The Uniaxial Stress–Strain Relationship of Hyperelastic Material Models of Rubber Cracks in the Platens of Papermaking Machines Based on Nonlinear Strain and Stress Measurements with the Finite Element Method
Abstract
:1. Introduction
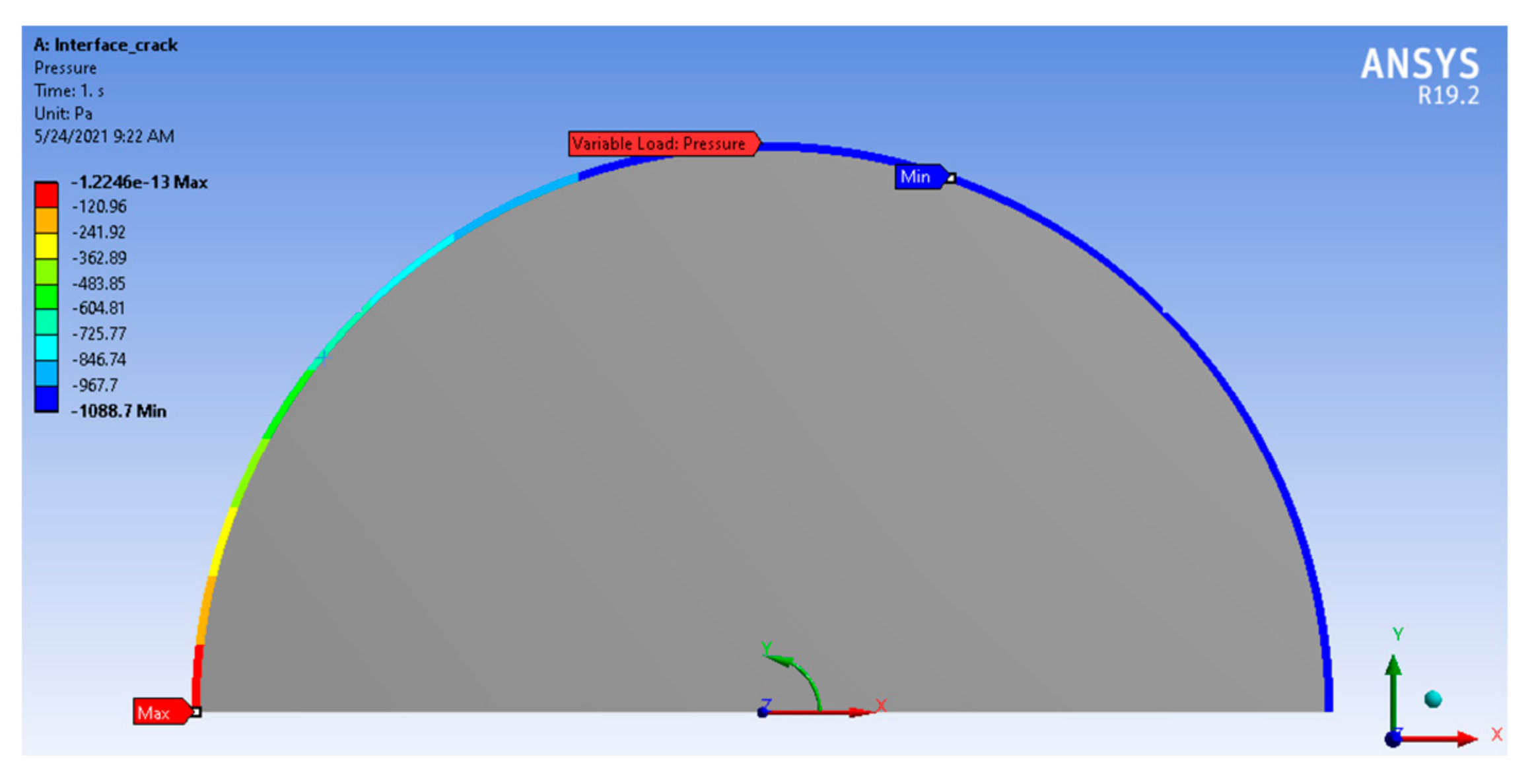
2. The Crack Problem
3. Finite Element Analysis
3.1. Models
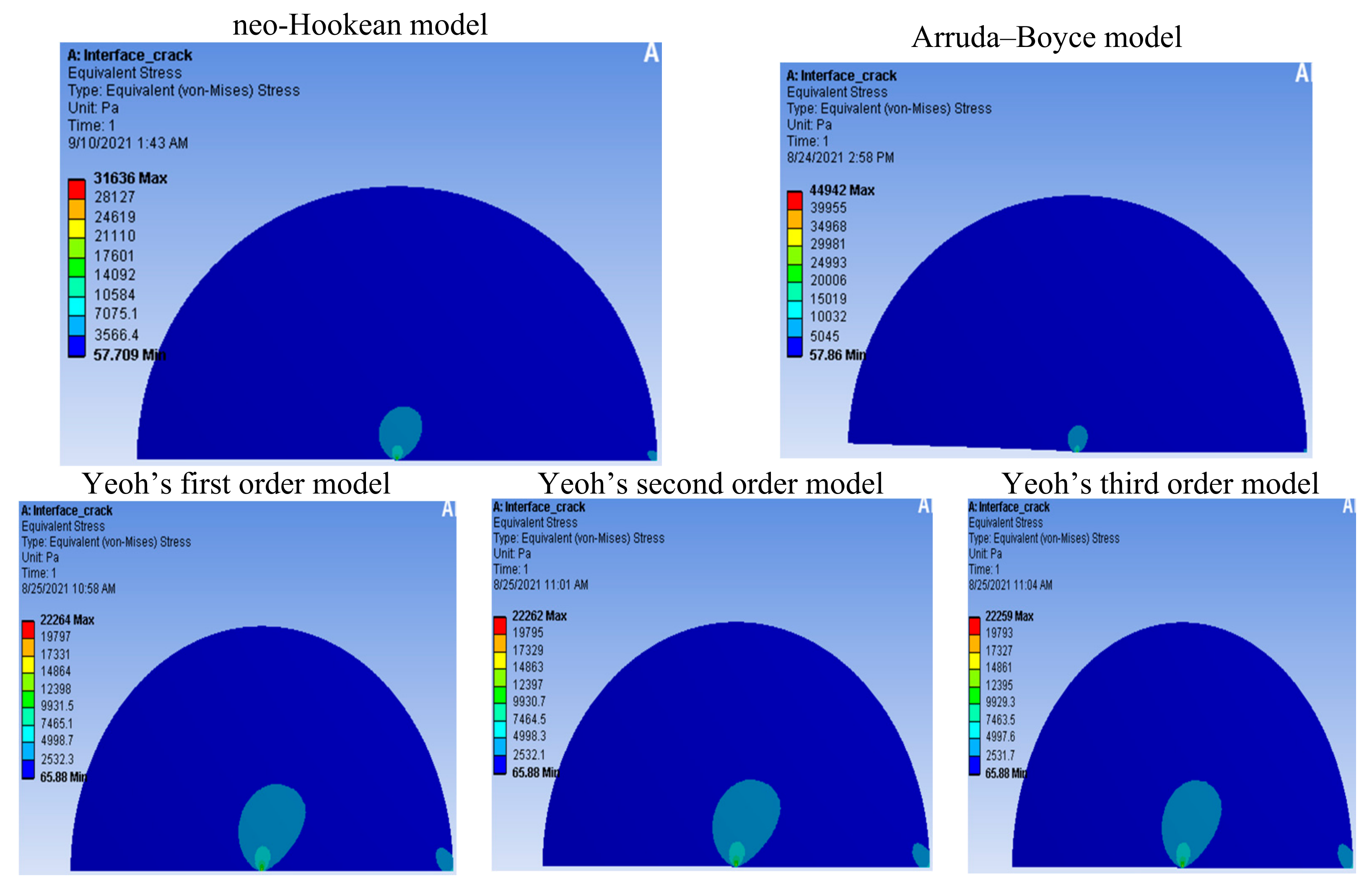
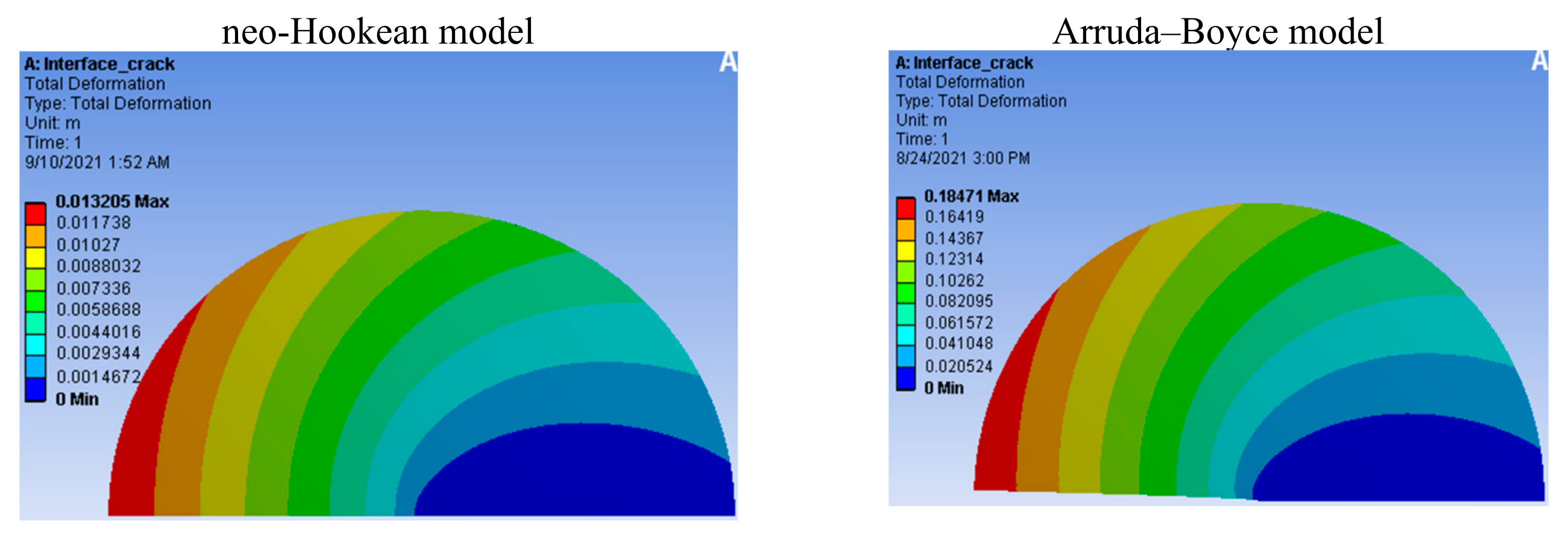
3.1.1. Neo-Hookean Model
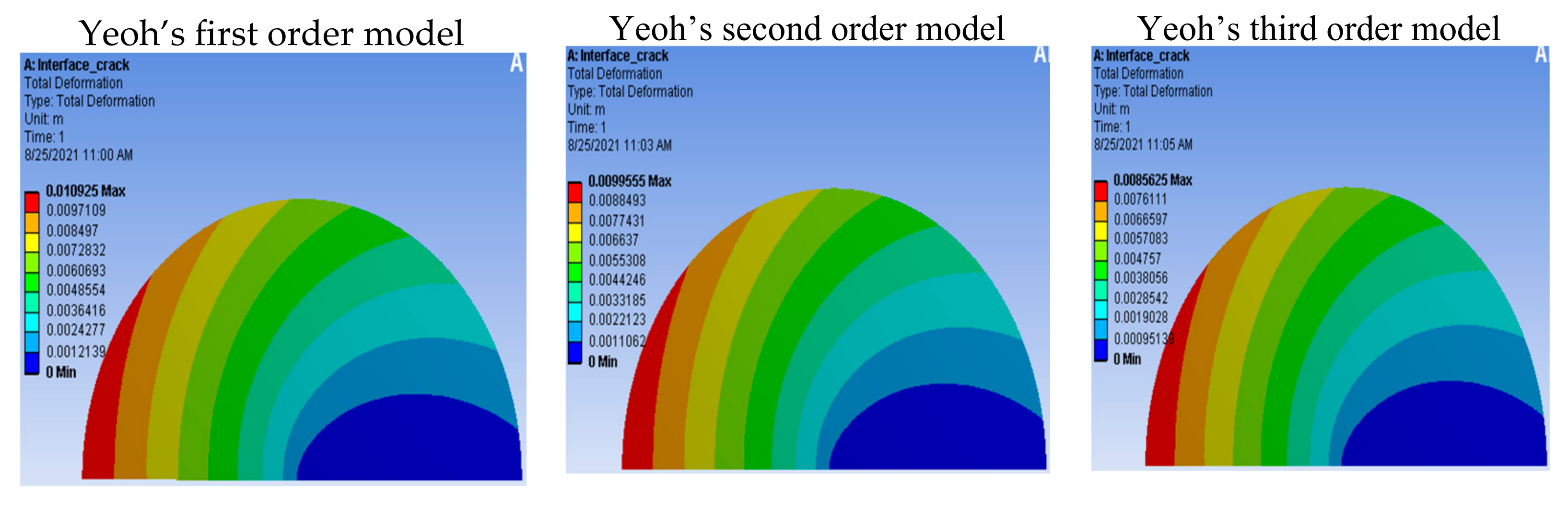
3.1.2. Yeoh Model
3.1.3. Arruda–Boyce Model
3.2. Meshing
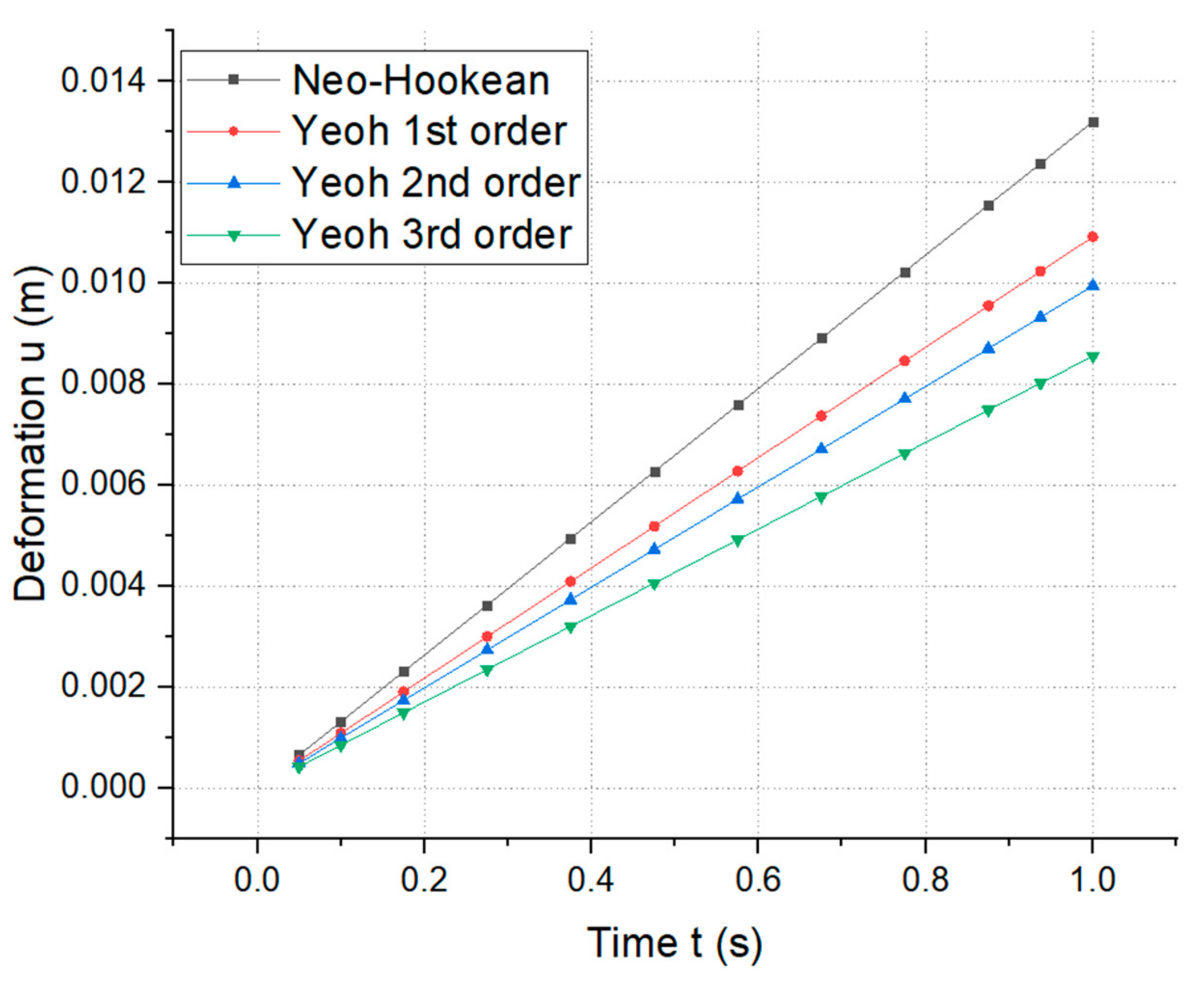
3.3. Computation
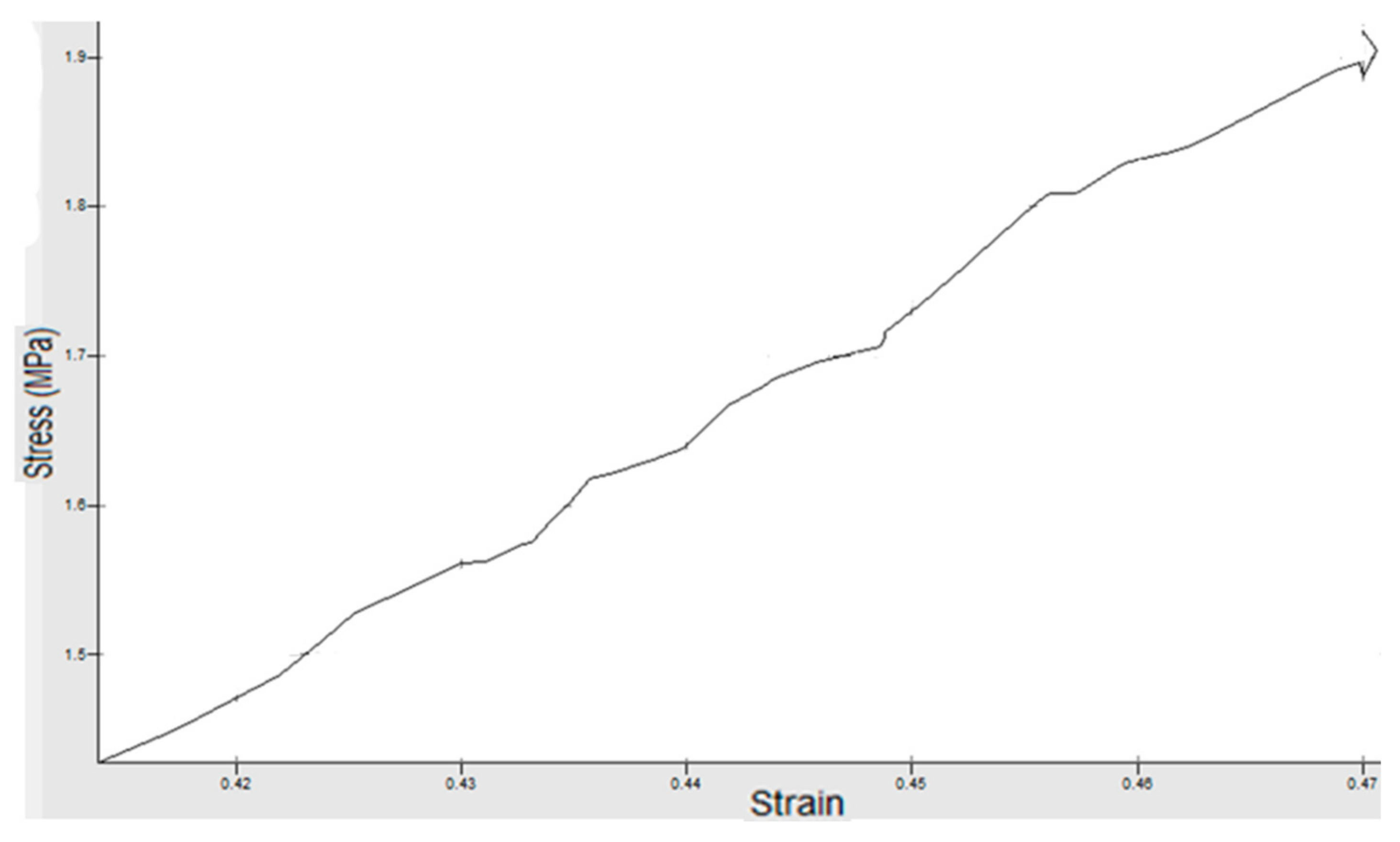
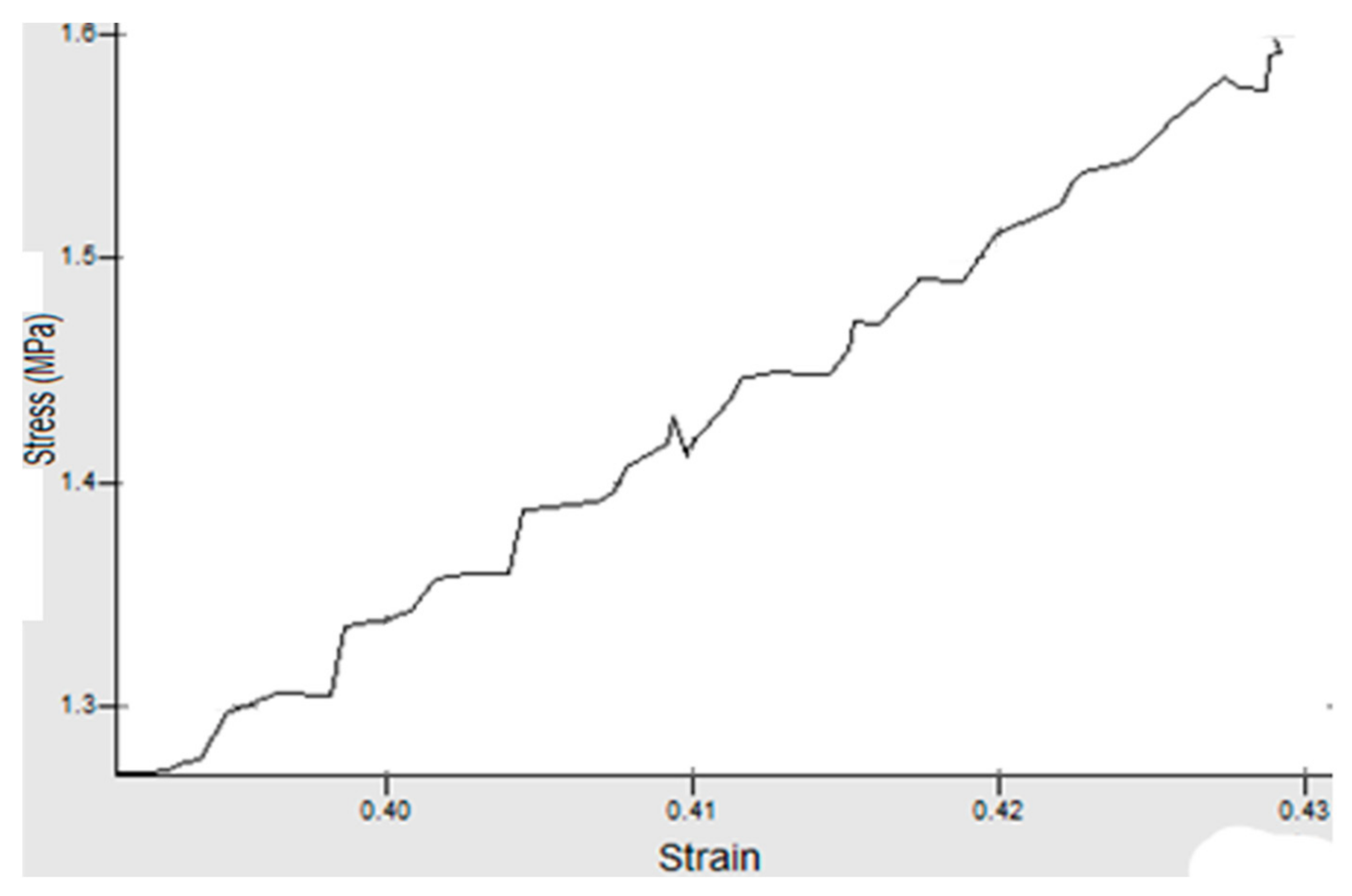
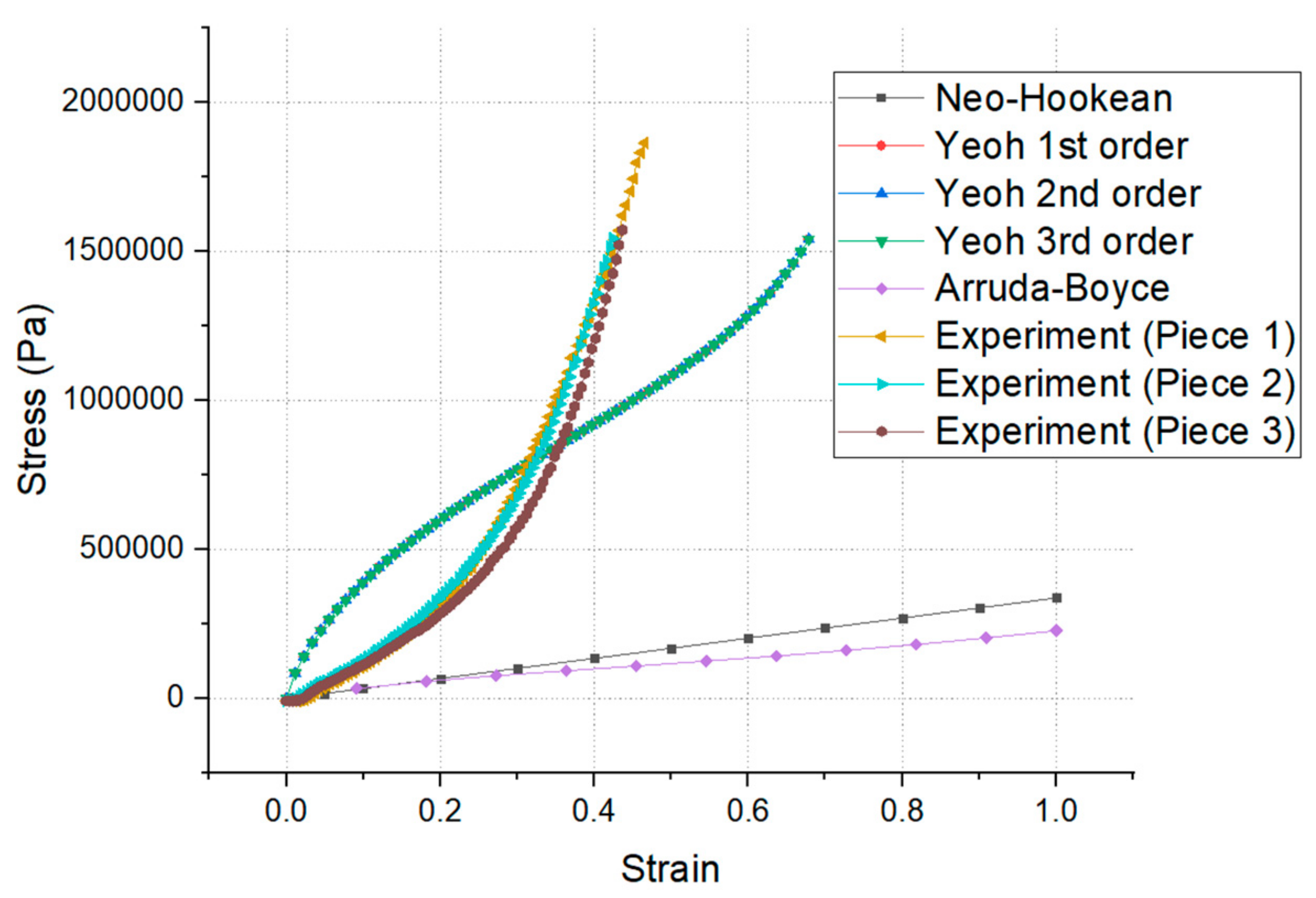
4. Experimental Work
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mankovits, T.; Szabó, T. Finite Element Analysis of Rubber Bumper used in Air-Springs. Procedia Eng. 2012, 48, 388–395. [Google Scholar] [CrossRef] [Green Version]
- Yeoh, O.H. Some forms of the strain energy function for rubber. Rubber Chem. Technol. 2012, 66, 754–771. [Google Scholar] [CrossRef]
- Arruda, E.M.; Boyce, M.C. A three-dimensional constitutive model for the large stretch behavior of rubber elastic materials. J. Mech. Phys. Solids 1993, 41, 389–412. [Google Scholar] [CrossRef] [Green Version]
- Mihai, L.A.; Budday, S.; Holzapfel, G.A.; Kuhl, E.; Goriely, A. A family of hyperelastic models for human brain tissue. J. Mech. Phy. Solids 2017, 106, 60–79. [Google Scholar] [CrossRef]
- Lin, D.C.; Horkay, F. Nanomechanics of polymer gels and biological tissues: A critical review of analytical approaches in the Hertzian regime and beyond. Soft Matter. 2008, 4, 669. [Google Scholar] [CrossRef]
- Hyun, H.C.; Lee, J.H.; Kim, M.; Lee, H. A spherical indentation technique for property evaluation of hyperelastic rubber. J. Mater. Res. 2012, 27, 2677–2690. [Google Scholar] [CrossRef]
- Giannakopoulos, A.E.; Triantafyllou, A. Spherical indentation of incompressible rubber-like materials. J. Mech. Phys. Solids 2007, 55, 1196–1211. [Google Scholar] [CrossRef]
- Liu, D.X.; Zhang, Z.D.; Sun, L.Z. Nonlinear elastic load-displacement relation for spherical indentation on rubberlike materials. J. Mater. Res. 2010, 25, 2197–2202. [Google Scholar] [CrossRef]
- Zhang, Q.; Yang, Q.S. The analytical and numerical study on the nanoindentation of nonlinear elastic materials. Comput. Mater. Contin. 2013, 37, 123–134. [Google Scholar] [CrossRef] [Green Version]
- Ho, M.P.; Wang, H.; Lee, J.H.; Ho, C.K.; Lau, K.T.; Leng, J.; Hui, D. Critical factors on manufacturing processes of natural fibre composites. Compos. Part B Eng. 2012, 43, 3549–3562. [Google Scholar] [CrossRef]
- Huang, Z.M.; Zhang, Y.Z.; Kotaki, M.; Ramakrishna, S. A review on polymer nanofibers by electrospinning and their applications in nanocomposites. Compos. Sci. Technol. 2013, 63, 2223–2253. [Google Scholar] [CrossRef]
- Fattahi, A.M.; Roozpeikar, S.; Ahmed, N.A. FEM modelling based on molecular results for PE/SWCNT nanocomposites. Int. J. Eng. Technol. 2018, 7, 4345–4356. [Google Scholar] [CrossRef]
- Fattahi, A.M.; Safaei, B. Buckling analysis of CNT-reinforced beams with arbitrary boundary conditions. Microsyst. Technol. 2017, 23, 5079–5091. [Google Scholar] [CrossRef]
- Tebeta, R.T.; Fattahi, A.M.; Ahmed, N.A. Experimental and numerical study on HDPE/SWCNT nanocomposite elastic properties considering the processing techniques effect. Microsyst. Technol. 2020, 26, 2423–2441. [Google Scholar] [CrossRef]
- Huri, D.; Mankovits, T. Comparison of the material models in rubber finite element analysis. IOP Conf. Ser. Mater. Sci. Eng. 2018, 393, 012018. [Google Scholar] [CrossRef]
- Patel, D.K.; Kalidindi, S.R. Correlation of spherical nanoindentation stress-strain curves to simple compression stress-strain curves for elastic-plastic isotropic materials using finite element models. Acta Mater. 2016, 112, 295–302. [Google Scholar] [CrossRef] [Green Version]
- Hossain, M.; Steinmann, P. More Hyperelastic Models for Rubber-Like Materials: Consistent Tangent Operators and Comparative Study. J. Mech. Behav. Mater. 2013, 22, 1–24. [Google Scholar] [CrossRef]
- Ogden, R.W. Non-Linear Elastic Deformations; Dover Publications: New York, NY, USA, 1997. [Google Scholar]
- Monfared, M.; Ayatollahi, M.; Bagheri, R. In-plane stress analysis of dissimilar materials with multiple interface cracks. Appl. Math. Modell. 2019, 40, 8464–8474. [Google Scholar] [CrossRef]
- Monfared, M.; Pourseifi, M.; Bagheri, R. Computation of mixed mode stress intensity factors for multiple axisymmetric cracks in an FGM medium under transient loading. Int. J. Solids Struct. 2019, 158, 220–231. [Google Scholar] [CrossRef]
- Mansouri, K.; Arfaoui, M.; Trifa, M.; Hassis, H.; Renard, Y. Singular elastostatic fields near the notch vertex of a Mooney–Rivlin hyperelastic body. Int. J. Solids Struct. 2020, 80, 532–544. [Google Scholar] [CrossRef]
- Geubelle, P.H.; Knauss, W.G. Finite strains at the tip of a crack in a sheet of hyperelastic material: I. Homogeneous case. J. Elast. 2017, 135, 161–198. [Google Scholar] [CrossRef]
- Rivlin, R.; Thomas, A.G. Rupture of rubber. I. Characteristic energy for tearing. J. Polym. Sci. A Polym. Chem. 1953, 10, 291–318. [Google Scholar] [CrossRef]
- Griffith, A.A. The phenomena of flow and rupture in solids. Philos. Trans. R. Soc. Lond. Ser. A 1920, 221, 163–198. [Google Scholar] [CrossRef]
- Aït-Bachir, M.; Mars, W.; Verron, E. Energy release rate of small cracks in hyperelastic materials. Int. J. Non Linear Mech. 2012, 47, 22–29. [Google Scholar] [CrossRef] [Green Version]
- Gao, Y. Elastostatic crack tip behavior for a rubber-like material. Theor. Appl. Fract. Mech. 2020, 14, 219–231. [Google Scholar] [CrossRef]
- Gao, Y. Large deformation field near a crack tip in rubber-like material. Theor. Appl. Fract. Mech. 2019, 26, 155–162. [Google Scholar] [CrossRef]





| Hyperelastic Material Models | Incompressibility Parameter lD | ||
|---|---|---|---|
| Neo-Hookean model | 1.5012 × 105 (Pa) | 0 (Pa−1) | - |
| Yeoh 1st order model | 6.0392× 105 (Pa) | 0 (Pa−1) | - |
| Yeoh 2nd order model | C1 = 6.6275 × 105 (Pa) | D1 = 0 (Pa−1) | - |
| C2 = −62,451 (Pa) | D2 = 0 (Pa−1) | ||
| Yeoh 3rd order model | C1 = 7.7062 × 105 (Pa) | D1 = 0 (Pa−1) | - |
| C2 = −3.8631 × 105 (Pa) | D2 = 0 (Pa−1) | ||
| C3 = 1.9685 × 105 (Pa) | D3 = 0 (Pa−1) | ||
| Arruda-Boyce model | 23,157 (Pa) | 1.5011 × 10−7(Pa−1) | 5.3334 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, H.-D.; Huang, S.-C. The Uniaxial Stress–Strain Relationship of Hyperelastic Material Models of Rubber Cracks in the Platens of Papermaking Machines Based on Nonlinear Strain and Stress Measurements with the Finite Element Method. Materials 2021, 14, 7534. https://doi.org/10.3390/ma14247534
Nguyen H-D, Huang S-C. The Uniaxial Stress–Strain Relationship of Hyperelastic Material Models of Rubber Cracks in the Platens of Papermaking Machines Based on Nonlinear Strain and Stress Measurements with the Finite Element Method. Materials. 2021; 14(24):7534. https://doi.org/10.3390/ma14247534
Chicago/Turabian StyleNguyen, Huu-Dien, and Shyh-Chour Huang. 2021. "The Uniaxial Stress–Strain Relationship of Hyperelastic Material Models of Rubber Cracks in the Platens of Papermaking Machines Based on Nonlinear Strain and Stress Measurements with the Finite Element Method" Materials 14, no. 24: 7534. https://doi.org/10.3390/ma14247534
APA StyleNguyen, H.-D., & Huang, S.-C. (2021). The Uniaxial Stress–Strain Relationship of Hyperelastic Material Models of Rubber Cracks in the Platens of Papermaking Machines Based on Nonlinear Strain and Stress Measurements with the Finite Element Method. Materials, 14(24), 7534. https://doi.org/10.3390/ma14247534






