Estimation of C* Integral for Mismatched Welded Compact Tension Specimen
Abstract
:1. Introduction
2. Numerical Analysis
2.1. Geometry and Loading
2.2. Material Properties
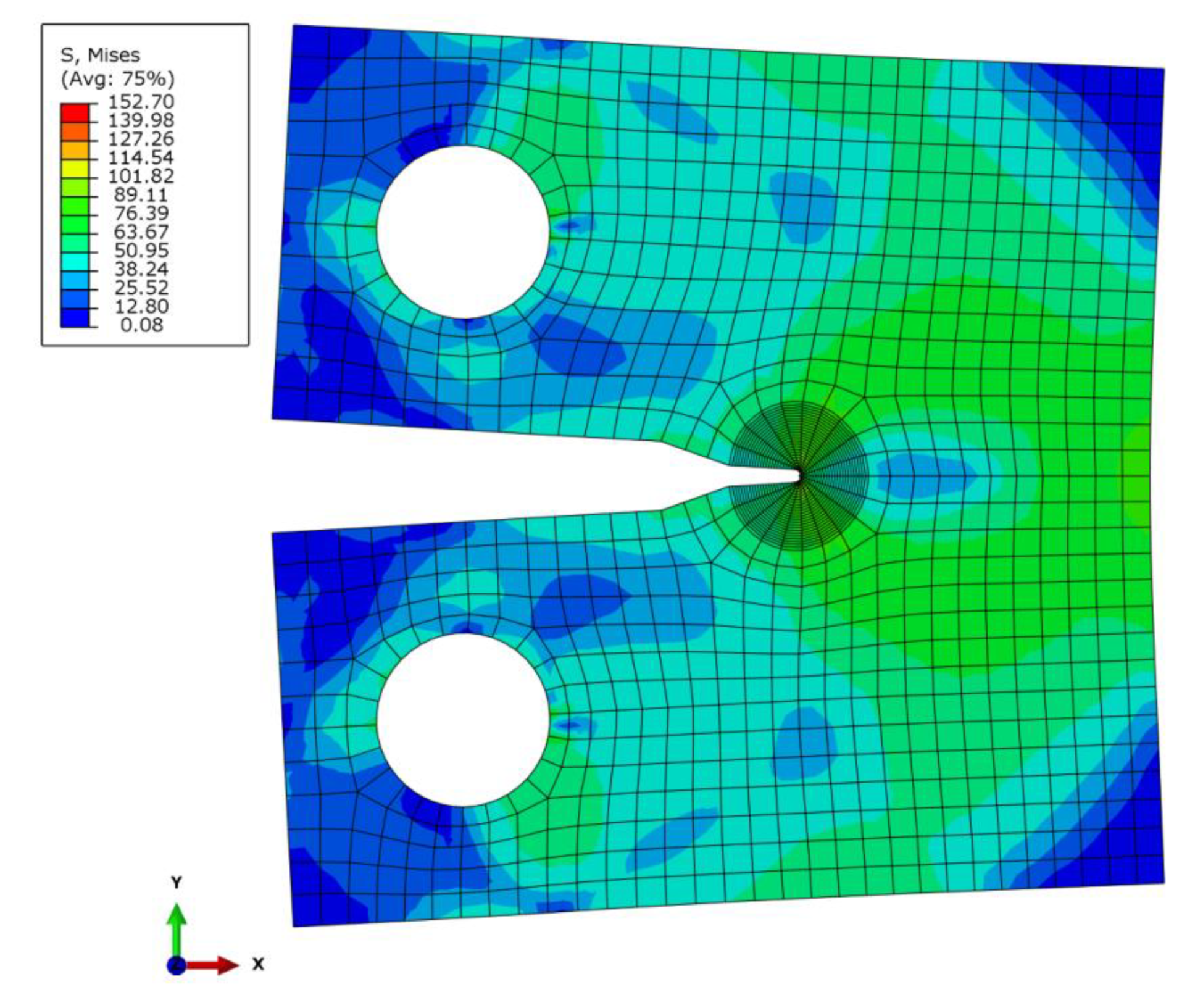
2.3. Finite Element Analysis
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Dake, Y.; Sridrah, I.; Zhongmin, Z.; Kumar, S.B. Fracture capacity of girth welded pipelines with 3D surface cracks subjected to biaxial loading conditions. Int. J. Press. Vessels Pip. 2012, 92, 115–126. [Google Scholar] [CrossRef]
- Dake, Y.; Zhong, M.X.; Sridrah, I.; Kumar, S.B. Fracture analysis of girth welded pipelines with 3D embedded cracks subjected to biaxial loading conditions. Eng. Fract. Mech. 2012, 96, 570–587. [Google Scholar]
- Xuan, F.-Z.; Tu, S.-T.; Wang, Z. A modification of ASTM E 1457 C* estimation equation for compact tension specimen with a mismatched cross-weld. Eng. Fract. Mech. 2005, 72, 2602–2614. [Google Scholar] [CrossRef]
- Abe, F.; Tabuchi, M.; Tsukamoto, S.; Shirane, T. Microstructure evolution in HAZ and suppression of Type IV fracture in advanced ferritic power plant steels. Int. J. Press. Vessel. Pip. 2010, 87, 598–604. [Google Scholar] [CrossRef]
- Dogan, B. Proceedings of CREEP8, Eighth International Conference on Creep and Fatigue at Elevated Temperatures (Joint with PVP07); University of Limerick: Limerick, Ireland, 2007; pp. 299–305. [Google Scholar]
- Tabuchi, M.; Hongo, H.; Watanabe, T., Jr.; Yokobori, A.T. Creep crack growth analysis of welded joints for high Cr heat resisting steel. ASTM Spec. Tech. Publ. 2007, 1480, 93–101. [Google Scholar]
- Yatomi, M.; Fuji, A.; Tabuchi, M.; Hasegawa, Y.; Kobayashi KI, I.; Yokobori, T.; Yokobori, T. Creep crack growth of P92 welds. In Proceedings of the ASME 2008 Pressure Vessels and Piping Division Conference, Chicago, IL, USA, 27–31 July 2008; pp. 1207–1214. [Google Scholar]
- Hyde, T.; Saber, M.; Sun, W. Testing and modelling of creep crack growth in compact tension specimens from a P91 weld at 650 °C. Eng. Fract. Mech. 2010, 77, 2946–2957. [Google Scholar] [CrossRef]
- Lee, K.-H.; Kim, Y.-J.; Yoon, K.-B.; Nikbin, K.; Dean, D. Quantification of stress redistribution due to mismatch in creep properties in welded branch pipes. Fatigue Fract. Eng. Mater. Struct. 2010, 33, 238–251. [Google Scholar] [CrossRef]
- Tu, S.-T.; Segle, P.; Gong, J.-M. Creep damage and fracture of weldments at high temperature. Int. J. Press. Vessel. Pip. 2003, 81, 199–209. [Google Scholar] [CrossRef]
- Tu, S.-T.; Yoon, K.-B. The influence of material mismatch on the evaluation of time-dependent fracture mechanics parameters. Eng. Fract. Mech. 1999, 64, 765–780. [Google Scholar] [CrossRef]
- Xuan, F.-Z.; Wang, Z.-F.; Tu, S.-T. Creep finite element simulation of multilayered system with interfacial cracks. Mater. Des. 2009, 30, 563–569. [Google Scholar] [CrossRef]
- Chen, G.; Wang, G.; Xuan, F.; Tu, S. Mismatch effect in creep properties on creep crack growth behavior in welded joints. Mater. Des. 2014, 63, 600–608. [Google Scholar] [CrossRef]
- Chen, G.; Wang, G.; Zhang, J.; Xuan, F.; Tu, S. Effects of initial crack positions and load levels on creep failure behavior in P92 steel welded joint. Eng. Fail. Anal. 2015, 47, 56–66. [Google Scholar] [CrossRef]
- Chen, G.; Wang, G.Z.; Xuan, F.Z.; Tu, S.T. Effects of HAZ widths on creep crack growth properties of welded joints. Weld. World 2015, 59, 851–860. [Google Scholar] [CrossRef]
- Zhao, L.; Jing, H.; Xiu, J.; Han, Y.; Xu, L. Experimental investigation of specimen size effect on creep crack growth behavior in P92 steel welded joint. Mater. Des. 2014, 57, 736–743. [Google Scholar] [CrossRef]
- Mehmanparast, A.; Maleki, S.; Yatomi, M.; Nikbin, K.M. Specimen Geometry and Size Effects on the Creep Crack Growth Behaviour of P91 Weldments. In Proceedings of the ASME 2013 Pressure Vessels and Piping, Division Conference, Paris, France, 14–18 July 2013. [Google Scholar]
- Li, Y.; Wang, G.Z.; Xuan, F.Z.; Tu, S.T. Geometry and Material Constraint Effects on Creep Crack Growth Behavior in Welded Joints. High Temp. Mater. Process. 2016, 36, 155–162. [Google Scholar] [CrossRef]
- ASTM Standard, E1457-15. Standard Test Method for Measurement of Creep Crack Growth Times in Metals; ASTM International: West Conshohocken, PA, USA, 2015. [Google Scholar]
- ABAQUS /CAE 2016 User’s Manual. Inc. and Dassault Systems. Available online: http://130.149.89.49:2080/v2016/index.html (accessed on 15 June 2021).
- Katinić, M.; Konjatić, P.; Kozak, D.; Turk, D. Numerical analysis of the effect of residual stress on transient creep in SENB specimen. Int. J. Press. Vessels Pip. 2020, 188, 104222. [Google Scholar] [CrossRef]
- Tada, H.; Paris, P.; Irwin, G. The Stress Analysis of Cracks Handbook; Paris Productions Inc.: St. Louis, MO, USA, 1985. [Google Scholar]
- Kumar, V.; German, D.; Shih, C.F. An Engineering Approach for Elastic-Plastic Fracture Analysis; EPRI Report NP-1931; EPRI: Washington, DC, USA, 1981. [Google Scholar]
- Goldman, N.L.; Hutchinson, J.W. Fully Plastic Crack Problems: The Center Cracked Strip Under Plane Strain. Int. J. Solids Struct. 1975, 11, 575–591. [Google Scholar] [CrossRef]
- TuringBot Software, Sao Paulo, Brazil. 2021. Available online: https://turingbotsoftware.com/ (accessed on 12 August 2021).



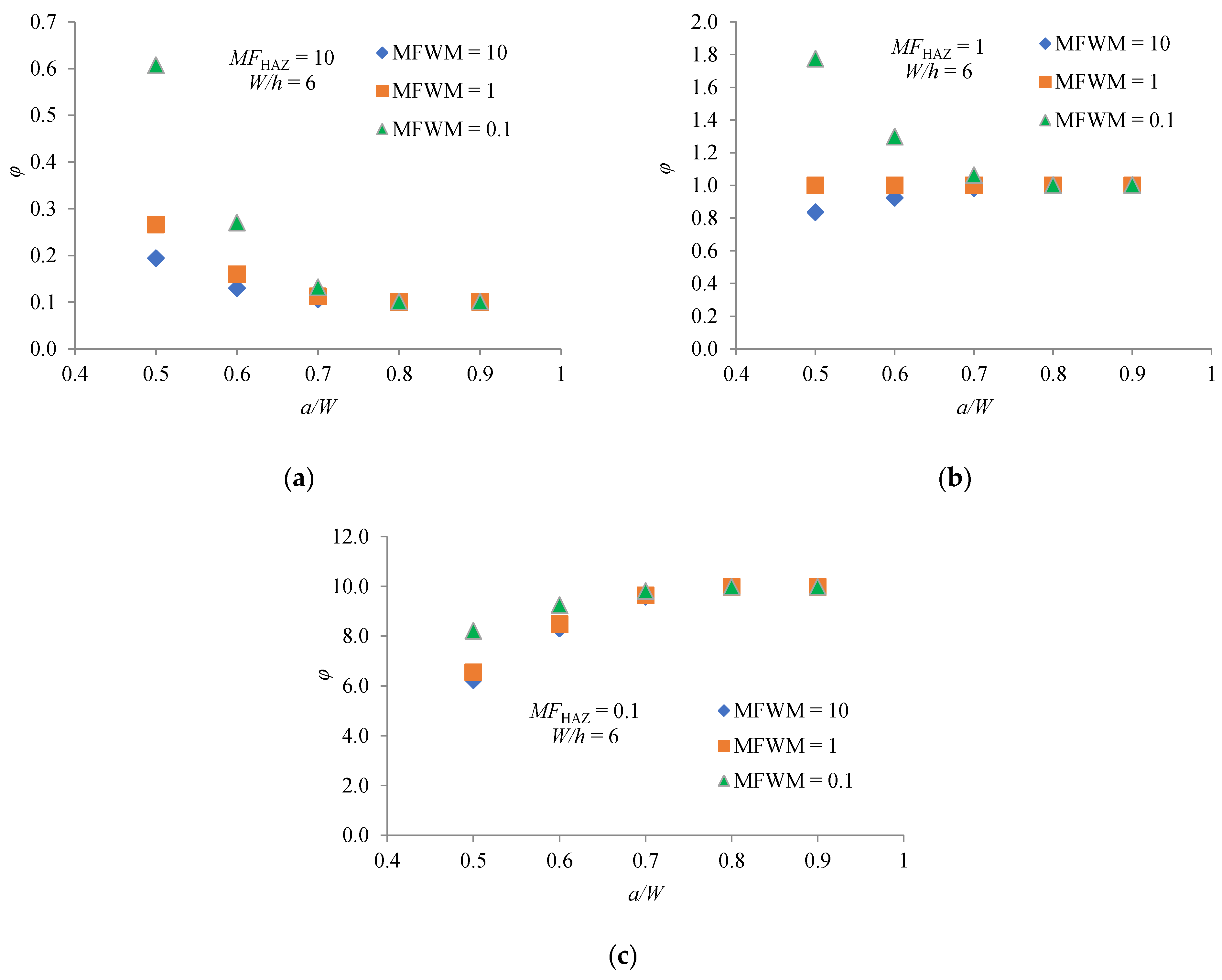
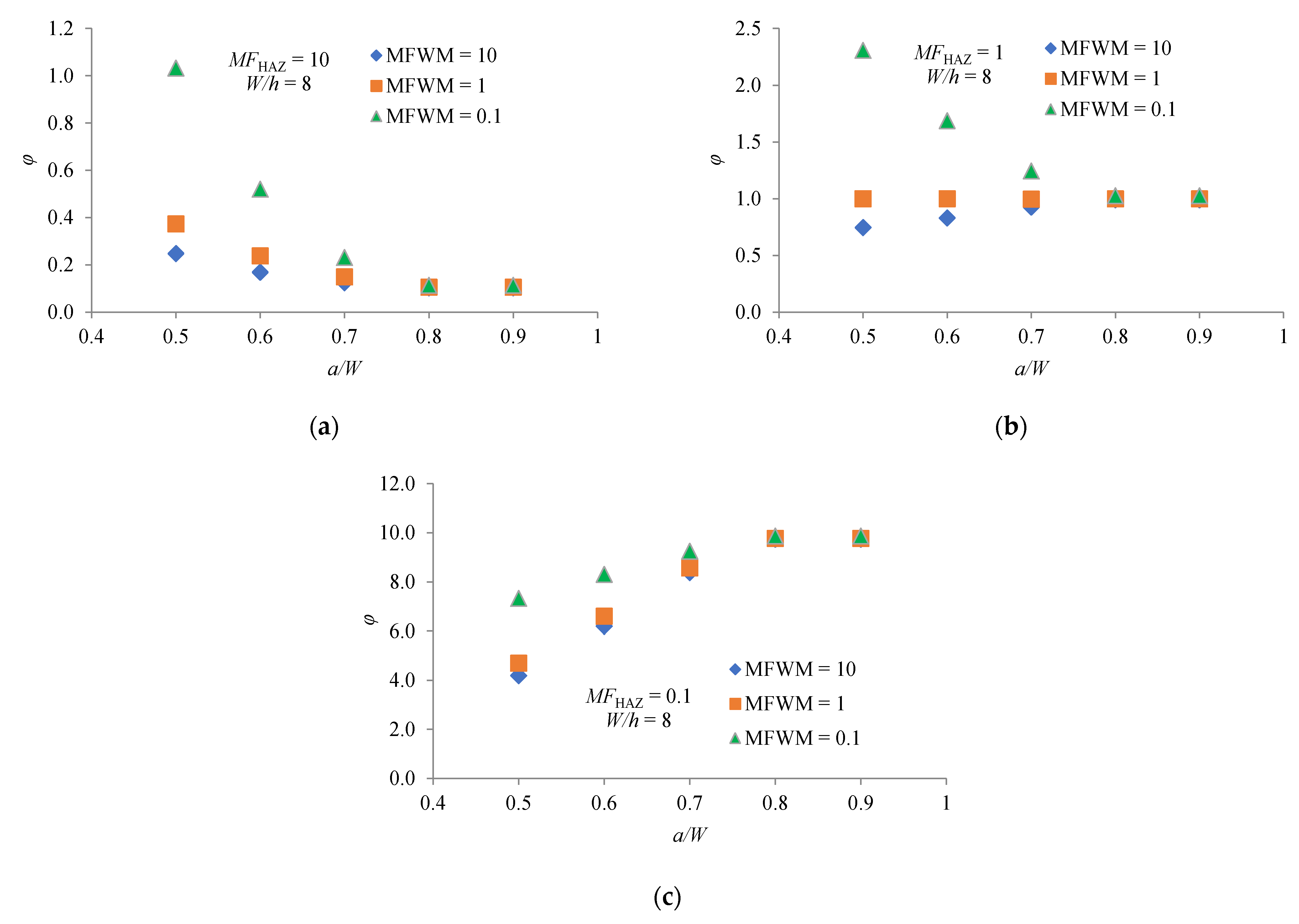
| MFWM | MFHAZ |
|---|---|
| 10 | 0.1 |
| 10 | 1 |
| 10 | 10 |
| 1 | 0.1 |
| 1 | 1 |
| 1 | 10 |
| 0.1 | 0.1 |
| 0.1 | 1 |
| 0.1 | 10 |
| KI(FE)/KI | 1.005 | |
| C*(FE)/C* | n = 5 | 0.978 |
| n = 10 | 0.982 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Katinić, M.; Turk, D.; Konjatić, P.; Kozak, D. Estimation of C* Integral for Mismatched Welded Compact Tension Specimen. Materials 2021, 14, 7491. https://doi.org/10.3390/ma14247491
Katinić M, Turk D, Konjatić P, Kozak D. Estimation of C* Integral for Mismatched Welded Compact Tension Specimen. Materials. 2021; 14(24):7491. https://doi.org/10.3390/ma14247491
Chicago/Turabian StyleKatinić, Marko, Dorian Turk, Pejo Konjatić, and Dražan Kozak. 2021. "Estimation of C* Integral for Mismatched Welded Compact Tension Specimen" Materials 14, no. 24: 7491. https://doi.org/10.3390/ma14247491
APA StyleKatinić, M., Turk, D., Konjatić, P., & Kozak, D. (2021). Estimation of C* Integral for Mismatched Welded Compact Tension Specimen. Materials, 14(24), 7491. https://doi.org/10.3390/ma14247491









