Numerical Study on the Dynamic Fracture Energy of Concrete Based on a Rate-Dependent Cohesive Model
Abstract
1. Introduction
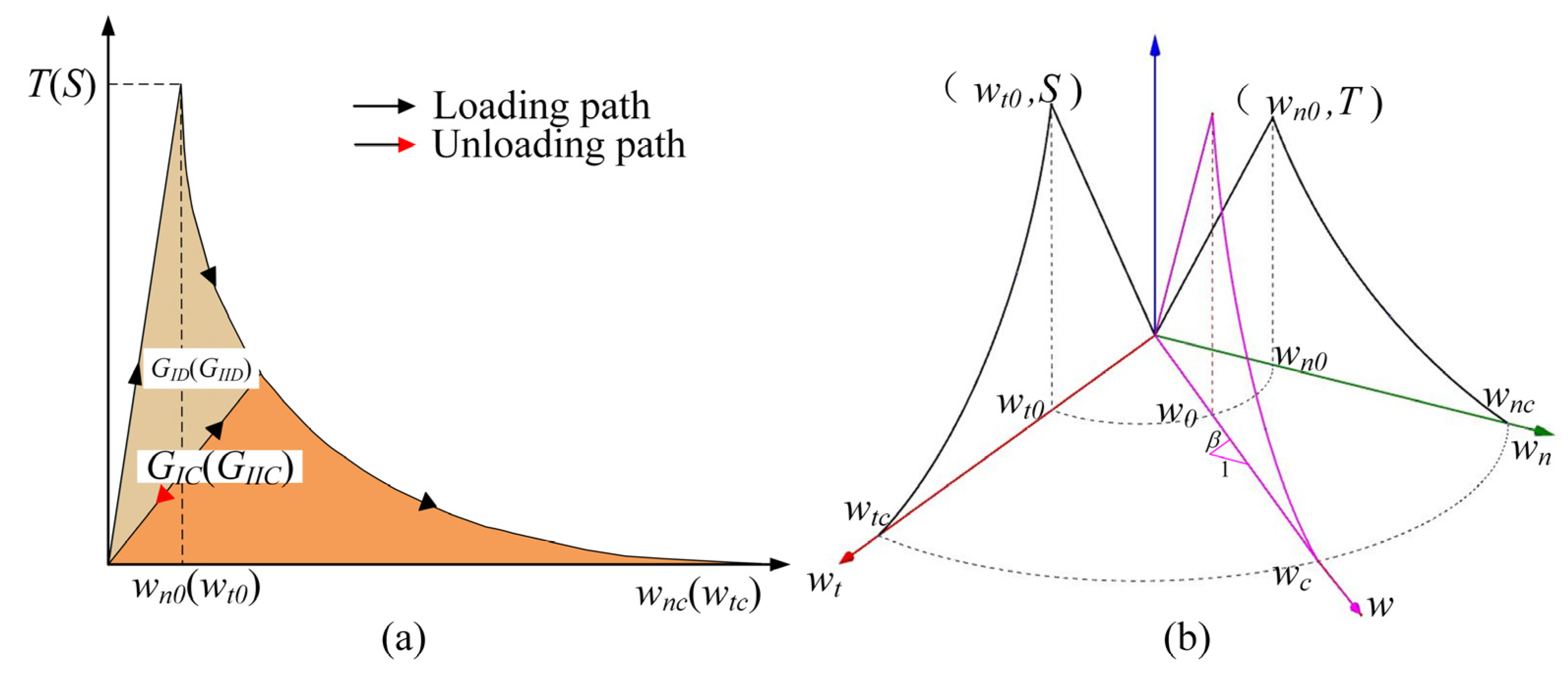
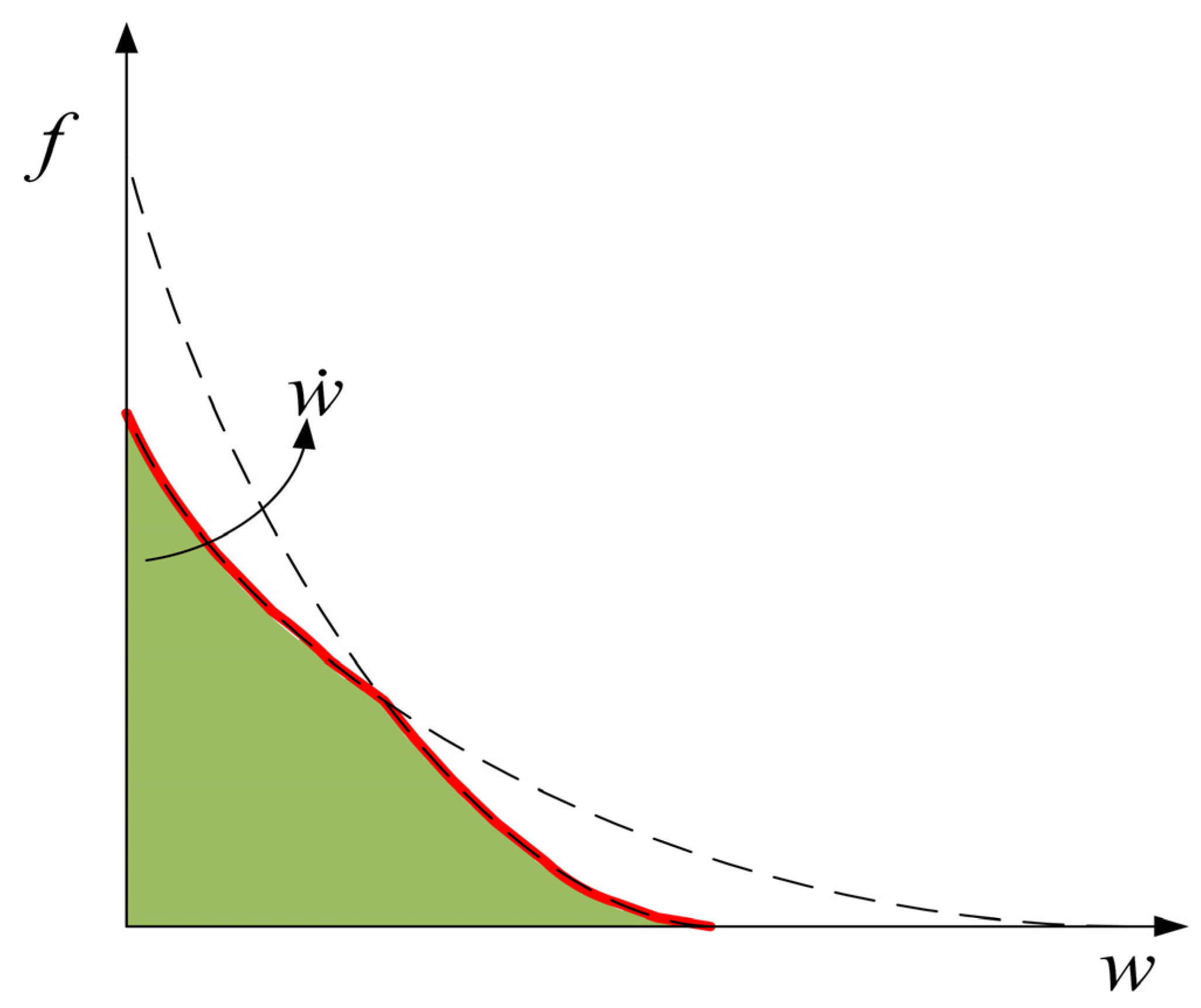
2. Constitutive Law of the Rate-Dependent Cohesive Model
3. Model Setup and Calibration
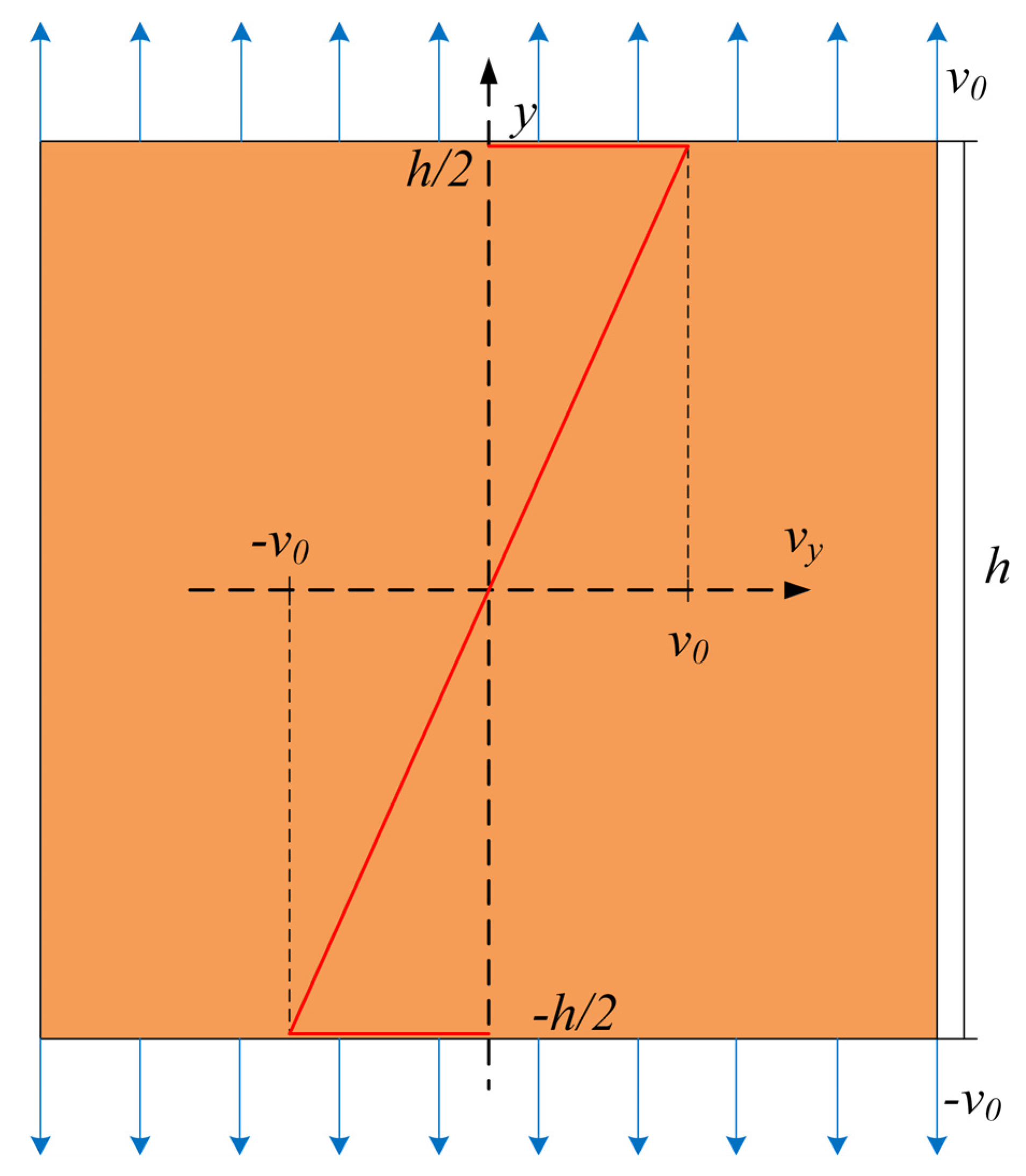
3.1. Specimen Geometry and Loading Method
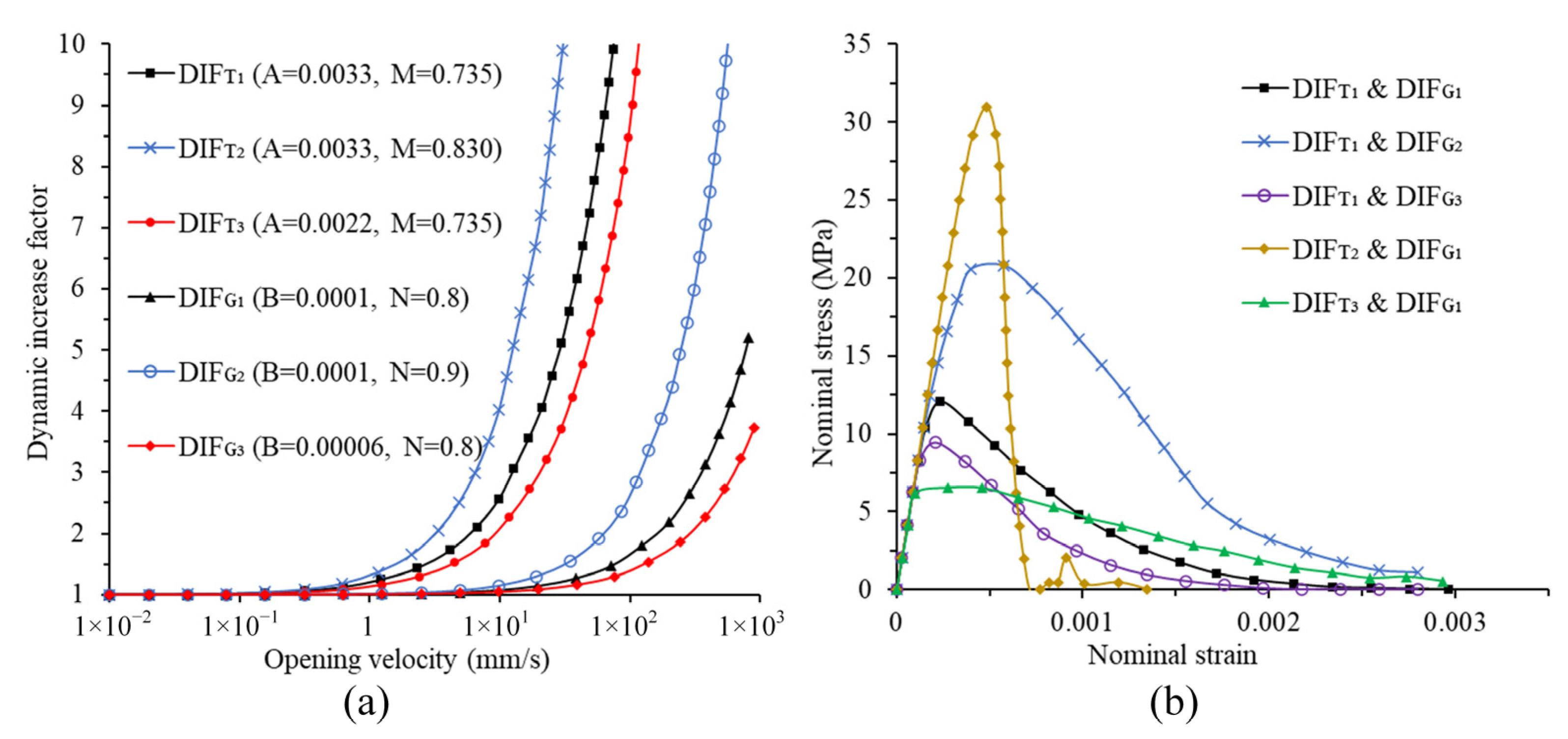
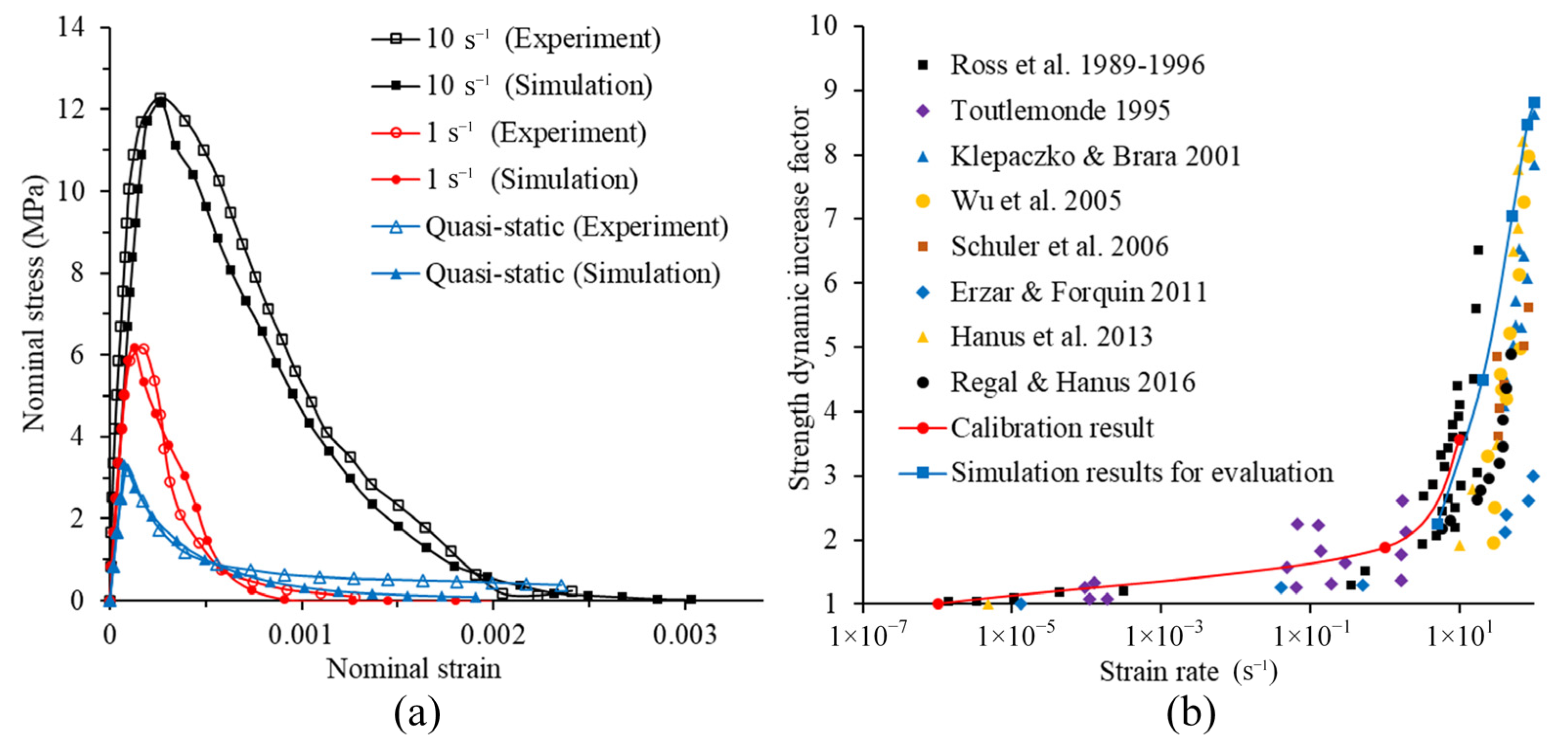
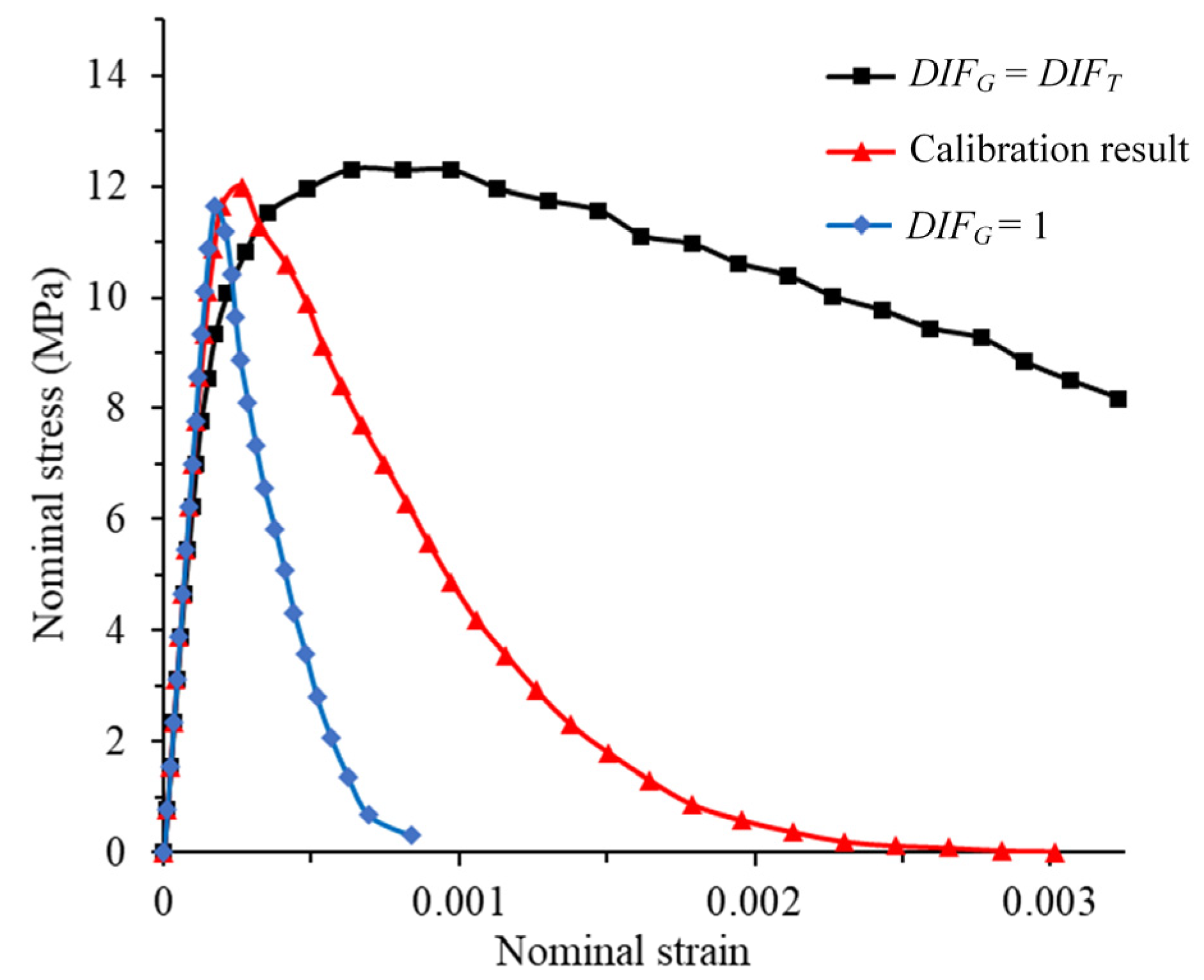
3.2. Model Calibration and Evaluation of DIF
3.3. Mesh Sensitivity Analysis
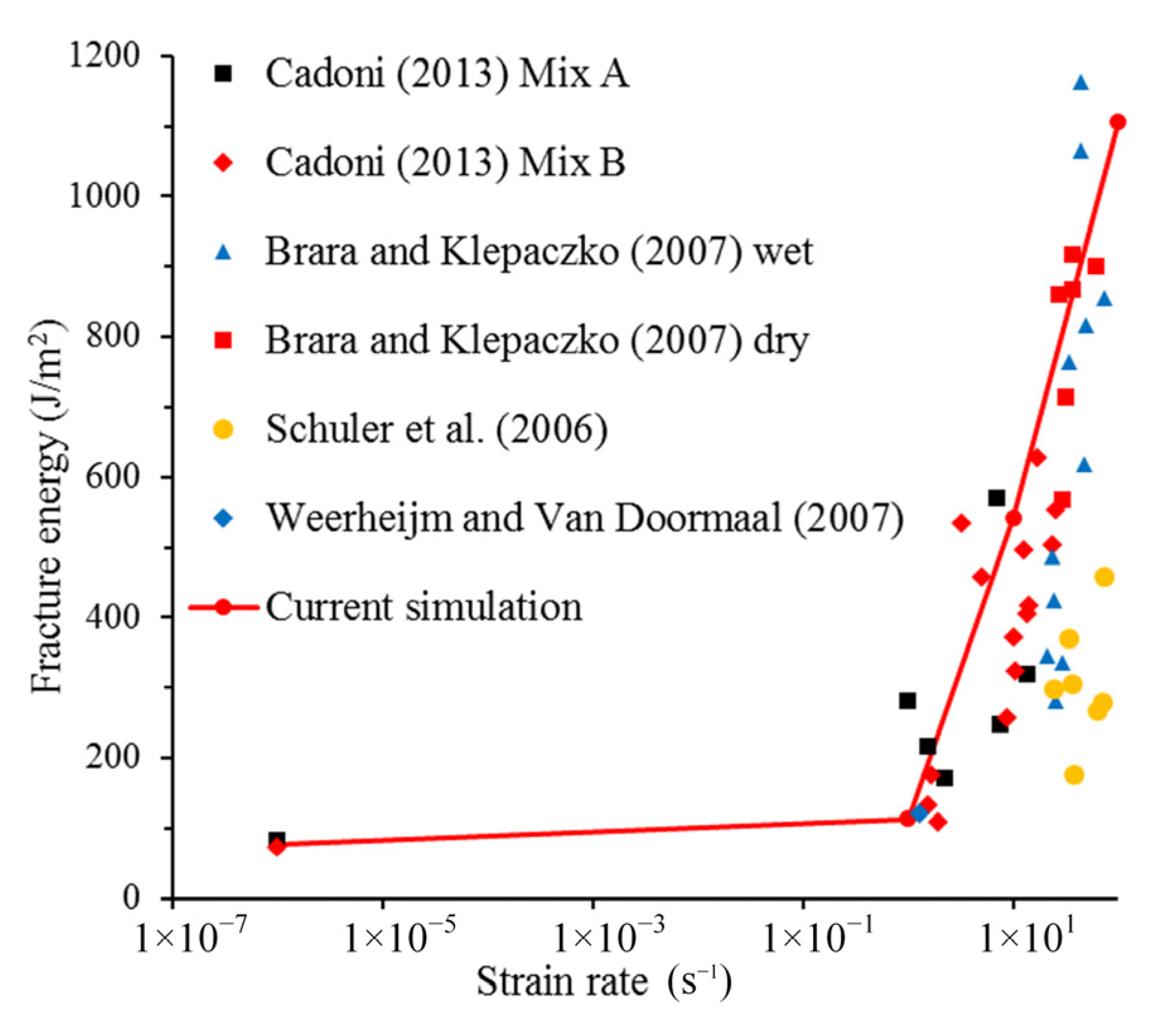
4. Numerical Investigation on Dynamic Fracture Energy
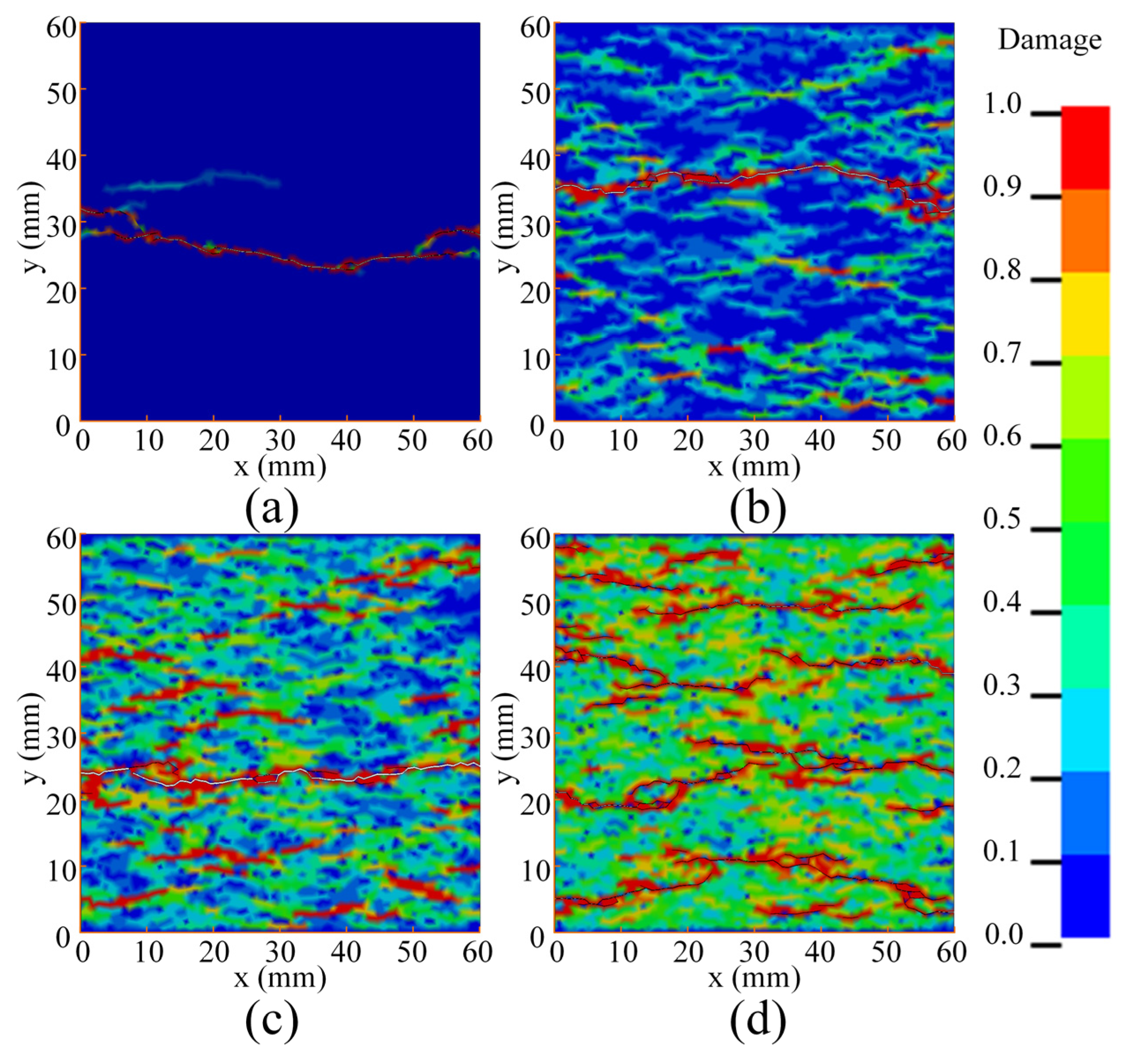
4.1. Damage and Unpenetrated Crack
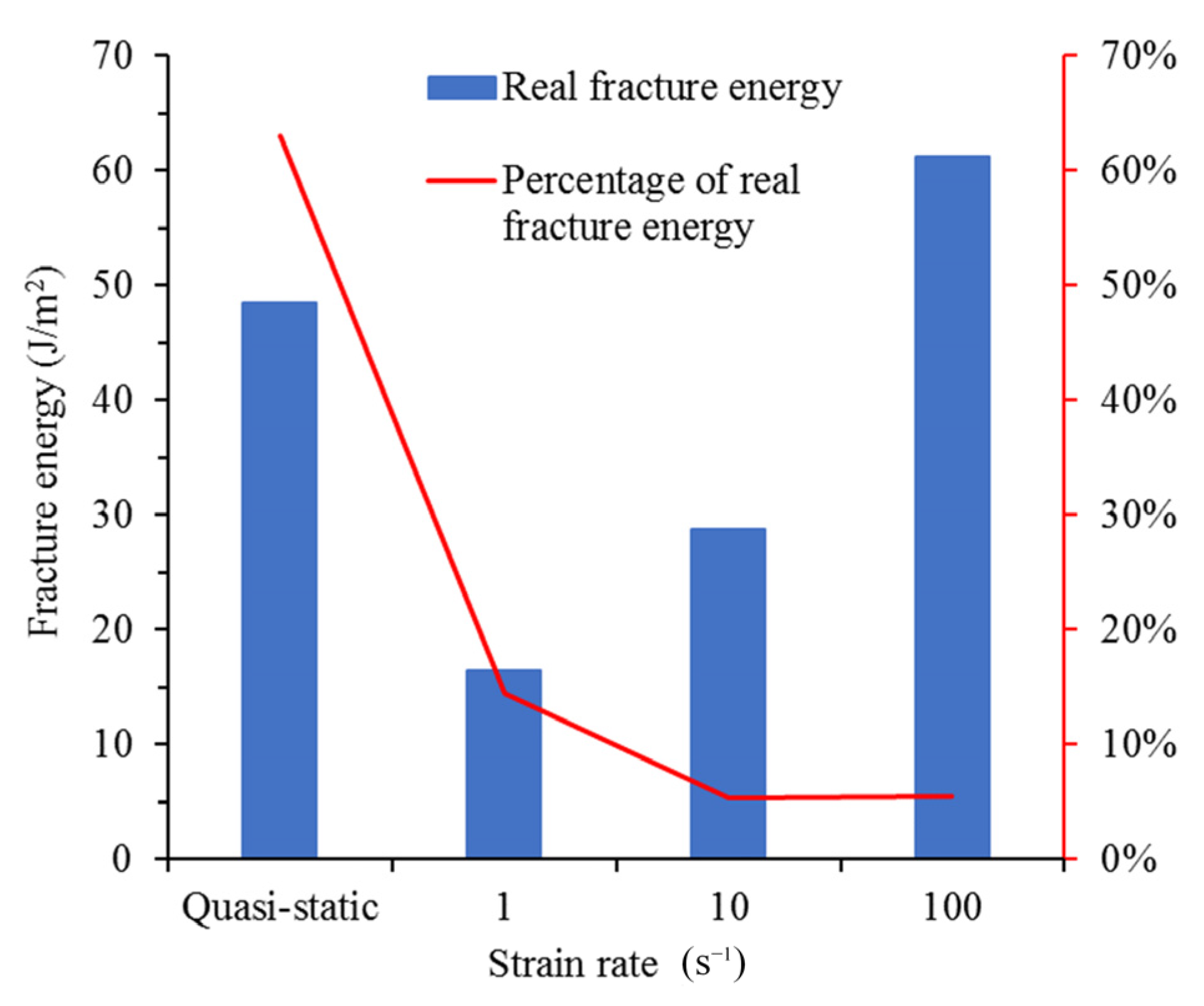
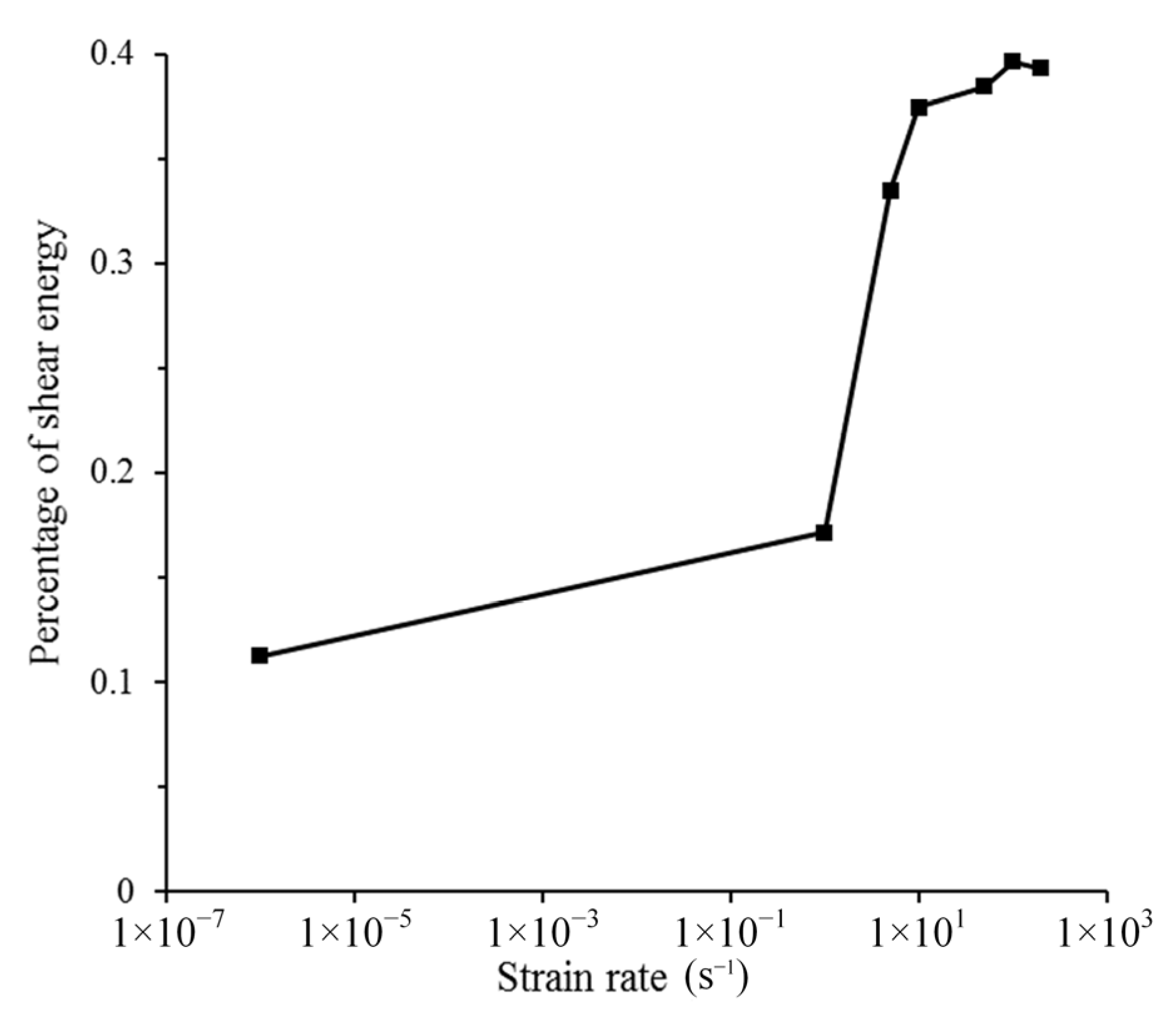
4.2. The Real Fracture Energy
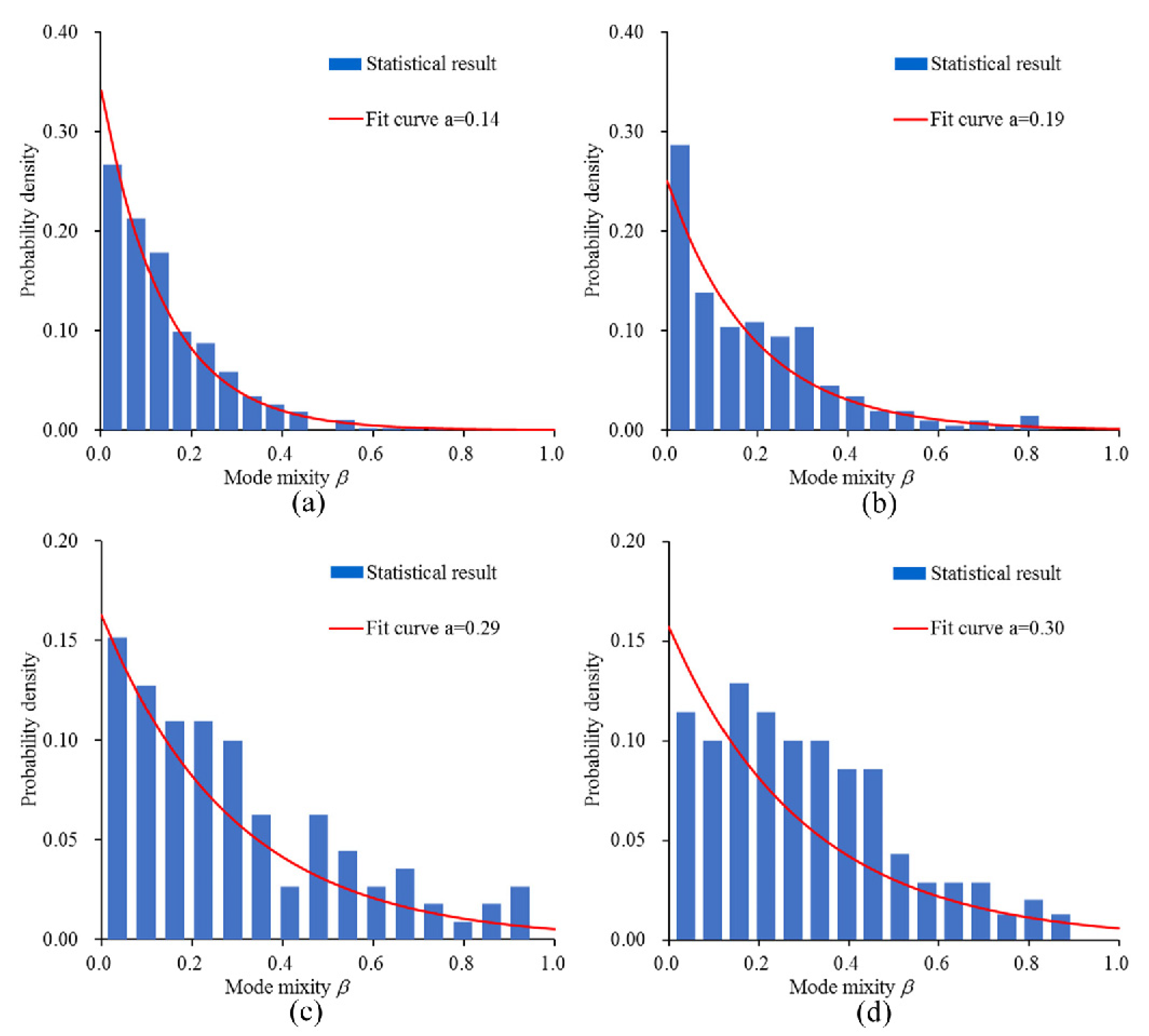
4.3. The Failure Mode of Microcracks
5. Conclusions
- (1)
- Two reasons contribute to the fact that fracture energy changes when increasing the strain rate. One is that the damage range and unmeasurable cracks of concrete increase with the increase in strain rate (structural effect), and the other is the rate dependence of concrete real fracture energy;
- (2)
- As the strain rate increases, the damage range on the specimen becomes larger, and the number of unpenetrated cracks increases, which leads to more pronounced structural effects;
- (3)
- There is a sub-interval in the range of strain rate from 1 ×10−6 to 1 s−1, where the real fracture energy decreases with the increase in strain rate. With the strain further increasing to 1 s−1, the real fracture energy increases with the increase in strain rate. However, despite the increase in real fracture energy at this stage, the proportion of real fracture energy in fracture energy drops, indicating that structural effects dominate the increase in fracture energy;
- (4)
- As the strain rate increases, more microcracks will change from mode-I type to mixed fracture mode. Meanwhile, change in fracture mode has obvious effects on real fracture energy.
Author Contributions
Funding
Conflicts of Interest
References
- Yan, D.; Lin, G. Dynamic properties of concrete in direct tension. Cem. Concr. Res. 2006, 36, 1371–1378. [Google Scholar] [CrossRef]
- Cadoni, E.; Solomos, G.; Albertini, C. Concrete behaviour in direct tension tests at high strain rates. Mag. Concr. Res. 2013, 65, 660–672. [Google Scholar] [CrossRef]
- Brara, A.; Klepaczko, J.R. Fracture energy of concrete at high loading rates in tension. Int. J. Impact Eng. 2007, 34, 424–435. [Google Scholar] [CrossRef]
- Schuler, H.; Mayrhofer, C.; Thoma, K. Spall experiments for the measurement of the tensile strength and fracture energy of concrete at high strain rates. Int. J. Impact Eng. 2006, 32, 1635–1650. [Google Scholar] [CrossRef]
- Levi-Hevroni, D.; Kochavi, E.; Kofman, B.; Gruntman, S.; Sadot, O. Experimental and numerical investigation on the dynamic increase factor of tensile strength in concrete. Int. J. Impact Eng. 2018, 114, 93–104. [Google Scholar] [CrossRef]
- Chen, X.; Ge, L.; Zhou, J.; Wu, S. Dynamic Brazilian test of concrete using split Hopkinson pressure bar. Mater. Struct. Constr. 2017, 50, 1. [Google Scholar] [CrossRef]
- Liu, P.; Zhou, X.; Qian, Q.; Berto, F.; Zhou, L. Dynamic splitting tensile properties of concrete and cement mortar. Fatigue Fract. Eng. Mater. Struct. 2020, 43, 757–770. [Google Scholar] [CrossRef]
- Luo, X.; Xu, J.Y. Dynamic splitting-tensile testing of highly fluidised geopolymer concrete. Mag. Concr. Res. 2013, 65, 837–843. [Google Scholar] [CrossRef]
- Erzar, B.; Forquin, P. An Experimental Method to Determine the Tensile Strength of Concrete at High Rates of Strain. Exp. Mech. 2010, 1, 941–955. [Google Scholar] [CrossRef]
- Zhang, X.X.; Ruiz, G.; Yu, R.C.; Tarifa, M. Fracture behaviour of high-strength concrete at a wide range of loading rates. Int. J. Impact Eng. 2009, 36, 1204–1209. [Google Scholar] [CrossRef]
- Ruiz, G.; Zhang, X.X.; Yu, R.C.; Porras, R.; Poveda, E.; del Viso, J.R. Effect of Loading Rate on Fracture Energy of High-Strength Concrete. Strain 2011, 47, 518–524. [Google Scholar] [CrossRef]
- Wittmann, F.H.; Roelfstra, P.E.; Mihashi, H.; Huang, Y.-Y.; Zhang, X.-H.; Nomura, N. Influence of age of loading, water-cement ratio and rate of loading on fracture energy of concrete. Mater. Struct. 1987, 20, 103–110. [Google Scholar] [CrossRef]
- Snozzi, L.; Caballero, A.; Molinari, J.F. Influence of the meso-structure in dynamic fracture simulation of concrete under tensile loading. Cem. Concr. Res. 2011, 41, 1130–1142. [Google Scholar] [CrossRef]
- Erzar, B.; Forquin, P. Experiments and mesoscopic modelling of dynamic testing of concrete. Mech. Mater. 2011, 43, 505–527. [Google Scholar] [CrossRef]
- Forquin, P.; Lukić, B. On the Processing of Spalling Experiments. Part I: Identification of the Dynamic Tensile Strength of Concrete. J. Dyn. Behav. Mater. 2018, 4, 34–55. [Google Scholar] [CrossRef]
- Lu, Y.B.; Li, Q.M. About the dynamic uniaxial tensile strength of concrete-like materials. Int. J. Impact Eng. 2011, 38, 171–180. [Google Scholar] [CrossRef]
- Ruiz, G.; Zhang, X.; Tarifa, M.; Yu, R.C.; Camara, M. Fracture Energy of High-Strength Concrete Under Different Loading Rates. An. Mecánica Fract. 2009, 26, 513–518. [Google Scholar]
- Chen, C.; Fan, X.; Chen, X. Experimental investigation of concrete fracture behavior with different loading rates based on acoustic emission. Constr. Build. Mater. 2020, 237, 117472. [Google Scholar] [CrossRef]
- Bless, S.; Peden, B.; Guzman, I.; Omidvar, M.; Iskander, M. Poncelet coefficients of granular media. In Dynamic Behavior of Materials, Volume 1; Springer: Berlin, Germany, 2014; pp. 373–380. [Google Scholar]
- Weerheijm, J.; Van Doormaal, J.C.A.M. Tensile failure of concrete at high loading rates: New test data on strength and fracture energy from instrumented spalling tests. Int. J. Impact Eng. 2007, 34, 609–626. [Google Scholar] [CrossRef]
- Lukić, B.B.; Saletti, D.; Forquin, P. On the Processing of Spalling Experiments. Part II: Identification of Concrete Fracture Energy in Dynamic Tension. J. Dyn. Behav. Mater. 2018, 4, 56–73. [Google Scholar] [CrossRef]
- Hao, Y.; Hao, H.; Zhang, X.H. Numerical analysis of concrete material properties at high strain rate under direct tension. Int. J. Impact Eng. 2012, 39, 51–62. [Google Scholar] [CrossRef]
- Xu, H.; Wen, H.M. A computational constitutive model for concrete subjected to dynamic loadings. Int. J. Impact Eng. 2016, 91, 116–125. [Google Scholar] [CrossRef]
- Wu, H.; Zhang, Q.; Huang, F.; Jin, Q. Experimental and numerical investigation on the dynamic tensile strength of concrete. Int. J. Impact Eng. 2005, 32, 605–617. [Google Scholar] [CrossRef]
- Khosravani, M.R.; Silani, M.; Weinberg, K. Fracture studies of Ultra-High Performance Concrete using dynamic Brazilian tests. Theor. Appl. Fract. Mech. 2018, 93, 302–310. [Google Scholar] [CrossRef]
- Unger, J.F.; Eckardt, S.; Könke, C. Modelling of cohesive crack growth in concrete structures with the extended finite element method. Comput. Methods Appl. Mech. Eng. 2007, 196, 4087–4100. [Google Scholar] [CrossRef]
- Huang, Y.; Guan, Y.; Wang, L.; Zhou, J.; Ge, Z.; Hou, Y. Characterization of mortar fracture based on three point bending test and XFEM. Int. J. Pavement Res. Technol. 2018, 11, 339–344. [Google Scholar] [CrossRef]
- Brara, A.; Camborde, F.; Klepaczko, J.R.; Mariotti, C. Experimental and numerical study of concrete at high strain rates in tension. Mech. Mater. 2001, 33, 33–45. [Google Scholar] [CrossRef]
- Hentz, S.; Donzé, F.V.; Daudeville, L. Discrete element modelling of concrete submitted to dynamic loading at high strain rates. Comput. Struct. 2004, 82, 2509–2524. [Google Scholar] [CrossRef]
- Wu, Z.; Cui, W.; Fan, L.; Liu, Q. Mesomechanism of the dynamic tensile fracture and fragmentation behaviour of concrete with heterogeneous mesostructure. Constr. Build. Mater. 2019, 217, 573–591. [Google Scholar] [CrossRef]
- Zhou, R.; Chen, H.M.; Lu, Y. Mesoscale modelling of concrete under high strain rate tension with a rate-dependent cohesive interface approach. Int. J. Impact Eng. 2020, 139, 103500. [Google Scholar] [CrossRef]
- Yılmaz, O.; Molinari, J.F. A mesoscale fracture model for concrete. Cem. Concr. Res. 2017, 97, 84–94. [Google Scholar] [CrossRef]
- Zhou, R.; Lu, Y. A mesoscale interface approach to modelling fractures in concrete for material investigation. Constr. Build. Mater. 2018, 165, 608–620. [Google Scholar] [CrossRef]
- Ozbolt, J.; Sharma, A.; Irhan, B.; Sola, E. Tensile behavior of concrete under high loading rates. Int. J. Impact Eng. 2014, 69, 55–68. [Google Scholar] [CrossRef]
- Ožbolt, J.; Sharma, A.; Reinhardt, H.W. Dynamic fracture of concrete—Compact tension specimen. Int. J. Solids Struct. 2011, 48, 1534–1543. [Google Scholar] [CrossRef]
- Rosa, A.L.; Yu, R.C.; Ruiz, G.; Saucedo, L.; Sousa, J.L.A.O. A loading rate dependent cohesive model for concrete fracture. Eng. Fract. Mech. 2012, 82, 195–208. [Google Scholar] [CrossRef]
- Yu, R.C.; Rosa, A.L.; Ruiz, G.; Sousa, J. A loading-rate dependent cohesive model to simulate concrete fracture. In Proceedings of the 12th International Conference on Fracture 2009, ICF-12, Ottawa, ON, Canada, 12–17 July 2009; Volume 8, pp. 6468–6476. [Google Scholar]
- Turon, A.; Dávila, C.G.; Camanho, P.P.; Costa, J. An engineering solution for mesh size effects in the simulation of delamination using cohesive zone models. Eng. Fract. Mech. 2007, 74, 1665–1682. [Google Scholar] [CrossRef]
- Wu, Z.; Zhang, P.; Fan, L.; Liu, Q. Debris characteristics and scattering pattern analysis of reinforced concrete slabs subjected to internal blast loads–a numerical study. Int. J. Impact Eng. 2019, 131, 1–16. [Google Scholar] [CrossRef]
- Peng, Y.; Wang, Q.; Ying, L.; Mahmoud, M.M.; Peng, H. Numerical simulation of dynamic mechanical properties of concrete under uniaxial compression. Materials 2019, 12, 643. [Google Scholar] [CrossRef] [PubMed]
- Saksala, T. Numerical modelling of concrete fracture processes under dynamic loading: Meso-mechanical approach based on embedded discontinuity finite elements. Eng. Fract. Mech. 2018, 201, 282–297. [Google Scholar] [CrossRef]
- Régal, X.; Hanus, J.L. Experimental Study of the Dynamic Flexural Strength of Concrete. Exp. Mech. 2017, 57, 427–442. [Google Scholar] [CrossRef][Green Version]
- Ožbolt, J.; Sharma, A. Numerical simulation of dynamic fracture of concrete through uniaxial tension and L-specimen. Eng. Fract. Mech. 2012, 85, 88–102. [Google Scholar] [CrossRef]
- Ozbolt, J.; Rah, K.K.; Mestrovic, D. Influence of loading rate on concrete cone failure. Int. J. Fract. 2006, 139, 239–252. [Google Scholar] [CrossRef]


| Bulk Element | Density ρ (kg/m3) | Young’s Modulus E (GPa) | Poisson’s Ratio υ | ||
|---|---|---|---|---|---|
| 2418 | 44.9 | 0.2 | |||
| cohesive element | T0 (MPa) | S0 (MPa) | GIC0 (J/m2) | GIIC0 (J/m2) | α |
| 3.3 | 13.2 | 40 | 400 | 50 | |
| A | B | M | N | (mm/s) | |
| 0.0033 | 0.0001 | 0.735 | 0.8 | 0.01 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, P.; Wu, Z.; Liu, Y.; Chu, Z. Numerical Study on the Dynamic Fracture Energy of Concrete Based on a Rate-Dependent Cohesive Model. Materials 2021, 14, 7421. https://doi.org/10.3390/ma14237421
Zhang P, Wu Z, Liu Y, Chu Z. Numerical Study on the Dynamic Fracture Energy of Concrete Based on a Rate-Dependent Cohesive Model. Materials. 2021; 14(23):7421. https://doi.org/10.3390/ma14237421
Chicago/Turabian StyleZhang, Penglin, Zhijun Wu, Yang Liu, and Zhaofei Chu. 2021. "Numerical Study on the Dynamic Fracture Energy of Concrete Based on a Rate-Dependent Cohesive Model" Materials 14, no. 23: 7421. https://doi.org/10.3390/ma14237421
APA StyleZhang, P., Wu, Z., Liu, Y., & Chu, Z. (2021). Numerical Study on the Dynamic Fracture Energy of Concrete Based on a Rate-Dependent Cohesive Model. Materials, 14(23), 7421. https://doi.org/10.3390/ma14237421






