Investigation of the Size Effects on the Elongation of Ti-2.5Al-1.5Mn Foils with Digital Image Correlation Method
Abstract
:1. Introduction
2. Materials and Methods
- (1)
- First, a layer of white paint was sprayed on the specimen surface as the background color, and black speckles were evenly sprayed so achieve each 50% of black and white. Then, specimens were installed in the material testing machine.
- (2)
- At the same time, when the material testing machine started running, the CCD camera, which was controlled by the GOM Correlate software, collected specimen images at the frequency of 1 image per second.
- (3)
- The changes in marked speckle information were calculated via the GOM Correlate software, and then, the displacement and strain field information were obtained.
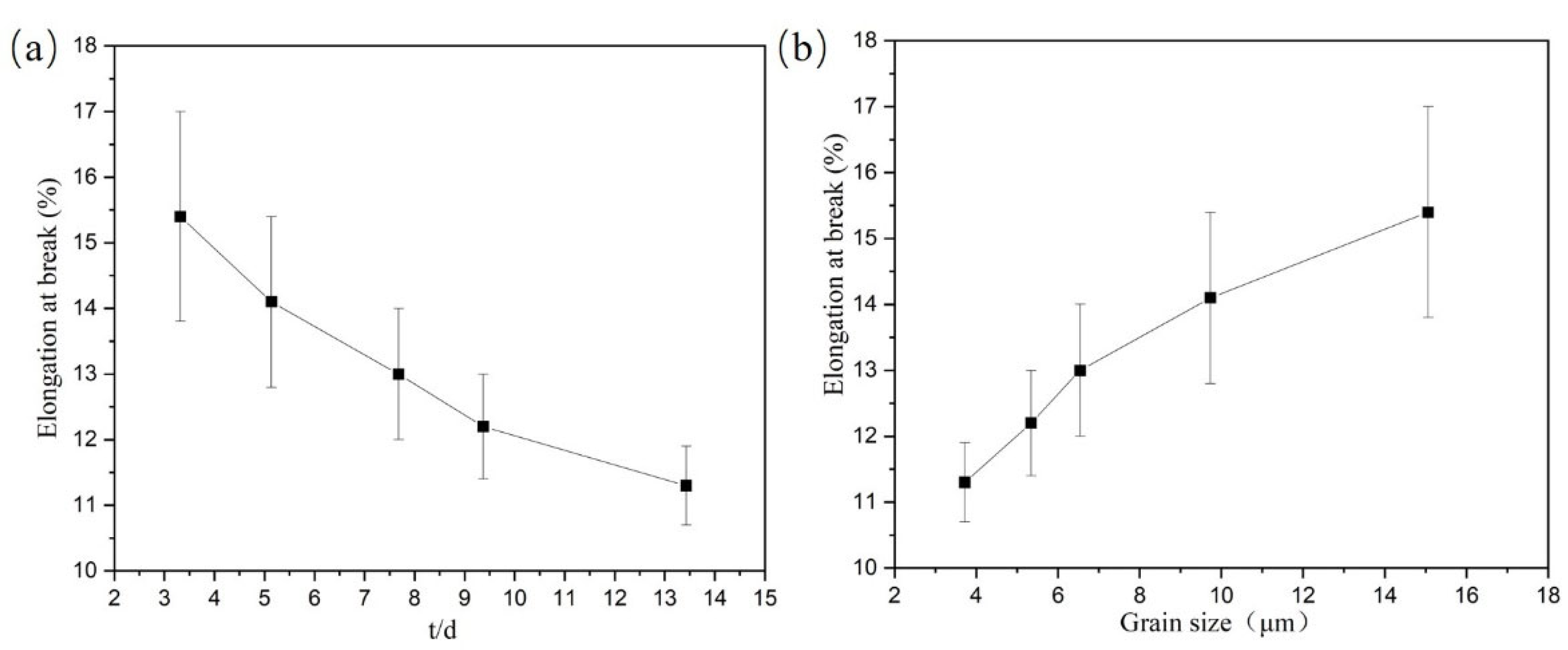
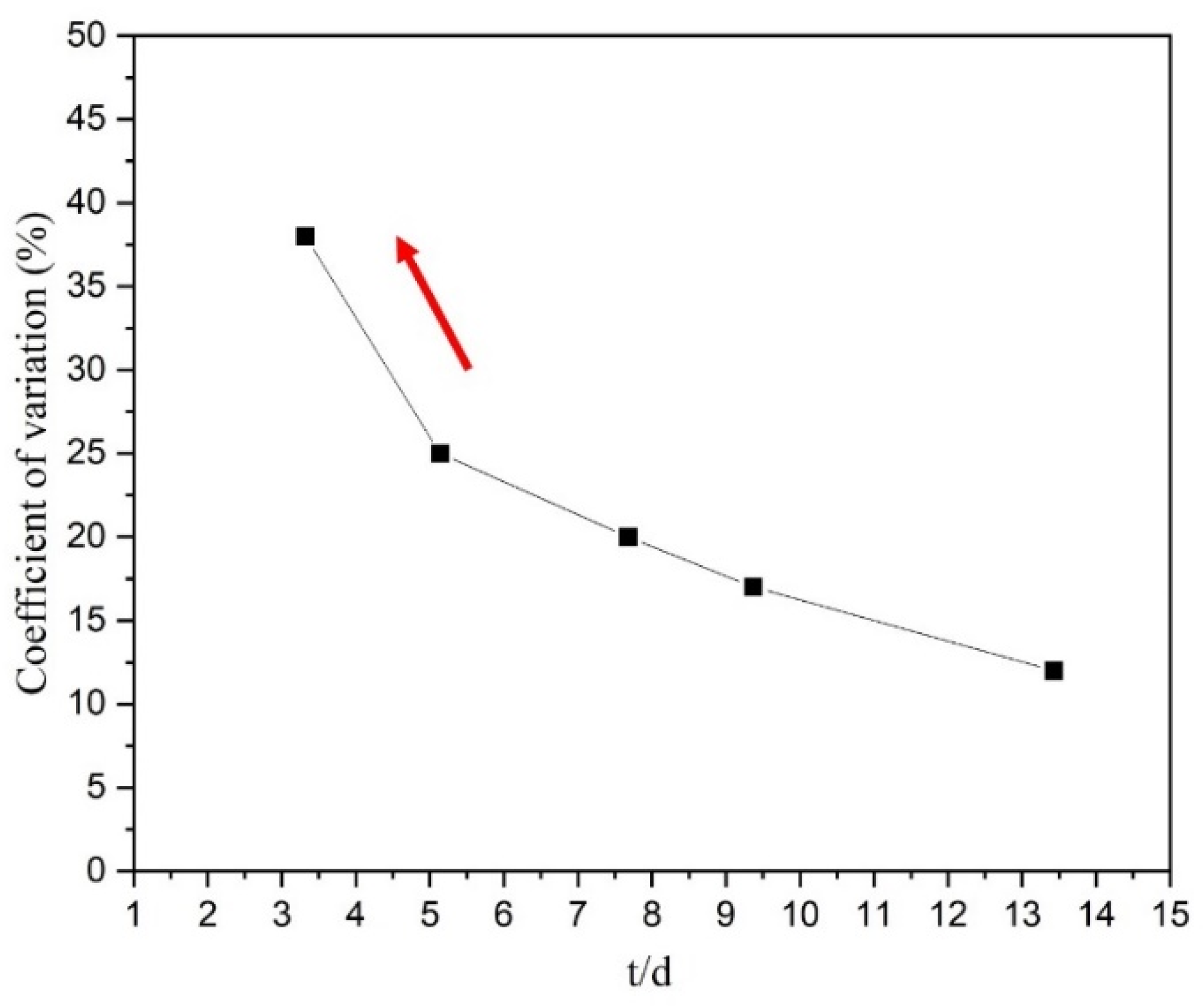
3. Results and Discussion
4. Conclusions
- (1)
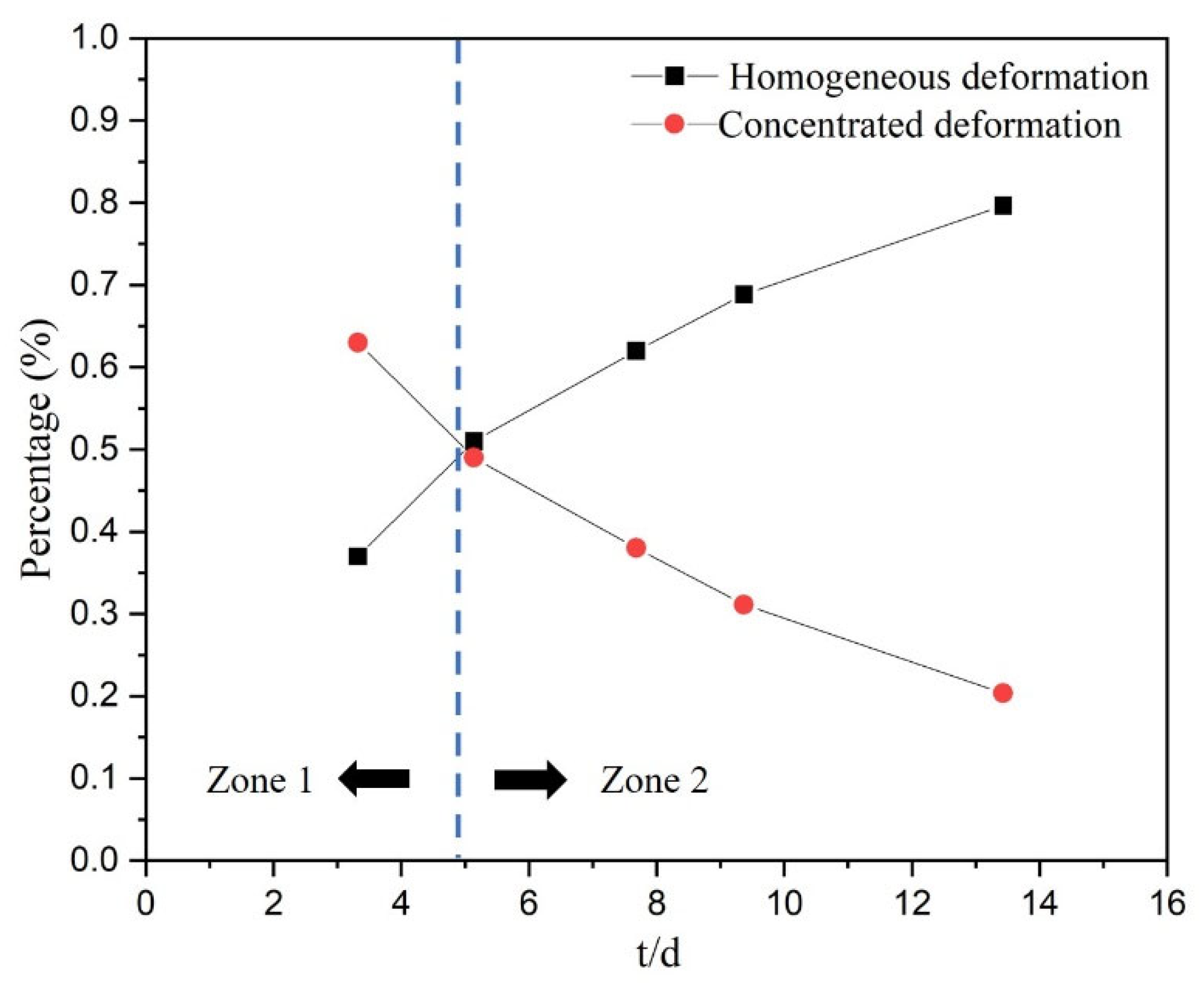
- The influence of individual grain heterogeneity increases during the deformation process, which results in the premature formation of concentrated deformation zones, contributing to the increased role of concentrated deformation in the foil elongation.
- (2)
- The proportion of homogeneous deformation amount and concentrated deformation amount can be divided into two different zones by a certain critical t/d value, which is near 5 for Ti-2.5Al-1.5Mn foils.
- (3)
- It is feasible to increase the plasticity of Ti-2.5Al-1.5Mn foils with a thickness of 50 μm by increasing the grain size, but foils with the t/d value in zone 1 should be avoided for forming parts that require high uniformity.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Feng, F.; Li, J.; Chen, R.; Peng, Y.; Su, H.; Zhang, Q.; Huang, P.; Zheng, Z. Effect of Die Geometry on the Formability of 5052 Aluminum Alloy in Electromagnetic Impaction Deformation. Materials 2018, 11, 1379. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.J.; Shan, D.B.; Zhou, J.; Guo, B.; Sun, L.N. Size effects of the cavity dimension on the microforming ability during coining process. J. Mater. Process. Technol. 2007, 187, 256–259. [Google Scholar] [CrossRef]
- Wang, C.J.; Wang, H.Y.; Chen, G.; Zhu, Q.; Zhang, G.W.; Cui, L.J.; Zhang, P. Size effects affected uniaxial tensile properties and formability in rubber pad micro-forming process of pure nickel thin sheets. Int. J. Mech. Sci. 2020, 182, 105757–105763. [Google Scholar] [CrossRef]
- Gu, X.; Wang, X.; Ma, Y.J.; Zhang, H.K.; Lu, J.X.; Wang, K.Y.; Liu, H.X. Investigation on grain size effect and forming mechanism of laser shock hydraulic micro-forming of copper foil. Int. J. Adv. Manuf. Technol. 2021, 114, 1049–1064. [Google Scholar] [CrossRef]
- Huang, K.L.; Yang, Y.; Yin, D.Q.; Yang, X.Z.; Qin, Y. Effect of Electric Current Magnitude on Particles Deformation during the Densification Process of Micro-FAST. Rare. Metal. Mat. Eng. 2015, 44, 365–369. [Google Scholar]
- Ma, Z.W.; Tong, G.Q.; Chen, F.; Wang, Q.; Wang, S.C. Grain size effect on springback behavior in bending of Ti-2.5Al-1.5Mn foils. J. Mater. Process. Technol. 2015, 224, 11–17. [Google Scholar] [CrossRef]
- Peng, L.F.; Hu, P.; Lai, X.M.; Mei, D.Q.; Ni, J. Investigation of micro/meso sheet soft punch stamping process—Simulation and experiments. Mater. Des. 2009, 30, 783–790. [Google Scholar] [CrossRef]
- Ma, Z.W.; Peng, X.; Wang, C.J.; Cao, Z.Y. Modeling of material deformation behavior in micro-forming under consideration of individual grain heterogeneity. Trans. Nonferrous Met. Soc. China 2020, 30, 2994–3005. [Google Scholar] [CrossRef]
- Wang, C.J.; Wang, C.J.; Guo, B.; Shan, D.B.; Guan, H. Size effect on flow stress in uniaxial compression of pure nickel cylinders with a few grains across thickness. Mater. Lett. 2013, 106, 294–296. [Google Scholar] [CrossRef]
- Vollertsen, F.; Hu, Z.; Schulzeniehoff, H.; Theiler, C. State of the art in micro forming and investigations into micro deep drawing. J. Mater. Process. Technol. 2004, 151, 70–79. [Google Scholar] [CrossRef]
- Michel, J.F.; Picart, P. Size effects on the constitutive behavior for brass in sheet metal forming. J. Mater. Process. Technol. 2003, 141, 439–446. [Google Scholar] [CrossRef]
- Raulea, L.V.; Goijaerts, A.M.; Govaert, L.E.; Baaijens, F.P.T. Size effects in the processing of thin metal sheets. J. Mater. Process. Technol. 2001, 115, 44–48. [Google Scholar] [CrossRef]
- Wang, C.J.; Liu, Y.; Guo, B.; Shan, D.B.; Zhang, B. Acoustic softening and stress superposition in ultrasonic vibration assisted uniaxial tension of copper foil: Experiments and modeling. Mater. Des. 2016, 112, 246–253. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.G.; Fu, M.W.; Chan, W.L. A constitutive model for modeling of the deformation behavior in microforming with a consideration of grain boundary strengthening. Comp. Mater. Sci. 2012, 55, 85–94. [Google Scholar] [CrossRef]
- Takeuchi, S. The mechanism of the inverse Hall-Petch relation of nanocrystals. Scr. Mater. 2001, 44, 1483–1487. [Google Scholar] [CrossRef]
- Mahabunphachai, S.; Ko, M. Investigation of size effects on material behavior of thin sheet metals using hydraulic bulge testing at micro/meso-scales. Int. J. Mach. Tools Manuf. 2008, 48, 1014–1029. [Google Scholar] [CrossRef]
- Chan, W.L.; Fu, M.W.; Lu, J.; Liu, J.G. Modeling of grain size effect on micro deformation behavior in micro-forming of pure copper. Mater. Sci. Eng. A 2010, 527, 6638–6648. [Google Scholar] [CrossRef]
- Chan, W.L.; Fu, M.W. Experimental studies and numerical modeling of the specimen and grain size effects on the flow stress of sheet metal in microforming. Mater. Sci. Eng. A 2011, 528, 7674–7683. [Google Scholar] [CrossRef]
- Engel, U.; Eckstein, R. Microforming—From basic research to its realization. J. Mater. Process. Technol. 2002, 125, 35–44. [Google Scholar] [CrossRef]
- Saotome, Y.; Yasuda, K.; Kaga, H. Microdeep drawability of very thin sheet steels. J. Mater. Process. Technol. 2001, 113, 641–647. [Google Scholar] [CrossRef]
- Ma, Z.W.; Cao, Z.Y.; Lu, J.B.; Zhang, Y.J.; Liu, W. Size effects on springback behavior of H80 foils. Rare Met. 2018, 37, 1082–1090. [Google Scholar] [CrossRef]
- Lu, H.N.; Wei, D.B.; Jiang, Z.Y.; Liu, X.H. Modelling of size effects in microforming process with consideration of grained heterogeneity. Comp. Mater. Sci. 2013, 77, 44–52. [Google Scholar] [CrossRef] [Green Version]
- Fang, Z.; Jiang, Z.Y.; Wei, D.B.; Liu, X.H. Study on springback in micro V-bending with consideration of grain heterogeneity. Int. J. Adv. Manuf. Technol. 2015, 78, 1075–1085. [Google Scholar] [CrossRef]
- Ha, N.S.; Le, V.T.; Goo, N.S. Investigation of punch resistance of the Allomyrira dichtoloma beetle forewing. J. Bionic Eng. 2018, 15, 57–68. [Google Scholar] [CrossRef]
- Ha, N.S.; Le, V.T.; Goo, N.S.; Kim, J.Y. Thermal Strain Measurement of Austin Stainless Steel (SS304) during a Heating-cooling Process. Int. J. Aeronaut. Space Sci. 2017, 18, 206–214. [Google Scholar] [CrossRef]
- Chin, G.Y.; Mammel, W.L. Computer solutions of the Taylor analysis for axisymmetric flow. Trans. TMS AIME 1967, 239, 1400–1405. [Google Scholar]
- Chan, W.L.; Fu, M.W. Experimental and simulation based study on micro-scaled sheet metal deformation behavior in microembossing process. Mater. Sci. Eng. A 2012, 556, 60–67. [Google Scholar] [CrossRef]
- Xue, S.; Wang, C.; Chen, P.; Xu, Z.; Cheng, L.; Guo, B.; Shan, D. Investigation of Electrically-Assisted Rolling Process of Corrugated Surface Microstructure with T2 Copper Foil. Materials 2019, 12, 4144. [Google Scholar] [CrossRef] [Green Version]
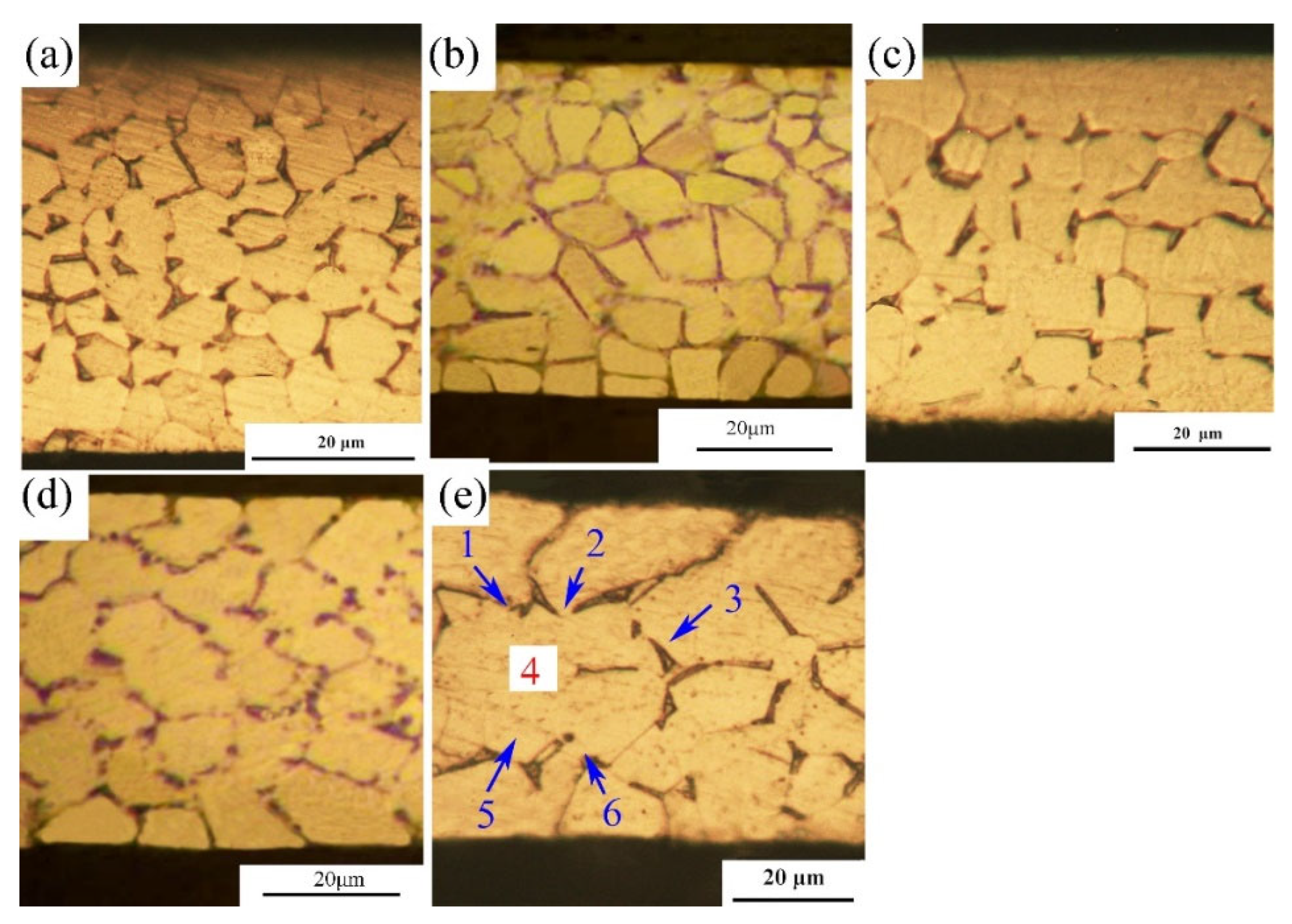



| Number | Annealing Parameters | Grain Size d (μm) | t/d |
|---|---|---|---|
| a | 700 °C, 1.5 h | 3.72 ± 1.23 | 13.43 |
| b | 720 °C, 2.5 h | 5.34 ± 2.13 | 9.37 |
| c | 750 °C, 3.5 h | 6.52 ± 2.46 | 7.68 |
| d | 800 °C, 3.5 h | 9.73 ± 3.15 | 5.14 |
| e | 850 °C, 7 h | 15.06 ± 4.67 | 3.32 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Zhang, W.; Ma, Z. Investigation of the Size Effects on the Elongation of Ti-2.5Al-1.5Mn Foils with Digital Image Correlation Method. Materials 2021, 14, 7353. https://doi.org/10.3390/ma14237353
Wang C, Zhang W, Ma Z. Investigation of the Size Effects on the Elongation of Ti-2.5Al-1.5Mn Foils with Digital Image Correlation Method. Materials. 2021; 14(23):7353. https://doi.org/10.3390/ma14237353
Chicago/Turabian StyleWang, Chunju, Weiwei Zhang, and Zhenwu Ma. 2021. "Investigation of the Size Effects on the Elongation of Ti-2.5Al-1.5Mn Foils with Digital Image Correlation Method" Materials 14, no. 23: 7353. https://doi.org/10.3390/ma14237353
APA StyleWang, C., Zhang, W., & Ma, Z. (2021). Investigation of the Size Effects on the Elongation of Ti-2.5Al-1.5Mn Foils with Digital Image Correlation Method. Materials, 14(23), 7353. https://doi.org/10.3390/ma14237353








