Electron-Optical In Situ Imaging for the Assessment of Accuracy in Electron Beam Powder Bed Fusion
Abstract
1. Introduction
2. Materials and Methods
2.1. PBF-EB Process and Part Design
2.2. ELO Imaging
2.3. XCT Measurement
2.4. Simulation
2.5. Data Analysis and Comparison
3. Results
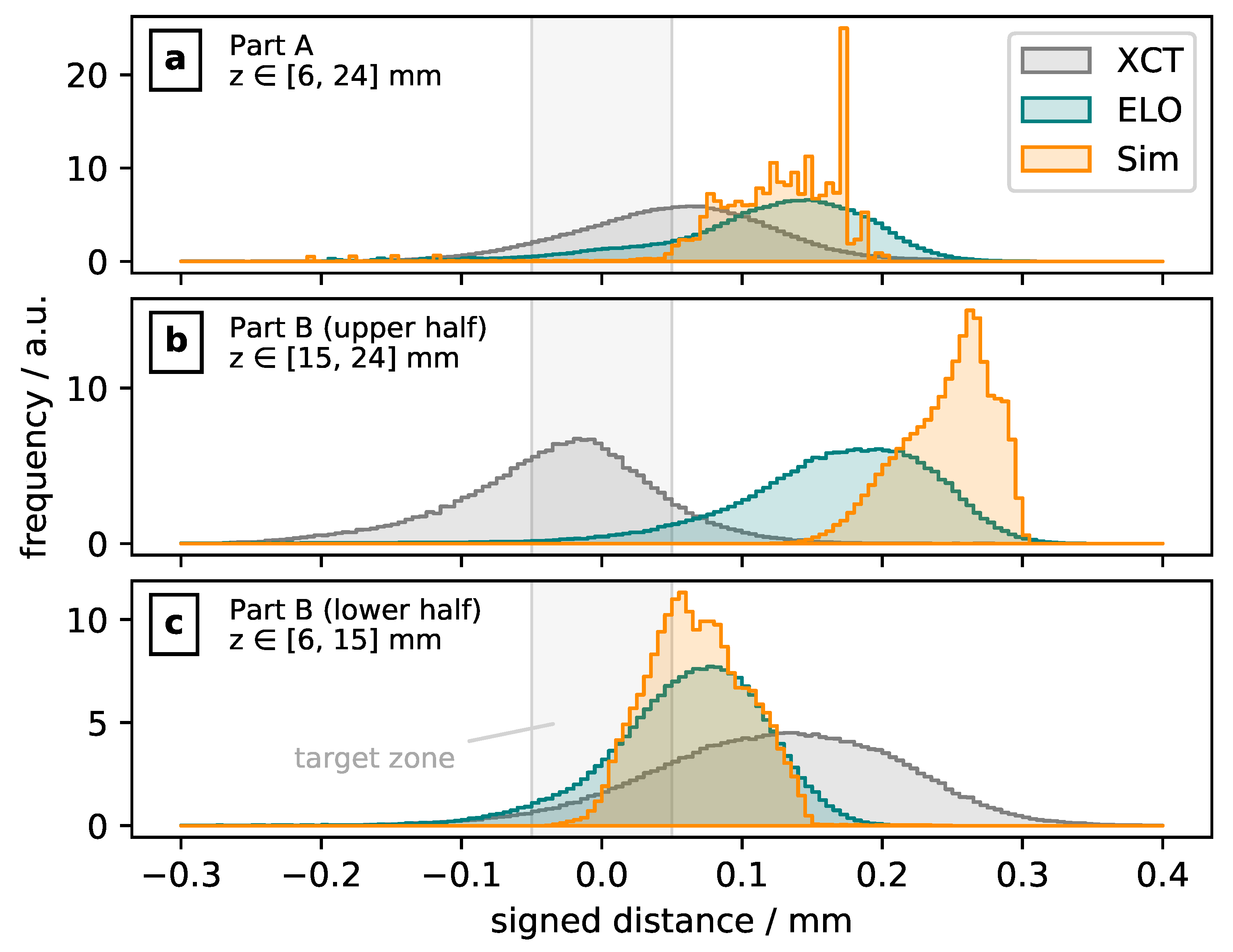
3.1. XCT Measurement
3.2. ELO Reconstruction
3.3. Simulation
4. Discussion
4.1. Dimensional Accuracy
4.2. Side Surface Roughness
5. Conclusions
- In situ ELO imaging can be used to monitor the accuracy of the molten layers and to quantitatively detect deviations from the corresponding reference cross-sections.
- In situ ELO imaging can be used for making predictions about the out-of-plane surface roughness of the as-built part since it is capable of resolving undesired displacements between consecutive layers.
- In situ ELO imaging is not capable of predicting all geometrical defects of the as-built PBF-EB parts (e.g., the edge loss effect) because of its limitation to layer-wise imaging of the current surface.
- The combination of in situ ELO imaging and post-process measurement of the as-built part (e.g., via XCT) enables the distinction between the inaccuracy created during melting of a specific layer and the inaccuracies developed during melting of subsequent layers.
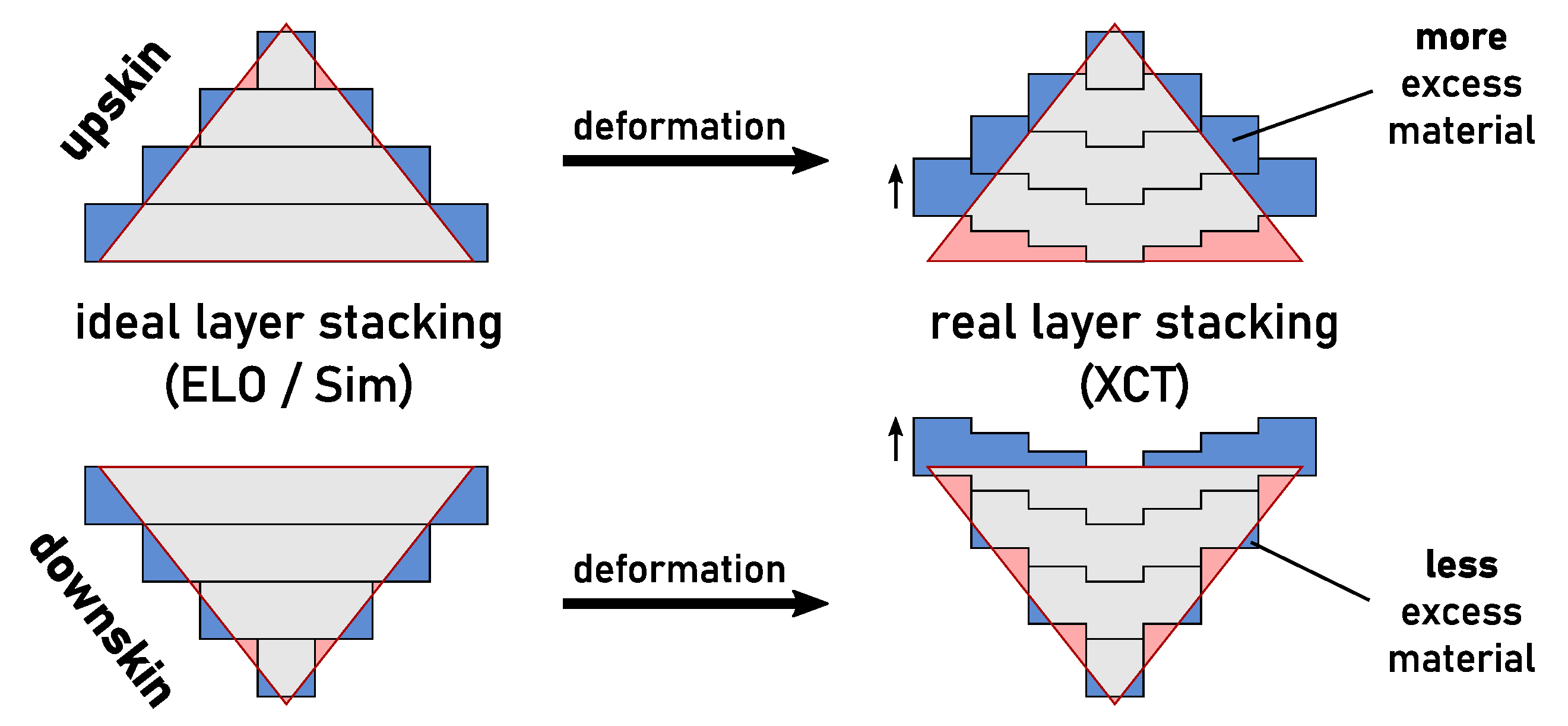
- Thermals stresses may induce severe plastic deformation which creates systematic deviations from the reference geometry. Both direction and magnitude of these deviations strongly depend on the characteristics of the involved geometric features (upskin or downskin surface, overhang, edge, etc.). The observed effects might be explained with an up-warping of layers induced by melting of subsequent layers.
- Thermodynamic simulation of the layer-wise melting process and the solidifying volume was demonstrated to be in excellent agreement with experimental in situ data.
- The thermodynamic simulation delivered additional sub-surface information about the molten layers which is important for the full assessment of accuracy and surface roughness, especially for downskin surfaces. In the future, the simulation might be used as a viable tool to optimize scanning strategies in advance in order to improve both accuracy and surface roughness.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
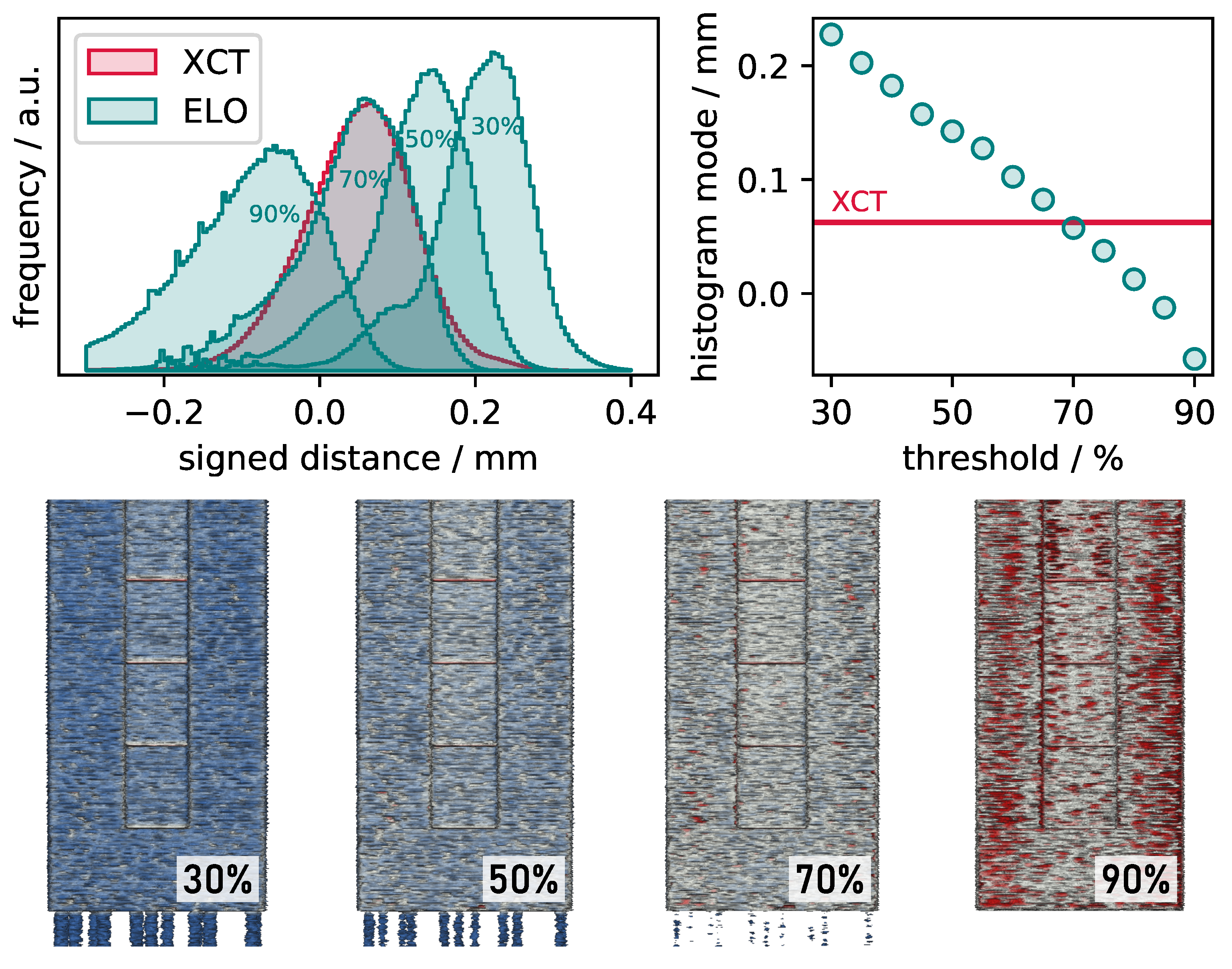
Appendix A. Sensitivity Analysis on ELO Thresholding
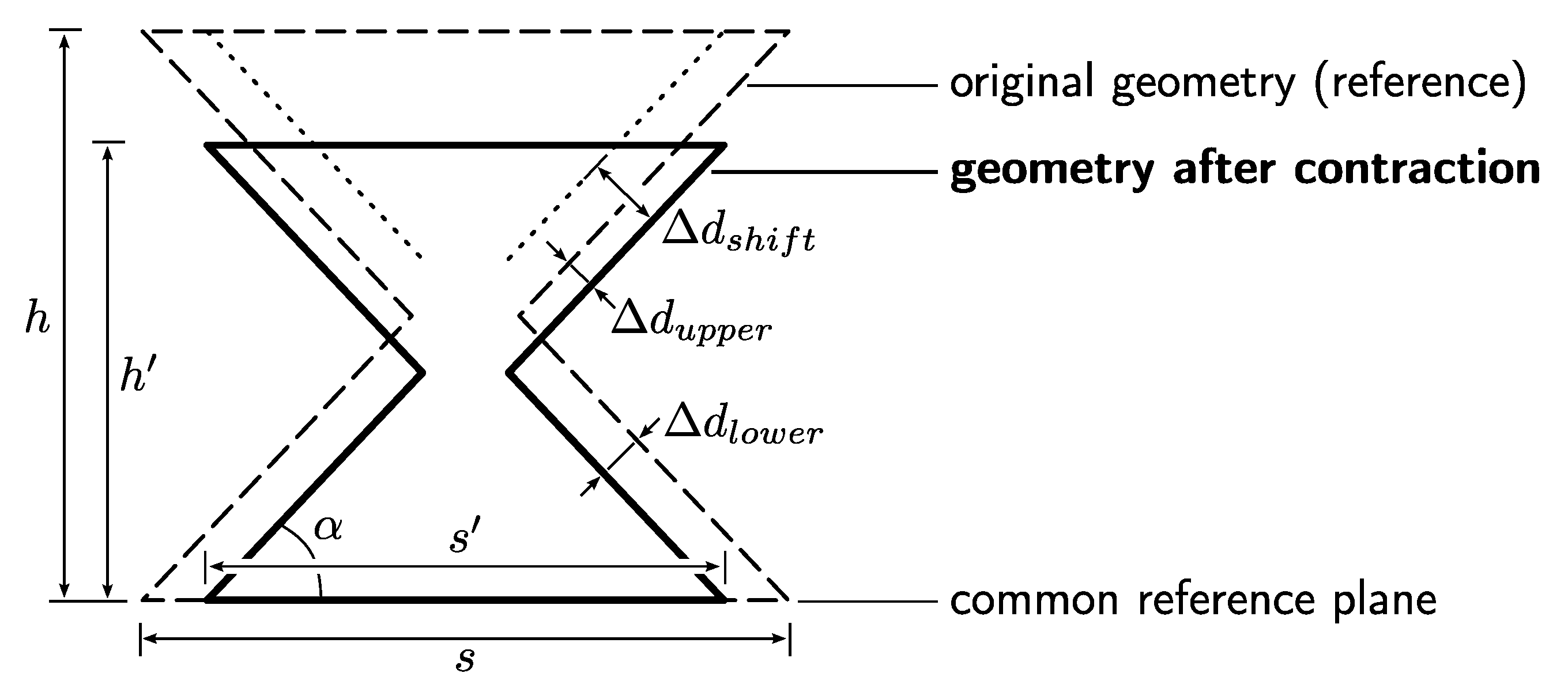
Appendix B. Offset Shift Due to Data Registration
References
- Leach, R.K.; Bourell, D.; Carmignato, S.; Donmez, A.; Senin, N.; Dewulf, W. Geometrical metrology for metal additive manufacturing. CIRP Ann. 2019, 68, 677–700. [Google Scholar] [CrossRef]
- Moylan, S.; Cooke, A.; Jurrens, K.; Slotwinski, J.; Donmez, M.A. A Review of Test Artifacts for Additive Manufacturing (Report Number: NISTIR 7858); National Institute of Standards and Technology (NIST): Gaithersburg, MD, USA, 2012. [CrossRef]
- Rebaioli, L.; Fassi, I. A review on benchmark artifacts for evaluating the geometrical performance of additive manufacturing processes. Int. J. Adv. Manuf. Technol. 2017, 93, 2571–2598. [Google Scholar] [CrossRef]
- Gruber, S.; Grunert, C.; Riede, M.; López, E.; Marquardt, A.; Brueckner, F.; Leyens, C. Comparison of dimensional accuracy and tolerances of powder bed based and nozzle based additive manufacturing processes. J. Laser Appl. 2020, 32, 032016. [Google Scholar] [CrossRef]
- Smith, C.J.; Derguti, F.; Hernandez Nava, E.; Thomas, M.; Tammas-Williams, S.; Gulizia, S.; Fraser, D.; Todd, I. Dimensional accuracy of Electron Beam Melting (EBM) additive manufacture with regard to weight optimized truss structures. J. Mater. Process. Technol. 2016, 229, 128–138. [Google Scholar] [CrossRef]
- Plotkowski, A.; Ferguson, J.; Stump, B.; Halsey, W.; Paquit, V.; Joslin, C.; Babu, S.S.; Marquez Rossy, A.; Kirka, M.M.; Dehoff, R.R. A stochastic scan strategy for grain structure control in complex geometries using electron beam powder bed fusion. Addit. Manuf. 2021, 46, 102092. [Google Scholar] [CrossRef]
- Pistor, J.; Breuning, C.; Körner, C. A single crystal process window for electron beam powder bed fusion additive manufacturing of a cmsx-4 type ni-based superalloy. Materials 2021, 14, 3785. [Google Scholar] [CrossRef]
- Cooke, A.; Soons, J. Variability in the Geometric Accuracy of Additively Manufactured Test Parts. In Proceedings of the 21st Annual Solid Freeform Fabrication Symposium: An Additive Manufacturing Conference, Austin, TX, USA, 9–11 August 2010. [Google Scholar] [CrossRef]
- Borrelli, R.; Franchitti, S.; Pirozzi, C.; Carrino, L.; Nele, L.; Polini, W.; Sorrentino, L.; Corrado, A. Ti6Al4V Parts Produced by Electron Beam Melting: Analysis of Dimensional Accuracy and Surface Roughness. J. Adv. Manuf. Syst. 2020, 19, 107–130. [Google Scholar] [CrossRef]
- Bartlett, J.L.; Li, X. An overview of residual stresses in metal powder bed fusion. Addit. Manuf. 2019, 27, 131–149. [Google Scholar] [CrossRef]
- Prabhakar, P.; Sames, W.J.; Dehoff, R.; Babu, S.S. Computational modeling of residual stress formation during the electron beam melting process for Inconel 718. Addit. Manuf. 2015, 7, 83–91. [Google Scholar] [CrossRef]
- Tadano, S.; Nakatani, Y.; Hino, T.; Ohnishi, H.; Tsuji, D.; Tanaka, T. Inherent strain analysis using experimental multi-layer model for electron-beam-melted parts. Yosetsu Gakkai Ronbunshu/Q. J. Jpn. Weld. Soc. 2021, 39, 1–10. [Google Scholar] [CrossRef]
- Cheng, B.; Chou, K. Thermal stresses associated with part overhang geometry in electron beam additive manufacturing: Process parameter effects. In Proceedings of the 25th Annual International Solid Freeform Fabrication Symposium, An Additive Manufacturing Conference, SFF 2014, Austin, TX, USA, 4–6 August 2014; pp. 1076–1087. [Google Scholar]
- Cheng, B.; Chou, K. Geometric consideration of support structures in part overhang fabrications by electron beam additive manufacturing. CAD Comput. Aided Des. 2015, 69, 102–111. [Google Scholar] [CrossRef]
- Cheng, B.; Chou, K. A numerical investigation of support structure designs for overhangs in powder bed electron beam additive manufacturing. J. Manuf. Process. 2020, 49, 187–195. [Google Scholar] [CrossRef]
- Ghaoui, S.; Ledoux, Y.; Vignat, F.; Museau, M.; Vo, T.; Villeneuve, F.; Ballu, A. Analysis of geometrical defects in overhang fabrications in electron beam melting based on thermomechanical simulations and experimental validations. Addit. Manuf. 2020, 36, 101557. [Google Scholar] [CrossRef]
- Everton, S.K.; Hirsch, M.; Stravroulakis, P.; Leach, R.K.; Clare, A.T. Review of In Situ process monitoring and In Situ metrology for metal additive manufacturing. Mater. Design 2016, 95, 431–445. [Google Scholar] [CrossRef]
- Grasso, M.; Colosimo, B.M. Process defects and in situ monitoring methods in metal powder bed fusion: A review. Meas. Sci. Technol. 2017, 28, 044005. [Google Scholar] [CrossRef]
- Mani, M.; Lane, B.M.; Donmez, M.A.; Feng, S.C.; Moylan, S.P. A review on measurement science needs for real-time control of additive manufacturing metal powder bed fusion processes. Int. J. Prod. Res. 2017, 55, 1400–1418. [Google Scholar] [CrossRef]
- Grasso, M.; Remani, A.; Dickins, A.; Colosimo, B.M.; Leach, R.K. In Situ measurement and monitoring methods for metal powder bed fusion: An updated review. Meas. Sci. Technol. 2021, 32, 112001. [Google Scholar] [CrossRef]
- Foster, B.; Reutzel, E.W.; Nassar, A.R.; Hall, B.T.; Brown, S.W.; Dickman, C.J. Optical, layerwise monitoring of powder bed fusion. In Proceedings of the Solid Freeform Fabrication Symposium 2015, Austin, TX, USA, 10–12 August 2015; pp. 295–307. [Google Scholar]
- Nassar, A.R.; Reutzel, E.W.; Brown, S.W.; Morgan, J.P.; Morgan, J.P.; Natale, D.J.; Tutwiler, R.L.; Feck, D.P.; Banks, J.C. Sensing for directed energy deposition and powder bed fusion additive manufacturing at Penn State University. In Laser 3D Manufacturing III; Gu, B., Helvajian, H., Piqué, A., Eds.; SPIE: Bellingham, WA, USA, 2016; Volume 9738, p. 97380R. [Google Scholar] [CrossRef]
- Aminzadeh, M.; Kurfess, T. Vision-based inspection system for dimensional accuracy in powder-bed additive manufacturing. In Proceedings of the ASME 2016 11th International Manufacturing Science and Engineering Conference, MSEC 2016, Blacksburg, VA, USA, 27 June–1 July 2016; Volume 2, pp. 1–13. [Google Scholar] [CrossRef]
- Abdelrahman, M.; Reutzel, E.W.; Nassar, A.R.; Starr, T.L. Flaw detection in powder bed fusion using optical imaging. Addit. Manuf. 2017, 15, 1–11. [Google Scholar] [CrossRef]
- Li, Z.; Liu, X.; Wen, S.; He, P.; Zhong, K.; Wei, Q.; Shi, Y.; Liu, S. In situ 3D monitoring of geometric signatures in the powder-bed-fusion additive manufacturing process via vision sensing methods. Sensors 2018, 18, 1180. [Google Scholar] [CrossRef]
- Caltanissetta, F.; Grasso, M.; Petrò, S.; Colosimo, B.M. Characterization of In Situ measurements based on layerwise imaging in laser powder bed fusion. Addit. Manuf. 2018, 24, 183–199. [Google Scholar] [CrossRef]
- Zur Jacobsmühlen, J.; Achterhold, J.; Kleszczynski, S.; Witt, G.; Merhof, D. In situ measurement of part geometries in layer images from laser beam melting processes. Prog. Addit. Manuf. 2019, 4, 155–165. [Google Scholar] [CrossRef]
- He, P.; Zhong, K.; Liu, X.; Zhou, G.; Wang, C.; Wei, Q.; Shi, Y.; Li, Z. A phase-guided method for extracting the contour of the fusion area in laser powder bed fusion. In Proceedings of the Seventh International Conference on Optical and Photonic Engineering (icOPEN 2019), Phuket, TH, USA, 16–20 July 2019; Fujigaki, M., Xie, H., Zhang, Q., Zhang, S., Zhu, J., Kemao, Q., Asundi, A., Eds.; SPIE: Bellingham, WA, USA, 2019; p. 37. [Google Scholar] [CrossRef]
- Pagani, L.; Grasso, M.; Scott, P.J.; Colosimo, B.M. Automated layerwise detection of geometrical distortions in laser powder bed fusion. Addit. Manuf. 2020, 36, 101435. [Google Scholar] [CrossRef]
- Rodriguez, E.; Mireles, J.; Terrazas, C.A.; Espalin, D.; Perez, M.A.; Wicker, R.B. Approximation of absolute surface temperature measurements of powder bed fusion additive manufacturing technology using in situ infrared thermography. Addit. Manuf. 2015, 5, 31–39. [Google Scholar] [CrossRef]
- Raplee, J.; Plotkowski, A.; Kirka, M.M.; Dinwiddie, R.; Okello, A.; Dehoff, R.R.; Babu, S.S. Thermographic Microstructure Monitoring in Electron Beam Additive Manufacturing. Sci. Rep. 2017, 7, 43554. [Google Scholar] [CrossRef] [PubMed]
- Price, S.; Lydon, J.; Cooper, K.; Chou, K. Experimental Temperature Analysis of Powder-Based Electron Beam Additive Manufacturing. In Proceedings of the Solid Freeform Fabrication Symposium, Austin, TX, USA, 12–14 August 2013; pp. 162–173. [Google Scholar]
- Ridwan, S.; Mireles, J.; Gaytan, S.; Espalin, D.; Wicker, R. Automatic Layerwise Acquisition of Thermal and Geometric Data of the Electron Beam Melting Process Using Infrared Thermography. In Proceedings of the International Symposium Solid Freeform Fabrication, Austin, TX, USA, 4–6 August 2014; Volume 343, pp. 343–352. [Google Scholar]
- Croset, G.; Martin, G.; Josserond, C.; Lhuissier, P.; Blandin, J.J.; Dendievel, R. In Situ layerwise monitoring of electron beam powder bed fusion using near-infrared imaging. Addit. Manuf. 2021, 38, 101767. [Google Scholar] [CrossRef]
- Arnold, C.; Körner, C. Electron-optical In Situ metrology for electron beam powder bed fusion: Calibration and validation. Meas. Sci. Technol. 2021, 33, 014001. [Google Scholar] [CrossRef]
- Lorensen, W.E.; Cline, H.E. Marching cubes: A high resolution 3D surface construction algorithm. In Proceedings of the 14th Annual Conference on Computer Graphics and Interactive Techniques, SIGGRAPH 1987, Anaheim, CA, USA, 27–31 July 1987; Volume 21, pp. 163–169. [Google Scholar] [CrossRef]
- Van der Walt, S.; Schönberger, J.L.; Nunez-Iglesias, J.; Boulogne, F.; Warner, J.D.; Yager, N.; Gouillart, E.; Yu, T. Scikit-image: Image processing in Python. PeerJ 2014, 2, e453. [Google Scholar] [CrossRef]
- Sanders, D.J. Temperature distributions produced by scanning Gaussian laser beams. Appl. Opt. 1984, 23, 30. [Google Scholar] [CrossRef]
- Smith, C.J.; Tammas-Williams, S.; Hernandez-Nava, E.; Todd, I. Tailoring the thermal conductivity of the powder bed in Electron Beam Melting (EBM) Additive Manufacturing. Sci. Rep. 2017, 7, 10514. [Google Scholar] [CrossRef]
- Rausch, A.M.; Markl, M.; Körner, C. Predictive simulation of process windows for powder bed fusion additive manufacturing: Influence of the powder size distribution. Comput. Math. Appl. 2019, 78, 2351–2359. [Google Scholar] [CrossRef]
- Samet, Y.K.; Robert, R.N.; Vincent, A.M. A Comparative Study of the Harmonic and Arithmetic Averaging of Diffusion Coefficients for Non-Linear Heat Conduction Problems; Technical Report INL/EXT-08-13999; Idaho National Laboratory: Idaho Falls, ID, USA, 2008. [CrossRef][Green Version]
- CloudCompare (Version 2.12. Alpha) [GPL Software]. 2021. Available online: http://www.cloudcompare.org/ (accessed on 28 October 2021).
- Breuning, C.; Arnold, C.; Markl, M.; Körner, C. A multivariate meltpool stability criterion for fabrication of complex geometries in electron beam powder bed fusion. Addit. Manuf. 2021, 45, 102051. [Google Scholar] [CrossRef]
- Vo, T.H.; Museau, M.; Vignat, F.; Villeneuve, F.; Ledoux, Y.; Ballu, A. Typology of geometrical defects in Electron Beam Melting. Procedia CIRP 2018, 75, 92–97. [Google Scholar] [CrossRef]
- Kanaya, K.; Okayama, S. Penetration and energy-loss theory of electrons in solid targets. J. Phys. D Appl. Phys. 1972, 5, 308. [Google Scholar] [CrossRef]
- Safdar, A.; He, H.Z.; Wei, L.Y.; Snis, A.; Chavez De Paz, L.E. Effect of process parameters settings and thickness on surface roughness of EBM produced Ti-6Al-4V. Rapid Prototyp. J. 2012, 18, 401–408. [Google Scholar] [CrossRef]
- Prisco, U.; Astarita, A.; El Hassanin, A.; Franchitti, S. Influence of processing parameters on microstructure and roughness of electron beam melted Ti-6Al-4V titanium alloy. Mater. Manuf. Process. 2019, 34, 1753–1760. [Google Scholar] [CrossRef]
- Arnold, C.; Pobel, C.; Osmanlic, F.; Körner, C. Layerwise monitoring of electron beam melting via backscatter electron detection. Rapid Prototyp. J. 2018, 24, 1401–1406. [Google Scholar] [CrossRef]
- Pobel, C.R.; Arnold, C.; Osmanlic, F.; Fu, Z.; Körner, C. Immediate development of processing windows for selective electron beam melting using layerwise monitoring via backscattered electron detection. Mater. Lett. 2019, 249, 70–72. [Google Scholar] [CrossRef]




| Property | Unit | Value |
|---|---|---|
| Thermal diffusivity solid | m2/s | |
| Thermal diffusivity powder | m2/s | |
| Density | kg/m3 | 4122 |
| Specific heat | J/(kg K) | 670 |
| Absorption coefficient | 0.85 | |
| Liquidus temperature | K | 1928 |
| Preheat temperature | K | 1023 |
| Beam diameter | μm | 400 |
| Lattice spacing | μm | 25 |
| Time step | μs | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arnold, C.; Breuning, C.; Körner, C. Electron-Optical In Situ Imaging for the Assessment of Accuracy in Electron Beam Powder Bed Fusion. Materials 2021, 14, 7240. https://doi.org/10.3390/ma14237240
Arnold C, Breuning C, Körner C. Electron-Optical In Situ Imaging for the Assessment of Accuracy in Electron Beam Powder Bed Fusion. Materials. 2021; 14(23):7240. https://doi.org/10.3390/ma14237240
Chicago/Turabian StyleArnold, Christopher, Christoph Breuning, and Carolin Körner. 2021. "Electron-Optical In Situ Imaging for the Assessment of Accuracy in Electron Beam Powder Bed Fusion" Materials 14, no. 23: 7240. https://doi.org/10.3390/ma14237240
APA StyleArnold, C., Breuning, C., & Körner, C. (2021). Electron-Optical In Situ Imaging for the Assessment of Accuracy in Electron Beam Powder Bed Fusion. Materials, 14(23), 7240. https://doi.org/10.3390/ma14237240








