Forecasting Strength of CFRP Confined Concrete Using Multi Expression Programming
Abstract
:1. Introduction
2. Research Methodology
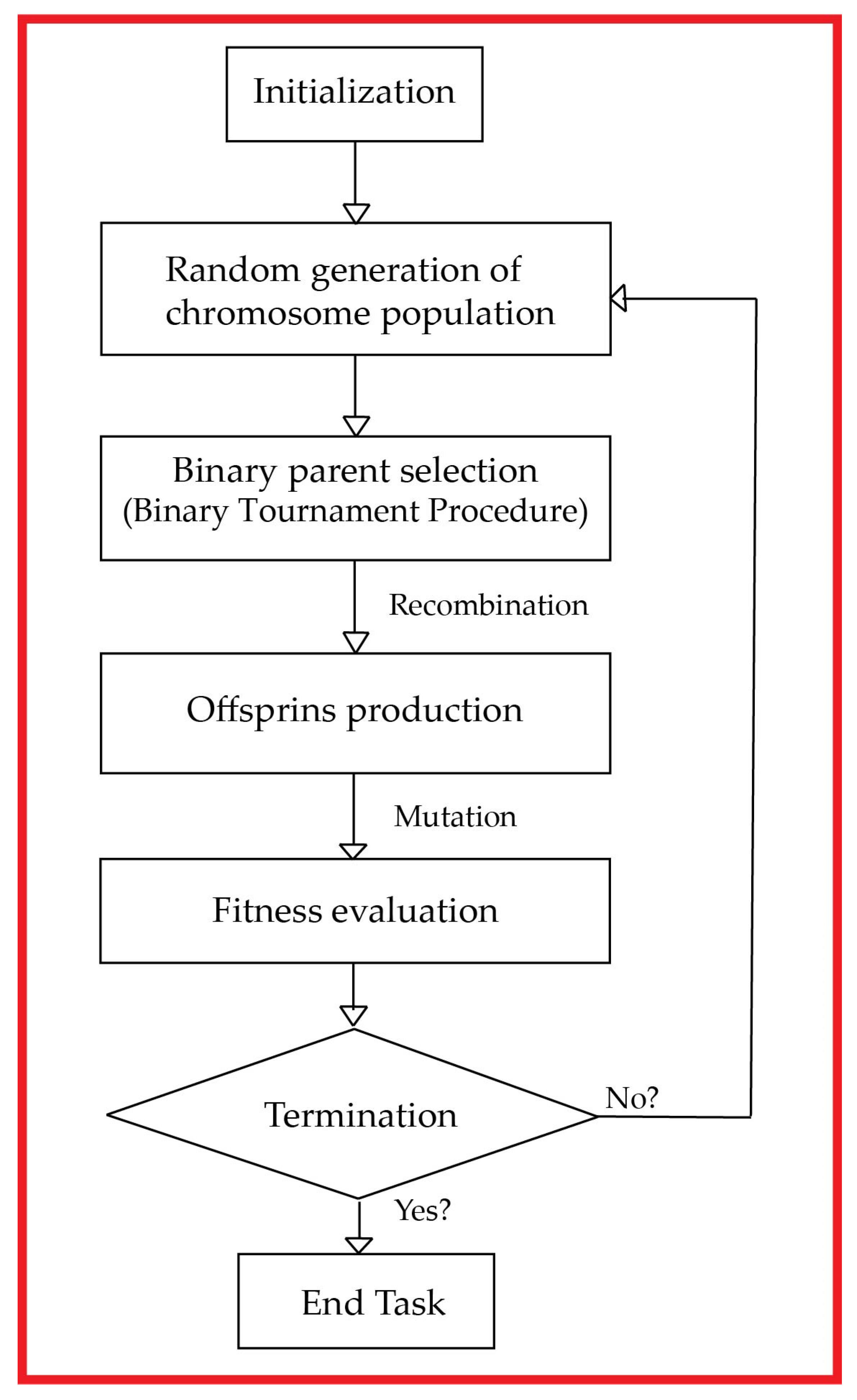
2.1. Multi Expression Programming
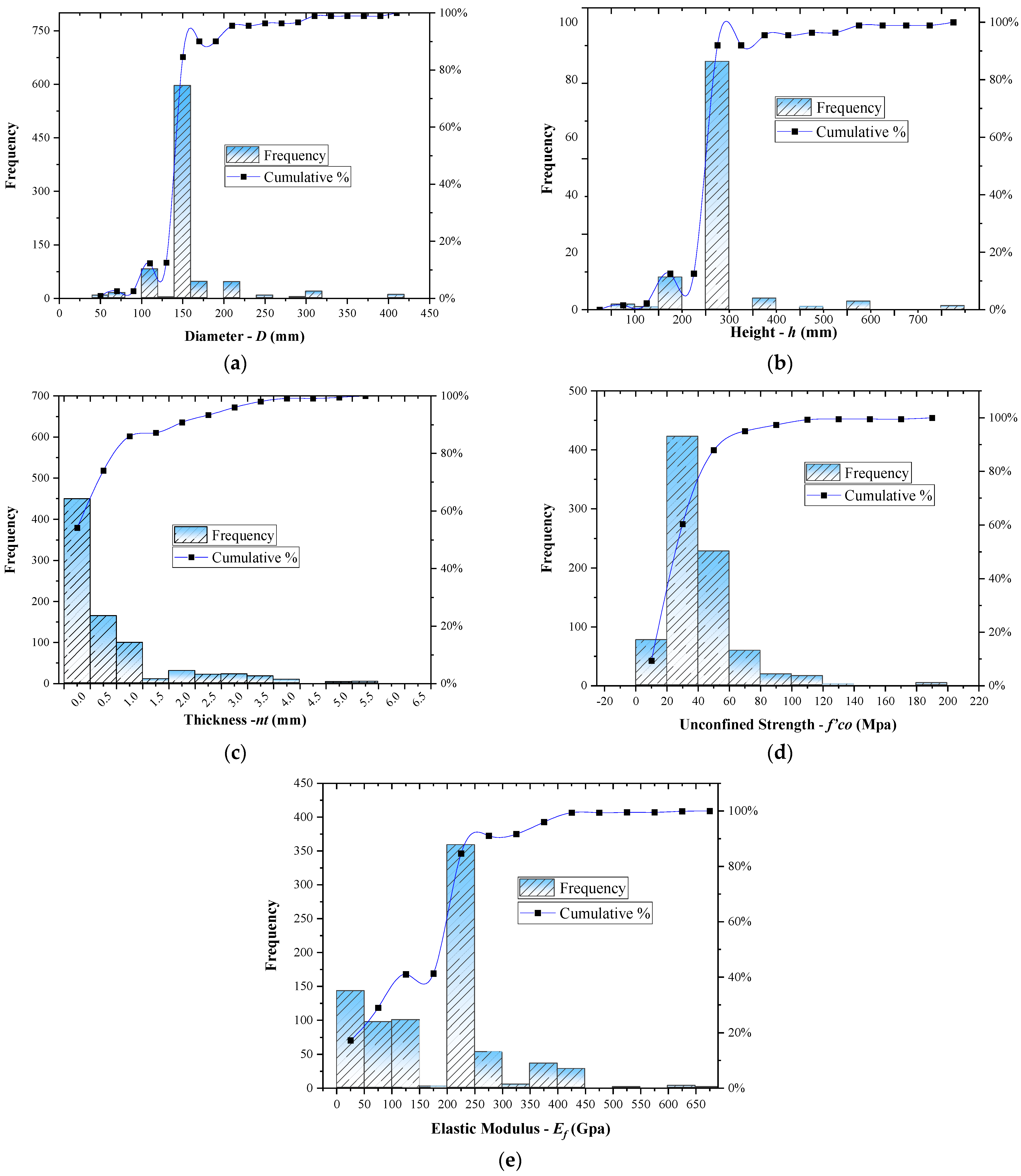
2.2. Experimental Database
2.3. Modeling Parameters
- To exist a correlation between the observed and expected values |R| needs to be between 0.2 < |R| < 0.8.
- If |R| evaluated to be < 0.2, that depicts a weak correlation among the actual and predicted values.
- |R| has to be larger than 0.8 to maintain a strong correlation between expected and actual values.
3. Results and Discussion
3.1. Mechanical Properties and Formulation
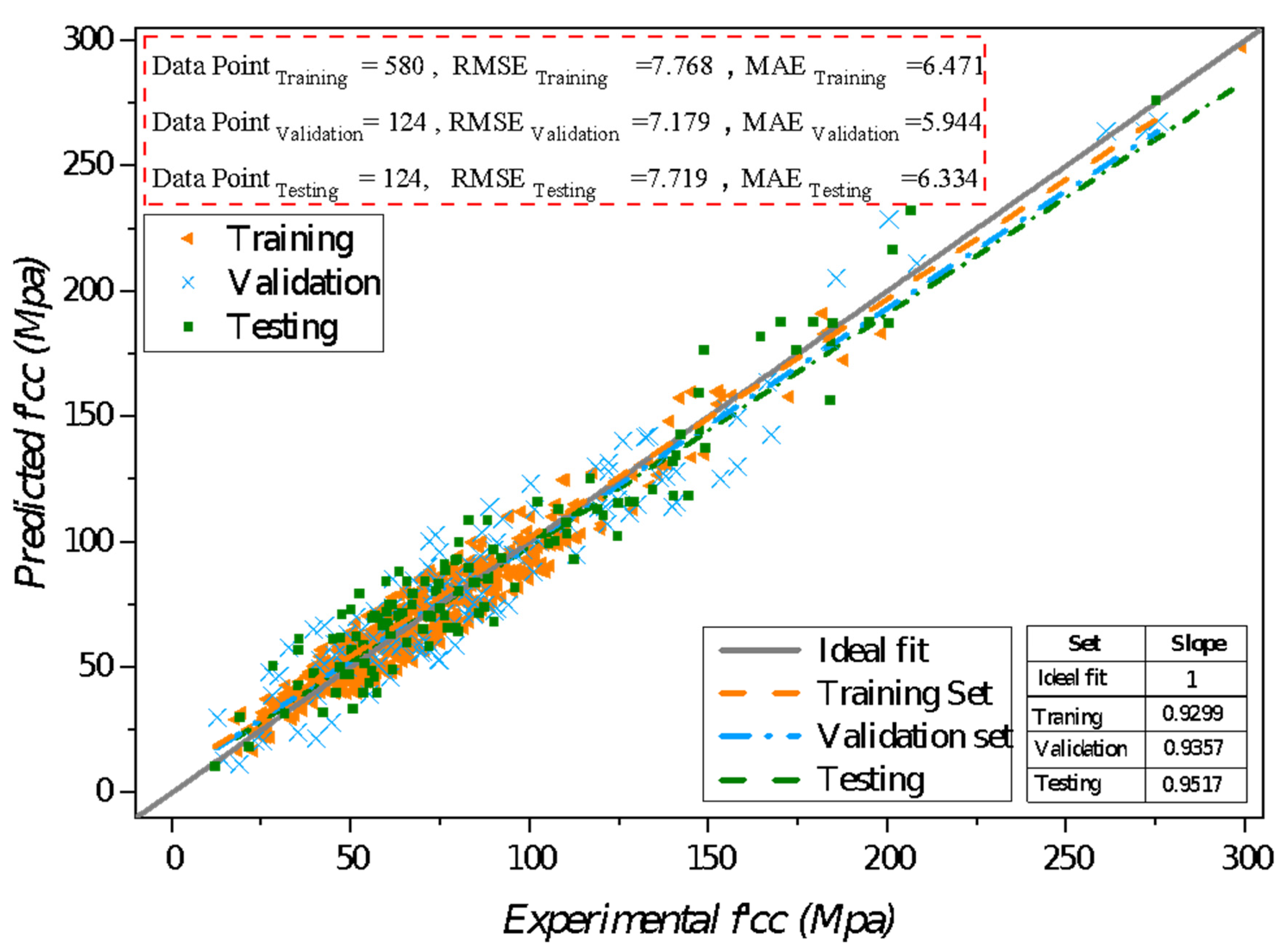
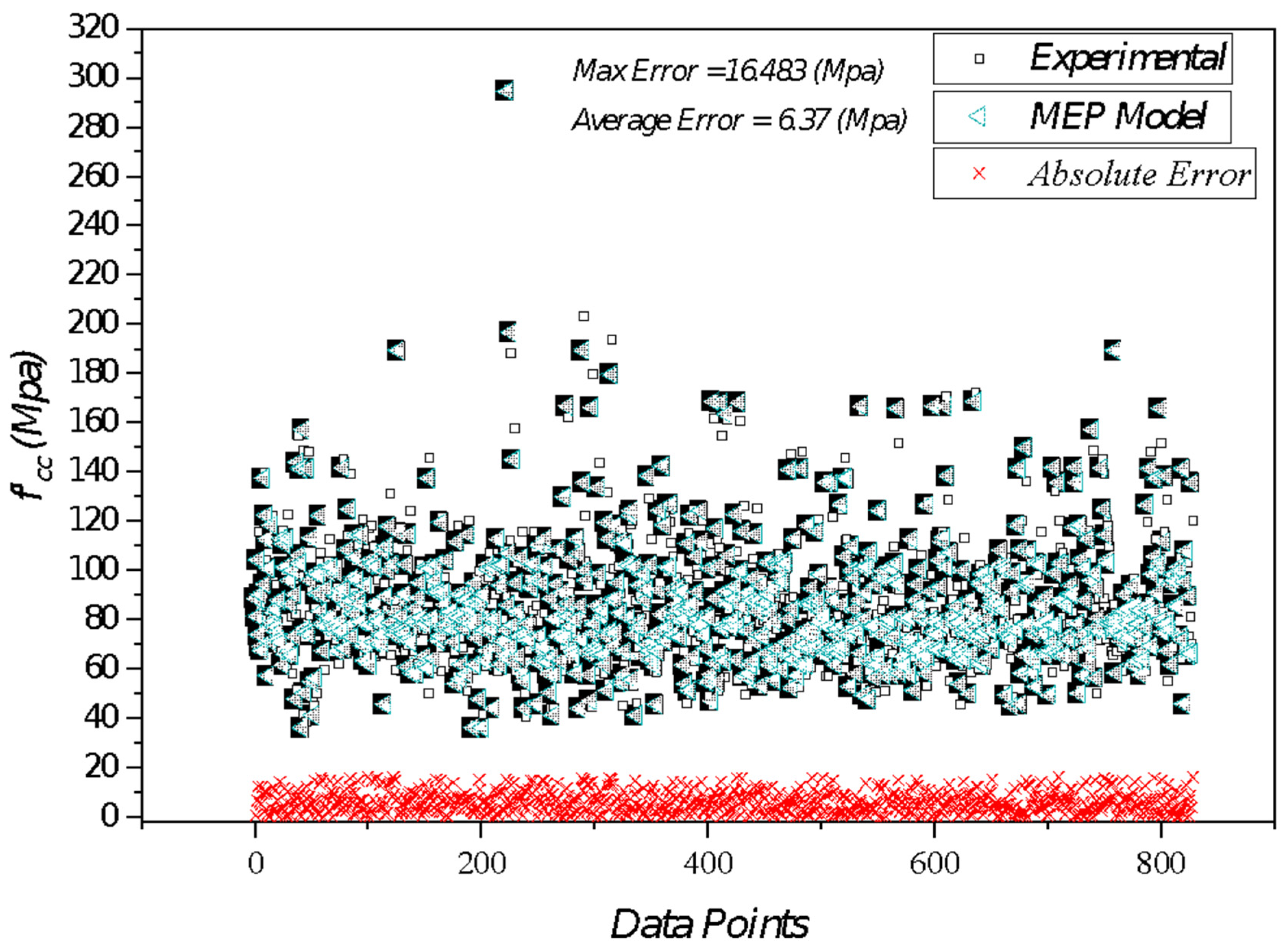
3.2. Model Performance and Evaluation:
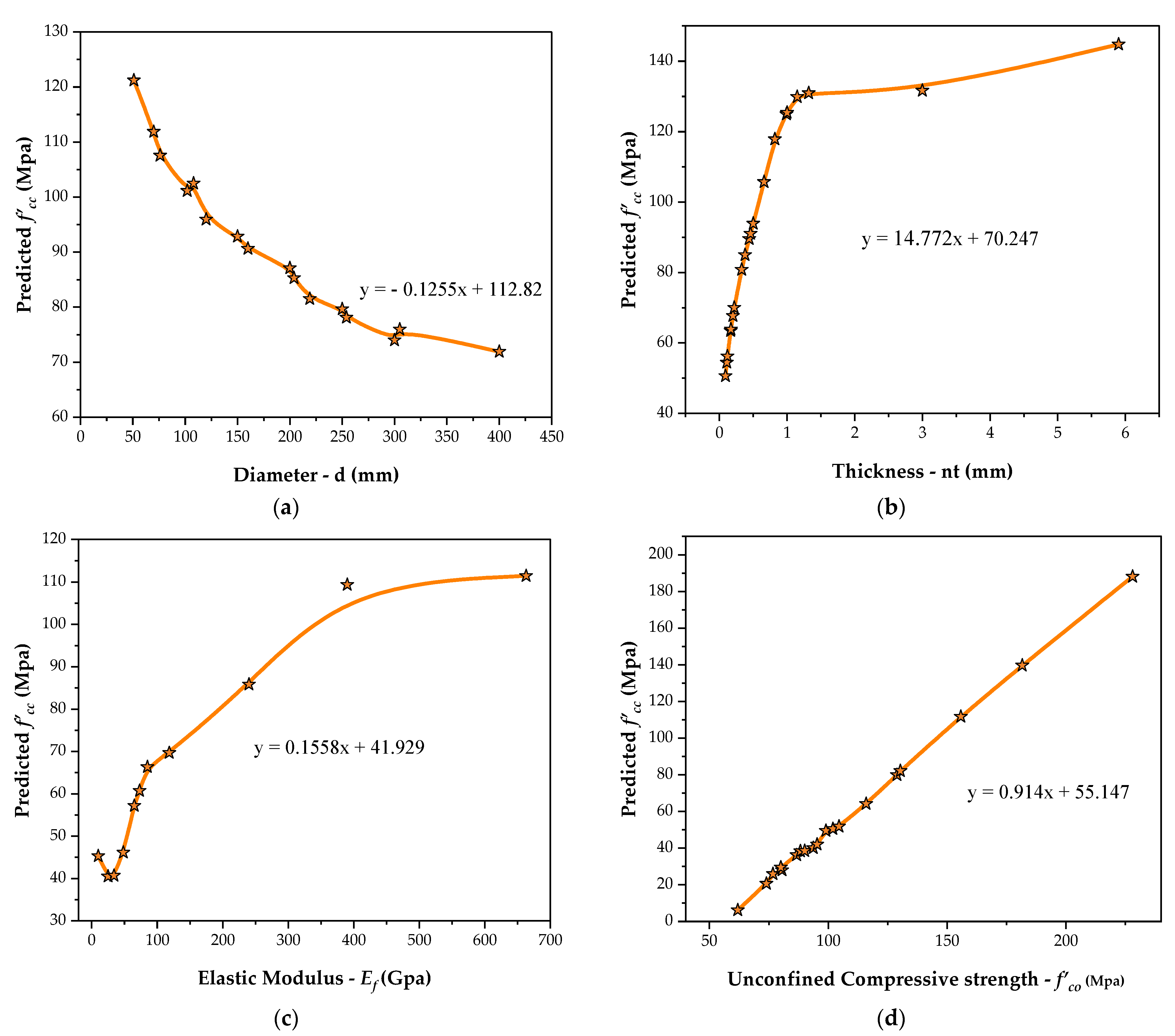
3.3. Parametric Analysis
- (i)
- Material properties such as modulus of elasticity (E) of FRP, unconfined concrete (f′co) strength;
- (ii)
- Geometric properties such as thickness (nt) of FRP composites, and cylinder diameter (d).
3.3.1. Effect of Diameter (d)
3.3.2. Effect of Thickness of FRP Layers (nt)
3.3.3. Effect of Elastic Modulus of FRP (Ef)
3.3.4. Effect of Concrete Compressive Strength (f′co)
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kawashima, K.; Shoji, G.; Sakakibara, Y. A cyclic loading test for clarifying the plastic hinge length of reinforced concrete piers. J. Struct. Eng. A 2000, 46, 767–776. [Google Scholar]
- Takemura, H.K.K. Effect of loading hysteresis on ductility capacity of reinforced concrete bridge piers. J. Struct Eng. 1997, 43, 849–858. [Google Scholar]
- Hoshikuma, J.; Kawashima, K.; Nagaya, K.; Taylor, A.W. Stress-Strain Model for Confined Reinforced Concrete in Bridge Piers. J. Struct. Eng. 1997, 123, 624–633. [Google Scholar] [CrossRef]
- Sheikh, S.A.; Toklucu, M.T. Reinforced concrete columns confined by circular spirals and hoops. ACI Struct. J. 1993, 90, 542. [Google Scholar]
- Li, G.; Kidane, S.; Pang, S.-S.; Helms, J.; Stubblefield, M. Investigation into FRP repaired RC columns. Compos. Struct. 2003, 62, 83–89. [Google Scholar] [CrossRef]
- Delgado, P.; Arêde, A.; Pouca, N.V.; Rocha, P.; Costa, A.; Delgado, R. Retrofit of RC hollow piers with CFRP sheets. Compos. Struct. 2012, 94, 1280–1287. [Google Scholar] [CrossRef]
- Castillo, E.; Griffith, M.; Ingham, J. Seismic behavior of RC columns flexurally strengthened with FRP sheets and FRP anchors. Compos. Struct 2018, 203, 382–395. [Google Scholar] [CrossRef]
- Salawu, O.S.; Williams, C. Review of full-scale dynamic testing of bridge columns. Eng. Struct. 1993, 17, 113–121. [Google Scholar] [CrossRef]
- Cheok, G.S. Behavior of 1/6-scale model bridge columns subjected to inelastic cyclic loading. Struct. J. 1990, 87, 630–638. [Google Scholar]
- Tang, Y.; Fang, S.; Chen, J.; Ma, L.; Li, L.; Wu, X. Axial compression behavior of recycled-aggregate-concrete-filled GFRP–steel composite tube columns. Eng. Struct. 2020, 216, 110676. [Google Scholar] [CrossRef]
- Ruggieri, S.; Cardellicchio, A.; Leggieri, V.; Uva, G. Machine-learning based vulnerability analysis of existing buildings. Autom. Constr. 2021, 132, 103936. [Google Scholar] [CrossRef]
- Mangalathu, S.; Sun, H.; Nweke, C.; Yi, Z.; Burton, H.V. Classifying earthquake damage to buildings using machine learning. Earthq. Spectra 2020, 36, 183–208. [Google Scholar] [CrossRef]
- Xie, Y.; Sichani, M.E.; Padgett, J.; Desroches, R. The promise of implementing machine learning in earthquake engineering: A state-of-the-art review. Earthq. Spectra 2020, 36, 1769–1801. [Google Scholar] [CrossRef]
- Yumashev, A.; Ślusarczyk, B.; Kondrashev, S.; Mikhaylov, A. Global Indicators of Sustainable Development: Evaluation of the Influence of the Human Development Index on Consumption and Quality of Energy. Energies 2020, 13, 2768. [Google Scholar] [CrossRef]
- Nie, D.; Panfilova, E.; Samusenkov, V.; Mikhaylov, A. E-Learning Financing Models in Russia for Sustainable Development. Sustainability 2020, 12, 4412. [Google Scholar] [CrossRef]
- Bagheri, M.; He, X.; Oustriere, N.; Liu, W.; Shi, H.; Limmer, M.A.; Burken, J.G. Investigating plant uptake of organic contaminants through transpiration stream concentration factor and neural network models. Sci. Total Environ. 2021, 751, 141418. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Chen, L.; Tsang, D.C.; Guo, B.; Yang, J.; Shen, Z.; Hou, D.; Ok, Y.S.; Poon, C.S. Biochar as green additives in cement-based composites with carbon dioxide curing. J. Clean. Prod. 2020, 258, 120678. [Google Scholar] [CrossRef]
- Wang, F.; Song, G.; Mo, Y. Shear loading detection of through bolts in bridge structures using a percussion-based one-dimensional memory-augmented convolutional neural network. Comput. Civ. Infrastruct. Eng. 2021, 36, 289–301. [Google Scholar] [CrossRef]
- Ashteyat, A.; Obaidat, Y.T.; Murad, Y.Z.; Haddad, R. Compressive strength prediction of lightweight short columns at elevated temperature using gene expression programing and artificial neural network. J. Civ. Eng. Manag. 2020, 26, 189–199. [Google Scholar] [CrossRef]
- Getahun, M.A.; Shitote, S.M.; Gariy, Z.C.A. Artificial neural network based modelling approach for strength prediction of concrete incorporating agricultural and construction wastes. Constr. Build. Mater. 2018, 190, 517–525. [Google Scholar] [CrossRef]
- Golafshani, E.M.; Behnood, A.; Arashpour, M. Predicting the compressive strength of normal and High-Performance Concretes using ANN and ANFIS hybridized with Grey Wolf Optimizer. Constr. Build. Mater. 2020, 232, 117266. [Google Scholar] [CrossRef]
- Nguyen, T.; Kashani, A.; Ngo, T.; Bordas, S. Deep neural network with high-order neuron for the prediction of foamed concrete strength. Comput. Civ. Infrastruct. Eng. 2019, 34, 316–332. [Google Scholar] [CrossRef]
- Sadrmomtazi, A.; Sobhani, J.; Mirgozar, M. Modeling compressive strength of EPS lightweight concrete using regression, neural network and ANFIS. Constr. Build. Mater. 2013, 42, 205–216. [Google Scholar] [CrossRef]
- Öztaş, A.; Pala, M.; Özbay, E.; Kanca, E.; Caglar, N.; Bhatti, M.A. Predicting the compressive strength and slump of high strength concrete using neural network. Constr. Build. Mater. 2006, 20, 769–775. [Google Scholar] [CrossRef]
- Liu, Y.; Zhuge, Y.; Chow, C.W.; Keegan, A.; Pham, P.N.; Li, D.; Qian, G.; Wang, L. Recycling drinking water treatment sludge into eco-concrete blocks with CO2 curing: Durability and leachability. Sci. Total Environ. 2020, 746, 141182. [Google Scholar] [CrossRef] [PubMed]
- Liu, Q.-F.; Hu, Z.; Lu, X.-Y.; Yang, J.; Azim, I.; Sun, W. Prediction of Chloride Distribution for Offshore Concrete Based on Statistical Analysis. Materials 2020, 13, 174. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ghanizadeh, A.R.; Abbaslou, H.; Amlashi, A.T.; Alidoust, P. Modeling of bentonite/sepiolite plastic concrete compressive strength using artificial neural network and support vector machine. Front. Struct. Civ. Eng. 2019, 13, 215–239. [Google Scholar] [CrossRef]
- Khademi, F.; Akbari, M.; Jamal, S.M.; Nikoo, M. Multiple linear regression, artificial neural network, and fuzzy logic prediction of 28 days compressive strength of concrete. Front. Struct. Civ. Eng. 2017, 11, 90–99. [Google Scholar] [CrossRef]
- Reddy, T.C.S. Engineering, Predicting the strength properties of slurry infiltrated fibrous concrete using artificial neural network. Front. Struct. Civ. Eng. 2018, 12, 490–503. [Google Scholar] [CrossRef]
- Mansouri, I.; Gholampour, A.; Kisi, O.; Ozbakkaloglu, T. Evaluation of peak and residual conditions of actively confined concrete using neuro-fuzzy and neural computing techniques. Neural Comput. Appl. 2018, 29, 873–888. [Google Scholar] [CrossRef]
- Mansouri, I.; Kisi, O.; Sadeghian, P.; Lee, C.-H.; Hu, J.W. Prediction of Ultimate Strain and Strength of FRP-Confined Concrete Cylinders Using Soft Computing Methods. Appl. Sci. 2017, 7, 751. [Google Scholar] [CrossRef] [Green Version]
- Mozumder, R.A.; Roy, B.; Laskar, A.I. Support Vector Regression Approach to Predict the Strength of FRP Confined Concrete. Arab. J. Sci. Eng. 2016, 42, 1129–1146. [Google Scholar] [CrossRef]
- Cascardi, A.; Micelli, F.; Aiello, M.A. An Artificial Neural Networks model for the prediction of the compressive strength of FRP-confined concrete circular columns. Eng. Struct 2017, 140, 199–208. [Google Scholar] [CrossRef]
- Camoes, A.; Martins, F.F. Compressive strength prediction of CFRP confined concrete using data mining techniques. Comput. Concr. 2017, 19, 233–241. [Google Scholar] [CrossRef]
- Pham, T.M.; Hao, H. Axial Impact Resistance of FRP-Confined Concrete. J. Compos. Constr. 2017, 21, 04016088. [Google Scholar] [CrossRef] [Green Version]
- Cevik, A.; Cabalar, A.F. A genetic-programming-based formulation for the strength enhancement of fiber-reinforced-polymer-confined concrete cylinders. J. Appl. Polym. Sci. 2008, 110, 3087–3095. [Google Scholar] [CrossRef]
- Cevik, A.; Guzelbey, I.H. Neural network modeling of strength enhancement for CFRP confined concrete cylinders. Build. Environ. 2008, 43, 751–763. [Google Scholar] [CrossRef]
- Cevik, A.; Göğüş, M.T.; Güzelbey, I.H.; Filiz, H. Soft computing based formulation for strength enhancement of CFRP confined concrete cylinders. Adv. Eng. Softw. 2010, 41, 527–536. [Google Scholar] [CrossRef]
- Naderpour, H.; Kheyroddin, A.; Amiri, G.G. Prediction of FRP-confined compressive strength of concrete using artificial neural networks. Compos. Struct. 2010, 92, 2817–2829. [Google Scholar] [CrossRef]
- Wu, Y.-B.; Jin, G.-F.; Ding, T.; Meng, D. Modeling Confinement Efficiency of FRP-Confined Concrete Column Using Radial Basis Function Neural Network. In Proceedings of the 2010 2nd International Workshop on Intelligent Systems and Applications, Wuhan, China, 22–23 May 2010; pp. 1–6. [Google Scholar]
- Cevik, A. Modeling strength enhancement of FRP confined concrete cylinders using soft computing. Expert Syst. Appl. 2011, 38, 5662–5673. [Google Scholar] [CrossRef]
- Oreta, A.W.; Ongpeng, J. Ongpeng, and Concrete, Modeling the confined compressive strength of hybrid circular concrete columns using neural networks. Comput. Concr. 2011, 8, 597–616. [Google Scholar] [CrossRef]
- Elsanadedy, H.; Al-Salloum, Y.; Abbas, H.; Alsayed, S. Prediction of strength parameters of FRP-confined concrete. Compos. Part B Eng. 2012, 43, 228–239. [Google Scholar] [CrossRef]
- Jalal, M.; Ramezanianpour, A.A. Strength enhancement modeling of concrete cylinders confined with CFRP composites using artificial neural networks. Compos. Part B Eng. 2012, 43, 2990–3000. [Google Scholar] [CrossRef]
- Mashrei, M.A.; Seracino, R.; Rahman, M. Application of artificial neural networks to predict the bond strength of FRP-to-concrete joints. Constr. Build. Mater. 2013, 40, 812–821. [Google Scholar] [CrossRef]
- Pham, T.M.; Hadi, M.N. Predicting stress and strain of FRP-confined square/rectangular columns using artificial neural networks. J. Compos. Constr. 2014, 18, 04014019. [Google Scholar] [CrossRef] [Green Version]
- Oltean, M.; Groşan, C. Evolving Evolutionary Algorithms Using Multi Expression Programming. In Tools and Algorithms for the Construction and Analysis of Systems; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2003; pp. 651–658. [Google Scholar]
- Faris, H.; Mirjalili, S.; Aljarah, I. Automatic selection of hidden neurons and weights in neural networks using grey wolf optimizer based on a hybrid encoding scheme. Int. J. Mach. Learn. Cybern. 2019, 10, 2901–2920. [Google Scholar] [CrossRef]
- Azim, I.; Yang, J.; Javed, M.F.; Iqbal, M.F.; Mahmood, Z.; Wang, F.; Liu, Q.-F. Prediction model for compressive arch action capacity of RC frame structures under column removal scenario using gene expression programming. Structures 2020, 25, 212–228. [Google Scholar] [CrossRef]
- Aval, S.B.; Ketabdari, H.; Gharebaghi, S.A. Estimating Shear Strength of Short Rectangular Reinforced Concrete Columns Using Nonlinear Regression and Gene Expression Programming. Structures 2017, 12, 13–23. [Google Scholar] [CrossRef]
- Ferreira, C. Gene Expression Programming: Mathematical Modeling by an Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Hashmi, M.Z.; Shamseldin, A.Y.; Melville, B.W. Statistical downscaling of watershed precipitation using Gene Expression Programming (GEP). Environ. Model. Softw. 2011, 26, 1639–1646. [Google Scholar] [CrossRef]
- Murad, Y.; Ashteyat, A.; Hunaifat, R. Predictive model to the bond strength of frp-to-concrete under direct pullout using gene expression programming. J. Civ. Eng. Manag. 2019, 25, 773–784. [Google Scholar] [CrossRef] [Green Version]
- Murad, Y.; Imam, R.; Abu Hajar, H.; Habeh, D.; Hammad, A.; Shawash, Z. Predictive compressive strength models for green concrete. Int. J. Struct. Integr. 2019, 11, 169–184. [Google Scholar] [CrossRef]
- Nazari, A.; Torgal, F.P. Modeling the compressive strength of geopolymeric binders by gene expression programming-GEP. Expert Syst. Appl. 2013, 40, 5427–5438. [Google Scholar] [CrossRef] [Green Version]
- Fardis, M.; Khalili, H.H.; Marshall, A.L. Discussion: FRP-encased concrete as a structural material. Mag. Concr. Res. 1983, 35, 242–243. [Google Scholar] [CrossRef]
- Newman, K.; Newman, J.J.S. Solid mechanics, and e. design, Failure theories and design criteria for plain concrete. Expert Syst. Appl. 1971, 11, 963–995. [Google Scholar]
- Richart, F.E.; Brandtzag, A.; Brown, R.L. The Failure of Plain and Spirally Reinforced Concrete in Compression; University of Illinois at Urbana Champaign, College of Engineering: Champaign, IL, USA, 1929. [Google Scholar]
- Karbhari, V.M.; Gao, Y. Composite Jacketed Concrete under Uniaxial Compression—Verification of Simple Design Equations. J. Mater. Civ. Eng. 1997, 9, 185–193. [Google Scholar] [CrossRef]
- Samaan, M.; Mirmiran, A.; Shahawy, M. Model of Concrete Confined by Fiber Composites. J. Struct. Eng. 1998, 124, 1025–1031. [Google Scholar] [CrossRef]
- Saafi, M.; Toutanji, H.; Li, Z. Behavior of concrete columns confined with fiber reinforced polymer tubes. Mater. J. 1999, 96, 500–509. [Google Scholar]
- Lam, L.; Teng, J. Design-oriented stress–strain model for FRP-confined concrete. Constr. Build. Mater. 2003, 17, 471–489. [Google Scholar] [CrossRef]
- Mander, J.B.; Priestley, M.J.N.; Park, R. Theoretical Stress-Strain Model for Confined Concrete. J. Struct. Eng. 1988, 114, 1804–1826. [Google Scholar] [CrossRef] [Green Version]
- Bisby, L.A.; Dent, A.J.S.; Green, M.F. Comparison of confinement models for fiber reinforced polymer-wrapped concrete. ACI Struct J. 2005, 102, 62–72. [Google Scholar]
- Matthys, S. Axial load behavior of large-scale columns confined with fiber reinforced polymer composites. ACI Struct J. 2005, 102, 258. [Google Scholar]
- Shehata, I.A.E.M.; Carneiro, L.A.V.; Shehata, L.C.D. Strength of confined short concrete columns. In Proceedings of the 8th International Symposium on Fiber Reinforced Polymer Reinforcement for Concrete Structures; University of Patras: Patras, Greece, 2007. [Google Scholar]
- Al-Salloum, Y.; Siddiqui, N. Compressive strength prediction model for FRP confined concrete. In Proceedings, Ninth International Symposium on Fiber Reinforced Polymer Reinforcement for Concrete Structures; The University of Adelaide: Sydney, Australia, 2009. [Google Scholar]
- Teng, J.G.; Jiang, T.; Lam, L.; Luo, Y.Z. Refinement of a Design-Oriented Stress–Strain Model for FRP-Confined Concrete. J. Compos. Constr. 2009, 13, 269–278. [Google Scholar] [CrossRef] [Green Version]
- Realfonzo, R.; Napoli, A. Concrete confined by FRP systems: Confinement efficiency and design strength models. Compos. Part B Eng. 2011, 42, 736–755. [Google Scholar] [CrossRef]
- Oltean, M.; Grosan, C. A comparison of several linear genetic programming techniques. Complex. Syst. 2004, 14, 285–313. [Google Scholar]
- Arabshahi, A.; Gharaei-Moghaddam, N.; Tavakkolizadeh, M. Development of applicable design models for concrete columns confined with aramid fiber reinforced polymer using Multi-Expression Programming. Structures 2020, 23, 225–244. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Fogel, L.J.; Owens, A.J.; Walsh, M.J. Artificial Intelligence through Simulated Evolution; John Wiley & Sons: Hoboken, NJ, USA, 1966. [Google Scholar]
- Koza, J.R. Genetic Programming: On the Programming of Computers by Means of Natural Selection; MIT Press: Cambridge, MA, USA, 1992; pp. 17–63. [Google Scholar]
- Oltean, M.; Dumitrescu, D. Multi expression programming. J. Genet. Program. Evolvable Mach. Kluwer Second. Tour Rev. 2002. [Google Scholar]
- Oltean, M.; Dumitrescu, D. Evolving TSP Heuristics Using Multi Expression Programming. Comput. Vis. 2004, 670–673. [Google Scholar] [CrossRef] [Green Version]
- Alavi, A.H.; Gandomi, A.H.; Sahab, M.G.; Gandomi, M. Multi expression programming: A new approach to formulation of soil classification. Eng. Comput. 2010, 26, 111–118. [Google Scholar] [CrossRef]
- Gandomi, A.; Faramarzifar, A.; Rezaee, P.G.; Asghari, A.; Talatahari, S. New design equations for elastic modulus of concrete using multi expression programming. J. Civ. Eng. Manag. 2015, 21, 761–774. [Google Scholar] [CrossRef] [Green Version]
- Azim, I.; Yang, J.; Iqbal, M.F.; Javed, M.F.; Nazar, S.; Wang, F.; Liu, Q.-F. Semi-analytical model for compressive arch action capacity of RC frame structures. Structures 2020, 27, 1231–1245. [Google Scholar] [CrossRef]
- Azim, I.; Yang, J.; Iqbal, M.F.; Mahmood, Z.; Javed, M.F.; Wang, F.; Liu, Q.-F. Prediction of Catenary Action Capacity of RC Beam-Column Substructures under a Missing Column Scenario Using Evolutionary Algorithm. KSCE J. Civ. Eng. 2021, 25, 891–905. [Google Scholar] [CrossRef]
- Sharifi, S.; Abrishami, S.; Gandomi, A.H. Consolidation assessment using Multi Expression Programming. Appl. Soft Comput. 2020, 86, 105842. [Google Scholar] [CrossRef]
- Alavi, A.H.; Mollahasani, A.; Gandomi, A.H.; Bazaz, J.B. Formulation of Secant and Reloading Soil Deformation Moduli Using Multi Expression Programming. Eng. Comput. 2012, 11, 124. [Google Scholar]
- Gandomi, A.; Alavi, A.H.; MirzaHosseini, M.R.; Nejad, F.M. Nonlinear Genetic-Based Models for Prediction of Flow Number of Asphalt Mixtures. J. Mater. Civ. Eng. 2011, 23, 248–263. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Alavi, A.H.; Yun, G.J. Formulation of uplift capacity of suction caissons using multi expression programming. KSCE J. Civ. Eng. 2011, 15, 363–373. [Google Scholar] [CrossRef]
- Zhang, Q.; Yang, B.; Wang, L.; Zhu, F. Predicting Cement Compressive Strength Using Double-Layer Multi-expression Programming. In Proceedings of the 2012 Fourth International Conference on Computational and Information Sciences, Chongqing, China, 17–19 August 2012; pp. 94–97. [Google Scholar]
- Elwell, D.J.; Fu, G. Compression Testing of Concrete: Cylinders vs. Cubes; Newyork State Department of Transportation: New York, NY, USA, 1995. [Google Scholar]
- Smith, G.N. Probability and statistics in civil engineering. Collins Prof. Tech. Books 1986, 244, 145. [Google Scholar]
- Mousavi, S.; Alavi, A.H.; Gandomi, A.; Esmaeili, M.A.; Gandomi, M. A data mining approach to compressive strength of CFRP-confined concrete cylinders. Struct. Eng. Mech. 2010, 36, 759–783. [Google Scholar] [CrossRef]
- Qiu, R.; Wang, Y.; Wang, D.; Qiu, W.; Wu, J.; Tao, Y. Water temperature forecasting based on modified artificial neural network methods: Two cases of the Yangtze River. Sci. Total Environ. 2020, 737, 139729. [Google Scholar] [CrossRef]
- Pyo, J.; Hong, S.M.; Kwon, Y.S.; Kim, M.S.; Cho, K.H. Estimation of heavy metals using deep neural network with visible and infrared spectroscopy of soil. Sci. Total Environ. 2020, 741, 140162. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Babanajad, S.K.; Alavi, A.H.; Farnam, Y. Novel Approach to Strength Modeling of Concrete under Triaxial Compression. J. Mater. Civ. Eng. 2012, 24, 1132–1143. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Roke, D.A. Assessment of artificial neural network and genetic programming as predictive tools. Adv. Eng. Softw. 2015, 88, 63–72. [Google Scholar] [CrossRef]
- Sharifi, Y.; Hosseinpour, M. Adaptive neuro-fuzzy inference system and stepwise regression for compressive strength assessment of concrete containing metakaolin. Int. J. Optim. Civ. Eng. 2019, 9, 251–272. [Google Scholar]
- Tohidi, S.; Sharifi, Y. Neural networks for inelastic distortional buckling capacity assessment of steel I-beams. Thin-Walled Struct. 2015, 94, 359–371. [Google Scholar] [CrossRef]
- Hosseinpour, M.; Sharifi, H.; Sharifi, Y. Stepwise regression modeling for compressive strength assessment of mortar containing metakaolin. Int. J. Model. Simul. 2018, 38, 207–215. [Google Scholar] [CrossRef]
- Sharifi, Y.; Moghbeli, A.; Hosseinpour, M.; Sharifi, H. Neural networks for lateral torsional buckling strength assessment of cellular steel I-beams. Adv. Struct. Eng. 2019, 22, 2192–2202. [Google Scholar] [CrossRef]
- Sharifi, Y.; Moghbeli, A.; Rahmatian, M.; Moghbeli, K. Shear strength assessment of slender reinforced normal concrete beams using artificial neural networks. J. Concr. Struct. Mater. 2020, 4, 173–190. [Google Scholar]
- Smith, G.N. Probability and Statistics in Civil. Engineering; Collins: London, UK, 1986. [Google Scholar]
- Ali, M.; de Azevedo, A.; Marvila, M.; Khan, M.; Memon, A.; Masood, F.; Almahbashi, N.; Shad, M.; Khan, M.; Fediuk, R.; et al. The Influence of COVID-19-Induced Daily Activities on Health Parameters—A Case Study in Malaysia. Sustainability 2021, 13, 7465. [Google Scholar] [CrossRef]
- Despotovic, M.; Nedić, V.; Despotović, D.; Cvetanović, S. Evaluation of empirical models for predicting monthly mean horizontal diffuse solar radiation. Renew. Sustain. Energy Rev. 2016, 56, 246–260. [Google Scholar] [CrossRef]
- Roy, P.P.; Roy, K. On Some Aspects of Variable Selection for Partial Least Squares Regression Models. QSAR Comb. Sci. 2008, 27, 302–313. [Google Scholar] [CrossRef]
- Golbraikh, A.; Tropsha, A. Beware of q2! J. Mol. Graph. Model. 2002, 20, 269–276. [Google Scholar] [CrossRef]
- Gholampour, A.; Gandomi, A.; Ozbakkaloglu, T. New formulations for mechanical properties of recycled aggregate concrete using gene expression programming. Constr. Build. Mater. 2017, 130, 122–145. [Google Scholar] [CrossRef]
- Ali, M.; Abbas, S.; Salah, B.; Akhter, J.; Saleem, W.; Haruna, S.; Room, S.; Abdulkadir, I. Investigating Optimal Confinement Behaviour of Low-Strength Concrete through Quantitative and Analytical Approaches. Materials 2021, 14, 4675. [Google Scholar] [CrossRef] [PubMed]
- Ali, M.; Abbas, S.; Khan, M.I.; Gad, M.A.; Ammad, S.; Khan, A. Experimental Validation of Mander’s Model for Low Strength Confined Concrete Under Axial Compression. In Proceedings of the 2020 Second International Sustainability and Resilience Conference: Technology and Innovation in Building Designs(51154), Sakheer, Bahrain, 11–12 November 2020; pp. 1–6. [Google Scholar]
- Ziegel, E.R.; Frank, I.; Todeschini, R. Data Analysis Handbook. Technometrics 1996, 38, 193. [Google Scholar] [CrossRef]
- Gad, M.A.; Riad, A.M.; Nikbakht, E.; Ali, M.; Ghanem, G.M. Structural Behavior of Slender Reinforced Concrete Columns Wrapped with Fiber Reinforced Polymers Subjected to Eccentric Loads. In Proceedings of the 2020 Second International Sustainability and Resilience Conference: Technology and Innovation in Building Designs(51154), Sakheer, Bahrainm, 11–12 November 2020; pp. 1–5. [Google Scholar]
- Fediuk, R. High-strength fibrous concrete of Russian Far East natural materials. IOP Conf. Ser. Mater. Sci. Eng. 2016, 116, 012020. [Google Scholar] [CrossRef] [Green Version]
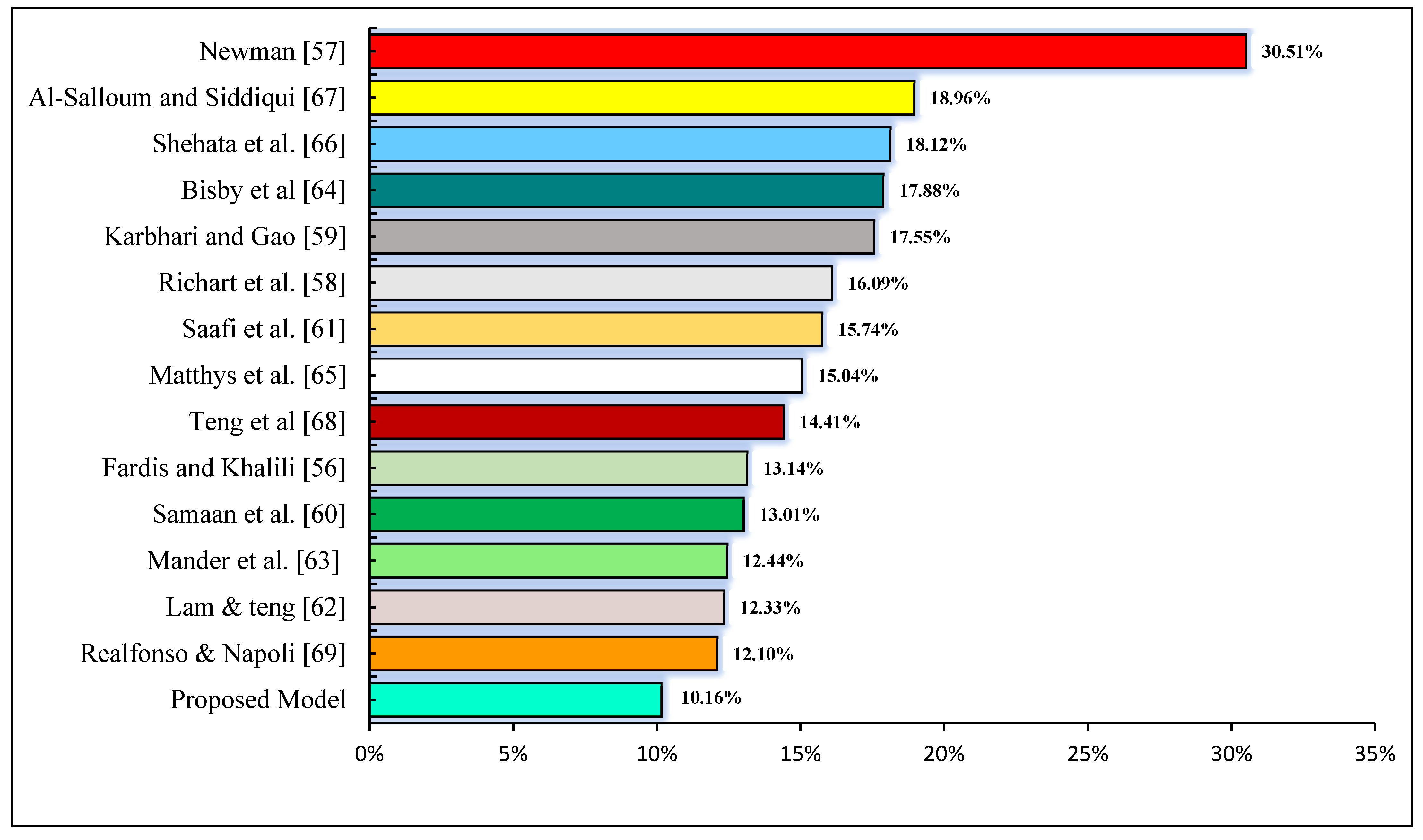
| Researcher | Year | Developed Model |
|---|---|---|
| Richart et al. [58] | 1928 | |
| Newman and Newman [57] | 1969 | |
| Fardis and Khalili [56] | 1982 | |
| Karbhari and Gao [59] | 1997 | |
| Samaan et al. [60] | 1998 | |
| - | - | thus = 0.872 + 0.371 + 6.258 |
| - | - | E2 = 245.610.2 + 1.3456 |
| Saafi et al. [61] | 1999 | |
| Lam and Teng [62] | 2003 | |
| Mander et al. [63] | 2005 | |
| Bisby et al. [64] | 2005 | |
| Matthys et al. [65] | 2006 | |
| Shehata et al. [66] | 2007 | |
| Al-Salloum and Siddiqui [67] | 2009 | |
| Teng et al. [68] | 2009 | |
| Realfonso and Napoli [69] | 2011 |
| Parameters | d | h | nt | E | f′co | f′cc | εco | εcc |
|---|---|---|---|---|---|---|---|---|
| - | (mm) | (mm) | (mm) | (Gpa) | (Mpa) | (Mpa) | (%) | (%) |
| Mean | 154.62 | 307.88 | 0.82 | 182.52 | 40.56 | 74.58 | 0.26 | 1.53 |
| Median | 152 | 304 | 0.38 | 230 | 36.3 | 66.78 | 0.24 | 1.35 |
| Mode | 150 | 300 | 0.33 | 230 | 24.5 | 63 | 0.24 | 0.95 |
| Sample Variance | 1927.85 | 7552.62 | 0.992 | 12,592.78 | 469.98 | 1125.324 | 0.0155 | 0.716 |
| Skewness | 2.71 | 2.85 | 2.355 | 0.4467 | 2.603 | 2.05988 | 7.428 | 0.957 |
| Standard Error | 1.53 | 3.02 | 0.03 | 3.899 | 0.75 | 1.17 | 0.004 | 0.031 |
| Kurtosis | 12.59 | 13.48 | 5.784 | 0.3353 | 11.696 | 8.54763 | 60.888 | 0.658 |
| Standard Deviation | 43.907 | 86.91 | 0.996 | 112.218 | 21.68 | 33.546 | 0.1246 | 0.846 |
| Minimum | 51 | 102 | 0.09 | 10 | 6.2 | 17.8 | 0.1676 | 0.083 |
| Maximum | 406 | 812 | 5.9 | 663 | 188.2 | 302.2 | 1.53 | 4.62 |
| Range | 355 | 710 | 5.81 | 653 | 182 | 284.4 | 1.3624 | 4.537 |
| - | d | h | t | E | f′co |
|---|---|---|---|---|---|
| d | 1 | 0.99 | 0.02 | 0.07 | −0.09 |
| h | 0.99 | 1 | 0.02 | 0.07 | −0.09 |
| t | 0.02 | 0.02 | 1 | −0.49 | 0.19 |
| E | 0.07 | 0.07 | −0.49 | 1 | −0.10 |
| f′co | −0.09 | −0.09 | 0.19 | −0.10 | 1 |
| Parameters | Settings |
|---|---|
| Size of subpopulations | 150 |
| Number of subpopulation | 100 |
| Mathematical operators | +, −, ×, ÷, Cosθ, Sinθ, tanθ |
| Crossover probability | 0.92 |
| Mutation probability | 0.01 |
| Variables | 0.5 |
| Operators | 0.5 |
| Number of generations | 10,000 |
| S. No. | Equation | Condition | Suggested by |
|---|---|---|---|
| 1 | (Roy and Roy, 2008) [101] | ||
| - | where | - | |
| - | - | ||
| 2 | (Golbraikh and Tropsha, 2002) [102] | ||
| 3 | [102] |
| - | RMSE | RSE | MAE | RRMSE | R | ρ | OF |
|---|---|---|---|---|---|---|---|
| Training | 7.768321 | 0.010346 | 6.471356 | 0.005 | 0.9948 | 0.002291 | 0.009156 |
| Validation | 7.17975 | 0.009859 | 5.944429 | 0.009 | 0.9950 | 0.004578 | - |
| Testing | 7.719133 | 0.009733 | 6.33431 | 0.010 | 0.9953 | 0.004921 | - |
| Database | 7.6756 | 0.0102 | 6.3719 | 0.004 | 0.9949 | 0.00189 | - |
| Sr. No. | Parameters | Sets | Database | ||
|---|---|---|---|---|---|
| Training | Validation | Testing | |||
| 1 | k | 0.991410 | 0.993896 | 1.011315 | 0.994896 |
| 2 | k′ | 0.998249 | 0.981181 | 0.979612 | 0.994932 |
| 3 | Rm | 0.889943 | 0.892999 | 0.896258 | 0.891061 |
| 4 | 0.999809 | 0.999783 | 0.999783 | 0.999802 | |
| 5 | 0.999823 | 0.999796 | 0.999794 | 0.999816 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ilyas, I.; Zafar, A.; Javed, M.F.; Farooq, F.; Aslam, F.; Musarat, M.A.; Vatin, N.I. Forecasting Strength of CFRP Confined Concrete Using Multi Expression Programming. Materials 2021, 14, 7134. https://doi.org/10.3390/ma14237134
Ilyas I, Zafar A, Javed MF, Farooq F, Aslam F, Musarat MA, Vatin NI. Forecasting Strength of CFRP Confined Concrete Using Multi Expression Programming. Materials. 2021; 14(23):7134. https://doi.org/10.3390/ma14237134
Chicago/Turabian StyleIlyas, Israr, Adeel Zafar, Muhammad Faisal Javed, Furqan Farooq, Fahid Aslam, Muhammad Ali Musarat, and Nikolai Ivanovich Vatin. 2021. "Forecasting Strength of CFRP Confined Concrete Using Multi Expression Programming" Materials 14, no. 23: 7134. https://doi.org/10.3390/ma14237134
APA StyleIlyas, I., Zafar, A., Javed, M. F., Farooq, F., Aslam, F., Musarat, M. A., & Vatin, N. I. (2021). Forecasting Strength of CFRP Confined Concrete Using Multi Expression Programming. Materials, 14(23), 7134. https://doi.org/10.3390/ma14237134










