Numerical Simulations of Laser-Induced Shock Experiments on Graphite
Abstract
1. Introduction
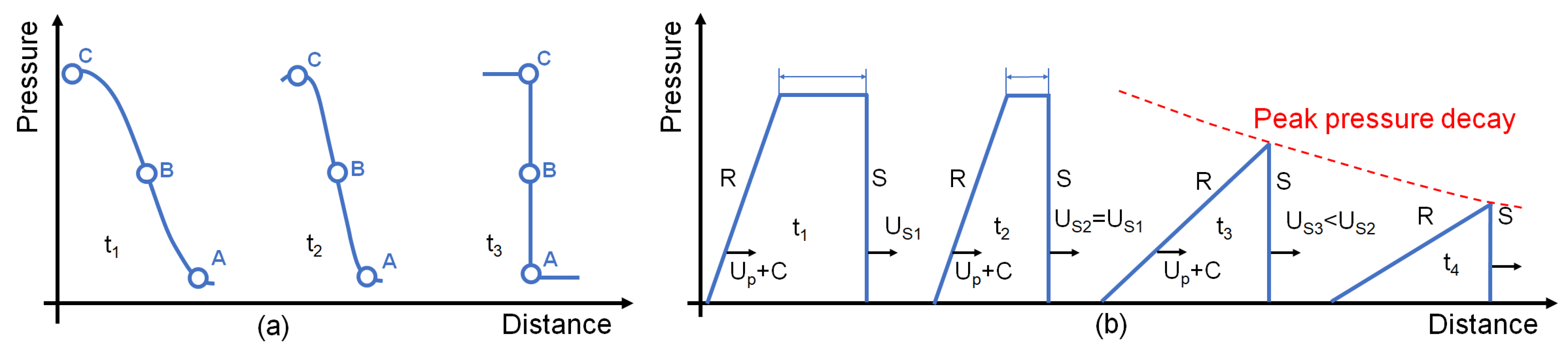
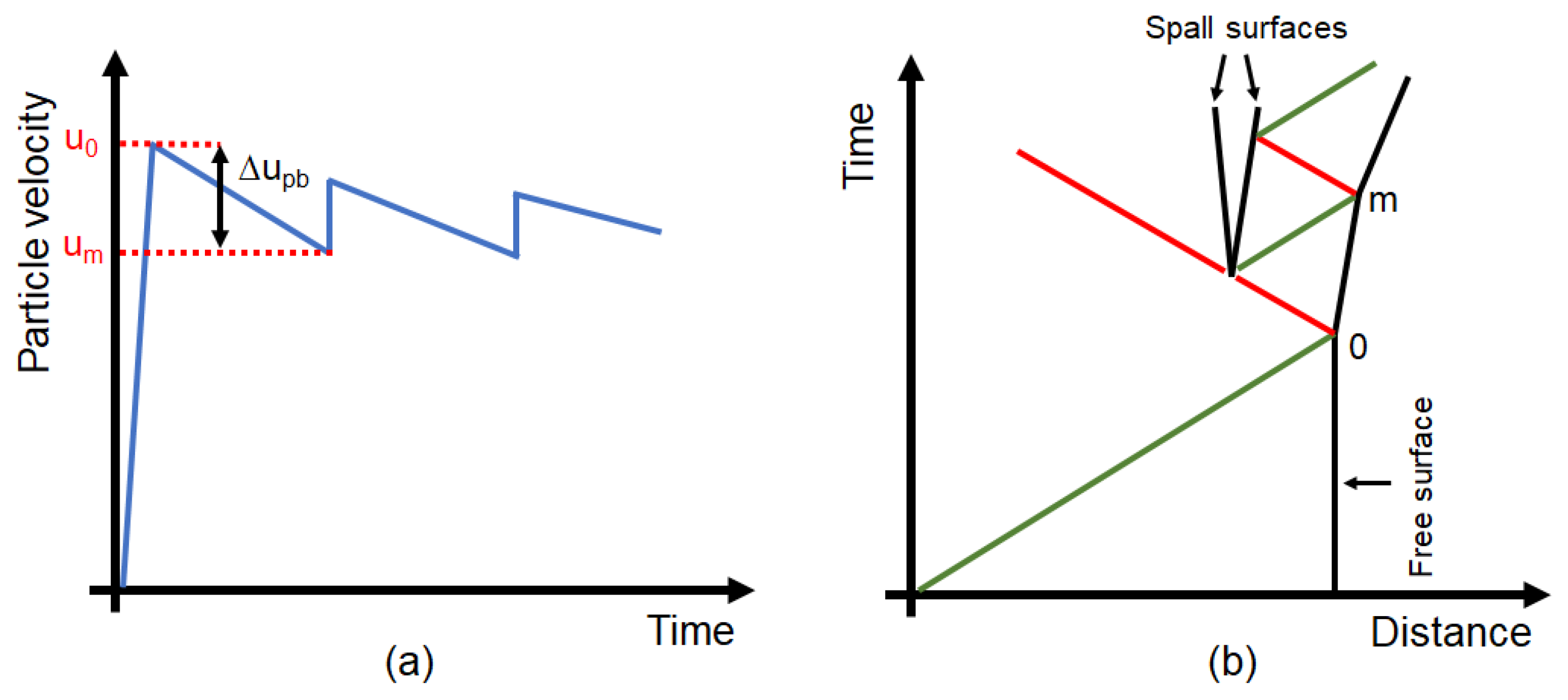
2. Laser-Induced Shockwaves in Solids
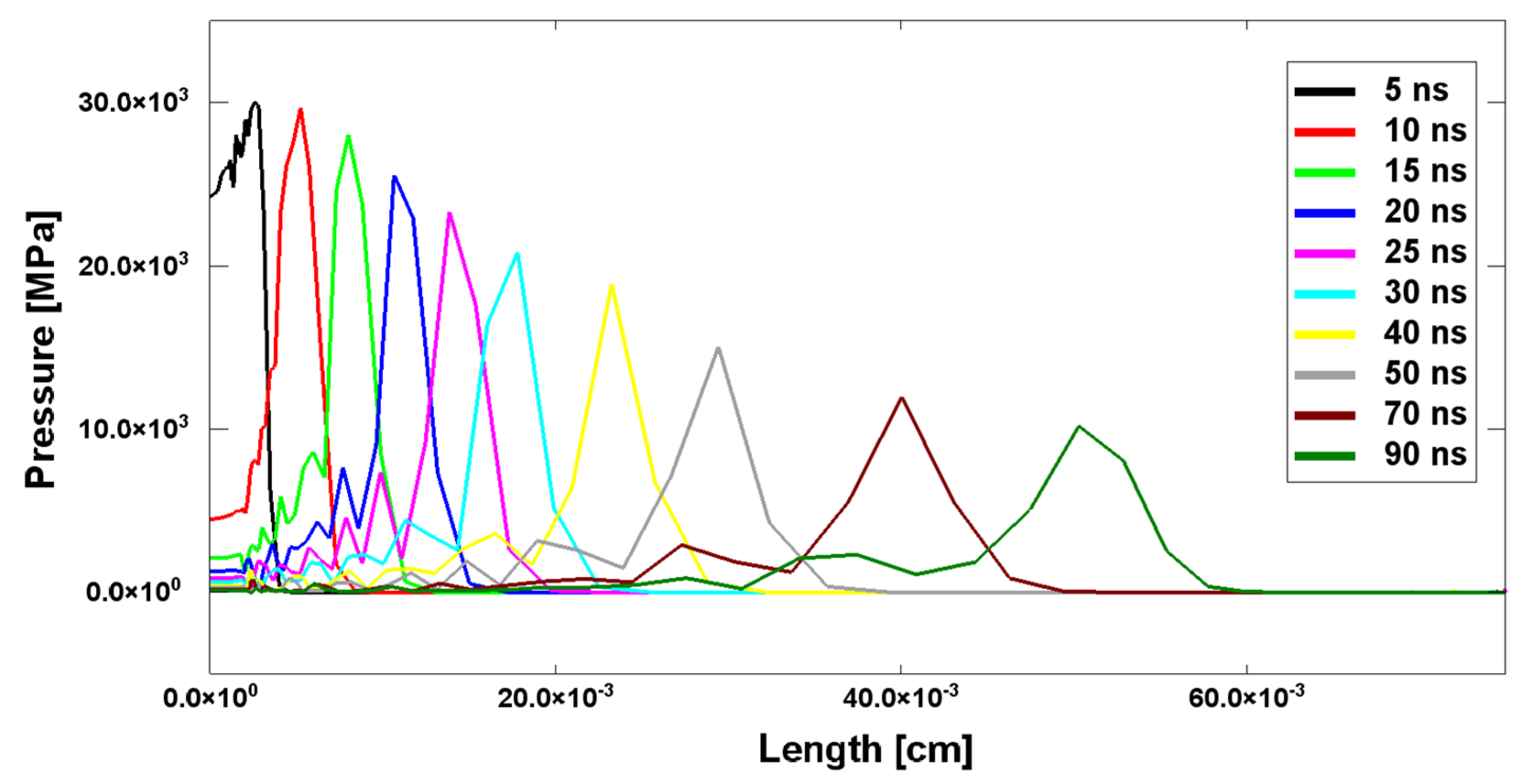
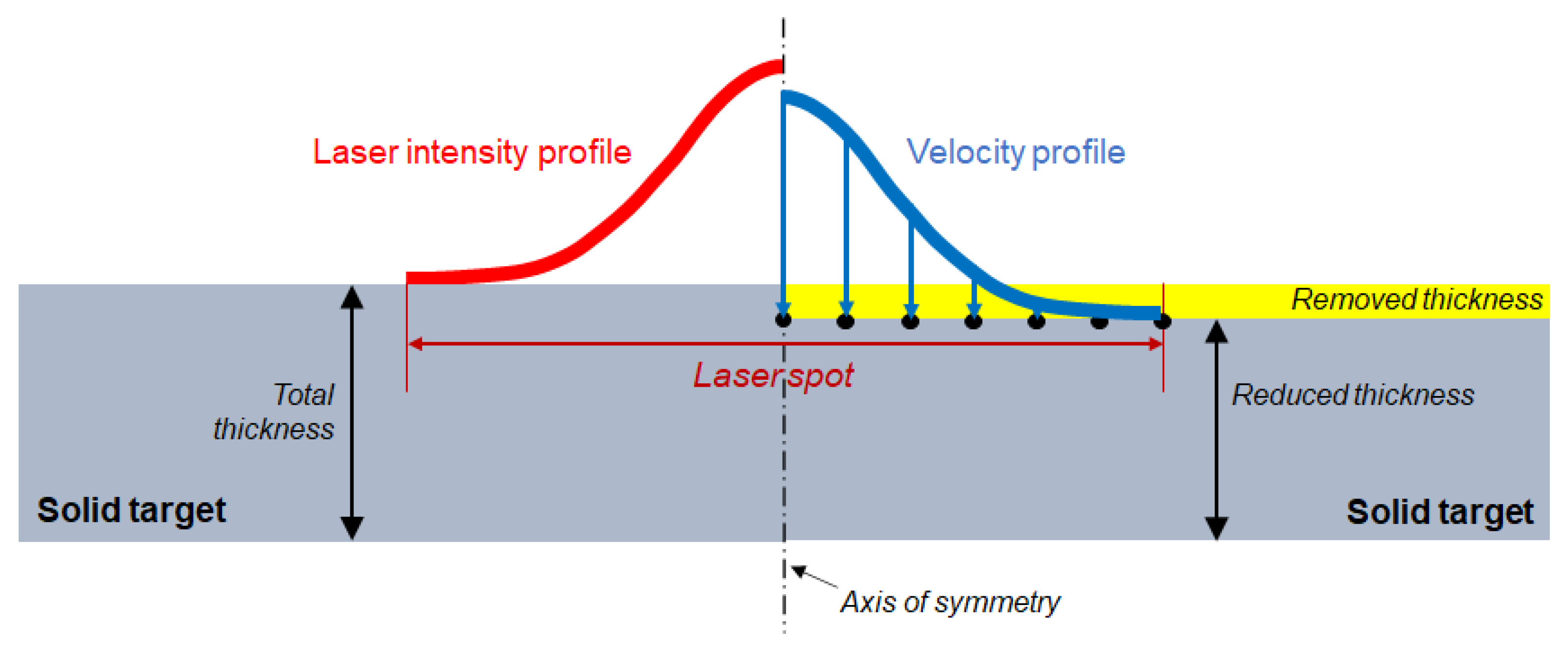
3. Numerical Simulation Case Study
4. Numerical Approach
4.1. Helios
4.2. LS-Dyna
Material Model
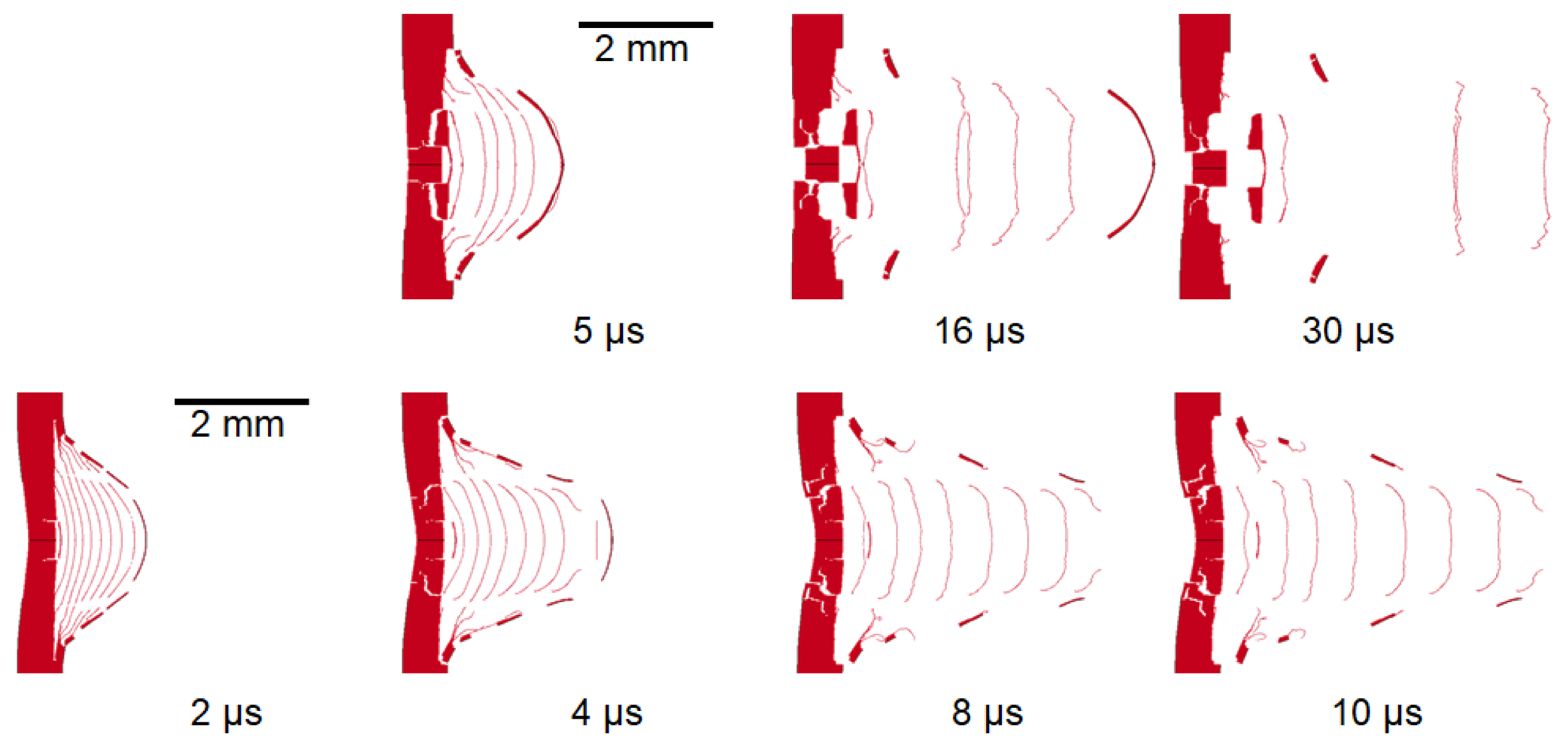
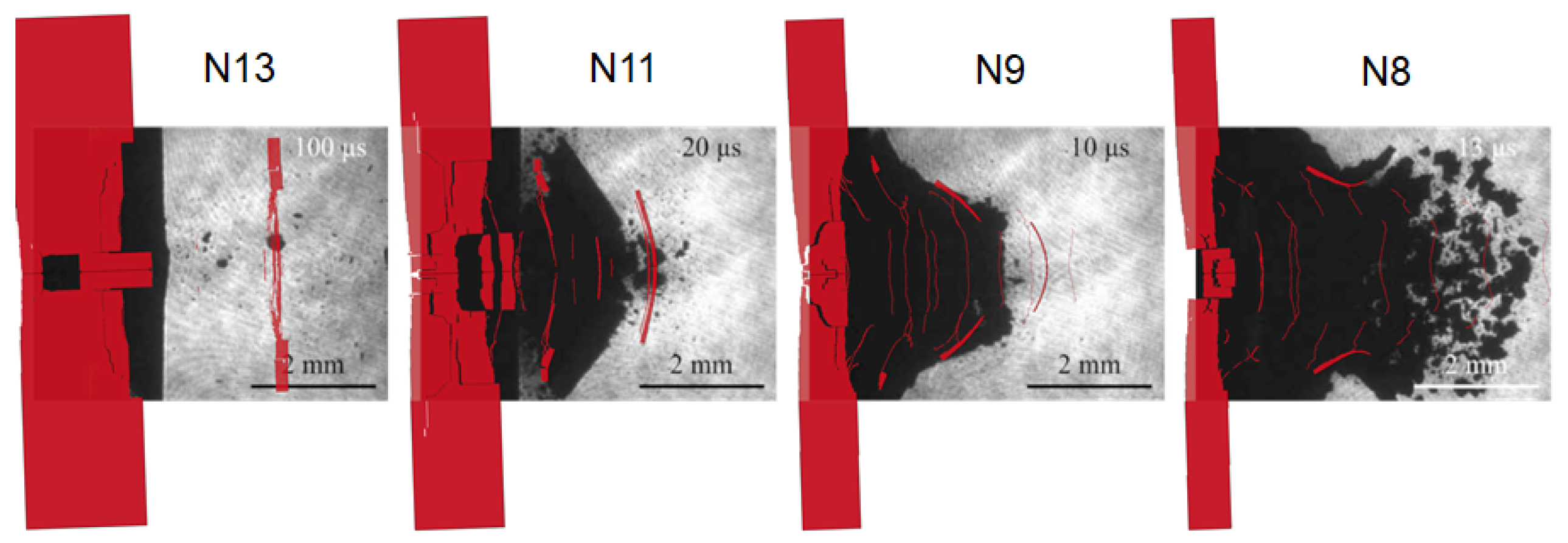
5. Results
5.1. South Beam Shots
5.2. North Beam Shots
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fox, J.A.; Barr, D.N. Laser-induced Shock Effects in Plexiglas and 6061-T6 Aluminum. Appl. Phys. Lett. 1973, 22, 594–596. [Google Scholar] [CrossRef]
- DeMichelis, C. Laser Interaction with Solids—A Bibliographical Review. IEEE J. Quantum Electron. 1970, 6, 630–641. [Google Scholar] [CrossRef]
- Sundar, R.; Ganesh, P.; Gupta, K.; Ragvendra, G.; Pant, B.K.; Kain, V.; Ranganathan, K.; Rakesh, K.; Bindra, K.S. Laser Shock Peening and Its Applications: A Review. Lasers Manuf. Mater. Process. 2019, 6, 424–463. [Google Scholar] [CrossRef]
- Berthe, L.; Arrigoni, M.; Boustie, M.; Cuq-Lelandais, J.; Broussillou, C.; Fabre, G.; Jeandin, M.; Guipont, V.; Nivard, M. State-of-the-Art Laser Adhesion Test (LASAT). Nondestruct. Test. Eval. 2011, 26, 303–317. [Google Scholar] [CrossRef]
- Steen, W.M.; Mazumder, J. Laser Material Processing; Springer: London, UK; New York, NY, USA, 2010; ISBN 9781849960625. [Google Scholar]
- Lu, Y.F.; Takai, M.; Komuro, S.; Shiokawa, T.; Aoyagi, Y. Surface Cleaning of Metals by Pulsed-Laser Irradiation in Air. Appl. Phys. A 1994, 59, 281–288. [Google Scholar] [CrossRef]
- Accelerator Research and Innovation for European Science and Society (ARIES)—CERN Web Page. Available online: https://aries.web.cern.ch/ (accessed on 8 July 2021).
- Brüning, O.S.; Collier, P.; Lebrun, P.; Myers, S.; Ostojic, R.; Poole, J.; Proudlock, P. LHC Design Report; CERN Yellow Reports: Monographs; CERN: Geneva, Switzerland, 2004. [Google Scholar]
- Apollinari, G.; Béjar Alonso, I.; Brüning, O.; Fessia, P.; Lamont, M.; Rossi, L.; Tavian, L. High-Luminosity Large Hadron Collider (HL-LHC): Technical Design Report V.0.1; CERN Yellow Reports: Geneva, Switzerland, 2017; Volume 4. [Google Scholar] [CrossRef]
- Assmann, R.; Bailey, R.; Brüning, O.; Dominguez Sanchez, O.; de Rijk, G.; Jimenez, J.M.; Myers, S.; Rossi, L.; Tavian, L.; Todesco, E.; et al. First Thoughts on a Higher-Energy LHC.; CERN: Geneva, Switzerland, 2010. [Google Scholar]
- Abada, A.; Abbrescia, M.; AbdusSalam, S.S.; Abdyukhanov, I.; Abelleira Fernandez, J.; Abramov, A.; Aburaia, M.; Acar, A.O.; Adzic, P.R.; Agrawal, P.; et al. FCC-Hh: The Hadron Collider. Eur. Phys. J. Spec. Top. 2019, 228, 755–1107. [Google Scholar] [CrossRef]
- Rossi, L. HL-LHC Preliminary Design Report: Deliverable: D1.5; CERN: Geneva, Switzerland, 2014. [Google Scholar]
- Mounet, N.; Bruce, R.; M´etral, E.; Redaelli, S.; Salvachua, B.; Salvant, B.; Valentino, G. Collimator Impedance Measurements in the LHC.; CERN: Geneva, Switzerland, 2013. [Google Scholar]
- Bertarelli, A. Beam-Induced Damage Mechanisms and Their Calculation; CERN: Geneva, Switzerland, 2016. [Google Scholar] [CrossRef]
- Carra, F.; Quaranta, E.; Bertarelli, A.; Dallocchio, A.; Garlasche, M.; Gentini, L.; Gradassi, P.; Guinchard, M.; Redaelli, S.; Rossi, A.; et al. Novel Materials for Collimators at LHC and Its Upgrades; CERN: Geneva, Switzerland, 2014. [Google Scholar]
- Gobbi, G.; Bertarelli, A.; Carra, F.; Guardia-Valenzuela, J.; Redaelli, S. Novel LHC Collimator Materials: High-Energy Hadron Beam Impact Tests and Nondestructive Postirradiation Examination. Mech. Adv. Mater. Struct. 2019, 27, 1518–1530. [Google Scholar] [CrossRef]
- Scapin, M.; Peroni, L.; Carra, F. Investigation and Mechanical Modelling of Pure Molybdenum at High Strain-Rate and Temperature. J. Dyn. Behav. Mater. 2016, 2, 460–475. [Google Scholar] [CrossRef]
- Scapin, M. Mechanical Characterization and Modeling of the Heavy Tungsten Alloy IT180. Int. J. Refract. Met. Hard Mater. 2015, 50, 258–268. [Google Scholar] [CrossRef]
- Scapin, M.; Peroni, L.; Torregrosa, C.; Perillo-Marcone, A.; Calviani, M. Effect of Strain-Rate and Temperature on Mechanical Response of Pure Tungsten. J. Dyn. Behav. Mater. 2019, 5, 296–308. [Google Scholar] [CrossRef]
- Scapin, M.; Peroni, L.; Torregrosa, C.; Perillo-Marcone, A.; Calviani, M.; Pereira, L.G.; Léaux, F.; Meyer, M. Experimental Results and Strength Model Identification of Pure Iridium. Int. J. Impact Eng. 2017, 106, 191–201. [Google Scholar] [CrossRef]
- Scapin, M.; Peroni, L.; Peroni, M. Parameters Identification in Strain-Rate and Thermal Sensitive Visco-Plastic Material Model for an Alumina Dispersion Strengthened Copper. Int. J. Impact Eng. 2012, 40–41, 58–67. [Google Scholar] [CrossRef][Green Version]
- Harden, F.J.; Bouvard, A.; Charitonidis, N.; Kadi, Y. HiRadMat: A Facility Beyond the Realms of Materials Testing. J. Phys. Conf. Ser. 2019, 1350, 012162. [Google Scholar] [CrossRef]
- Bertarelli, A.; Berthomé, E.; Boccone, V.; Carra, F.; Cerutti, F.; Charitonidis, N.; Charrondiere, C.; Dallocchio, A.; Fernandez Carmona, P.; Francon, P.; et al. An Experiment to Test Advanced Materials Impacted by Intense Proton Pulses at CERN HiRadMat Facility. Nucl. Instrum. Methods Phys. Res. A 2013, 308, 88–99. [Google Scholar] [CrossRef][Green Version]
- Bertarelli, A.; Boccone, V.; Carra, F.; Cerutti, F.; Dallocchio, A.; Mariani, N.; Peroni, L.; Scapin, M. Limits for Beam-Induced Damage: Reckless or Too Cautious? CERN: Geneva, Switzerland, 2011; pp. 183–188. [Google Scholar] [CrossRef]
- Peroni, L.; Scapin, M.; Dallocchio, A. Effects Induced by LHC High Energy Beam in Copper Structures. J. Nucl. Mater. 2011, 420, 463–472. [Google Scholar] [CrossRef]
- Krasyuk, I.K.; Semenov, A.Y.; Stuchebryukhov, I.A.; Belikov, R.S.; Khishchenko, K.V.; Rosmej, O.N.; Rienecker, T.; Schoenlein, A.; Tomut, M. Investigation of the Spall Strength of Graphite Using Nano- and Picosecond Laser Pulses. J. Phys. Conf. Ser. 2015, 653, 012002. [Google Scholar] [CrossRef]
- GSI Helmholtzzentrum Fur Schwerionenforschung GmbH Web Page–Current Laser and Experimental Parameters. Available online: https://www.gsi.de/work/forschung/appamml/plasmaphysikphelix/strahlzeit/current_laser_and_experimental_parameters (accessed on 30 August 2021).
- Seisson, G.; Prudhomme, G.; Frugier, P.-A.; Hébert, D.; Lescoute, E.; Sollier, A.; Videau, L.; Mercier, P.; Boustie, M.; Berthe, L. Dynamic Fragmentation of Graphite under Laser-Driven Shocks: Identification of Four Damage Regimes. Int. J. Impact Eng. 2016, 91, 68–79. [Google Scholar] [CrossRef]
- Phipps, C.R., Jr.; Turner, T.P.; Harrison, R.F.; York, G.W.; Osborne, W.Z.; Anderson, G.K.; Corlis, X.F.; Haynes, L.C.; Steele, H.S.; Spicochi, K.C.; et al. Impulse Coupling to Targets in Vacuum by KrF, HF, and CO2 Single-Pulse Lasers. J. Appl. Phys. 1988, 64, 1083–1096. [Google Scholar] [CrossRef]
- Fabbro, R.; Fournier, J.; Ballard, P.; Devaux, D.; Virmont, J. Physical Study of Laser-Produced Plasma in Confined Geometry. J. Appl. Phys. 1990, 68, 775–784. [Google Scholar] [CrossRef]
- Grun, J.; Decoste, R.; Ripin, B.H.; Gardner, J. Characteristics of Ablation Plasma from Planar, Laser-Driven Targets. Appl. Phys. Lett. 1981, 39, 545–547. [Google Scholar] [CrossRef]
- MacFarlane, J.J.; Golovkin, I.E.; Woodruff, P.R. HELIOS-CR—A 1-D Radiation-Magnetohydrodynamics Code with Inline Atomic Kinetics Modeling. J. Quant. Spectrosc. Radiat. Transf. 2006, 99, 381–397. [Google Scholar] [CrossRef]
- Ramis, R.; Meyer-ter-Vehn, J.; Ramirez, J. MULTI2D—A Computer Code for Two-Dimensional Radiation Hydrodynamics. Comput. Phys. Commun. 2009, 180, 977–994. [Google Scholar] [CrossRef]
- Colombier, J.P.; Combis, P.; Bonneau, F.; Le Harzic, R.; Audouard, E. Hydrodynamic Simulations of Metal Ablation by Femtosecond Laser Irradiation. Phys. Rev. B 2005, 71, 165406. [Google Scholar] [CrossRef]
- Pozdnyakov, V.; Keller, S.; Kashaev, N.; Klusemann, B.; Oberrath, J. Two-Step Simulation Approach for Laser Shock Peening. PAMM 2019, 19, e201900497. [Google Scholar] [CrossRef]
- Aubert, B.; Hebert, D.; Rullier, J.-L.; Lescoute, E.; Videau, L.; Berthe, L. 2D Characterization of the Pressure Generated by an Intense Laser Pulse on an Aluminum Target. AIP Conf. Proc. 2018, 1979, 160002. [Google Scholar] [CrossRef]
- Aubert, B.; Hebert, D.; Rullier, J.-L.; Chevalier, J.-M.; Berthe, L.; Brambrink, E.; Lescoute, E.; Videau, L.; Franzkowiak, J.-E.; Jodar, B.; et al. Numerical Simulations of Laser-Driven Cratering Experiments into Porous Graphite. EPJ Web Conf. 2018, 183, 01060. [Google Scholar] [CrossRef]
- ANSYS AUTODYN. User Manual; LSTC: Canonsburg, PA, USA, 2010. [Google Scholar]
- LS-DYNA® K. LS-DYNA® Keyword User’s Manual—Version 971; LSTC: Livermore, CA, USA, 2007; Volume I. [Google Scholar]
- Meyers, M.A. Dynamic Behavior of Materials; Wiley: Hoboken, NJ, USA, 1994; ISBN 978-0-471-58262-5. [Google Scholar]
- Zukas, J.A. High Velocity Impact Dynamics; Wiley: Hoboken, NJ, USA, 1990. [Google Scholar]
- Al’tshuler, L.V.; Divnov, I.I.; Novikov, S.A. Relationship between Critical Fracture Stresses and the Fracture Time Under Explosive Loading of Metals. Dokl. Akad. Nauk. 1966, 166, 67–70. [Google Scholar]
- Barker, L.M.; Hollenbach, R.E. Laser Interferometer for Measuring High Velocities of Any Reflecting Surface. J. Appl. Phys. 1972, 43, 4669–4675. [Google Scholar] [CrossRef]
- Neyer, B.T. Velocity Interferometer System for Any Reflector (VISAR). SPIE Proc. 1986, 0648. [Google Scholar] [CrossRef]
- Strand, O.T.; Goosman, D.R.; Martinez, C.; Whitworth, T.L.; Kuhlow, W.W. Compact System for High-Speed Velocimetry Using Heterodyne Techniques. Rev. Sci. Instrum. 2006, 77, 083108. [Google Scholar] [CrossRef]
- Naik, P.A.; Arora, V.; Prasad, Y.B.S.R.; Chakera, J.A.; Gupta, P.D. Chapter 14—Materials under Intense Laser Irradiation. In Materials Under Extreme Conditions; Tyagi, A.K., Banerjee, S., Eds.; Elsevier: Amsterdam, The Netherlands, 2017; pp. 501–532. ISBN 978-0-12-801300-7. [Google Scholar]
- Lescoute, E.; De Rességuier, T.; Chevalier, J.M.; Boustie, M.; Berthe, L.; Cuq-Lelandais, J.-P. Transverse Shadowgraphy And New Recovery Technique to Investigate Dynamic Fragmentation Of Laser Shock-Loaded Metals. AIP Conf. Proc. 2009, 1195, 1043–1046. [Google Scholar] [CrossRef]
- Amoruso, S.; Bruzzese, R.; Spinelli, N.; Velotta, R. Characterization of Laser-Ablation Plasmas. J. Phys. B: At. Mol. Opt. Phys. 1999, 32, R131–R172. [Google Scholar] [CrossRef]
- Marla, D.; Bhandarkar, U.; Joshi, S. Critical Assessment of the Issues in the Modeling of Ablation and Plasma Expansion Processes in the Pulsed Laser Deposition of Metals. J. Appl. Phys. 2011, 109, 021101. [Google Scholar] [CrossRef]
- Peroni, L.; Scapin, M.; Carra, F.; Mariani, N. Investigation of Dynamic Fracture Behavior of Graphite. Key Eng. Mater. 2013, 569–570, 103–110. [Google Scholar] [CrossRef]
- Hébert, D.; Seisson, G.; Bertron, I.; Chevalier, J.M.; Thessieux, C.; Quessada, J.H.; Tastet, S. Plate Impact Experiments and Simulation on Porous Graphite. J. Phys.: Conf. Ser. 2014, 500, 182016. [Google Scholar] [CrossRef]
- Hébert, D.; Seisson, G.; Bertron, I.; Hallo, L.; Chevalier, J.-M.; Thessieux, C.; Guillet, F.; Boustie, M.; Berthe, L. Simulations of Hypervelocity Impacts into Graphite. Procedia Eng. 2015, 103, 159–164. [Google Scholar] [CrossRef][Green Version]
- Seisson, G.; Hébert, D.; Bertron, I.; Chevalier, J.-M.; Lescoute, E.; Videau, L.; Combis, P.; Guillet, F.; Boustie, M.; Berthe, L. Dynamic Behavior of a Porous Brittle Material: Experiments and Modeling. Procedia Eng. 2013, 58, 715–723. [Google Scholar] [CrossRef][Green Version]
- Seisson, G.; Hébert, D.; Bertron, I.; Chevalier, J.-M.; Hallo, L.; Lescoute, E.; Videau, L.; Combis, P.; Guillet, F.; Boustie, M.; et al. Dynamic Cratering of Graphite: Experimental Results and Simulations. Int. J. Impact Eng. 2014, 63, 18–28. [Google Scholar] [CrossRef]
- Seisson, G.; Boustie, M.; Berthe, L.; Hébert, D. Experimental and Theoretical Study of the Damaging of Graphite under Dynamic Loading—Application to Hypervelocity Impacts, Etude expérimentale et Théorique de L’endommagement du Graphite Sous Sollicitation Dynamique—Application aux Impacts Hypervéloces; ISAE-ENSMA Ecole Nationale Supérieure de Mécanique et d’Aérotechique: Poitiers, France, 2014. [Google Scholar]
- POCO Web Page. Available online: https://poco.entegris.com/ (accessed on 28 April 2021).
- Kachur, V. Properties of ATJ Graphite; Westinghouse Electric Corp.: Pittsburgh, PA, USA, 1964. [Google Scholar] [CrossRef][Green Version]
- Marsh, P. (Ed.) Los Alamos series on dynamic material properties. In LASL Shock Hugoniot Data; University of California Press: Berkeley, CA, USA; London, UK, 1980; ISBN 0-520-04008-2. [Google Scholar]
- Hébert, D.; Seisson, G.; Rullier, J.-L.; Bertron, I.; Hallo, L.; Chevalier, J.-M.; Thessieux, C.; Guillet, F.; Boustie, M.; Berthe, L. Hypervelocity Impacts into Porous Graphite: Experiments and Simulations. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2017, 375, 20160171. [Google Scholar] [CrossRef]
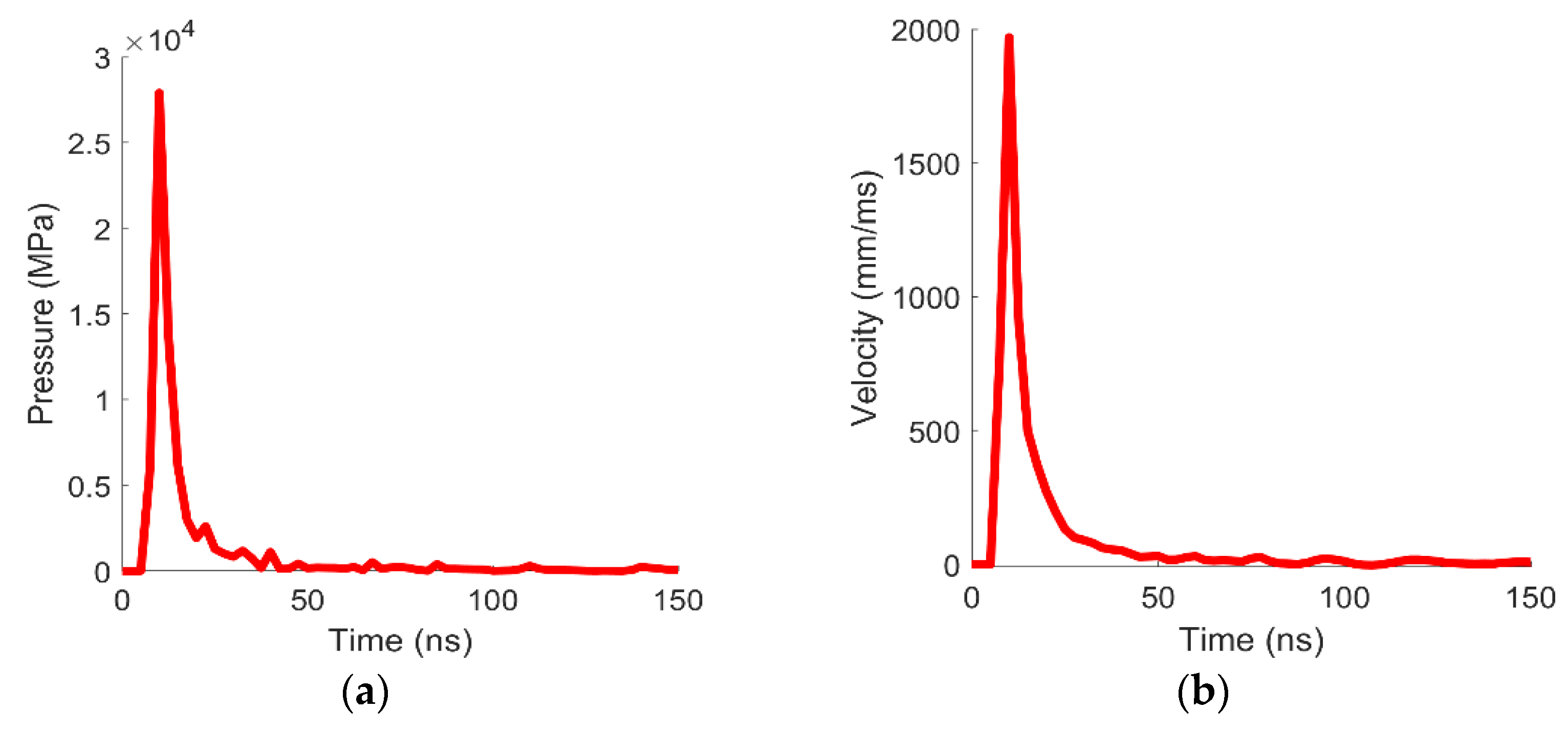
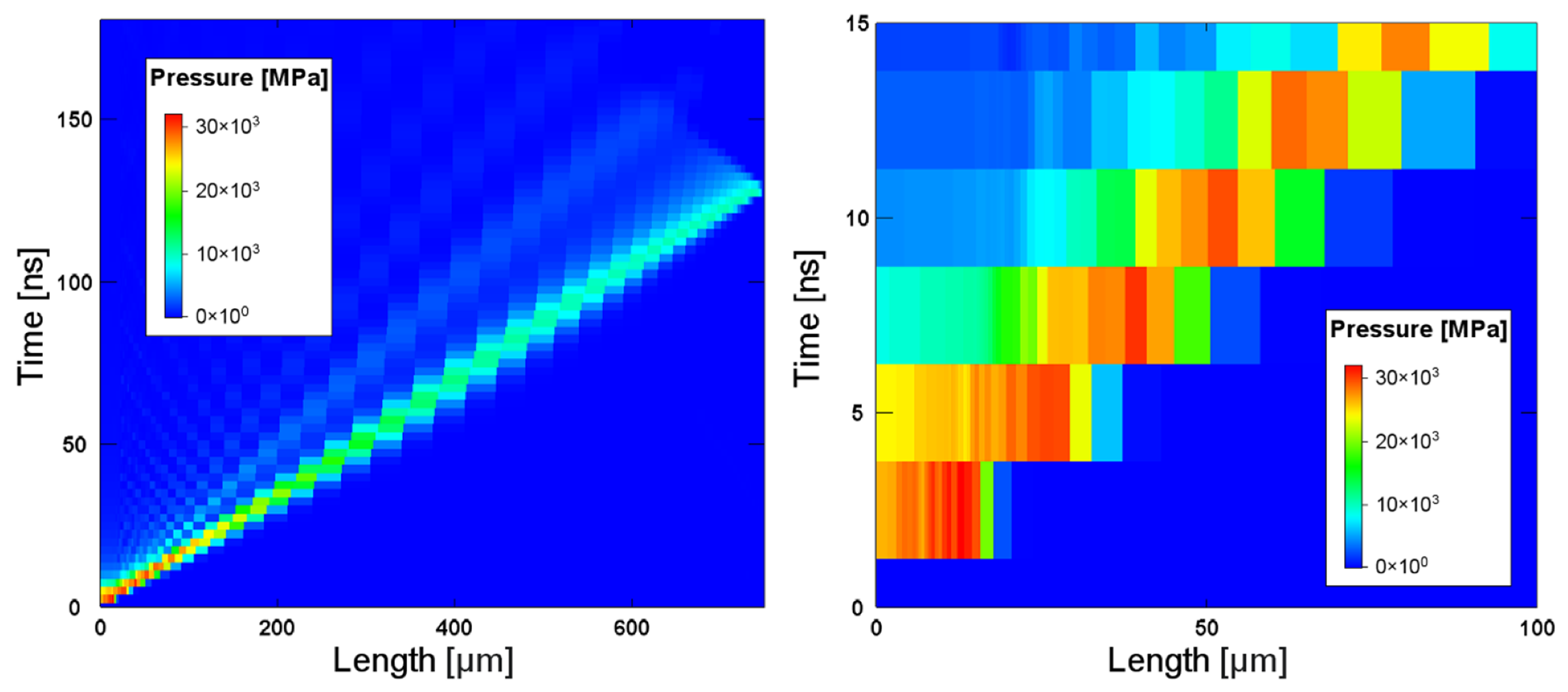
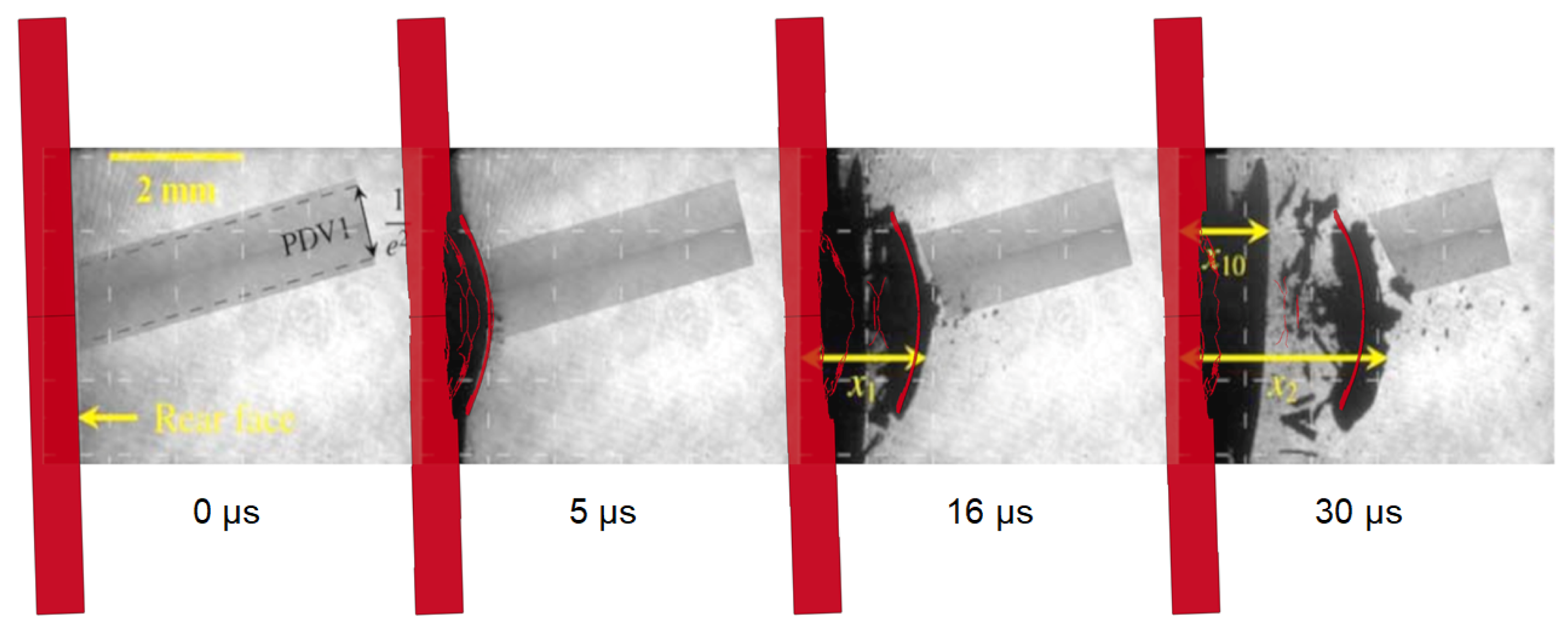
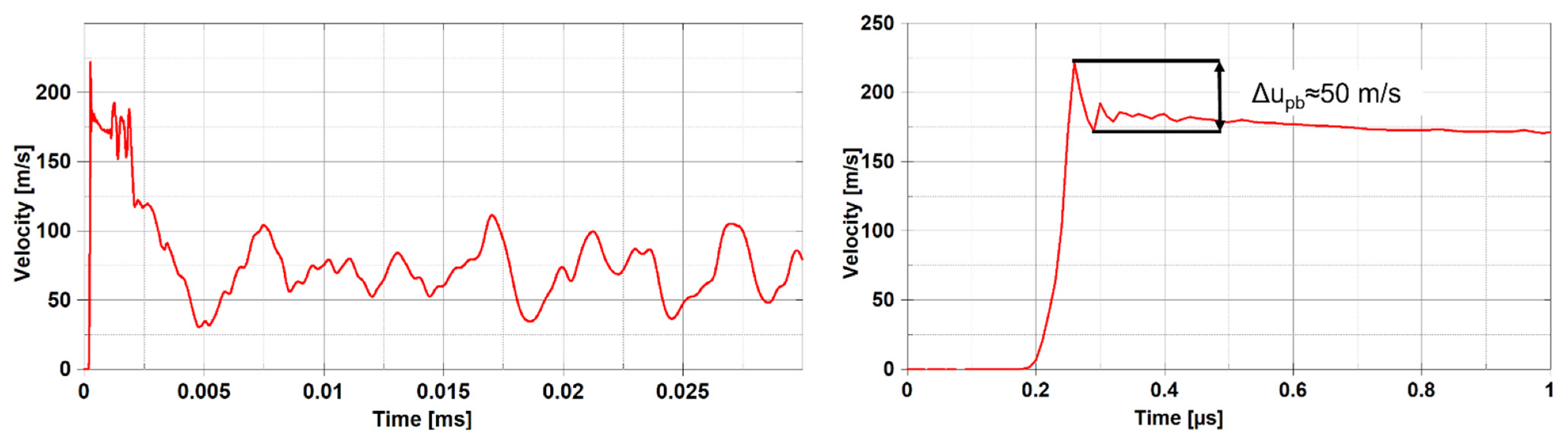



| Laser Beam | Shot | Damage Regime | ||||
|---|---|---|---|---|---|---|
| SOUTH BEAM | S10 | 1 | 235 | 1.72 | 46.7 | D1–D2 |
| S7 | 0.75 | 121 | 0.89 | 27.4 | D2 | |
| S15 | 0.75 | 259 | 1.89 | 50.4 | D3 | |
| S17 | 0.75 | 547 | 4 | 91.7 | D4 | |
| NORTH BEAM | N13 | 2 | 564 | 3.11 | 74.9 | D1 |
| N16 | 0.75 | 167 | 0.92 | 28.3 | D1–D2 | |
| N9 | 1 | 636 | 3.50 | 82.5 | D2 | |
| N8 | 0.75 | 652 | 3.59 | 84.2 | D3 | |
| N11 | 1.5 | 608 | 3.35 | 79.6 | D4 |
| Shot | ||
|---|---|---|
| S7 | 35 | 715 |
| S10 | 50 | 950 |
| S15 | 50 | 700 |
| S17 | 70 | 680 |
| N13 | 62 | 1938 |
| N11 | 63 | 1437 |
| N16 | 35 | 715 |
| N9 | 68 | 932 |
| N8 | 68 | 682 |
| Shot | Peak Velocity [m/s] | Average Debris Velocity [m/s] | |||
|---|---|---|---|---|---|
| Exp. (PDV) | Exp. (VISAR) | Simulation | Exp. (PDV) | Simulation | |
| Shot S7 | 150 | 169 | 145 | 75 | 70 |
| Shot S15 | 250 | 272 | 324 | 85 | 250 |
| Shot S17 | 400 | 564 | 558 | 100 | 517 |
| Shot | Peak Velocity [m/s] | Average Debris Velocity [m/s] | |||
|---|---|---|---|---|---|
| Exp. (PDV) | Exp. (VISAR) | Simulation | Exp. (PDV) | Simulation | |
| Shot N13 | 75 | 100 | 94 | 15 | 60 |
| Shot N11 | 140 | 163 | 169 | 80 | 123 |
| Shot N9 | 250 | 332 | 355 | 100 | 225 |
| Shot N8 | 360 | 511 | 486 | 100 | 391 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morena, A.; Peroni, L. Numerical Simulations of Laser-Induced Shock Experiments on Graphite. Materials 2021, 14, 7079. https://doi.org/10.3390/ma14227079
Morena A, Peroni L. Numerical Simulations of Laser-Induced Shock Experiments on Graphite. Materials. 2021; 14(22):7079. https://doi.org/10.3390/ma14227079
Chicago/Turabian StyleMorena, Alberto, and Lorenzo Peroni. 2021. "Numerical Simulations of Laser-Induced Shock Experiments on Graphite" Materials 14, no. 22: 7079. https://doi.org/10.3390/ma14227079
APA StyleMorena, A., & Peroni, L. (2021). Numerical Simulations of Laser-Induced Shock Experiments on Graphite. Materials, 14(22), 7079. https://doi.org/10.3390/ma14227079







