Colloidal Shear-Thickening Fluids Using Variable Functional Star-Shaped Particles: A Molecular Dynamics Study
Abstract
:1. Introduction
2. Materials and Methods
3. Results
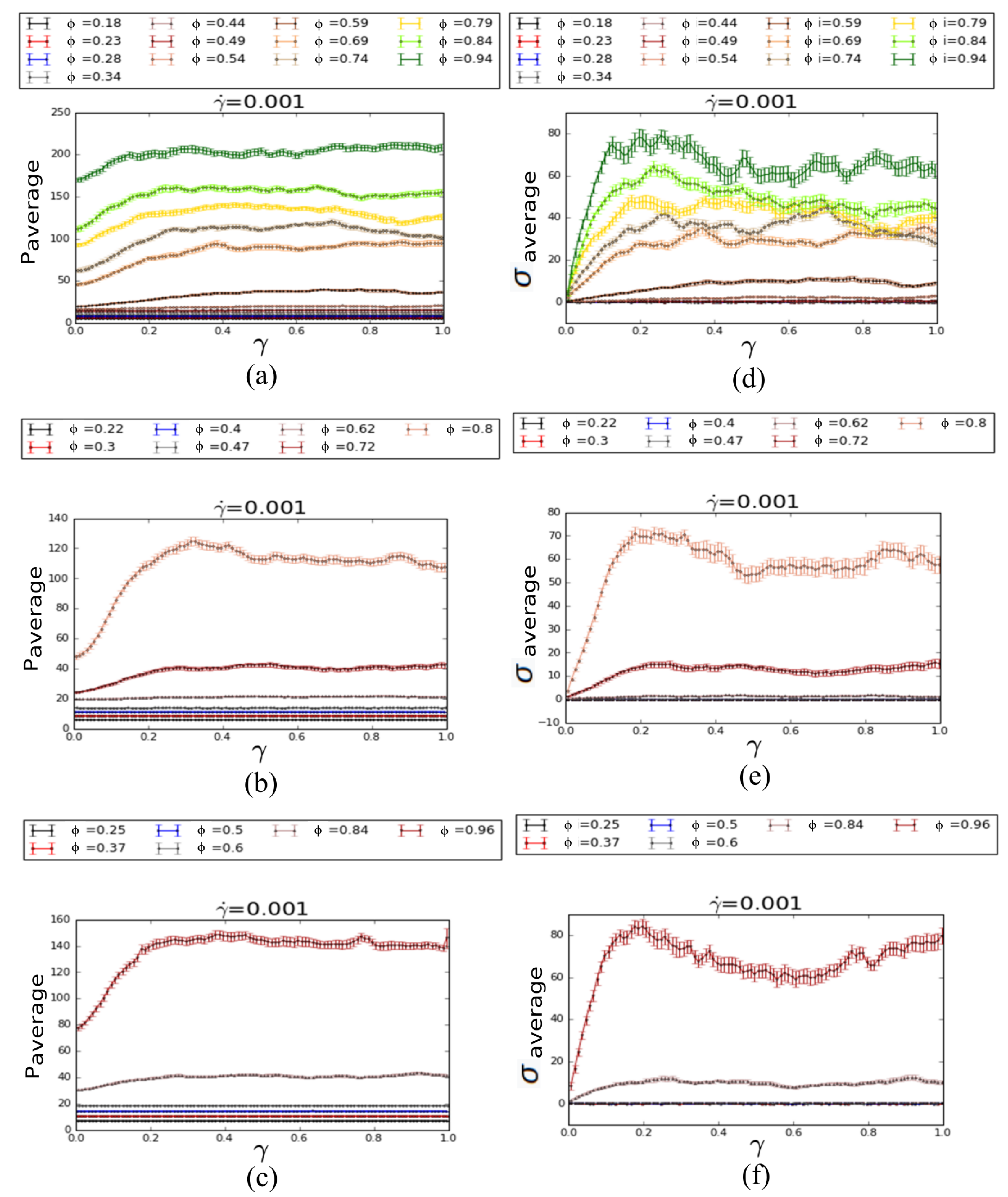
3.1. Shear Thickening Due to Functional Particle Infusion
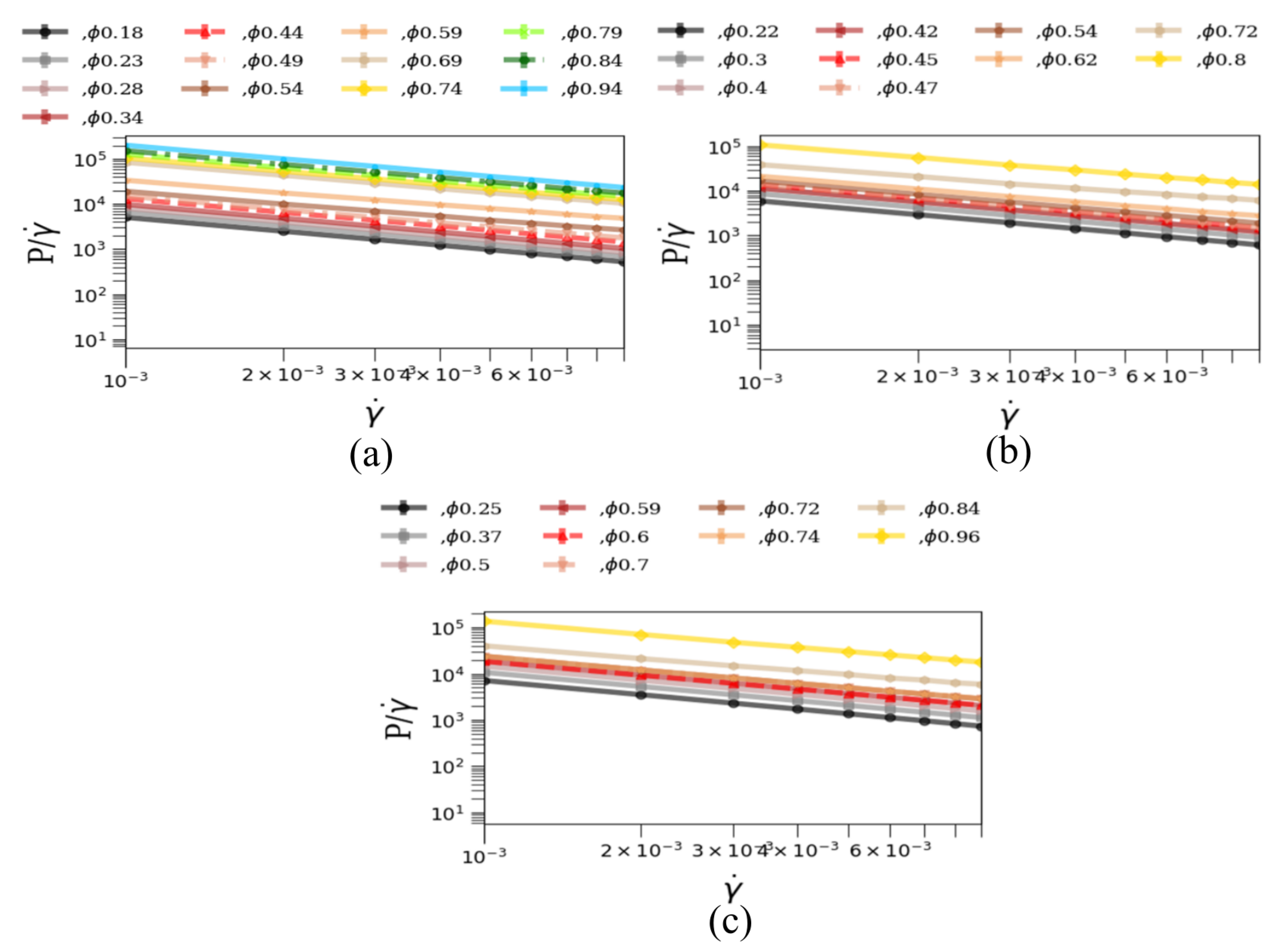
3.2. Pressure, Viscosity, Diffusivity and the Onset of Jamming
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MDPI | Multidisciplinary Digital Publishing Institute |
| MR | Magnetorheological |
| ER | Electrorheological |
| SRD | Stochastic rotation dynamics |
| DPD | Dissipative particle dynamics |
| LAMMPS | Large-scale Atomic/Molecular Massively Parallel Simulator |
| GA | Geometric asperity |
References
- De Vicente, J.; Klingenberg, D.J.; Hidalgo-Alvarez, R. Magnetorheological fluids: A review. Soft Matter 2011, 7, 3701–3710. [Google Scholar] [CrossRef]
- Jolly, M.R.; Carlson, J.D.; Munoz, B.C. A model of the behaviour of magnetorheological materials. Smart Mater. Struct. 1996, 5, 607. [Google Scholar] [CrossRef]
- Ruzicka, M. Electrorheological Fluids: Modeling and Mathematical Theory; Springer Science & Business Media: New York, NY, USA, 2000. [Google Scholar]
- Jordan, T.C.; Shaw, M.T. Electrorheology. IEEE Trans. Electr. Insul. 1989, 24, 849–878. [Google Scholar] [CrossRef]
- Coulter, J.P.; Weiss, K.D.; Carlson, J.D. Engineering applications of electrorheological materials. J. Intell. Mater. Syst. Struct. 1993, 4, 248–259. [Google Scholar] [CrossRef]
- Hong, S.; Choi, S.B.; Jung, W.; Jeong, W. Vibration isolation of structural systems using squeeze mode ER mounts. J. Intell. Mater. Syst. Struct. 2002, 13, 421–424. [Google Scholar] [CrossRef]
- Tan, K.; Stanway, R.; Bullough, W. Shear mode ER transfer function for robotic applications. J. Phys. D Appl. Phys. 2005, 38, 1838. [Google Scholar] [CrossRef]
- Atkin, R.; Ellam, D.; Bullough, W. Electro-structured fluid seals. J. Intell. Mater. Syst. Struct. 2002, 13, 459–464. [Google Scholar] [CrossRef]
- Ouellette, J. Smart fluids move into the marketplace. Ind. Phys. 2004, 9, 14–17. [Google Scholar]
- Janocha, H.; Clephas, B.; Claeyssen, F.; Hesselbach, J.; Bullough, W.; Carlson, J.D.; zur Megede, D.; Wurmus, H.; Kallenbach, M. Actuators in adaptronics. In Adaptronics and Smart Structures; Springer: Berlin/Heidelberg, Germany, 1999; pp. 99–240. [Google Scholar]
- Stanway, R. Smart fluids: Current and future developments. Mater. Sci. Technol. 2004, 20, 931–939. [Google Scholar] [CrossRef]
- Fox, R.W. AT McDonald. Introduction to Fluid Mechanics; Wiley: New York, NY, USA, 2011. [Google Scholar]
- Viswanath, D.S.; Ghosh, T.K.; Prasad, D.H.; Dutt, N.V.; Rani, K.Y. Theories of Viscosity. In Viscosity of Liquids; Springer: Berlin/Heidelberg, Germany, 2007; pp. 109–133. [Google Scholar]
- Müller-Plathe, F. Reversing the perturbation in nonequilibrium molecular dynamics: An easy way to calculate the shear viscosity of fluids. Phys. Rev. E 1999, 59, 4894. [Google Scholar] [CrossRef] [Green Version]
- Kirova, E.; Norman, G. Viscosity calculations at molecular dynamics simulations. J. Physics: Conf. Ser. 2015, 653, 012106. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.H.; Cummings, P.T. Shear viscosity of model mixtures by nonequilibrium molecular dynamics. I. Argon–krypton mixtures. J. Chem. Phys. 1993, 99, 3919–3925. [Google Scholar] [CrossRef] [Green Version]
- Olsson, P.; Teitel, S. Critical scaling of shear viscosity at the jamming transition. Phys. Rev. Lett. 2007, 99, 178001. [Google Scholar] [CrossRef] [Green Version]
- Hecht, M.; Harting, J.; Bier, M.; Reinshagen, J.; Herrmann, H.J. Shear viscosity of claylike colloids in computer simulations and experiments. Phys. Rev. E 2006, 74, 021403. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rao, M.A. Flow and functional models for rheological properties of fluid foods. In Rheology of Fluid, Semisolid, and Solid Foods; Springer: Berlin/Heidelberg, Germany, 2014; pp. 27–61. [Google Scholar]
- Gravish, N.; Franklin, S.V.; Hu, D.L.; Goldman, D.I. Entangled granular media. Phys. Rev. Lett. 2012, 108, 208001. [Google Scholar] [CrossRef] [Green Version]
- Heine, D.R.; Petersen, M.K.; Grest, G.S. Effect of particle shape and charge on bulk rheology of nanoparticle suspensions. J. Chem. Phys. 2010, 132, 184509. [Google Scholar] [CrossRef] [Green Version]
- Papanikolaou, S.; O’Hern, C.S.; Shattuck, M.D. Isostaticity at frictional jamming. Phys. Rev. Lett. 2013, 110, 198002. [Google Scholar] [CrossRef] [Green Version]
- Liu, A.; Nagel, S. (Eds.) Jamming and Rheology: Constrained Dynamics on Microscopic and Macroscopic Scales; Taylor&Francis: London, UK, 2001. [Google Scholar]
- Liu, A.J.; Nagel, S.R. Jamming is not just cool any more. Nature 1998, 396, 21–22. [Google Scholar] [CrossRef]
- Marschall, T.A.; Franklin, S.V.; Teitel, S. Compression-and shear-driven jamming of U-shaped particles in two dimensions. Granul. Matter 2015, 17, 121–133. [Google Scholar] [CrossRef] [Green Version]
- Bi, D.; Zhang, J.; Chakraborty, B.; Behringer, R.P. Jamming by shear. Nature 2011, 480, 355–358. [Google Scholar] [CrossRef]
- van Hecke, M. Jamming of soft particles: Geometry, mechanics, scaling and isostaticity. J. Phys. Condens. Matter 2009, 22, 033101. [Google Scholar] [CrossRef]
- Torquato, S.; Stillinger, F.H. Jammed hard-particle packings: From Kepler to Bernal and beyond. Rev. Mod. Phys. 2010, 82, 2633. [Google Scholar] [CrossRef] [Green Version]
- Shen, T.; Papanikolaou, S.; O’Hern, C.S.; Shattuck, M.D. Statistics of frictional families. Phys. Rev. Lett. 2014, 113, 128302. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, K.; Wang, M.; Papanikolaou, S.; Liu, Y.; Schroers, J.; Shattuck, M.D.; O’Hern, C.S. Computational studies of the glass-forming ability of model bulk metallic glasses. J. Chem. Phys. 2013, 139, 124503. [Google Scholar]
- Sims, N.D.; Stanway, R.; Johnson, A.R.; Peel, D.J.; Bullough, W.A. Smart fluid damping: Shaping the force/velocity response through feedback control. J. Intell. Mater. Syst. Struct. 2000, 11, 945–958. [Google Scholar] [CrossRef]
- Cho, S.W.; Jung, H.J.; Lee, I.W. Smart passive system based on magnetorheological damper. Smart Mater. Struct. 2005, 14, 707. [Google Scholar] [CrossRef]
- Jung, H.J.; Kim, I.H.; Koo, J.H. A multi-functional cable-damper system for vibration mitigation, tension estimation and energy harvesting. Smart Struct. Syst. 2011, 7, 379–392. [Google Scholar] [CrossRef]
- Shäfer, J.; Dippel, S.; Wolf, D. Force schemes in simulations of granular materials. J. Phys. I 1996, 6, 5–20. [Google Scholar] [CrossRef]
- Espanol, P. Fluid particle model. Phys. Rev. E 1998, 57, 2930. [Google Scholar] [CrossRef] [Green Version]
- Espanol, P.; Warren, P. Statistical mechanics of dissipative particle dynamics. EPL Europhys. Lett. 1995, 30, 191. [Google Scholar] [CrossRef] [Green Version]
- Hütter, M. Local structure evolution in particle network formation studied by brownian dynamics simulation. J. Colloid Interface Sci. 2000, 231, 337–350. [Google Scholar] [CrossRef] [PubMed]
- Ladd, A.; Verberg, R. Lattice-Boltzmann simulations of particle-fluid suspensions. J. Stat. Phys. 2001, 104, 1191–1251. [Google Scholar] [CrossRef]
- Komnik, A.; Harting, J.; Herrmann, H. Transport phenomena and structuring in shear flow of suspensions near solid walls. J. Stat. Mech. Theory Exp. 2004, 2004, P12003. [Google Scholar] [CrossRef] [Green Version]
- Brady, J.F.; Bossis, G. Stokesian dynamics. Annu. Rev. Fluid Mech. 1988, 20, 111–157. [Google Scholar] [CrossRef]
- Phung, T.N.; Brady, J.F.; Bossis, G. Stokesian dynamics simulation of Brownian suspensions. J. Fluid Mech. 1996, 313, 181–207. [Google Scholar] [CrossRef] [Green Version]
- Brady, J.F. The rheological behavior of concentrated colloidal dispersions. J. Chem. Phys. 1993, 99, 567–581. [Google Scholar] [CrossRef] [Green Version]
- Inoue, Y.; Chen, Y.; Ohashi, H. Development of a simulation model for solid objects suspended in a fluctuating fluid. J. Stat. Phys. 2002, 107, 85–100. [Google Scholar] [CrossRef]
- Gompper, G.; Ihle, T.; Kroll, D.; Winkler, R. Multi-particle collision dynamics: A particle-based mesoscale simulation approach to the hydrodynamics of complex fluids. In Advanced Computer Simulation Approaches for Soft Matter Sciences III; Holm, C., Kremer, K., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–87. [Google Scholar]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Lykov, K.; Li, X.; Lei, H.; Pivkin, I.V.; Karniadakis, G.E. Inflow/outflow boundary conditions for particle-based blood flow simulations: Application to arterial bifurcations and trees. PLoS Comput. Biol. 2015, 11, e1004410. [Google Scholar] [CrossRef] [PubMed]
- Miskin, M.Z.; Jaeger, H.M. Adapting granular materials through artificial evolution. Nat. Mater. 2013, 12, 326–331. [Google Scholar] [CrossRef]
- Li, Y.; Li, X.; Li, Z.; Gao, H. Surface-structure-regulated penetration of nanoparticles across a cell membrane. Nanoscale 2012, 4, 3768–3775. [Google Scholar] [CrossRef]
- Bogart, L.K.; Pourroy, G.; Murphy, C.J.; Puntes, V.; Pellegrino, T.; Rosenblum, D.; Peer, D.; Lévy, R. Nanoparticles for imaging, sensing, and therapeutic intervention. ACS Nano 2014, 8, 3107–3122. [Google Scholar] [CrossRef]
- Van Lehn, R.C.; Ricci, M.; Silva, P.H.; Andreozzi, P.; Reguera, J.; Voïtchovsky, K.; Stellacci, F.; Alexander-Katz, A. Lipid tail protrusions mediate the insertion of nanoparticles into model cell membranes. Nat. Commun. 2014, 5, 1–11. [Google Scholar] [CrossRef] [PubMed]
- O’hern, C.S.; Silbert, L.E.; Liu, A.J.; Nagel, S.R. Jamming at zero temperature and zero applied stress: The epitome of disorder. Phys. Rev. E 2003, 68, 011306. [Google Scholar] [CrossRef] [Green Version]
- Donev, A.; Torquato, S.; Stillinger, F.H.; Connelly, R. Jamming in hard sphere and disk packings. J. Appl. Phys. 2004, 95, 989–999. [Google Scholar] [CrossRef] [Green Version]
- Donev, A.; Connelly, R.; Stillinger, F.H.; Torquato, S. Underconstrained jammed packings of nonspherical hard particles: Ellipses and ellipsoids. Phys. Rev. E 2007, 75, 051304. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zeravcic, Z.; Xu, N.; Liu, A.; Nagel, S.; van Saarloos, W. Excitations of ellipsoid packings near jamming. EPL Europhys. Lett. 2009, 87, 26001. [Google Scholar] [CrossRef] [Green Version]
- Mailman, M.; Schreck, C.F.; O’Hern, C.S.; Chakraborty, B. Jamming in systems composed of frictionless ellipse-shaped particles. Phys. Rev. Lett. 2009, 102, 255501. [Google Scholar] [CrossRef] [Green Version]
- Hidalgo, R.C.; Zuriguel, I.; Maza, D.; Pagonabarraga, I. Role of particle shape on the stress propagation in granular packings. Phys. Rev. Lett. 2009, 103, 118001. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Desmond, K.; Franklin, S.V. Jamming of three-dimensional prolate granular materials. Phys. Rev. E 2006, 73, 031306. [Google Scholar] [CrossRef] [Green Version]
- Azéma, E.; Radjaï, F. Stress-strain behavior and geometrical properties of packings of elongated particles. Phys. Rev. E 2010, 81, 051304. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jiao, Y.; Torquato, S. Maximally random jammed packings of Platonic solids: Hyperuniform long-range correlations and isostaticity. Phys. Rev. E 2011, 84, 041309. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Frenkel, D.; Smit, B. Understanding Molecular Simulation: From Algorithms to Applications; Elsevier: Amsterdam, The Netherlands, 2001; Volume 1. [Google Scholar]
- Malevanets, A.; Kapral, R. Mesoscopic model for solvent dynamics. J. Chem. Phys. 1999, 110, 8605–8613. [Google Scholar] [CrossRef]
- Malevanets, A.; Kapral, R. Solute molecular dynamics in a mesoscale solvent. J. Chem. Phys. 2000, 112, 7260–7269. [Google Scholar] [CrossRef] [Green Version]
- Hecht, M.; Harting, J.; Ihle, T.; Herrmann, H.J. Simulation of claylike colloids. Phys. Rev. E 2005, 72, 011408. [Google Scholar] [CrossRef] [Green Version]
- Petersen, M.K.; Lechman, J.B.; Plimpton, S.J.; Grest, G.S.; in’t Veld, P.J.; Schunk, P. Mesoscale hydrodynamics via stochastic rotation dynamics: Comparison with Lennard-Jones fluid. J. Chem. Phys. 2010, 132, 174106. [Google Scholar] [CrossRef]
- Bair, S.; Winer, W. The high pressure high shear stress rheology of liquid lubricants. J. Tribol. 1992, 114, 1–9. [Google Scholar] [CrossRef]
- Moore, J.D.; Parsons, B. Scaling of viscous shear zones with depth-dependent viscosity and power-law stress–strain-rate dependence. Geophys. J. Int. 2015, 202, 242–260. [Google Scholar] [CrossRef] [Green Version]
- Kubečka, J.; Uhlík, F.; Košovan, P. Mean squared displacement from fluorescence correlation spectroscopy. Soft Matter 2016, 12, 3760–3769. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Olsson, P.; Teitel, S. Herschel-Bulkley shearing rheology near the athermal jamming transition. Phys. Rev. Lett. 2012, 109, 108001. [Google Scholar] [CrossRef] [PubMed]
- Stalter, S.; Yelash, L.; Emamy, N.; Statt, A.; Hanke, M.; Lukáčová-Medvid’ová, M.; Virnau, P. Molecular dynamics simulations in hybrid particle-continuum schemes: Pitfalls and caveats. Comput. Phys. Commun. 2018, 224, 198–208. [Google Scholar] [CrossRef] [Green Version]
- Grady, D. Strain-rate dependence of the effective viscosity under steady-wave shock compression. Appl. Phys. Lett. 1981, 38, 825–826. [Google Scholar] [CrossRef]
- Webb, S.L.; Dingwell, D.B. Non-Newtonian rheology of igneous melts at high stresses and strain rates: Experimental results for rhyolite, andesite, basalt, and nephelinite. J. Geophys. Res. Solid Earth 1990, 95, 15695–15701. [Google Scholar] [CrossRef] [Green Version]
- Magnin, A.; Piau, J. Cone-and-plate rheometry of yield stress fluids. Study of an aqueous gel. J. Non-Newton. Fluid Mech. 1990, 36, 85–108. [Google Scholar] [CrossRef]
- Olsson, P.; Teitel, S. Critical scaling of shearing rheology at the jamming transition of soft-core frictionless disks. Phys. Rev. E 2011, 83, 030302. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Otsuki, M.; Hayakawa, H. Critical scaling near jamming transition for frictional granular particles. Phys. Rev. E 2011, 83, 051301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mewis, J.; Wagner, N.J. Colloidal Suspension Rheology; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salehin, R.; Xu, R.-G.; Papanikolaou, S. Colloidal Shear-Thickening Fluids Using Variable Functional Star-Shaped Particles: A Molecular Dynamics Study. Materials 2021, 14, 6867. https://doi.org/10.3390/ma14226867
Salehin R, Xu R-G, Papanikolaou S. Colloidal Shear-Thickening Fluids Using Variable Functional Star-Shaped Particles: A Molecular Dynamics Study. Materials. 2021; 14(22):6867. https://doi.org/10.3390/ma14226867
Chicago/Turabian StyleSalehin, Rofiques, Rong-Guang Xu, and Stefanos Papanikolaou. 2021. "Colloidal Shear-Thickening Fluids Using Variable Functional Star-Shaped Particles: A Molecular Dynamics Study" Materials 14, no. 22: 6867. https://doi.org/10.3390/ma14226867
APA StyleSalehin, R., Xu, R.-G., & Papanikolaou, S. (2021). Colloidal Shear-Thickening Fluids Using Variable Functional Star-Shaped Particles: A Molecular Dynamics Study. Materials, 14(22), 6867. https://doi.org/10.3390/ma14226867





