Sensitivity Analysis of Stochastic Calculation of SCC Regarding Aggressive Environment
Abstract
:1. Introduction
2. Material
3. Stochastic and Sensitivity Analysis
4. Results and Discussion
4.1. Probability of Corrosion Initiation
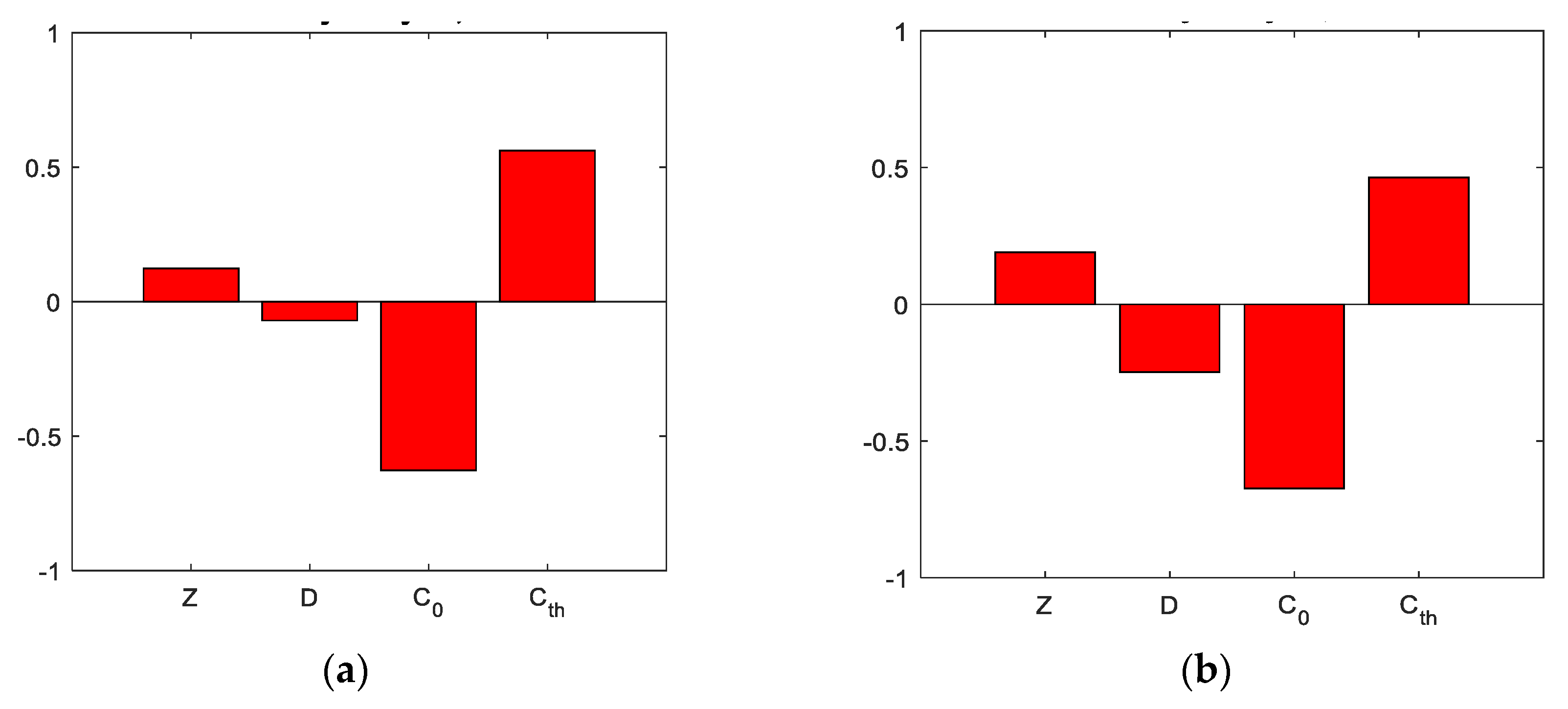
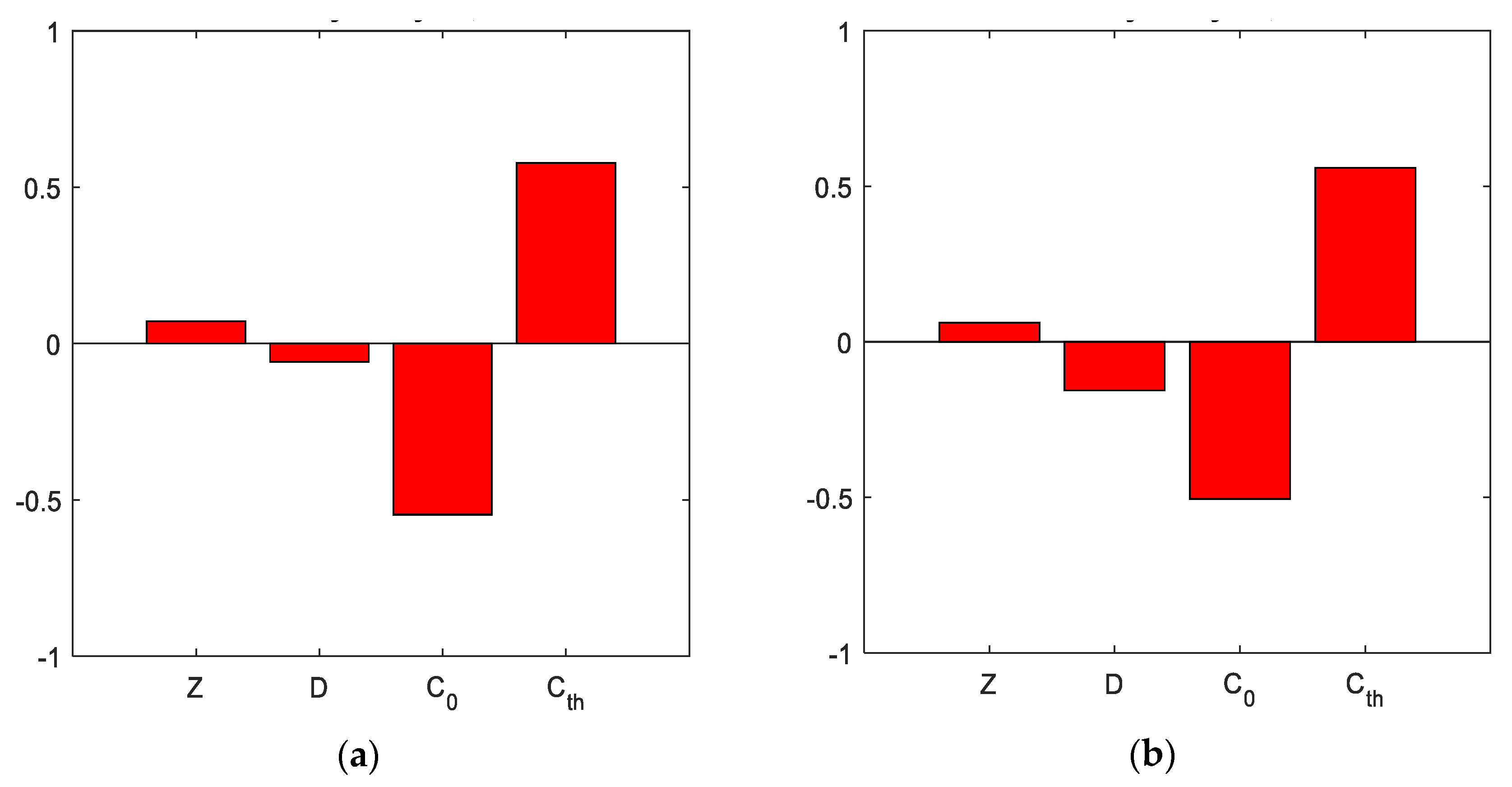
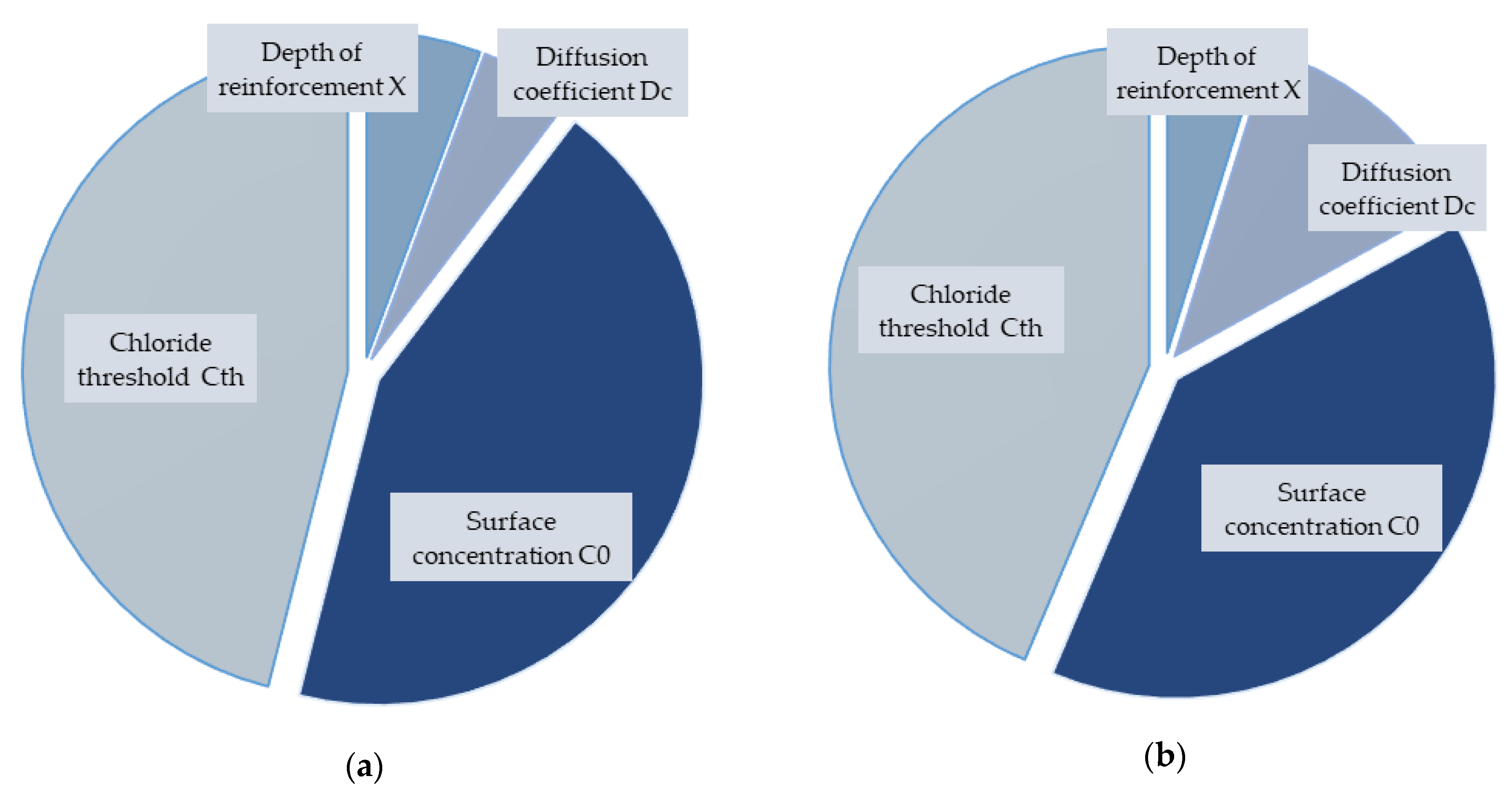
4.2. Coefficients of Correlation
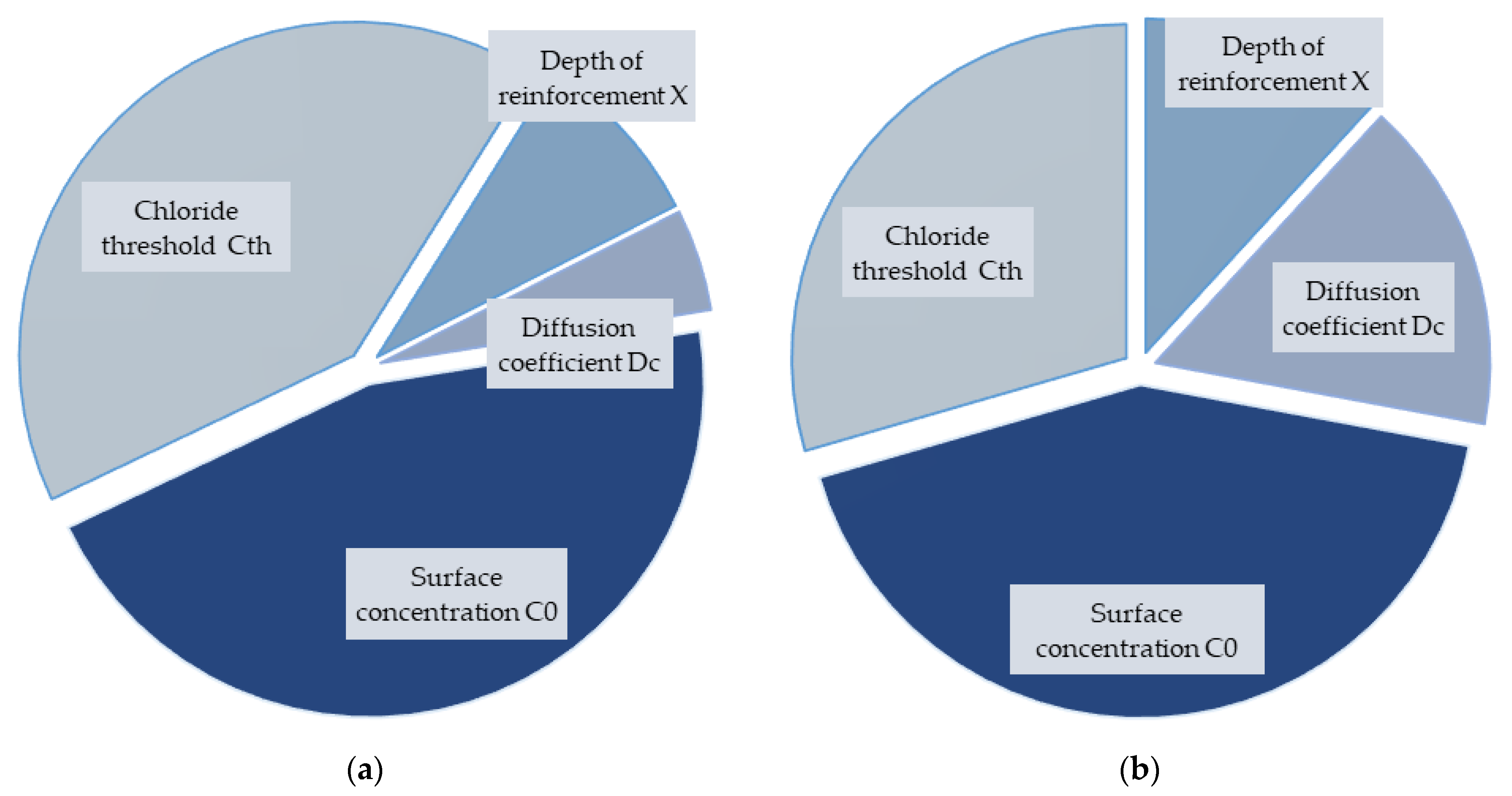
4.3. Significance Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yan, L.; Chouw, N. Sustainable Concrete and Structures with Natural Fibre Reinforcements. In Infrastructure Corrosion and Durability—A Sustainability Study; Lu, Y., Ed.; OMICS Group Incorporation: Hyderabad, India, 2014; pp. 1–25. [Google Scholar]
- Sharbatdar, M.K.; Abbasi, M.; Fakharian, P. Improving the Properties of Self-compacted Concrete with Using Combined Silica Fume and Metakaolin. Period. Polytech. Civ. Eng. 2020, 62, 535–544. [Google Scholar] [CrossRef] [Green Version]
- Kocot, A.; Ponikiewski, T. Influence of Artificial Waste Modification on Strength of Cementitious Composite. Trans. VSB—Tech. Univ. Ostrav. Civ. Eng. Ser. 2021, 21, 7. [Google Scholar] [CrossRef]
- Stevulova, N.; Vaclavik, V.; Hospodarova, V.; Dvorský, T. Recycled Cellulose Fiber Reinforced Plaster. Materials 2021, 14, 2986. [Google Scholar] [CrossRef]
- Gholampour, A.; Ozbakkaloglu, T. Time-dependent and long-term mechanical properties of concretes incorporating different grades of coarse recycled concrete aggregates. Eng. Struct. 2018, 157, 224–234. [Google Scholar] [CrossRef]
- Lee, D.; Son, S.; Kim, D.; Kim, S. Special-Length-Priority Algorithm to Minimize Reinforcing Bar-Cutting Waste for Sustainable Construction. Sustainability 2020, 12, 5950. [Google Scholar] [CrossRef]
- Svintsov, A.P.; Shchesnyak, E.L.; Galishnikova, V.V.; Fediuk, R.S.; Stashevskaya, N.A. Effect of nano-modified additives on properties of concrete mixtures during winter season. Constr. Build. Mater. 2020, 237, 117527. [Google Scholar] [CrossRef]
- Okrajnov-Bajic, R.; Vasovic, D. Self-compacting concrete and its application in contemporary architectural practice. Spatium 2009, 28–34. [Google Scholar] [CrossRef]
- Alberti, M.; Enfedaque, A.; Galvez, J. Fibre reinforced concrete with a combination of polyolefin and steel-hooked fibres. Compos. Struct. 2017, 171, 317–325. [Google Scholar] [CrossRef]
- Ponikiewski, T.; Katzer, J. Fresh Mix Characteristics of Self-Compacting Concrete Reinforced by Fibre. Period. Polytech. Civ. Eng. 2016, 61, 226–231. [Google Scholar] [CrossRef] [Green Version]
- Geiker, M.; Jacobsen, S. Self-compacting concrete (SCC). Dev. Formul. Reinf. Concr. 2019, 229–256. [Google Scholar] [CrossRef]
- Kessler, S.; Gehlen, C. Measurement Uncertainty and POD and Its Influence Remaining Service Life Evaluation. In Proceedings of the 3rd International fib Congress and Exhibition, Incorporating the PCI Annual Convention and Bridge Conference: Think Globally, Build Locally, Proceedings, Washington, DC, USA, 29 May–3 June 2010. [Google Scholar]
- Abrishambaf, A.; Barros, J.A.; Cunha, V.M. Tensile stress–crack width law for steel fibre reinforced self-compacting concrete obtained from indirect (splitting) tensile tests. Cem. Concr. Compos. 2015, 57, 153–165. [Google Scholar] [CrossRef] [Green Version]
- Faraj, R.H.; Mohammed, A.A.; Mohammed, A.; Omer, K.M.; Ahmed, H.U. Systematic multiscale models to predict the compressive strength of self-compacting concretes modified with nanosilica at different curing ages. Eng. Comput. 2021, 1–24. [Google Scholar] [CrossRef]
- Asteris, P.G.; Ashrafian, A.; Rezaie-Balf, M. Prediction of the Compressive Strength of Self-Compacting Concrete Using Surrogate Models. Comput. Concr. 2019, 24, 137–150. [Google Scholar] [CrossRef]
- Lehner, P.; Konečný, P.; Ponikiewski, T. Comparison of Material Properties of SCC Concrete with Steel Fibres Related to Ingress of Chlorides. Crystals 2020, 10, 220. [Google Scholar] [CrossRef] [Green Version]
- Stawiski, B.; Kania, T. Tests of Concrete Strength across the Thickness of Industrial Floor Using the Ultrasonic Method with Exponential Spot Heads. Materials 2020, 13, 2118. [Google Scholar] [CrossRef] [PubMed]
- Ganesha, M.; Umesh, S.S.; Anand, V.R. Research on the Strength Parameters of Poly Propylene Fiber Reinforced Concrete and Steel Fiber Reinforced Concrete. Int. J. Recent Technol. Eng. 2019, 8, 954–957. [Google Scholar] [CrossRef]
- da Silva, G.C.S.; Christ, R.; Pacheco, F.; de Souza, C.F.N.; Gil, A.M.; Tutikian, B.F. Evaluating steel fiber-reinforced self-consolidating concrete performance. Struct. Concr. 2020, 21, 448–457. [Google Scholar] [CrossRef]
- Safehian, M.; Ramezanianpour, A.A. Prediction of RC structure service life from field long term chloride diffusion. Comput. Concr. 2015, 15, 589–606. [Google Scholar] [CrossRef]
- Zhuo, W.; Yan, Q.; Yang, Z.; Lin, S.; Lin, K.; He, F. Chloride Penetration in Coastal Concrete Structures: Field Investigation and Model Development. Adv. Mater. Sci. Eng. 2019, 2019, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Kožar, I.; Malić, N.T.; Simonetti, D.; Božić, Ž. Stochastic properties of bond-slip parameters at fibre pull-out. Eng. Fail. Anal. 2020, 111, 104478. [Google Scholar] [CrossRef]
- Zambon, I.; Ariza, M.P.S.; e Matos, J.C.; Strauss, A. Value of Information (VoI) for the Chloride Content in Reinforced Concrete Bridges. Appl. Sci. 2020, 10, 567. [Google Scholar] [CrossRef] [Green Version]
- Loreto, G.; Di Benedetti, M.; De Luca, A.; Nanni, A. Assessment of reinforced concrete structures in marine environment: A case study. Corros. Rev. 2019, 37, 57–69. [Google Scholar] [CrossRef]
- Zięba, J.; Buda-Ożóg, L.; Skrzypczak, I. Probabilistic method and FEM analysis in the design and analysis of cracks widths. Eng. Struct. 2019, 209, 110022. [Google Scholar] [CrossRef]
- Arregui-Mena, J.D.; Margetts, L.; Mummery, P.M. Practical Application of the Stochastic Finite Element Method. Arch. Comput. Methods Eng. 2014, 23, 171–190. [Google Scholar] [CrossRef]
- Vu, K.A.T.; Stewart, M.G. Structural reliability of concrete bridges including improved chloride-induced corrosion models. Struct. Saf. 2000, 22, 313–333. [Google Scholar] [CrossRef]
- Metropolis, N.; Ulam, S. The Monte Carlo Method. J. Am. Stat. Assoc. 1949, 44, 335. [Google Scholar] [CrossRef] [PubMed]
- Marek, P.; Brozzetti, J.; Gustar, M.; Elishakoff, I. Probabilistic Assessment of Structures using Monte Carlo Simulations. Appl. Mech. Rev. 2002, 55, B31–B32. [Google Scholar] [CrossRef]
- Lehner, P.; Horňáková, M.; Konečný, P. Numerical Approximation of Time-Dependent Chloride Diffusion Model Parameters via Probabilistic Monte Carlo Method. AIP Conf. Proc. 2020, 2293, 130007. [Google Scholar]
- Rao, K.D.; Gopika, V.; Rao, V.S.; Kushwaha, H.; Verma, A.; Srividya, A. Dynamic fault tree analysis using Monte Carlo simulation in probabilistic safety assessment. Reliab. Eng. Syst. Saf. 2009, 94, 872–883. [Google Scholar] [CrossRef]
- Saltelli, A. Sensitivity Analysis for Importance Assessment. Risk Anal. 2002, 22, 579–590. [Google Scholar] [CrossRef]
- Faifer, M.; Ferrara, L.; Ottoboni, R.; Toscani, S. Low Frequency Electrical and Magnetic Methods for Non-Destructive Analysis of Fiber Dispersion in Fiber Reinforced Cementitious Composites: An Overview. Sensors 2013, 13, 1300–1318. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Y.; Blumenthal, W.R.; Lowe, T.C. Determination of Non-Symmetric 3-D Fiber-Orientation Distribution and Average Fiber Length in Short-Fiber Composites. J. Compos. Mater. 1997, 31, 1287–1301. [Google Scholar] [CrossRef]
- Balázs, G.L.; Czoboly, O.; Lublóy, É.; Kapitány, K.; Barsi, Á. Observation of steel fibres in concrete with Computed Tomography. Constr. Build. Mater. 2017, 140, 534–541. [Google Scholar] [CrossRef]
- Scannell, W.T.; Sohanghpurwala, A.A. Verification of Effectiveness of Epoxy-Coated Rebars; Epoxy-Coated Rebars, Final Report to Pennsylvania Department of Transportation, Project No 94-05; Concorr. Ing; Pennsylvania Department of Transportation: Harrisburg, PA, USA, 1998; pp. 5–96. [Google Scholar]
- Darwin, D.; Browning, J.; O’Reilly, M.; Xing, L.; Ji, J. Critical Chloride Corrosion Threshold of Galvanized Reinforcing Bars. ACI Mater. J. 2009, 106, 176–183. [Google Scholar]
- Weyers, R.E.; Pyc, W.; Sprinkel, M.M. Estimating the Service Life of Epoxy-Coated Reinforcing Steel. ACI Mater. J. 1998, 95, 546–557. [Google Scholar]
- Lehner, P.; Konečnỳ, P.; Ponikiewski, T. Relationship between Mechanical Properties and Conductivity of SCC Mixtures with Steel Fibres. In Research and Modelling in Civil Engineering 2018; Katzer, J., Cichocki, K., Domski, J., Eds.; Koszalin University of Technology: Koszalin, Poland, 2018. [Google Scholar]
- Konečný, P.; Lehner, P.; Ponikiewski, T.; Miera, P. Comparison of Chloride Diffusion Coefficient Evaluation Based on Electrochemical Methods. Procedia Eng. 2017, 190, 193–198. [Google Scholar] [CrossRef]
- Sucharda, O.; Lehner, P.; Konečný, P.; Ponikiewski, T. Investigation of Fracture Properties by Inverse Analysis on Selected SCC Concrete Beams with Different Amount of Fibres; Elsevier: Amsterdam, The Netherlands, 2018; Volume 13, pp. 1533–1538. [Google Scholar]
- Lehner, P.; Ghosh, P.; Konečný, P. Statistical analysis of time dependent variation of diffusion coefficient for various binary and ternary based concrete mixtures. Constr. Build. Mater. 2018, 183, 75–87. [Google Scholar] [CrossRef]
- Konečný, P.; Lehner, P.; Ghosh, P.; Morávková, Z.; Tran, Q. Comparison of procedures for the evaluation of time dependent concrete diffusion coefficient model. Constr. Build. Mater. 2020, 258, 119535. [Google Scholar] [CrossRef]
- Konečný, P.; Veselý, V.; Lehner, P.; Pieszka, D.; Žídek, L. Investigation of Selected Physical Parameters of Cementitious Composite during Sequential Fracture Test. Adv. Mater. Res. 2014, 969, 228–233. [Google Scholar] [CrossRef]
- Le, T.D.; Lehner, P.; Konečný, P. Probabilistic Modeling of Chloride Penetration with Respect to Concrete Heterogeneity and Epoxy-Coating on the Reinforcement. Materials 2019, 12, 4068. [Google Scholar] [CrossRef] [Green Version]
- Konečný, P.; Lehner, P. Effect of cracking and randomness of inputs on corrosion initiation of reinforced concrete bridge decks exposed to chlorides. Frat. Ed. Integrità Strutt. 2016, 11, 29–37. [Google Scholar] [CrossRef] [Green Version]
- Boddy, A.; Bentz, E.; Thomas, M.; Hooton, R. An overview and sensitivity study of a multimechanistic chloride transport model. Cem. Concr. Res. 1999, 29, 827–837. [Google Scholar] [CrossRef]
- Král, P.; Hradil, P.; Hušek, M.; Kala, J.; Kala, Z. Sensitivity analysis and optimization as tools for the inverse concrete material model parameter identification. In Proceedings of the International Conference of Numerical Analysis and Applied Mathematics (ICNAAM 2017), Thessaloniki, Greece, 25–30 September 2017; AIP Publishing: New York, NY, USA, 2018; Volume 1978, p. 430010. [Google Scholar]
- Kala, Z.; Kala, J.; Simos, T.E.; Psihoyios, G.; Tsitouras, C.; Anastassi, Z. Sensitivity Analysis of Stability Problems of Steel Structures using Shell Finite Elements and Nonlinear Computation Methods. AIP Conf. Proc. 2011, 1389, 1865. [Google Scholar]
- Schober, P.; Boer, C.; Schwarte, L.A. Correlation Coefficients. Anesth. Analg. 2018, 126, 1763–1768. [Google Scholar] [CrossRef]
- Ghosh, P.; Konečný, P.; Tikalsky, P.J. SBRA Model for Corrosion Initiation of Concrete Structures. Model. Corroding Concr. Struct. 2011, 5, 85–100. [Google Scholar] [CrossRef]
- Zhang, X.-G.; Zhao, Y.-G.; Xing, F.; Lu, Z.-H. Coupling effects of influence factors on probability of corrosion initiation time of reinforced concrete. J. Cent. South. Univ. Technol. 2011, 18, 223–229. [Google Scholar] [CrossRef]
- Ponikiewski, T.; Katzer, J.; Bugdol, M.; Rudzki, M. X-ray computed tomography harnessed to determine 3D spacing of steel fibres in self compacting concrete (SCC) slabs. Constr. Build. Mater. 2015, 74, 102–108. [Google Scholar] [CrossRef]
| Mixture No. | OPC | SCC 0% | SCC 1% | SCC 2% |
|---|---|---|---|---|
| Cement type I 42.5 R | 313 kg/m3 | 490 kg/m3 | 490 kg/m3 | 490 kg/m3 |
| Water | 164 kg/m3 | 201 kg/m3 | 201 kg/m3 | 201 kg/m3 |
| Sand | 387 kg/m3 | 807 kg/m3 | 807 kg/m3 | 807 kg/m3 |
| River gravel | 1546 kg/m3 | 807 kg/m3 | 807 kg/m3 | 807 kg/m3 |
| Super-plastificator | - | 12.25 kg/m3 | 12.25 kg/m3 | 12.25 kg/m3 |
| Stabilizer | - | 1.96 kg/m3 | 1.96 kg/m3 | 1.96 kg/m3 |
| Steel fibres | - | 0 kg/m3 | 80 kg/m3 | 160 kg/m3 |
| Water/cement ratio (W/C) | 0.52 | 0.41 | 0.41 | 0.41 |
| Mixture No. | Diffusion Coefficient (m2/s × 10−11) | Coefficient of Variation (-) | Ageing Factor (-) |
|---|---|---|---|
| OPC | 1.0723 | 0.035 | 0.1344 |
| SCC 0% | 1.1575 | 0.107 | 0.2779 |
| SCC 1% | 1.7311 | 0.036 | 0.1157 |
| SCC 2% | 2.1111 | 0.104 | 0.0932 |
| Parameter | Unit | Probabilistic Approach | |
|---|---|---|---|
| Range/Value | Function | ||
| Variation coefficient, cvRV | - | −1.00–1.00 | Constant |
| Width of the investigated cross-section, b | m | 1.00 | Constant |
| Height of the investigated cross-sectional surface, h | m | 0.20 | Constant |
| Depth of reinforcement, Z | m | 0.04–0.11 | Histogram [36] |
| Chloride threshold for corrosion initiation, Cth | % weight of cement | 0.09–0.51 | Histogram [37] |
| Concentration of chloride at the surface, C0 | % weight of cement | 0.21–1.63 | Histogram [46] |
| Initial concentration of chloride in the cross-section, Cb | % weight of cement | 0 | Constant |
| Monitored life span, t | years | 100 | Constant |
| Number of simulations | - | 100,000 | Constant |
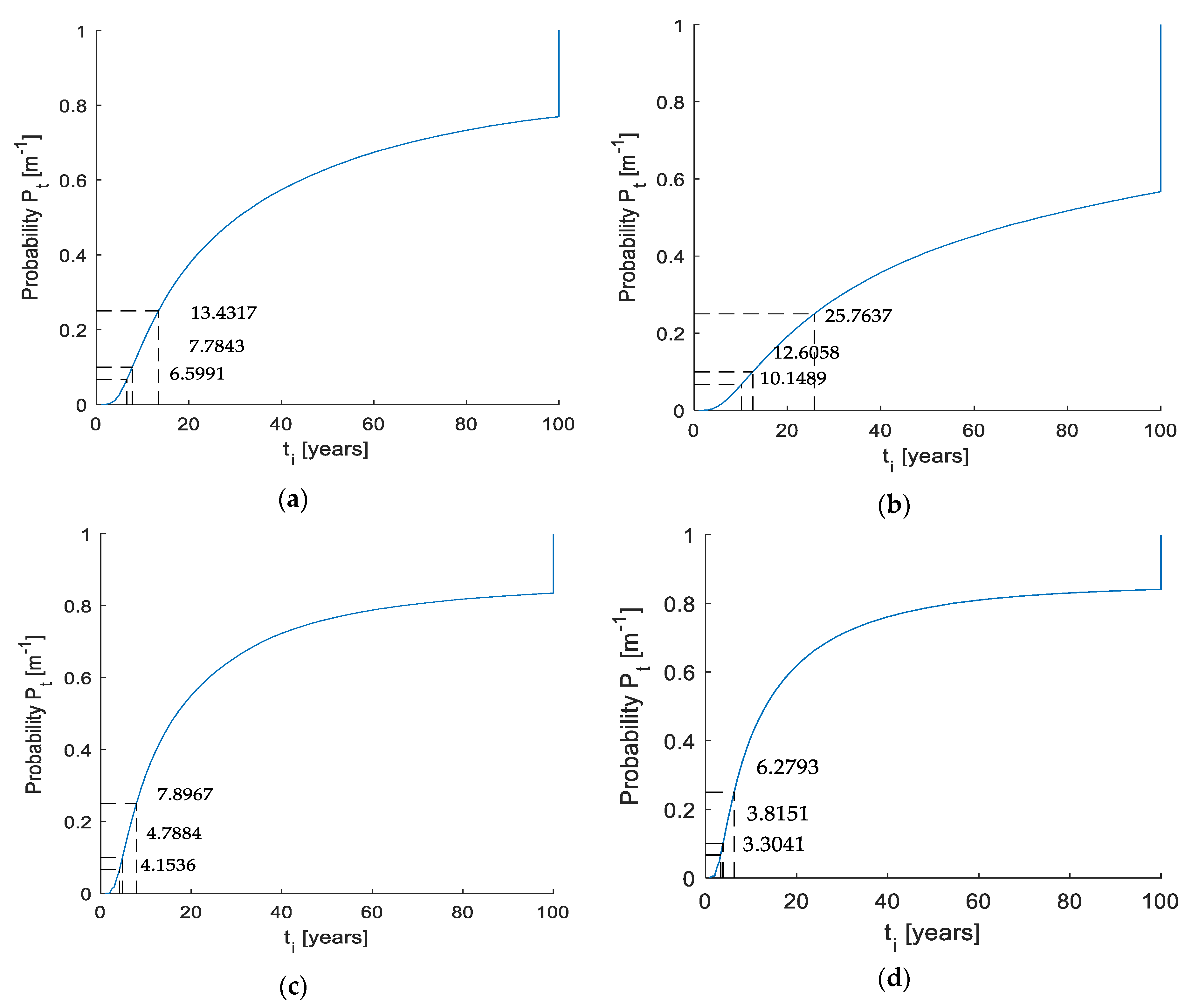
| Mixture No. | Probability of Corrosion Initiation Pf (%) | ||
|---|---|---|---|
| 5 | 10 | 25 | |
| OPC | 6.60 | 7.78 | 13.43 |
| SCC 0% | 10.15 | 12.61 | 25.76 |
| SCC 1% | 4.15 | 4.79 | 7.90 |
| SCC 2% | 3.31 | 3.82 | 6.28 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lehner, P.; Horňáková, M.; Hrabová, K. Sensitivity Analysis of Stochastic Calculation of SCC Regarding Aggressive Environment. Materials 2021, 14, 6838. https://doi.org/10.3390/ma14226838
Lehner P, Horňáková M, Hrabová K. Sensitivity Analysis of Stochastic Calculation of SCC Regarding Aggressive Environment. Materials. 2021; 14(22):6838. https://doi.org/10.3390/ma14226838
Chicago/Turabian StyleLehner, Petr, Marie Horňáková, and Kristýna Hrabová. 2021. "Sensitivity Analysis of Stochastic Calculation of SCC Regarding Aggressive Environment" Materials 14, no. 22: 6838. https://doi.org/10.3390/ma14226838
APA StyleLehner, P., Horňáková, M., & Hrabová, K. (2021). Sensitivity Analysis of Stochastic Calculation of SCC Regarding Aggressive Environment. Materials, 14(22), 6838. https://doi.org/10.3390/ma14226838






