Study on Penetration Performance of Rear Shaped Charge Warhead
Abstract
:1. Introduction
2. Jet Penetration Theory
2.1. Theory of the SCJ Breaking Armor
2.2. The Jet Penetrates the Multi-Layer Target
3. Structural Model
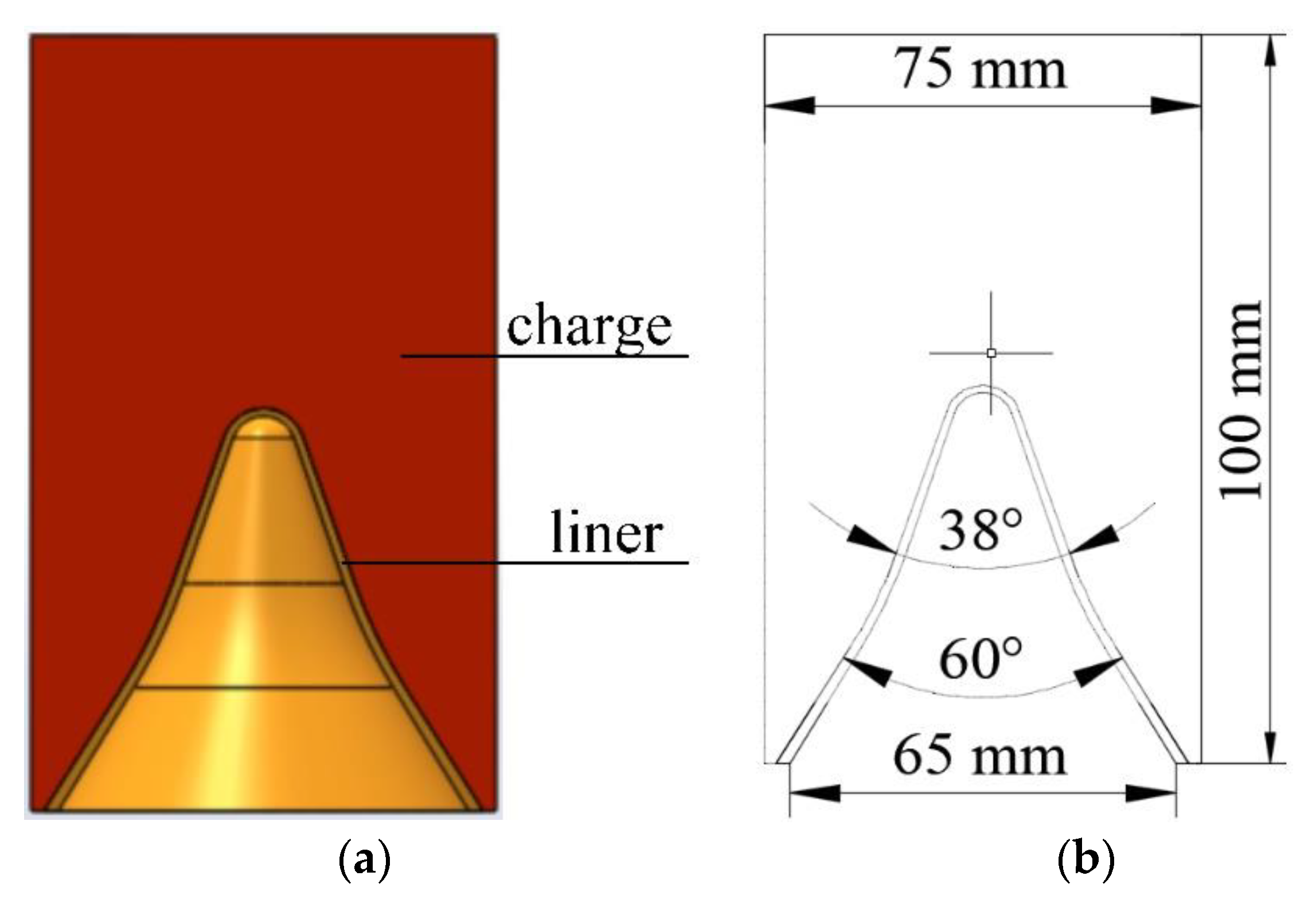
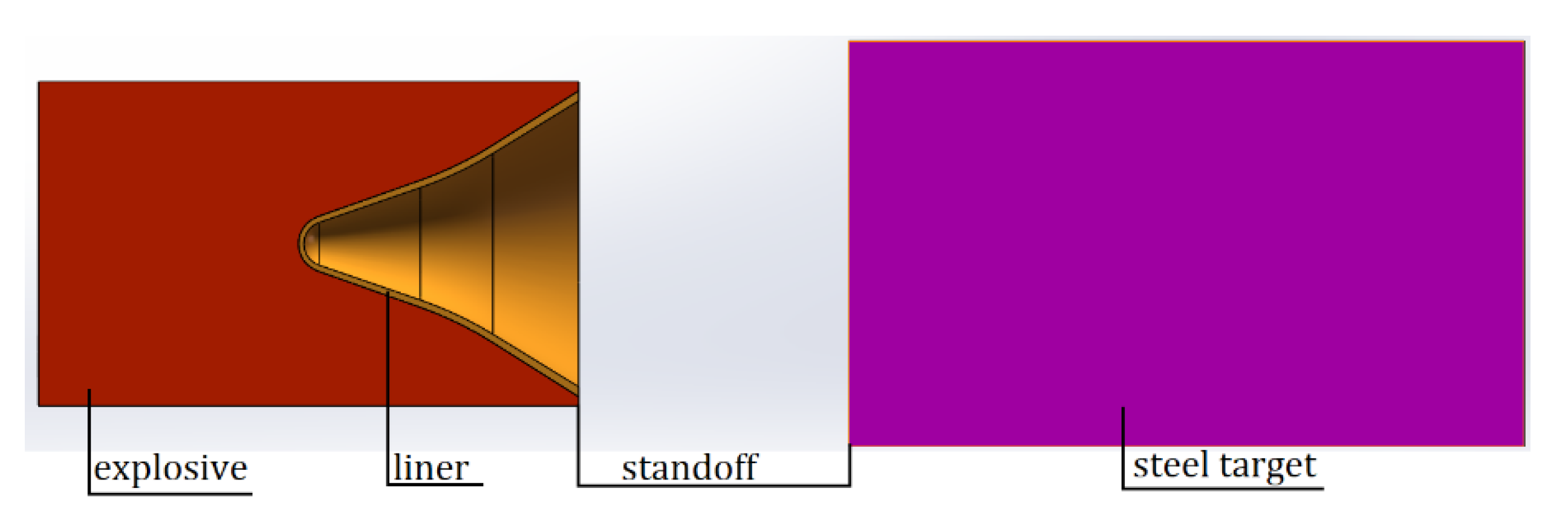
3.1. Warhead Structure Design
3.2. Penetration Model
4. Numerical Simulation
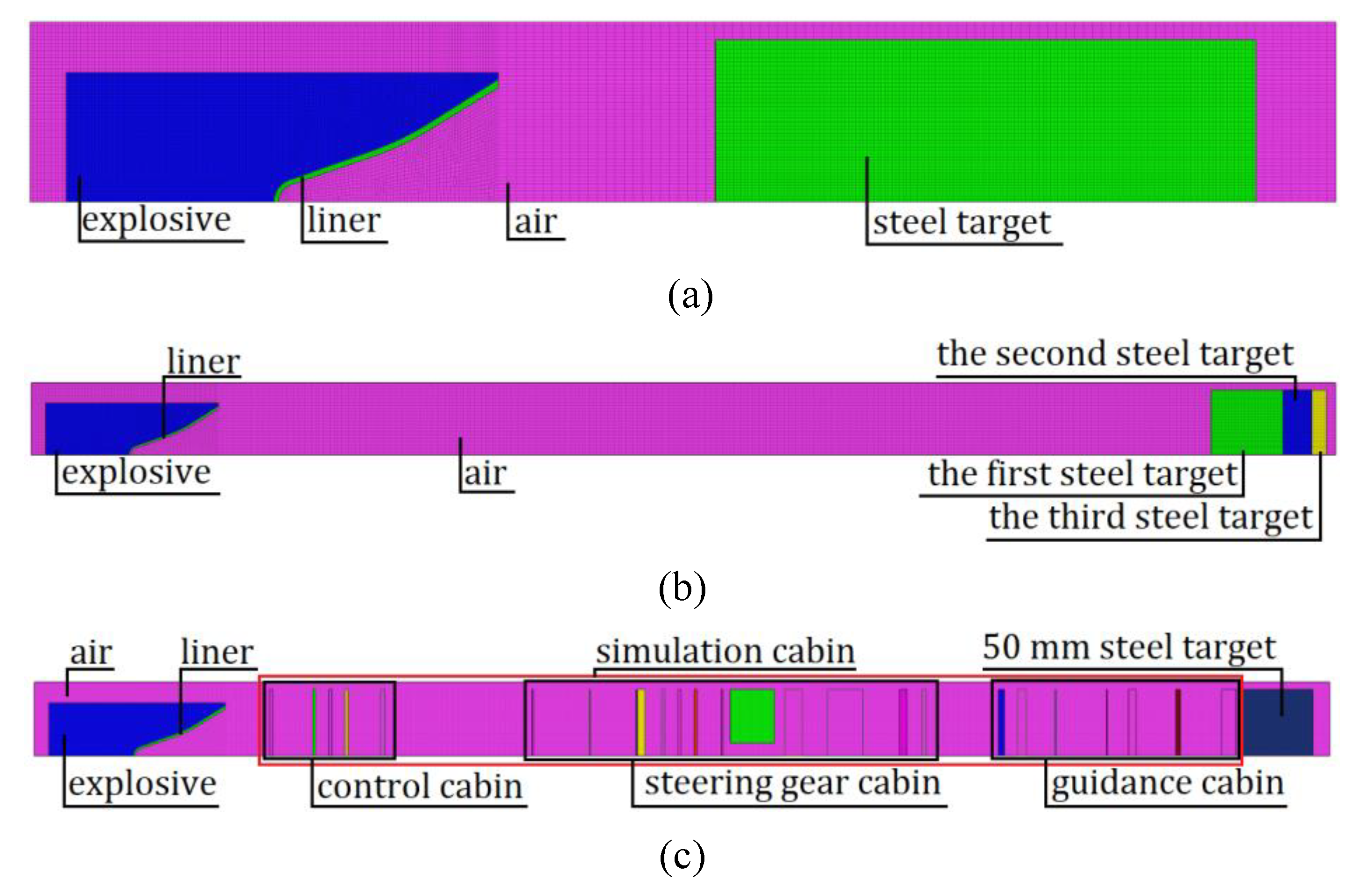
4.1. Finite Element Model
4.2. Material Constitutive Model and Parameters
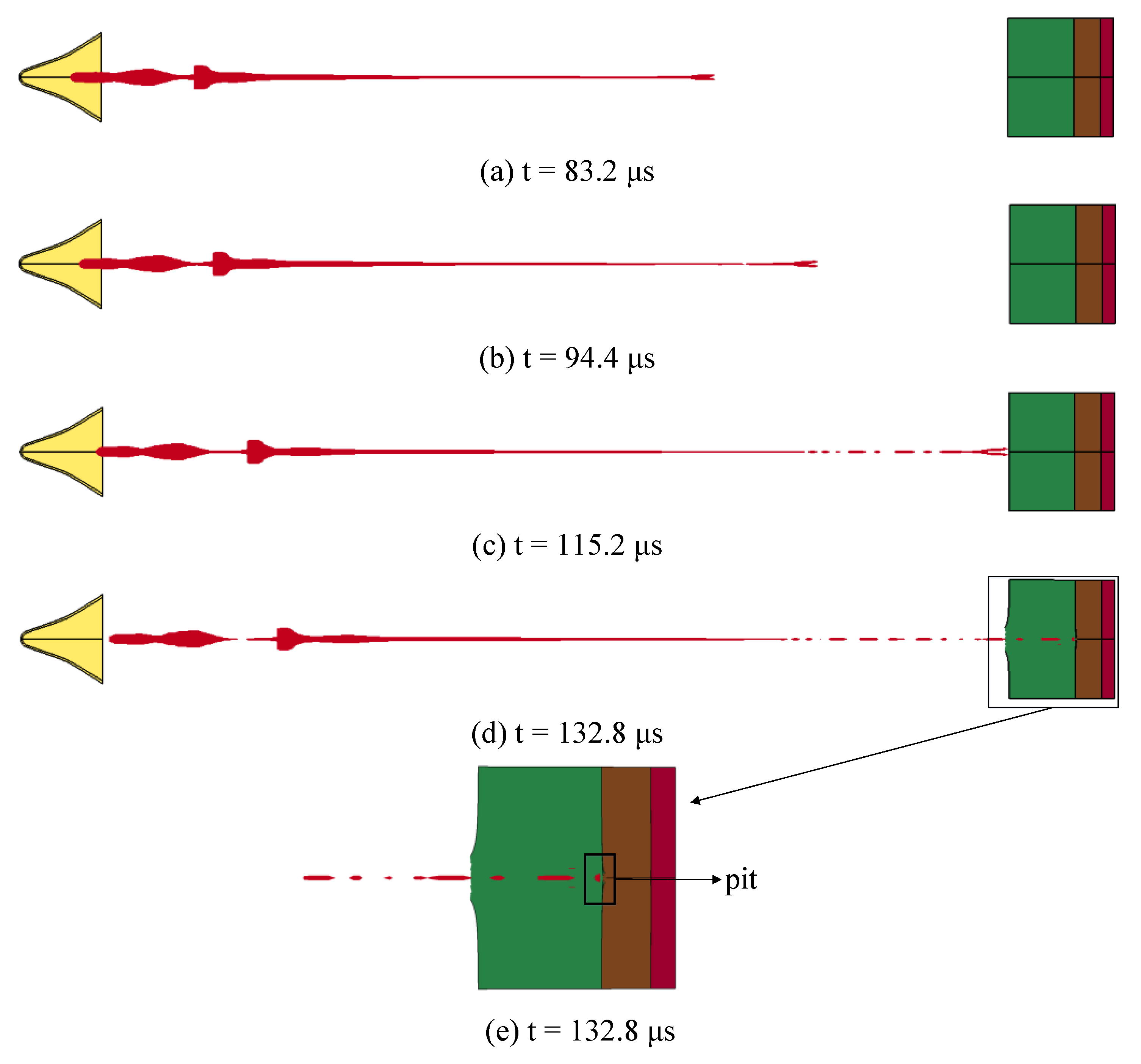
4.3. Numerical Simulation Results
5. Experimental Verification
5.1. Direct Penetration Test
5.1.1. Test Setup
5.1.2. Test Result
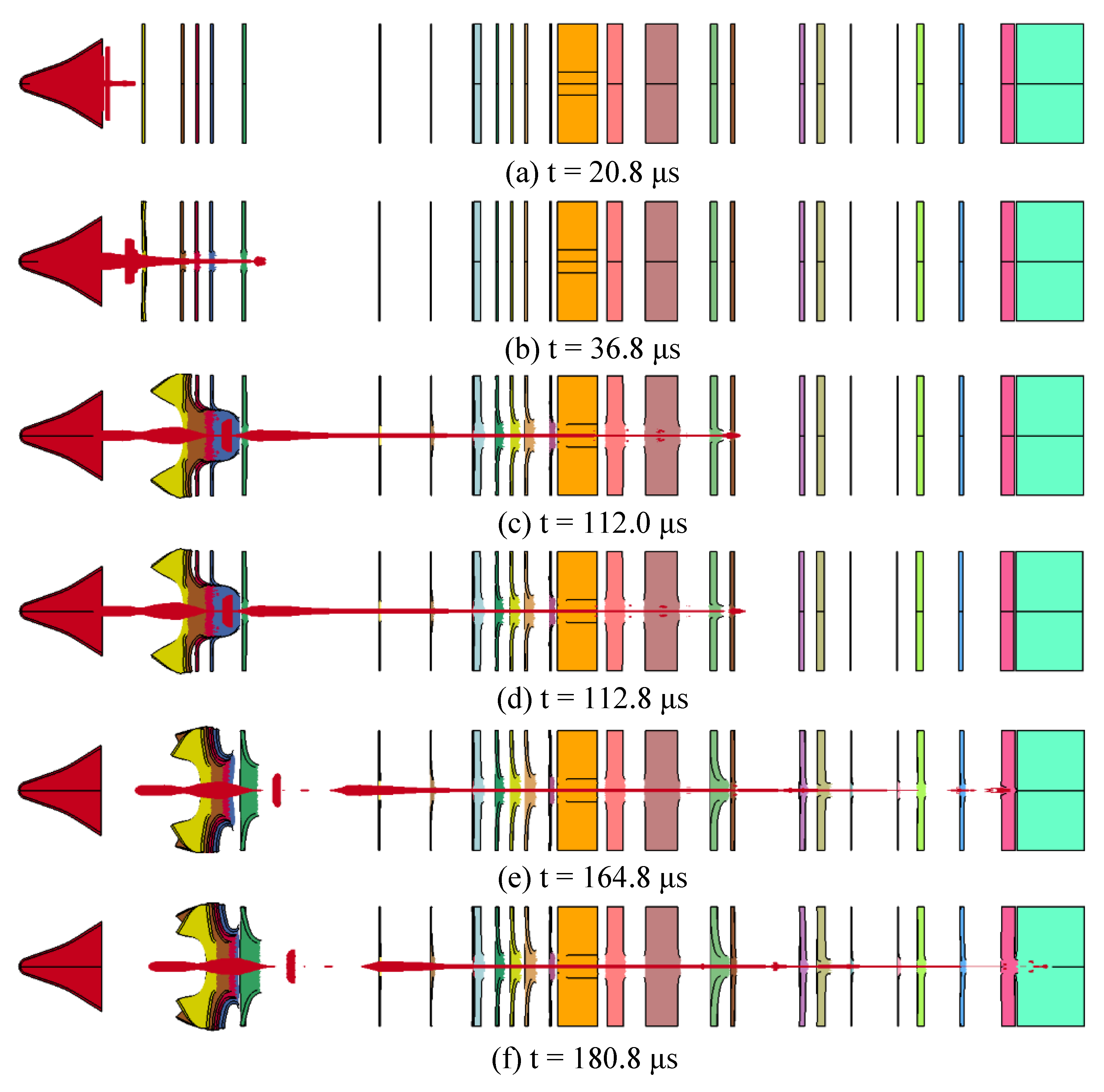
5.2. Penetration Simulation Cabin and Target Experiment
5.2.1. Test Setup
5.2.2. Test Result
6. Conclusions
- The optimal standoff of the SCJ warhead is 2 LD, and the DOP of the SCJ to the Q235 steel target is about 128 mm.
- The DOP of the SCJ into the Q235 steel target is about 50 mm at 10 LD standoff without the simulated cabin, compared with the DOP (128 mm) of the Q235 steel target at the optimal standoff, its penetration ability is reduced by about 61%. In other words, the penetration ability of the SCJ is weakened by 61% under the condition of non-optimal standoff.
- At 10 LD, the DOP of the residual jet into the Q235 steel target is about 30 mm after the penetration of the SCJ into the simulated cabin; compared with the penetration ability without the simulated cabin, the DOP decreases by 40%. In other words, the penetration ability of the SCJ is weakened by about 40% under the influence of the simulated cabin.
- Compared with the DOP of the Q235 steel target at the optimal standoff, the DOP of the SCJ to the Q235 steel target decreases by 76.5% under the combined influence of non-optimal standoff and simulated cabin, and the final DOP of the SCJ warhead is about 30 mm.
- When the diameter of the liner is 10 times the blast height, there is a certain error between the breach size of the first layer target plate obtained by the numerical simulation of direct penetration into the target plate and the test value. The error of the entry hole size is 0.3 mm × 0.5 mm and the error of the exit hole size is 0.6 mm × 0.2 mm. The penetration depth obtained by numerical simulation of penetration simulation cabin and target plate is also different from the experimental value, and the penetration depth error is 0.5 mm. The deviation may be caused by impurities in the fluid during the test, or a small amount of impurities on the target surface caused by the environment during the test, which will have an impact on the process of shaped charge jet penetrating the target. At the same time, the accuracy of the numerical simulation is also a reason. However, the error between the target opening size and the penetration depth is within 5%, which is in good agreement as a whole.
- If you want to eliminate this error, you can improve the mesh quality of the finite element model as much as possible and adopt more accurate numerical simulation calculations when the computer performance allows.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lu, F.Y.; Li, X.Y.; Lin, Y.L. Structure and Principle of Warhead; Science Press: Beijing, China, 2009. [Google Scholar]
- Yang, X.H.; Han, J.L.; Li, W.B. Design Method of Optimum Standoff for Bi-Conical Liner Shaped Charge Warhead. Trans. Beijing Inst. Technol. 2015, 35, 139–143. [Google Scholar]
- Lin, J.Q.; Zheng, Y.; Hao, Y.F.; Li, W.B.; Wang, X.M. Study on Impact Initiation of Cover Explosive by EFP at Different Explosion Height. Ordnance Ind. Autom. 2019, 38, 86–91. [Google Scholar]
- Liu, F.; Ren, X.J.; He, X. Engineering algorithm of shock wave propagation law in underground engineering under different blast height and explosion conditions. Energ. Mater. 2020, 28, 1076–1082. [Google Scholar]
- Zhu, M.J.; Gu, W.B.; Tang, Y.; Zeng, Z.; Xu, H.M. The Experimental and Numerical Simulation of the Standoff Effect to Penetration Properties. Explos. Mater. 2010, 39, 31–34. [Google Scholar]
- Held, M. Characterizing Shaped Charge Performance by Stand-Off Behavior. In Proceedings of the 7th International Symposium on Ballistics, Hague, The Netherlands, 19–21 April 1983; pp. 331–339. [Google Scholar]
- Held, M. Penetration Cutoff Velocities of Shaped Charge Jets. Propellants Explos. Pyrotech. 1988, 13, 111–119. [Google Scholar] [CrossRef]
- Shvetsov, G.A.; Matrosov, A.D.; Fedorov, S.V.; Babkin, A.V.; Lado, S.V. Effect of external magnetic fields on shaped-charge operation. Int. J. Impact Eng. 2011, 38, 521–526. [Google Scholar] [CrossRef]
- Ma, B.; Huang, Z.X.; Zu, X.D.; Xiao, Q.Q. Experimental study on external strong magnetic fields coupling with the shaped charge jet. Int. J. Impact Eng. 2016, 98, 88–96. [Google Scholar] [CrossRef]
- Ma, B.; Huang, Z.X.; Guan, Z.W.; Zu, X.D.; Jia, X.; Xiao, Q.Q. Research of the axial strong magnetic field applied at the initial period of inertial stretching stage of the shaped charge jet. Int. J. Impact Eng. 2018, 113, 54–60. [Google Scholar] [CrossRef]
- Ma, B.; Huang, Z.X.; Guan, Z.W.; Jia, X.; Xiao, Q.Q.; Zu, X.D. Theoretical analysis of the acceleration effect of the magnetic field on the shaped charge jet. Int. J. Mech. Sci. 2017, 133, 283–287. [Google Scholar] [CrossRef]
- Pyka, D.; Kurzawa, A.; Bocian, M.; Bajkowski, M.; Magier, M.; Sliwinski, J.; Jamroziak, K. Numerical and experimental studies of the Łk type shaped charge. Appl. Sci. 2020, 10, 6742. [Google Scholar] [CrossRef]
- Żochowski, P.; Warchoł, R.; Miszczak, M.; Nita, M.; Pankowski, Z.; Bajkowski, M. Experimental and Numerical Study on the PG-7VM Warhead Performance against High-Hardness Armor Steel. Materials 2021, 14, 3020. [Google Scholar] [CrossRef]
- Jia, X.; Huang, Z.X.; Zu, X.D.; Gu, X.H.; Xiao, Q.Q. Theoretical analysis of the disturbance of shaped charge jet penetrating a woven fabric rubber composite armor. Int. J. Impact Eng. 2014, 65, 69–78. [Google Scholar] [CrossRef]
- Jia, X.; Huang, Z.X.; Zu, X.D.; Gu, X.H.; Zhu, C.S.; Zhang, Z.W. Experimental study on the performance of woven fabric rubber composite armor subjected to shaped charge jet impact. Int. J. Impact Eng. 2013, 57, 134–144. [Google Scholar] [CrossRef]
- Wu, H.; Hu, F.; Fang, Q. A comparative study for the impact performance of shaped charge JET on UHPC targets. Def. Technol. 2019, 15, 506–518. [Google Scholar] [CrossRef]
- Wang, C.; Xu, W.L.; Yuen, S.C.K. Penetration of shaped charge into layered and spaced concrete targets. Int. J. Impact Eng. 2018, 112, 193–206. [Google Scholar] [CrossRef]
- Men, J.B.; Jiang, J.W.; Wang, S.Y. Fundamentals of Numerical Simulation for Explosion and Shock Problems; Beijing Institute of Technology Press: Beijing, China, 2015. [Google Scholar]
- Liu, J.F.; Long, Y.; Ji, C.; Zhong, M.S.; Liu, Q. The influence of liner material on the dynamic response of the finite steel target subjected to high velocity impact by explosively formed projectile. Int. J. Impact Eng. 2017, 109, 264–275. [Google Scholar] [CrossRef]
- Yin, J.P.; Han, Y.Y.; Wang, X.F.; Chang, B.H.; Dong, F.D.; Xu, Y.J. A new charge structure based on computer modeling and simulation analysis. J. Vis. Commun. Image Represent. 2019, 64, 102613. [Google Scholar] [CrossRef]
- Steinberg, D.J. Equation of State and Strength Properties of Selected Materials; UCRL-MA-106439; Lawrence Livermore National Laboratory: Livermore, CA, USA, 2003. [Google Scholar]

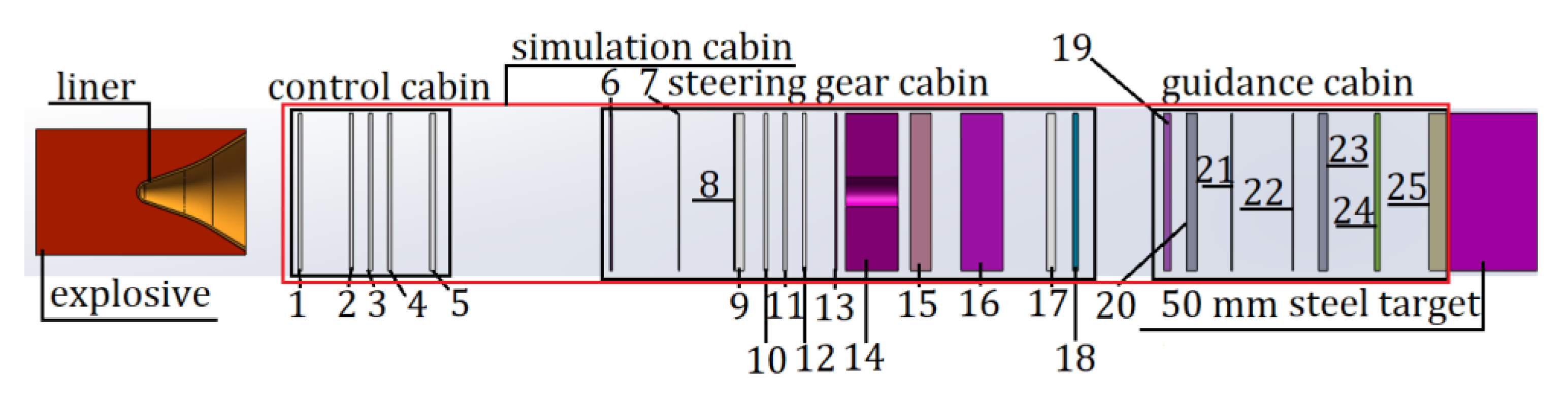






| Penetrating Medium | Layer | Name | Materials | Thickness | Distance to The Upper Layer | |
|---|---|---|---|---|---|---|
| Simulation Cabin | Control cabin | 1 | Control cabin shell | Aluminum | 2 mm | 0 |
| 2 | Circuit board 1 | Printed circuit board material | 2 mm | 27.3 mm | ||
| 3 | Circuit board 2 | 2 mm | 9 mm | |||
| 4 | Circuit board 3 | 2 mm | 9 mm | |||
| 5 | Control cabin shell | Aluminum | 3 mm | 22 mm | ||
| Steering Gear cabin | 6 | Power connector | Steel | 1 mm | 100 mm | |
| 7 | Analog power 1 | Aluminum | 0.5 mm | 38 mm | ||
| 8 | Analog power 2 | 0.5 mm | 31 mm | |||
| 9 | Steering gear cabin shell | 5 mm | 0.5 mm | |||
| 10 | Circuit board 1 | Printed circuit board material | 2 mm | 11.5 mm | ||
| 11 | Circuit board 2 | 2 mm | 9 mm | |||
| 12 | Circuit board 3 | 2 mm | 9 mm | |||
| 13 | Steering gear cabin shell | Aluminum | 1 mm | 16.5 mm | ||
| 14 | Steering gear shaft 1 | Steel | 30 mm | 5 mm | ||
| 15 | Steering gear shaft 2 | 12 mm | 7 mm | |||
| 16 | Electrical machinery | 24 mm | 17 mm | |||
| 17 | Circuit board 4 | Printed circuit board material | 5 mm | 25 mm | ||
| 18 | Power connector bracket | Steel | 3 mm | 10 mm | ||
| Guidance cabin | 19 | Guidance cabin shell | Aluminum | 4 mm | 49 mm | |
| 20 | Circuit board | Printed circuit board material | 6 mm | 9 mm | ||
| 21 | Analog power 1 | Aluminum | 0.5 mm | 19.5 mm | ||
| 22 | Analog power 2 | 0.5 mm | 34.5 mm | |||
| 23 | Analog gyroscope sensor | 5 mm | 14.5 mm | |||
| 24 | Guidance cabin shell | 3 mm | 27 mm | |||
| 25 | Glass hood | Printed circuit board material | 10 mm | 28 mm | ||
| Steel plate | 1 | The first steel plate | Q235 Steel | 50 mm | 2 mm | |
| Material | A | B | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Explosive | 1.71 | 0.83 | 28.6 | 8.5 | 524.23 | 7.678 | 34 | 1.1 | 0.34 | 1 |
| Material | G (GPa) | A (MPa) | B (MPa) | C | S | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Copper | 8.93 | 46.5 | 90 | 292 | 0.31 | 0.025 | 1.09 | 1356 | 293 | 0.39 | 1.49 |
| Material | E (GPa) | NUXY | Yield Stress (MPa) | |
|---|---|---|---|---|
| Q235 steel | 7.8 | 207 | 0.3 | 355 |
| Aluminum | 2.7 | 71 | 0.33 | 90 |
| Printed circuit board material | 1.19 | 7.8 | - | - |
| Material | T (K) | |||||
|---|---|---|---|---|---|---|
| Air | 1.225 | 1.4 | 1.005 | 0.718 | 288.2 | 206,800 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, Y.; He, G.; Liu, Y.; Guo, Z.; Qiao, Z. Study on Penetration Performance of Rear Shaped Charge Warhead. Materials 2021, 14, 6526. https://doi.org/10.3390/ma14216526
Du Y, He G, Liu Y, Guo Z, Qiao Z. Study on Penetration Performance of Rear Shaped Charge Warhead. Materials. 2021; 14(21):6526. https://doi.org/10.3390/ma14216526
Chicago/Turabian StyleDu, Yanan, Guanglin He, Yukuan Liu, Zhaoxuan Guo, and Zenghui Qiao. 2021. "Study on Penetration Performance of Rear Shaped Charge Warhead" Materials 14, no. 21: 6526. https://doi.org/10.3390/ma14216526
APA StyleDu, Y., He, G., Liu, Y., Guo, Z., & Qiao, Z. (2021). Study on Penetration Performance of Rear Shaped Charge Warhead. Materials, 14(21), 6526. https://doi.org/10.3390/ma14216526






