Effect of Elevated Temperatures on the Mechanical Properties of a Direct Laser Deposited Ti-6Al-4V
Abstract
:1. Introduction
2. Materials and Methods
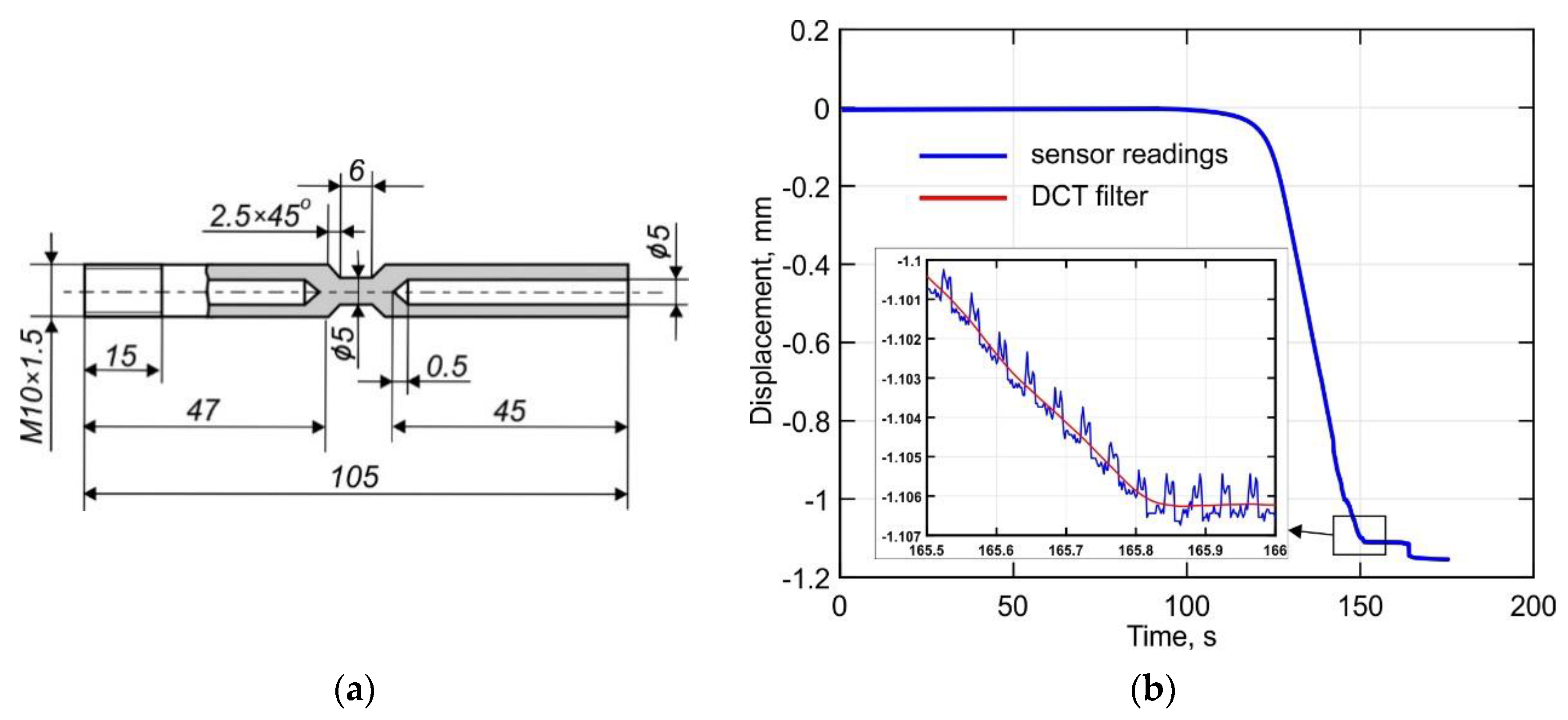
2.1. Specimens
2.2. Optical and Scanning Electron Microscopy
2.3. Tensile Tests at Elevated Temperatures
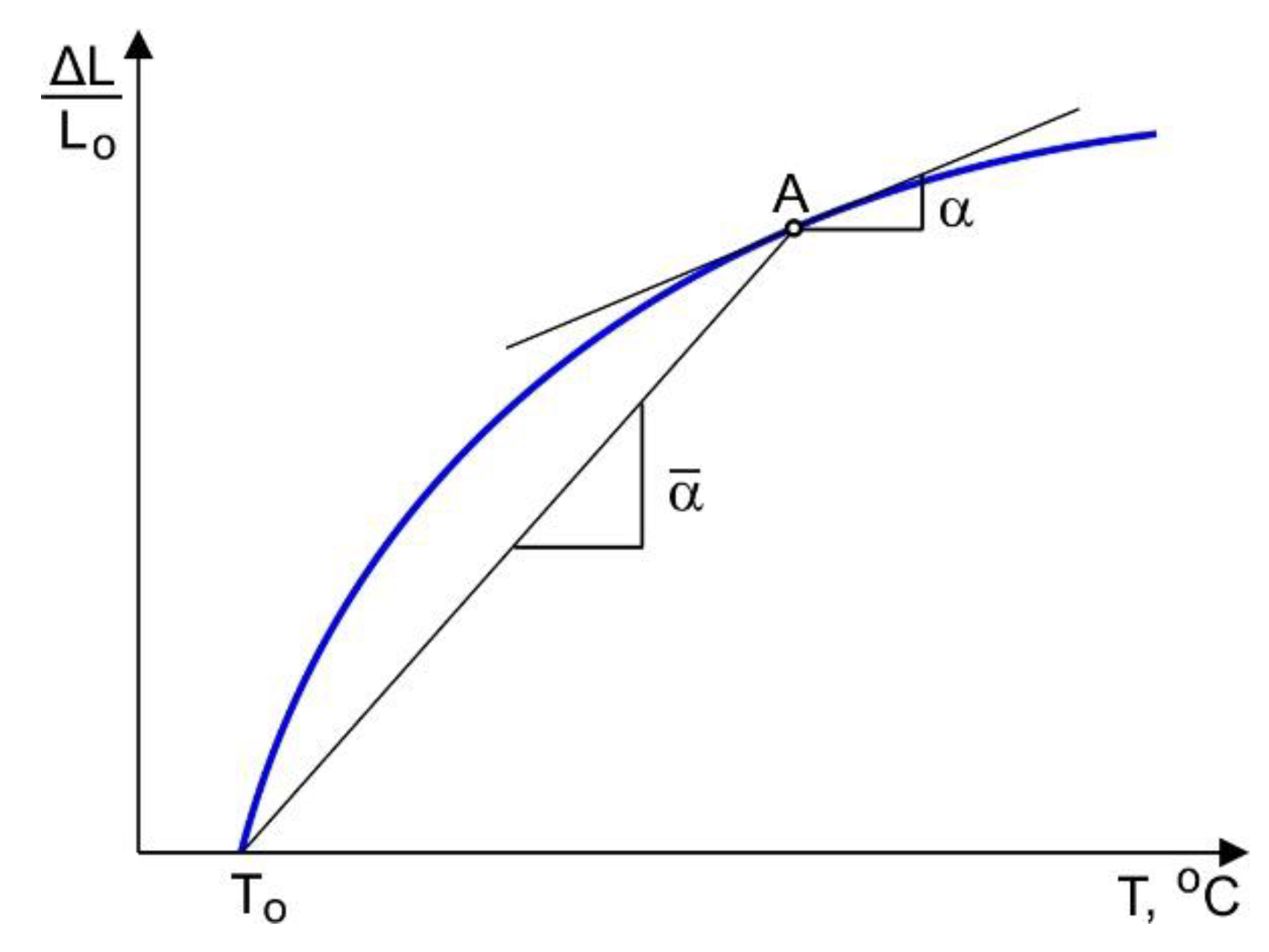
2.4. Thermal Expansion Tests
- -
- for instantaneous CTE:
- -
- for secant CTE:
2.5. Stress Relaxation Tests
3. Results and Discussion
3.1. Microstructure of the DLD-Processed Ti-6Al-4V Alloy
3.2. Effect of the Temperature on the Fracture Behavior
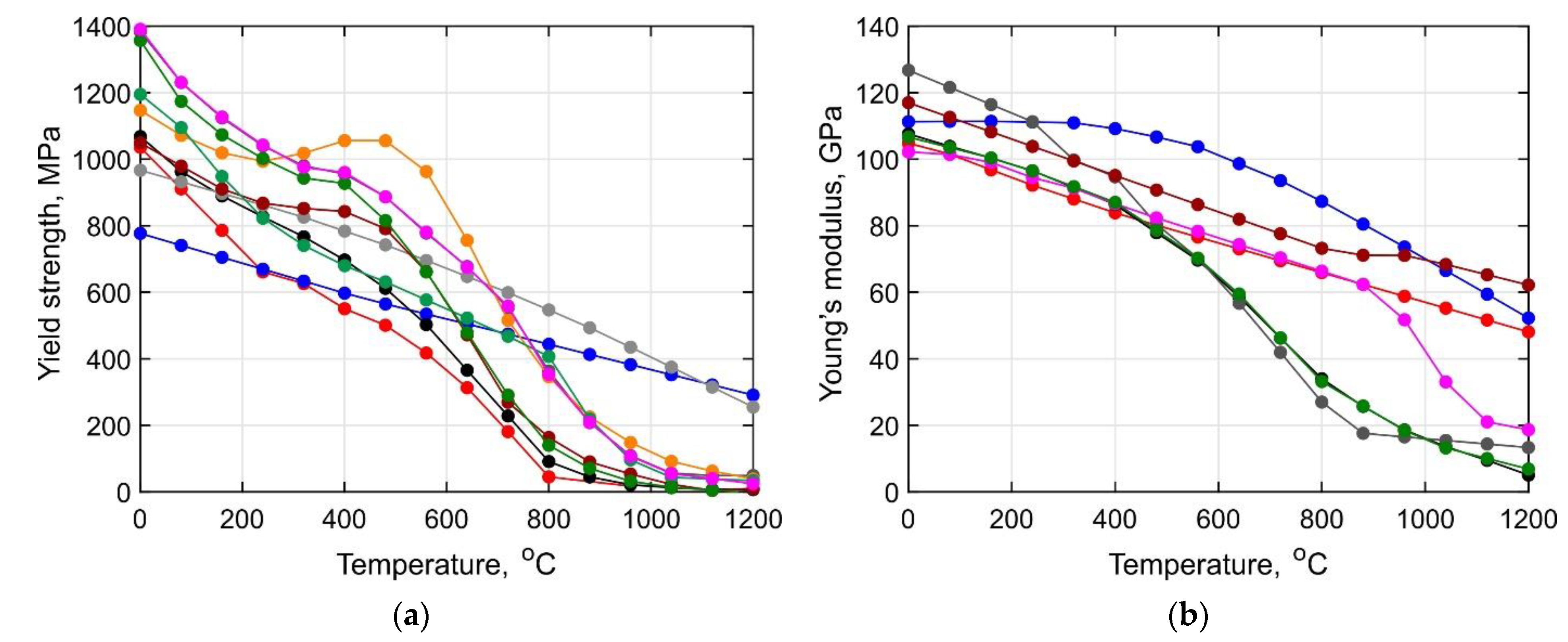
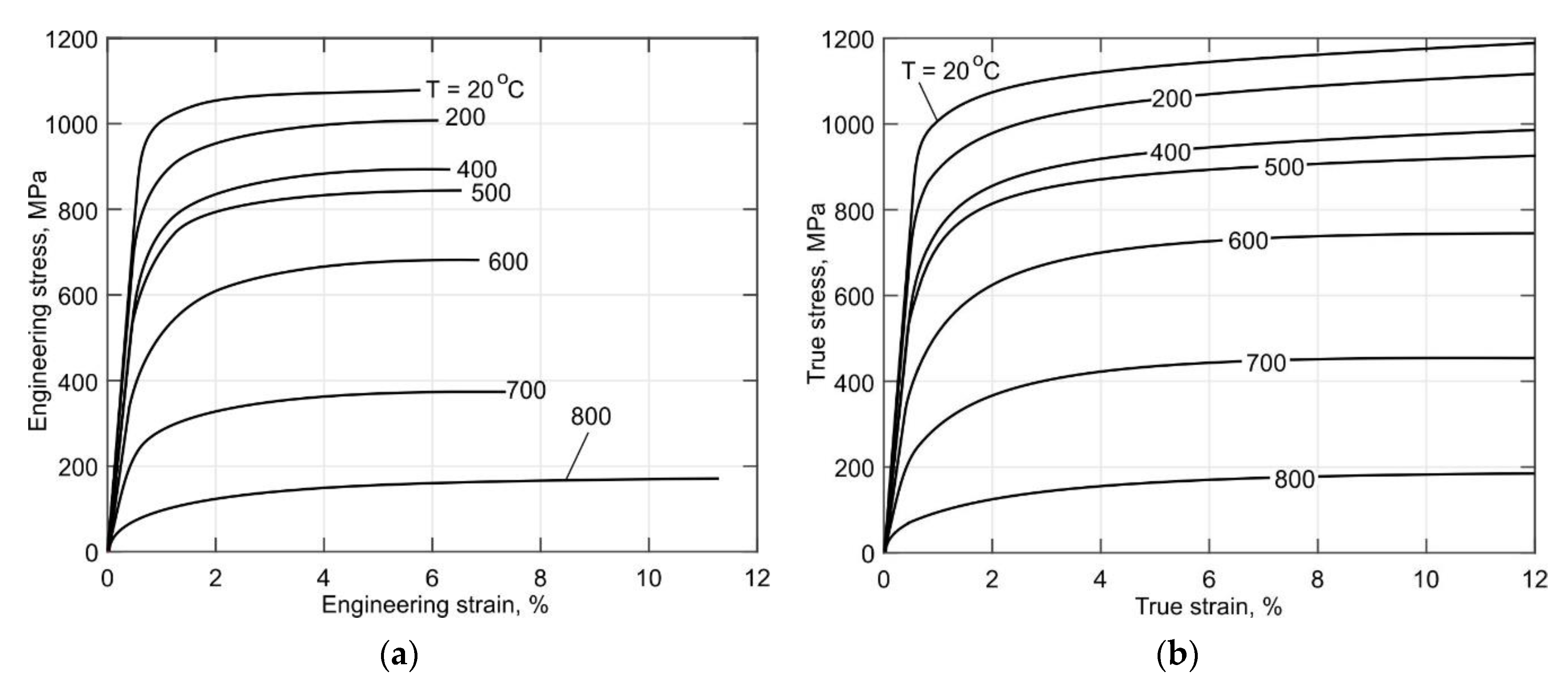
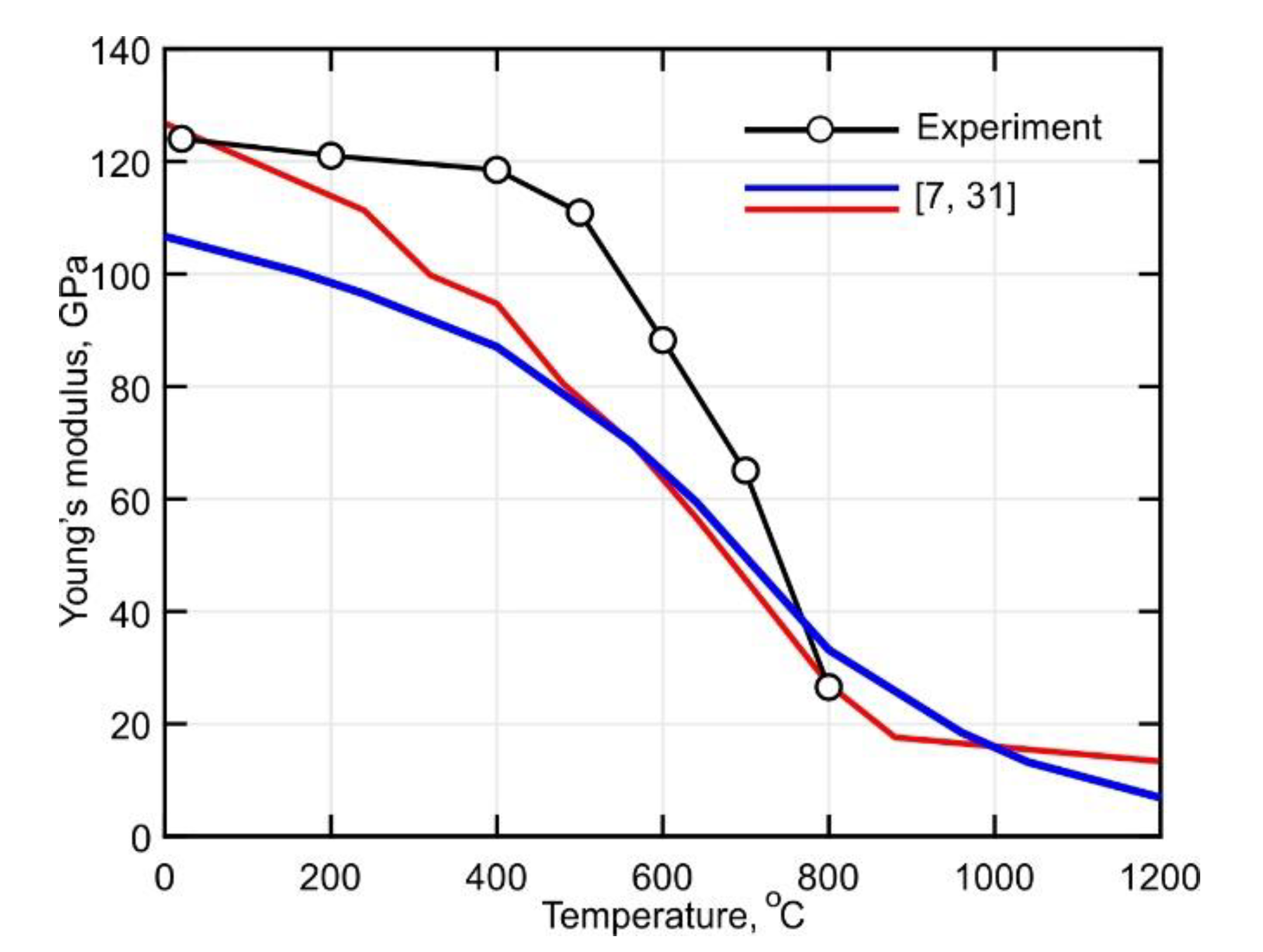
3.3. Short-Term Mechanical Properties of the Ti-6Al-4V Alloy over a Wide Temperature Range
3.4. Temperature Dependence of the Thermal Expansion Coefficient
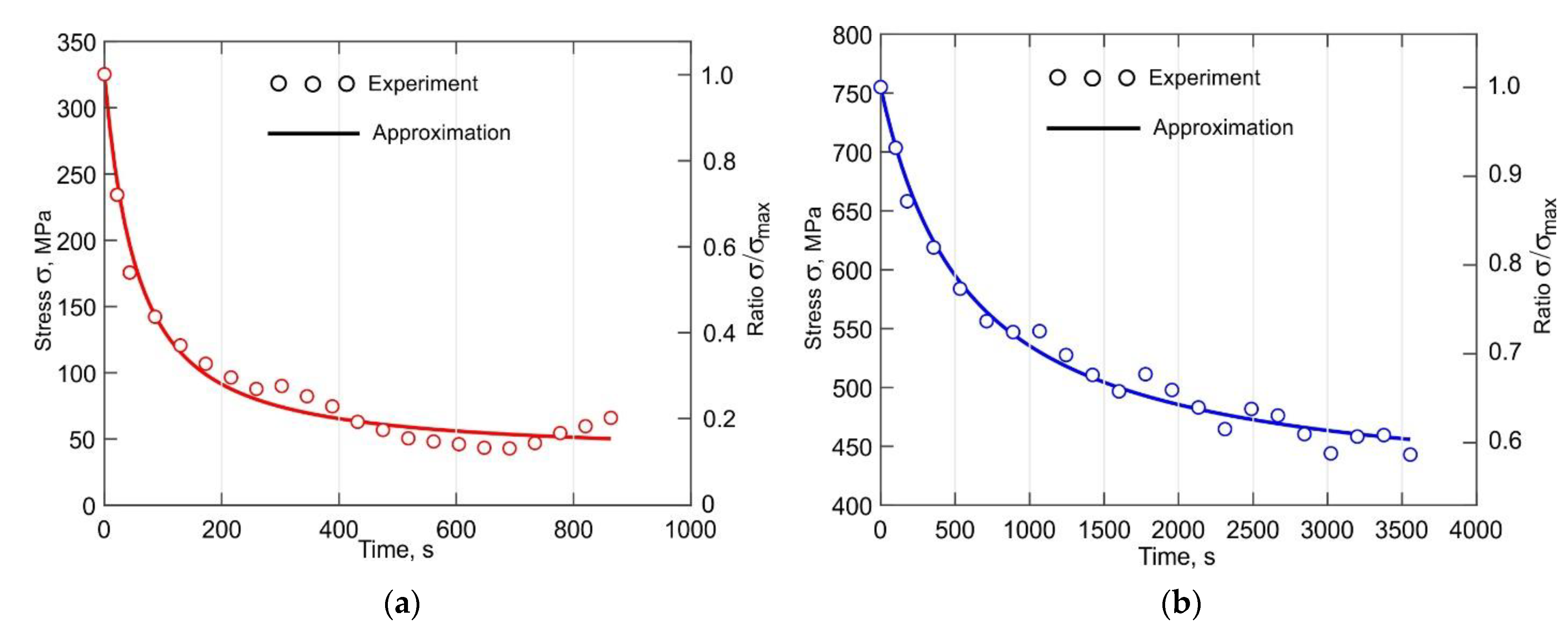
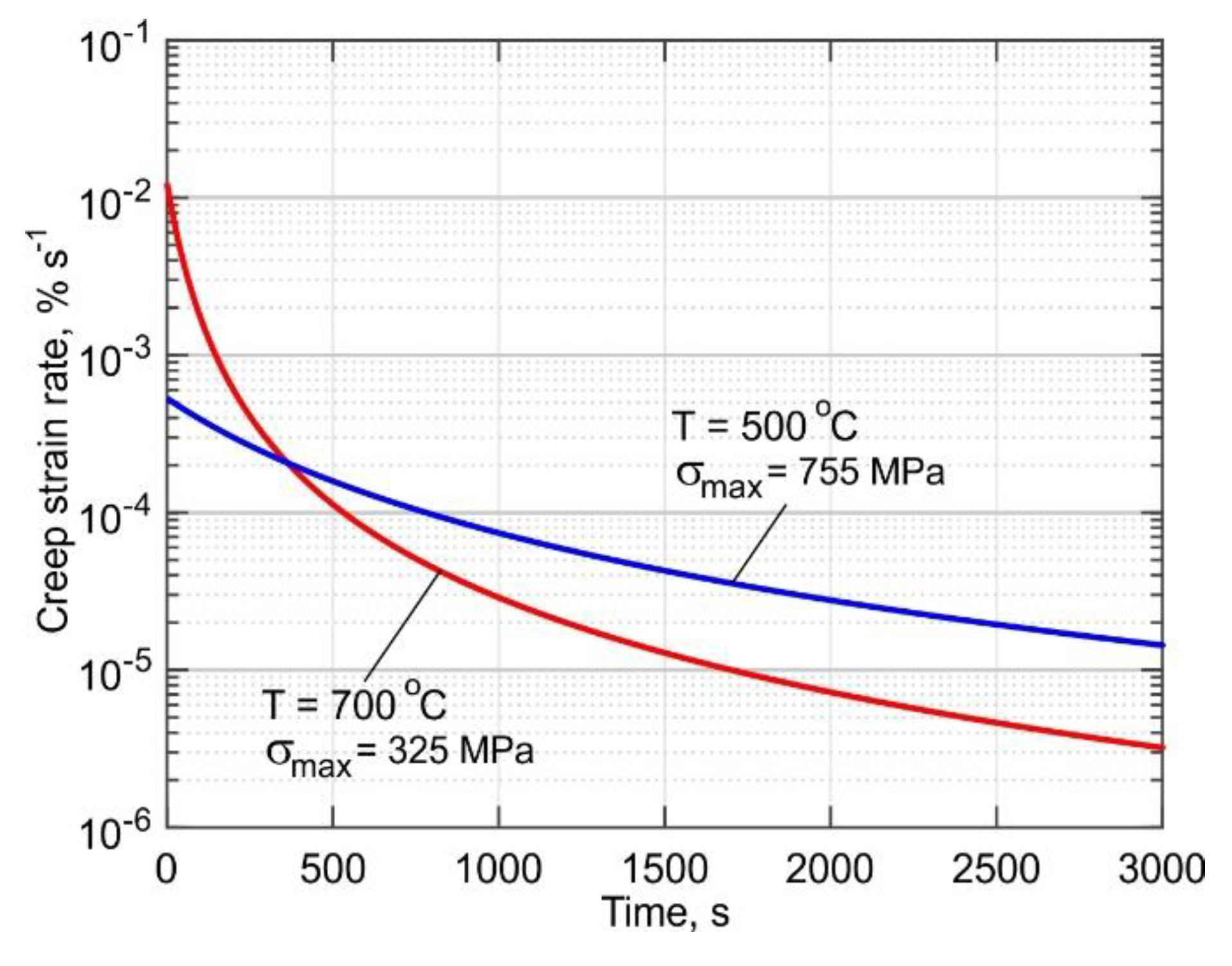
3.5. Analysis of the Stress Relaxation
4. Conclusions
- The microstructure of the buildup obtained by direct laser deposition with inter-pass temperatures in the range of 60–80 °C consists of a lamellar α’-phase and a small amount of residual β-phase.
- According to the obtained stress curves, the yield strength decreases gradually by approximately 40% when the temperature increases to 500 °C. Furthermore, it was determined that the softening rate increases significantly upon further heating
- It was found that the DLD-processed Ti-6Al-4V alloy has a Young’s modulus with greater thermal stability than conventionally processed alloys. At 500 °C, the Young’s modulus of the alloy is about 46% higher than that of the wrought alloy.
- The analysis of the CTE curves showed that a diffusion-controlled transformation of α’→ α + β in the temperature range between 400 °C and 600 °C leads to a 20% decrease in the CTE. In addition, the α + β → β transformation was determined to start at temperatures above 800 °C.
- The stress relaxation process was found to have a decisive influence on the formation of the residual stresses at temperatures above 700 °C, which is especially important in the production of small-sized parts by the DLD method.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- DebRoy, T.; Wei, H.L.; Zuback, J.S.; Mukherjee, T.; Elmer, J.W.; Milewski, J.O.; Beese, A.M.; Wilson-Heid, A.; De, A.; Zhang, W. Additive manufacturing of metallic components-Process, structure and properties. Prog. Mater. Sci. 2018, 92, 112–224. [Google Scholar] [CrossRef]
- Mukherjee, T.; Zuback, J.S.; Zhang, W.; DebRoy, T. Residual stresses and distortion in additively manufactured compositionally graded and dissimilar joints. Comput. Mater. Sci. 2018, 143, 325–337. [Google Scholar] [CrossRef]
- Blakey-Milner, B.; Gradl, P.; Snedden, G.; Brooks, M.; Pitot, J.; Lopez, E.; Leary, M.; Berto, F.; du Plessis, A. Metal additive manufacturing in aerospace: A review. Mater. Des. 2021, 209, 110008. [Google Scholar] [CrossRef]
- Gouge, M.; Michaleris, P. Thermo-Mechanical Modeling of Additive Manufacturing, 1st ed.; Butterworth-Heinemann: Oxford, UK, 2017. [Google Scholar]
- Papadakis, L. Experimental and computational appraisal of the shape accuracy of a thin-walled virole aero-engine casing manufactured by means of laser metal deposition. Prod. Eng. Res. Devel. 2017, 11, 389–399. [Google Scholar] [CrossRef]
- Babkin, K.; Zemlyakov, E.; Ivanov, S.; Vildanov, A.; Topalov, I.; Turichin, G. Distortion prediction and compensation in direct laser deposition of large axisymmetric Ti-6Al-4V part. Procedia CIRP 2020, 94, 357–361. [Google Scholar] [CrossRef]
- Mukherjee, T.; Zhang, W.; DebRoy, T. An improved prediction of residual stresses and distortion in additive manufacturing. Comput. Mater. Sci. 2017, 126, 360–372. [Google Scholar] [CrossRef] [Green Version]
- Seshacharyulu, T.; Medeiros, S.C.; Frazier, W.G.; Prasad, Y.V.R.K. Microstructural mechanisms during hot working of commercial grade Ti–6Al–4V with lamellar starting structure. Mater. Sci. Eng. A 2002, 325, 112–125. [Google Scholar] [CrossRef]
- Rangaswamy, P.; Choo, H.; Prime, M.B.; Bourke, M.A.; Larsen, J.M. High temperature stress assessment in SCS-6/Ti-6Al-4V composite using neutron diffraction and finite element modeling. In International Conference on Processing & Manufacturing of Advanced Materials; Los Alamos National Laboratory: Las Vegas, NV, USA, 2000. [Google Scholar]
- Denlinger, E.R.; Michaleris, P. Effect of stress relaxation on distortion in additive manufacturing process modeling. Addit. Manuf. 2016, 12, 51–59. [Google Scholar] [CrossRef] [Green Version]
- Lu, X.; Lin, X.; Chiumenti, M.; Cervera, M.; Li, J.; Ma, L.; Wei, L.; Hu, Y.; Huang, W. Finite element analysis and experimental validation of the thermomechanical behavior in laser solid forming of Ti-6Al-4V. Addit. Manuf. 2018, 21, 30–40. [Google Scholar] [CrossRef]
- Tiley, J.S. Modeling of Microstructure Property Relationships in Ti-6Al-4V. Ph.D. Thesis, Ohio State University, Columbus, OH, USA, 2002. [Google Scholar]
- Donachie, M.J. Titanium: A Technical Guide, 2nd ed.; ASM International: Materials Park, OH, USA, 1988. [Google Scholar]
- Moiseyev, V.N. Titanium Alloys: Russian Aircraft and Aerospace Applications; CRC Press Taylor & Francis Group: Boca Raton, FL, USA, 2006. [Google Scholar]
- Boyer, R.; Collings, E.W.; Welsch, G. Properties Handbook: Titanium Alloys; ASM International: Materials Park, OH, USA, 1994. [Google Scholar]
- Mills, K.C. Recommended Values of Thermophysical Properties for Selected Commercial Alloys; Woodhead Publishing: Cambridge, UK, 2002. [Google Scholar]
- Ilyin, A.A.; Kolachev, B.A.; Polkin, I.S. Titanium Alloys. Composition, Structure, Properties. Handbook; VILS-MATI: Moscow, Russia, 2009. (In Russian) [Google Scholar]
- ASTM F2924-14 Standard Specification for Additive Manufacturing Titanium-6 Aluminum-4 Vanadium with Powder Bed Fusion; ASTM International: West Conshohocken, PA, USA, 2021.
- Ding, R.; Guo, Z.X.; Wilson, A. Microstructural evolution of a Ti-6Al-4V alloy during thermomechanical processing. Mater. Sci. Eng. A 2002, 327, 233–245. [Google Scholar] [CrossRef]
- Weiss, I.; Froes, F.H.; Eylon, D.; Welsch, D.G.E. Modification of alpha morphology in Ti-6Al-4V by thermomechanical processing. Metall. Mater. Trans. A 1986, 17, 1935–1947. [Google Scholar] [CrossRef]
- Liu, S.; Shin, Y.C. Additive manufacturing of Ti6Al4V alloy: A review. Mater. Des. 2019, 164, 107552. [Google Scholar] [CrossRef]
- Lewandowski, J.J.; Seifi, M. Metal Additive Manufacturing: A Review of Mechanical Properties. Annu. Rev. Mater. Res. 2016, 46, 151–186. [Google Scholar] [CrossRef] [Green Version]
- Lin, Y.C.; Jiang, X.-Y.; Shuai, C.; Zhao, C.-Y.; He, D.-G.; Chen, M.-S.; Chen, C. Effects of initial microstructures on hot tensile deformation behaviors and fracture characteristics of Ti-6Al-4V alloy. Mater. Sci. Eng. A 2018, 711, 293–302. [Google Scholar] [CrossRef]
- Paghandeh, M.; Zarei-Hanzaki, A.; Abedi, H.R.; Vahidshad, Y. On the warm temperature strain accommodation mechanisms of Ti-6Al-4V alloy holding different starting microstructures. J. Mater. Res. Technol. 2021, 14, 496–506. [Google Scholar] [CrossRef]
- Rangaswamy, P. Comparison of residual strains measured by X-ray and neutron diffraction in a titanium (Ti–6Al–4V) matrix composite. Mater. Sci. Eng. A 1999, 259, 209–219. [Google Scholar] [CrossRef] [Green Version]
- Zhao, X.; Iyer, A.; Promoppatum, P.; Yao, S.-C. Numerical modeling of the thermal behavior and residual stress in the direct metal laser sintering process of titanium alloy products. Addit. Manuf. 2017, 14, 126–136. [Google Scholar] [CrossRef]
- Chiumenti, M.; Cervera, M.; Dialami, N.; Wu, B.; Jinwei, L.; Agelet de Saracibar, C. Numerical modeling of the electron beam welding and its experimental validation. Finite Elem. Anal. Des. 2016, 121, 118–133. [Google Scholar] [CrossRef] [Green Version]
- Cao, J.; Gharghouri, M.A.; Nash, P. Finite-element analysis and experimental validation of thermal residual stress and distortion in electron beam additive manufactured Ti-6Al-4V build plates. J. Mater. Process. Technol. 2016, 237, 409–419. [Google Scholar] [CrossRef]
- Robert, Y. Simulation Numérique du Soudage du TA6V par Laser YAG Impulsionnel: Caractérisation Expérimentale et Modélisation des Aspects Thermomécaniques Associés à ce Proceed. Ph.D. Thesis, École Nationale Supérieure des Mines de Paris, Paris, France, 2007. (In French). [Google Scholar]
- MSC Software, Simufact Additive, Material Database. 2016. Available online: https://www.mscsoftware.com/product/simufact-additive (accessed on 28 September 2021).
- Babu, B. Physically Based Model for Plasticity and Creep of Ti-6Al-4V. Ph.D. Thesis, Luleå University of Technology, Luleå, Sweden, 2008. [Google Scholar]
- Babu, B.; Lundbäck, A.; Lindgren, L.-E. Simulation of Ti-6Al-4V Additive Manufacturing Using Coupled Physically Based Flow Stress and Metallurgical Model. Materials 2019, 12, 3844. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Liu, Y.J.; Chen, J.; Wang, H.L.; Zhang, Z.Q.; Lu, Y.J.; Wu, S.Q.; Lin, J.X. Crystallographic features of α variants and β phase for Ti-6Al-4Valloy fabricated by selective laser melting. Mater. Sci. Eng. A 2017, 707, 548–558. [Google Scholar] [CrossRef]
- Saboori, A.; Abdi, A.; Fetami, S.A.; Marchese, G.; Biamino, S.; Mirzadeh, H. Hot deformation behavior and flow stress modeling of Ti–6Al–4V alloy produced via electron beam melting additive manufacturing technology in single β-phase field. Mater. Sci. Eng. A 2020, 792, 139822. [Google Scholar] [CrossRef]
- Bambach, M.; Sizova, I.; Szyndler, J.; Bennett, J.; Hyatt, G.; Cao, J.; Papke, T.; Merklein, M. On the hot deformation behavior of Ti-6Al-4V made by additive manufacturing. J. Mater. Process. Technol. 2021, 288, 116840. [Google Scholar] [CrossRef]
- Song, J.; Han, Y.; Fang, M.; Hu, F.; Ke, L.; Li, Y.; Lei, L.; Lu, W. Temperature sensitivity of mechanical properties and microstructure during moderate temperature deformation of selective laser melted Ti-6Al-4V alloy. Mater. Charact. 2020, 165, 110342. [Google Scholar] [CrossRef]
- Li, P.-H.; Guo, W.-G.; Huang, W.-D.; Su, Y.; Lin, X.; Yuan, K.-B. Thermomechanical response of 3D laser-deposited Ti-6Al-4V alloy over a wide range of strain rates and temperatures. Mater. Sci. Eng. A 2015, 647, 34–42. [Google Scholar] [CrossRef]
- Motoyama, Y.; Tokunaga, H.; Kajino, S.; Okane, T. Stress-strain behavior of a selective laser melted Ti-6Al-4V at strain rates of 0.001–1/s and temperatures 20–1000 °C. J. Mater. Process. Technol. 2021, 294, 117141. [Google Scholar] [CrossRef]
- ASTM F136-02a Standard Specification for Wrought Titanium-6 Aluminum-4 Vanadium ELI (Extra Low Interstitial) Alloy for Surgical Implant Applications (UNS R56401); ASTM International: West Conshohocken, PA, USA, 2002.
- ASM Handbook, Metallography and Microstructures; ASM Handbook series; ASM International: Materials Park, OH, USA, 2004; Volume 9.
- Garcia, D. Robust smoothing of gridded data in one and higher dimensions with missing values. Comput. Stat. Data Anal. 2010, 54, 1167–1178. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Oppenheim, A.V.; Schafer, R.W. Discrete-Time Signal Processing, 3rd ed.; Prentice-Hall: Hoboken, NJ, USA, 2010. [Google Scholar]
- Dennis, J.E., Jr. Nonlinear Least-Squares. In The State of the Art in Numerical Analysis; Jacobs, D., Ed.; Academic Press: New York, NY, USA, 1977; pp. 269–312. [Google Scholar]
- ASTM E328-21, Standard Test Methods for Stress Relaxation for Materials and Structures; ASTM International: West Conshohocken, PA, USA, 2021.
- Wu, B.; Pan, Z.; Ding, D.; Cuiuri, D.; Li, H. Effects of heat accumulation on microstructure and mechanical properties of Ti6Al4V alloy deposited by wire arc additive manufacturing. Addit. Manuf. 2018, 23, 151–160. [Google Scholar] [CrossRef]
- Foster, B.K.; Beese, A.M.; Keist, J.S.; McHale, E.T.; Palmer, T.A. Impact of Interlayer Dwell Time on Microstructure and Mechanical Properties of Nickel and Titanium Alloys. Metall. Mater. Trans. A 2017, 48, 4411–4422. [Google Scholar] [CrossRef]
- Song, T.; Dong, T.; Lu, S.L.; Kondoh, K.; Das, R.; Brandt, M.; Qian, M. Simulation-informed laser metal powder deposition of Ti-6Al-4V with ultrafine α-β lamellar structures for desired tensile properties. Addit. Manuf. 2021, 46, 102139. [Google Scholar]
- Xiao, Y.; Cagle, M.; Mujahid, S.; Liu, P.; Wang, Z.; Yang, W.; Chen, L. A gleeble-assisted study of phase evolution of Ti-6Al-4V induced by thermal cycles during additive manufacturing. J. Alloys Compd. 2021, 860, 158409. [Google Scholar] [CrossRef]
- Li, X.; Tan, W. Numerical investigation of effects of nucleation mechanisms on grain structure in metal additive manufacturing. Comput. Mater. Sci. 2018, 153, 159–169. [Google Scholar] [CrossRef]
- Lin, J.J.; Lv, Y.H.; Liu, Y.X.; Xu, B.S.; Sun, Z.; Li, Z.G.; Wu, Y.X. Microstructural evolution and mechanical properties of Ti-6Al-4V wall deposited by pulsed plasma arc additive manufacturing. Mater. Des. 2016, 102, 30–40. [Google Scholar] [CrossRef]
- Klimova-Korsmik, O.G.; Turichin, G.A.; Shalnova, S.A.; Gushchina, M.O.; Cheverikin, V.V. Structure and properties of Ti-6Al-4V titanium alloy products obtained by direct laser deposition and subsequent heat treatment. J. Phys. Conf. Ser. 2018, 1109, 012061. [Google Scholar] [CrossRef]
- Shalnova, S.A.; Klimova-Korsmik, O.G.; Turichin, G.A.; Gushchina, M. Effect of process parameters on quality of Ti-6Al-4V multi-layer single pass wall during direct laser deposition with beam oscillation. Solid State Phenom. 2020, 299, 716–722. [Google Scholar] [CrossRef]
- Gushchina, M.O.; Ivanov, S.Y.; Vildanov, A.M. Effect of Temperature Field on Mechanical Properties of Direct Laser Deposited Ti-6Al-4V Alloy. IOP Conf. Ser. Mater. Sci. Eng. 2020, 969, 012103. [Google Scholar] [CrossRef]
- Safyari, M.; Moshtaghi, M.; Kuramoto, S. Environmental hydrogen embrittlement associated with decohesion and void formation at soluble coarse particles in a cold-rolled Al-Cu based alloy. Mater. Sci. Eng. A 2021, 799, 139850. [Google Scholar] [CrossRef]
- Davis, J.R. Tensile Testing, 2nd ed.; ASM International: Materials Park, OH, USA, 2004. [Google Scholar]
- Kassner, M.E. Fundamentals of Creep in Metals and Alloys, 3rd ed.; Butterworth-Heinemann: Oxford, UK, 2015. [Google Scholar]
- Oding, I.A. Creep and Stress Relaxation in Metals; Oliver & Boyd: Edinburgh, UK; London, UK, 1965. [Google Scholar]









| T, °C | σ0.2, MPa | E, GPa | True Tensile Curve | Engineering Tensile Curve | ||||
|---|---|---|---|---|---|---|---|---|
| p1 | p2 | p3 | p1 | p2 | p3 | |||
| 20 | 1000 | 124.0 | 0.49292 | 1.16000 | 0.012126 | −0.34052 | 1.110000 | 0.0100000 |
| 200 | 845.0 | 121.0 | 0.49292 | 1.30004 | 0.012126 | −0.34052 | 1.245515 | 0.0096846 |
| 400 | 704.8 | 118.5 | 0.47779 | 1.37959 | 0.009724 | −0.33283 | 1.328941 | 0.0087338 |
| 500 | 600.0 | 110.9 | 0.39231 | 1.52868 | 0.007098 | −0.64584 | 1.483647 | 0.0064257 |
| 600 | 418.8 | 88.2 | −0.69472 | 1.93472 | 0.012777 | −1.49563 | 1.842861 | 0.0115448 |
| 700 | 245 | 65.0 | −1.5021 | 2.15010 | 0.018110 | −2.46304 | 1.806981 | 0.0165517 |
| 800 | 70 | 26.5 | −2.11940 | 3.33223 | 0.028902 | −2.71973 | 3.036418 | 0.0238623 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ivanov, S.; Gushchina, M.; Artinov, A.; Khomutov, M.; Zemlyakov, E. Effect of Elevated Temperatures on the Mechanical Properties of a Direct Laser Deposited Ti-6Al-4V. Materials 2021, 14, 6432. https://doi.org/10.3390/ma14216432
Ivanov S, Gushchina M, Artinov A, Khomutov M, Zemlyakov E. Effect of Elevated Temperatures on the Mechanical Properties of a Direct Laser Deposited Ti-6Al-4V. Materials. 2021; 14(21):6432. https://doi.org/10.3390/ma14216432
Chicago/Turabian StyleIvanov, Sergei, Marina Gushchina, Antoni Artinov, Maxim Khomutov, and Evgenii Zemlyakov. 2021. "Effect of Elevated Temperatures on the Mechanical Properties of a Direct Laser Deposited Ti-6Al-4V" Materials 14, no. 21: 6432. https://doi.org/10.3390/ma14216432
APA StyleIvanov, S., Gushchina, M., Artinov, A., Khomutov, M., & Zemlyakov, E. (2021). Effect of Elevated Temperatures on the Mechanical Properties of a Direct Laser Deposited Ti-6Al-4V. Materials, 14(21), 6432. https://doi.org/10.3390/ma14216432








