Temperature Influence on Additive Manufactured Carbon Fiber Reinforced Polymer Composites
Abstract
:1. Introduction
2. Materials and Methods
2.1. Numerical Modelling
2.1.1. Model Description
2.1.2. Material Properties
- fibre and matrix are assumed to be isotropic and linear elastic.
- The strains in the longitudinal direction are the same in the matrix and in the fibres (Voigt assumption)
- The stresses in the transverse direction are constant (Reuss assumption)
- The homogenised macroscopic stresses in the lamina are zero, i.e., the assumption L = T = 0 is used.
2.1.3. Boundary Problem Formulation
2.1.4. Non-Linear Transient Heat Transfer Formulation
2.2. Experimental Method
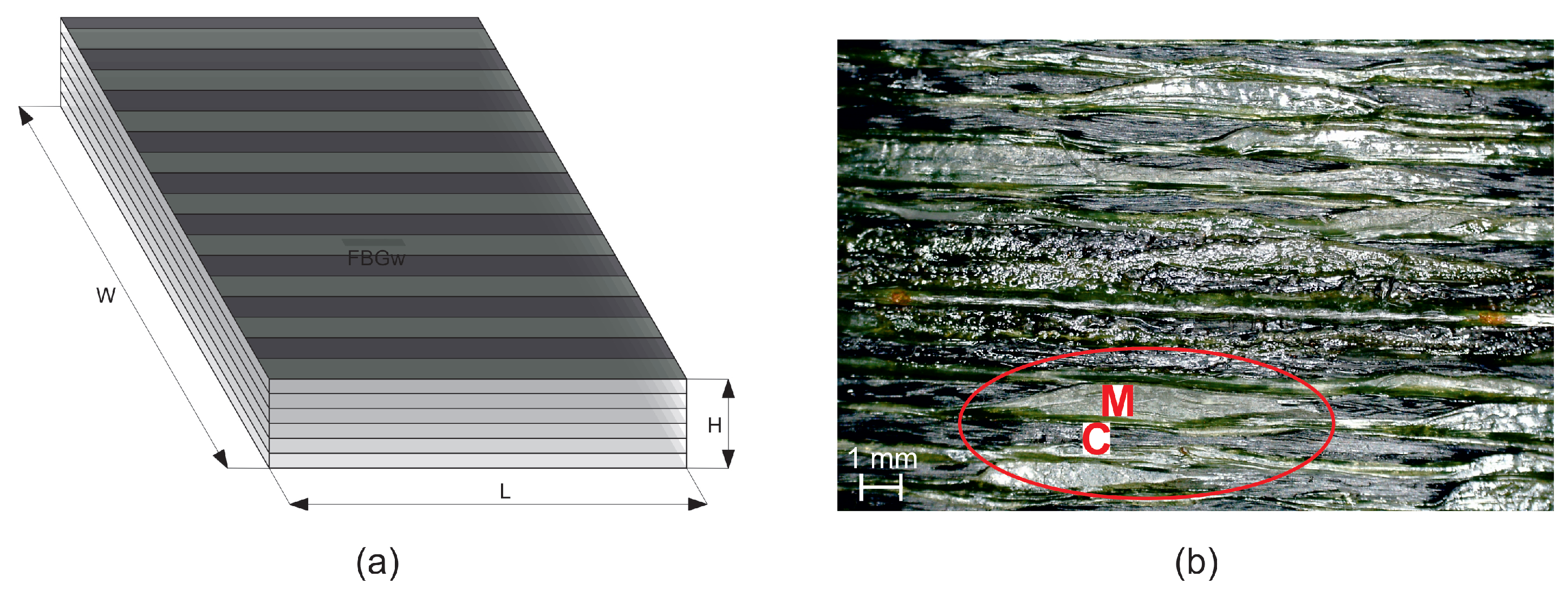
2.2.1. Materials and Sample
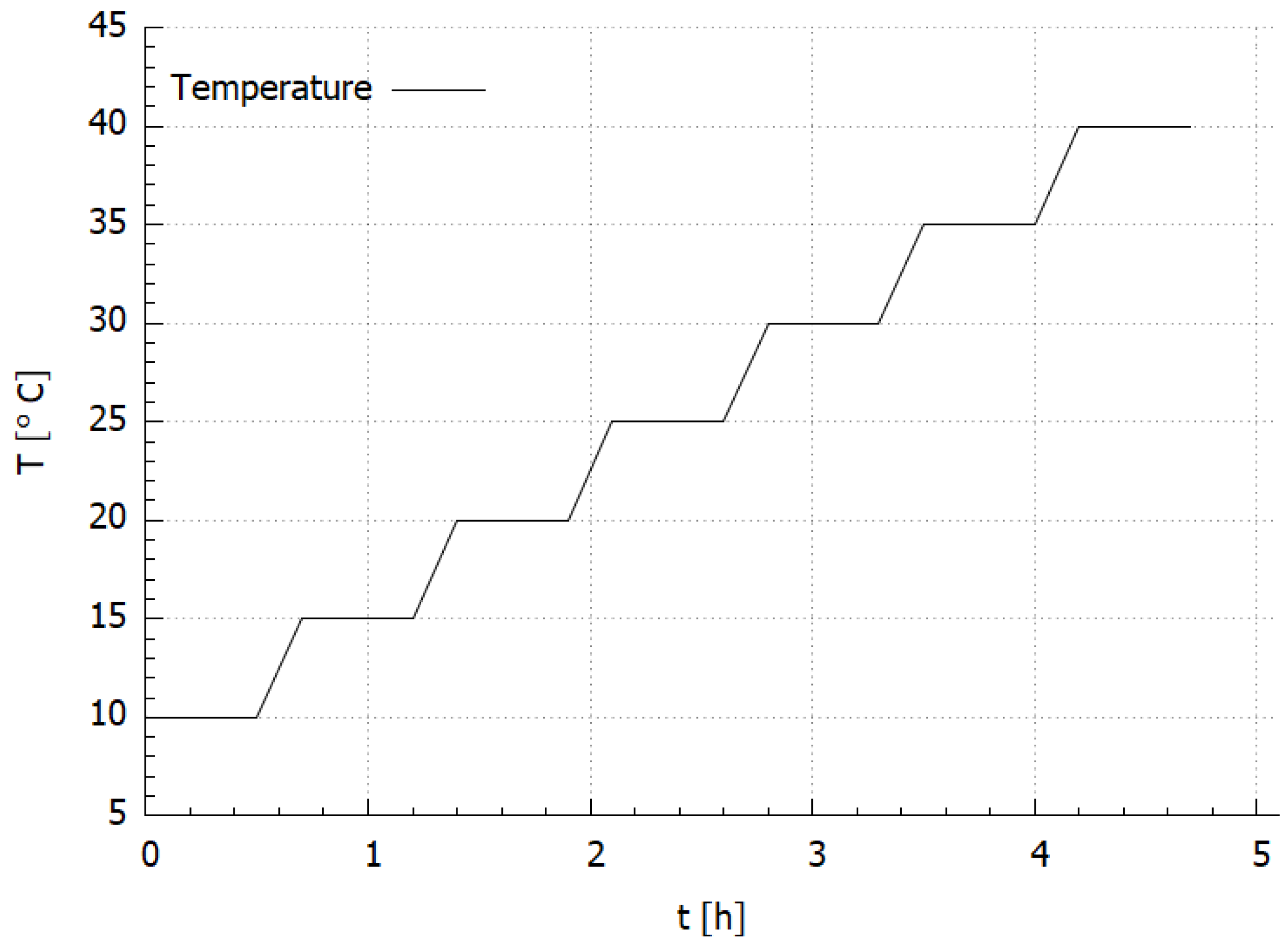
2.2.2. Measurement Method
3. Results
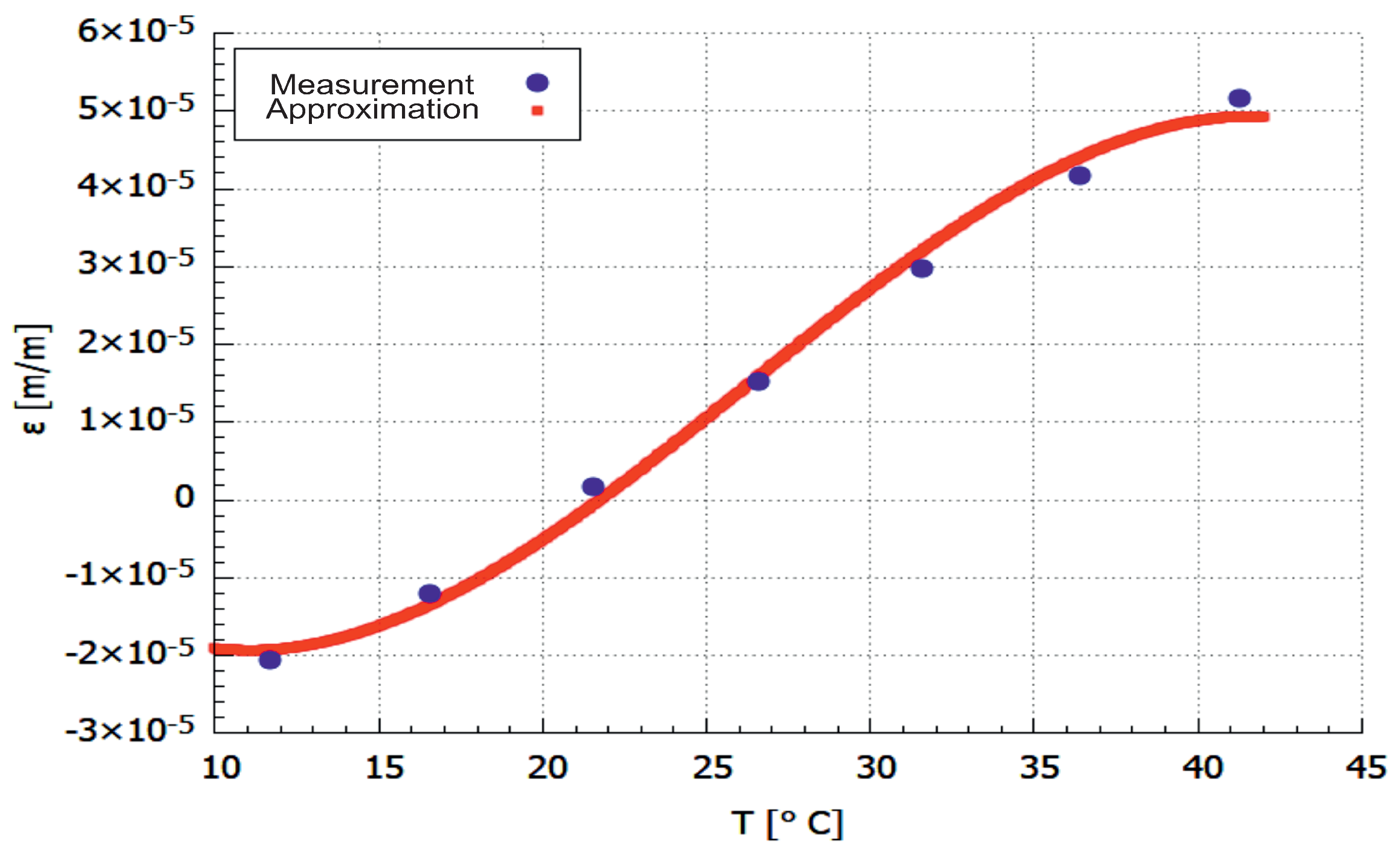
3.1. Experimental Results
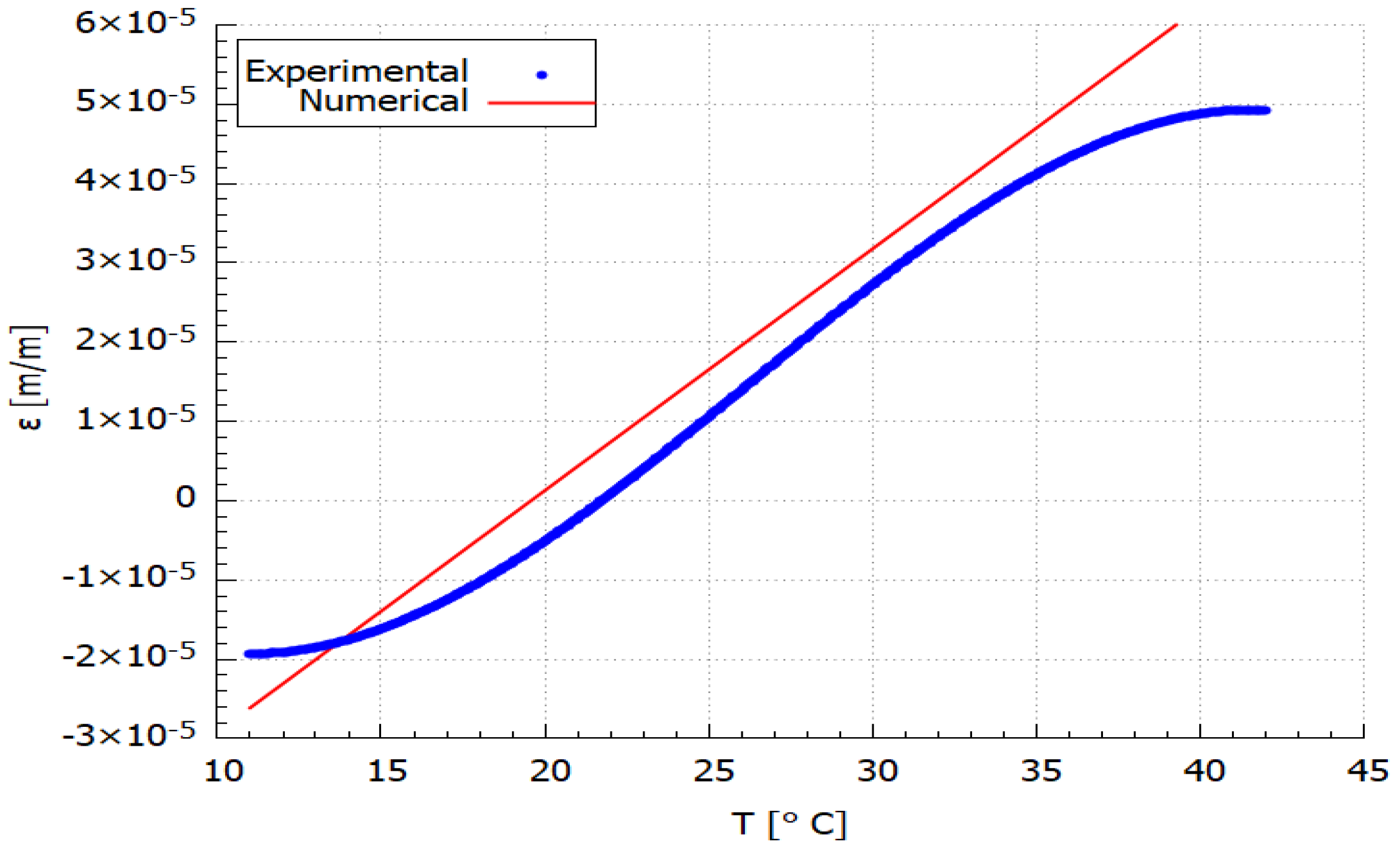
3.2. Model Validation
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kodama, H. A scheme for three-dimensional display by automatic fabrication of three-dimensional model. IEICE Trans. Electron 1981, J64, 237–241. [Google Scholar]
- Kodama, H. Automatic method for fabricating a three-dimensional plastic model with photo-hardening polymer. Rev. Sci. Instrum. 1981, 52, 1770–1773. [Google Scholar] [CrossRef]
- Hull, C.W. Apparatus for Production of Three-Dimensional Objects by Stereolithography. U.S. Patent 638905, 8 August 1984. [Google Scholar]
- Najmon, J.C.; Raeisi, S.; Tovar, A. Review of additive manufacturing technologies and applications in the aerospace industry. Addit. Manuf. Aerosp. Ind. 2019, 7–31. [Google Scholar] [CrossRef]
- Schubert, C.; Van Langeveld, M.C.; Donoso, L.A. Innovations in 3D printing: A 3D overview from optics to organs. Br. J. Ophthalmol. 2014, 98, 159–161. [Google Scholar] [CrossRef] [PubMed]
- Dawood, A.; Marti, B.M.; Sauret-Jackson, V.; Darwood, A. 3D printing in dentistry. Br. Dent. J. 2015, 219, 521–529. [Google Scholar] [CrossRef]
- Bogers, M.; Hadar, R.; Bilberg, A. Additive manufacturing for consumer-centric business models: Implications for supply chains in consumer goods manufacturing. Technol. Forecast. Soc. Chang. 2016, 102, 225–239. [Google Scholar] [CrossRef]
- Sun, C.; Wang, Y.; McMurtrey, M.D.; Jerred, N.D.; Liou, F.; Li, J. Additive manufacturing for energy: A review. Appl. Energy 2021, 282, 116041. [Google Scholar] [CrossRef]
- Bergeron, A.; Crigger, J. Early progress on additive manufacturing of nuclear fuel materials. J. Nucl. Mater. 2018, 508, 344–347. [Google Scholar] [CrossRef]
- Pikul, J.H.; Zhang, H.G.; Cho, J.; Braun, P.V.; King, W.P. High-power lithium ion microbatteries from interdigitated three-dimensional bicontinuous nanoporous electrodes. Nat. Commun. 2013, 4, 1–5. [Google Scholar] [CrossRef] [PubMed]
- Lacey, S.D.; Kirsch, D.J.; Li, Y.; Morgenstern, J.T.; Zarket, B.C.; Yao, Y.; Dai, J.; Garcia, L.Q.; Liu, B.; Gao, T.; et al. Extrusion-based 3D printing of hierarchically porous advanced battery electrodes. Adv. Mater. 2018, 30, 1705651. [Google Scholar] [CrossRef]
- Maurel, A.; Courty, M.; Fleutot, B.; Tortajada, H.; Prashantha, K.; Armand, M.; Grugeon, S.; Panier, S.; Dupont, L. Highly loaded graphite–polylactic acid composite-based filaments for lithium-ion battery three-dimensional printing. Chem. Mater. 2018, 30, 7484–7493. [Google Scholar] [CrossRef]
- You, J.; Preen, R.J.; Bull, L.; Greenman, J.; Ieropoulos, I. 3D printed components of microbial fuel cells: Towards monolithic microbial fuel cell fabrication using additive layer manufacturing. Sustain. Energy Technol. Assess. 2017, 19, 94–101. [Google Scholar] [CrossRef]
- Wei, L.; Zhang, J.; Yu, F.; Zhang, W.; Meng, X.; Yang, N.; Liu, S. A novel fabrication of yttria-stabilized-zirconia dense electrolyte for solid oxide fuel cells by 3D printing technique. Int. J. Hydrogen Energy 2019, 44, 6182–6191. [Google Scholar] [CrossRef]
- Guo, N.; Leu, M.C. Effect of different graphite materials on the electrical conductivity and flexural strength of bipolar plates fabricated using selective laser sintering. Int. J. Hydrogen Energy 2012, 37, 3558–3566. [Google Scholar] [CrossRef]
- Hughes, J.P.; dos Santos, P.L.; Down, M.P.; Foster, C.W.; Bonacin, J.A.; Keefe, E.M.; Rowley-Neale, S.J.; Banks, C.E. Single step additive manufacturing (3D printing) of electrocatalytic anodes and cathodes for efficient water splitting. Sustain. Energy Fuels 2020, 4, 302–311. [Google Scholar] [CrossRef] [Green Version]
- Tofail, S.A.; Koumoulos, E.P.; Bandyopadhyay, A.; Bose, S.; O’Donoghue, L.; Charitidis, C. Additive manufacturing: Scientific and technological challenges, market uptake and opportunities. Mater. Today 2018, 21, 22–37. [Google Scholar] [CrossRef]
- Mani, M.; Lyons, K.W.; Gupta, S. Sustainability characterization for additive manufacturing. J. Res. Natl. Inst. Stand. Technol. 2014, 119, 419. [Google Scholar] [CrossRef]
- Kousiatza, C.; Karalekas, D. In-situ monitoring of strain and temperature distributions during fused deposition modeling process. Mater. Des. 2016, 97, 400–406. [Google Scholar] [CrossRef]
- Penumakala, P.K.; Santo, J.; Thomas, A. A critical review on the fused deposition modeling of thermoplastic polymer composites. Compos. Part B Eng. 2020, 201, 108336. [Google Scholar] [CrossRef]
- Wickramasinghe, S.; Do, T.; Tran, P. FDM-based 3D printing of polymer and associated composite: A review on mechanical properties, defects and treatments. Polymers 2020, 12, 1529. [Google Scholar] [CrossRef]
- Ning, F.; Cong, W.; Qiu, J.; Wei, J.; Wang, S. Additive manufacturing of carbon fiber reinforced thermoplastic composites using fused deposition modeling. Compos. Part B Eng. 2015, 80, 369–378. [Google Scholar] [CrossRef]
- Zhang, W.; Cotton, C.; Sun, J.; Heider, D.; Gu, B.; Sun, B.; Chou, T.W. Interfacial bonding strength of short carbon fiber/acrylonitrile-butadiene-styrene composites fabricated by fused deposition modeling. Compos. Part B Eng. 2018, 137, 51–59. [Google Scholar] [CrossRef]
- Tekinalp, H.L.; Kunc, V.; Velez-Garcia, G.M.; Duty, C.E.; Love, L.J.; Naskar, A.K.; Blue, C.A.; Ozcan, S. Highly oriented carbon fiber–polymer composites via additive manufacturing. Compos. Sci. Technol. 2014, 105, 144–150. [Google Scholar] [CrossRef] [Green Version]
- Ferreira, R.T.L.; Amatte, I.C.; Dutra, T.A.; Bürger, D. Experimental characterization and micrography of 3D printed PLA and PLA reinforced with short carbon fibers. Compos. Part B Eng. 2017, 124, 88–100. [Google Scholar] [CrossRef]
- Matsuzaki, R.; Ueda, M.; Namiki, M.; Jeong, T.K.; Asahara, H.; Horiguchi, K.; Nakamura, T.; Todoroki, A.; Hirano, Y. Three-dimensional printing of continuous-fiber composites by in-nozzle impregnation. Sci. Rep. 2016, 6, 1–7. [Google Scholar] [CrossRef]
- Li, N.; Li, Y.; Liu, S. Rapid prototyping of continuous carbon fiber reinforced polylactic acid composites by 3D printing. J. Mater. Process. Technol. 2016, 238, 218–225. [Google Scholar] [CrossRef]
- Tian, X.; Liu, T.; Yang, C.; Wang, Q.; Li, D. Interface and performance of 3D printed continuous carbon fiber reinforced PLA composites. Compos. Part A Appl. Sci. Manuf. 2016, 88, 198–205. [Google Scholar] [CrossRef]
- Dickson, A.N.; Barry, J.N.; McDonnell, K.A.; Dowling, D.P. Fabrication of continuous carbon, glass and Kevlar fibre reinforced polymer composites using additive manufacturing. Addit. Manuf. 2017, 16, 146–152. [Google Scholar] [CrossRef]
- Goh, G.D.; Dikshit, V.; Nagalingam, A.P.; Goh, G.L.; Agarwala, S.; Sing, S.L.; Wei, J.; Yeong, W.Y. Characterization of mechanical properties and fracture mode of additively manufactured carbon fiber and glass fiber reinforced thermoplastics. Mater. Des. 2018, 137, 79–89. [Google Scholar] [CrossRef]
- Ashby, M.F.; Johnson, K. Materials and Design: The Art and Science of Material Selection in Product Design; Butterworth-Heinemann: Oxford, UK, 2013. [Google Scholar]
- Zhou, F.; Zhang, J.; Song, S.; Yang, D.; Wang, C. Effect of temperature on material properties of carbon fiber reinforced polymer (CFRP) tendons: Experiments and model assessment. Materials 2019, 12, 1025. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jia, Z.; Li, T.; Chiang, F.P.; Wang, L. An experimental investigation of the temperature effect on the mechanics of carbon fiber reinforced polymer composites. Compos. Sci. Technol. 2018, 154, 53–63. [Google Scholar] [CrossRef]
- Ejeh, C.J.; Barsoum, I.; Chizindu, G.O.; Kodie, G.M.; Anachuna, J.I. Thermo-elastic behaviour of carbon-fiber reinforced polymer and the effect of adding nanoparticles at elevated heat intensity. Heliyon 2020, 6, e03622. [Google Scholar] [CrossRef] [PubMed]
- Lüders, C.; Kalinka, G.; Li, W.; Sinapius, M.; Wille, T. Experimental and numerical multiscale approach to thermally cycled FRP. Compos. Struct. 2020, 244, 112303. [Google Scholar] [CrossRef]
- Nye, J.F. Physical Properties of Crystals: Their Representation by Tensors and Matrices; Oxford University Press: Oxford, UK, 1985. [Google Scholar]
- Somireddy, M.; Czekanski, A. Anisotropic material behavior of 3D printed composite structures–Material extrusion additive manufacturing. Mater. Des. 2020, 195, 108953. [Google Scholar] [CrossRef]
- Rimašauskas, M.; Kuncius, T.; Rimašauskienė, R. Processing of carbon fiber for 3D printed continuous composite structures. Mater. Manuf. Process. 2019, 34, 1528–1536. [Google Scholar] [CrossRef]
- Behrens, E. Thermal conductivities of composite materials. J. Compos. Mater. 1968, 2, 2–17. [Google Scholar] [CrossRef]
- Schapery, R.A. Thermal expansion coefficients of composite materials based on energy principles. J. Compos. Mater. 1968, 2, 380–404. [Google Scholar] [CrossRef]
- Fan, M.; Fu, F. Advanced High Strength Natural Fibre Composites in Construction; Woodhead Publishing: Duxford, UK, 2016. [Google Scholar]
- Jiménez-Fortunato, I.; Bull, D.J.; Thomsen, O.T.; Dulieu-Barton, J.M. On the source of the thermoelastic response from orthotropic fibre reinforced composite laminates. Compos. Part A Appl. Sci. Manuf. 2021, 149, 106515. [Google Scholar] [CrossRef]
- Newnham, P.; Abrate, S. Finite element analysis of heat transfer in anisotropic solids: Application to manufacturing problems. J. Reinf. Plast. Compos. 1993, 12, 854–864. [Google Scholar] [CrossRef]
- Wilson, E.; Bathe, K.; Peterson, F. Finite element analysis of linear and nonlinear heat transfer. Nucl. Eng. Des. 1974, 29, 110–124. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Chauhan, S. Fast explicit dynamics finite element algorithm for transient heat transfer. Int. J. Therm. Sci. 2019, 139, 160–175. [Google Scholar] [CrossRef] [Green Version]
- Compton, B.G.; Kemp, J.W.; Novikov, T.V.; Pack, R.C.; Nlebedim, C.I.; Duty, C.E.; Rios, O.; Paranthaman, M.P. Direct-write 3D printing of NdFeB bonded magnets. Mater. Manuf. Process. 2018, 33, 109–113. [Google Scholar] [CrossRef]
- Mieloszyk, M.; Andrearczyk, A.; Majewska, K.; Jurek, M.; Ostachowicz, W. Polymeric structure with embedded fiber Bragg grating sensor manufactured using multi-jet printing method. Measurement 2020, 166, 108229. [Google Scholar] [CrossRef]
- Chawla, K.K. Composite Materials: Science and Engineering; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Wei, Y.; Jian, W.; Guangxuan, L. Grid-independent issue in numerical heat transfer. arXiv 2006, arXiv:math-ph/0609066. [Google Scholar]
- Zanjanijam, A.R.; Major, I.; Lyons, J.G.; Lafont, U.; Devine, D.M. Fused filament fabrication of peek: A review of process-structure-property relationships. Polymers 2020, 12, 1665. [Google Scholar] [CrossRef]
- Wang, P.; Zou, B.; Xiao, H.; Ding, S.; Huang, C. Effects of printing parameters of fused deposition modeling on mechanical properties, surface quality, and microstructure of PEEK. J. Mater. Process. Technol. 2019, 271, 62–74. [Google Scholar] [CrossRef]
- Wu, F.; Misra, M.; Mohanty, A.K. Studies on why the heat deflection temperature of polylactide bioplastic cannot be improved by overcrosslinking. Polym. Cryst. 2019, 2, e10088. [Google Scholar] [CrossRef]
- Barczewski, M.; Mysiukiewicz, O.; Hejna, A.; Biskup, R.; Szulc, J.; Michałowski, S.; Piasecki, A.; Kloziński, A. The Effect of Surface Treatment with Isocyanate and Aromatic Carbodiimide of Thermally Expanded Vermiculite Used as a Functional Filler for Polylactide-Based Composites. Polymers 2021, 13, 890. [Google Scholar] [CrossRef]
- Cristea, M.; Ionita, D.; Iftime, M.M. Dynamic mechanical analysis investigations of pla-based renewable materials: How are they useful? Materials 2020, 13, 5302. [Google Scholar] [CrossRef]
- Ray, S.; Cooney, R.P. Thermal degradation of polymer and polymer composites. In Handbook of Environmental Degradation of Materials; Elsevier: Amsterdam, The Netherlands, 2018; pp. 185–206. [Google Scholar]
- Aou, K.; Kang, S.; Hsu, S.L. Morphological study on thermal shrinkage and dimensional stability associated with oriented poly (lactic acid). Macromolecules 2005, 38, 7730–7735. [Google Scholar] [CrossRef]
- Yu, F.; Liu, T.; Zhao, X.; Yu, X.; Lu, A.; Wang, J. Effects of talc on the mechanical and thermal properties of polylactide. J. Appl. Polym. Sci. 2012, 125, E99–E109. [Google Scholar] [CrossRef]
- Hao, Y.; Li, Y.; Liu, Z.; Yan, X.; Tong, Y.; Zhang, H. Thermal, mechanical and rheological properties of poly (lactic acid) chain extended with polyaryl polymethylene isocyanate. Fibers Polym. 2019, 20, 1766–1773. [Google Scholar] [CrossRef]
- Akindoyo, J.O.; Beg, M.D.H.; Ghazali, S.; Heim, H.P.; Feldmann, M.; Mariatti, M. Simultaneous impact modified and chain extended glass fiber reinforced poly (lactic acid) composites: Mechanical, thermal, crystallization, and dynamic mechanical performance. J. Appl. Polym. Sci. 2021, 138, 49752. [Google Scholar] [CrossRef]
- Espinach, F.; Boufi, S.; Delgado-Aguilar, M.; Julián, F.; Mutjé, P.; Méndez, J. Composites from poly (lactic acid) and bleached chemical fibres: Thermal properties. Compos. Part B Eng. 2018, 134, 169–176. [Google Scholar] [CrossRef]
- Ferreira, W.H.; Andrade, C.T. The role of graphene on thermally induced shape memory properties of poly (lactic acid) extruded composites. J. Therm. Anal. Calorim. 2021, 143, 3107–3115. [Google Scholar] [CrossRef]
- Yazdaninia, A.; Khonakdar, H.A.; Jafari, S.H.; Asadi, V. Influence of trifluoropropyl-POSS nanoparticles on the microstructure, rheological, thermal and thermomechanical properties of PLA. RSC Adv. 2016, 6, 37149–37159. [Google Scholar] [CrossRef]
- Cao, Y.; Ju, Y.; Liao, F.; Jin, X.; Dai, X.; Li, J.; Wang, X. Improving the flame retardancy and mechanical properties of poly (lactic acid) with a novel nanorod-shaped hybrid flame retardant. RSC Adv. 2016, 6, 14852–14858. [Google Scholar] [CrossRef]
- Ali, F.; Chang, Y.W.; Kang, S.C.; Yoon, J.Y. Thermal, mechanical and rheological properties of poly (lactic acid)/epoxidized soybean oil blends. Polym. Bull. 2009, 62, 91–98. [Google Scholar] [CrossRef]



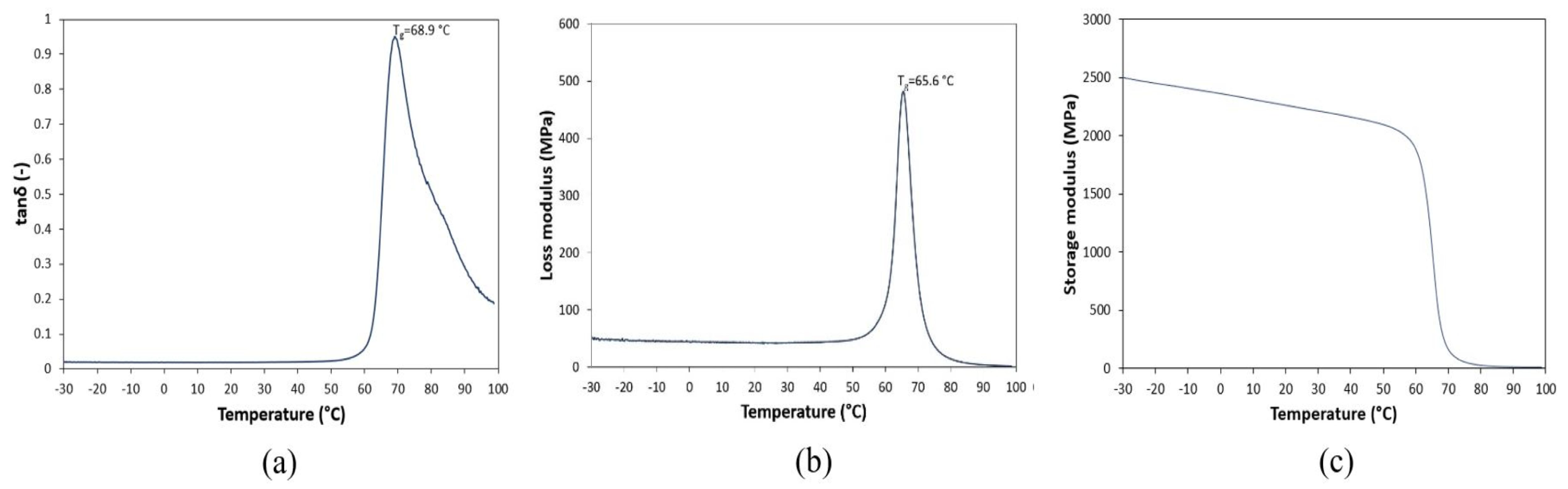


| Volume Fraction [%] | Young’s Modulus [Pa] | Shear’s Modulus [Pa] | Poisson’s Ratio [-] | Density [kg/m3] | |
|---|---|---|---|---|---|
| Fiber | 15.05 | 230 × 109 | 17 × 109 | 0.2 | 1760 |
| Matrix | 84.95 | 2.315 × 109 | 24 × 108 | 0.3 | 1240 |
| E11 [Pa] | E22 [Pa] | E33 [Pa] | ν12 [-] | ν13 [-] | ν23 [-] | G12 [Pa] | G13 [Pa] | G23 [Pa] |
|---|---|---|---|---|---|---|---|---|
| 36,580 | 2720 | 2720 | 0.3 | 0.3 | 0.3 | 14,070 | 14,070 | 14,070 |
| α11 [m/mK] | α22 [m/mK] | κ11 [m/mK] | κ22 [m/mK] | Cv [J/kgK] |
|---|---|---|---|---|
| 3.09 × 10 | 7.41 × 10 | 1.62 | 0.15 | 1438.91 |
| C | C | C | C |
|---|---|---|---|
| −0.000002011647241 | 0.000108722592509 | 0.001514056918440 | −0.172701442544788 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muna, I.I.; Mieloszyk, M. Temperature Influence on Additive Manufactured Carbon Fiber Reinforced Polymer Composites. Materials 2021, 14, 6413. https://doi.org/10.3390/ma14216413
Muna II, Mieloszyk M. Temperature Influence on Additive Manufactured Carbon Fiber Reinforced Polymer Composites. Materials. 2021; 14(21):6413. https://doi.org/10.3390/ma14216413
Chicago/Turabian StyleMuna, Isyna Izzal, and Magdalena Mieloszyk. 2021. "Temperature Influence on Additive Manufactured Carbon Fiber Reinforced Polymer Composites" Materials 14, no. 21: 6413. https://doi.org/10.3390/ma14216413
APA StyleMuna, I. I., & Mieloszyk, M. (2021). Temperature Influence on Additive Manufactured Carbon Fiber Reinforced Polymer Composites. Materials, 14(21), 6413. https://doi.org/10.3390/ma14216413






