Analysing the Contact Conduction Influence on the Heat Transfer Intensity in the Rectangular Steel Bars Bundle
Abstract
:1. Introduction
2. Materials and Methods
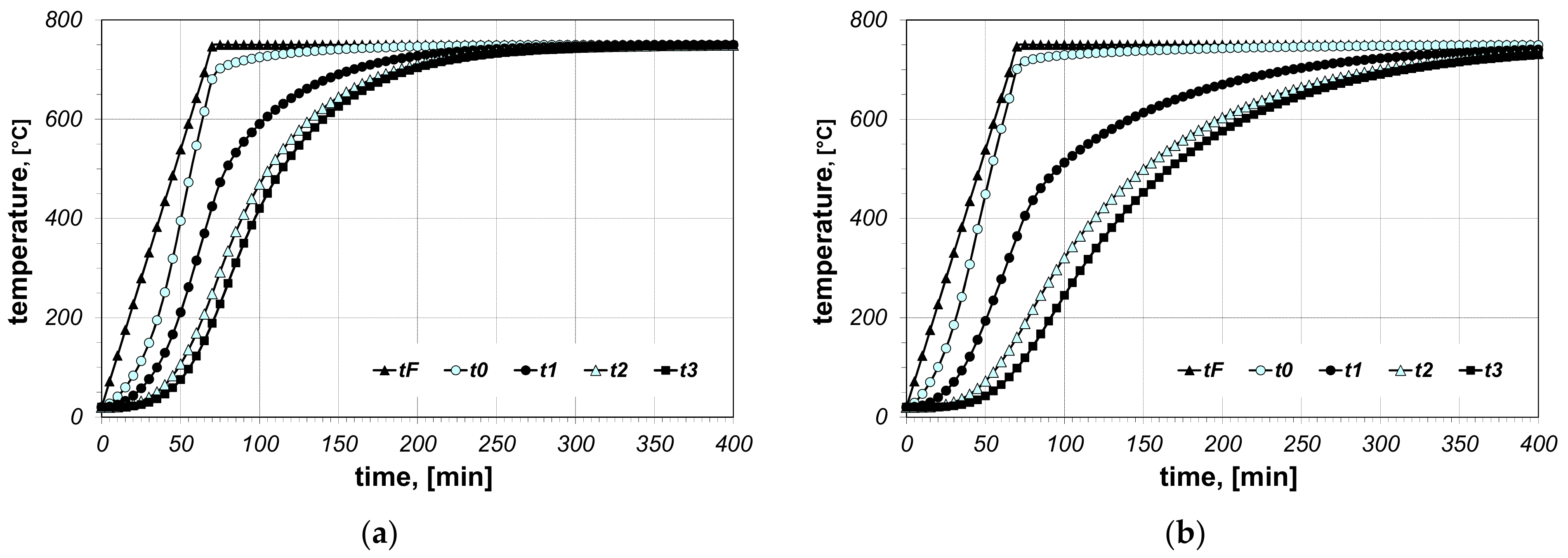
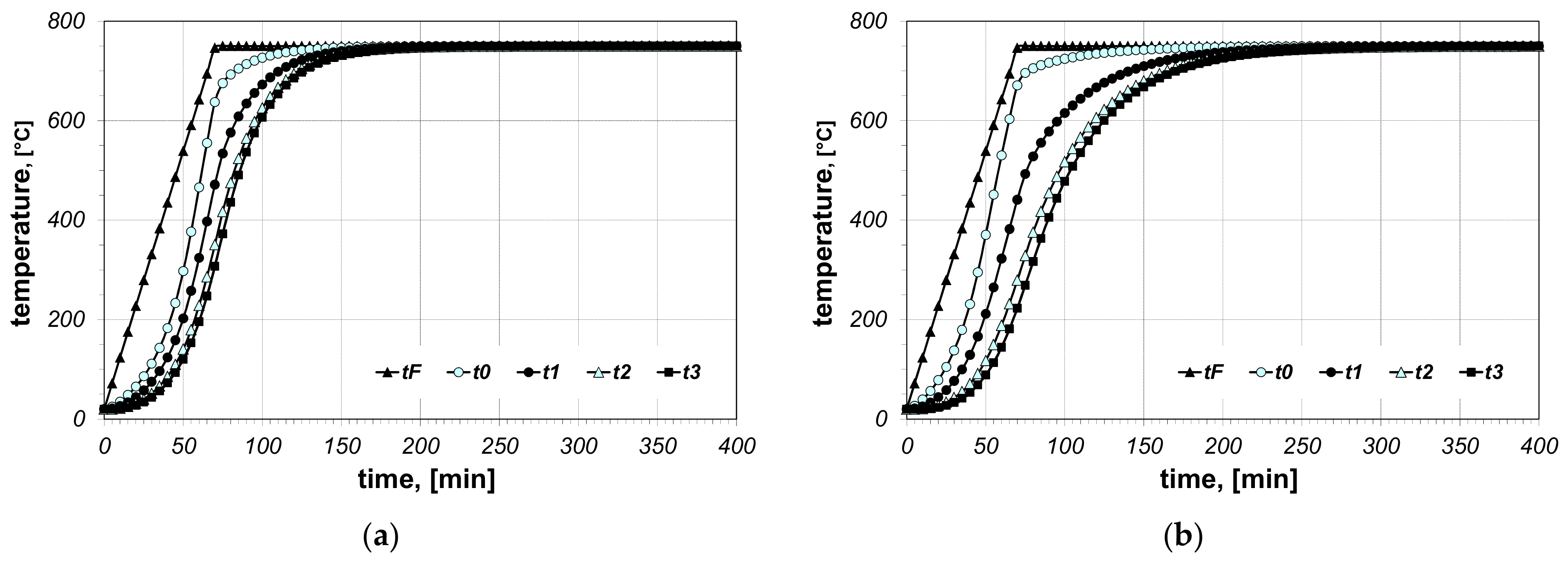
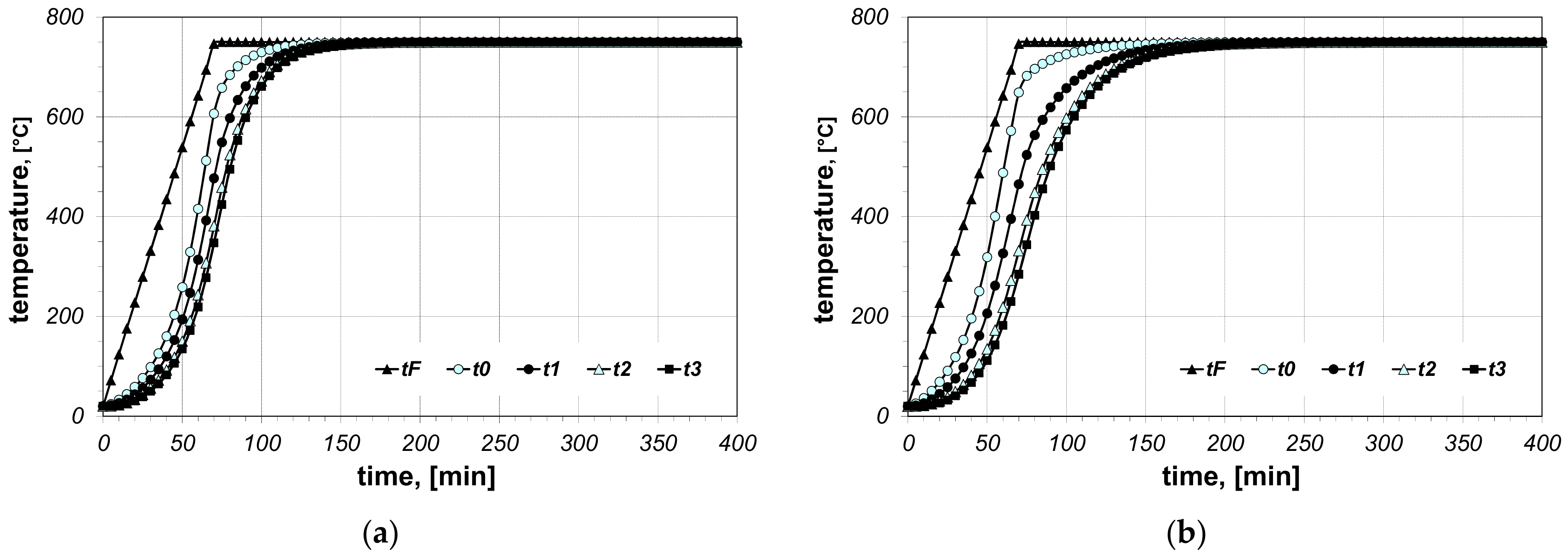
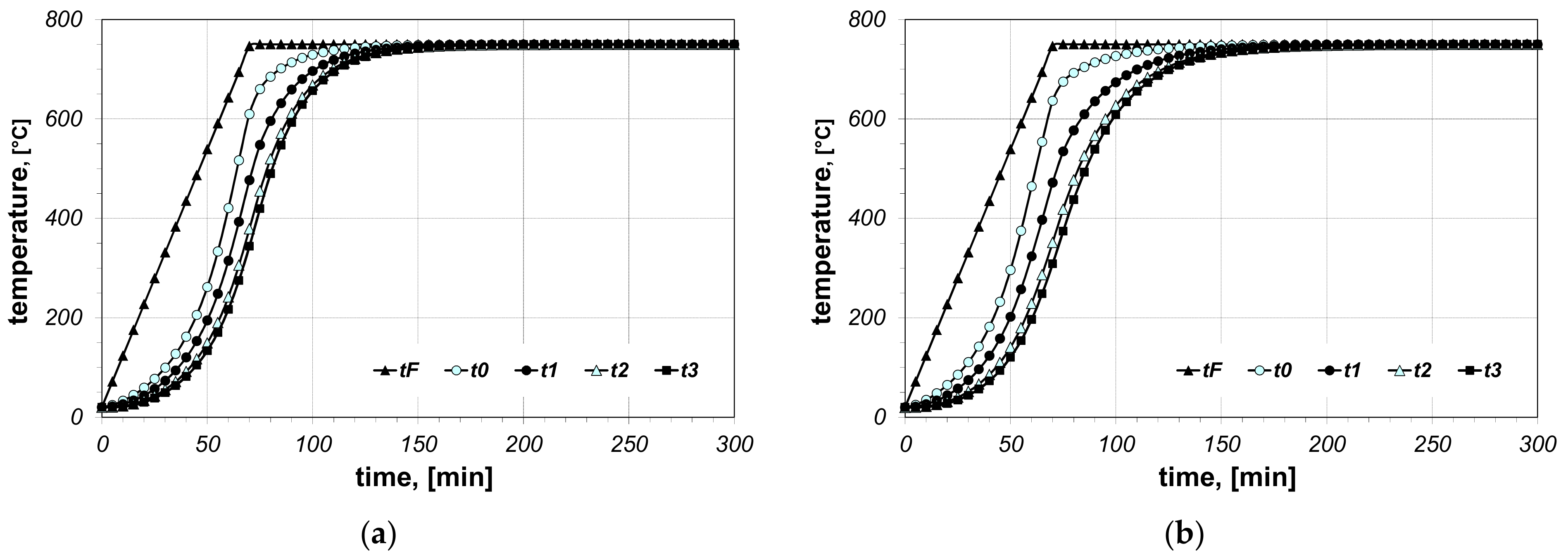
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kolmasiak, C.; Wyleciał, T. Heat treatment of steel products as an example of transport phenomenon in porous media. Metalurgija 2018, 57, 363–366. Available online: https://hrcak.srce.hr/201766 (accessed on 20 September 2021).
- Musiał, M. Numerical Analysis of the Process of Heating of a Bed of Steel Bars. Arch. Metall. Mater. 2013, 1, 63–66. [Google Scholar] [CrossRef]
- Wyczółkowski, R.; Urbaniak, D. Modeling of Radiation in Bar Bundles Using the Thermal Resistance Concept. J. Thermophys. Heat Transf. 2016, 30, 721–729. [Google Scholar] [CrossRef]
- Wyczółkowski, R.; Bagdasaryan, V.; Szwaja, S. On Determination of the Effective Thermal Conductivity of a Bundle of Steel Bars Using the Krischer Model and Considering Thermal Radiation. Materials 2021, 14, 4378. [Google Scholar] [CrossRef] [PubMed]
- Wyczółkowski, R.; Gała, M.; Szwaja, S.; Piotrowski, A. Determination of the Radiation Exchange Factor in the Bundle of Steel Round Bars. Energies 2021, 14, 5263. [Google Scholar] [CrossRef]
- Kaviany, M. Principles of Heat Transfer in Porous Media, 2nd ed.; Springer: New York, NY, USA, 1995. [Google Scholar]
- Van Antwerpen, W.; du Toit, C.G.; Rousseau, P.G.A. Review of Correlations to Model the Packing Structure and Effective Thermal Conductivity in Packed Beds of Mono-Sized Spherical Particles. Nucl. Engine Des. 2010, 240, 1803–1818. [Google Scholar] [CrossRef]
- Wyczółkowski, R.; Benduch, A. The experimental study of the effective thermal conductivity of bundles of rectangular steel sections. CEER 2014, 14, 119–132. [Google Scholar] [CrossRef] [Green Version]
- Kula, D.; Wodzyński, Ł. Transfer of thermal fluctuations through the building partition formed by periodic composite material. Acta Sci. Pol. Arch. 2020, 19, 21–30. [Google Scholar] [CrossRef]
- Wągrowska, M.; Szlachetka, O. Distribution of temperature in multicomponent functionally graded multilayered composites. Acta Sci. Pol. Arch. 2016, 15, 27–39. [Google Scholar]
- Wozniak, C.; Wagrowska, M.; Szlachetka, O. On the tolerance modelling of heat conduction in functionally graded laminated media. J. Appl. Mech. Tech. Phys. 2015, 56, 274–281. [Google Scholar] [CrossRef]
- Sahay, S.S.; Krishnan, K. Model Based Optimization of Continuous Annealing Operation for Bundle of Packed Rods. Ironmak. Steelmak. 2007, 29, 89–94. [Google Scholar] [CrossRef]
- Dutkowski, K.; Kruzel, M. Experimental Investigation of the Apparent Thermal Conductivity of Microencapsulated Phase-Change-Material Slurry at the Phase-Transition Temperature. Materials 2021, 14, 4124. [Google Scholar] [CrossRef]
- Du, Y.; Ge, Y. Multiphase Model for Predicting the Thermal Conductivity of Cement Paste and Its Applications. Materials 2021, 14, 4525. [Google Scholar] [CrossRef] [PubMed]
- Cengel, Y.A. Numerical Methods in Heat Conduction. In Heat Transfer and Mass Transfer—A Practical Approach, 3rd ed.; McGraw–Hill: New York, NY, USA, 2002; Chapter 5; pp. 285–354. [Google Scholar]
- Malinowski, Z. Numerical Modeling in Plastic Processing and Heat Transfer; Uczelniane Wydawnictwa Naukow-Dydaktyczne AGH: Kraków, Poland, 2005. (In Polish) [Google Scholar]
- Cengel, Y.A. Natural Convection. In Heat Transfer and Mass Transfer—A Practical Approach, 3rd ed.; McGraw–Hill: New York, NY, USA, 2002; Chapter 9; pp. 503–560. [Google Scholar]
- Cengel, Y.A. Table A-15 Properties of air at 1 atm pressure. In Heat Transfer and Mass Transfer—A Practical Approach, 3rd ed.; McGraw–Hill: New York, NY, USA, 2002; Appendix 1; p. 860. [Google Scholar]
- Coquard, R.; Rochais, D.; Baillis, D. Conductive and Radiative Heat Transfer in Ceramic and Metal Foams at Fire Temperatures. Fire Technol. 2012, 48, 699–732. [Google Scholar] [CrossRef]
- Trevisan, S.; Wang, W.; Laumert, B. Coatings utilization to modify the effective properties of high temperature packed bed thermal energy storage. Appl. Ther. Eng. 2021, 185, 116–128. [Google Scholar] [CrossRef]
- Wyczółkowski, R.; Gała, M.; Bagdasaryan, V. Model of complex heat transfer in the package of steel rectangular steel sections. Appl. Sci. 2020, 10, 9044. [Google Scholar] [CrossRef]
- Wyczółkowski, R. Computational model of complex heat flow in the area of steel rectangular section. Proc. Eng. 2016, 157, 185–192. [Google Scholar] [CrossRef] [Green Version]
- Öchsner, A.; Murcg, G.E.; de Lemos, M.J.S. (Eds.) Cellular and Porous Materials: Thermal Properties Simulation and Prediction; WILEY-VCH Verlag GmbH & Co, KGaA: Wenheim, Germany, 2008. [Google Scholar]
- European Steel and Alloy Grades/Numbers Steel Number. Available online: http://www.steelnumber.com/en/steel_composition_eu.php?name_id=645 (accessed on 30 July 2021).
- Standard Practice for Using a Guarded-Hot-Plate Apparatus or Thin-Heater Apparatus in the Single-Sided Mode; ASTM C1044-12; ASTM International: West Conshohocken, PA, USA, 2012.
- Standard Test Method for Steady-State Heat Flux Measurements and Thermal Transmissions Properties by Means of Guarded-Hot-Plate Apparatus; ASTM C177-13; ASTM International: West Conshohocken, PA, USA, 2013.
- Wyczolkowski, R.; Radomiak, H.; Wylecial, T. Computational model of effective thermal conductivity of the steel section bundle. In Proceedings of the 10th International Conference on Computational Heat Mass and Momentum Transfer (ICCHM2T 2017), Seoul, Korea, 28 May–1 June 2017. Paper Number 160149. [Google Scholar]
- Wyczółkowski, R.; Boryca, J. Analysis of Thermal Radiation in the Heating of Steel Round Bar Bundles. Acta Phys. Pol. A 2019, 135, 256–262. [Google Scholar] [CrossRef]

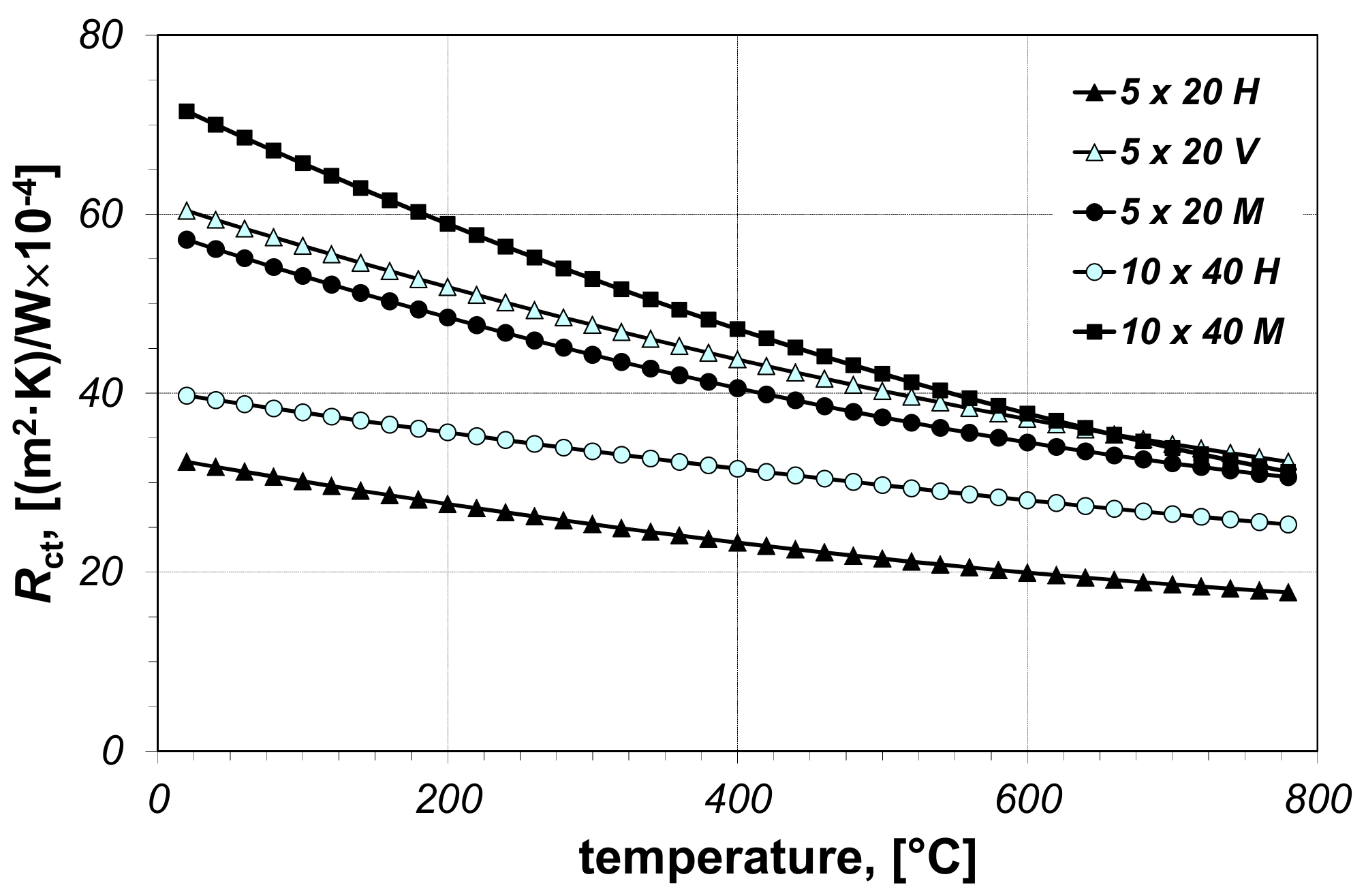


| Sample | A1 | A2 | A3 | lcell, m |
|---|---|---|---|---|
| 5 × 20 H | 1.2 × 10−5 | −0.0288 | 32.91 | 0.0050 |
| 5 × 20 V | 1.8 × 10−5 | −0.0513 | 61.41 | 0.0200 |
| 5 × 20 M | 2.3 × 10−5 | −0.0533 | 58.16 | 0.0125 |
| 10 × 40 H | 6.7 × 10−6 | −0.0243 | 40.21 | 0.0100 |
| 10 × 40 M | 2.9 × 10−5 | −0.0762 | 72.86 | 0.0250 |
| Sample | τmin, min | τmax, min | Δτ, % |
|---|---|---|---|
| 5 × 20 H | 222 | 365 | 39.2 |
| 5 × 20 V | 139 | 192 | 27.6 |
| 5 × 20 M | 120 | 151 | 20.5 |
| 10 × 40 H | 152 | 220 | 30.9 |
| 10 × 40 M | 121 | 138 | 12.3 |
| Sample | τmin, min | τmax, min | Δτ, % |
|---|---|---|---|
| 5 × 20 H | 177 | 280 | 36.8 |
| 5 × 20 V | 117 | 155 | 24.5 |
| 5 × 20 M | 103 | 126 | 18.3 |
| 10 × 40 H | 125 | 175 | 28.6 |
| 10 × 40 M | 105 | 116 | 9.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kolmasiak, C.; Bagdasaryan, V.; Wyleciał, T.; Gała, M. Analysing the Contact Conduction Influence on the Heat Transfer Intensity in the Rectangular Steel Bars Bundle. Materials 2021, 14, 5655. https://doi.org/10.3390/ma14195655
Kolmasiak C, Bagdasaryan V, Wyleciał T, Gała M. Analysing the Contact Conduction Influence on the Heat Transfer Intensity in the Rectangular Steel Bars Bundle. Materials. 2021; 14(19):5655. https://doi.org/10.3390/ma14195655
Chicago/Turabian StyleKolmasiak, Cezary, Vazgen Bagdasaryan, Tomasz Wyleciał, and Marek Gała. 2021. "Analysing the Contact Conduction Influence on the Heat Transfer Intensity in the Rectangular Steel Bars Bundle" Materials 14, no. 19: 5655. https://doi.org/10.3390/ma14195655
APA StyleKolmasiak, C., Bagdasaryan, V., Wyleciał, T., & Gała, M. (2021). Analysing the Contact Conduction Influence on the Heat Transfer Intensity in the Rectangular Steel Bars Bundle. Materials, 14(19), 5655. https://doi.org/10.3390/ma14195655







