Stability Loss Analysis for Thin-Walled Shells with Elliptical Cross-Sectional Area
Abstract
:1. Introduction
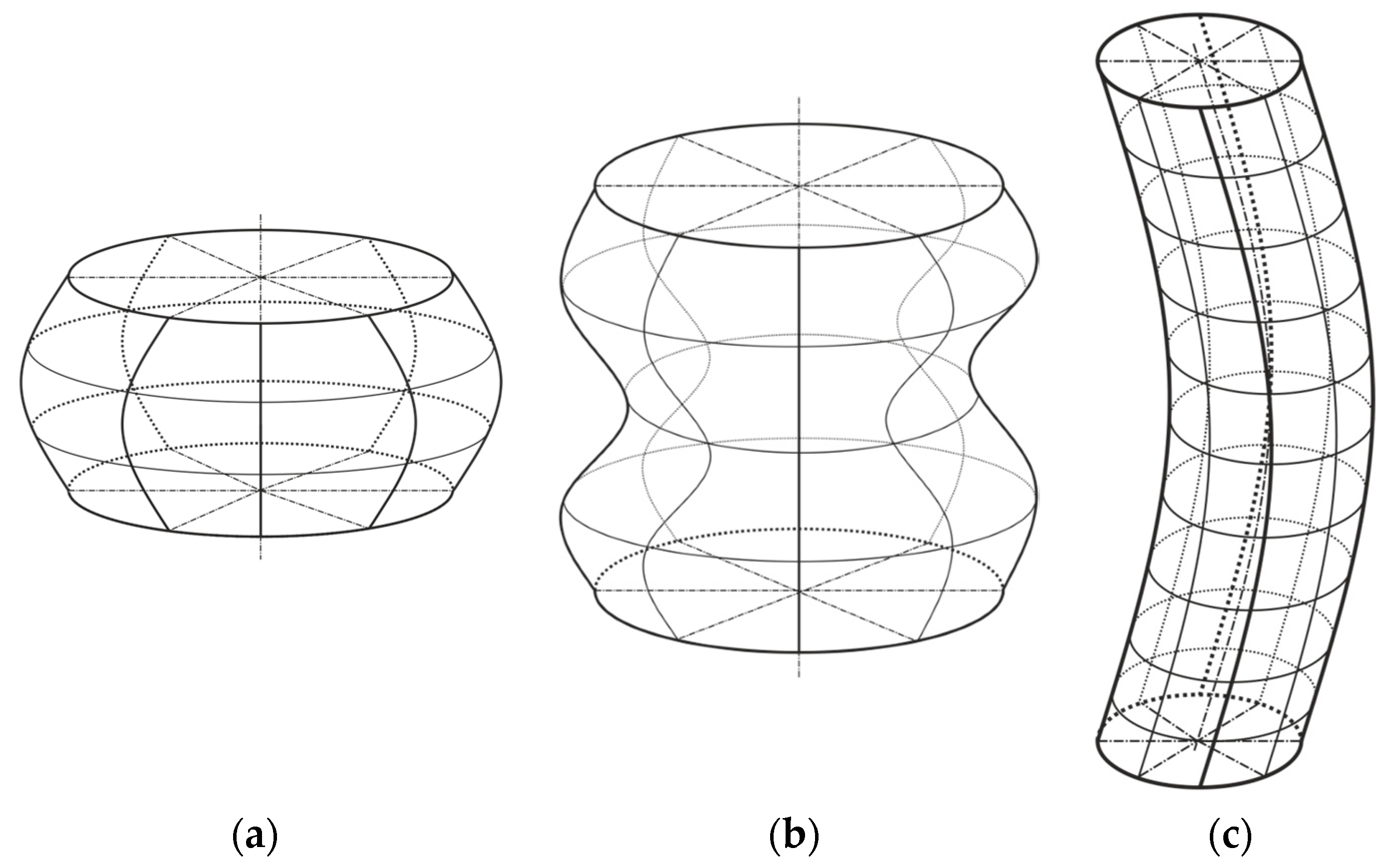
2. Stability Concept of Thin-Walled Shells, Proposal of Fixture with Elliptical Cross-Section, and Manufacturing Shell Specimen
- is the upper critical load and can be defined as the largest load to which the original shell equilibrium configuration remains stable with respect to minimal imperfections;
- is the upper critical load and can be defined as the lowest load to which the original shell equilibrium configuration of the shell remains stable with respect to minimal imperfections;
- is the critical load of the real shell element, referred to as the buckling load, and can be defined as a load with a certain value at which the deflection of the actual shell surface occurs, i.e., such a critical load value for which the original equilibrium state of the shell ceases to be stable [26].
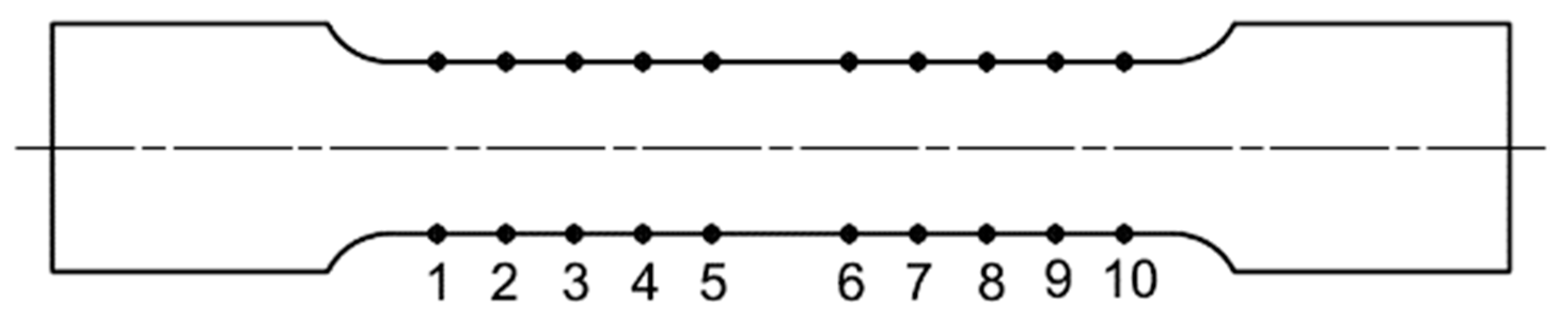
- Total length of specimen is ,
- Length of surface working part is L = 100 mm,
- Specimen radius is .
2.1. Static Tensile Test for Determining Material Parameters of Aluminium Alloy
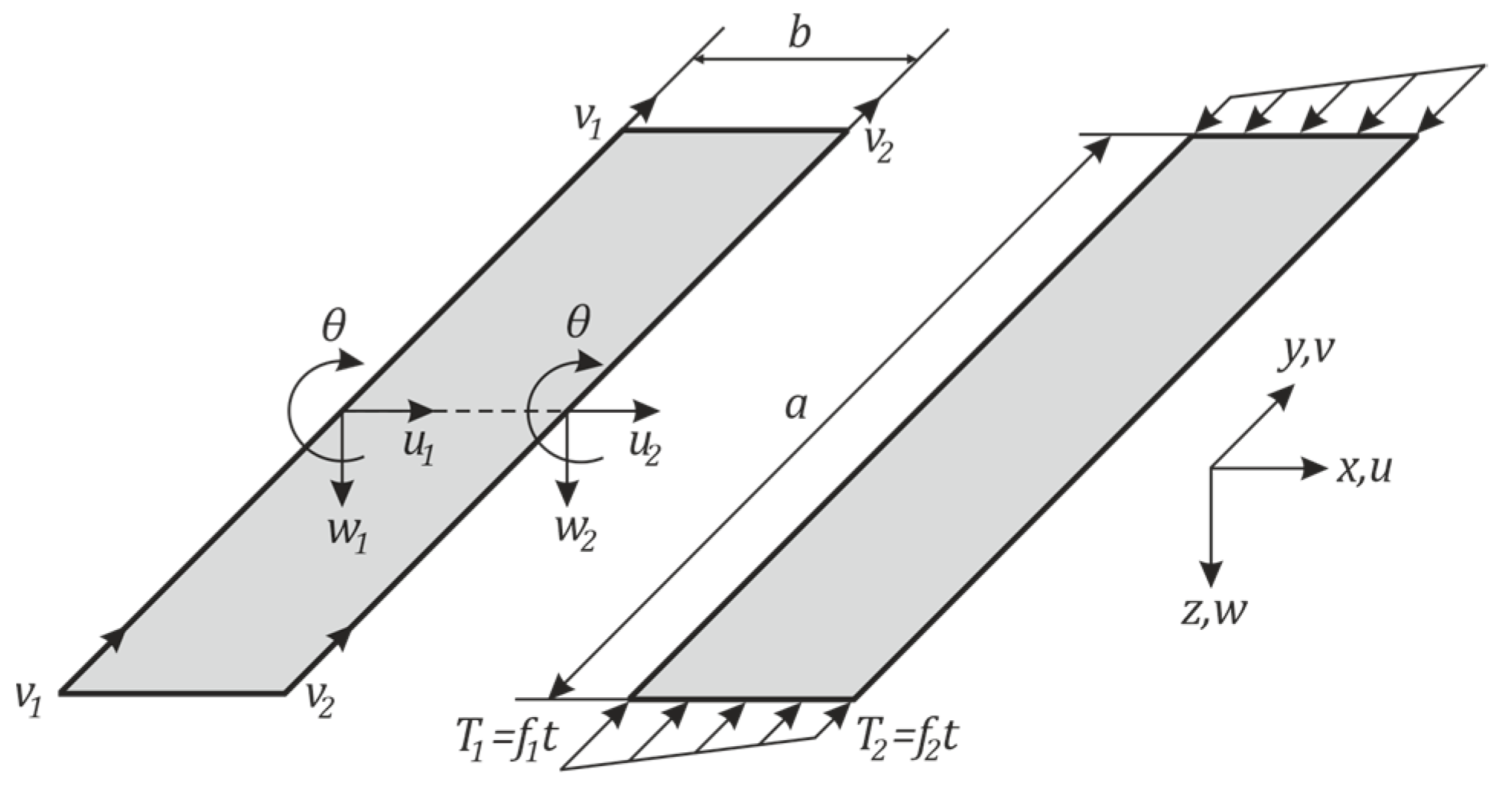
2.2. Proposed Numerical Solution for Finite Strip Method
3. Proposed Elliptical Cross-Section Shapes and Its Solid Mechanical Fixtures, Results of Experimental and Numerical Measurements
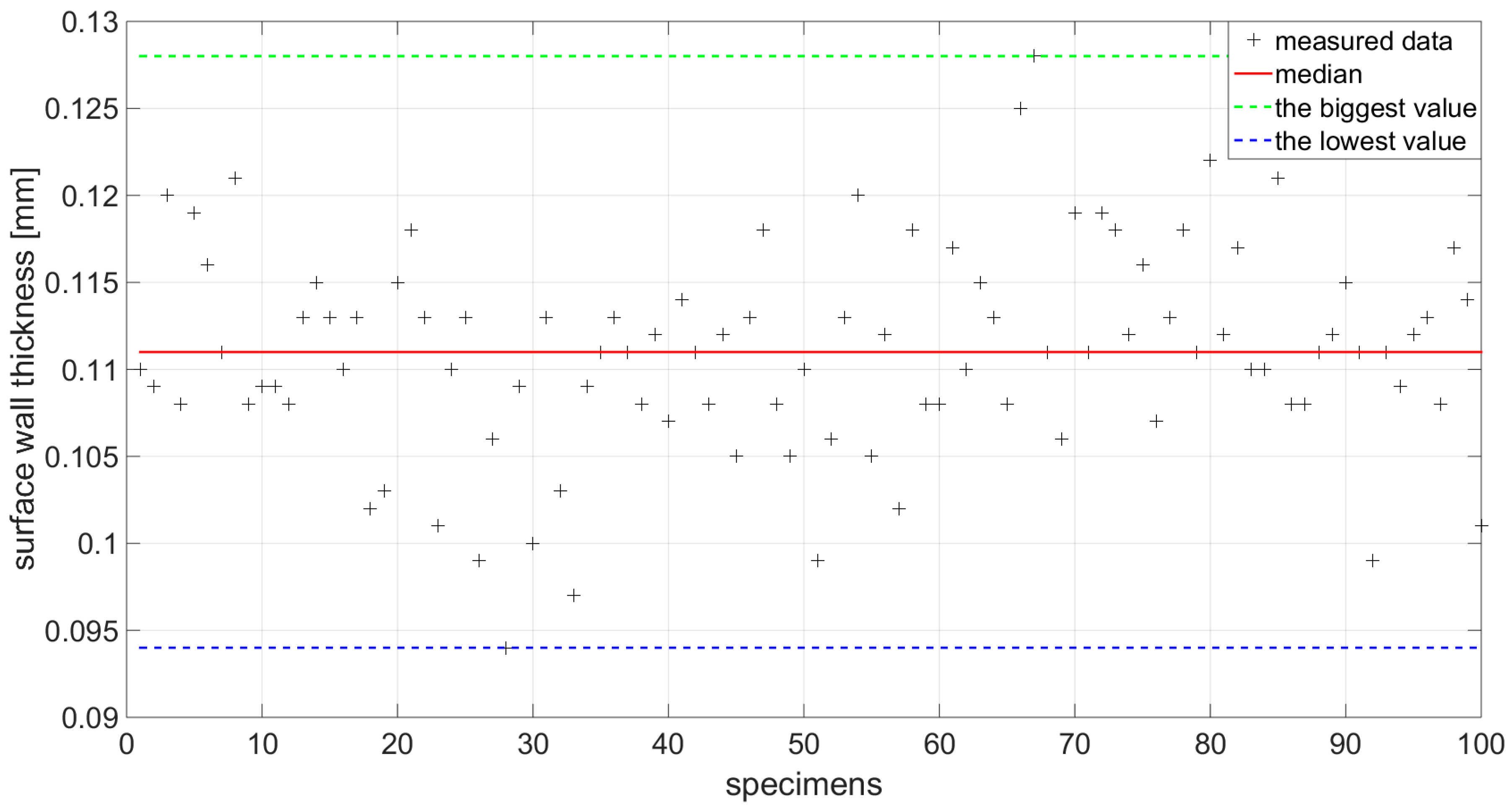
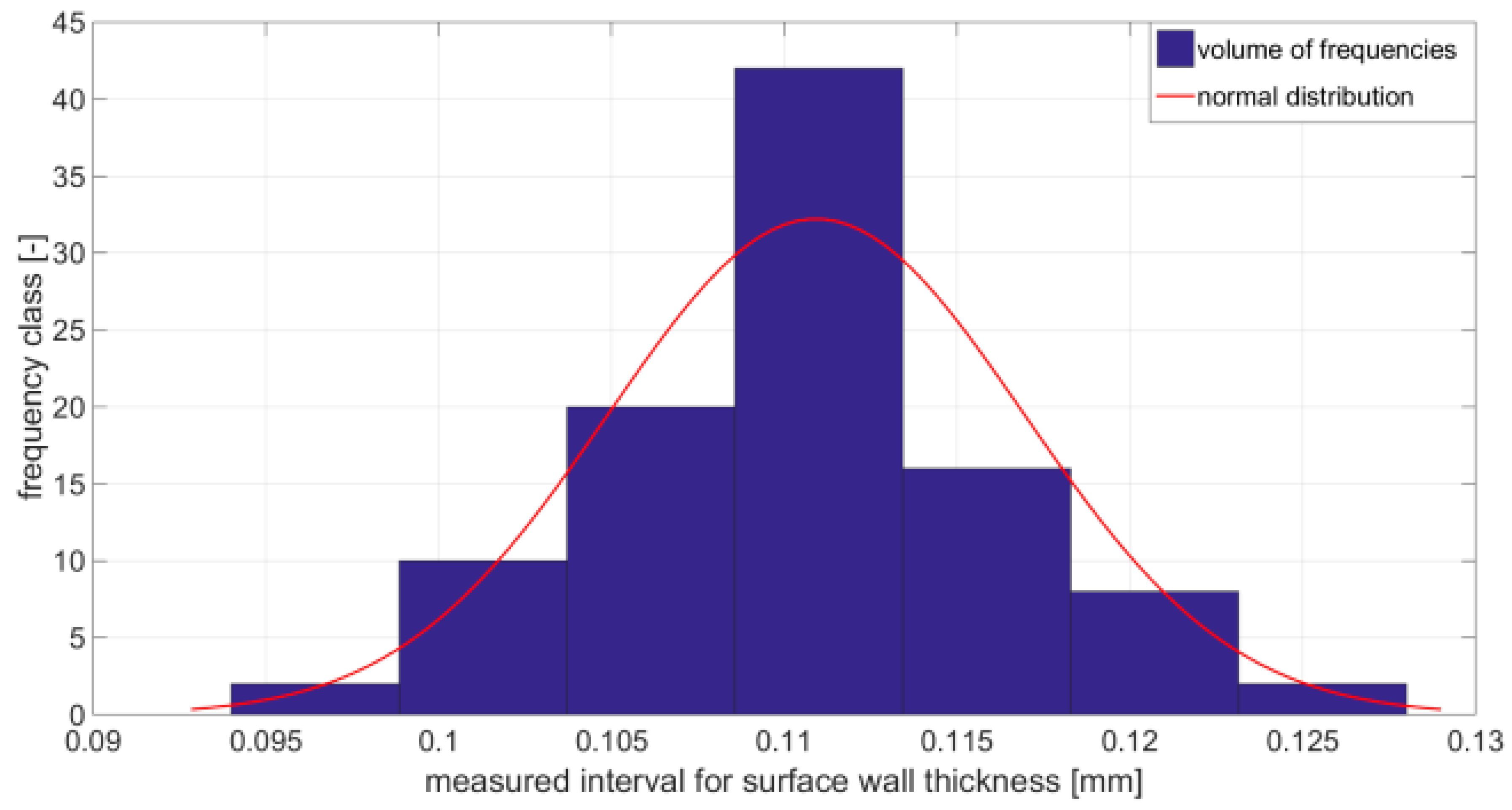
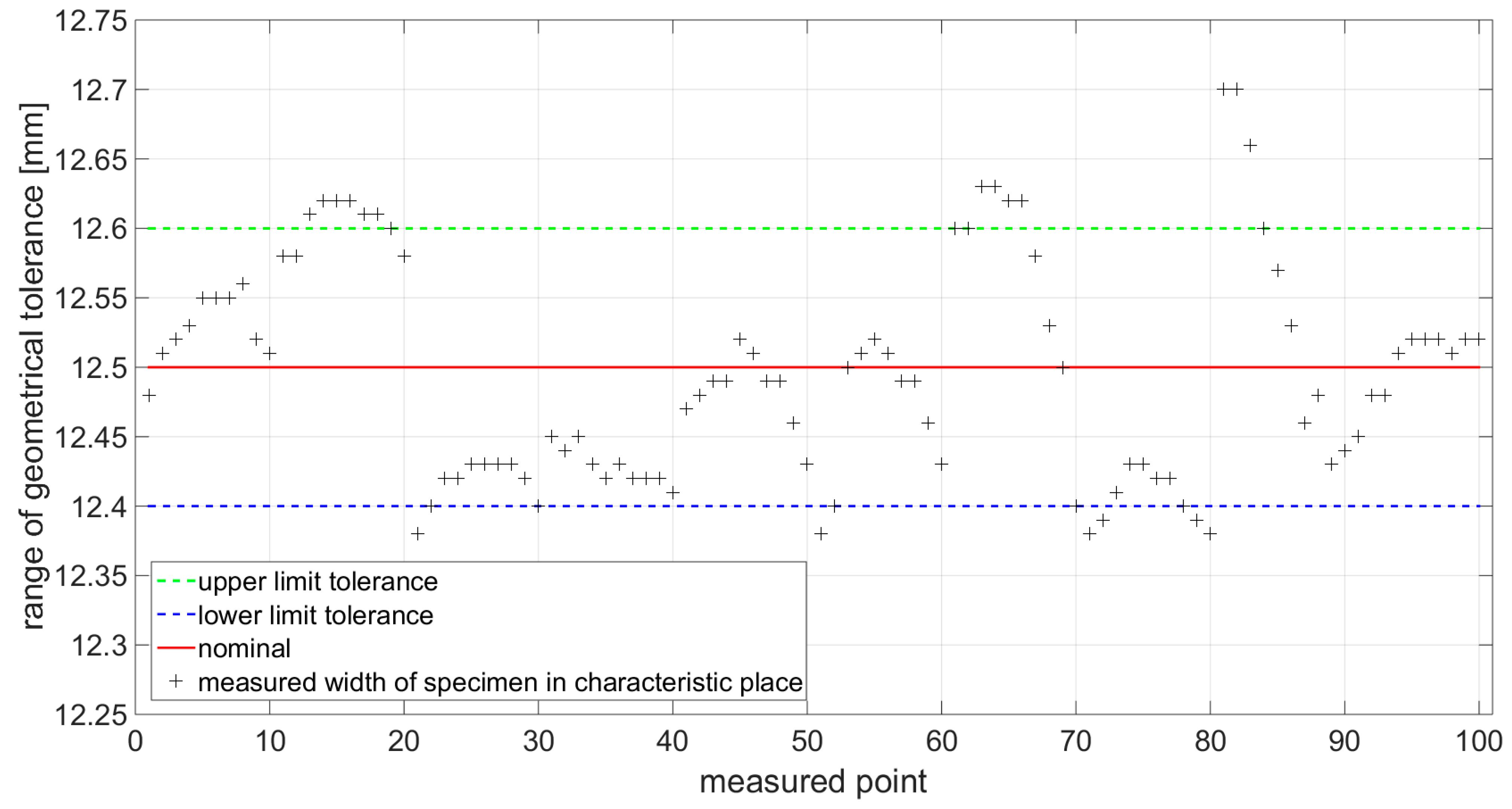
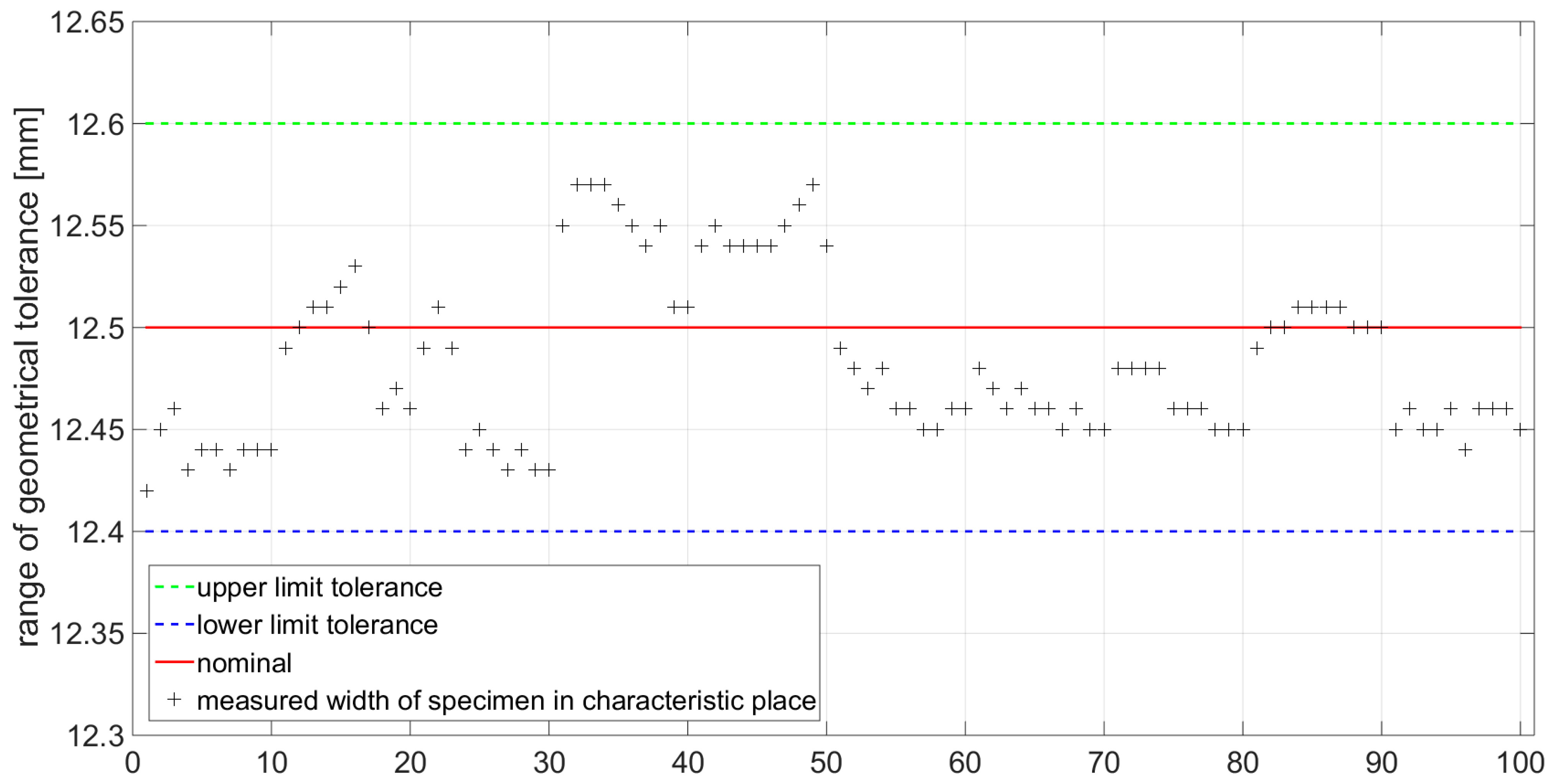
3.1. Result of Dimensional Measurement for Surface Wall Thickness and Specimen Width Used for Static Tensile Test
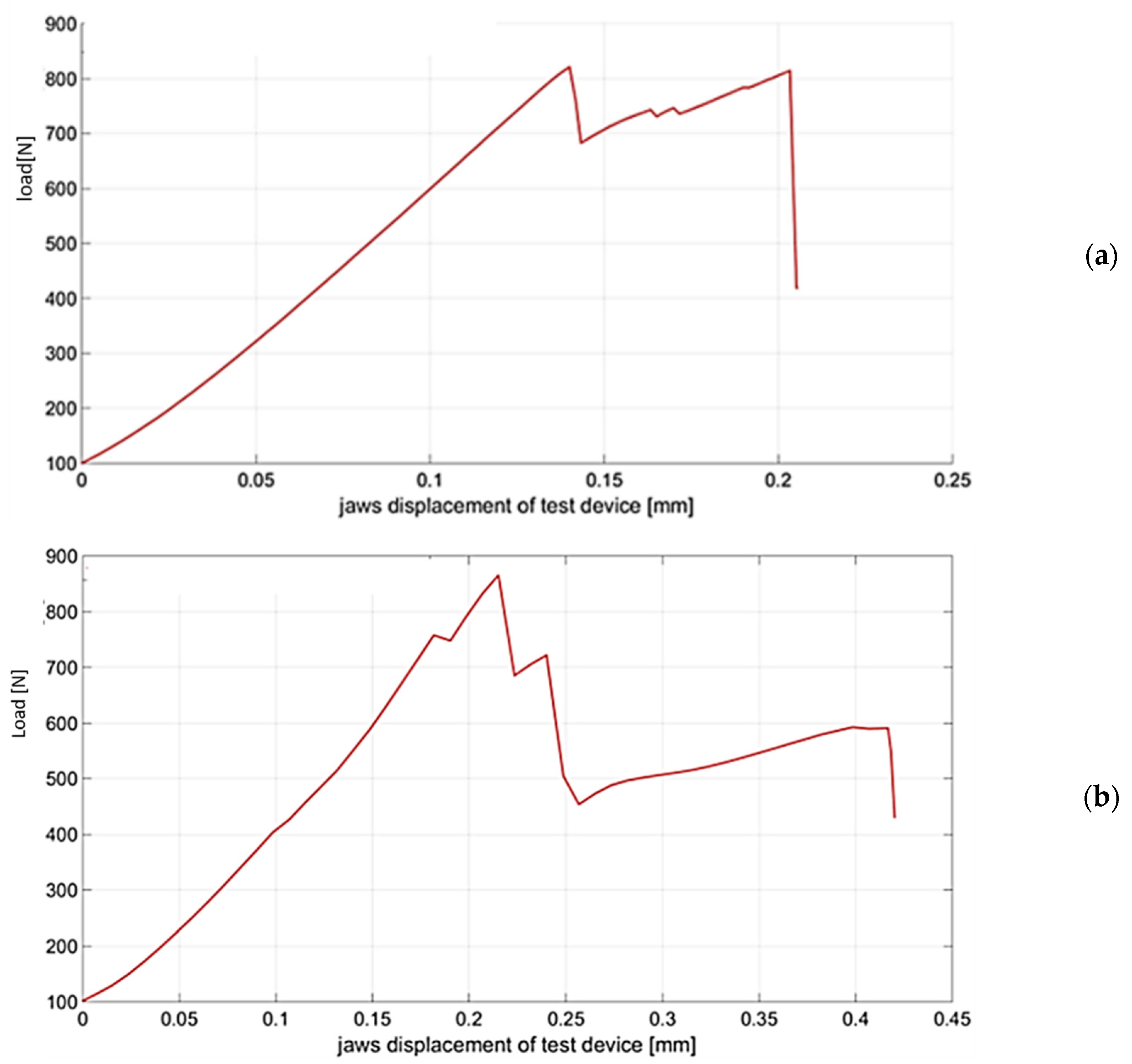
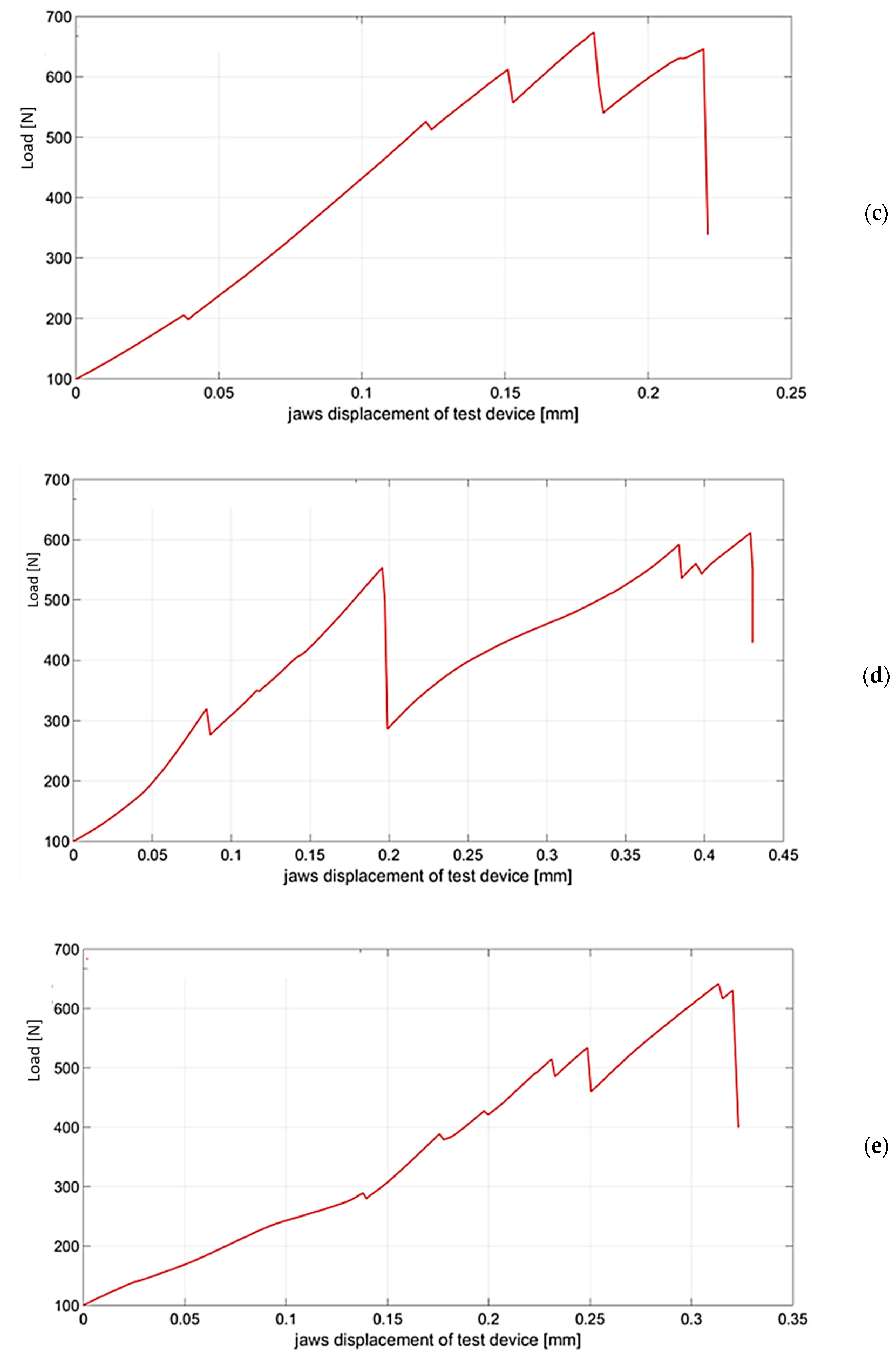
3.2. Experimental Results of Critical Force Measurement
3.3. Result of Static Tensile Test
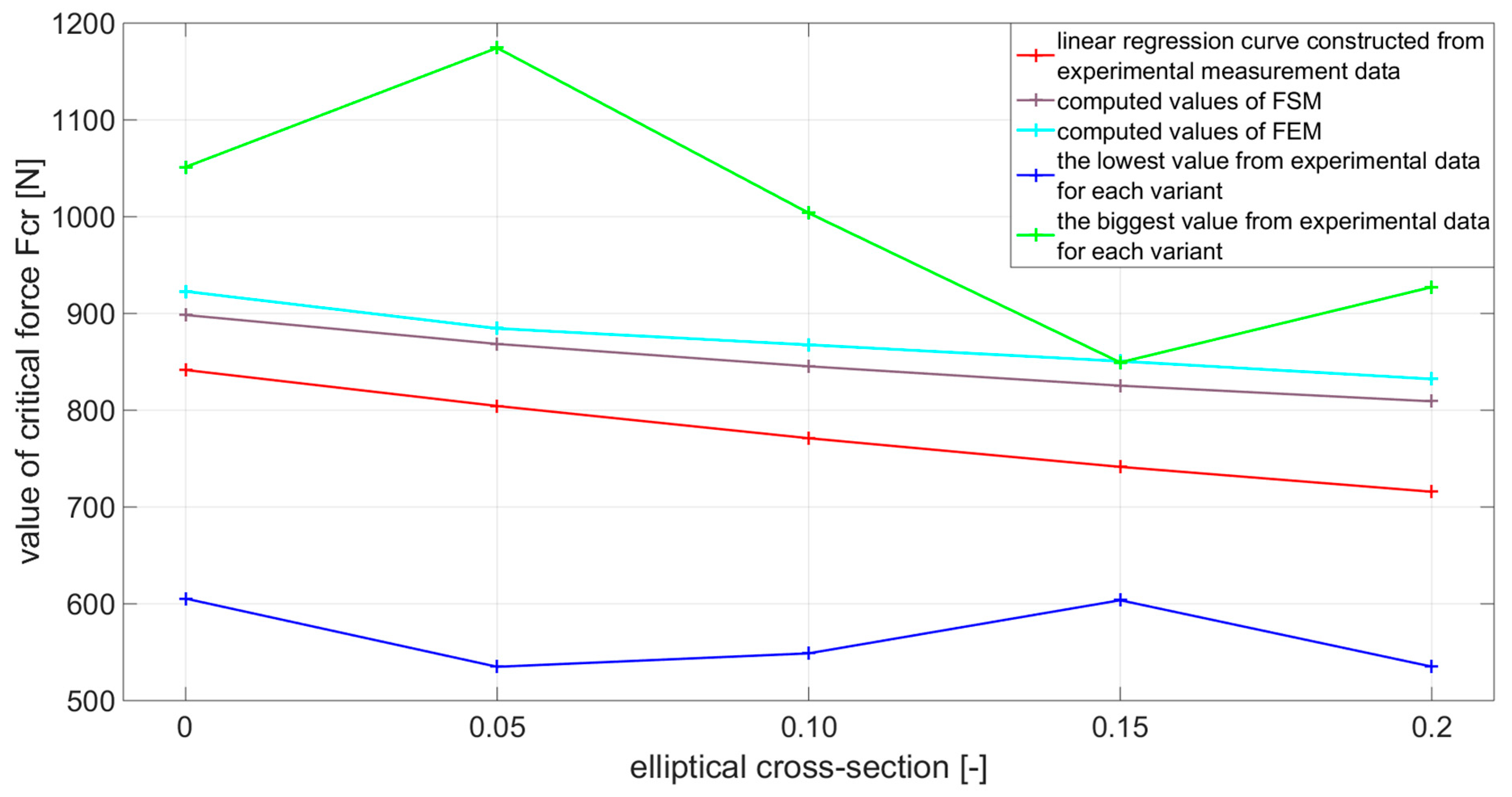
3.4. Computed Numerical Solutions
4. Discussion
- Geometric deviations of the test specimen surface,
- Geometric deviations of the mechanical fixtures,
- Incorrect placed of the test specimen in the mechanical fixtures,
- Inconsistency of the manufacturing tolerances of the roundness of the casing of the test specimen and the mechanical fixtures,
- Hidden material damage and residual stresses caused by the can manufacturing process,
- Unknown impact.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Brown, W.S. Stress and strain in a thin elliptic cylinder under internal pressure. The Engineer 1936, 162. [Google Scholar]
- Marguerre, K. Stability of cylindrical shell of variable curvature. NACA 1951, 1302. [Google Scholar]
- Kempner, J.; Nissel, N.; Vafakos, W.P. Energy solution for simply supported oval shells. AIAA J. 1964, 2, 555–557. [Google Scholar]
- Kempner, J.; Chen, Y.N. Large deflections of an axially compressed oval cylindrical shell. In Proceedings of the Eleventh International Congress of Applied Mechanics, Munich, Germany, 1 January 1964; Springer: Berlin, Germany, 1964; pp. 299–306. [Google Scholar]
- Chen, Y.N. Buckling and Postbuckling of an Oval Cylindrical Shell under Axial Compression. Ph.D. Thesis, Polytechnic Institute of Brooklyn, Brooklyn, NY, USA, June 1964. [Google Scholar]
- Kempner, J.; Chen, Y.N. Buckling and Postbuckling of an Axially Compressed Oval Cylindrical Shell. Polytechnic Institute of Brooklyn, PIBAL Report No. 917. Presented at the Seventh Anniversary Symposium on Shells to Honour Lloyd, H. Donnell, April 1966. [Google Scholar]
- Kempner, J.; Chen, Y.N. Buckling and Postbuckling of an Axially Compressed Oval Cylindrical Shell; PIBAL Report. 917; McCutchan Publishing Corporation: San Pablo, CA USA, 1967; pp. 141–183. [Google Scholar]
- Hutchinson, J.W. Buckling and Initial postbuckling behaviour of oval cylindrical shells under axial compression. Transactions of the american society of mechanical engineers. J. Appl. Mech. 1968, 35, 66–72. [Google Scholar] [CrossRef]
- Kempner, J.; Chen, Y.N. Postbuckling of an axially compressed oval cylindrical shell. Applied mechanics. In Proceedings of the 12th International Congress of Applied Mechanics, Stanford, CA, USA, 26–31 August 1968; Stanford University: Stanford, CA, USA, 1968. [Google Scholar]
- Feinstein, G.; Chen, Y.N.; Kempner, J. Buckling of clamped oval cylindrical shells under axial loads. AIAA J. 1971, 9, 1733–1738. [Google Scholar] [CrossRef]
- Feinstein, G.; Erickson, B.; Kempner, J. Stability of oval cylindrical shells. J. Exp. Mech. 1971, 11, 514–520. [Google Scholar] [CrossRef]
- Tennyson, R.C.; Booton, M.; Caswell, R.D. Buckling of imperfect elliptical cylindrical shells under axial compression. AIAA J. 1971, 9, 250–255. [Google Scholar] [CrossRef]
- Holland, M.; Lalor, M.J.; Walsh, J. Principal displacements in a pressurized elliptic cylinder: Theoretical predictions with experimental verification by laser interferometer. J. Strain Anal. 1974, 9, 159–165. [Google Scholar] [CrossRef]
- Kempner, J.; Chen, Y.N. Buckling and Initial postbuckling of oval cylindrical shells under combined axial compression and bending. Trans. N. Y. Acad. Sci. 1974, 36, 143–244. [Google Scholar] [CrossRef]
- Chen, Y.N.; Kempner, J. Buckling of oval cylindrical shells under compression and asymmetric bending. AIAA J. 1976, 14, 1235–1240. [Google Scholar] [CrossRef]
- Suzuki, K.; Shikanai, G.; Leissa, A.W. Free Vibrations of laminated composite thin non-circular cylindrical shell. J. Appl. Mech. 1994, 61, 861–871. [Google Scholar] [CrossRef]
- Meyers, C.A.; Hyer, M.W. Response of elliptical composite cylinders to axial compression loading. Mech. Adv. Mater. Struct. 1996, 6, 169–194. [Google Scholar] [CrossRef]
- Gardner, L. Structural behaviour of oval hollow sections. Int. J. Adv. Steel Constr. 2005, 1, 26–50. [Google Scholar]
- Zhu, Y.; Wilkinson, T. Finite element analysis of structural steel elliptical hollow sections in pure compression. In Tubular Structures XI; Routledge: London, UK, 2017; pp. 179–186. [Google Scholar]
- Chan, T.M.; Gardner, L. Compressive resistance of hot-rolled elliptical hollow sections. Eng. Struct. 2008, 30, 522–532. [Google Scholar] [CrossRef]
- Silvestre, N. Buckling behaviour of elliptical cylindrical shells and tubes under compression. Int. J. Solids Struct. 2008, 45, 4427–4447. [Google Scholar] [CrossRef] [Green Version]
- Northcutt, A.; Datir, P.; Han, H.C. Computational simulations of buckling of oval and tapered arteries. In Tributes to Yuan-Cheng Fung on His 90th Birthday; World Scientific: Singapore, 2009; pp. 53–64. [Google Scholar]
- Wan, L.; Chen, L. Buckling behavior of elliptical shells of changing thickness under uniform axial compression. In Applied Mechanics and Materials; Trans Tech Publications Ltd.: Stafa-Zurich, Switzerland, 2013; Volume 351, pp. 492–496. [Google Scholar]
- Lomakin, E.V.; Rabinskiy, L.; Radchenko, V.; Solyaev, Y.; Zhavornok, S.; Babaytsev, A.V. Analytical estimates of the contact zone area for a pressurized flat-oval cylindrical shell placed between two parallel rigid plates. Meccanica 2018, 53, 3831–3838. [Google Scholar] [CrossRef]
- Coman, C.D. Oval cylindrical shells under asymmetric bending: A singular-perturbation solution. Zeitschrift für Angewandte Mathematik und Physik 2018, 69, 1–16. [Google Scholar] [CrossRef]
- Trebuňa, F.; Šimčák, F. Robustness of Elements of Mechanical Systems; Emilena: Košice, Slovakia, 2004. [Google Scholar]
- Samuelson, L.Å.; Eggwertz, S. Shell Stability Handbook; Elsevier Science Publishers LTD: London, UK, 1992; p. 283. ISBN 1-85166-954-X. [Google Scholar]
- Koiter, W.T. Elastic Stability of Solid and Structures; Cambridge University Press: New York, NY, USA, 2009; p. 229. ISBN 978-0-511-43674-1. [Google Scholar]
- Singer, J.; Arbocz, J.; Weller, T. Buckling Experiments: Experimental Methods in Buckling of Thin-Walled Structures; John Wiley & Sons: New York, NY, USA, 2002; p. 1707. ISBN 0-471-97450-1. [Google Scholar]
- Bigoni, D. Nonlinear Solid Mechanics: Bifurcation Theory and Material Instability; Cambridge University Press: Cambridge, UK, 2012; p. 527. ISBN 978-1-107-02541-7. [Google Scholar]
- Chen, D.H. Crush Mechanics of Thin-Walled Tubes; CRC Press: Boca Raton, FL, USA, 2016; p. 329. ISBN 978-1-4987-5518-4. [Google Scholar]
- Narayanan, R. Shell Structures, Stability and Strength; Elsevier: London, UK, 1985. [Google Scholar]
- International Standard ISO 6892-1. Metallic Material-Tensile Testing-Part 1: Method of Test at Room Temperature. Reference Number, ISO 6892-1:2009(E), 1st ed.; ISO: Geneva, Switzerland, 2009. [Google Scholar]
- Li, Z.; Schafer, B.W. Buckling analysis of cold-formed steel members with general boundary conditions using cufsm: Conventional and constrained finite strip method. In Proceedings of the 20th International Specialty Conference on Cold-Formed Steel Structures, Saint Luis, MO, USA, 3 November 2010. [Google Scholar]
- Cheung, Y.K. Finite Strip Method in Structural Analysis; Paramount Press: Budapest, Hungary, 1976; p. 233. ISBN 0-08-018308-5. [Google Scholar]
- Zinkiewich, O.C.; Cheung, Y.K. The Finite Element Method in Structural and Continuum Mechanics; McGraw-Hill: New York, NY, USA, 1967. [Google Scholar]
- Schafer, B.W.; Ádány, S. Buckling analysis of cold-formed steel members using CUFSM: Conventional and constrained finite strip methods. In Proceedings of the 18th International Specialty Conference on Cold-Formed Steel Structures: Recent Research and Developments in Cold-Formed Steel Design and Construction, Orlando, FL, USA, 26–27 October 2006. [Google Scholar]
- Maláková, S.; Urbanský, M.; Fedorko, G.; Molnár, V.; Sivak, S. Design of geometrical parameters and kinematical characteristics of a non-circular gear transmission for given parameters. Appl. Sci. 2021, 11, 1000. [Google Scholar] [CrossRef]
- Maláková, S.; Puškár, M.; Frankovský, P.; Sivák, S.; Palko, M.; Palko, M. Meshing Stiffness—A Parameter Affecting the Emission of Gearboxes. Appl. Sci. 2020, 10, 8678. [Google Scholar] [CrossRef]
- Blatnický, M.; Sága, M.; Dizo, J.; Bruna, M. Application of Light Metal Alloy EN AW 6063 to Vehicle Frame Construction with an Innovated Steering Mechanism. Materials 2020, 13, 817. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sága, M.; Blatnická, M.; Blatnický, M.; Dižo, J.; Gerlici, J. Research of the fatigue life of welded joints of high strength steel S960 QL created using laser and electron beams. Materials 2020, 13, 2539. [Google Scholar] [CrossRef]
- Frankovský, P.; Delyová, I.; Sivák, P.; Kurylo, P.; Pivarčiová, E.; Neumann, V. Experimental assessment of time-limited operation and rectification of a bridge crane. Materials 2020, 13, 2708. [Google Scholar] [CrossRef]
- Kuryło, P.; Klekiel, T.; Pruszyński, P. A mechanical study of novel additive manufactured modular mandible fracture fixation plates-Preliminary Study with finite element analysis. Injury 2020, 51, 1527–1535. [Google Scholar]
- Casuso, M.; Polvorosa, R.; Veiga, F.; Suárez, A.; Lamikiz, A. Residual stress and distortion modeling on aeronautical aluminum alloy parts for machining sequence optimization. Int. J. Adv. Manuf. Technol. 2020, 110, 1219–1232. [Google Scholar] [CrossRef]
- Dean, W.R. On the theory of elastic stability. Proc. R. Soc. Lond. 1925, 107, 734–759. [Google Scholar]
- Schwerin, E. Die Torsionsstabilität des dünnwandigen Rohres. Zeitschrift für Angewandte Mathematik und Mechanik 1925, 5, 235–243. [Google Scholar] [CrossRef]
- Brazier, L.G. On the flexure of thin cylindrical shells and other “thin” sections. Proc. R. Soc. Lond. 1927, 116, 104–114. [Google Scholar]
- Robertson, A. The strength of tubular struts. Proc. R. Soc. Lond. 1928, 121, 558–585. [Google Scholar]
- Donnell, L.H. Stability of Thin-Walled Tubes Under Torsion; Technical Report NACA Rep. 479; NACA: Boston, MA, USA, 1933. [Google Scholar]
- Kromm, A. Die Stabilitätsgrenze der Kreiszylinderschale bei Beanspruchung durch Schub-und Längskräfte. In Jahrbuch 1942 der Deutschen Luftfahrtforschung; Wiley: Hoboken, NJ, USA, 1942; pp. 602–616. [Google Scholar]
- Batdorf, S.B. A Simplified Method of Elastic Stability Analysis for Thin Cylindrical Shells; Technical Report NACA Rep. 874; NACA: Boston, MA, USA, 1947. [Google Scholar]
- Batdorf, S.B.; Stein, M.; Schildcrout, M. Critical Combinations of Torsion and Direct Axial Stress for Thin-Walled Cylinders; Technical Report NACA TN-1345; NACA: Boston, MA, USA, 1947. [Google Scholar]










| Ellipse Shape | ||
|---|---|---|
 | ||
 | ||
 | ||
 | ||
 |
| Standard deviation [mm] | 0.006014595 |
| Arithmetic mean [mm] | 0.111 |
| Median [mm] | 0.111 |
| The biggest value [mm] | 0.128 |
| The lowest value [mm] | 0.094 |
| Specimens with Axial Orientation of the Material Fibers | Specimens with Radial Orientation of the Material Fibers | ||
|---|---|---|---|
| Standard deviation [mm] | 0.0302 | Standard deviation [mm] | 0.0079 |
| Arithmetic mean [mm] | 12.496 | Arithmetic mean [mm] | 12.483 |
| Median [mm] | 12.503 | Median [mm] | 12.460 |
| The lowest measured value [mm] | 12.38 | The lowest measured value [mm] | 12.43 |
| The biggest measured value [mm] | 12.70 | The biggest measured value [mm] | 12.57 |
| Statistical Parameters | Standard Deviation [N] | Arithmetic Mean [N] | Median [N] |
|---|---|---|---|
| Ref. variant | 120.2447 | 805.891 | 783.580 |
| Variant | 150.7167 | 799.594 | 773.765 |
| Variant | 112.8161 | 780.684 | 754.933 |
| Variant | 84.3076 | 743.717 | 736.544 |
| Variant | 103.1899 | 687.421 | 688.285 |
| Specimens with Axial Orientation of the Material Fibers 1 | Specimens with Radial Orientation of the Material Fibers 2 | ||||
|---|---|---|---|---|---|
| [GPa] | [MPa] | [-] | [GPa] | [MPa] | [-] |
| 20.53 | 5632 | 0.33 | 12.51 | 5632 | 0.54 |
| Variant | % Difference | ||
|---|---|---|---|
| Ref. | 898.4 | 922.8 | 2.6 |
| 868.5 | 884.5 | 1.8 | |
| 845.4 | 867.6 | 2.5 | |
| 825.4 | 850.7 | 2.9 | |
| 809.2 | 832.3 | 2.7 |
| Variant | 1 Linear Regression of | % Difference between 1 and 2 | |||
|---|---|---|---|---|---|
| Ref. | 605.4 | 1051.3 | 841.6 | 805.8 | 4.4 |
| 534.9 | 1285.5 | 804.4 | 799.5 | 0.6 | |
| 548.8 | 1003.8 | 771.1 | 780.6 | 1.2 | |
| 603.7 | 849.4 | 741.5 | 743.7 | 0.3 | |
| 535.1 | 927.3 | 715.8 | 687.4 | 4.2 |
| Variant | Linear Regresion 1 | 2 FSM | 3 FEM | % Difference between 1 and 2 | % Difference between 2 and 3 |
|---|---|---|---|---|---|
| Ref. | 841.6 | 898.4 | 922.8 | 6.3 | 2.6 |
| 804.4 | 868.5 | 884.5 | 7.3 | 1.8 | |
| 771.1 | 845.4 | 867.6 | 8.7 | 2.5 | |
| 741.5 | 825.4 | 850.7 | 10.1 | 2.9 | |
| 715.8 | 809.2 | 832.3 | 11.5 | 2.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kostka, J.; Bocko, J.; Frankovský, P.; Delyová, I.; Kula, T.; Varga, P. Stability Loss Analysis for Thin-Walled Shells with Elliptical Cross-Sectional Area. Materials 2021, 14, 5636. https://doi.org/10.3390/ma14195636
Kostka J, Bocko J, Frankovský P, Delyová I, Kula T, Varga P. Stability Loss Analysis for Thin-Walled Shells with Elliptical Cross-Sectional Area. Materials. 2021; 14(19):5636. https://doi.org/10.3390/ma14195636
Chicago/Turabian StyleKostka, Ján, Jozef Bocko, Peter Frankovský, Ingrid Delyová, Tomáš Kula, and Patrik Varga. 2021. "Stability Loss Analysis for Thin-Walled Shells with Elliptical Cross-Sectional Area" Materials 14, no. 19: 5636. https://doi.org/10.3390/ma14195636
APA StyleKostka, J., Bocko, J., Frankovský, P., Delyová, I., Kula, T., & Varga, P. (2021). Stability Loss Analysis for Thin-Walled Shells with Elliptical Cross-Sectional Area. Materials, 14(19), 5636. https://doi.org/10.3390/ma14195636






