Width Dependent Elastic Properties of Graphene Nanoribbons
Abstract
1. Introduction
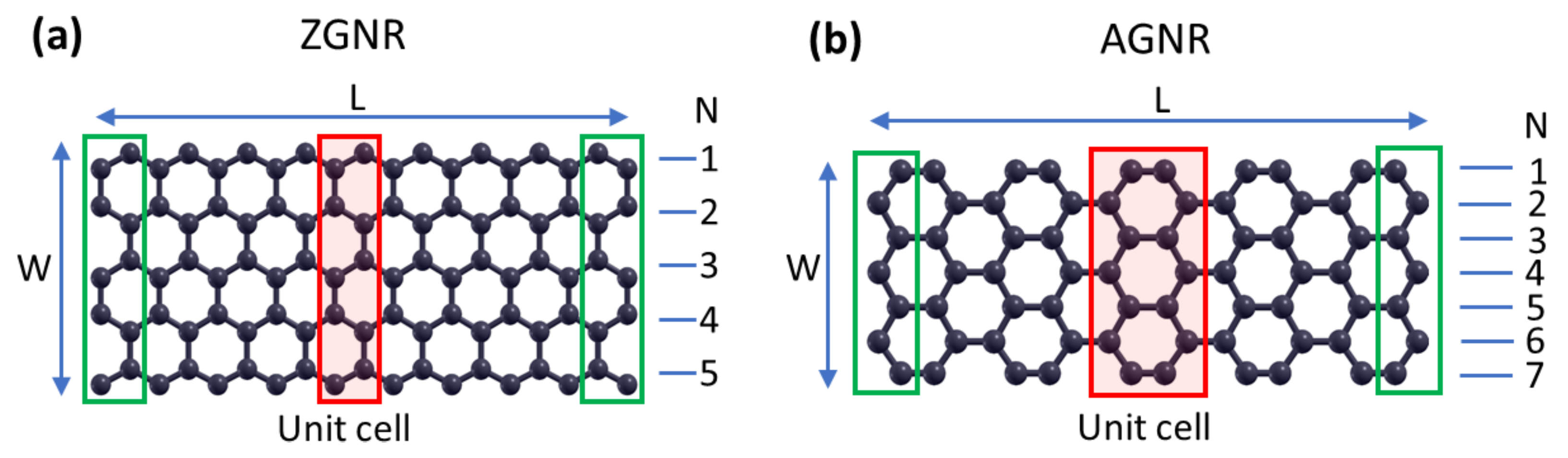
2. Methods
2.1. Density Functional Theory Calculations
2.2. Molecular Dynamics Simulations
3. Results and Discussion
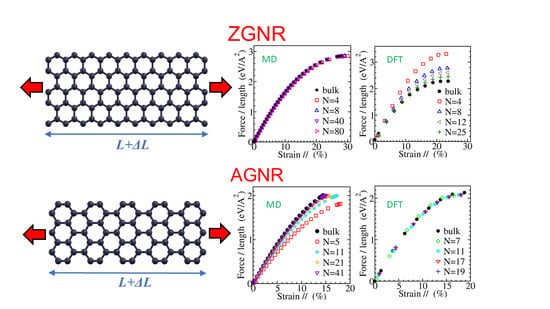
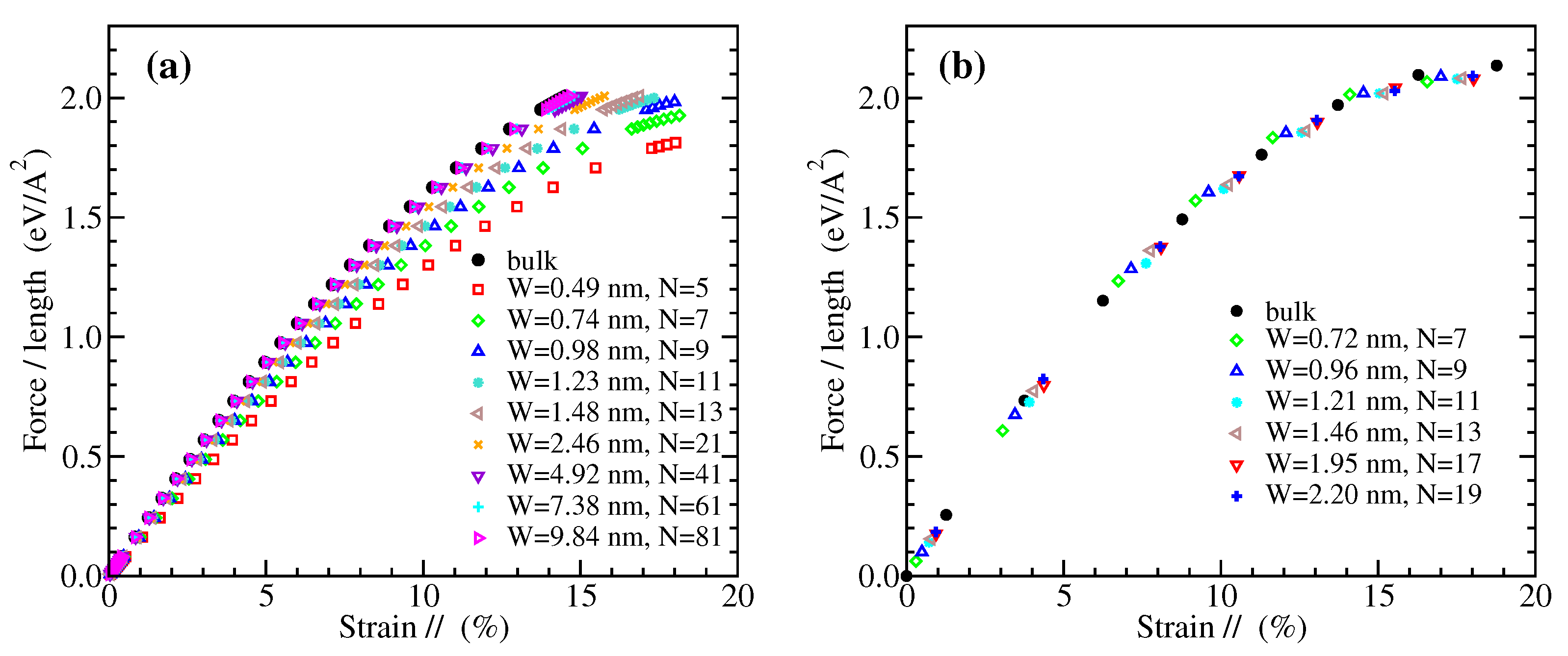
3.1. Stress-Strain Curves
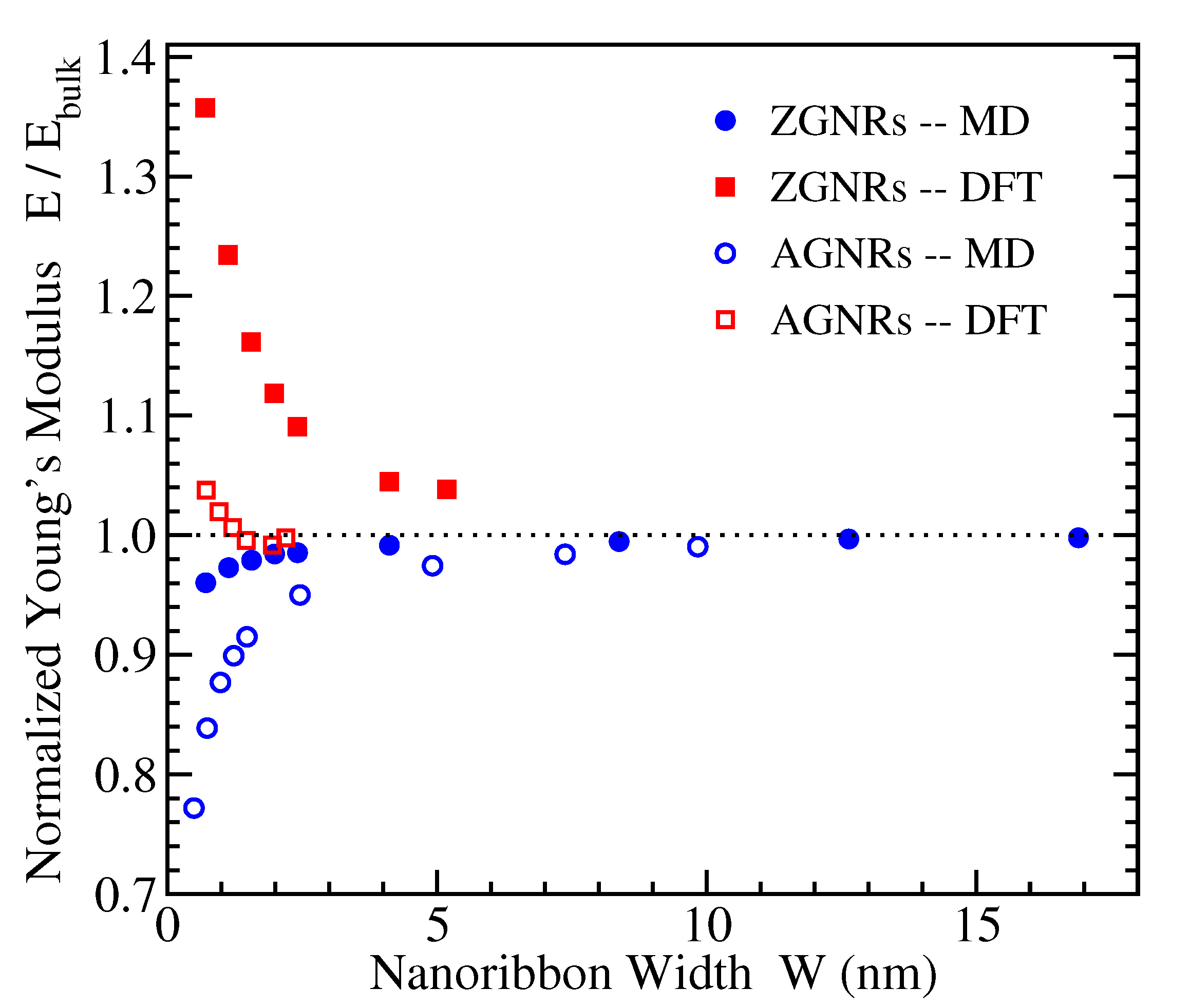
3.2. Young’s Modulus
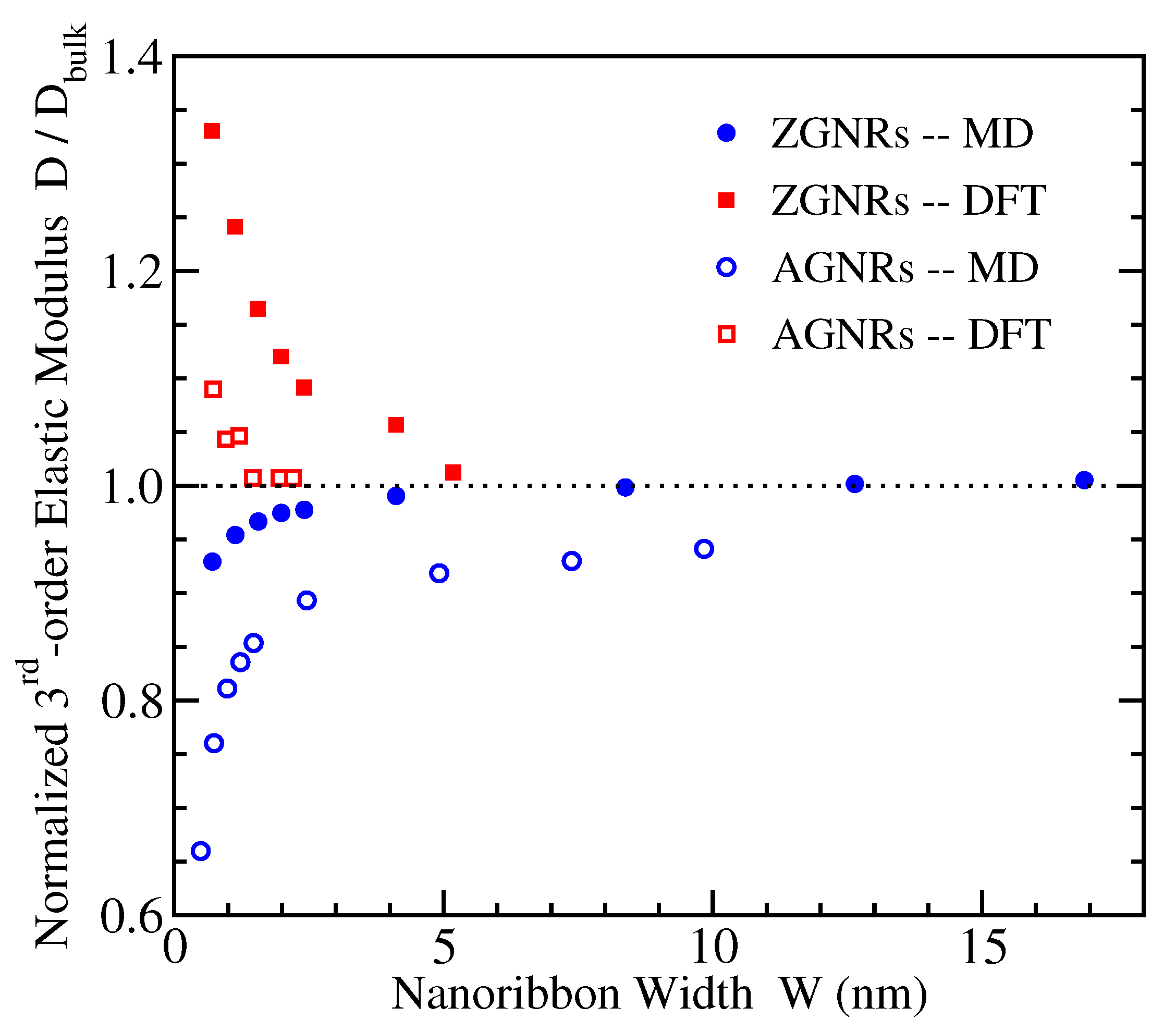
3.3. Third-Order Elastic Modulus
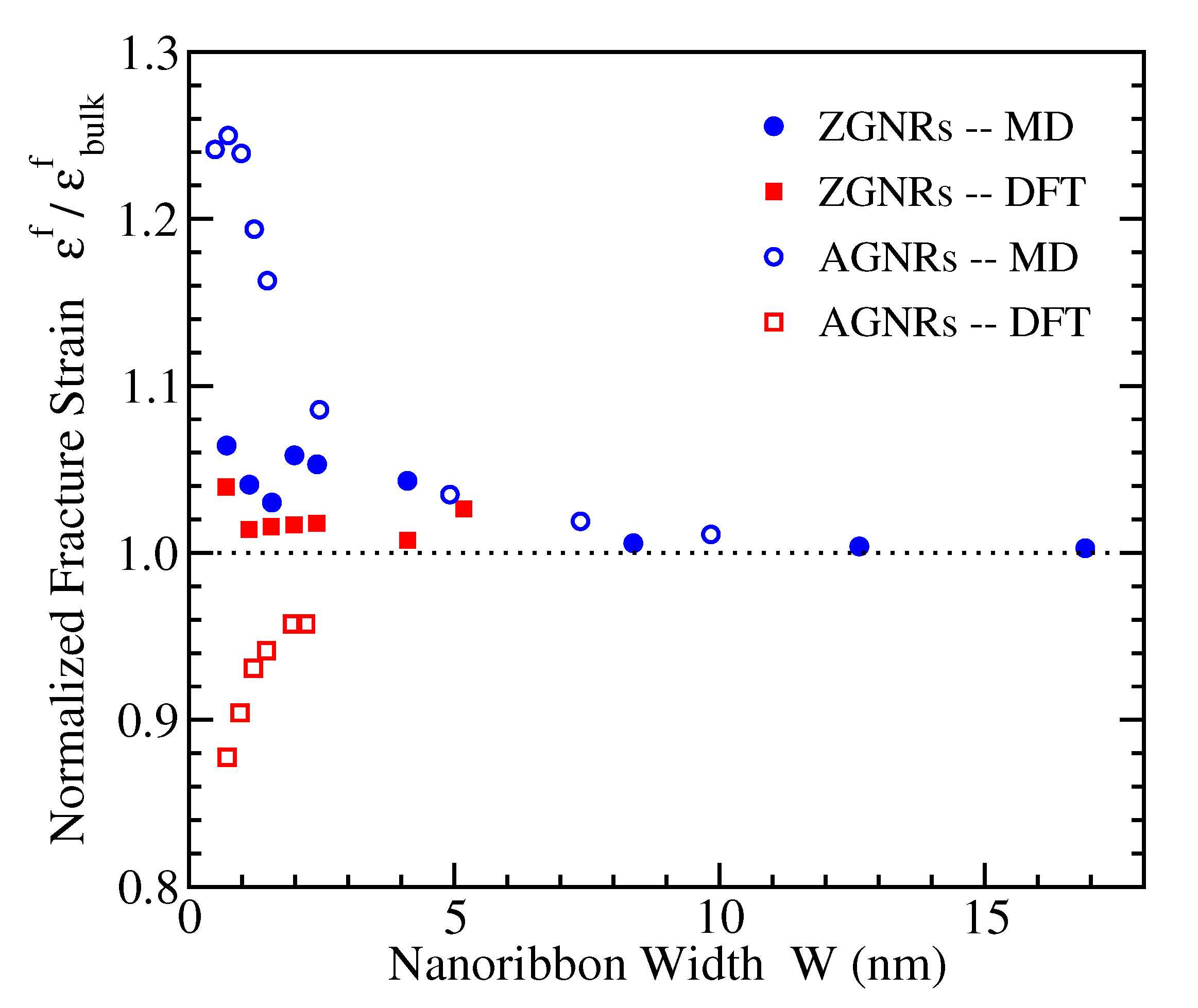
3.4. Fracture Strain
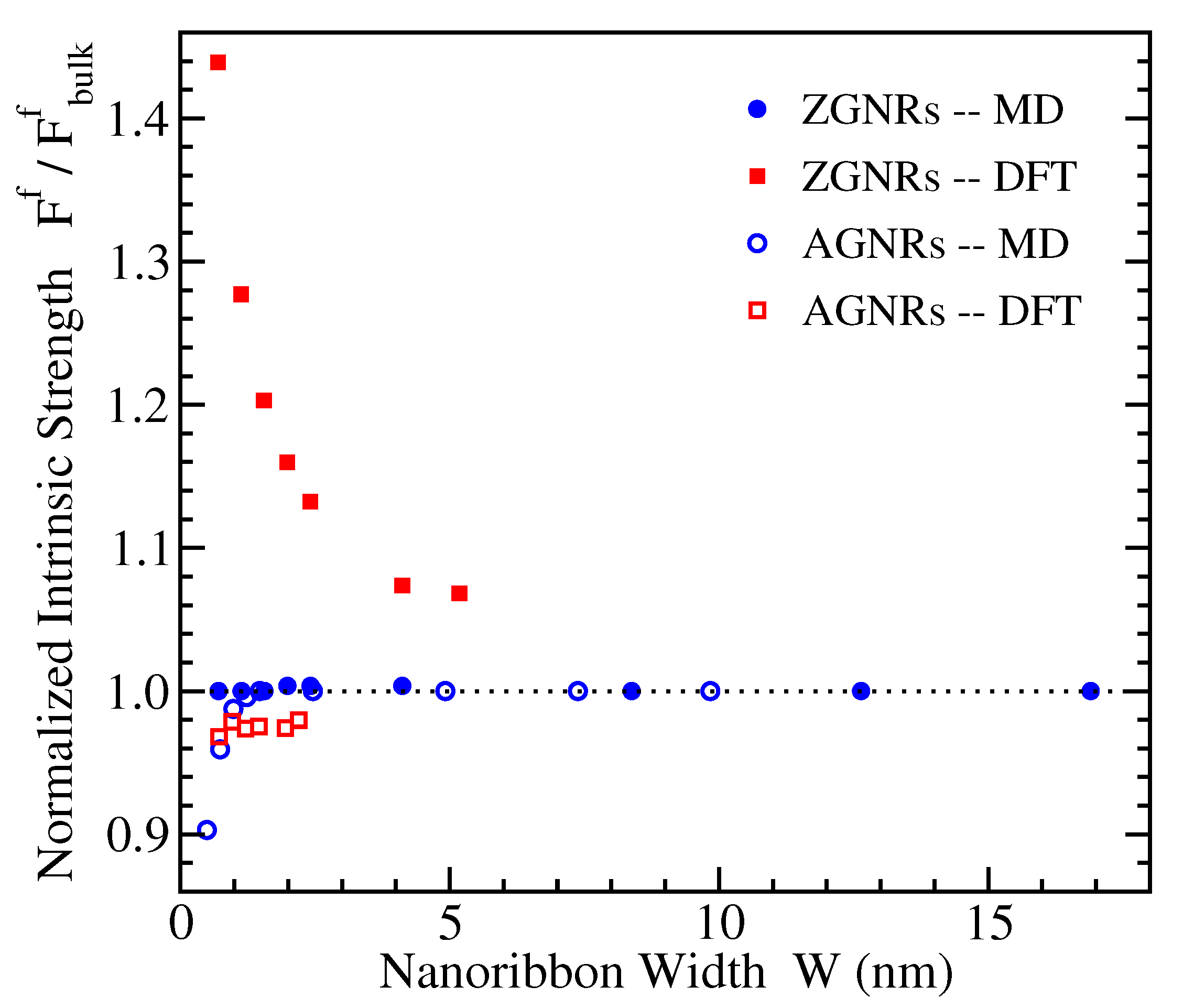
3.5. Intrinsic Strength
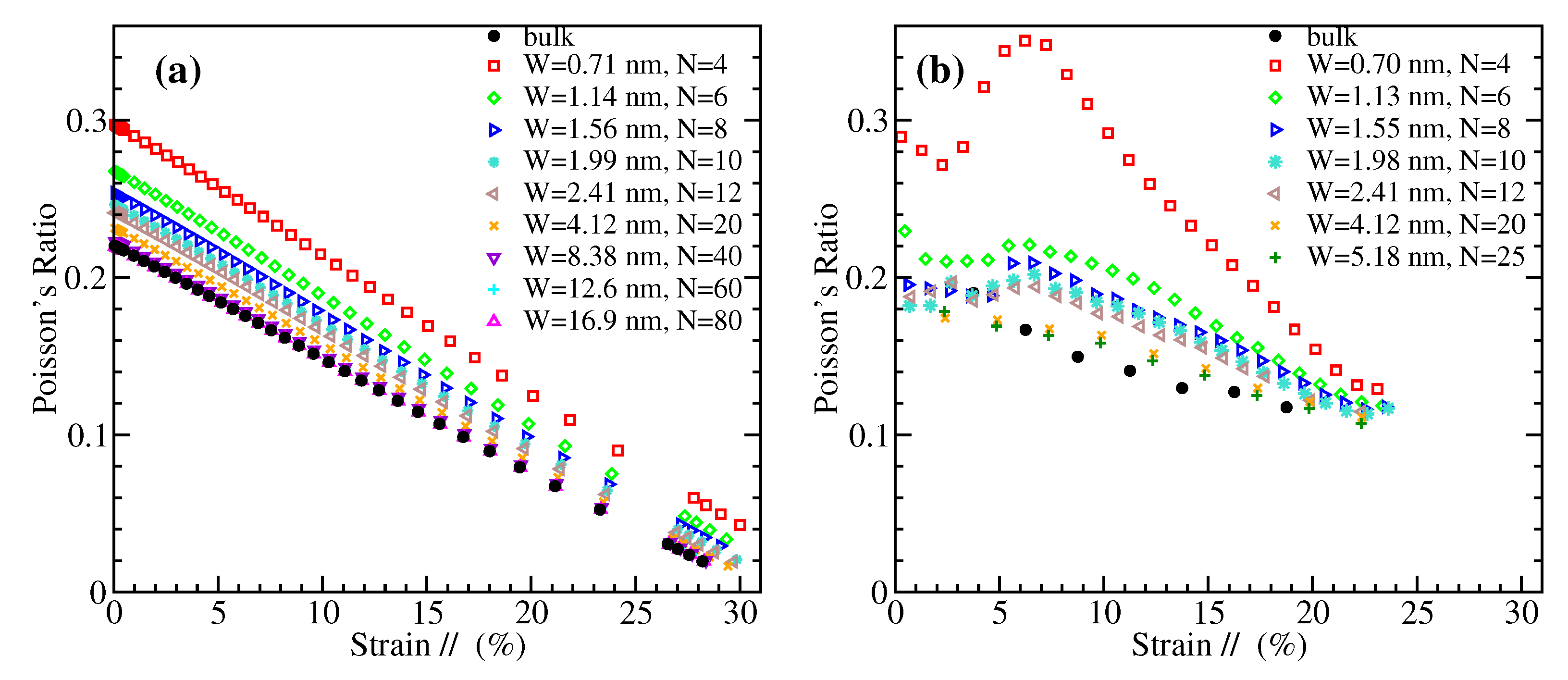
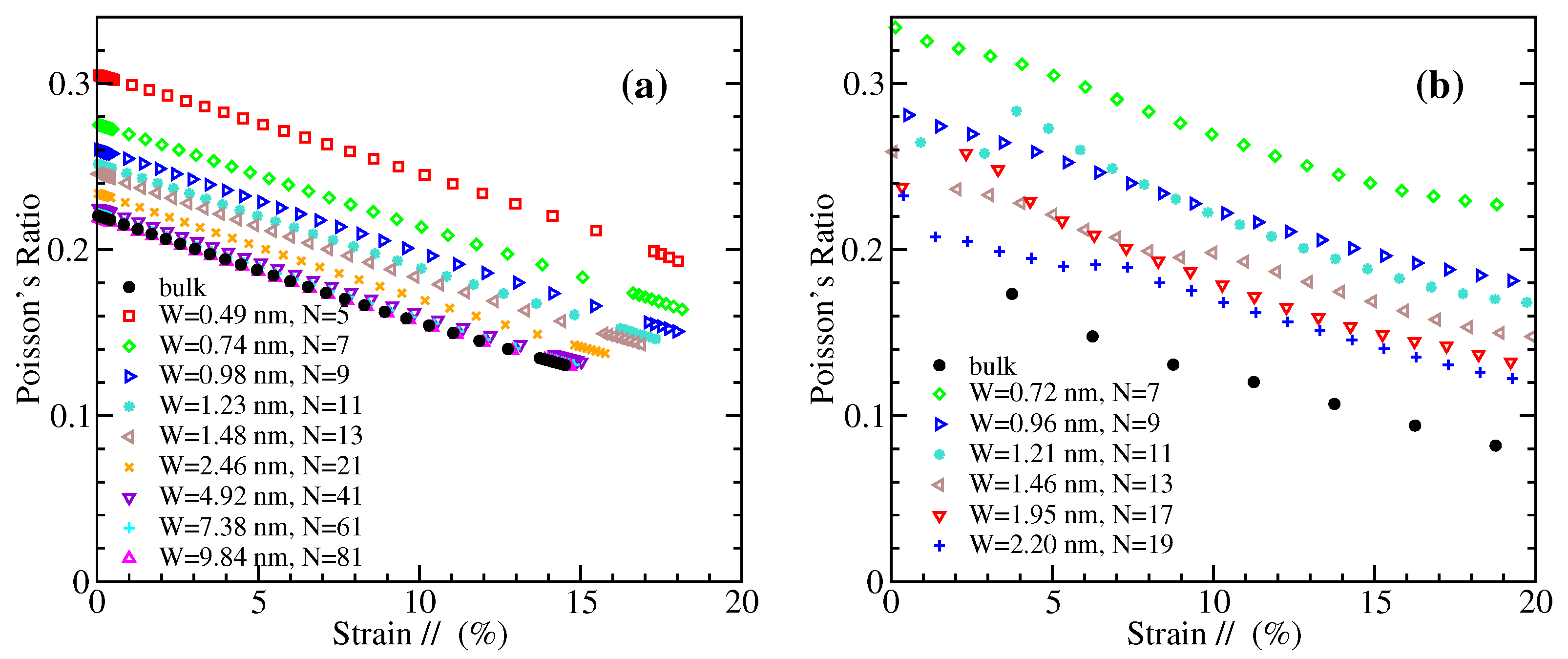
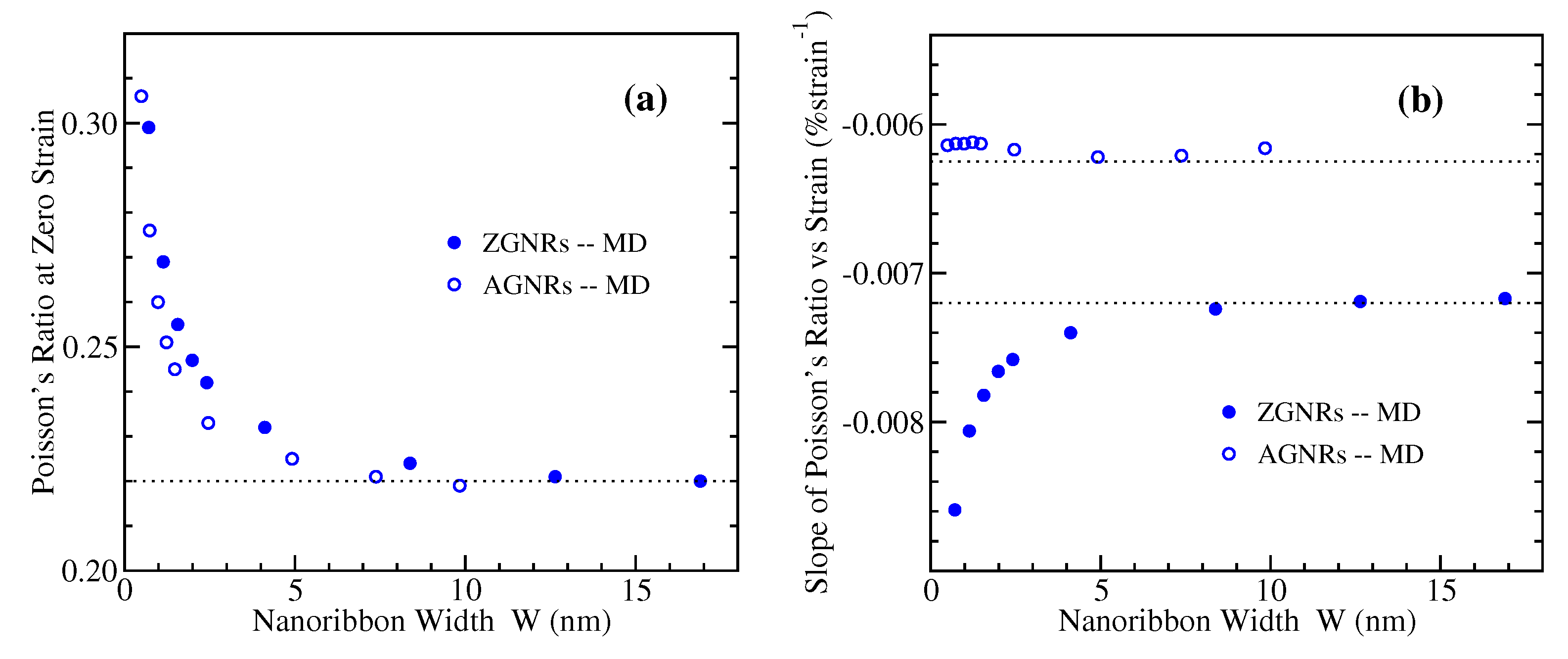
3.6. Poisson’s Ratio
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| GNR | Graphene NanoRibbon |
| AGNR | Armchair Graphene NanoRibbon |
| ZGNR | Zigzag Graphene NanoRibbon |
| MD | Molecular Dynamics |
| GGA | Generalized Gradient Approximation |
| DFT | Density Functional Theory |
| 2D | 2-Dimensional |
References
- Castro Neto, A.H.; Guinea, F.; Peres, N.M.R.; Novoselov, K.S.; Geim, A.K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109–162. [Google Scholar]
- Sarma, S.D.; Adam, S.; Hwang, E.H.; Rossi, E. Electronic transport in two-dimensional graphene. Rev. Mod. Phys. 2011, 83, 407–470. [Google Scholar] [CrossRef]
- McCann, E.; Koshino, M. The electronic properties of bilayer graphene. Rep. Prog. Phys. 2013, 76, 056503. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Katsnelson, M.I.; Grigorieva, I.V.; Dubonos, S.V.; Firsov, A.A. Two-dimensional gas of massless Dirac fermions in graphene. Nature 2005, 438, 197–200. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Tan, Y.-W.; Stormer, H.L.; Kim, P. Experimental observation of the quantum Hall effect and Berry’s phase in graphene. Nature 2005, 438, 201–204. [Google Scholar] [CrossRef] [PubMed]
- Nika, D.L.; Balandin, A.A. Phonons and thermal transport in graphene and graphene-based materials. Rep. Prog. Phys. 2017, 80, 036502. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, S.; Calizo, I.; Teweldebrhan, D.; Pokatilov, E.P.; Nika, D.L.; Balandin, A.A.; Bao, W.; Miao, F.; Lau, C.N. Extremely high thermal conductivity of graphene: Prospects for thermal management applications in nanoelectronic circuits. Appl. Phys. Lett. 2008, 92, 151911. [Google Scholar] [CrossRef]
- Chen, S.; Moore, A.L.; Cai, W.; Suk, J.W.; An, J.; Mishra, C.; Amos, C.; Magnuson, C.W.; Kang, J.; Shi, L.; et al. Raman measurements of thermal transport in suspended monolayer graphene of variable sizes in vacuum and gaseous environments. ACS Nano 2011, 5, 321–328. [Google Scholar] [CrossRef]
- Chen, S.; Wu, Q.; Mishra, C.; Kang, J.; Zhang, H.; Cho, K.; Cai, W.; Balandin, A.A.; Ruoff, R.S. Thermal conductivity of isotopically modified graphene. Nat. Mater. 2012, 11, 203–207. [Google Scholar] [CrossRef]
- Mohr, M.; Maultzsch, J.; Dobardzic, E.; Reich, S.; Milosevic, I.; Damnjanovic, M.; Bosak, A.; Krisch, M.; Thomsen, C. Phonon dispersion of graphite by inelastic X-ray scattering. Phys. Rev. B 2007, 76, 035439. [Google Scholar] [CrossRef]
- Koukaras, E.N.; Kalosakas, G.; Galiotis, C.; Papagelis, K. Phonon properties of graphene derived from molecular dynamics simulations. Sci. Rep. 2015, 5, 12923. [Google Scholar] [CrossRef] [PubMed]
- Kopidakis, G.; Wang, C.Z.; Soukoulis, C.M.; Ho, K.M. A tight-binding molecular dynamics study of phonon anharmonic effects in diamond and graphite. J. Phys. Condens. Matter 1997, 9, 7071–7080. [Google Scholar] [CrossRef][Green Version]
- Michel, K.H.; Costamagna, S.; Peeters, F.M. Theory of anharmonic phonons in two-dimensional crystals. Phys. Rev. B 2015, 91, 134302. [Google Scholar] [CrossRef]
- Raj, A.; Eapen, J. Phonon dispersion using the ratio of zero-time correlations among conjugate variables: Computing full phonon dispersion surface of graphene. Comp. Phys. Commun. 2019, 238, 124–137. [Google Scholar] [CrossRef]
- Daniels, C.; Horning, A.; Phillips, A.; Massote, D.V.P.; Liang, L.; Bullard, Z.; Sumpter, B.G.; Meunier, V. Elastic plastic and fracture mechanisms in graphene materials. J. Phys. Condens. Matter 2015, 27, 373002. [Google Scholar] [CrossRef]
- Liu, F.; Ming, P.; Li, J. Ab initio calculation of ideal strength and phonon instability of graphene under tension. Phys. Rev. B 2007, 76, 064120. [Google Scholar] [CrossRef]
- Lee, C.; Wei, X.; Kysar, J.W.; Hone, J. Measurement of the elastic properties and intrinsic strength of monolayer graphene. Science 2008, 321, 385–388. [Google Scholar] [CrossRef]
- Zakharchenko, K.V.; Katsnelson, M.I.; Fasolino, A. Finite temperature lattice properties of graphene beyond the quasiharmonic approximation. Phys. Rev. Lett. 2009, 102, 046808. [Google Scholar] [CrossRef]
- Lu, Q.; Huang, R. Nonlinear mechanics of single-atomic-layer graphene sheets. Int. J. Appl. Mech. 2009, 1, 443–467. [Google Scholar] [CrossRef]
- Kalosakas, G.; Lathiotakis, N.N.; Galiotis, C.; Papagelis, K. In-plane force fields and elastic properties of graphene. J. Appl. Phys. 2013, 113, 134307. [Google Scholar] [CrossRef]
- Zhang, P.; Ma, L.; Fan, F.; Zeng, Z.; Peng, C.; Loya, P.E.; Liu, Z.; Gong, Y.; Zhang, J.; Zhang, X.; et al. Fracture toughness of graphene. Nat. Common. 2014, 5, 3782. [Google Scholar] [CrossRef]
- Yang, K.; Chen, Y.; Pan, F.; Wang, S.; Ma, Y.; Liu, Q. Buckling behavior of substrate supported graphene sheets. Materials 2016, 9, 32. [Google Scholar] [CrossRef] [PubMed]
- Sgouros, A.P.; Kalosakas, G.; Galiotis, C.; Papagelis, K. Uniaxial compression of suspended single and multilayer graphenes. 2D Mater. 2016, 3, 025033. [Google Scholar] [CrossRef]
- RNicholl, J.T.; Lavrik, N.V.; Vlassiouk, I.; Srijanto, B.R.; Bolotin, K.I. Hidden area and mechanical nonlinearities in freestanding graphene. Phys. Rev. Lett. 2017, 118, 266101. [Google Scholar] [CrossRef] [PubMed]
- Baimova, J.A.; Rysaeva, L.K.; Dmitriev, S.V.; Lisovenko, D.S.; Gorodtsov, V.A.; Indeitsev, D.A. Auxetic behaviour of carbon nanostructures. Mater. Phys. Mech. 2017, 33, 1–11. [Google Scholar]
- Sgouros, A.P.; Androulidakis, C.; Tsoukleri, G.; Kalosakas, G.; Delikoukos, N.; Signetti, S.; Pugno, N.M.; Parthenios, J.; Galiotis, C.; Papagelis, K. Efficient mechanical stress transfer in multilayer graphene with a ladder-like architecture. ACS Appl. Mater. Interfaces 2021, 13, 4473–4484. [Google Scholar] [CrossRef]
- Ferrari, A.C. Raman spectroscopy of graphene and graphite: Disorder, electron-phonon coupling, doping and nonadiabatic effects. Solid State Commun. 2007, 143, 47–57. [Google Scholar] [CrossRef]
- Malard, L.M.; Pimenta, M.A.; Dresselhaus, G.; Dresselhaus, M.S. Raman spectroscopy in graphene. Phys. Rep. 2009, 473, 51–87. [Google Scholar] [CrossRef]
- Yang, L.; Deslippe, J.; Park, C.-H.; Cohen, M.L.; Louie, S.G. Excitonic effects on the optical response of graphene and bilayer graphene. Phys. Rev. Lett. 2009, 103, 186802. [Google Scholar] [CrossRef]
- Mohr, M.; Papagelis, K.; Maultzsch, J.; Thomsen, C. Two-dimensional electronic and vibrational band structure of uniaxially strained graphene from ab initio calculations. Phys. Rev. B 2009, 80, 205410. [Google Scholar] [CrossRef]
- Frank, O.; Mohr, M.; Maultzsch, J.; Thomsen, C.; Riaz, I.; Jalil, R.; Novoselov, K.S.; Tsoukleri, G.; Parthenios, J.; Papagelis, K.; et al. Raman 2D-band splitting in graphene: Theory and experiment. ACS Nano 2011, 5, 2231–2239. [Google Scholar] [CrossRef] [PubMed]
- Schedin, F.; Lidorikis, E.; Lombardo, A.; Kravets, V.G.; Geim, A.K.; Grigorenko, A.N.; Novoselov, K.S.; Ferrari, A.C. Surface-enhanced Raman spectroscopy of graphene. ACS Nano 2010, 4, 5617–5626. [Google Scholar] [CrossRef]
- Merthe, D.J.; Kresin, V.V. Transparency of graphene and other direct-gap two-dimensional materials. Phys. Rev. B 2016, 94, 205439. [Google Scholar] [CrossRef]
- Los, J.H.; Ghiringhelli, L.M.; Meijer, E.J.; Fasolino, A. Improved long-range reactive bond-order potential for carbon. I. Construction. Phys. Rev. B 2005, 72, 214102. [Google Scholar] [CrossRef]
- Lindsay, L.; Broido, D.A. Optimized Tersoff and Brenner empirical potential parameters for lattice dynamics and phonon thermal transport in carbon nanotubes and graphene. Phys. Rev. B 2010, 81, 205441. [Google Scholar] [CrossRef]
- Wei, D.; Song, Y.; Wang, F. A simple molecular mechanics potential for μm scale graphene simulations from the adaptive force matching method. J. Chem. Phys. 2011, 134, 184704. [Google Scholar] [CrossRef]
- Srinivasan, S.G.; van Duin, A.C.T.; Ganesh, P. Development of a ReaxFF potential for carbon condensed phases and its application to the thermal fragmentation of a large fullerene. J. Phys. Chem. A 2015, 119, 571–580. [Google Scholar] [CrossRef]
- Fthenakis, Z.G.; Kalosakas, G.; Chatzidakis, G.D.; Galiotis, C.; Papagelis, K.; Lathiotakis, N.N. Atomistic potential for graphene and other sp2 carbon systems. Phys. Chem. Chem. Phys. 2017, 19, 30925–30932. [Google Scholar] [CrossRef]
- Xu, Z.; Buehler, M.J. Geometry controls conformation of graphene sheets: Membranes, ribbons, and scrolls. ACS Nano 2010, 4, 3869–3876. [Google Scholar] [CrossRef]
- Katsnelson, M.I.; Fasolino, A. Graphene as a prototype crystalline membrane. Acc. Chem. Res. 2012, 46, 97–105. [Google Scholar] [CrossRef]
- Islam, M.Z.; Mahboob, M.; Lowe, R.L.; Bechtel, S.E. Characterization of the thermal expansion properties of graphene using molecular dynamics simulations. J. Phys. D Appl. Phys. 2013, 46, 435302. [Google Scholar] [CrossRef]
- Hillebrand, M.; Manda, B.M.; Kalosakas, G.; Gerlach, E.; Skokos, C. Chaotic dynamics of graphene and graphene nanoribbons. Chaos 2020, 30, 063150. [Google Scholar] [CrossRef] [PubMed]
- Terrones, H.; Lv, R.; Terrones, M.; Dresselhaus, M.S. The role of defects and doping in 2D graphene sheets and 1D nanoribbons. Rep. Prog. Phys. 2012, 75, 062501. [Google Scholar] [CrossRef] [PubMed]
- Cockayne, E.; Rutter, G.M.; Guisinger, N.P.; Crain, J.N.; First, P.N.; Stroscio, J.A. Grain boundary loops in graphene. Phys. Rev. B 2011, 83, 195425. [Google Scholar] [CrossRef]
- Ugeda, M.M.; Brihuega, I.; Hiebel, F.; Mallet, P.; Veuillen, J.-Y.; Gomez-Rodriguez, J.M.; Yndurain, F. Electronic and structural characterization of divacancies in irradiated graphene. Phys. Rev. B 2012, 85, 121402. [Google Scholar] [CrossRef]
- Susi, T.; Kotakoski, J.; Arenal, R.; Kurasch, S.; Jiang, H.; Skakalova, V.; Stephan, O.; Krasheninnikov, A.V.; Kauppinen, E.I.; Kaiser, U.; et al. Atomistic description of electron beam damage in nitrogen-doped graphene and single-walled carbon nanotubes. ACS Nano 2012, 6, 8837–8846. [Google Scholar] [CrossRef] [PubMed]
- Becton, M.; Zhang, L.; Wang, X. Effects of surface dopants on graphene folding by molecular simulations. Chem. Phys. Lett. 2013, 584, 135–141. [Google Scholar] [CrossRef]
- Sgouros, A.P.; Kalosakas, G.; Sigalas, M.M.; Papagelis, K. Exotic carbon nanostructures obtained through controllable defect engineering. RSC Adv. 2015, 5, 39930–39937. [Google Scholar] [CrossRef]
- Fthenakis, Z.G.; Lathiotakis, N.N. Graphene allotropes under extreme uniaxial strain: An ab initio theoretical study. Phys. Chem. Chem. Phys. 2015, 17, 16418–16427. [Google Scholar] [CrossRef]
- Grima, J.N.; Winczewski, S.; Mizzi, L.; Grech, M.C.; Cauchi, R.; Gatt, R.; Attard, D.; Wojciechowski, K.W.; Rybicki, J. Auxetic behaviour of carbon nanostructures. Adv. Mater. 2015, 27, 1455–1459. [Google Scholar] [CrossRef]
- Xiao, J.R.; Staniszewski, J.; Gillespie, J.W., Jr. Fracture and progressive failure of defective graphene sheets and carbon nanotubes. Comp. Struct. 2009, 88, 602–609. [Google Scholar] [CrossRef]
- Neek-Amal, M.; Peeters, F.M. Defected graphene nanoribbons under axial compression. Appl. Phys. Lett. 2010, 97, 153118. [Google Scholar] [CrossRef]
- Lin, Y.-M.; Valdes-Garcia, A.; Han, S.-J.; Farmer, D.B.; Meric, I.; Sun, Y.; Wu, Y.; Dimitrakopoulos, C.; Grill, A.; Avouris, P.; et al. Wafer-scale graphene integrated circuit. Science 2011, 332, 1294–1297. [Google Scholar] [CrossRef]
- Wang, Y.; Li, Z.; Wang, J.; Li, J.; Lin, Y. Graphene and graphene oxide: Biofunctionalization and applications in biotechnology. Trends Biotechnol. 2011, 29, 205–212. [Google Scholar] [CrossRef]
- Ratinac, K.R.; Yang, W.; Gooding, J.J.; Thordarson, P.; Braeta, F. Graphene and related materials in electrochemical sensing. Electroanalysis 2011, 23, 803–826. [Google Scholar] [CrossRef]
- Long, Y.; Zhao, X.; Jiang, X.; Zhang, L.; Zhang, H.; Liu, Y.; Zhu, H. A porous graphene/polydimethylsiloxane composite by chemical foaming for simultaneous tensile and compressive strain sensing. Flat Chem 2018, 10, 1–7. [Google Scholar] [CrossRef]
- Walsh, E.D.; Efetov, D.K.; Lee, G.-H.; Heuck, M.; Crossno, J.; Ohki, T.A.; Kim, P.; Englund, D.; Fong, K.C. Graphene-based Josephson-junction single-photon detector. Phys. Rev. Applied 2017, 8, 024022. [Google Scholar] [CrossRef]
- Casalino, M.; Sassi, U.; Goykhman, I.; Eiden, A.; Lidorikis, E.; Milana, S.; Fazio, D.D.; Tomarchio, F.; Iodice, M.; Coppola, G.; et al. Vertically illuminated, resonant cavity enhanced, graphene-silicon Schottky photodetectors. ACS Nano 2017, 11, 10955–10963. [Google Scholar] [CrossRef] [PubMed]
- Niu, W.; Liu, J.; Mai, Y.; Mullen, K.; Feng, X. Synthetic engineering of graphene nanoribbons with excellent liquid-phase processability. Trends Chem. 2019, 1, 549–558. [Google Scholar] [CrossRef]
- Han, M.Y.; Ozyilmaz, B.; Zhang, Y.; Kim, P. Energy band-gap engineering of graphene nanoribbons. Phys. Rev. Lett. 2007, 98, 206805. [Google Scholar] [CrossRef]
- Chen, Z.; Lin, Y.-M.; Rooks, M.J.; Avouris, P. Graphene nano-ribbon electronics. Physica E 2007, 40, 228–232. [Google Scholar] [CrossRef]
- Kosynkin, D.V.; Higginbotham, A.L.; Sinitskii, A.; Lomeda, J.R.; Dimiev, A.; Price, B.K.; Tour, J.M. Longitudinal unzipping of carbon nanotubes to form graphene nanoribbons. Nature 2009, 458, 872–876. [Google Scholar] [CrossRef] [PubMed]
- Jiao, L.; Zhang, L.; Wang, X.; Diankov, G.; Dai, H. Narrow graphene nanoribbons from carbon nanotubes. Nature 2009, 458, 877–880. [Google Scholar] [CrossRef] [PubMed]
- Cai, J.; Ruffieux, P.; Jaafar, R.; Bieri, M.; Braun, T.; Blankenburg, S.; Muoth, M.; Seitsonen, A.P.; Saleh, M.; Feng, X.; et al. Atomically precise bottom-up fabrication of graphene nanoribbons. Nature 2010, 466, 470–473. [Google Scholar] [CrossRef] [PubMed]
- Talirz, L.; Sode, H.; Cai, J.; Ruffieux, P.; Blankenburg, S.; Jafaar, R.; Berger, R.; Feng, X.; Mullen, K.; Passerone, D.; et al. Termini of bottom-up fabricated graphene nanoribbons. J. Am. Chem. Soc. 2013, 135, 2060–2063. [Google Scholar] [CrossRef]
- Jordan, R.S.; Wang, Y.; McCurdy, R.D.; Yeung, M.T.; Marsh, K.L.; Khan, S.I.; Kaner, R.B.; Rubin, Y. Synthesis of graphene nanoribbons via the topochemical polymerization and subsequent aromatization of a diacetylene precursor. Chem 2016, 1, 78–90. [Google Scholar] [CrossRef]
- Talirz, L.; Ruffieux, P.; Fasel, R. On-surface synthesis of atomically precise graphene nanoribbons. Adv. Mater. 2016, 28, 6222–6231. [Google Scholar] [CrossRef]
- Son, Y.-W.; Cohen, M.L.; Louie, S.G. Energy gaps in graphene nanoribbons. Phys. Rev. Lett. 2006, 97, 216803. [Google Scholar] [CrossRef]
- Gillen, R.; Mohr, M.; Thomsen, C.; Maultzsch, J. Vibrational properties of graphene nanoribbons by first-principles calculations. Phys. Rev. B 2009, 80, 155418. [Google Scholar] [CrossRef]
- Huang, B.; Liu, M.; Su, N.; Wu, J.; Duan, W.; Gu, B.-L.; Liu, F. Quantum manifestations of graphene edge stress and edge instability: A first-principles study. Phys. Rev. Lett. 2009, 102, 166404. [Google Scholar] [CrossRef]
- Lu, Q.; Huang, R. Excess energy and deformation along free edges of graphene nanoribbons. Phys. Rev. B 2010, 81, 155410. [Google Scholar] [CrossRef]
- Haskins, J.; Kinaci, A.; Sevik, C.; Sevincli, H.; Cuniberti, G.; Cagin, T. Control of thermal and electronic transport in defect-engineered graphene nanoribbons. ACS Nano 2011, 5, 3779–3787. [Google Scholar] [CrossRef]
- Lin, M.-W.; Ling, C.; Agapito, L.A.; Kioussis, N.; Zhang, Y.; Cheng, M.M.-C.; Wang, W.L.; Kaxiras, E.; Zhou, Z. Approaching the intrinsic band gap in suspended high-mobility graphene nanoribbons. Phys. Rev. B 2011, 84, 125411. [Google Scholar] [CrossRef]
- Bennett, P.B.; Pedramrazi, Z.; Madani, A.; Chen, Y.-C.; de Oteyza, D.G.; Chen, C.; Fischer, F.R.; Crommie, M.F.; Bokor, J. Bottom-up graphene nanoribbon field-effect transistors. Appl. Phys. Lett. 2013, 103, 253114. [Google Scholar] [CrossRef]
- Sgouros, A.; Sigalas, M.M.; Papagelis, K.; Kalosakas, G. Transforming graphene nanoribbons into nanotubes by use of point defects. J. Phys. Condens. Matter 2014, 26, 125301. [Google Scholar] [CrossRef] [PubMed]
- Villegas, C.E.P.; Mendonca, P.B.; Rocha, A.R. Optical spectrum of bottom-up graphene nanoribbons: Towards efficient atom-thick excitonic solar cells. Sci. Rep. 2014, 4, 6579. [Google Scholar] [CrossRef] [PubMed]
- Saiz-Bretin, M.; Dominguez-Adame, F.; Malyshev, A.V. Twisted graphene nanoribbons as nonlinear nanoelectronic devices. Carbon 2019, 149, 587–593. [Google Scholar] [CrossRef]
- Zhao, H.; Min, K.; Aluru, N.R. Size and chirality dependent elastic properties of graphene nanoribbons under uniaxial tension. Nano Lett. 2009, 9, 3012–3015. [Google Scholar] [CrossRef] [PubMed]
- Faccio, R.; Denis, P.A.; Pardo, H.; Goyenola, C.; Mombru, A.W. Mechanical properties of graphene nanoribbons. J. Phys. Condens. Matter 2009, 21, 285304. [Google Scholar] [CrossRef]
- Tabarraei, A.; Shadalou, S.; Song, J.-H. Mechanical properties of graphene nanoribbons with disordered edges. Comput. Mater. Sci. 2015, 96, 10–19. [Google Scholar] [CrossRef]
- Lu, Q.; Gao, W.; Huang, R. Atomistic simulation and continuum modeling of graphene nanoribbons under uniaxial tension. Model. Simul. Mater. Sci. Eng. 2011, 19, 054006. [Google Scholar] [CrossRef]
- Chu, Y.; Ragab, T.; Basaran, C. The size effect in mechanical properties of finite-sized graphene nanoribbon. Comput. Mater. Sci. 2014, 81, 269–274. [Google Scholar] [CrossRef]
- Giannopoulos, G.I.; Liosatos, I.A.; Moukanidis, A.K. Parametric study of elastic mechanical properties of graphene nanoribbons by a new structural mechanics approach. Physica E 2011, 44, 124–134. [Google Scholar] [CrossRef]
- Damasceno, D.A.; Mesquita, E.; Rajapakse, R.K.N.D.; Pavanello, R. Atomic-scale finite element modelling of mechanical behaviour of graphene nanoribbons. Int. J. Mech. Mater. Des. 2019, 15, 145–157. [Google Scholar] [CrossRef]
- Fu, Y.; Ragab, T.; Basaran, C. The effect of Stone-Wales defects on the mechanical behavior of graphene nano-ribbons. Comput. Mater. Sci. 2016, 124, 142–150. [Google Scholar] [CrossRef]
- Senturk, A.E.; Oktem, A.S.; Konukman, A.E.S. Influence of defect locations and nitrogen doping configurations on the mechanical properties of armchair graphene nanoribbons. J. Molec. Model. 2018, 24, 43. [Google Scholar] [CrossRef] [PubMed]
- Damasceno, D.A.; Rajapakse, R.K.N.D.N.; Mesquita, E. Atomistic modelling of size-dependent mechanical properties and fracture of pristine and defective cove-edged graphene nanoribbons. Nanomaterials 2020, 10, 1422. [Google Scholar] [CrossRef]
- Sgouros, A.P.; Kalosakas, G.; Papagelis, K.; Galiotis, C. Compressive response and buckling of graphene nanoribbons. Sci. Rep. 2018, 8, 9593. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1997, 77, 3865–3868. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baseggio, O.; Bonfà, P.; Brunato, D.; Car, R.; Carnimeo, I.; Cavazzoni, C.; de Gironcoli, S.; Delugas, P.; Ruffino, F.F.; et al. Quantum ESPRESSO toward the exascale. J. Chem. Phys. 2020, 152, 154105. [Google Scholar] [CrossRef] [PubMed]
- Rappe, A.M.; Rabe, K.M.; Kaxiras, E.; Joannopoulos, J.D. Optimized pseudopotentials. Phys. Rev. B 1990, 41, 1227–1230. [Google Scholar] [CrossRef] [PubMed]
- Mounet, N.; Marzari, N. First-principles determination of the structural, vibrational and thermodynamic properties of diamond, graphite, and derivatives. Phys. Rev. B 2005, 71, 205214. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kalosakas, G.; Lathiotakis, N.N.; Papagelis, K. Width Dependent Elastic Properties of Graphene Nanoribbons. Materials 2021, 14, 5042. https://doi.org/10.3390/ma14175042
Kalosakas G, Lathiotakis NN, Papagelis K. Width Dependent Elastic Properties of Graphene Nanoribbons. Materials. 2021; 14(17):5042. https://doi.org/10.3390/ma14175042
Chicago/Turabian StyleKalosakas, George, Nektarios N. Lathiotakis, and Konstantinos Papagelis. 2021. "Width Dependent Elastic Properties of Graphene Nanoribbons" Materials 14, no. 17: 5042. https://doi.org/10.3390/ma14175042
APA StyleKalosakas, G., Lathiotakis, N. N., & Papagelis, K. (2021). Width Dependent Elastic Properties of Graphene Nanoribbons. Materials, 14(17), 5042. https://doi.org/10.3390/ma14175042