Numerical Study on Surface Roughness Measurement Based on Nonlinear Ultrasonics in Through-Transmission and Pulse-Echo Modes
Abstract
:1. Introduction
2. Higher Harmonic Generation in Solid Media
3. Ultrasonic Scattering from Rough Surfaces
4. FE Modelling for Nonlinear Ultrasound
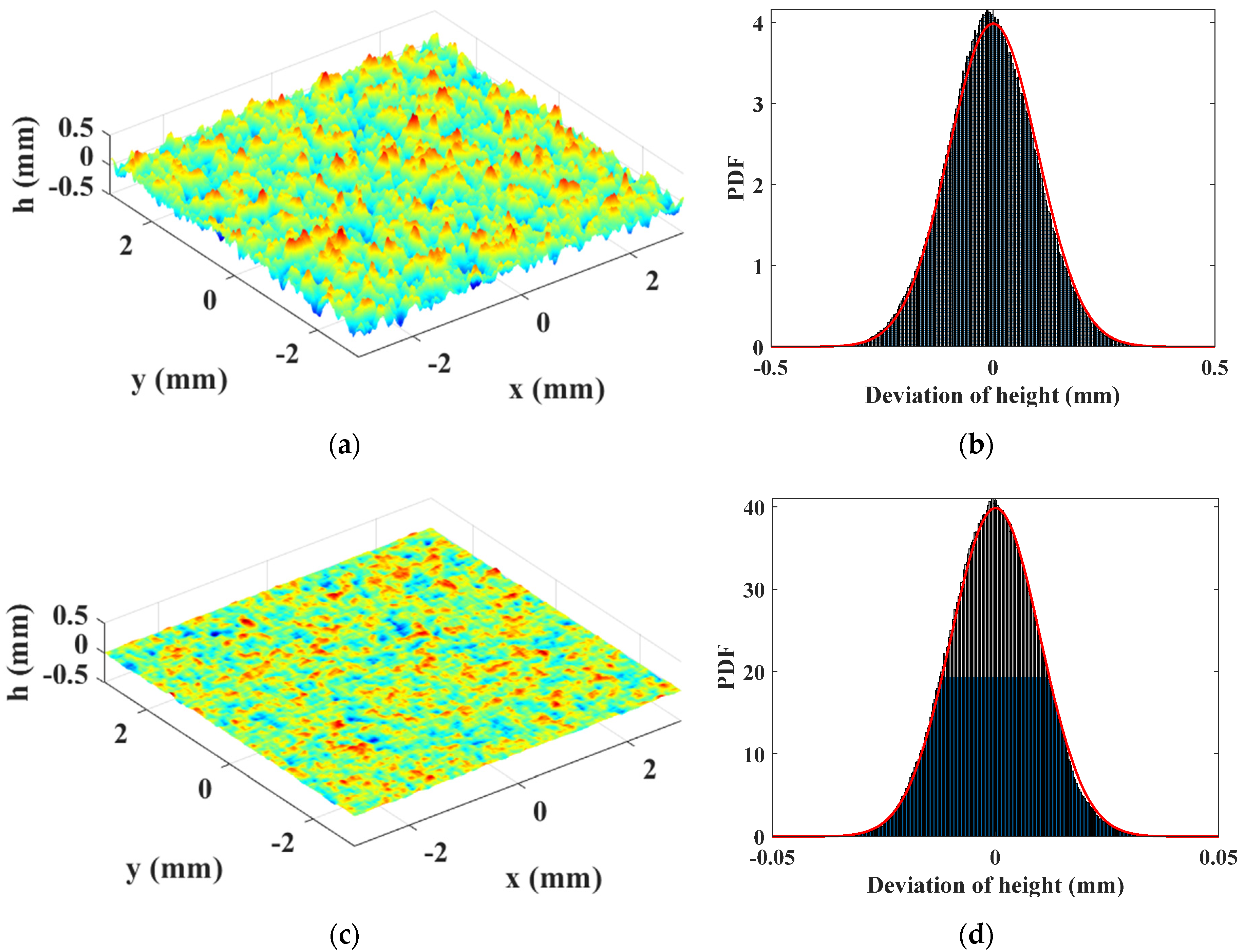
4.1. Unit-Cell Model Setup
4.2. Model Verification
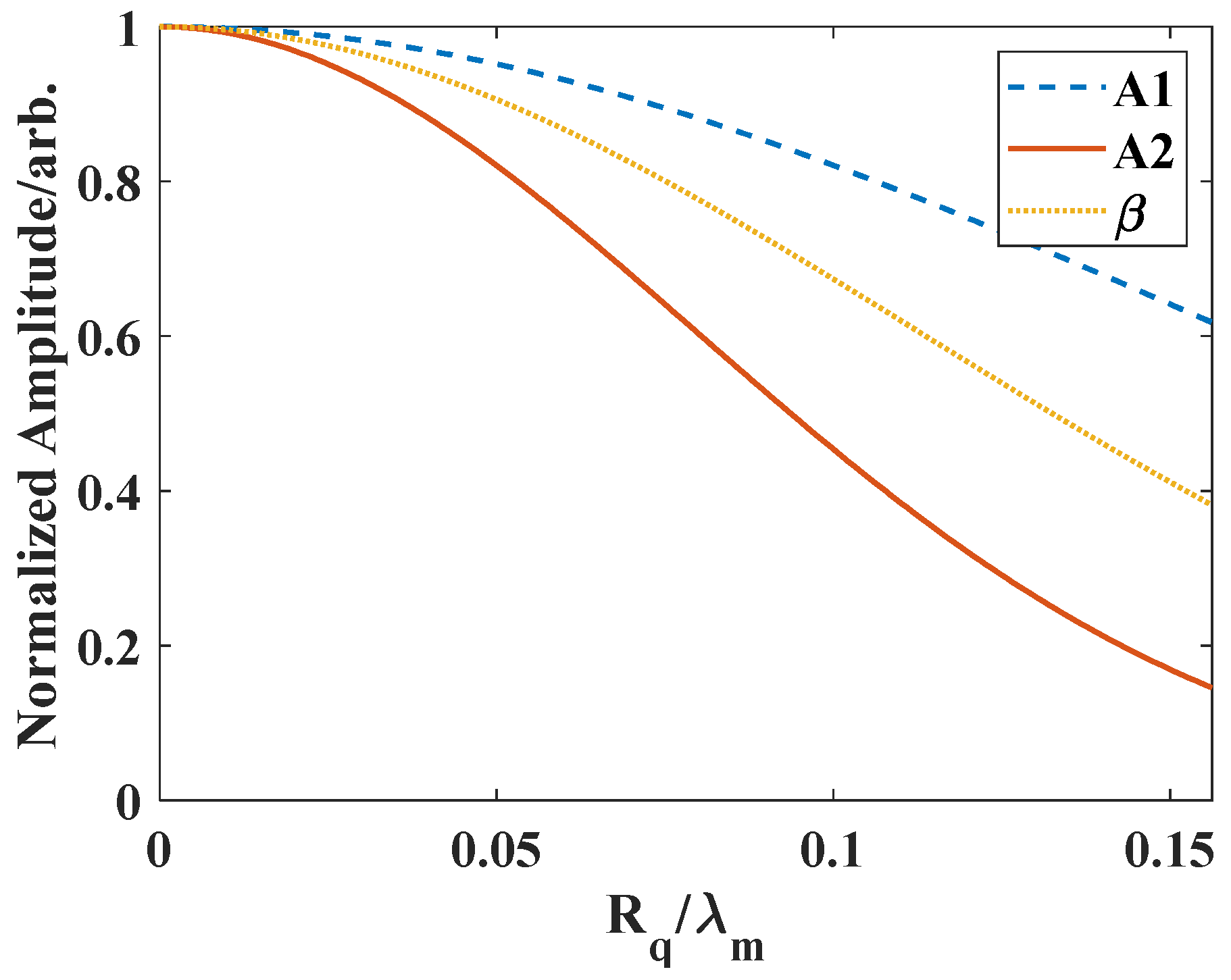
5. Results and Discussion
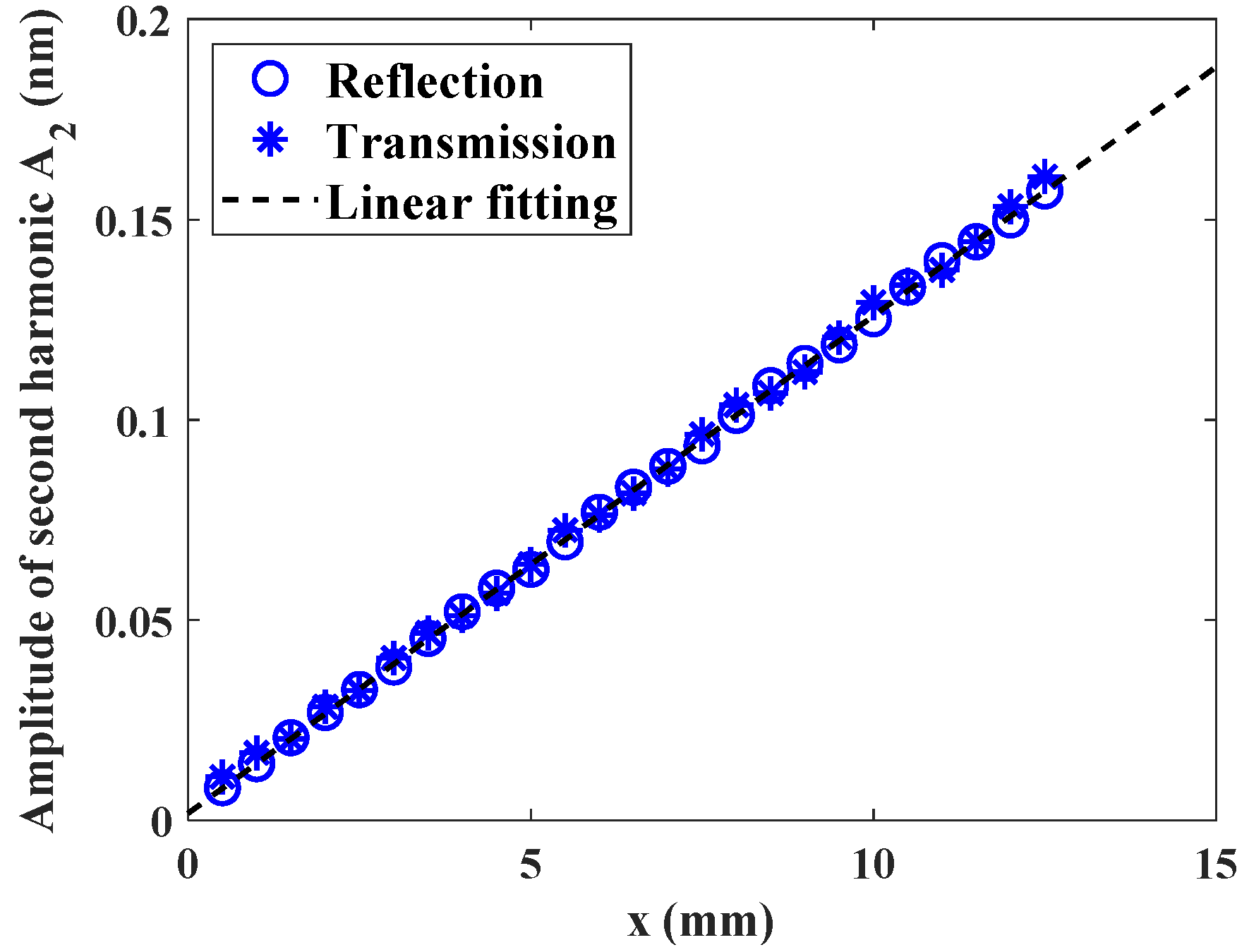
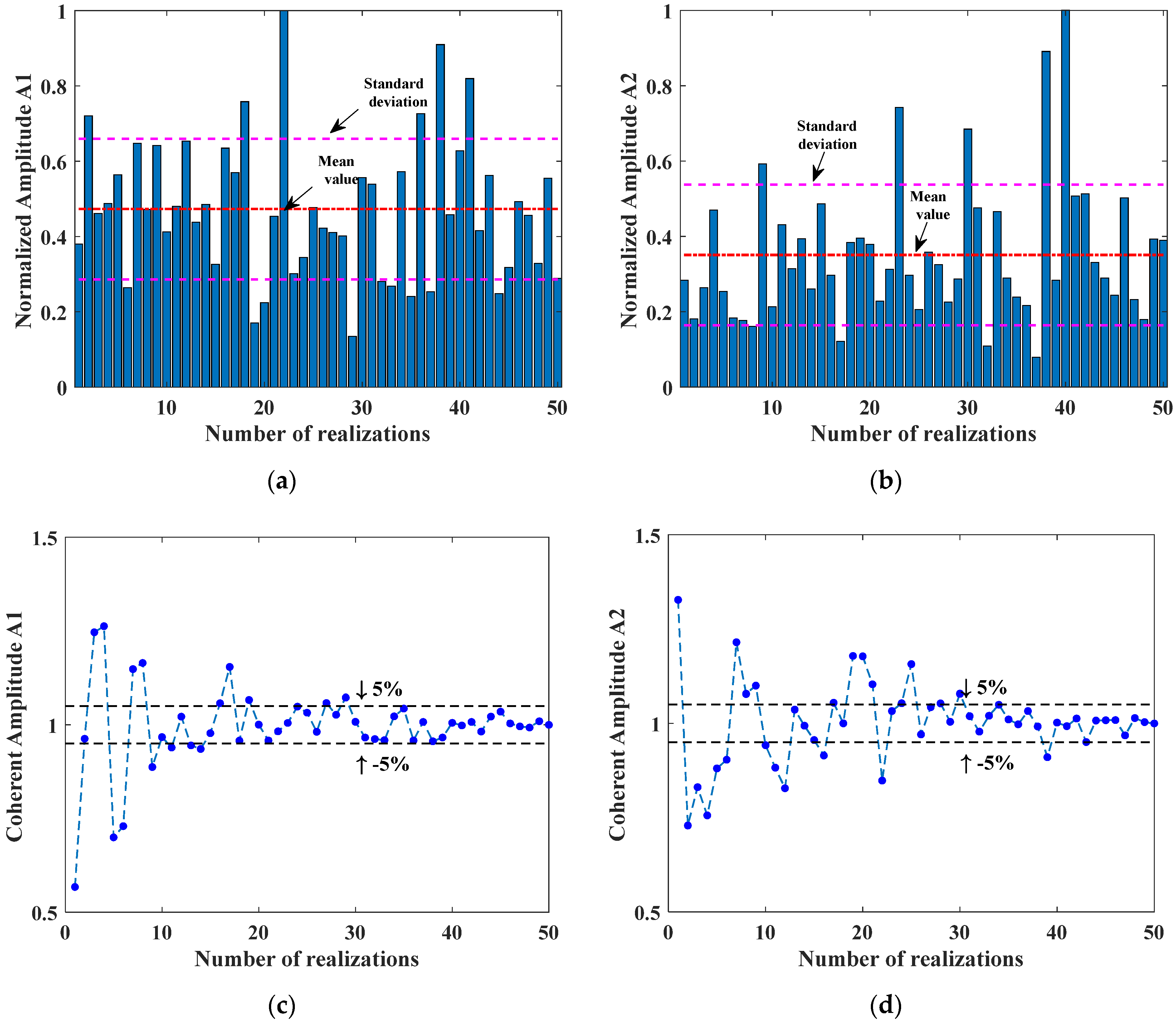
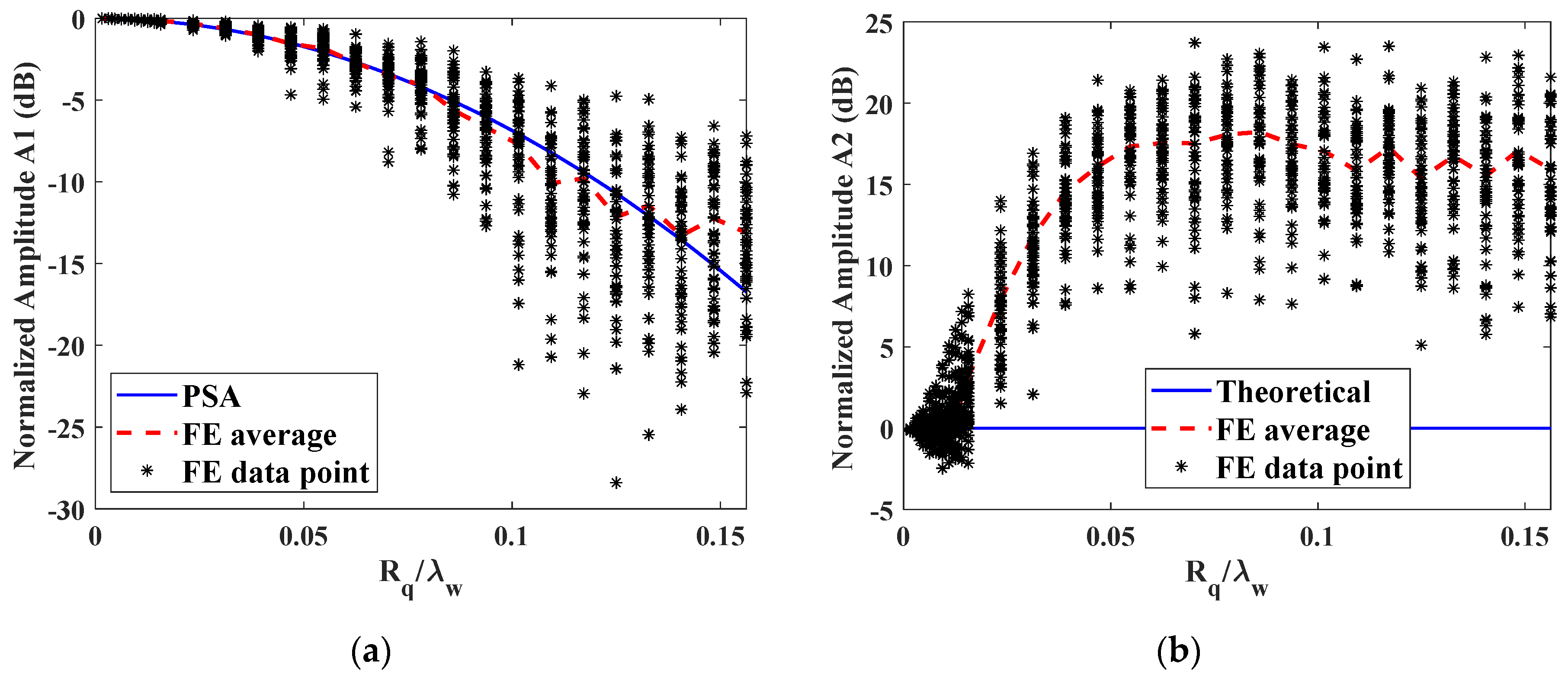
5.1. Through-Transmission Mode
5.2. Pulse-Echo Mode
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ma, Z.; Luo, Z.; Lin, L.; Krishnaswamy, S.; Lei, M. Quantitative characterization of the interfacial roughness and thickness of inhomogeneous coatings based on ultrasonic reflection coefficient phase spectrum. NDT E Int. 2019, 102, 16–25. [Google Scholar] [CrossRef]
- Ma, Z.; Lin, L.; Jin, S.; Lei, M. Identification of the velocity, thickness, and interfacial roughness of coating using full time-domain urcps: Cross-correlation-based inverse problem. J. Nondestruct. Eval. Diagn. Progn. Eng. Syst. 2019, 2, 011008. [Google Scholar] [CrossRef]
- Benstock, D.; Cegla, F.; Stone, M. The influence of surface roughness on ultrasonic thickness measurements. J. Acoust. Soc. Am. 2014, 136, 3028. [Google Scholar] [CrossRef] [Green Version]
- Ogilvy, J.A. An estimate of the accuracy of the kirchhoff approximation in acoustic wave scattering from rough surfaces. J. Phys. D Appl. Phys. 1986, 19, 2085–2113. [Google Scholar] [CrossRef]
- De Billy, M.; Quentin, G. Backscattering of acoustic waves by randomly rough surfaces of elastic solids immersed in water. J. Acoust. Soc. Am. 1982, 72, 591–601. [Google Scholar] [CrossRef]
- Nagy, P.B.; Adler, L. Surface roughness induced attenuation of reflected and transmitted ultrasonic waves. J. Acoust. Soc. Am. 1987, 82, 193–197. [Google Scholar] [CrossRef]
- Nagy, P.B.; Rose, J.H. Surface roughness and the ultrasonic detection of subsurface scatterers. J. Appl. Phys. 1993, 73, 566–580. [Google Scholar] [CrossRef]
- Lian, M.; Liu, H.; Zhou, L.; Zhang, T.; Liu, B.; Wang, Y. Ultrasonic roughness measurement based on scattering attenuation. Surf. Topogr. Metrol. Prop. 2019, 7, 015001. [Google Scholar] [CrossRef]
- Shi, F.; Choi, W.; Lowe, M.J.S.; Skelton, E.A.; Craster, R.V. The validity of kirchhoff theory for scattering of elastic waves from rough surfaces. Proc. R. Soc. A Math. Phys. Eng. Sci. 2015, 471, 20140977. [Google Scholar] [CrossRef]
- Shi, F.; Lowe, M.J.S.; Xi, X.; Craster, R.V. Diffuse scattered field of elastic waves from randomly rough surfaces using an analytical kirchhoff theory. J. Mech. Phys. Solids 2016, 92, 260–277. [Google Scholar] [CrossRef] [Green Version]
- Shi, F.; Lowe, M.; Craster, R. Diffusely scattered and transmitted elastic waves by random rough solid-solid interfaces using an elastodynamic kirchhoff approximation. Phys. Rev. B 2017, 95, 214305. [Google Scholar] [CrossRef] [Green Version]
- Shi, F.; Lowe, M.J.S.; Craster, R.V. Recovery of correlation function of internal random rough surfaces from diffusely scattered elastic waves. J. Mech. Phys. Solids 2017, 99, 483–494. [Google Scholar] [CrossRef]
- Choi, W.; Shi, F.; Lowe, M.J.S.; Skelton, E.A.; Craster, R.V.; Daniels, W.L. Rough surface reconstruction of real surfaces for numerical simulations of ultrasonic wave scattering. NDT E Int. 2018, 98, 27–36. [Google Scholar] [CrossRef] [Green Version]
- Haslinger, S.G.; Lowe, M.J.S.; Huthwaite, P.; Craster, R.V.; Shi, F. Appraising kirchhoff approximation theory for the scattering of elastic shear waves by randomly rough defects. J. Sound Vib. 2019, 460, 114872. [Google Scholar] [CrossRef]
- Liu, M.; Kim, J.-Y.; Jacobs, L.; Qu, J. Experimental study of nonlinear rayleigh wave propagation in shot-peened aluminum plates—feasibility of measuring residual stress. NDT E Int. 2011, 44, 67–74. [Google Scholar] [CrossRef]
- Matlack, K.H.; Kim, J.Y.; Jacobs, L.J.; Qu, J. Review of second harmonic generation measurement techniques for material state determination in metals. J. Nondestruct. Eval. 2015, 34, 273. [Google Scholar] [CrossRef]
- Yuan, M.; Lee, T.; Kang, T.; Zhang, J.; Song, S.J.; Kim, H.J. Absolute measurement of ultrasonic non-linearity parameter at contact interface. Nondestruct. Test. Eval. 2015, 30, 356–372. [Google Scholar] [CrossRef]
- Yuan, M.; Zhang, J.; Song, S.-J.; Kim, H.-J. Numerical simulation of rayleigh wave interaction with surface closed cracks under external pressure. Wave Motion 2015, 57, 143–153. [Google Scholar] [CrossRef]
- Bovsunovsky, A.; Surace, C. Non-linearities in the vibrations of elastic structures with a closing crack: A state of the art review. Mech. Syst. Signal Process. 2015, 62, 129–148. [Google Scholar] [CrossRef]
- Na, J.K.; Yost, W.T.; Cantrell, J.H.; Kessel, G.L. Effects of surface roughness and nonparallelism on the measurement of the acoustic nonlinearity parameter in steam turbine blades. Aip. Conf. Proc. 2000, 509, 1417–1424. [Google Scholar]
- Chakrapani, S.K.; Howard, A.; Barnard, D. Influence of surface roughness on the measurement of acoustic nonlinearity parameter of solids using contact piezoelectric transducers. Ultrasonics 2018, 84, 112–118. [Google Scholar] [CrossRef]
- Kim, J.; Ha, H.P.; Kim, K.M.; Jhang, K.Y. Analysis of the influence of surface roughness on measurement of ultrasonic nonlinearity parameter using contact-type transducer. Appl. Sci. 2020, 10, 8661. [Google Scholar] [CrossRef]
- Romer, A.; Kim, J.Y.; Qu, J.M.; Jacobs, L.J. The second harmonic generation in reflection mode: An analytical, numerical and experimental study. J. Nondestruct. Eval. 2016, 35, 10. [Google Scholar] [CrossRef]
- Best, S.R.; Croxford, A.J.; Neild, S.A. Pulse-echo harmonic generation measurements for non-destructive evaluation. J. Nondestruct. Eval. 2014, 33, 205–215. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S.; Li, X.; Jeong, H.; Cho, S.; Hu, H. Theoretical and experimental investigation of the pulse-echo nonlinearity acoustic sound fields of focused transducers. Appl. Acoust. 2017, 117, 145–149. [Google Scholar] [CrossRef]
- Jeong, H.; Zhang, S.; Li, X. Improvement of pulse-echo harmonic generation from a traction-free boundary through phase shift of a dual element transducer. Ultrasonics 2018, 87, 145–151. [Google Scholar] [CrossRef] [PubMed]
- Jeong, H.; Cho, S.; Shin, H.; Zhang, S.; Li, X. Optimization and validation of dual element ultrasound transducers for improved pulse-echo measurements of material nonlinearity. IEEE Sens. J. 2020, 20, 13596–13606. [Google Scholar] [CrossRef]
- Choi, W.; Skelton, E.; Lowe, M.J.S.; Craster, R. Unit cell finite element modelling for ultrasonic scattering from periodic surfaces. AIP Conf. Proc. 2013, 1511, 83–90. [Google Scholar]
- Wang, Z.; Cheng, J. Numerical and analytical study for ultrasonic testing of internal delamination defects considering surface roughness. Ultrasonics 2021, 110, 106290. [Google Scholar] [CrossRef]
- Zhang, J.; Drinkwater, B.W.; Wilcox, P.D. Effect of roughness on imaging and sizing rough crack-like defects using ultrasonic arrays. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2012, 59, 939–948. [Google Scholar] [CrossRef]
- Li, X.; Fu, Y.; Zhang, F.; Rao, Y. Detecting small flaws in two-phase ti-6al-4v with rough surfaces. Ultrasonics 2020, 106, 106128. [Google Scholar] [CrossRef] [PubMed]
- Green, R.E. Ultrasonic Investigation of Mechanical Properties; Academic Press: Cambridge, MA, USA, 1973; Volume 3. [Google Scholar]
- Murnaghan, F.D. Finite deformations of an elastic solid. Am. J. Math. 1937, 59, 235–260. [Google Scholar] [CrossRef]
- Rushchitsky, J.J. Analysis of a quadratic nonlinear hyperelastic longitudinal plane wave. Int. Appl. Mech. 2009, 45, 148–158. [Google Scholar] [CrossRef]
- Yuan, M.D.; Tse, P.W.; Xuan, W.M.; Xu, W.J. Extraction of least-dispersive ultrasonic guided wave mode in rail track based on floquet-bloch theory. Shock Vib. 2021, 2021. [Google Scholar] [CrossRef]
- Smith, R.T.; Stern, R.; Stephens, R.W.B. Third—order elastic moduli of polycrystalline metals from ultrasonic velocity measurements. J. Acoust. Soc. Am. 1966, 40, 1002–1008. [Google Scholar] [CrossRef]







| Density | Lame Parameters | Murnaghan Third-Order Elastic Constants | |||
|---|---|---|---|---|---|
| ρ | λ | μ | l | m | n |
| 2737 kg/m3 | 57.0 GPa | 27.6 GPa | −311 GPa | −401 GPa | −408 GPa |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, M.; Dai, A.; Liao, L.; Chen, Y.; Ji, X. Numerical Study on Surface Roughness Measurement Based on Nonlinear Ultrasonics in Through-Transmission and Pulse-Echo Modes. Materials 2021, 14, 4855. https://doi.org/10.3390/ma14174855
Yuan M, Dai A, Liao L, Chen Y, Ji X. Numerical Study on Surface Roughness Measurement Based on Nonlinear Ultrasonics in Through-Transmission and Pulse-Echo Modes. Materials. 2021; 14(17):4855. https://doi.org/10.3390/ma14174855
Chicago/Turabian StyleYuan, Maodan, Anbang Dai, Lin Liao, Yan Chen, and Xuanrong Ji. 2021. "Numerical Study on Surface Roughness Measurement Based on Nonlinear Ultrasonics in Through-Transmission and Pulse-Echo Modes" Materials 14, no. 17: 4855. https://doi.org/10.3390/ma14174855
APA StyleYuan, M., Dai, A., Liao, L., Chen, Y., & Ji, X. (2021). Numerical Study on Surface Roughness Measurement Based on Nonlinear Ultrasonics in Through-Transmission and Pulse-Echo Modes. Materials, 14(17), 4855. https://doi.org/10.3390/ma14174855







