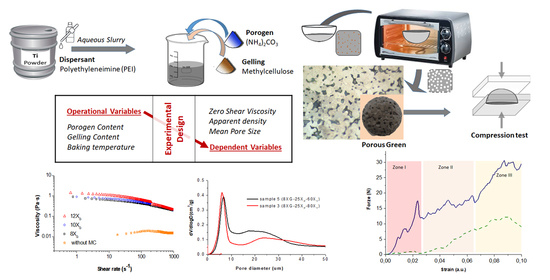
3.1. Study of the Influence of the Operation Variables on the Properties of the Ti Sponges
Ti slurries were formulated by incorporating ammonium bicarbonate as the porogen agent and MC as the shaping additive. Dispersion of the Ti powders in water has been previously reported by authors in terms of zeta potential and rheological behavior using an anionic and a cationic dispersant as well as bare powders [
26,
27]. On those papers, the Krieger Dougherty’s rheological model showed that using PEI (cationic dispersant) in the slurries formulation the values of maximum packing density were as high as 74% while the use of an anionic polyelectrolyte (Polyacrylic Acid-PAA, Mw = 2000, Acros) generated a maximum packing density value of 56%. Additionally, the Ti suspensions with solid content of 50 vol.% prepared with 1 wt.% of PEI as dispersant enabled the use of different shaping technologies. For that reason, in this paper the same solid content (50 vol.%) as well as the same dispersant concentration (1 wt.% of PEI referred to powder) has been used to the rheological studies of the slurries with the gelation agent.
Experimental design method consisting of a central test and 14 peripheral tests on the sides and vertices of a cube were used to study the influence of three different variables on the processing of Ti porous structures by gel casting from colloidal aqueous suspensions (with a solids content of 50 vol.% and 1 wt.% of PEI at pH 9). The aim of applying this statistical tool was to define the equations that predict the final properties of a similar material (dependent variables) from the parameters of the process (operating variables). Operating variables were the gelation agent concentrations (XG), the porogen concentrations (XP) and temperature (XT).
The amount of gelation agent (X
G variable) determines the polymerization degree and the gel structure during the gelation process, being also the responsible of changes in the rheological behavior of the suspensions. For this reason, the addition of different amounts of MC to the Ti slurries was firstly studied in terms of its rheological behaviour. Methylcelluloses are common thickeners for liquids used in food industries, biotechnology and materials processing. Rheological modification depends on intrinsic characteristic properties such as the molecular weight and substitutions of the anhydroglucose repeat unit as well as concentration of additive. Amounts can range from a few grams per litter [
28] to tens of grams [
29].
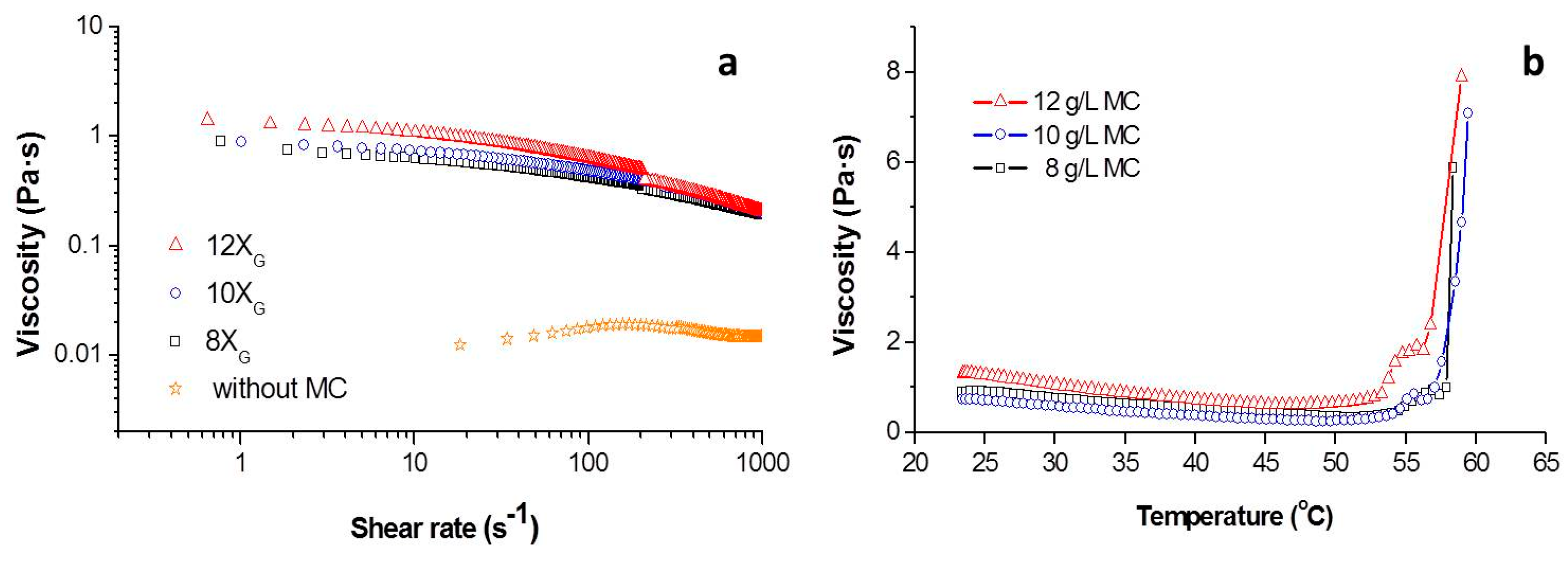
Figure 2a shows the viscosity vs. the shear rate for slurries of Ti with 50 vol.% of solids contents in DI water (without gelation agent or porogen) and in an aqueous media containing 8, 10 and 12 g/L of MC (X
G8, X
G10 and X
G12). For each of the slurries the curves were made overlapping the decreasing shear rate of the CR and CS experiments. It should be noted that for the thicker slurries the CR and CS curves do not coincide on the overlapping zone, as the CR experiment shears the slurry more energetically leaving no time for rearrangement of interparticle forces, while the CS experiment is less energetic allowing a faster formation of the mentioned interparticles forces and consequently higher viscosity values.
The decreasing on the viscosity values with the increment of shear rate indicated a pseudoplastic behavior of Ti + MC slurries. As expected, the addition of the gelation agent increased the viscosity, being this increment more significant at the low shear rates. In addition, the thickening effect of the initial Ti suspension disappeared as consequence of the MC addition. All experimental curves were fitted to the Cross model in order to obtain the values for the zero-shear viscosity (
η0) and the infinite shear viscosity (
η∞). High values of zero-shear viscosity are indicative of the capacity of samples to keep the shape and avoid segregation of phases in a resting state (out of external forces or stirring). On the other hand, low infinite shear viscosity values are indicative of efficiency on the mixing and milling processes. These values are collected in
Table 1 together to the values of viscosity at shear rates of 10 and 100 s
−1 which are reference values for casting.
It can be clearly observed that under similar dispersion conditions (1 wt.% PEI) the media containing 12 g/L of MC presented a higher zero-shear viscosity, denoting a higher capability to keep the shape after the forming processes and consequently prevent the formation of closed porosity into the slurry. Furthermore, the media containing 8 g/L of MC resulted in values of η∞ below 100 mPa·s which indicates a higher homogenization capability. The viscosity values of all MC slurries in the shear range of 10–100 s−1 fulfilled the requirements to be processed by gel casting.
In
Figure 2b the variation of the viscosity of the slurries recorded at a shear rate of 10 s
−1 containing MC with the temperature was plotted. Two sections were identified on these plots. In the low temperature zone, the viscosity decreases with the raise of the temperature. This behavior was also observed in slurries dispersed with polyelectrolytes of both ceramic [
30] and metallic powders [
31]. As the temperature achieves the 50 °C, this decreasing in the viscosity is compensated and starts to increase as the MC already dissolved into the liquid medium starts to gel. The gelation process of MC occurs during heating due to the hydrophobic association between methyl groups on cellulose chains [
32,
33]. The points where derivate of the curves included in
Figure 2b equals to 0 indicate the temperature where gelation process become predominant on the rheological behavior of the slurries. This temperature is 51, 49 and 47 °C, respectively, for the concentrations of MC of 8, 10 and 12 g/L.
For the three concentrations when the temperature of the slurries overcome the 52 °C a significant increment in the viscosity was observed, as the gelation process become massive and the hydrophobic effective units starts to join the MC chains in a 3D structure [
33]. Finally, at temperatures over 57 °C the viscosity increases exponentially, this temperature was reported as gelation temperature by Knarr and Bayer for cordierite slurries with MC [
34]. All the previous results indicate that slurries will keep the shape of the container when they are heated at temperatures over 57 °C, due to the increment of viscosity induced by temperature. In addition to the shape, the material could keep the internal structure or microstructure that could be formed inside the slurry, such as gradient or porosity. These temperatures are coincident with the studies on dynamic viscoelasticity behavior with temperature for methylcelluloses solution which also reported that hysteresis curve finish at 70 °C [
35].
Furthermore, the addition of the ammonium bicarbonate to the slurries formulation as a gas porogen by thermal decomposition produces the pores formation at the same time that temperature increases the viscosity, leading to stable pores inside the final sample. A picture of a dome shaped sample and a detail of the internal porous structure after gelation and drying are show in
Figure 3 staging the proposed approach.
The flow curves of the slurries formulated dissolving different amounts of the MC (8, 10 and 12 g/L) and the porogen agent (15, 20 and 25 wt.% of ammonium bicarbonate related to the solid content) were determined. The plot in
Figure 4 presents the rheograms of the viscosity evolution versus the shear rate for slurries with 12 g/L of MC and three contents of porogen (slurries (8X
G−15X
P), (8X
G−20X
P) and (8X
G−25X
P)). Similar rheograms for MC concentrations of 8 and 10 g/L were measured (no show here) with similar results and evolution of the slurries viscosity.
For a given amount of MC, the addition of 15 wt.% of ammonium bicarbonate leads to a decreasing in the viscosity of the slurry. This rheology sub serves the filling processed of the mold and is explained by the temperature dependence of a relatively big anions (bicarbonate anions) to the media [
36,
37]. Further additions of ammonium bicarbonate show an increment in the viscosity of the samples, as the increment of the ionic concentration led to a constriction on the electrical double layer and formation of short-range repulsive forces [
38]. The rheological behavior of these slurries is plastic or pseudoplastic, similarly to the curves of the
Figure 2, and they were adjusted to the Cross model to obtain the characteristic viscosity values of zero-shear viscosity (
η0), infinite shear viscosity (
η∞) and viscosity at 100 s
−1 (
η100).
After demolding, the apparent density of dome bulk pieces was calculated and the pore size distribution was determined by MIP for the Ti green samples shaped under the 15 experimental conditions of the experimental design method (
Table S1, supplementary material).
Figure 5 shows the pore size distributions measured when the porogen concentration varies for 4 fixed conditions of MC concentration and temperature considered in the experimental design (corresponding to (a) samples 9 (8X
G−15X
P−60X
T) and 7 (8X
G−15X
P−80X
T), (b) samples 5 (8X
G−25X
P−60X
T) and 3 (8X
G−25X
P−80X
T), (c) samples 8 (12X
G−15X
P−60X
T) and 6 (12X
G−15X
P−80X
T), (d) samples 4 (12X
G−25X
P−60X
T) and 2 (12X
G−25X
P−80X
T)). Similar pore size distributions were determined for other samples in
Table S1 (data and plots can be found as
supplementary material) with similar results that those discussed below.
The experimental values (also included as
Supplementary Material, Table S2) of the formulated slurries, viscosities (
η0,
η∞ and
η100 s−1), the apparent densities (D) and the mean pore diameter (P) resulting from the characterization of Ti sponges obtained at the 15 proposed experiments. Reported values show that viscosity in resting conditions varies from 1720 to 250 mPa·s and the mean pore size diameters range from 6.09 to 9.93 µm while the green density of Ti sponges varies from 1.77 to 2.56 g/cm
3 (from 39.25% to 56.76%).
To study the influence of each processing variable (X
G, X
P and X
T) in the apparent density, data in
Table S2 and the plots in
Figure 4 and similar (show as
Supplementary Material, Figure S1) were analyzed. As a function of the ammonium bicarbonate concentration (when X
G and X
T were fixed varying the X
P) and the MC concentration (X
P and X
T are fixed), whatever it is the values of other two variables, the apparent density decreases due to the higher amount of gas generated by the ammonium bicarbonate decomposition and the stronger gel structure formed by the slurry which is retaining the gas bubbles. In fact, from the microstructural inspection, pores in the green samples obtained with higher MC contents are lower in size and better distributed (
Figure 3). However, the increment of the process temperature promotes the increase of the apparent density. This could be due to the faster gas formation when temperature increases that promotes the coalescence of the bubbles at low gel concentrations and high porogen contents, avoiding an effective formation of the gel. In those cases, even the full structure of the green sponge can collapse.
The influence of the variables in the pore sizes deriving from the data collected in
Table S2 and the plots of pore distributions from the MIP such as those presented in
Figure 5 and other similar with different X
P at the same X
T or X
G. (not show here, but in the
Supplementary Material, Figure S2) were also analyzed. As a function of the ammonium bicarbonate concentration (when X
G and X
T were fixed varying the X
P), although the full width at half maximum for the main peak in the pore size distribution graphs ranges between 4 and 10 µm in all the cases, for the higher concentration of porogen a second broad area of porosity over the 10 µm is detected (
Figure 5b,d). Similarly occurs if the temperature is considered as the variable (when X
G and X
P were fixed varying the X
T), the higher is the temperature the wider is the population of pores with diameters higher than 10 µm. An in both cases, the higher is the concentration of the gelation agent (when X
P and X
T are fixed being X
G the variable) the lower is the extension of this second population of pores. Those results indicate that the gel strength prevents the coalescence of pores. However, for the highest gelation temperature tested, even the highest concentration of MC is not enough to keep the pores isolated, and then they coalesce to generate pores of bigger sizes.
The size of the pores is a critical parameter into the biological and mechanical response of the Ti based biomaterials. Furthermore, the porosity determines the mechanical response of the green sponges during handling. In order to evaluate the mechanical response of Ti green sponges, compression tests were performed on dome shaped samples at a displacement speed of 0.02 mm/s. In this test the applied compressive force distributes inside the sample transmitting the applied force in a simple elastic-plastic behavior [
39]. The dome configuration makes the compressive forces to develop circular tensile stresses on the surface of the sample [
40,
41,
42]. It has to be noted that this analysis considers a homogeneous and isotropic pore distribution without pore orientation, but orientation arising from the processing technologies can conditions the mechanical properties [
43].
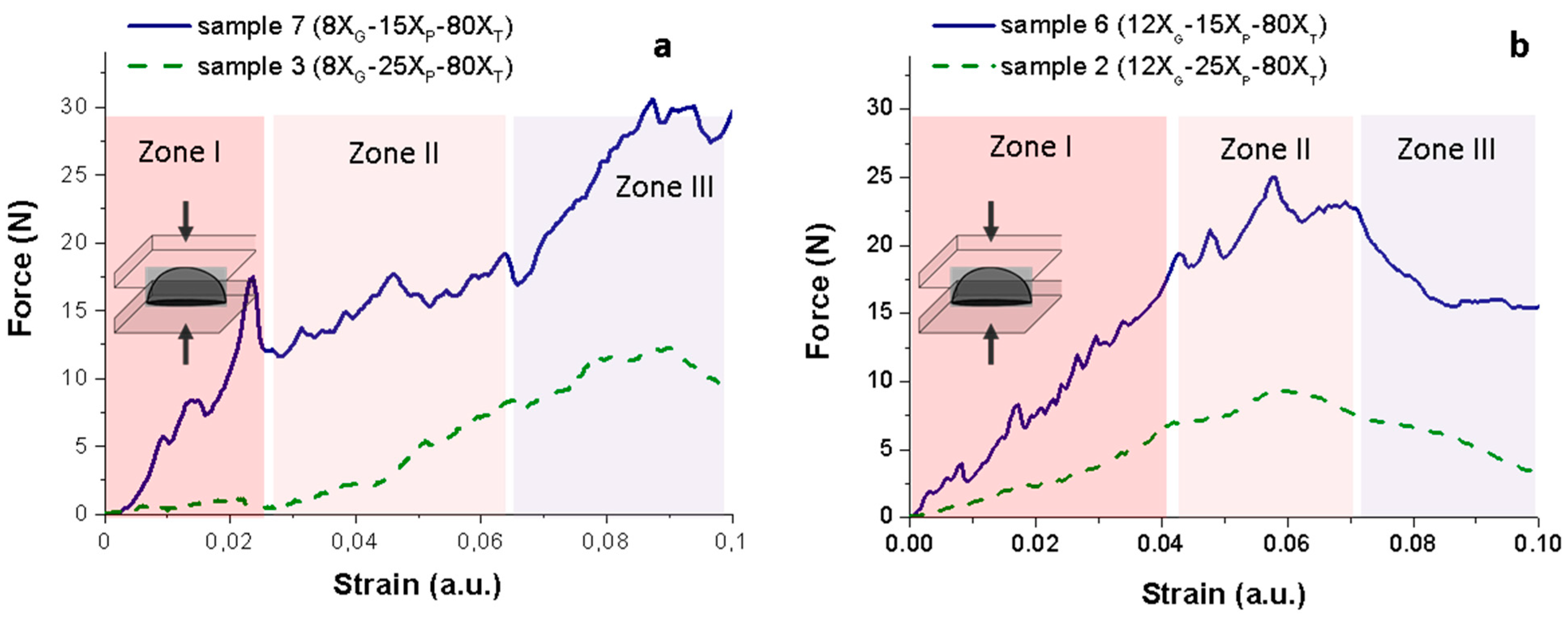
Plot in
Figure 6 shows the force-strain curve recorded in these mechanical tests where three regions of deformation corresponding to different phenomena can be identified [
44]. Initially the sponge response is nearly elastic (Zone I), where random tensile drops are due to the cracks initiated on the pores, i.e., properly are the structural defects and the rearrangement of the compacted powders. The strain value reached for zone I on
Figure 6a,b is different because the higher content of gelling agent in 12 X
G samples provide a plastic binder between particles, what allows higher strain (and stress) without breaking. The second zone (Zone II) consists in a stress plateau where multiple cracks grow and propagate easily throughout the materials collapsing the structure. The transition from the Zone I to the Zone II define a yield point which depends on the size, connectivity and number of pores. The final evolution of the force-strain curve (Zone III) can be identified with a densification process forced by the uniaxial pressure that compression plates exert onto the broken sample. As the broken pieces are not confined into a die, the Zone III can’t be clearly identified [
40]. In this study we were focused on the Zones I and II where the structural integrity of green sponges is mainly conditioned by the porosity and then by the selected operation variables (X
G, X
P and X
T).
Plots of
Figure 6a,b shows the load vs. deformation curves for the samples. In this case, 7 (8X
G−15X
P−80X
T) and 3 (8X
G−25X
P−80X
T), and samples. 6 (12X
G−15X
P−80X
T) and 2 (12X
G−25X
P−80X
T), respectively, which illustrate the mechanical response of Ti sponges obtained formulating slurries with 8 g/L and 12 g/L of MC, respectively, when the content of porogen change from 15 to 25 wt.% for a similar thermal treatment at 80 °C.
Results show that the porogen content strongly determines the structural integrity of the Ti sponges. In good agreement with the results described above, the curves force-strain exhibiting a higher slope correspond to the sponges obtained formulating the lower amount of ammonium bicarbonate (XP = 15 wt.%), that means to the structures with a lower level of porosity. In fact, samples 7 (8XG−15XP−80XT) and 6 (12XG−15XP−80XT) have similar apparent densities (2.44 and 2.37 g/cm3, respectively) and mean pore sizes (6.22 and 6.62 µm, respectively). However, the comparative examination of the whole curve evolution of both samples suggests a structure reinforcement achieved by the incorporation of a higher amount of the MC. At the plots, the higher is the amount of CM in the slurry formulation the higher is the compressive force required to achieve the plateau at the Zone II. Moreover, the tensile drops are less abrupt in the sponge num. 6 (12XG−15XP−80XT). Those effects can be related to the joining effect of the gelation agent over the particles and that the porosity generated by the ammonium bicarbonate decomposition is clearly trapped by a stiffer and stronger gel structure, respectively.
On the other hand, samples 3 (8X
G−25X
P−80X
T) and 2 (12X
G−25X
P−80X
T) have dissimilar apparent densities (2.15 and 1.77 g/cm
3, respectively) and mean pore sizes (7.17 and 6.27 µm, respectively). A low stiffness is observed for these sponges since they show a higher displacement for the application of smaller compressive forces. However, it is important to note that the whole behavior of the force-strain curves is similar to the curves measured for lower porogen contents (samples 7 and 6
Supplementary Material). So we can intuit that MC concentration influences the pore size and the porosity distribution, being both values higher as more porogen is added.
3.2. A Multiple Regression Analysis of the Experimental Data
In order to evaluate the weight of the main variables of the process, into the final properties of the shaped materials, a multiple regression analysis of the experimental data collected in
Table S2 was made with the software BMDP© to obtain a second-order polynomial equations relating each dependent variable (
η0, D and P) with the operational variables (X
T, X
G and X
P), resulting in:
The values of apparent density, viscosity and mean pore size of the bulk pieces are satisfactorily adjusted to the equation of the polynomial model tested, with 5, 6 and 7, different terms that contain the independent variables (operation variables), their square values or binary combinations of the aforementioned variables, respectively. As observed in the previous equations, there are significant interactions between the three selected input variables (XT, XG and XP) in each of the output variables (η0, D and P).
The polynomial models tested provide a good fit of the experimental data for the calculation of all response variables, as indicated by the values of multiple R, R2 and adjusted-R2 of the adjustments of Equations (5)–(7), as well as the higher
p-values and the lower values of the Snedecor’s F parameter (for a 95% confidence interval). They are all summarized in
Table 2.
The values estimated using the above Equations (5)–(7), reproduce the experimental results of the different dependent variables considered with errors less than of 10% in the most of cases. The following
Table 3 shows the errors determined experimentally and the estimated data from the aforementioned equations.
The analysis of the values collected in
Table 3 shows that the worst estimation for the apparent density, D, with respect to the experimental values has an error of 12.53%, however this test corresponds to limit conditions of the proposed experiment, that is it corresponds to the maximum values of the three operation variables: 12 g/L of MC, 25 wt.% of porogen and 80 °C. Therefore, the adjustment made is more precise with medium-low values of the operation variables. The other estimated data reproduce the experimental values with errors lower than 7%, which is the lowest error of the three estimated variables. On the other hand, the calculated values of the zero-shear viscosity (
η0) fits the experimental measured values with errors lower that 9%, the average value of the errors being lower than the rest of the variables, which indicates a good adjustment of the experimental results. Finally, the fitting values for the mean pore size (P) adjust to the experimental values with error lower than 15%. In this case, there is a greater disparity in the errors calculated on this variable from this model.
According to these results it can be concluded that calculated equations through a second order polynomic model for the processing of porous materials by a gelation technique conducts to error values lower than 7, 9 and 15%, in the worst case, for the apparent density, zero-shear viscosity and mean pore size, respectively. In this study, the errors assigned to the output variables are not significant within the range of the experimentally determined values, since the errors are within the range of variability and therefore the proposed model can be considered acceptable.
Those equations were used to determine the influence of the operational variables (input variables) on the properties of the slurries and the green structure of Ti bulk pieces (output variables). In this sense, the maximum and minimum values for each parameter (
η0, D and P) were estimated from Equations (5)–(7), and the values of the corresponding operational variables (X
T, X
G and X
P) were determined, and collected in
Table 4.
Matrices (x; y; z) correspond to XG, XP and XT, respectively. The viscosity values only depend on two variables, XG and XP, as the temperature was applied after the determination of the slurry viscosity. To determine the influence of the input variables on the properties considered it is necessary to determine the optimum conditions for each of the mentioned properties. For that, a non-linear programming as implemented in the More and Toraldo method was used. The values of two of the input variables were fixed and the other one was varied until the maximum and minimum value of each output parameter was reached, and with them the error was calculated. The maximum error corresponds to the most influential operational variable on the output parameter (η0, D or P).
To avoid particles segregation or sedimentation, the highest value of the zero-shear viscosity should be considered. For that reason, the optimum are the values which make maximize this parameter (−0.2; 1). As we previously said, the temperature value wasn’t a determinant factor, so the study is reduced only to two variables in which one or another is fixed, until achieving the maximum and minimum viscosity values. If XG was fixed and XP was the variable, the maximum and minimum viscosity values are 0.36 and 2.05, respectively, with error values of the 82.18%. Otherwise, when XP was fixed and XG was the variable, the values were 1.34 and 2.05 with and error of 34.38%. Consequently, the most influential variable in the zero-shear viscosity is XP.
In the other way, it has to be considered that the final objective was to achieve the lowest apparent density, which corresponds to the conditions for the highest porosity (1; 0.43; −1). Therefore, when XG and XP were fixed and XT was varied, the maximum and minimum density values were 1.73 and 1.94 g/cm3 with an error of 10.80%. When XG and XT were fixed and XP was varied, there are obtained minimum and maximum density values of 1.73 and 2.04 g/cm3 with an error of 15.00%. In addition, when XP and XT were fixed and XG was varied, there were obtained minimum and maximum values of 1.73 and 2.16 g/cm3 with an error of 19.66%. So, the most influential variable in the density is XG, followed by the XP and the lower influential was XT.
Finally, for the porosity, it was desirable the higher values for the mean pores size, which resulted in the following conditions (−1; 1; −0.32). Fixing XG and XP and changing the XT, the maximum and minimum pore sizes were 9.4 and 8.0, respectively, with error of 14.92%. Fixing XG and XT and changing the XP, the maximum and minimum pore sizes were 9.4 and 7.2 µm, respectively, with an error value of 22.98%. In addition, fixing XP and XT and changing the XG, the maximum and minimum mean pore sizes were 9.4 and 7.93 µm, respectively, with an error value of 15.77%. Based on this data the most influential variable in the mean pore size is XP, followed by XG and XT.
Table 5 summarizes the results of the study about the estimation of the influence of operational variables in the processing parameters of the green Ti sponges.
3.3. Sintering and Characterization of Ti Sponges
The porosity and the structure of the Ti structures after sintering were also studied. The Ti sponges were grouped in four categories: A, B, C and D. The Category A corresponds to the lower conditions for the operation variables (samples 8 and 9 in
Table S1). These materials have the lower porosity. The low viscosity promotes the displacement of big pores (supra-macro porosity, P
supra-macro) to the surface of the piece and burst lowering the porosity. Category B (samples 6, 7 and 11 in
Table S1) is associated to the materials with bigger pores in which the pores can internally merge into big pores but has only a limited capability to move up to the surface and once they burst, do not lose the shape. This porosity was opened, tubular and directional to the surface. Category C (samples 1, 4, 13 and 14 in
Table S1) corresponds to structures with a higher amount of pores, homogeneously distributed in the structure. In these cases, the viscosities were higher enough to keep the size of the pores without merges them in bigger ones but with open junctions. Finally, the Category D (samples 2, 3, 5, 10, 12 and 15 in
Table S1) corresponds to the higher values of the operational variables. The processing of these slurries is complicated due to both, the high viscosity and porosity, promotes the structure collapse. Those materials are hardly handling and then category D has not been considered for further characterizations.
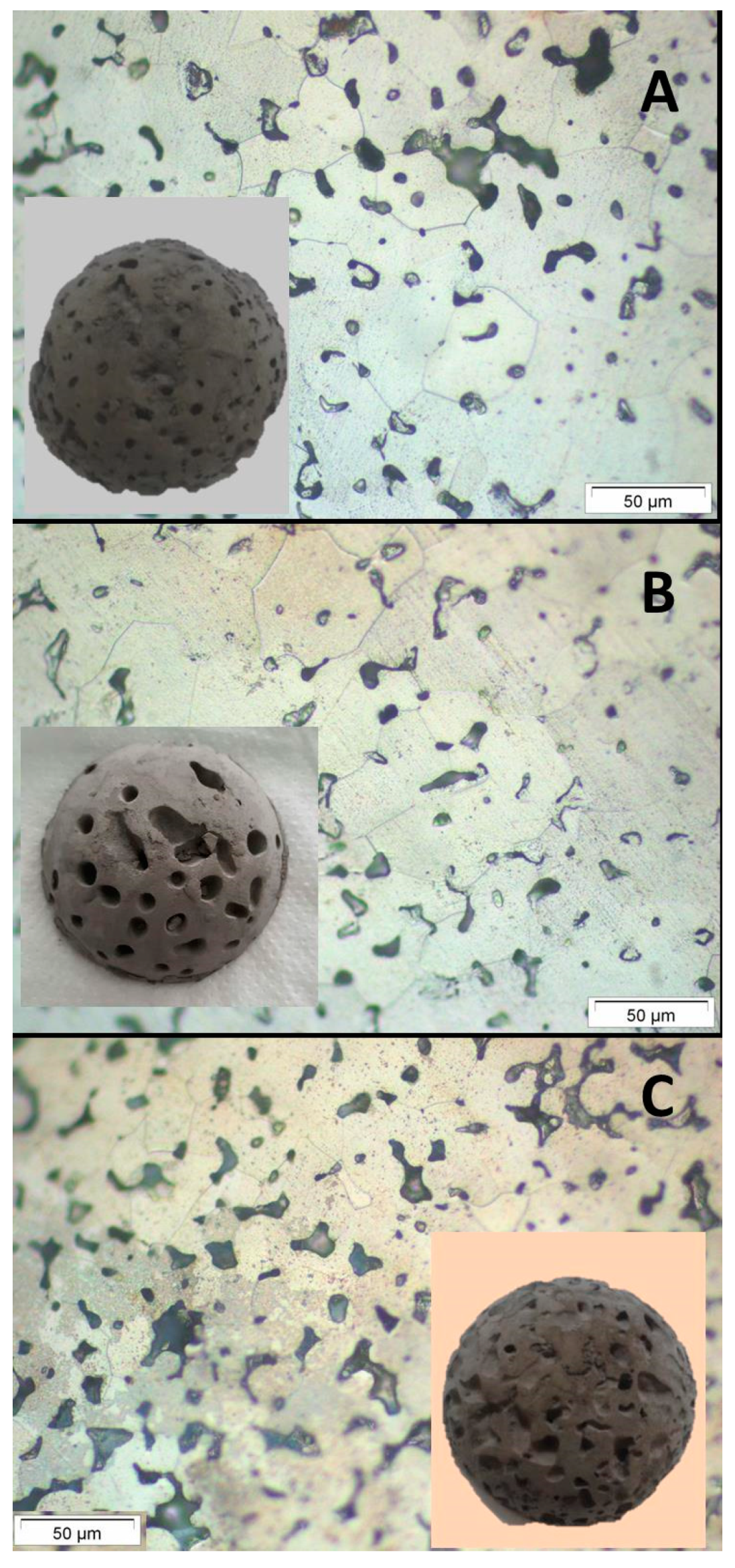
Figure 7 shows the pictures and micrographs of the materials which represents the categories A, B and C, while
Table 6 collects the characterization of the porosity and oxygen content (O
2) of these materials after sintering.
Materials have open porosities ranging from 19 to 39%, being the macro-porosity (P
macro ranging 50 nm < P < 200 µm) the more representative pore size in the Ti sponge microstructure. Samples on group A are denser than others and mainly present macroporosity. Materials on group B exhibit higher porosities which correspond mainly to the macro and supra-macro porosity. The high value on the supra-macro porosity was due to the coalescence of pores in the conditions where the gelation agent does not provide enough strength. Finally, materials of group C present the higher porosity, mainly macro porosity. The oxygen content ranges from 1.31 to 2.22 wt.%, close to the values of Ti processed by other aqueous colloidal techniques [
19,
22], being the structures on group C have the higher oxygen content, as a consequence of the higher total porosity.
It is important to note that samples of group B (6, 7 and 11 in
Table S2) has the highest apparent green densities (2.37–2.50 g/cm
3 corresponding to 51.40–54.23%) and a narrow pore size distribution with mean size ranging 6–7 µm. After sintering, these samples have the lowest closed porosity (0.2%) denoting the homogeneous and high degree of particles packing achieved during shaping. Moreover, these sponges exhibit the best compressive behavior (
Figure 6) as a result of the homogeneous distribution of the generated porosity in the stiff green structure. Finally, the macro porosity in this category of sponges is balanced between macro- and supra-macro pores leading to sintered Ti sponges with 39% of open porosity and almost null close porosity.