Temperature Effect on Stability of Clamped–Clamped Composite Annular Plate with Damages
Abstract
1. Introduction
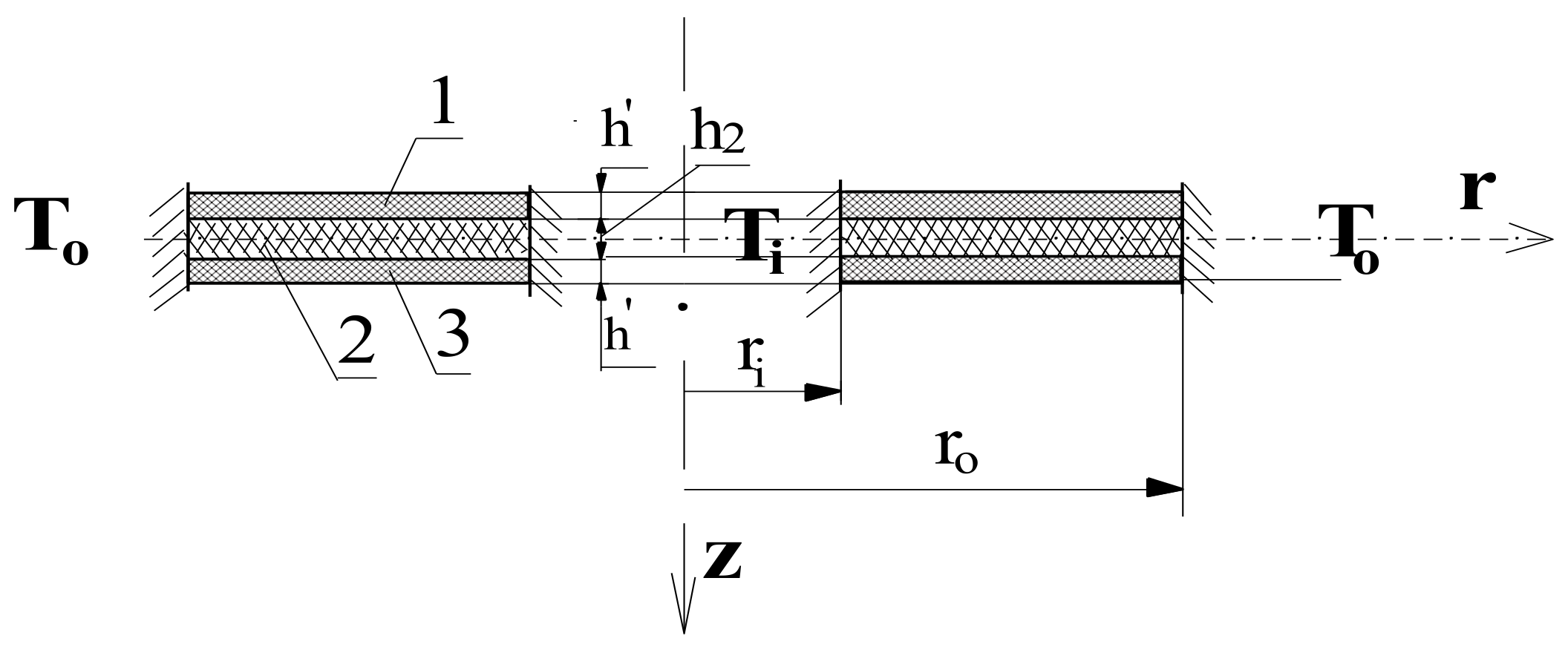
2. Problem Formulation
3. Problem Solution
3.1. Thermo-Mechanical Model of Fibrous Composite
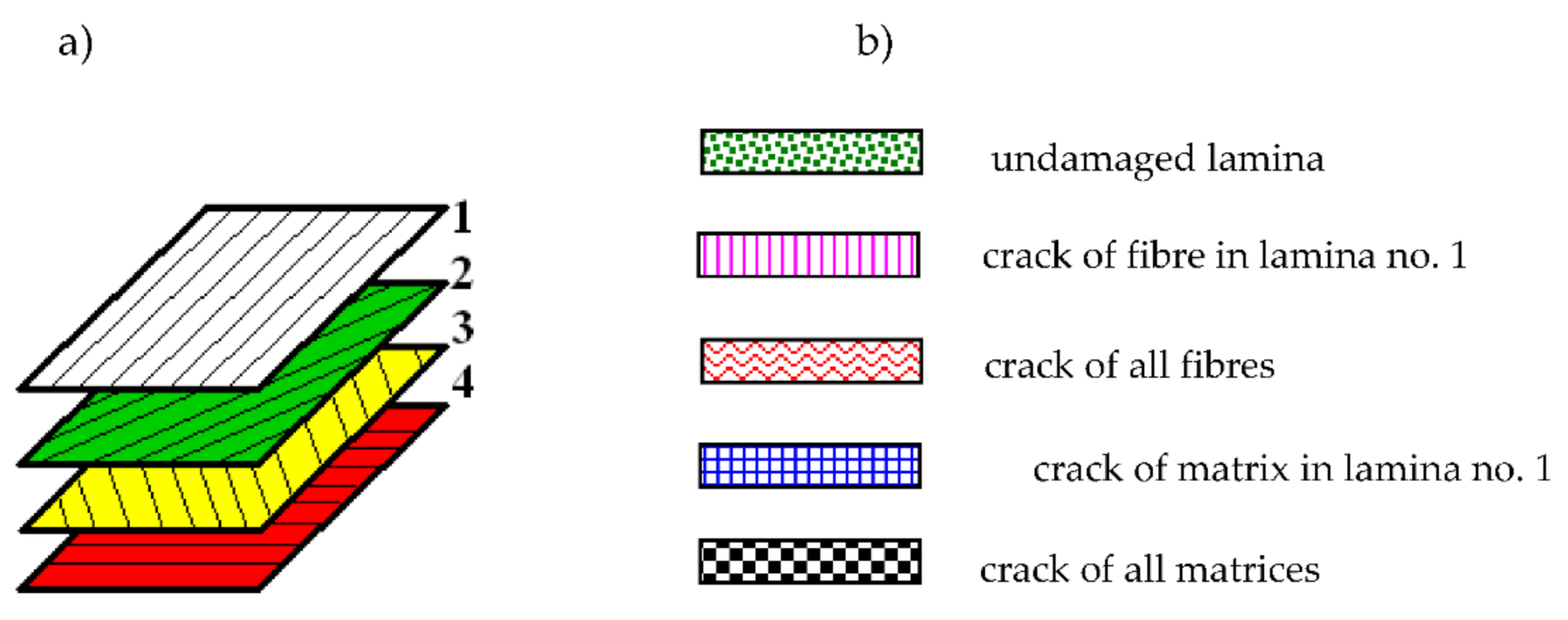
3.2. Composite Degradation Model
3.3. Plate Model Built Using the Finite Element Method
3.4. Plate Model Built with Finite Difference Method
4. Example Analyses
4.1. Plate Structure Parameters and Loading Coefficients
4.2. Convergence Analysis for FDM Plate Model and Comparison of FDM and FEM Results
- temperature differences cause plate buckling in a circumferentially wavy form;
- the thermal environment with the temperature growth in time increases the critical value of temperature differences, which are the reason for the plate dynamic stability loss;
- failure of lamina structure changes the response of the plate to thermal loading. Then, plate buckling occurs for higher values of critical temperature differences;
- the comparison of ∆Tcr and ∆Tcrdyn values calculated using the FDM and FEM plate models shows their comparability and a similar nature of changes;
- the critical deformation expressed by the values of the critical deflections does not differ for the examined plate models with health facings and fully damaged ones by fiber cracks.
4.3. Static Temperature Field
- both the thermal model of temperature field and properties of facings laminate material are of significance in the process of evaluation of the plate reaction to the impact of the surrounding environment;
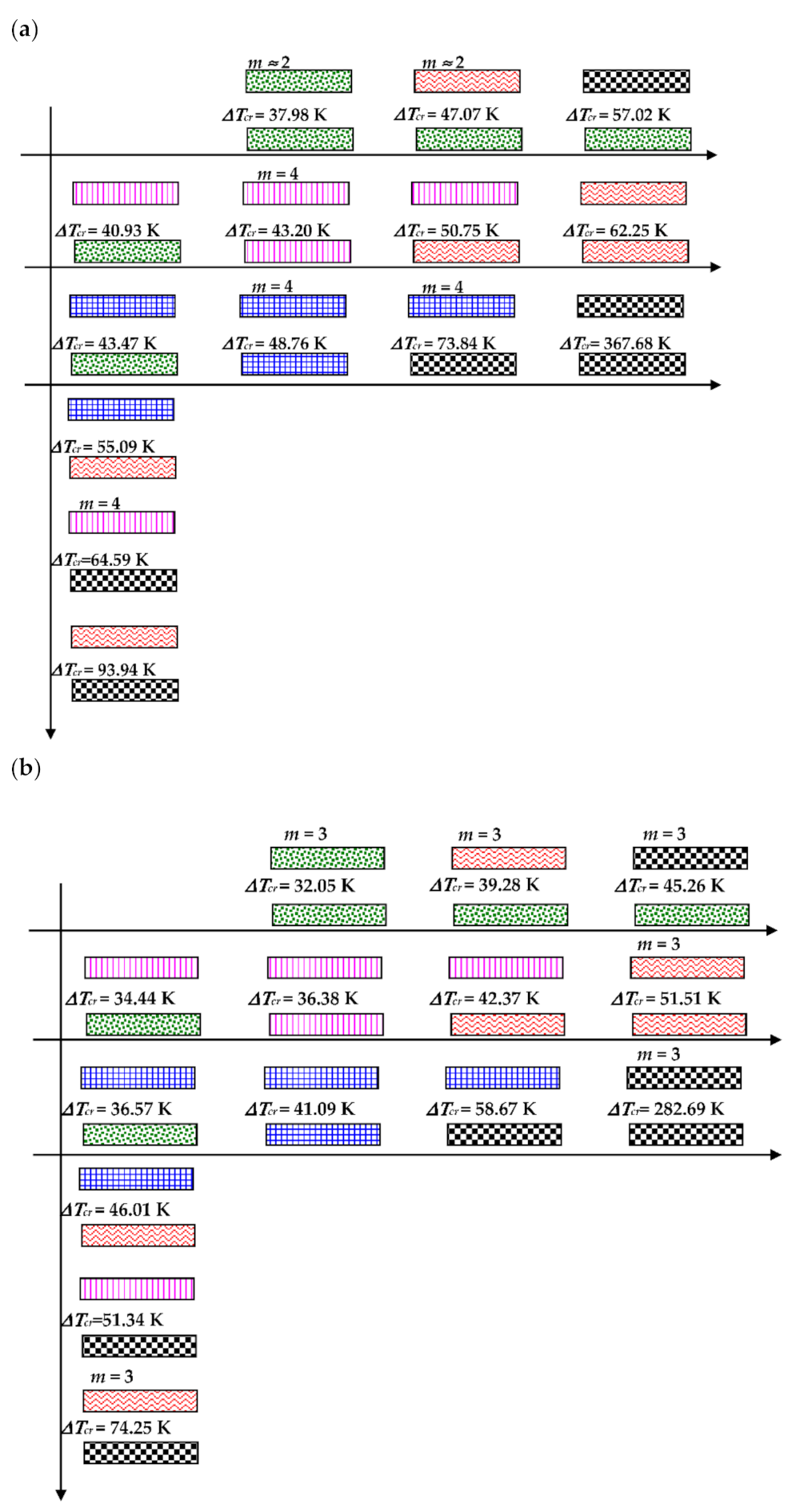
- damaged plates with a transversal symmetry of structure and a smaller failure in the form of cracks located only in the single lamina lose their stability for smaller values of temperature differences ∆Tcr than other destroyed plates. Smaller ∆Tcr values are observed for plates with an asymmetrical structure when one of the facings is healthy;
- the temperature gradient direction influences the values ∆Tcr;
- the buckling mode is circumferentially waved;
- the reaction of plates with heavy failures to the temperature environment is smaller than when plates are insignificantly damaged or completely healthy. Such an observation can be helpful in the process of diagnosing laminate composite structures with different damages.
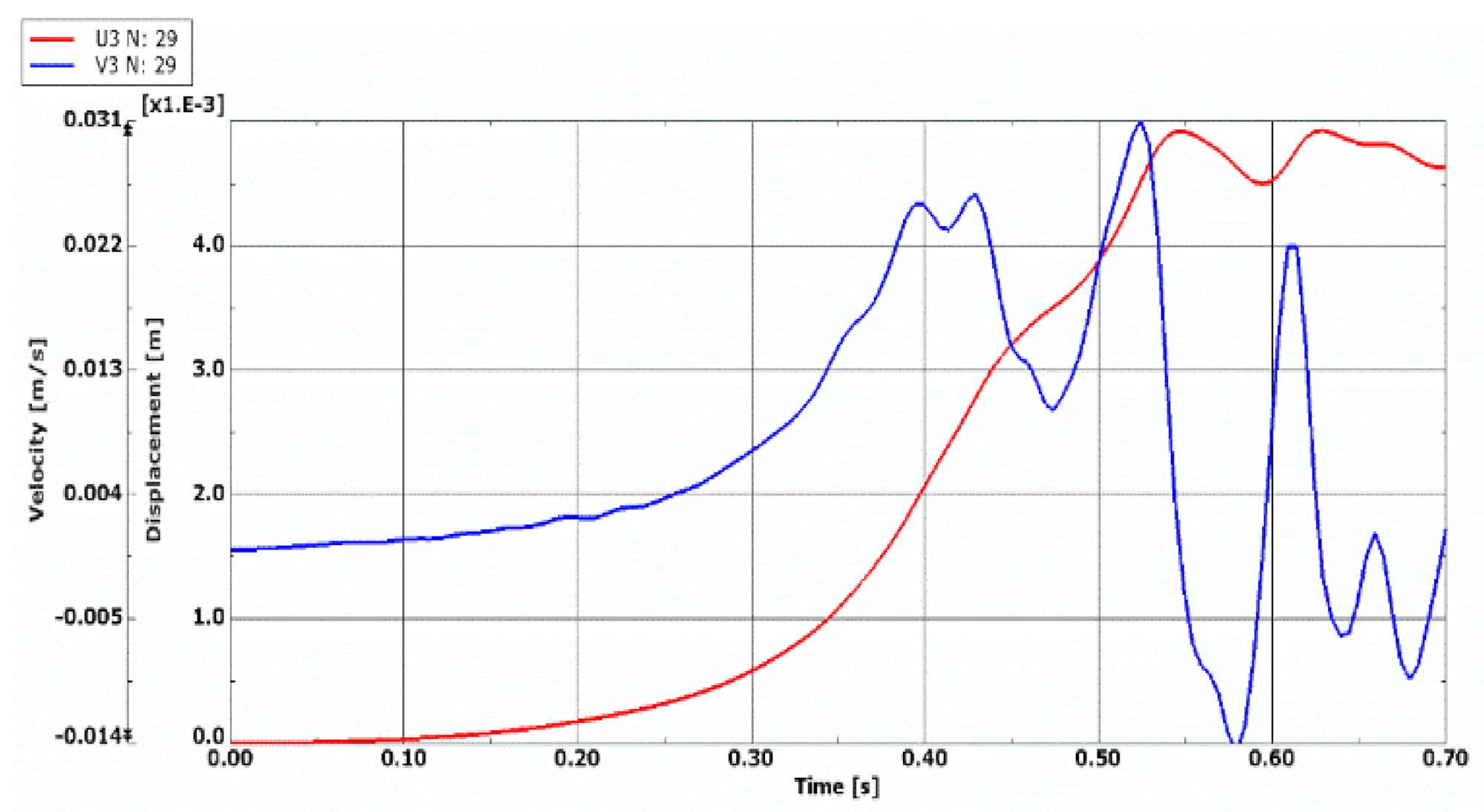
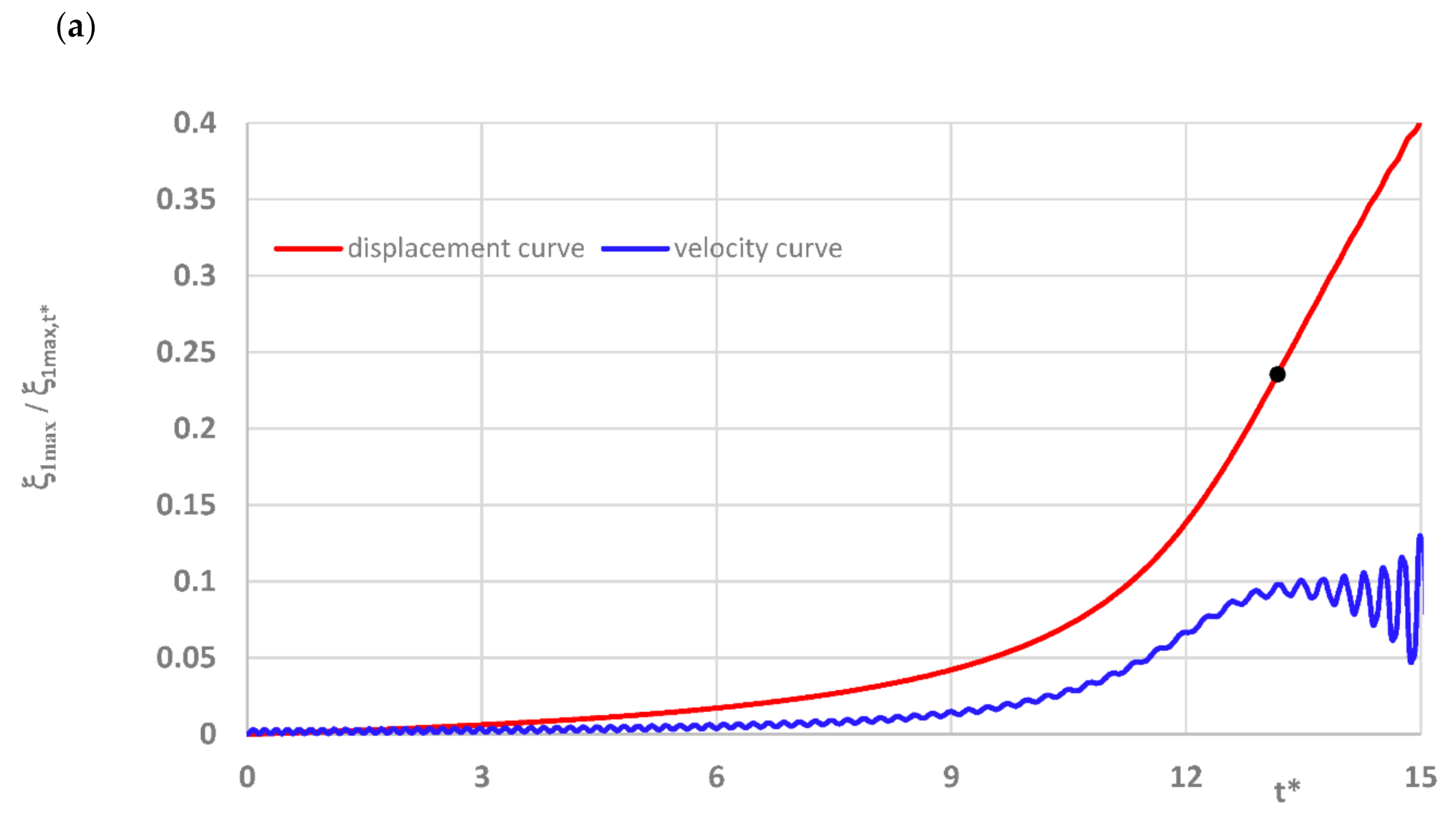
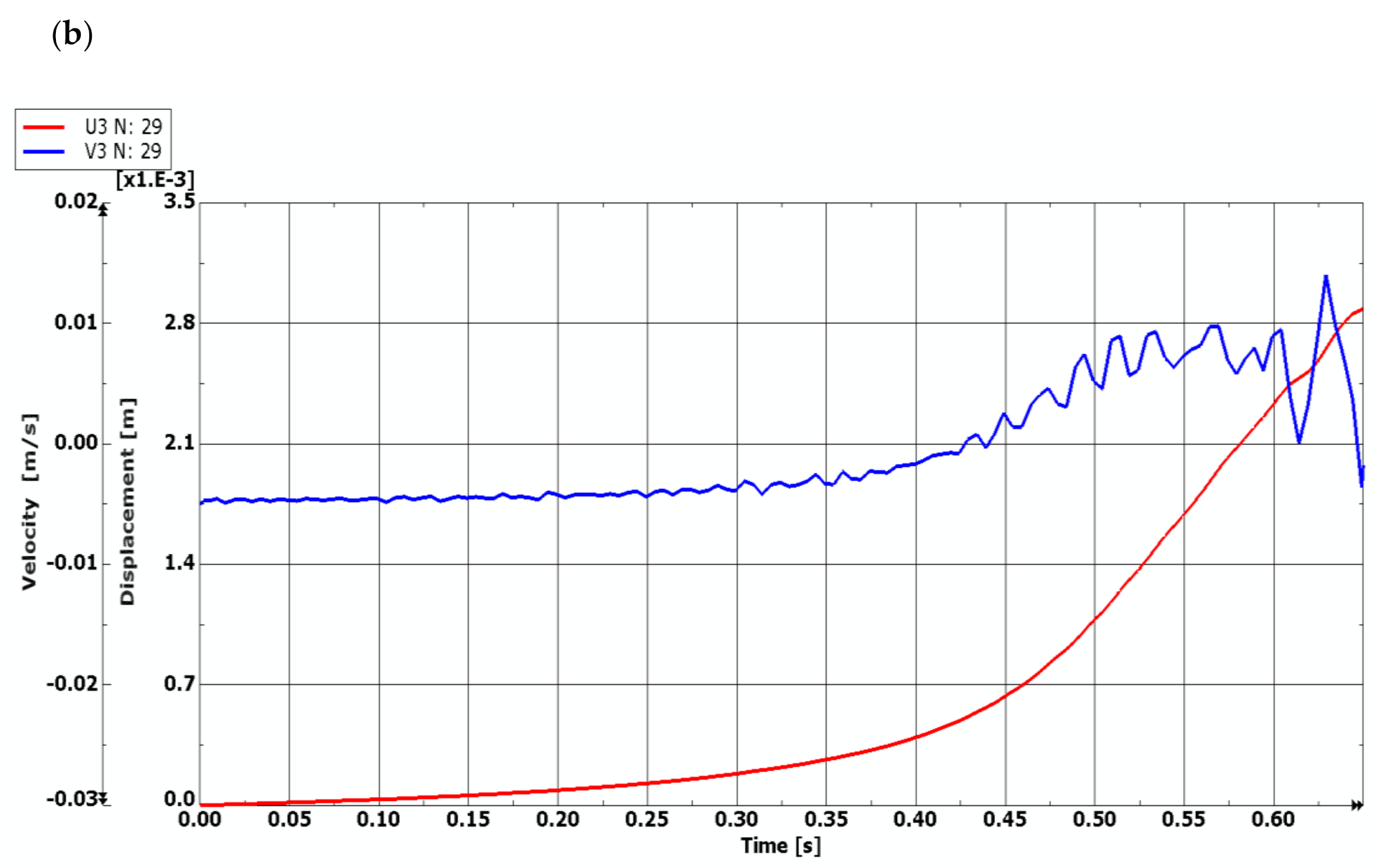
4.4. Dynamic Temperature Field
- presented results show the influence of dynamic temperature model on response of the composite plate;
- values of dynamic temperature difference ∆Tcrdyn are higher than those calculated in the static analysis but correspond with the changes of the static ones and confirm the observed effect of the static temperature environment on the buckling phenomenon of plates with varying grade of failure;
- numerical analyses show a possibility to use the temperature field in the failure diagnostic process.
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Appendix A
| Symbols | Definition |
| ri, ro | inner and outer radii of the annular plate |
| r, θ, z | cylindrical coordinates |
| r, ρ | plate radius and dimensionless radius |
| tl | thickness of laminate |
| h’, h2 | thickness of facings and core thickness |
| h” | thickness of each lamina |
| h = 2h’ + h2 | total thickness of plate |
| t, t* | time and dimensionless time |
| ∆T | temperature difference |
| Ti, To | inner and outer temperature |
| ∆Tcr, ∆Tcrdyn | static and dynamic critical temperature difference |
| a | rate of temperature loading growth |
| ∆Tf | fixed temperature difference |
| m | number of circumferential waves corresponding to the form of plate buckling |
| wd, wo | additional and preliminary plate deflection |
| ζ1(ρ,θ,t), ζo(ρ,θ) | Shape functions of dimensionless additional and preliminary plate deflection |
| E1, E2, G12, ν12 | Young’s and Kirchhoff’s moduli and Poisson’s ratio of the facings orthotropic material |
| E, G, ν | engineering constants: Young’s and Kirchhoff’s moduli and Poisson’s ratio of the facings quasi-isotropic material |
| E2, G2, ν2 | core Young’s and Kirchhoff’s moduli and Poisson’s ratio |
| μ, μ2 | facing and core mass density |
| α, α2 | linear expansion coefficient for isotropic material of facings and core |
| α11, α22 | linear expansion coefficient for orthotropic material |
| ηo = f(ρ) | form of plate pre-deflection |
| η | correction parameter η in damage theory |
| (),x | partial derivative |
References
- Chen, Y.R.; Chen, L.W.; Wang, C.C. Axisymmetric dynamic instability of rotating polar orthotropic sandwich annular plates with a constrained damping layer. Compos. Struct. 2006, 73, 290–302. [Google Scholar] [CrossRef]
- Wang, H.J.; Chen, L.W. Axisymmetric dynamic stability of rotating sandwich circular plates. J. Vib. Acoust. 2004, 126, 407–415. [Google Scholar] [CrossRef]
- Jianquiao, Y.E. Axisymmetric buckling analysis of homogeneous and laminated annular plates. Int. J. Pres. Ves. Pip. 1995, 62, 153–159. [Google Scholar]
- Jianquiao, Y.E. Laminated composite plates and shells; Springer: London, UK, 2003. [Google Scholar]
- Pawlus, D. Dynamic stability of three-layered annular plates with wavy forms of buckling. Acta Mech. 2011, 216, 123–138. [Google Scholar] [CrossRef]
- Pawlus, D. Solution to the problem of axisymmetric and asymmetric dynamic instability of three-layered annular plates. Thin Walled Struct. 2011, 49, 660–668. [Google Scholar] [CrossRef]
- Pawlus, D. Stability of three-layered annular plate with composite facings. Appl. Compos. Mater. 2017, 24, 141–158. [Google Scholar] [CrossRef]
- Lee, J.; Soutis, C. Prediction of impact-induced fibre damage in circular composite plates. Appl. Compos. Mater. 2005, 12, 109–131. [Google Scholar] [CrossRef]
- Muc, A.; Zuchara, P. Buckling and failure analysis of FRP faced sandwich plates. Compos. Struct. 2000, 48, 145–150. [Google Scholar] [CrossRef]
- Khoroshun, L.P.; Babich, D.V. Stability of plates made of fibrous composite with components subject to long-term damage. Int. Appl. Mech. 2010, 46, 573–579. [Google Scholar] [CrossRef]
- Maimi, P.; Camanho, P.P.; Mayugo, J.A.; Turon, A. Matrix cracking and delamination in laminated composites. Part II: Evaluation of crack density and delamination. Mech. Mater. 2011, 43, 194–211. [Google Scholar] [CrossRef]
- Ahmed, A.; Sluys, L.J. Computational modelling of impact damage in laminated composite plates. In Proceedings of the ECCM-16th European Conference on Composite Materials, Seville, Spain, 22–26 June 2014. [Google Scholar]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M.; Viola, E. Mechanical behaviour of damaged laminated composites plates and shells: Higher-order shear deformation theories. Compos. Struct. 2018, 189, 304–329. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M. Linear static behaviour of damaged laminated composite plates and shells. Materials 2017, 10, 811. [Google Scholar] [CrossRef]
- Meng, Q.; Wang, Z. Micromechanical modeling of impact damage mechanisms un unidirectional composite laminates. Appl. Compos. Mater. 2016, 23, 1099–1116. [Google Scholar] [CrossRef]
- Rokotonarivo, S.T.; Payan, C.; Moysan, J.; Hochard, C. Local damage evaluation of a laminate composite plate using ultrasonic birefringence of shear wave. Compos. Part B 2018, 142, 287–292. [Google Scholar] [CrossRef]
- Ghosh, A.; Sinha, P.K. Dynamic and impact response of damaged laminated composite plates. Aircr. Eng. Aerosp. Technol. 2004, 76, 29–37. [Google Scholar] [CrossRef]
- Pawlus, D. Evaluation of critical static loads of three-layered annular plates with damaged composite facings. Eng. Trans. 2016, 64, 613–619. [Google Scholar]
- Pawlus, D. Dynamic response of three-layer annular plate with damaged composite facings. Arch. Mech. Eng. 2018, LXV,1, 83–105. [Google Scholar] [CrossRef]
- Pawlus, D. Critical state evaluation of three-layered annular plates with symmetry and asymmetry damaged composite structure. In Proceedings of the Mechcomp 3–3rd International Conference on Mechanics of Composites, Bologna, Italy, 4–7 July 2017. [Google Scholar]
- Muc, A. Mechanics of Fibrous Composites; Księgarnia Akademicka: Kraków, Poland, 2003. (In Polish) [Google Scholar]
- Eslami, M.R. Buckling and Postbuckling of Beams, Plates and Shells; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Kiani, Y.; Eslami, M.R. An exact solution for thermal buckling of annular FGM plates on an elastic medium. Compos. Part B 2013, 45, 101–110. [Google Scholar] [CrossRef]
- Kiani, Y.; Eslami, M.R. Instability of heated circular FGM plates on a partial Winkler–type foundation. Acta Mech. 2013, 224, 1045–1060. [Google Scholar] [CrossRef]
- Ghiasian, S.E.; Bagheri, H.; Sadighi, M.; Eslami, M.R. Thermal buckling of shear deformable temperature dependent circular/annular FGM plates. Int. J. Mech. Sci. 2014, 81, 137–148. [Google Scholar] [CrossRef]
- Bagheri, H.; Kiani, Y.; Eslami, M.R. Asymmetric thermo-inertial buckling of annular plates. Acta Mech. 2017, 228, 1493–1509. [Google Scholar] [CrossRef]
- Bagheri, H.; Kiani, Y.; Eslami, M.R. Asymmetric thermal buckling of annular plates on a partial elastic foundation. J. Therm. Stresses 2017, 40, 1015–1029. [Google Scholar] [CrossRef]
- Bagheri, H.; Kiani, Y.; Eslami, M.R. Asymmetric thermal buckling of temperature dependent annular FGM plates on a partial elastic foundation. Comput. Math. Appl. 2018, 75, 1566–1581. [Google Scholar] [CrossRef]
- Jafarinezhad, M.R.; Eslami, M.R. Coupled thermoelasticity of FGM annular plate under lateral thermal shock. Compos. Struct. 2017, 168, 758–771. [Google Scholar] [CrossRef]
- Zhang, J.; Pan, S.; Chen, L. Dynamic thermal buckling and postbuckling of clamped-clamped imperfect functionally graded annular plates. Nonlinear Dyn. 2019, 95, 565–577. [Google Scholar] [CrossRef]
- Li, S.R.; Zhou, Y.H.; Song, X. Non-linear vibration and thermal buckling of an orthotropic annular plate with a centric rigid mass. J. Sound Vib. 2002, 251, 141–152. [Google Scholar] [CrossRef]
- Kidawa-Kukla, J. Thermally induced vibration of an annular plate subjected to the oscillating, heat stream. Sci. Res. Inst. Math. Comput. Sci. 2012, 4, 65–74. [Google Scholar] [CrossRef][Green Version]
- Aghelinejad, M.; Zare, K.; Ebrahimi, F.; Rastgoo, A. Nonlinear thermomechanical post-buckling analysis of thin functionally graded annular plates based on von-Karman’s plate theory. Mech. Adv. Mater. Struct. 2011, 18, 319–326. [Google Scholar] [CrossRef]
- Malekzadeh, P.M.R. Haghighi, G.M.M. Atashi, free vibration analysis of elastically supported functionally graded annular plates subjected to thermal environment. Meccanica 2011, 46, 893–913. [Google Scholar] [CrossRef]
- Pawlus, D. Stability of three-layered annular plate in stationary temperature field. Thin Walled Struct. 2019, 144, 106280. [Google Scholar] [CrossRef]
- Pawlus, D. Dynamic response of three-layered annular plates in time-dependent temperature field. Int. J. Struct. Stab. Dyn. 2020, 20, 2050139. [Google Scholar] [CrossRef]
- Pawlus, D. Dynamic stability of mechanical and thermal loaded three-layered annular plate with viscoelastic core. Vib. Phys. Syst. 2020, 31, 2020223. [Google Scholar] [CrossRef]
- Volmir, A.S. Nonlinear Dynamics of Plates and Shells; Science: Moskwa, Russian, 1972. (In Russian) [Google Scholar]
- German, J. Fundamentals of Mechanics of Fibrous Composites; Politechnika Krakowska: Kraków, Poland, 1996. (In Polish) [Google Scholar]
- Jones, R.M. Mechanics of Composite Materials; Scripta Book Company: Washington, DC, USA, 1975. [Google Scholar]
- ABAQUS/Standard; User’s manual; Hibbit, Karlsson & Sorensen, Inc.: Providence, RI, USA, 1998.
- Pawlus, D. Dynamic Stability of Three-Layered Annular Plates with Viscoelastic Core; Scientific Bulletin of the Technical University of Lodz, 1075: Lodz, Poland, 2010. (in Polish) [Google Scholar]
- Timoshenko, S.; Goodier, J.N. Theory of Elasticity; Arkady: Warszawa, Poland, 1962. [Google Scholar]
- Kowal-Michalska, K. Dynamic Stability of Composite Slab Structures; WNT: Warsaw, Poland, 2007. (In Polish) [Google Scholar]






| m | ∆Tcr [K] | ||||
|---|---|---|---|---|---|
| N = 11 | N = 14 | N = 17 | N = 21 | N = 26 | |
| 0 | 112.86 | 111.95 | 111.46 | 111.11 | 110.85 |
| 1 | 111.02 | 110.21 | 109.77 | 109.45 | 109.23 |
| 2 | 107.51 | 106.96 | 106.67 | 106.45 | 106.31 |
| 3 | 106.54 | 106.26 | 106.12 | 106.03 | 105.98 |
| 4 | 109.08 | 109.03 | 109.02 | 109.03 | 109.06 |
| 5 | 112.69 | 112.82 | 112.92 | 113.03 | 113.13 |
| Number N | 11 | 14 | 17 | 21 | 26 |
| ∆Tcrdyn [K] | 139.1 | 131.7 | 125.6 | 121.9 | 120.6 |
| Geometrical Parameters | |||
|---|---|---|---|
| inner radius ri, m | 0.2 | ||
| outer radius ro, m | 0.5 | ||
| total facing thickness h’, mm | 0.5 | ||
| thickness of each lamina h”, mm | 0.125 | ||
| core thickness h2, m | 0.005 | ||
| Material Parameters | |||
| orthotropic glass/epoxy composite of facing lamina | polyurethane foam of core | ||
| Young’s modulus E1, GPa | 53.781 | E2, MPa | 13 |
| Young’s modulus E2, GPa | 17.927 | ||
| Kirchhoff’s modulus G12, GPa | 8.964 | G2, MPa | 5 |
| Poisson’s ratio ν12 | 0.25 | ν2 | 0.3 |
| mass density μ, kg/m3 | 2900 | μ2, kg/m3 | 64 |
| linear expansion coefficient α, 1/K for material thermally isotropic | 1.96 × 10−5 | α2, 1/K | 70 × 10−6 |
| linear expansion coefficient α11, 1/K linear expansion coefficient α22, 1/K for material thermally orthotropic | 6.295 × 10−6 20.504 × 10−6 | - | - |
| calculated engineering constants of quasi-isotropic facings | |||
| facings with undamaged laminas | facings with damaged all laminas (fiber cracks) | ||
| Young’s modulus E, GPa | 31.1 | 18.71 | |
| Kirchhoff’s modulus G, GPa | 12.5 | 7.91 | |
| Poisson’s ratio ν | 0.245 | 0.182 | |
| loading parameters | |||
| rate of thermal loading growth a, K/s | 200 | ||
| fixed temperature difference ∆Tf, K | 10 | ||
| Plate Model | Asymmetric Plate m ≠ 0 | Axisymmetric Plate m = 0 | |
|---|---|---|---|
| Static Analysis | Static Analysis | Dynamic Analysis | |
| ∆Tcr [K] | ∆Tcr [K] | ∆Tcrdyn [K] | |
| Undamaged Facings | |||
| FDM | 69.36/3 | 72.14 | 86.70 |
| FEM | 62.20/2 | 64.35 | 70.82 |
| Damaged Facings | |||
| FDM | 106.26/3 | 111.95 | 131.70 |
| FEM | 94.05/3 | 98.06 | 113.82 |
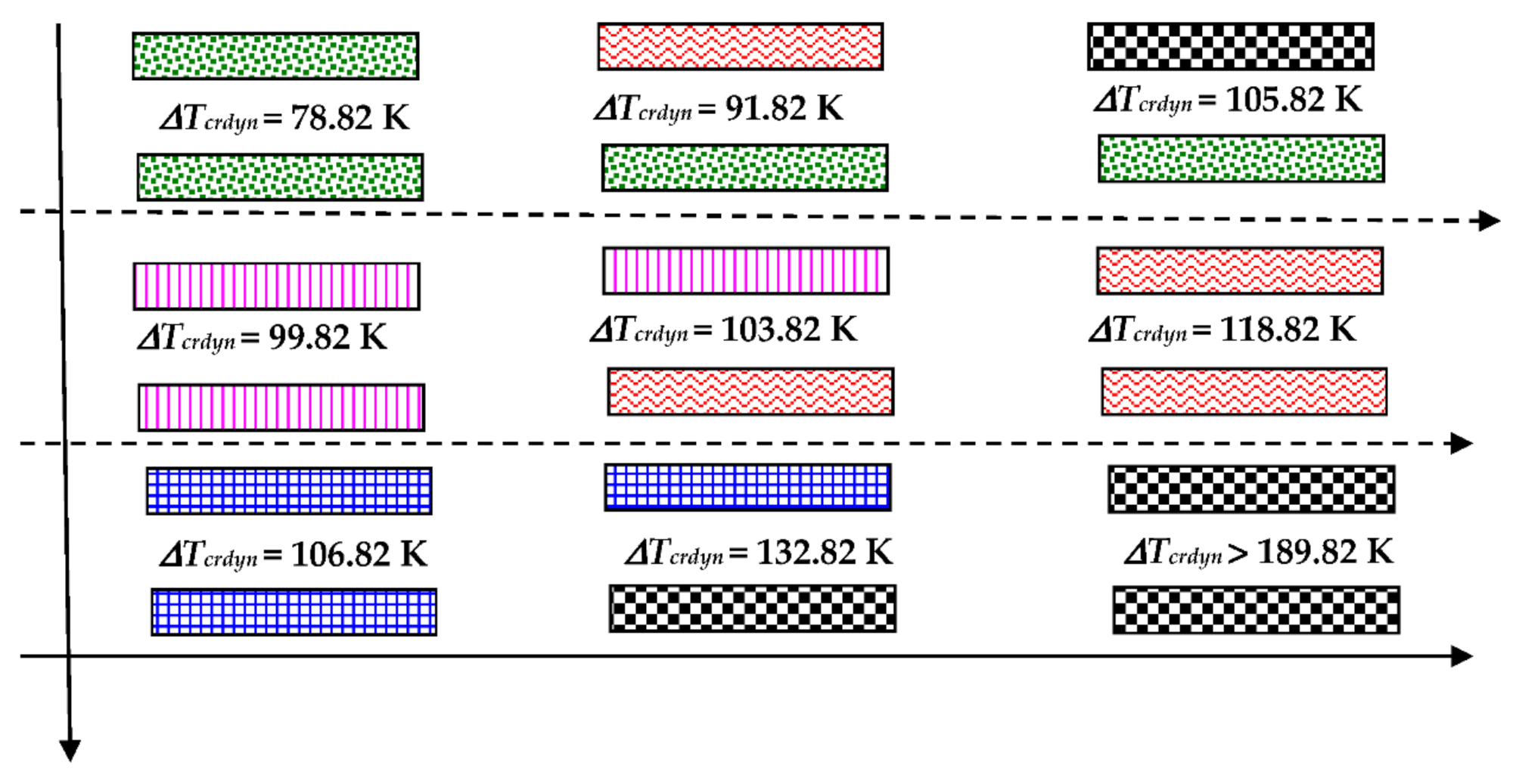
| Plate Mode | ∆Tcrdyn [K] | |||
|---|---|---|---|---|
| Undamaged Facings | Damaged Facings | |||
| FDM Model | FEM Model | FDM Model | FEM Model | |
| 0 | 86.7 | 70.82 | 131.7 | 113.82 |
| 1 | 84.9 | 67.82 | 130.3 | 99.82 |
| 2 | 81.7 | 67.82 | 123.5 | 103.82 |
| 3 | 78.5 | 66.82 | 119.0 | 105.82 |
| 4 | 77.5 | 70.82 | 119.4 | 109.82 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pawlus, D. Temperature Effect on Stability of Clamped–Clamped Composite Annular Plate with Damages. Materials 2021, 14, 4559. https://doi.org/10.3390/ma14164559
Pawlus D. Temperature Effect on Stability of Clamped–Clamped Composite Annular Plate with Damages. Materials. 2021; 14(16):4559. https://doi.org/10.3390/ma14164559
Chicago/Turabian StylePawlus, Dorota. 2021. "Temperature Effect on Stability of Clamped–Clamped Composite Annular Plate with Damages" Materials 14, no. 16: 4559. https://doi.org/10.3390/ma14164559
APA StylePawlus, D. (2021). Temperature Effect on Stability of Clamped–Clamped Composite Annular Plate with Damages. Materials, 14(16), 4559. https://doi.org/10.3390/ma14164559





