Optical Microscopy Observations and Construction of Dupin Cyclides at the Isotropic/Smectic A Phase Transition
Abstract
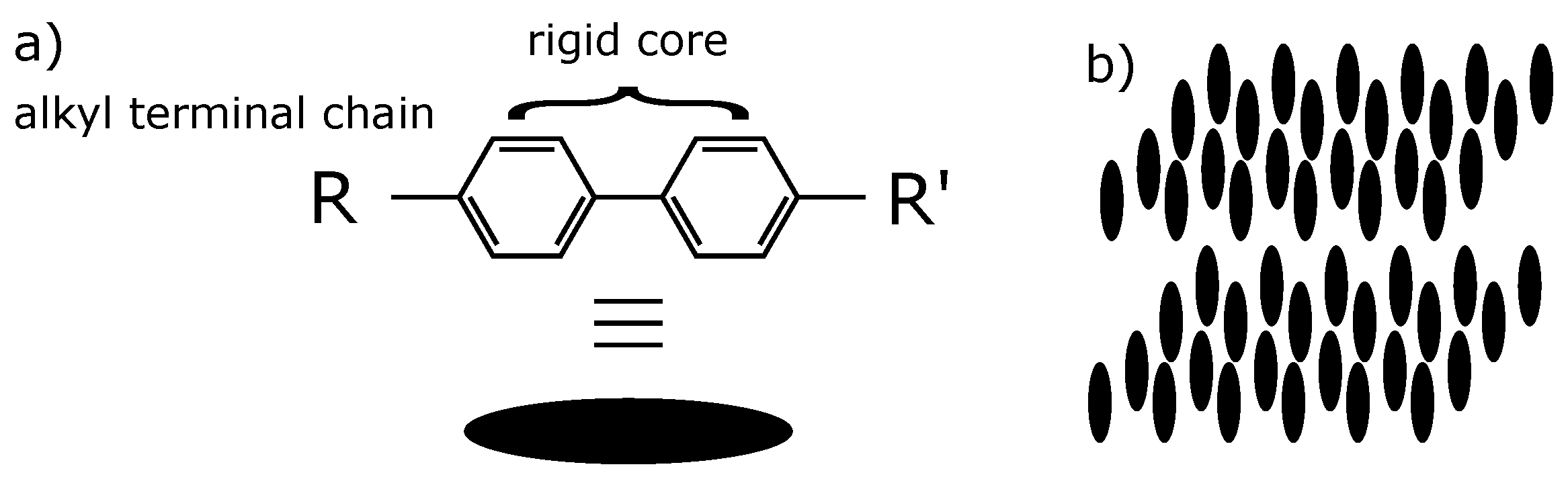
1. Introduction
2. Results
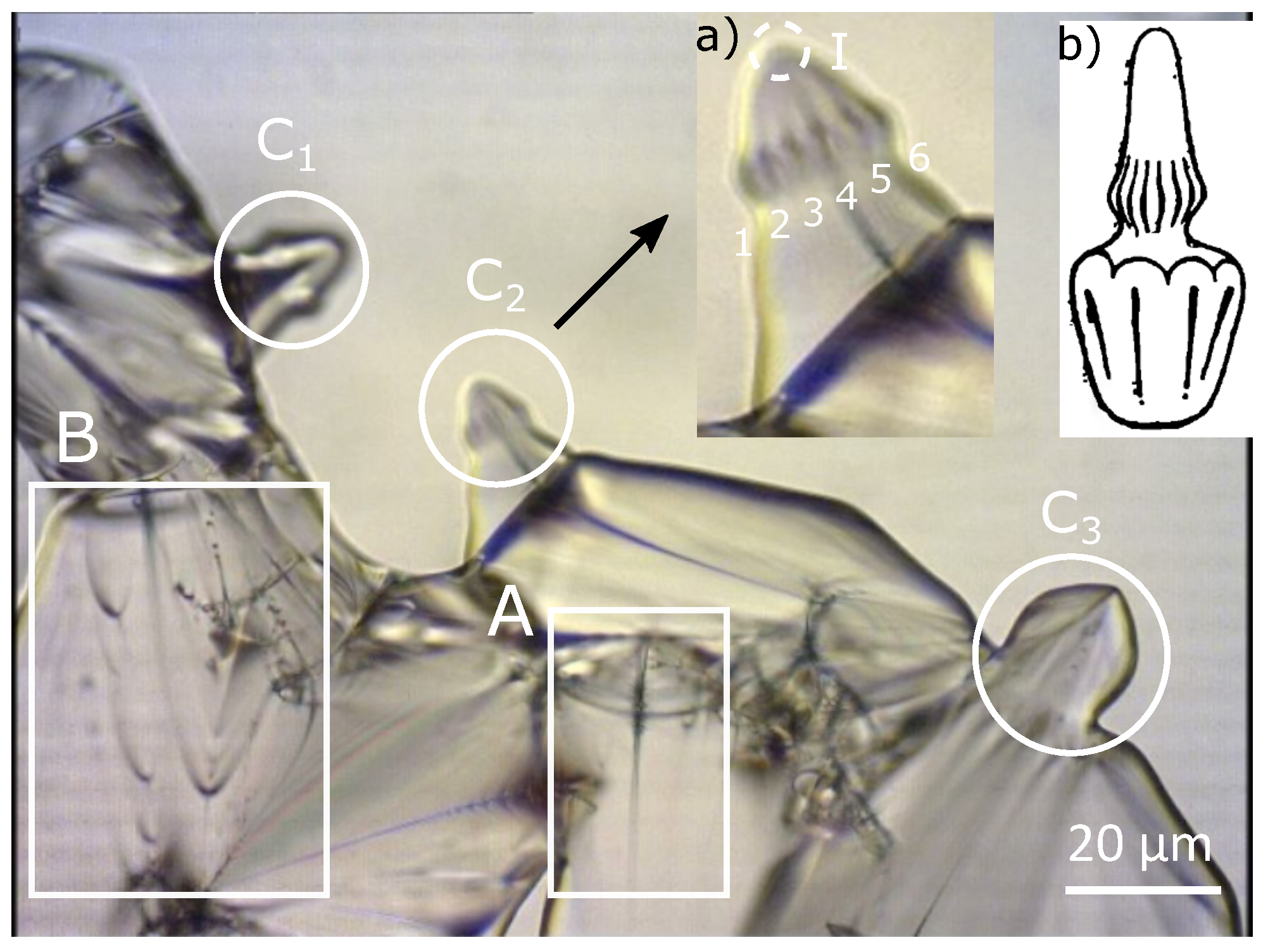
2.1. Polarized Optical Microscopy
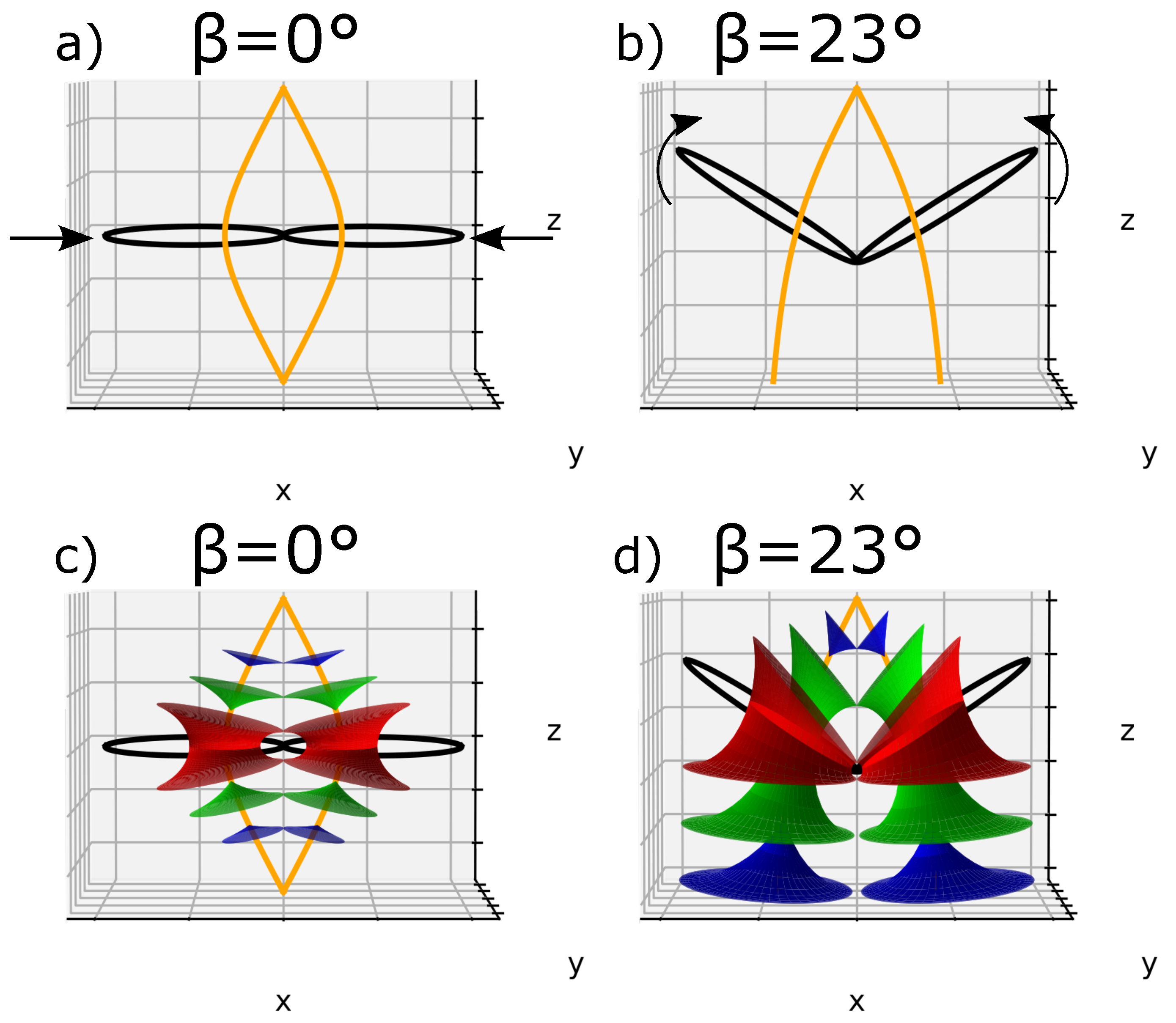
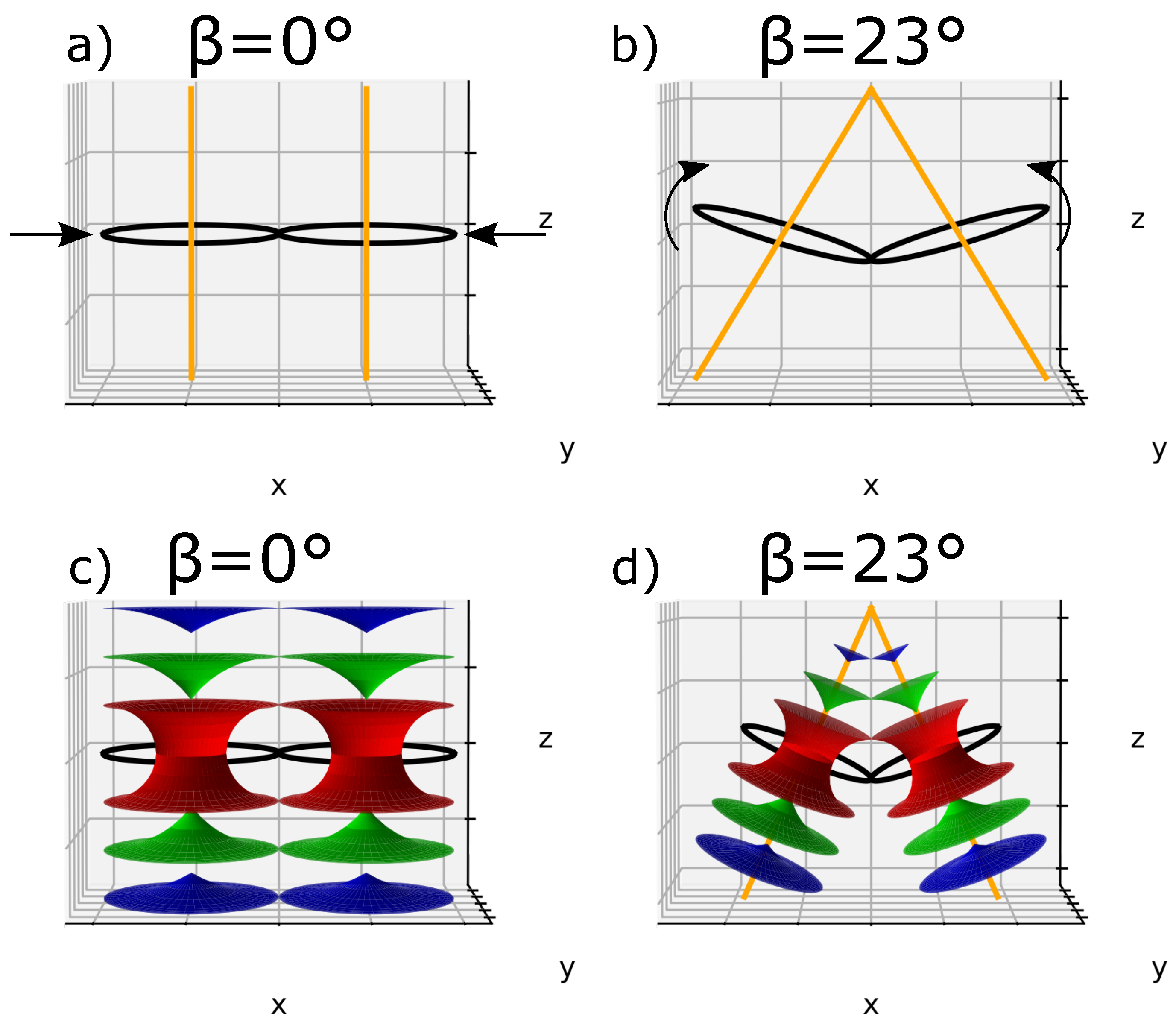
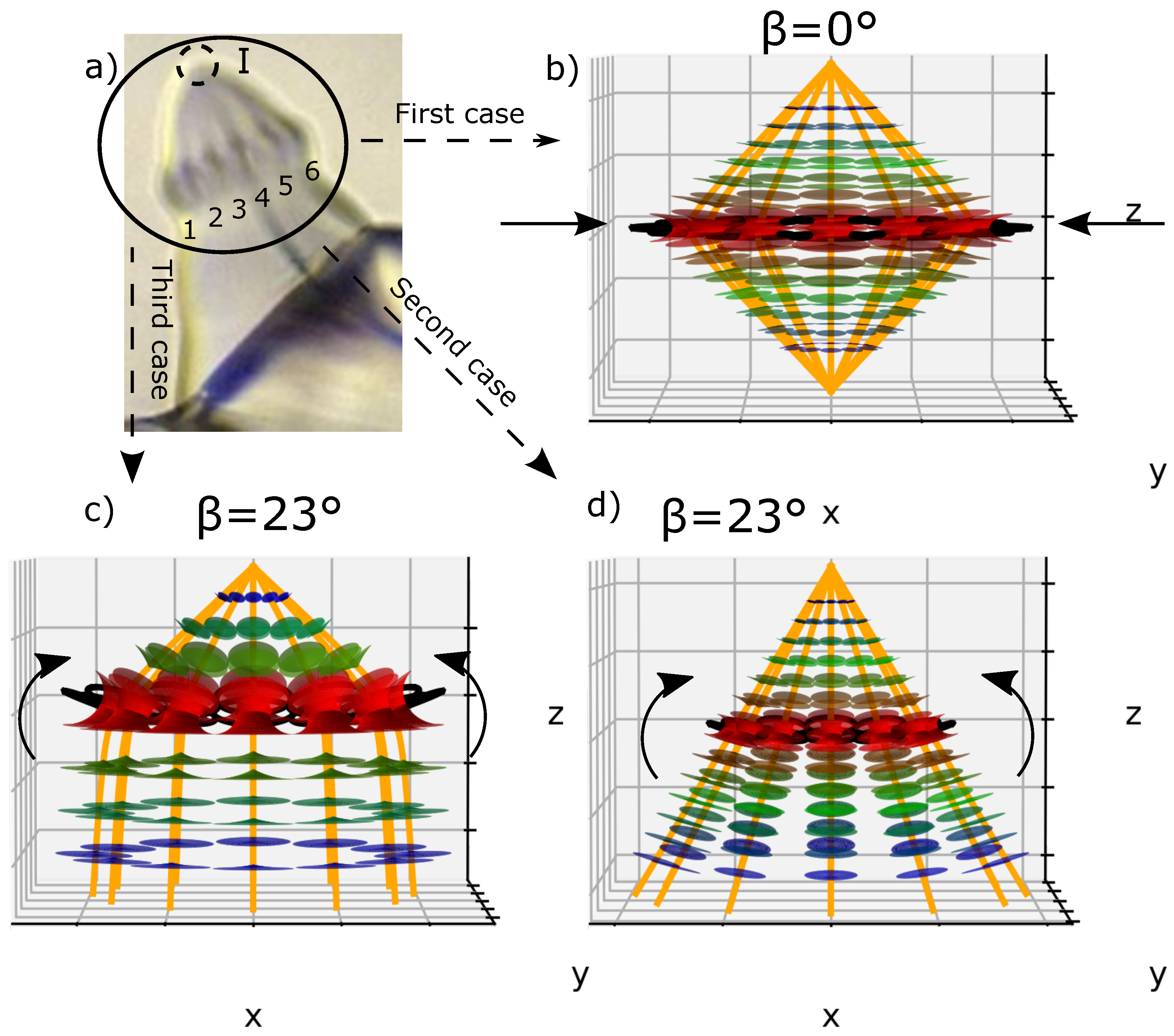
2.2. Focal Conic Assembly Corresponding to Friedel’s Law
- First, the domains of two adjacent focal groups (FC) cannot overlap;
- Second, in the case where two conics are tangent at a point M, the cones of revolution with apex M and resting on the focal lengths of the conics coincide; they share a common generatrix, this is the Law of Corresponding Cones (L.C.C.).
3. Discussion
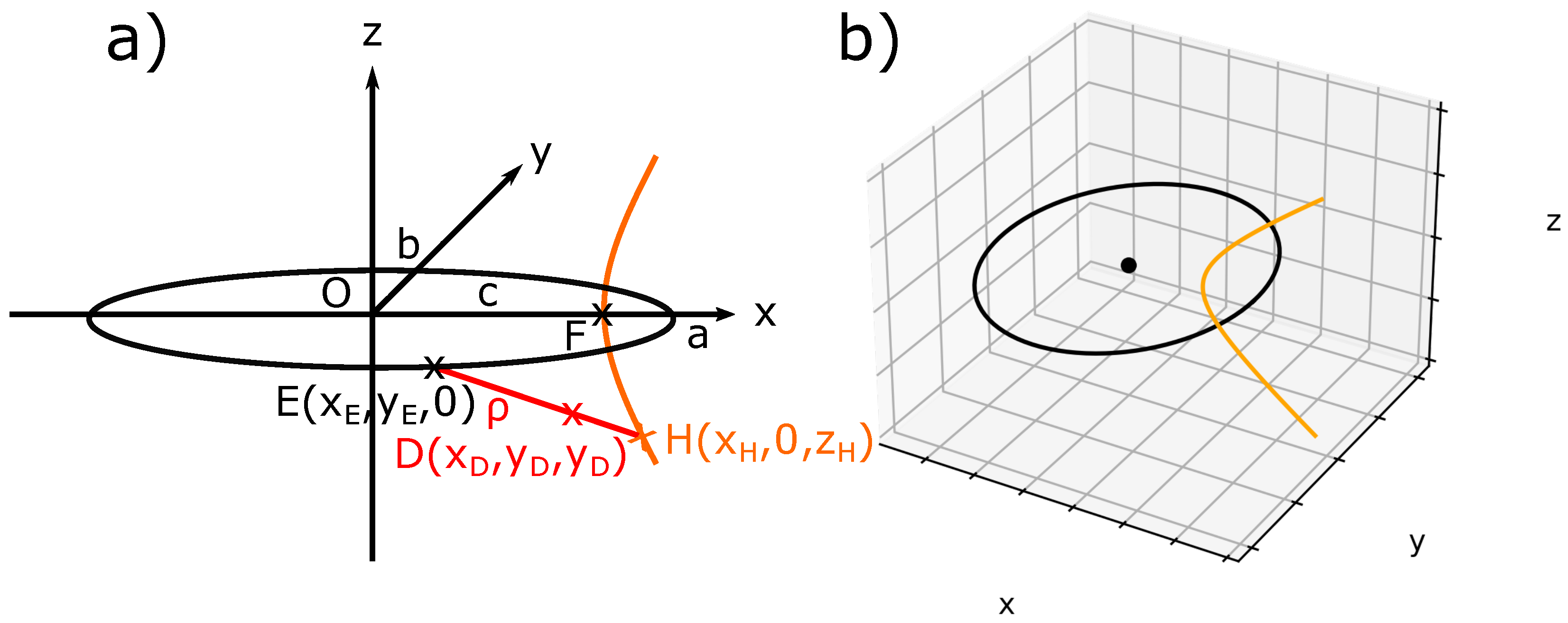
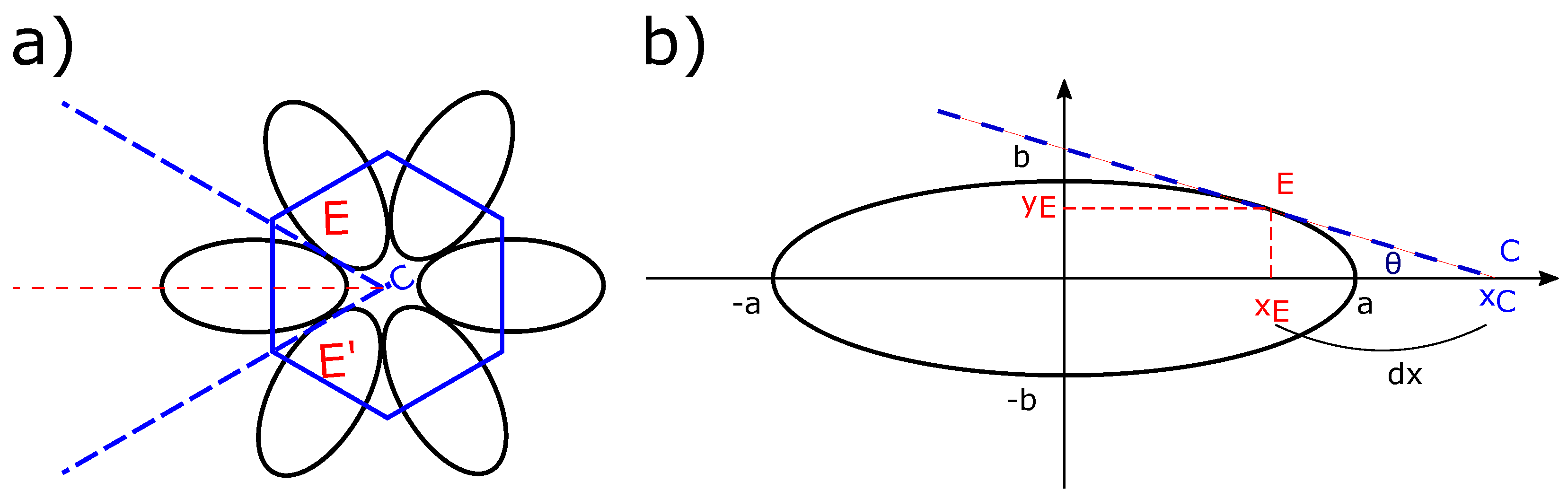
3.1. Geometrical Model
- First:
- Plot one set: ellipse and confocal hyperbola, which will define one single FCD.
- Second:
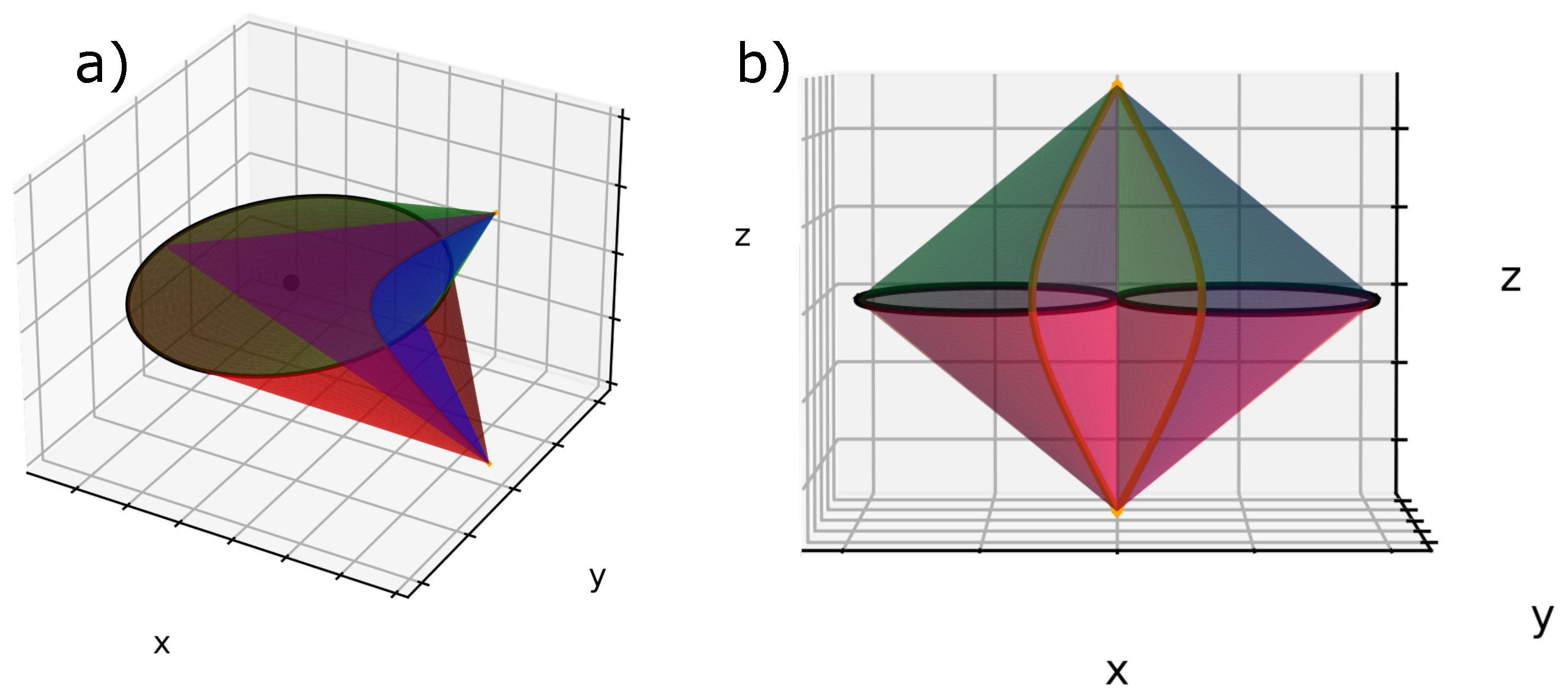
- Decorate the predefined domain by adding their respective smectic layers using the Dupin cyclides’ equation system.These two first steps will define one single domain (see Figure 3).
- Third:
- Plot the other focal conic domains based on Friedel’s law of focal conics’ assemblies and mainly on the fact that these ellipses that have been shown in Figure 4a should be tangent to each other and cannot interfere.The third step is the crucial one, which we will detail in the next paragraph, but mainly our idea is to copy the first domain and to rotate it with an angle depending on the number of focal conic domains needed.
3.1.1. Geometrical Definitions
- First:
- Plot an arbitrary FC with the corresponding smectic layers (Figure 3);
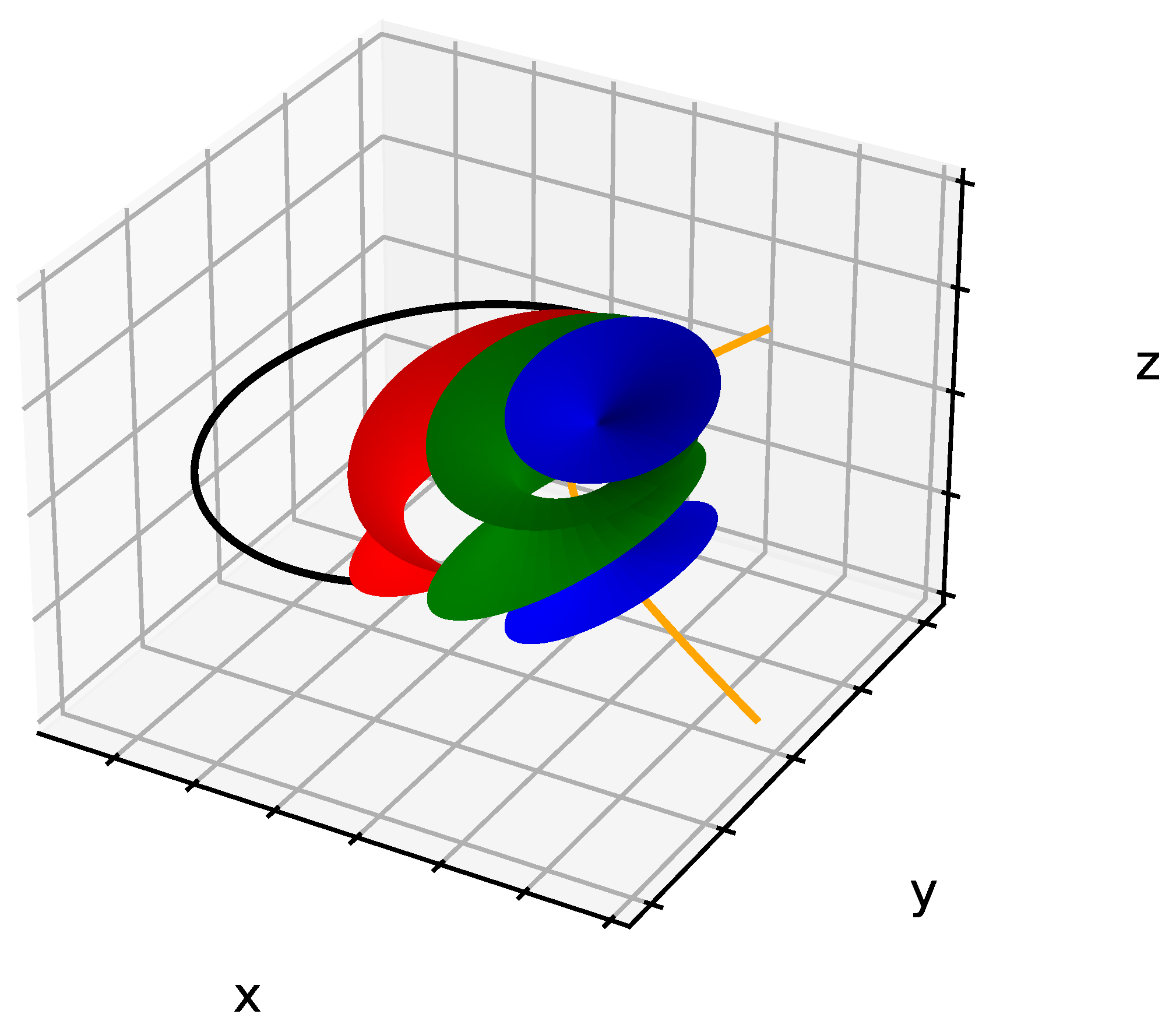
- Second:
- Copy the graph obtained in the first step and then rotate it with a specific angle and with center C, which is the center of the hexagon. For this, in Python code (see Supplementary Materials), we will use a for loop that will enable us to plot as many ellipses as we like, and, for each loop, the FCDs and the corresponding smectic layers have been rotated using a rotational matrix. This task can be repeated as many times as needed independently from the number of FCDs contained inside the bâtonnets, see areas and in Figure 4.
3.1.2. Application on Two FCDs
3.1.3. Application on Sets of FCDs
4. Materials and Methods
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| LC | Liquid Crystal |
| FCs | Focal Conics |
| FCDs | Focal Conic Domains |
| TFCDs | Toroidal Focal Conic Domains |
| Smectic A | SmA |
References
- De Gennes, P.G.; Prost, J. The Physics of Liquid Crystals; International Series of Monographs on Physics; Clarendon Press Publication: Oxford, UK, 1995. [Google Scholar]
- Friedel, G. Les états mésomorphes de la matière. Ann. Phys. 1922, 9, 273–474. [Google Scholar] [CrossRef]
- Suisse, J.M.; Bellemin-Laponnaz, S.; Douce, L.; Maisse-François, A.; Welter, R. A new liquid crystal compound based on an ionic imidazolium salt. Tetrahedron Lett. 2005, 46, 4303–4305. [Google Scholar] [CrossRef]
- Beaulieu, R.; Gottis, S.; Meyer, C.; Grand, E.; Deveaux, V.; Kovensky, J.; Stasik, I. Cholesteryl and diosgenyl glycosteroids: Synthesis and characterization of new smectic liquid crystals. Carbohydr. Res. 2015, 404, 70–78. [Google Scholar] [CrossRef]
- Malkar, D.; Monika, M.; Prasad, V.; Roy, A. Pseudopolar smectic-C phases of azo-substituted achiral bent-core hockey-stick-shaped molecules. Phys. Rev. E 2020, 101, 012701. [Google Scholar] [CrossRef] [PubMed]
- Chaveriat, L.; Meyer, C.; Beaupère, D.; Demailly, G.; Stasik, I. 6-S-Alkyl-6-thiohexonolactones and 6-S-Alkyl-6-thiohexitols: Efficient synthesis and new smectic liquid crystal phases. J. Mol. Liq. 2008, 142, 17–21. [Google Scholar] [CrossRef]
- Stasik, I.; Gottis, S.; Falentin-Daudré, C.; Meyer, C. Influence of alkyl chain length on the mesomorphism of 5-S-alkyl-5-thiopentonolactones and 5-S-alkyl-5-thiopentitols. Carbohydr. Res. 2014, 392, 31–39. [Google Scholar] [CrossRef]
- Meyer, C.; Stoenescu, D.; Luckhurst, G.R.; Davidson, P.; Dozov, I. Smectic-like bâtonnets in nematic/twist-bend nematic biphasic samples. Liq. Cryst. 2017, 44, 232–243. [Google Scholar] [CrossRef]
- Krishnamurthy, K.S.; Shankar Rao, D.S.; Kanakala, M.B.; Yelamaggad, C.V.; Madhusudana, N.V. Saddle-splay-induced periodic edge undulations in smectic-A disks immersed in a nematic medium. Phys. Rev. E 2020, 101, 032704. [Google Scholar] [CrossRef] [PubMed]
- Davidson, P.; Bourgaux, C.; Schoutteten, L.; Sergot, P.; Williams, C.; Livage, J. A Structural Study of the Lyotropic Nematic Phase of Vanadium Pentoxide Gels. J. Phys. II 1995, 5, 1577–1596. [Google Scholar] [CrossRef]
- Jamali, V.; Behabtu, N.; Senyuk, B.; Lee, J.A.; Smalyukh, I.I.; van der Schoot, P.; Pasquali, M. Experimental realization of crossover in shape and director field of nematic tactoids. Phys. Rev. E 2015, 91, 042507. [Google Scholar] [CrossRef] [PubMed]
- Prinsen, P.; van der Schoot, P. Shape and director-field transformation of tactoids. Phys. Rev. E 2003, 68, 021701. [Google Scholar] [CrossRef] [PubMed]
- Dierking, I.; Russell, C. Universal scaling laws for the anisotropic growth of SmA liquid crystal bâtonnets. Phys. B Condens. Matter 2003, 325, 281–286. [Google Scholar] [CrossRef]
- Fournier, J.B.; Durand, G. Focal conic faceting in smectic-A liquid crystals. J. Phys. II 1991, 1, 845–870. [Google Scholar] [CrossRef]
- Blanc, C. Etude de l’Interface Lamellaire-Eponge des Systèmes Lyotropes Gonflés: Du Facetage Volumique et des Formes de Croissance aux Modèles Microscopiques. Ph.D. Thesis in Physics, Thèse de doctorat de Physique dirigée par Kleman, Maurice. Sorbonne Université Campus Pierre et Marie Curie, Paris, Frence, 2000. [Google Scholar]
- Blanc, C.; Kleman, M. On the Shapes of Lamellar Droplets in Sponge Phase. Mol. Cryst. Liq. Cryst. Sci. Technol. Sect. A Mol. Cryst. Liq. Cryst. 1999, 332, 585–592. [Google Scholar] [CrossRef]
- Metselaar, L.; Dozov, I.; Antonova, K.; Belamie, E.; Davidson, P.; Yeomans, J.M.; Doostmohammadi, A. Electric-field-induced shape transition of nematic tactoids. Phys. Rev. E 2017, 96, 022706. [Google Scholar] [CrossRef] [PubMed]
- Kaznacheev, A.V.; Bogdanov, M.M.; Sonin, A.S. The influence of anchoring energy on the prolate shape of tactoids in lyotropic inorganic liquid crystals. J. Exp. Theor. Phys. 2003, 97, 1159–1167. [Google Scholar] [CrossRef]
- Kleman, M.; Laverntovich, O.D. Soft Matter Physics: An Introduction; Springer: New York, NY, USA, 2003. [Google Scholar]
- Williams, C. Défauts linéaires des mésophases smectiques A. J. Phys. Colloq. 1978, 39, C2-48–C2-57. [Google Scholar] [CrossRef][Green Version]
- Meyer, C.; Rabette, C.; Gisse, P.; Antonova, K.; Dozov, I. DH* in chiral smectics under electric field. Eur. Phys. J. E 2016, 39, 76. [Google Scholar] [CrossRef] [PubMed]
- Boltenhagen, P.; Kleman, M.; Lavrentovich, O.D. Focal Conics Domains in Smectics. In Soft Order in Physical Systems; Rabin, Y., Bruinsma, R., Eds.; Springer: Boston, MA, USA, 1994; pp. 5–32. [Google Scholar] [CrossRef]
- Boltenhagen, P. Quelques aspects des défauts dans les phases lamellaires gonflées. Ph.D. Thesis, Thèse de doctorat de Chimie dirigée par M. Kléman. Universite De Paris Sud Campus Scientifique D’orsay, Paris, Frence, 1993. [Google Scholar]
- Elston, S.J.; Sambles, J.R. (Eds.) The Optics of Thermotropic Liquid Crystals, 1st ed.; CRC Press: Boca Raton, FL, USA, 1998. [Google Scholar] [CrossRef]
- Meyer, C.; Le Cunff, L.; Belloul, M.; Foyart, G. Focal Conic Stacking in Smectic A Liquid Crystals: Smectic Flower and Apollonius Tiling. Materials 2009, 2, 499–513. [Google Scholar] [CrossRef]
- Beller, D.A.; Gharbi, M.A.; Honglawan, A.; Stebe, K.J.; Yang, S.; Kamien, R.D. Focal Conic Flower Textures at Curved Interfaces. Phys. Rev. X 2013, 3, 041026. [Google Scholar] [CrossRef]
- Yoon, D.K.; Choi, M.C.; Kim, Y.H.; Kim, M.W.; Lavrentovich, O.D.; Jung, H.T. Internal structure visualization and lithographic use of periodic toroidal holes in liquid crystals. Nat. Mater. 2007, 6, 866–870. [Google Scholar] [CrossRef] [PubMed]
- Designolle, V.; Herminghaus, S.; Pfohl, T.; Bahr, C. AFM Study of Defect-Induced Depressions of the Smectic-A/Air Interface. Langmuir 2006, 22, 363–368. [Google Scholar] [CrossRef]
- Guo, W.; Herminghaus, S.; Bahr, C. Controlling Smectic Focal Conic Domains by Substrate Patterning. Langmuir 2008, 24, 8174–8180. [Google Scholar] [CrossRef] [PubMed]
- Guo, W.; Bahr, C. Influence of anchoring strength on focal conic domains in smectic films. Phys. Rev. E 2009, 79, 011707. [Google Scholar] [CrossRef]
- Guo, W.; Bahr, C. Influence of phase sequence on focal conic domains in smectic films. Phys. Rev. E 2009, 79, 061701. [Google Scholar] [CrossRef] [PubMed]
- Honglawan, A.; Beller, D.A.; Cavallaro, M.; Kamien, R.D.; Stebe, K.J.; Yang, S. Topographically induced hierarchical assembly and geometrical transformation of focal conic domain arrays in smectic liquid crystals. Proc. Natl. Acad. Sci. USA 2013, 110, 34–39. [Google Scholar] [CrossRef]
- Honglawan, A.; Beller, D.A.; Cavallaro, M.; Kamien, R.D.; Stebe, K.J.; Yang, S. Pillar-Assisted Epitaxial Assembly of Toric Focal Conic Domains of Smectic-A Liquid Crystals. Adv. Mater. 2011, 23, 5519–5523. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.; Son, B.; Jung, H.; Lee, Y. Generation of optical vortex array from Toric Focal Conic Domains (TFCDs). In Proceedings of the 2012 17th Opto-Electronics and Communications Conference, Busan, Korea, 2–6 July 2012; pp. 97–98. [Google Scholar] [CrossRef]
- Friedel, G.; Grandjean, F. Observations Géométriques sur les Liquides à Coniques Focales; Persée: Lyon, France, 1910. [Google Scholar] [CrossRef]
- Lehmann, O. Cristaux liquides. Réponse à MM. G. Friedel et F. Grandjean; Persée: Lyon, France, 1910. [Google Scholar] [CrossRef]
- Kleman, M.; Lavrentovich, O.D. Liquids with conics. Liq. Cryst. 2009, 36, 1085–1099. [Google Scholar] [CrossRef]
- Meyer, C.; Jonckheere, B.; Penaud, C. The Construction of the Dupin Cyclides in a Smectic A Polygonal Texture. J. Mater. 2014, 2014, 145375. [Google Scholar] [CrossRef]
- Kléman, M.; Lavrentovich, O.D. Grain boundaries and the law of corresponding cones in smectics. Eur. Phys. J. E 2000, 2, 47–57. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Halaby Macary, M.; Damême, G.; Gibek, A.; Dubuffet, V.; Dupuy, B.; Picart, J.; Dimeni, R.F.; Meyer, C. Optical Microscopy Observations and Construction of Dupin Cyclides at the Isotropic/Smectic A Phase Transition. Materials 2021, 14, 4539. https://doi.org/10.3390/ma14164539
Halaby Macary M, Damême G, Gibek A, Dubuffet V, Dupuy B, Picart J, Dimeni RF, Meyer C. Optical Microscopy Observations and Construction of Dupin Cyclides at the Isotropic/Smectic A Phase Transition. Materials. 2021; 14(16):4539. https://doi.org/10.3390/ma14164539
Chicago/Turabian StyleHalaby Macary, Mikhael, Gauthier Damême, Antoine Gibek, Valentin Dubuffet, Benoît Dupuy, Justin Picart, Roll Freddy Dimeni, and Claire Meyer. 2021. "Optical Microscopy Observations and Construction of Dupin Cyclides at the Isotropic/Smectic A Phase Transition" Materials 14, no. 16: 4539. https://doi.org/10.3390/ma14164539
APA StyleHalaby Macary, M., Damême, G., Gibek, A., Dubuffet, V., Dupuy, B., Picart, J., Dimeni, R. F., & Meyer, C. (2021). Optical Microscopy Observations and Construction of Dupin Cyclides at the Isotropic/Smectic A Phase Transition. Materials, 14(16), 4539. https://doi.org/10.3390/ma14164539






