Size-Dependent Solute Segregation at Symmetric Tilt Grain Boundaries in α-Fe: A Quasiparticle Approach Study
Abstract
:1. Introduction
2. Quasiparticle Approach (QA)
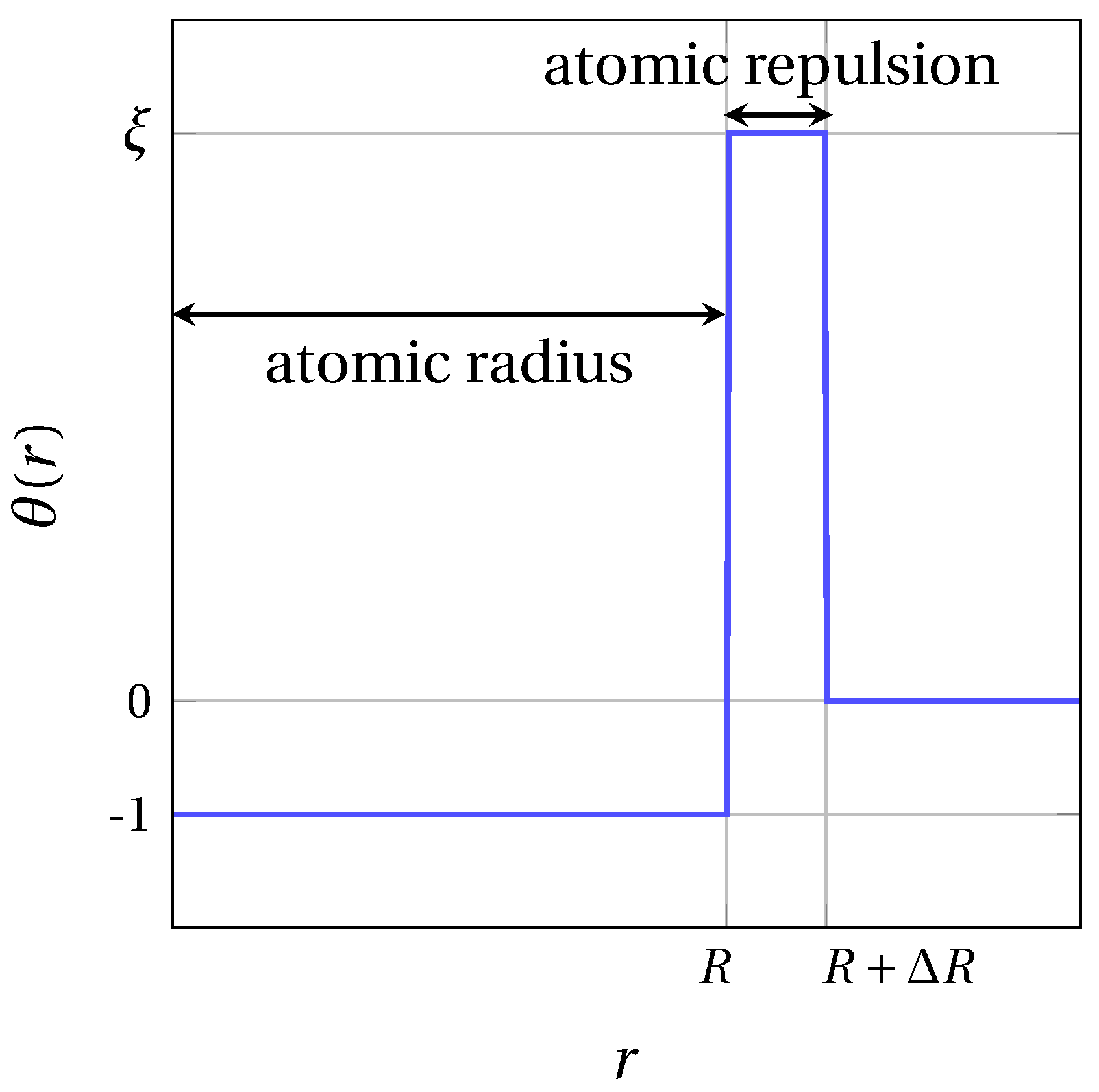
2.1. Basic Equation
2.2. Model Parameters
- Hydrostatic:
- Orthorhombic:
- Monoclinic:
3. Results
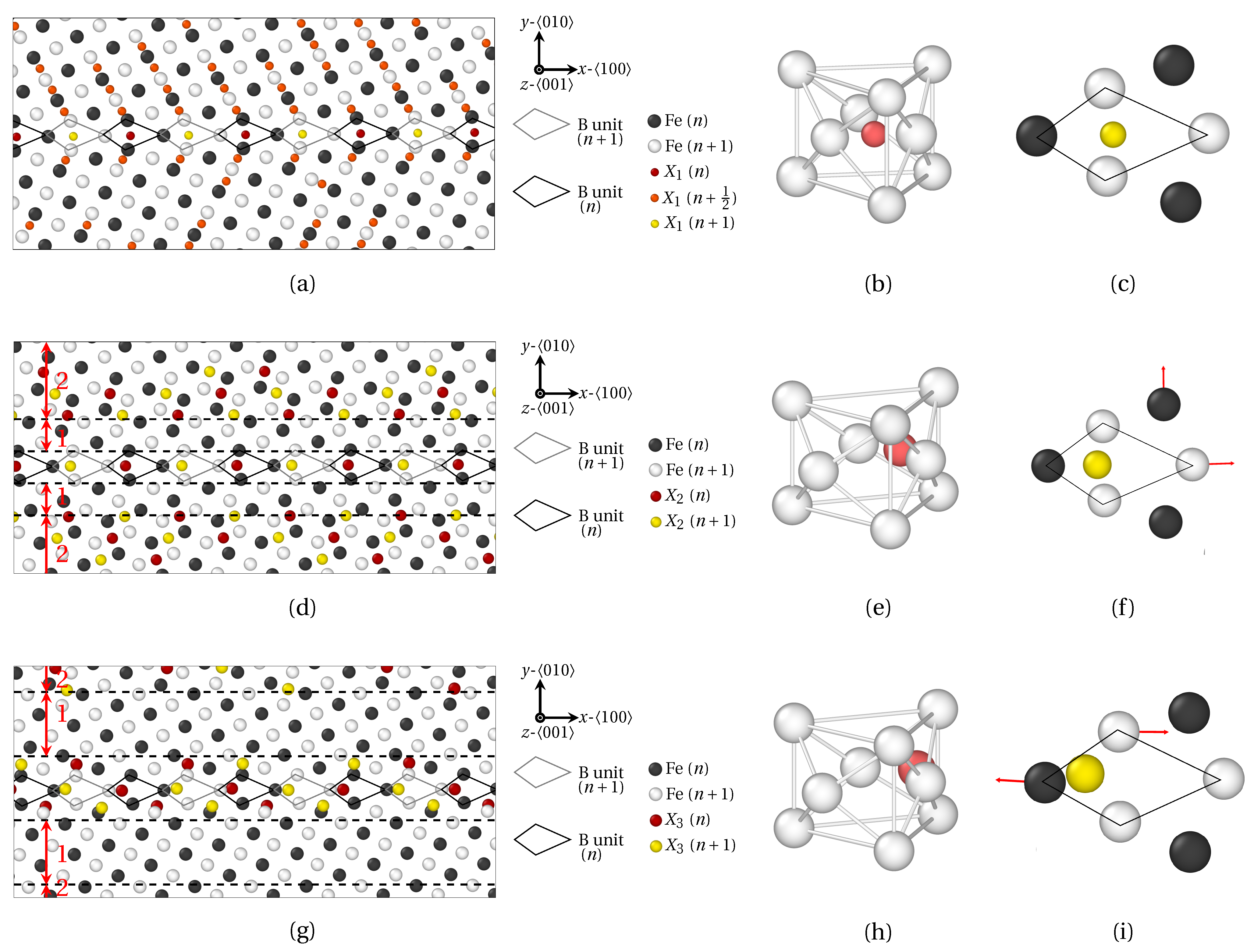
3.1. Segregation Pattern at GB
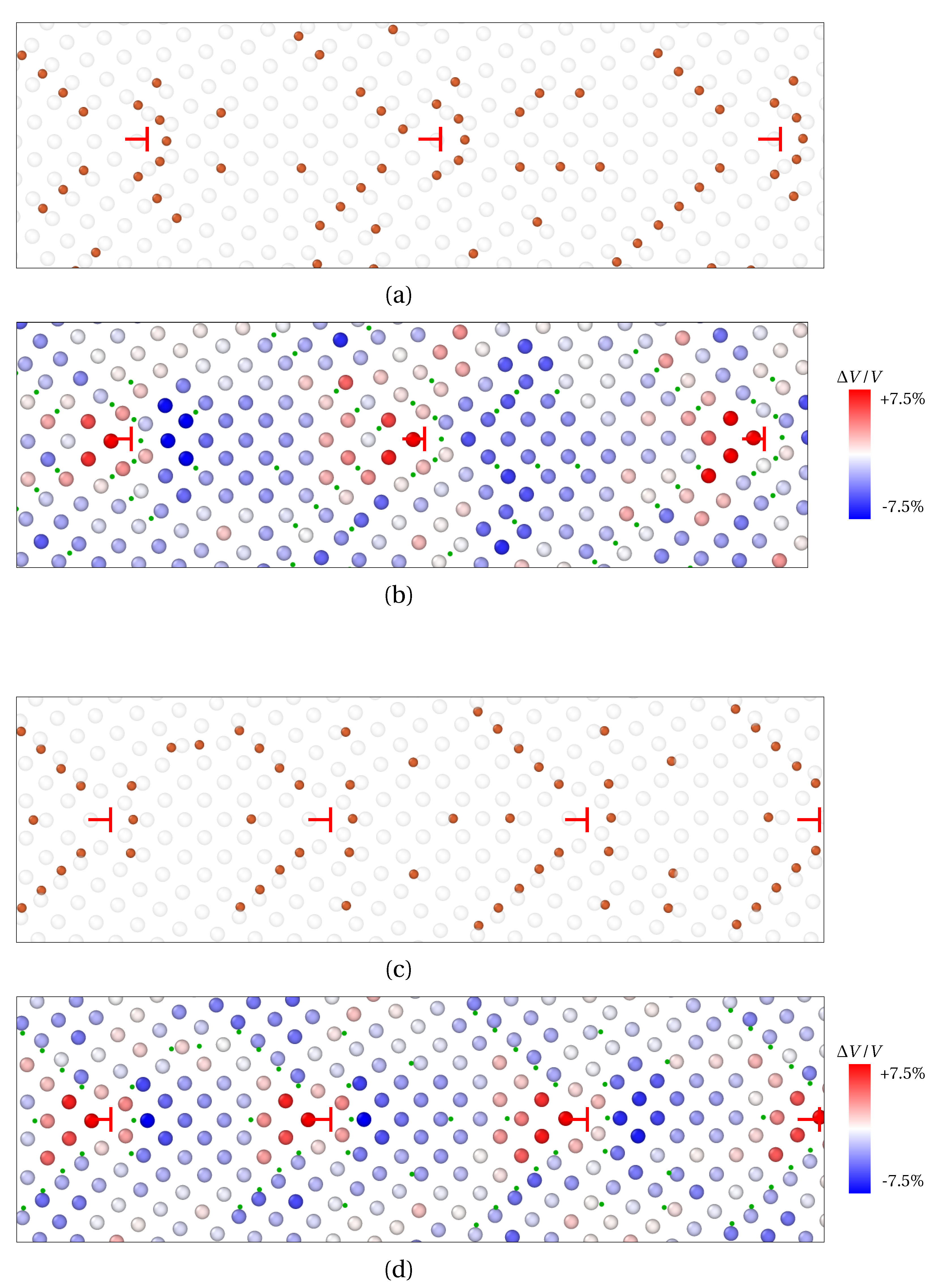
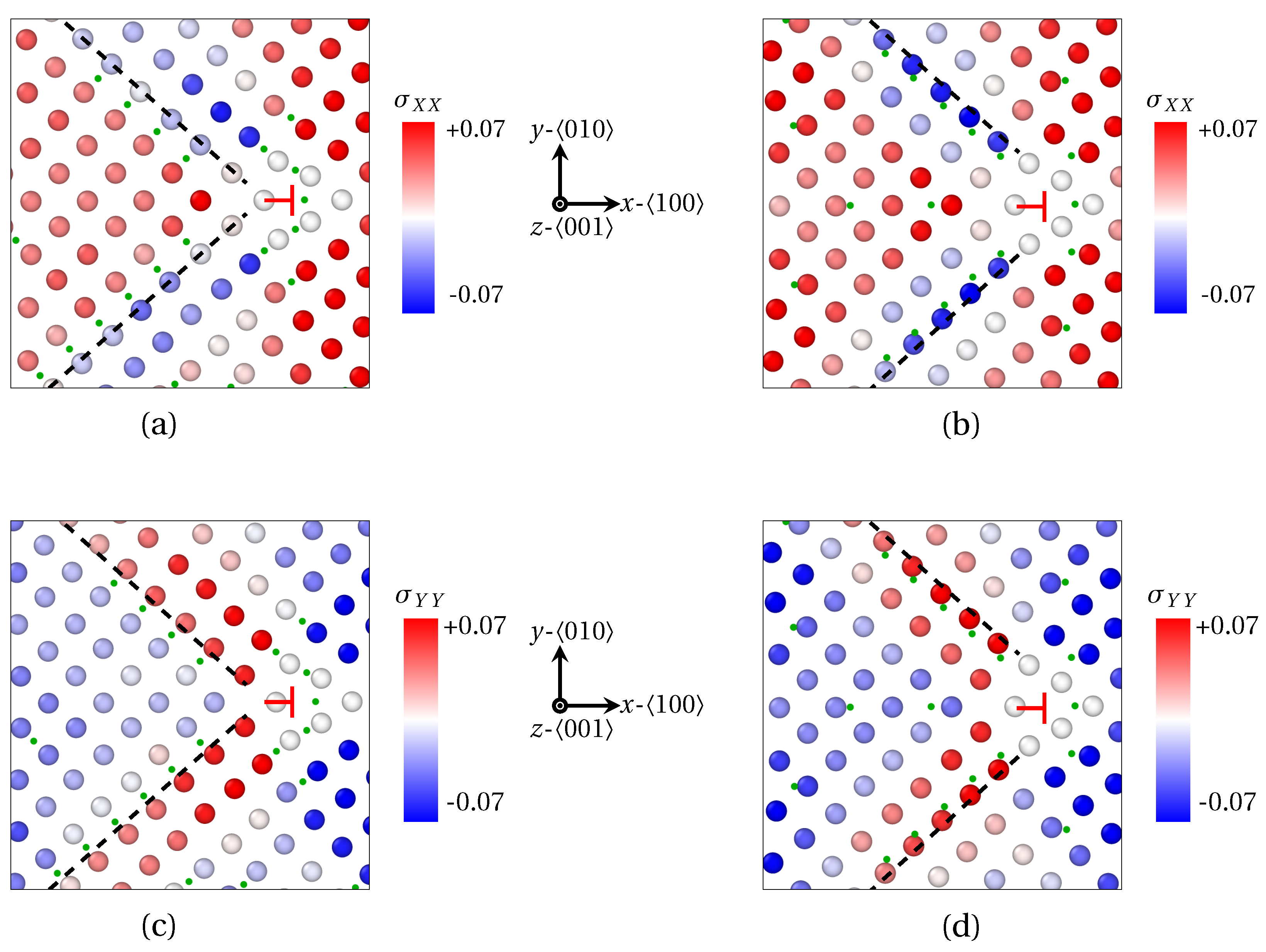
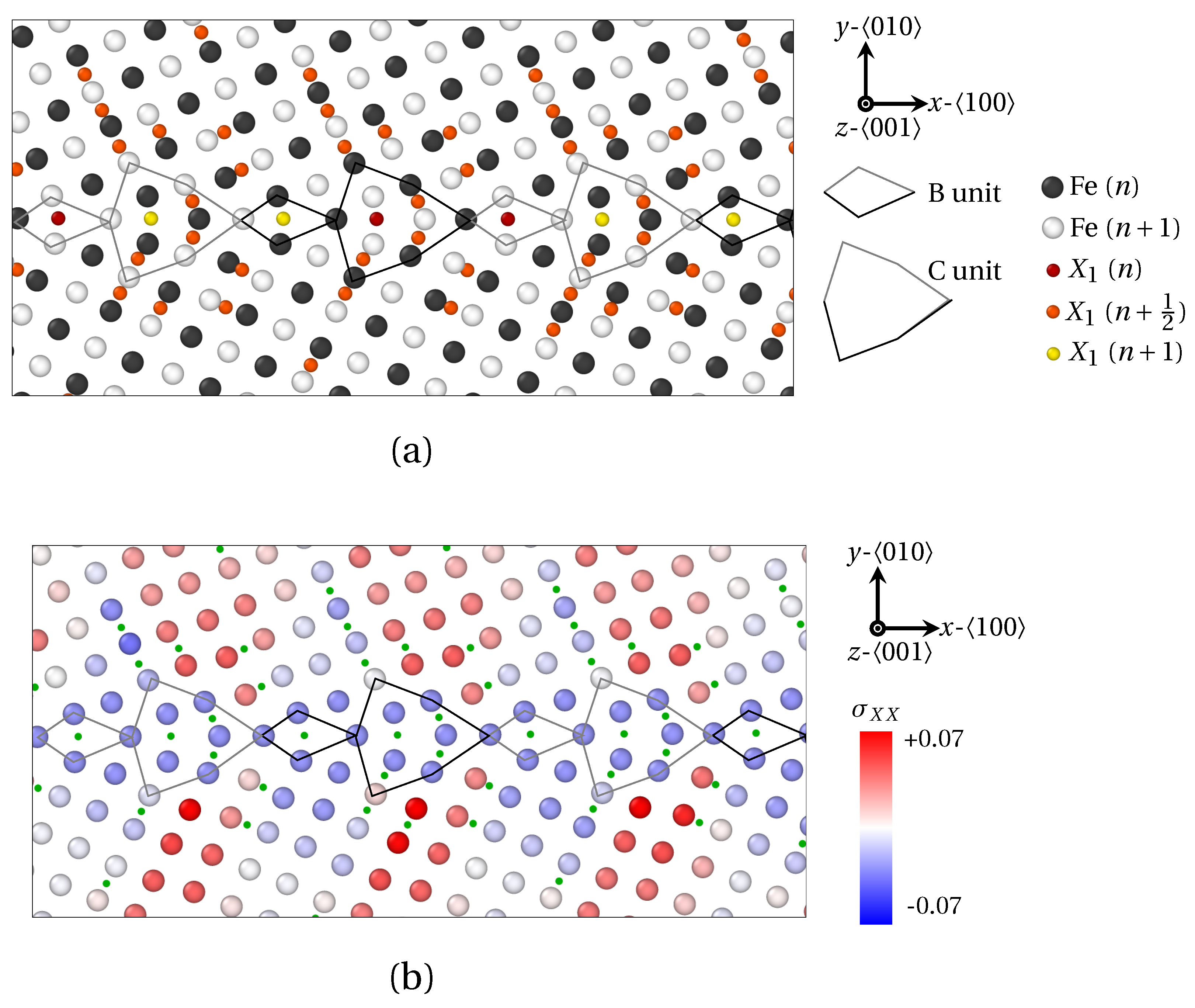
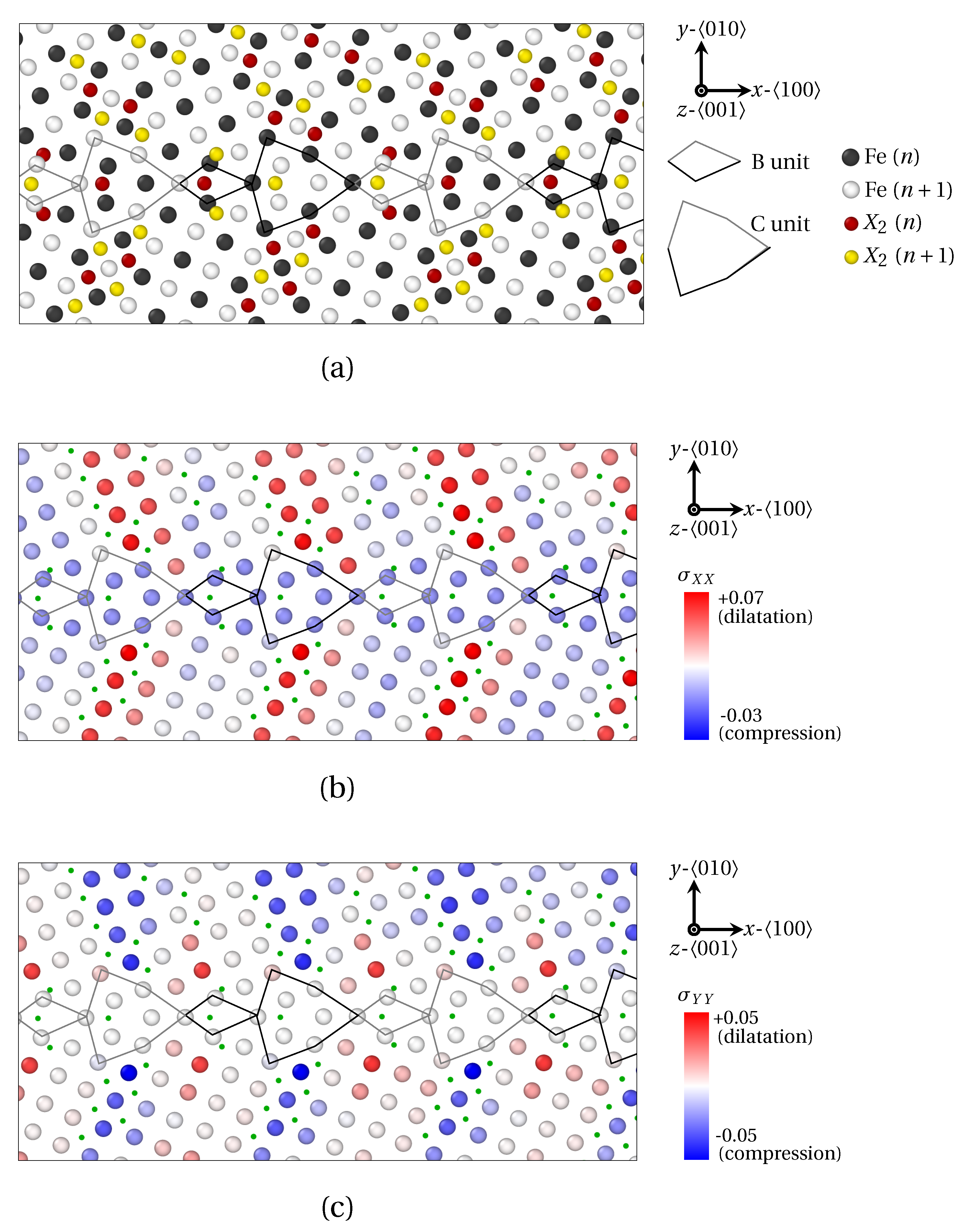
3.1.1. Low Angle GB
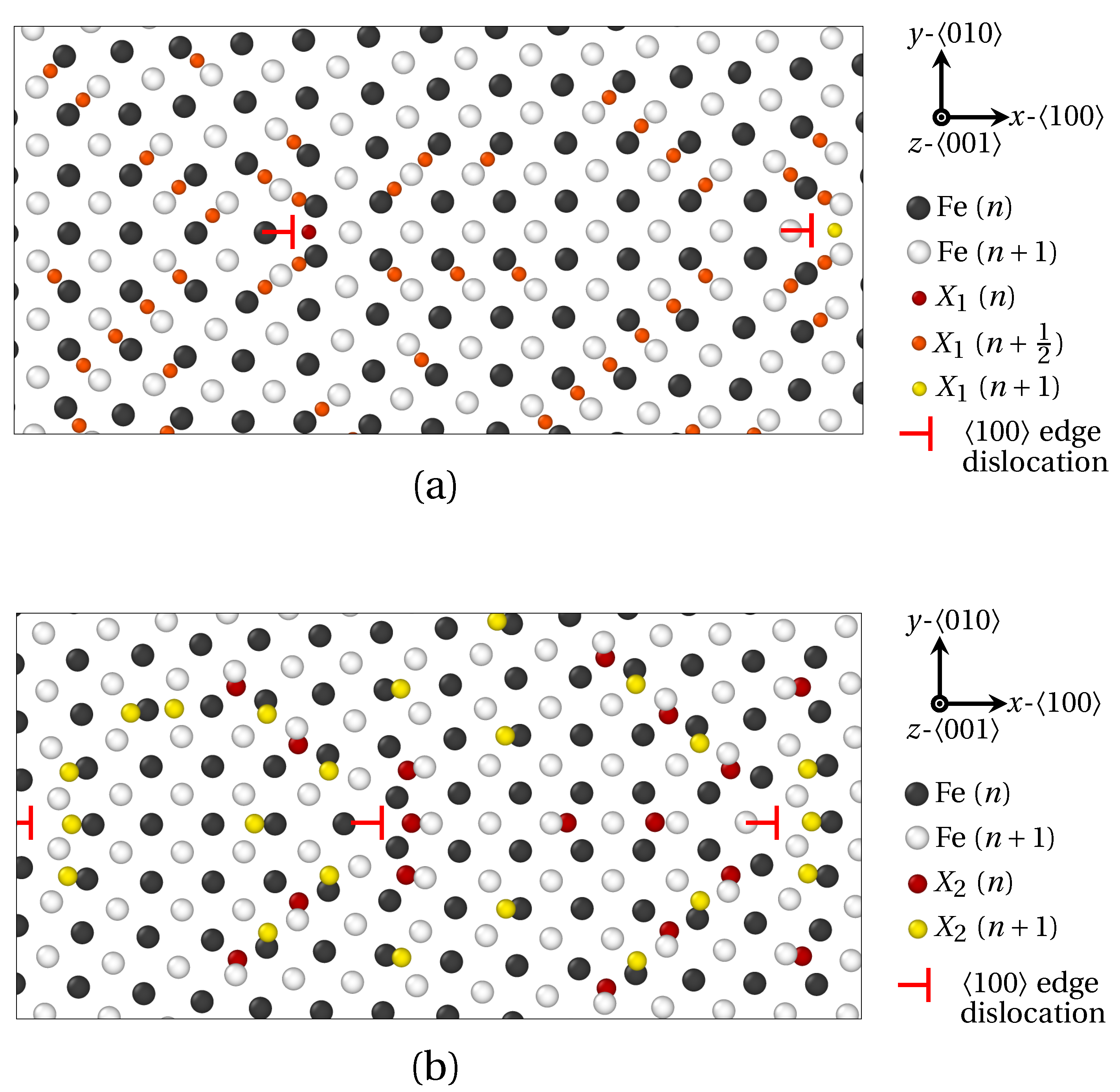
3.1.2. High Angle GB
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- McLean, D.; Maradudin, A. Grain boundaries in metals. Phys. Today 1958, 11, 35. [Google Scholar] [CrossRef]
- Balluffi, R.; Sutton, A. Why should we be interested in the atomic structure of interfaces? In Materials Science Forum; Trans Tech Publications Ltd.: Freienbach, Switzerland, 1996; Volume 207, pp. 1–12. [Google Scholar]
- Watanabe, T.; Tsurekawa, S. The control of brittleness and development of desirable mechanical properties in polycrystalline systems by grain boundary engineering. Acta Mater. 1999, 47, 4171–4185. [Google Scholar] [CrossRef]
- Lejček, P.; Hofmann, S.; Paidar, V. Solute segregation and classification of [100] tilt grain boundaries in α-iron: Consequences for grain boundary engineering. Acta Mater. 2003, 51, 3951–3963. [Google Scholar] [CrossRef]
- Randle, V. Twinning-related grain boundary engineering. Acta Mater. 2004, 52, 4067–4081. [Google Scholar] [CrossRef]
- Krakauer, B.; Seidman, D. Subnanometer scale study of segregation at grain boundaries in an Fe (Si) alloy. Acta Mater. 1998, 46, 6145–6161. [Google Scholar] [CrossRef]
- Raabe, D.; Herbig, M.; Sandlöbes, S.; Li, Y.; Tytko, D.; Kuzmina, M.; Ponge, D.; Choi, P.P. Grain boundary segregation engineering in metallic alloys: A pathway to the design of interfaces. Curr. Opin. Solid State Mater. Sci. 2014, 18, 253–261. [Google Scholar] [CrossRef]
- Xing, W.; Kalidindi, A.R.; Amram, D.; Schuh, C.A. Solute interaction effects on grain boundary segregation in ternary alloys. Acta Mater. 2018, 161, 285–294. [Google Scholar] [CrossRef]
- Divinski, S.V.; Edelhoff, H.; Prokofjev, S. Diffusion and segregation of silver in copper Σ 5 (310) grain boundary. Phys. Rev. B 2012, 85, 144104. [Google Scholar] [CrossRef]
- Herbig, M.; Raabe, D.; Li, Y.; Choi, P.; Zaefferer, S.; Goto, S. Atomic-scale quantification of grain boundary segregation in nanocrystalline material. Phys. Rev. Lett. 2014, 112, 126103. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yamaguchi, M. First-principles study on the grain boundary embrittlement of metals by solute segregation: Part I. iron (Fe)-solute (B, C, P, and S) systems. Metall. Mater. Trans. A 2011, 42, 319–329. [Google Scholar] [CrossRef]
- Scheiber, D.; Pippan, R.; Puschnig, P.; Romaner, L. Ab initio calculations of grain boundaries in bcc metals. Model. Simul. Mater. Sci. Eng. 2016, 24, 035013. [Google Scholar] [CrossRef]
- Yamaguchi, M.; Ebihara, K.I.; Itakura, M.; Kadoyoshi, T.; Suzudo, T.; Kaburaki, H. First-principles study on the grain boundary embrittlement of metals by solute segregation: Part II. Metal (Fe, Al, Cu)-hydrogen (H) systems. Metall. Mater. Trans. A 2011, 42, 330–339. [Google Scholar] [CrossRef]
- Tahir, A.; Janisch, R.; Hartmaier, A. Ab initio calculation of traction separation laws for a grain boundary in molybdenum with segregated C impurites. Model. Simul. Mater. Sci. Eng. 2013, 21, 075005. [Google Scholar] [CrossRef] [Green Version]
- Razumovskiy, V.I.; Ruban, A.V.; Razumovskii, I.; Lozovoi, A.; Butrim, V.; Vekilov, Y.K. The effect of alloying elements on grain boundary and bulk cohesion in aluminum alloys: An ab initio study. Scr. Mater. 2011, 65, 926–929. [Google Scholar] [CrossRef]
- Razumovskiy, V.I.; Lozovoi, A.; Razumovskii, I. First-principles-aided design of a new Ni-base superalloy: Influence of transition metal alloying elements on grain boundary and bulk cohesion. Acta Mater. 2015, 82, 369–377. [Google Scholar] [CrossRef]
- Yamaguchi, M.; Nishiyama, Y.; Kaburaki, H. Decohesion of iron grain boundaries by sulfur or phosphorous segregation: First-principles calculations. Phys. Rev. B 2007, 76, 035418. [Google Scholar] [CrossRef]
- Wang, J.; Janisch, R.; Madsen, G.K.; Drautz, R. First-principles study of carbon segregation in bcc iron symmetrical tilt grain boundaries. Acta Mater. 2016, 115, 259–268. [Google Scholar] [CrossRef]
- Hu, Y.J.; Wang, Y.; Wang, W.Y.; Darling, K.A.; Kecskes, L.J.; Liu, Z.K. Solute effects on the Σ3 111 [11-0] tilt grain boundary in BCC Fe: Grain boundary segregation, stability, and embrittlement. Comput. Mater. Sci. 2020, 171, 109271. [Google Scholar] [CrossRef]
- Daw, M.S.; Baskes, M.I. Semiempirical, quantum mechanical calculation of hydrogen embrittlement in metals. Phys. Rev. Lett. 1983, 50, 1285. [Google Scholar] [CrossRef]
- Barrera, O.; Bombac, D.; Chen, Y.; Daff, T.; Galindo-Nava, E.; Gong, P.; Haley, D.; Horton, R.; Katzarov, I.; Kermode, J.; et al. Understanding and mitigating hydrogen embrittlement of steels: A review of experimental, modeling and design progress from atomistic to continuum. J. Mater. Sci. 2018, 53, 6251–6290. [Google Scholar] [CrossRef] [Green Version]
- Rhodes, N.; Tschopp, M.; Solanki, K. Quantifying the energetics and length scales of carbon segregation to α-Fe symmetric tilt grain boundaries using atomistic simulations. Model. Simul. Mater. Sci. Eng. 2013, 21, 035009. [Google Scholar] [CrossRef] [Green Version]
- Wagih, M.; Larsen, P.M.; Schuh, C.A. Learning grain boundary segregation energy spectra in polycrystals. Nat. Commun. 2020, 11, 1–9. [Google Scholar] [CrossRef]
- Elder, K.; Katakowski, M.; Haataja, M.; Grant, M. Modeling elasticity in crystal growth. Phys. Rev. Lett. 2002, 88, 245701. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Elder, K.; Grant, M. Modeling elastic and plastic deformations in nonequilibrium processing using phase field crystals. Phys. Rev. E 2004, 70, 051605. [Google Scholar] [CrossRef] [Green Version]
- Elder, K.R.; Provatas, N.; Berry, J.; Stefanovic, P.; Grant, M. Phase-field crystal modeling and classical density functional theory of freezing. Phys. Rev. B 2007, 75, 064107. [Google Scholar] [CrossRef] [Green Version]
- Greenwood, M.; Ofori-Opoku, N.; Rottler, J.; Provatas, N. Modeling structural transformations in binary alloys with phase field crystals. Phys. Rev. B 2011, 84, 064104. [Google Scholar] [CrossRef] [Green Version]
- Smith, N.; Provatas, N. Generalization of the binary structural phase field crystal model. Phys. Rev. Mater. 2017, 1, 053407. [Google Scholar] [CrossRef]
- Mellenthin, J.; Karma, A.; Plapp, M. Phase-field crystal study of grain-boundary premelting. Phys. Rev. B 2008, 78, 184110. [Google Scholar] [CrossRef] [Green Version]
- Khachaturian, A. Ordering in substitutional and interstitial solid solutions. Prog. Mater. Sci. 1978, 22, 1–150. [Google Scholar] [CrossRef]
- Jin, Y.M.; Khachaturyan, A.G. Atomic density function theory and modeling of microstructure evolution at the atomic scale. J. Appl. Phys. 2006, 100, 013519. [Google Scholar] [CrossRef]
- Kapikranian, O.; Zapolsky, H.; Domain, C.; Patte, R.; Pareige, C.; Radiguet, B.; Pareige, P. Atomic structure of grain boundaries in iron modeled using the atomic density function. Phys. Rev. B 2014, 89, 014111. [Google Scholar] [CrossRef] [Green Version]
- Kapikranian, O.; Zapolsky, H.; Patte, R.; Pareige, C.; Radiguet, B.; Pareige, P. Point defect absorption by grain boundaries in α-iron by atomic density function modeling. Phys. Rev. B 2015, 92, 224106. [Google Scholar] [CrossRef] [Green Version]
- Vaugeois, A. Modélisation de L’influence de la Structure des Joints de Grains sur les Phénomènes de Ségrégation. Ph.D. Thesis, Normandie Université, Caen, France, 2017. [Google Scholar]
- Lavrskyi, M.; Zapolsky, H.; Khachaturyan, A.G. Quasiparticle approach to diffusional atomic scale self-assembly of complex structures: From disorder to complex crystals and double-helix polymers. NPJ Comput. Mater. 2016, 2, 1–9. [Google Scholar] [CrossRef]
- Demange, G.; Lavrskyi, M.; Chen, K.; Chen, X.; Wang, Z.; Patte, R.; Zapolsky, H. Fcc-> bcc phase transition kinetics in an immiscible binary system: Atomistic evidence of the twinning mechanism of transformation. arXiv 2021, arXiv:2103.12384. [Google Scholar]
- Bollmann, W. Crystal Defects and Crystalline Interfaces; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Sutton, A.; Balluffi, R. Interfaces in Crystalline Solids, Clarendon; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Read, W.T.; Shockley, W. Dislocation models of crystal grain boundaries. Phys. Rev. 1950, 78, 275. [Google Scholar] [CrossRef]
- Jaatinen, A.; Achim, C.; Elder, K.; Ala-Nissila, T. Thermodynamics of bcc metals in phase-field-crystal models. Phys. Rev. E 2009, 80, 031602. [Google Scholar] [CrossRef] [Green Version]
- Demange, G.; Chamaillard, M.; Zapolsky, H.; Lavrskyi, M.; Vaugeois, A.; Luneville, L.; Simeone, D.; Patte, R. Generalization of the fourier-spectral eyre scheme for the phase-field equations: Application to self-assembly dynamics in materials. Comput. Mater. Sci. 2018, 144, 11–22. [Google Scholar] [CrossRef]
- Müller, M.; Erhart, P.; Albe, K. Analytic bond-order potential for bcc and fcc iron—Comparison with established embedded-atom method potentials. J. Phys. Condens. Matter 2007, 19, 326220. [Google Scholar] [CrossRef]
- Simonelli, G.; Pasianot, R.; Savino, E. Embedded-atom-method interatomic potentials for bcc-iron. MRS Online Proc. Libr. Arch. 1992, 291. [Google Scholar] [CrossRef]
- Ackland, G.; Bacon, D.; Calder, A.; Harry, T. Computer simulation of point defect properties in dilute Fe-Cu alloy using a many-body interatomic potential. Philos. Mag. A 1997, 75, 713–732. [Google Scholar] [CrossRef]
- Mendelev, M.; Han, S.; Srolovitz, D.; Ackland, G.; Sun, D.; Asta, M. Development of new interatomic potentials appropriate for crystalline and liquid iron. Philos. Mag. 2003, 83, 3977–3994. [Google Scholar] [CrossRef]
- Dudarev, S.; Derlet, P. A ‘magnetic’interatomic potential for molecular dynamics simulations. J. Phys. Condens. Matter 2005, 17, 7097. [Google Scholar] [CrossRef]
- Hashimoto, M.; Ishida, Y.; Yamamoto, R.; Doyama, M. Atomistic studies of grain boundary segregation in Fe-P and Fe-B alloys—I. Atomic structure and stress distribution. Acta Metall. 1984, 32, 1–11. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2009, 18, 015012. [Google Scholar] [CrossRef]
- Cottrell, A.H.; Bilby, B.A. Dislocation theory of yielding and strain ageing of iron. Proc. Phys. Soc. Sect. A 1949, 62, 49. [Google Scholar] [CrossRef]
- Wilde, J.; Cerezo, A.; Smith, G. Three-dimensional atomic-scale mapping of a Cottrell atmosphere around a dislocation in iron. Scr. Mater. 2000, 43, 39–48. [Google Scholar] [CrossRef]
- Portavoce, A.; Tréglia, G. Theoretical investigation of Cottrell atmosphere in silicon. Acta Mater. 2014, 65, 1–9. [Google Scholar] [CrossRef]
- Nguyen-Manh, D.; Horsfield, A.; Dudarev, S. Self-interstitial atom defects in bcc transition metals: Group-specific trends. Phys. Rev. B 2006, 73, 020101. [Google Scholar] [CrossRef]
- Bishop, G.H.; Chalmers, B. A coincidence—Ledge—Dislocation description of grain boundaries. Scr. Metall. 1968, 2, 133–139. [Google Scholar] [CrossRef]
- Sutton, A.P.; Vitek, V. On the structure of tilt grain boundaries in cubic metals I. Symmetrical tilt boundaries. Philos. Trans. R. Soc. Lond. Ser. Math. Phys. Sci. 1983, 309, 1–36. [Google Scholar]
- Tschopp, M.A.; Solanki, K.; Gao, F.; Sun, X.; Khaleel, M.A.; Horstemeyer, M. Probing grain boundary sink strength at the nanoscale: Energetics and length scales of vacancy and interstitial absorption by grain boundaries in α-Fe. Phys. Rev. B 2012, 85, 064108. [Google Scholar] [CrossRef] [Green Version]



| Fe | 16 | 6.15 | 5.0 | 0.5 | 0.555 | 0.242 | 0.348 | 0.5 | 0.1 | 0.1 | 0.0275 | 0.104 | 1.0 | 0.5 | |
| X1 | - | 4.2 | 3.0 | 0.5 | - | - | - | 0.5 | 0.1 | 0.1 | 0.0275 | 1.0 | 0.5 | ||
| X2 | - | 5.7 | 3.0 | 0.5 | - | - | - | 0.5 | 0.1 | 0.1 | 0.0275 | 1.0 | 0.5 | ||
| X3 | - | 6.64 | 3.0 | 0.5 | - | - | - | 0.5 | 0.1 | 0.1 | 0.0275 | 1.0 | 0.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zapolsky, H.; Vaugeois, A.; Patte, R.; Demange, G. Size-Dependent Solute Segregation at Symmetric Tilt Grain Boundaries in α-Fe: A Quasiparticle Approach Study. Materials 2021, 14, 4197. https://doi.org/10.3390/ma14154197
Zapolsky H, Vaugeois A, Patte R, Demange G. Size-Dependent Solute Segregation at Symmetric Tilt Grain Boundaries in α-Fe: A Quasiparticle Approach Study. Materials. 2021; 14(15):4197. https://doi.org/10.3390/ma14154197
Chicago/Turabian StyleZapolsky, Helena, Antoine Vaugeois, Renaud Patte, and Gilles Demange. 2021. "Size-Dependent Solute Segregation at Symmetric Tilt Grain Boundaries in α-Fe: A Quasiparticle Approach Study" Materials 14, no. 15: 4197. https://doi.org/10.3390/ma14154197
APA StyleZapolsky, H., Vaugeois, A., Patte, R., & Demange, G. (2021). Size-Dependent Solute Segregation at Symmetric Tilt Grain Boundaries in α-Fe: A Quasiparticle Approach Study. Materials, 14(15), 4197. https://doi.org/10.3390/ma14154197






