Flow Field Analysis Inside and at the Outlet of the Abrasive Head
Abstract
:1. Introduction
1.1. Background of AWJ Calculations
1.2. Background of Abrasive Particle Velocity Measurement
1.3. Background Summary
2. Methods
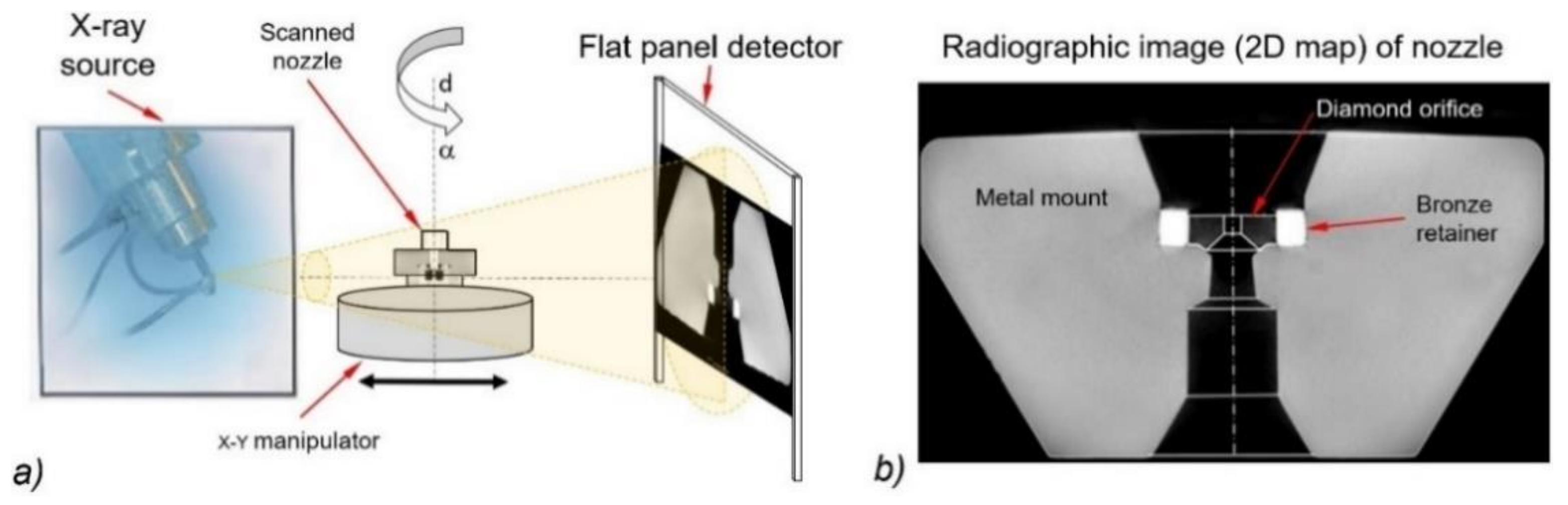
2.1. Water Nozzle Geometrical Reconstruction Based on X-ray CT
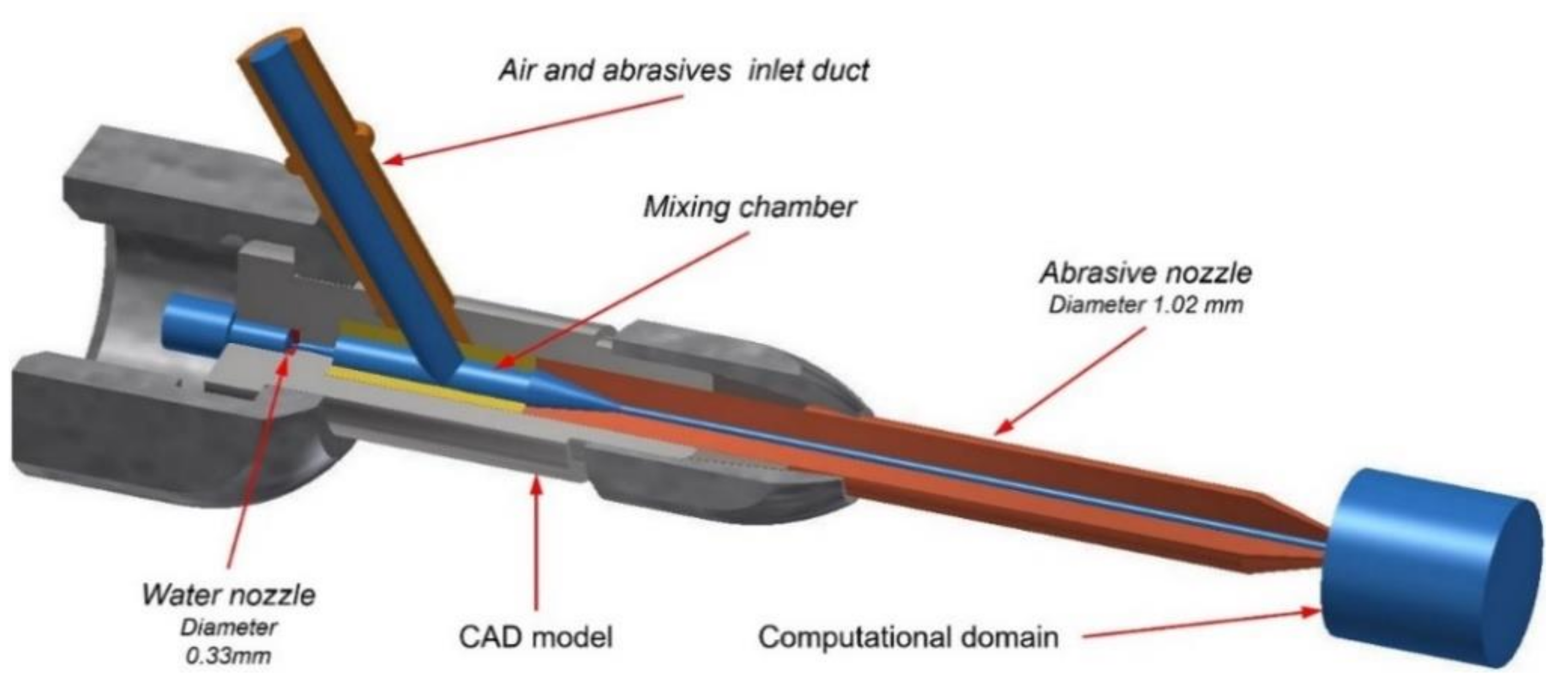
2.2. CFD Geometry of Computational Mesh, Model Settings, and Calculations
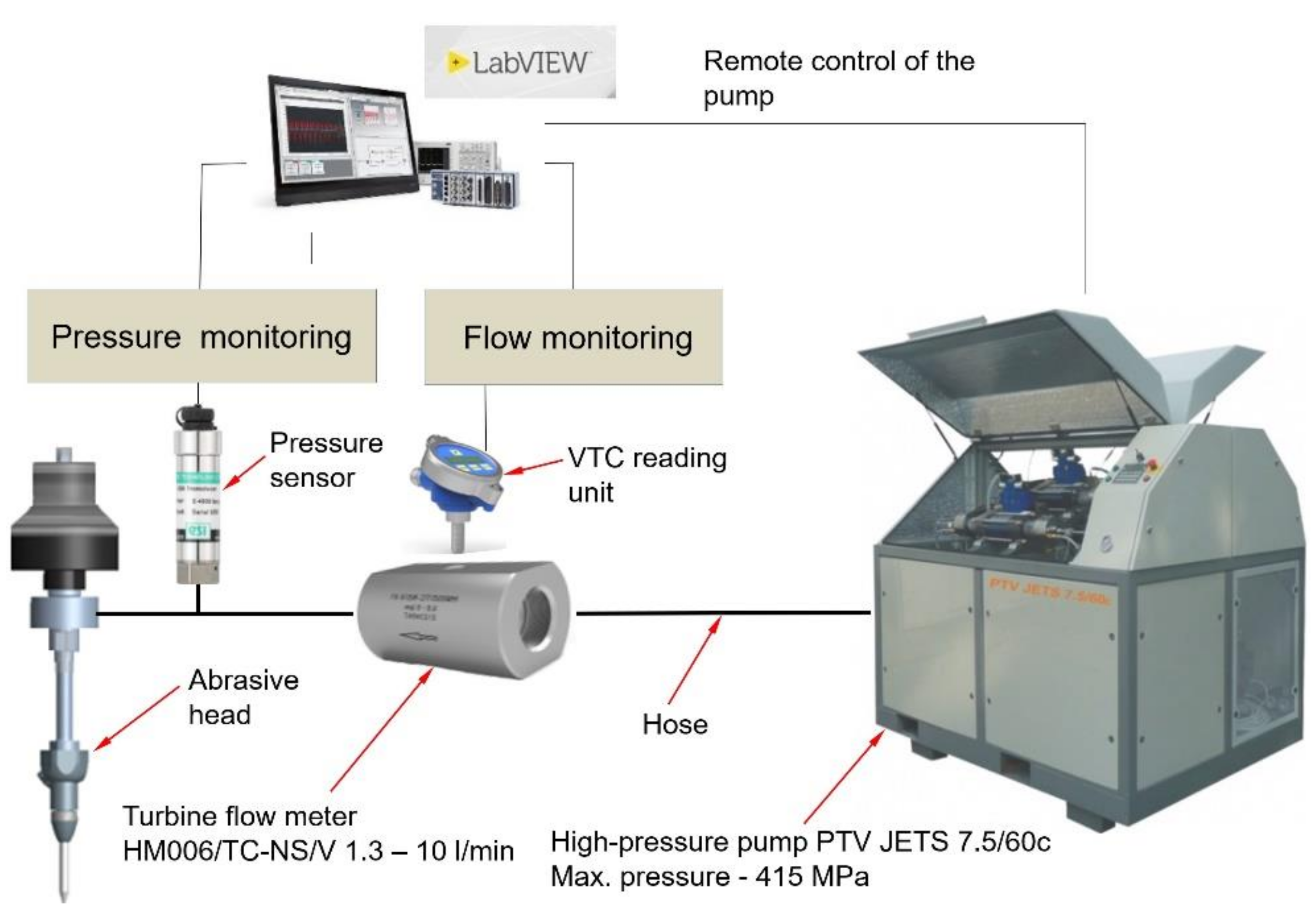
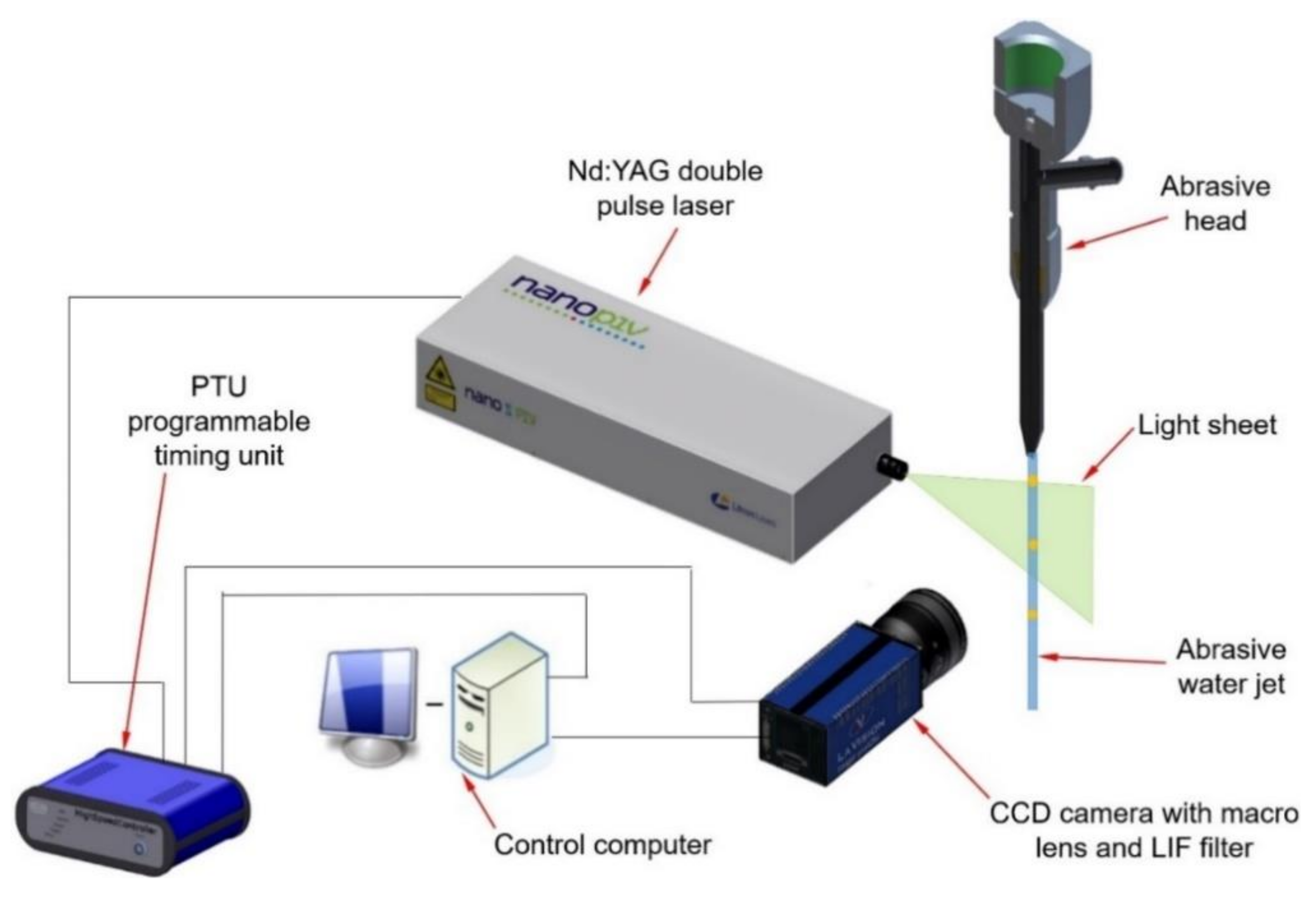
2.3. High-Pressure Water Flow Monitoring in the Abrasive Head
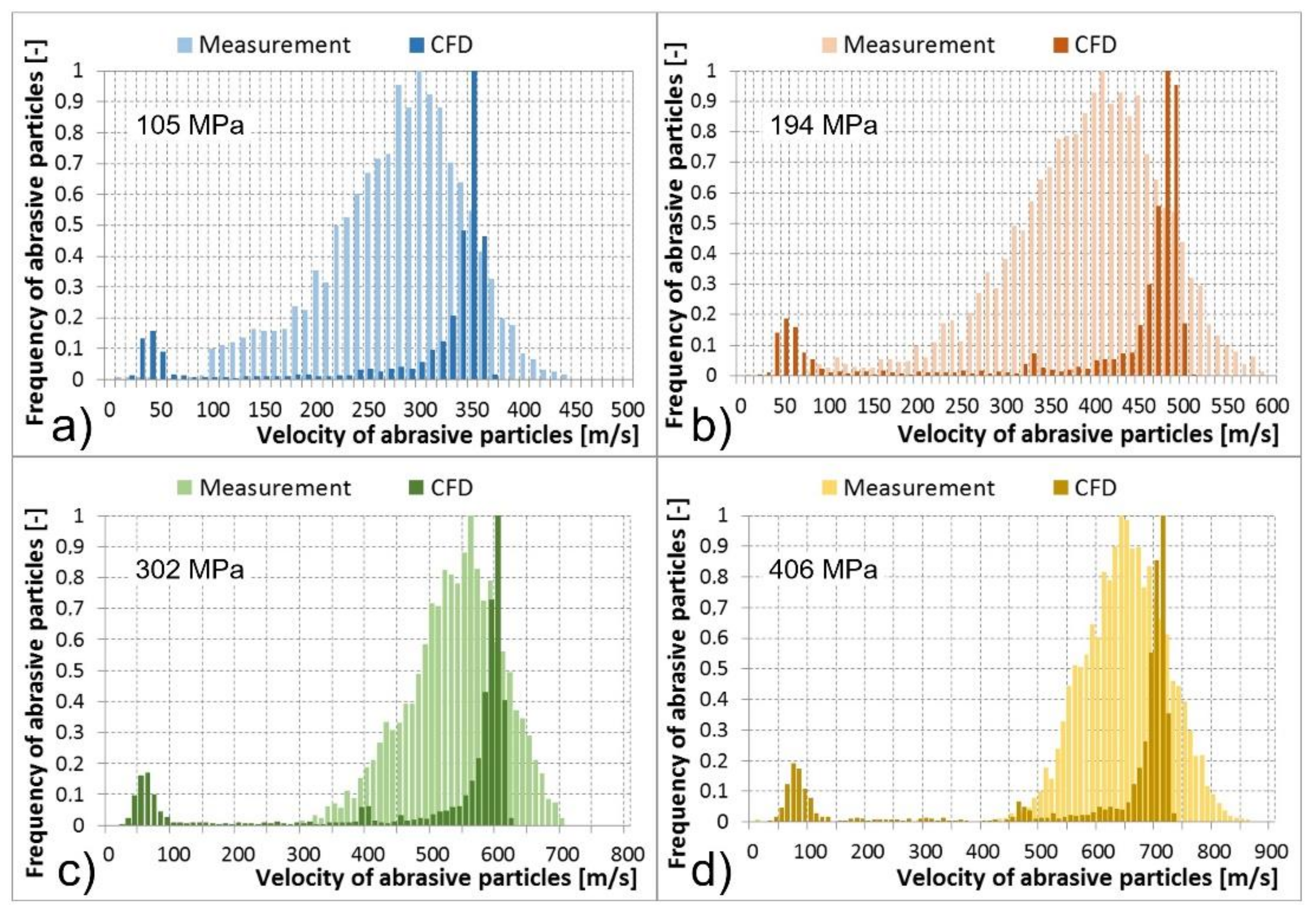
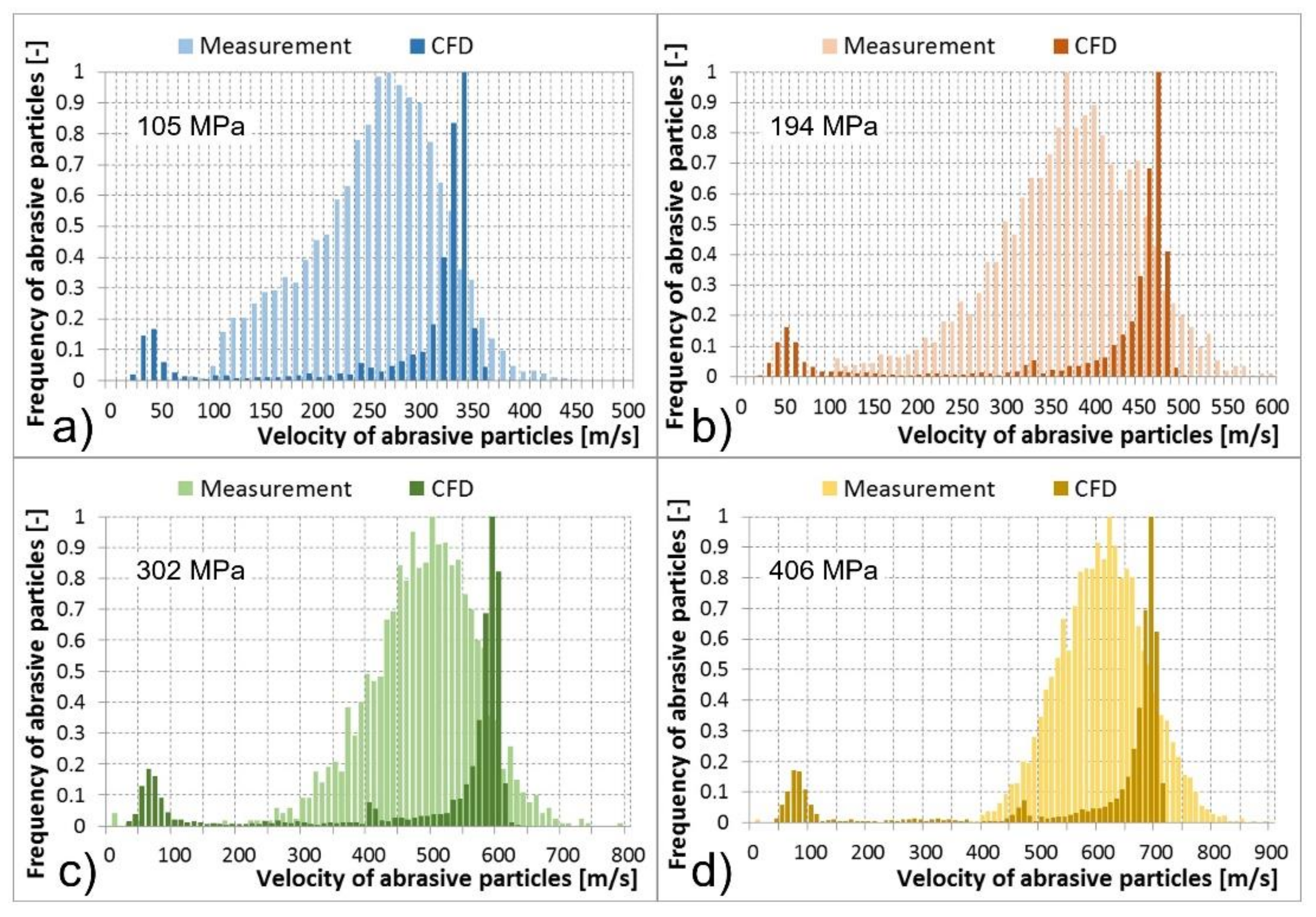
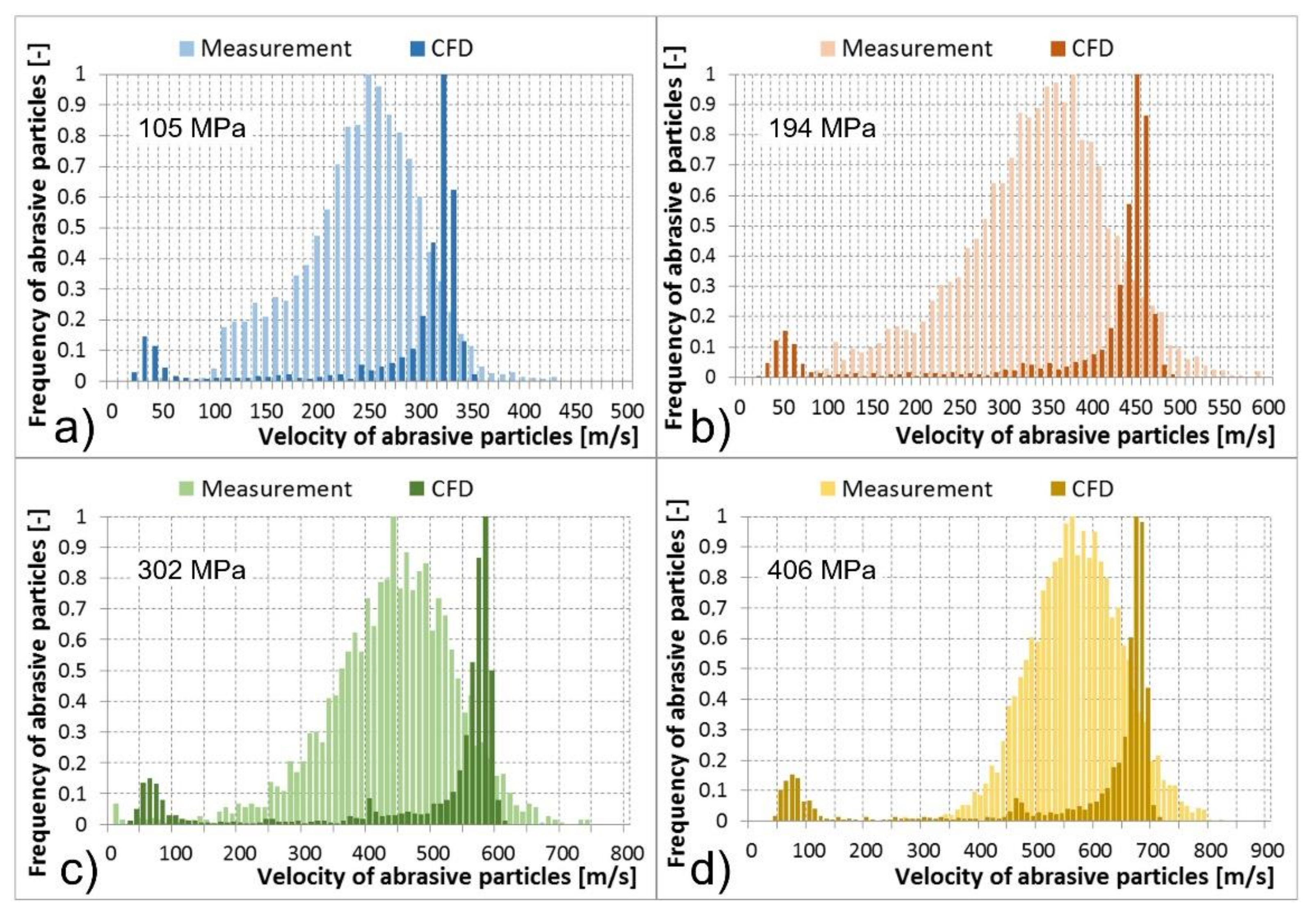
2.4. Measurement of Abrasive Particle Velocities at the Outlet of the Abrasive Head
3. Results and Discussions
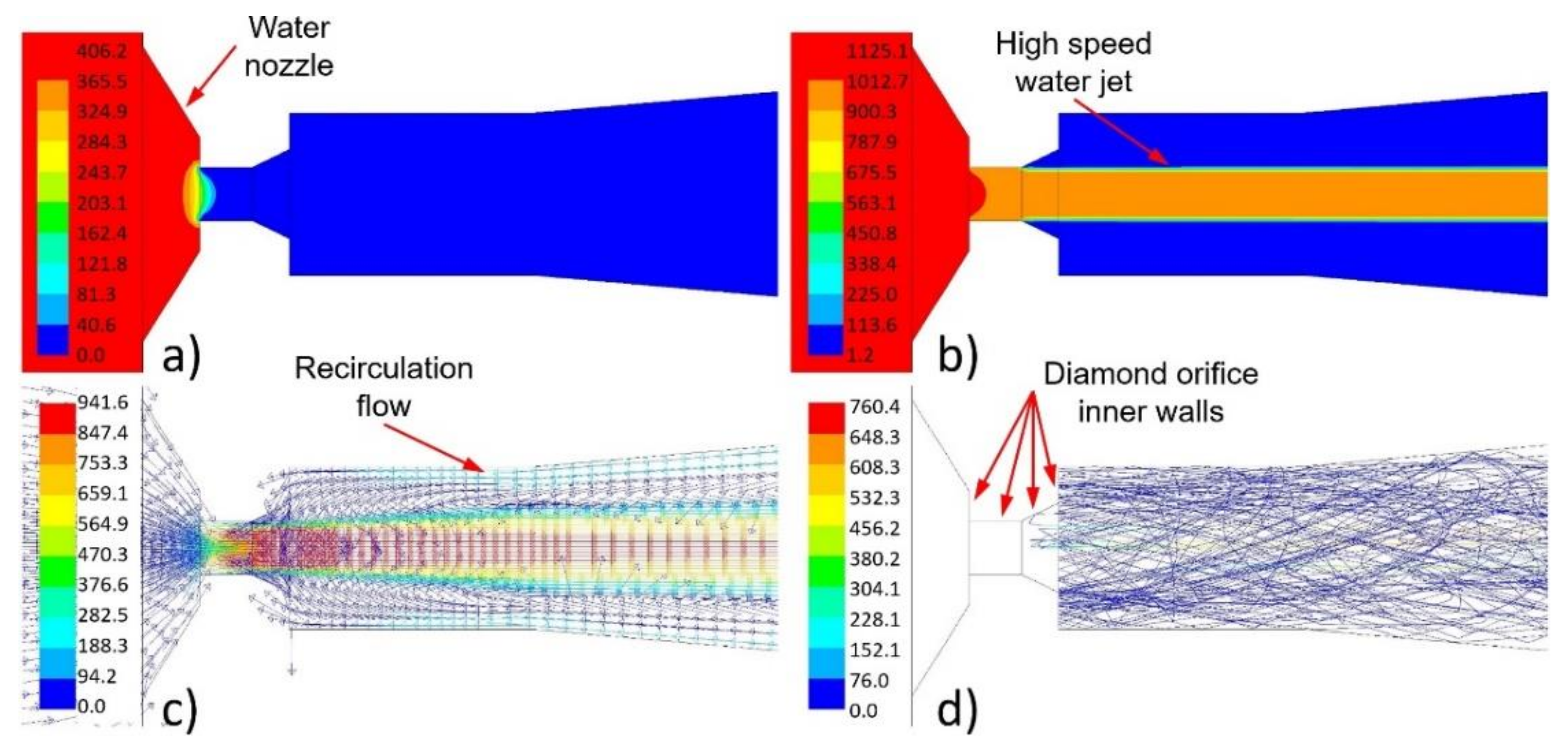
3.1. Water Nozzle Space
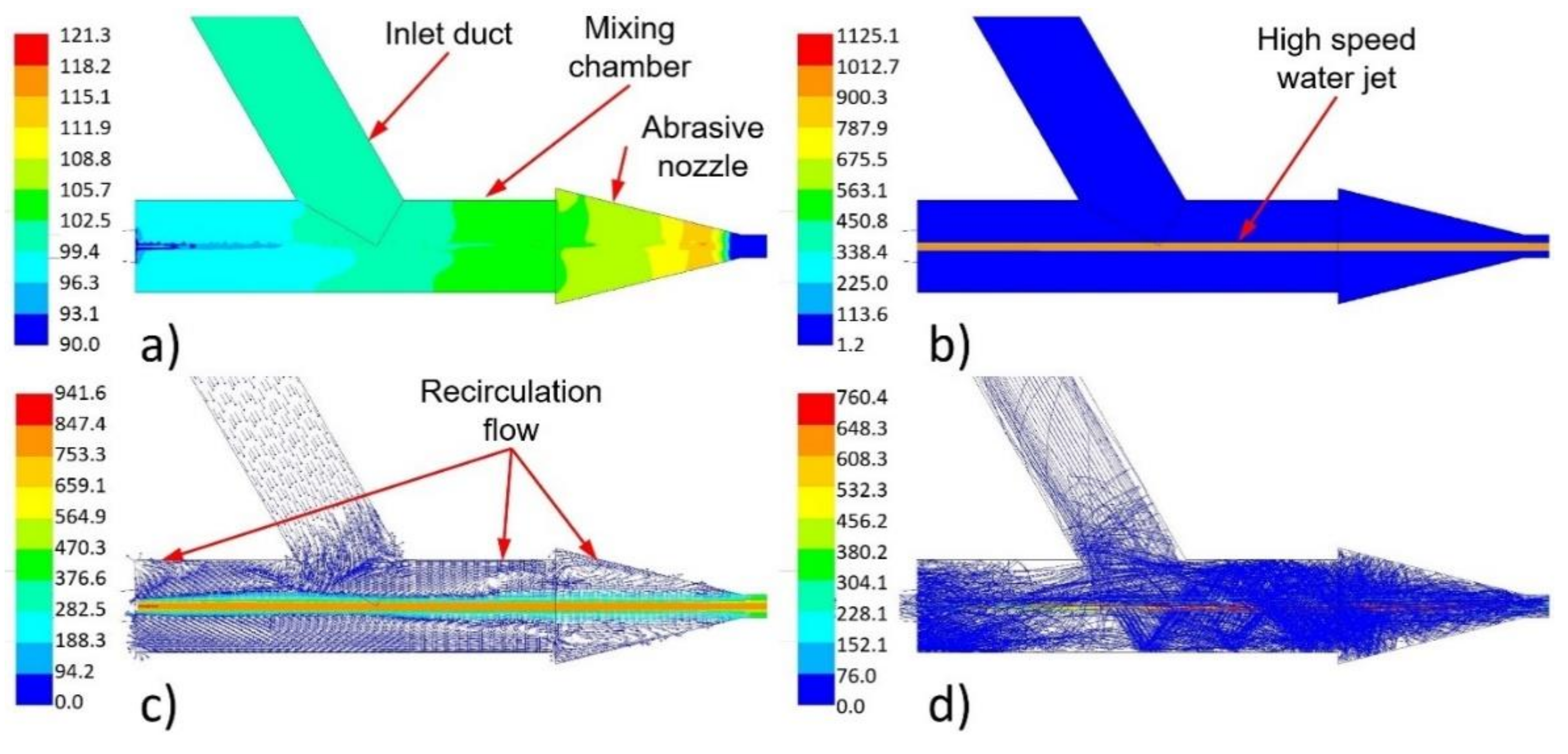
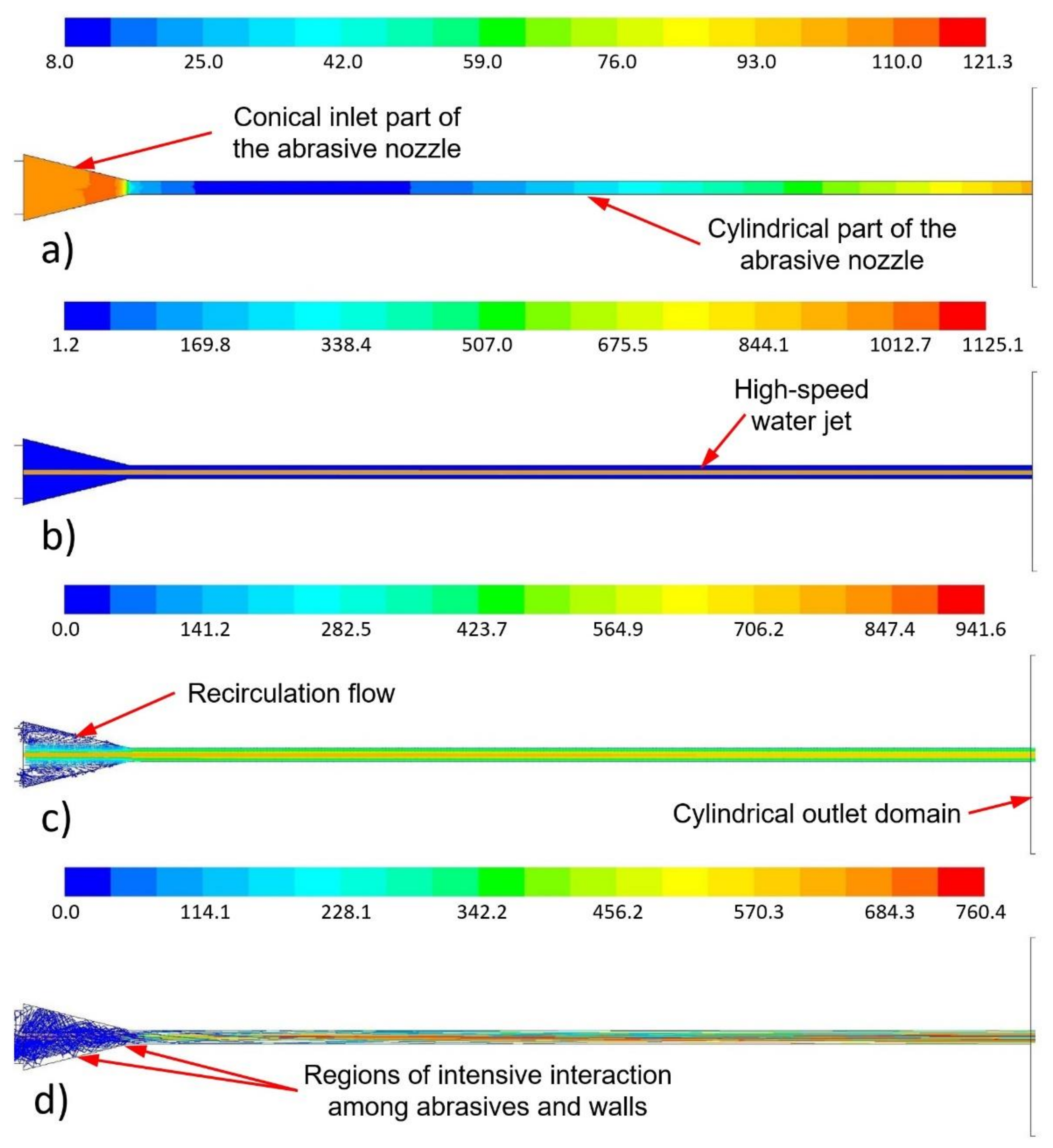
3.2. Mixing Chamber and Abrasive Nozzle Space
3.3. Outlet Space of Abrasive Head
4. Conclusions
- In the water nozzle, the calculated values of the volume flow rates were in very good conformity with the measured values under the determined feeding water pressures due to the exact geometry of the abrasive head that was included in the numerical model without simplifications. The exact geometry of the studied domain is thus a crucial part for creating and developing a numerical model which generates reasonable data;
- In the abrasive nozzle, a very good conformity of the pressure distribution in measurements and in calculations was observed. The shapes of dependences were similar with those published in other studies [38]. In the cylindrical part of the abrasive nozzle, the pressure decreased at first, then hit the minimum and, finally, grew up to the value of the atmospheric pressure. For both measurements and calculations, the increase in the high-speed water jet velocity caused a decrease in the minimum pressure;
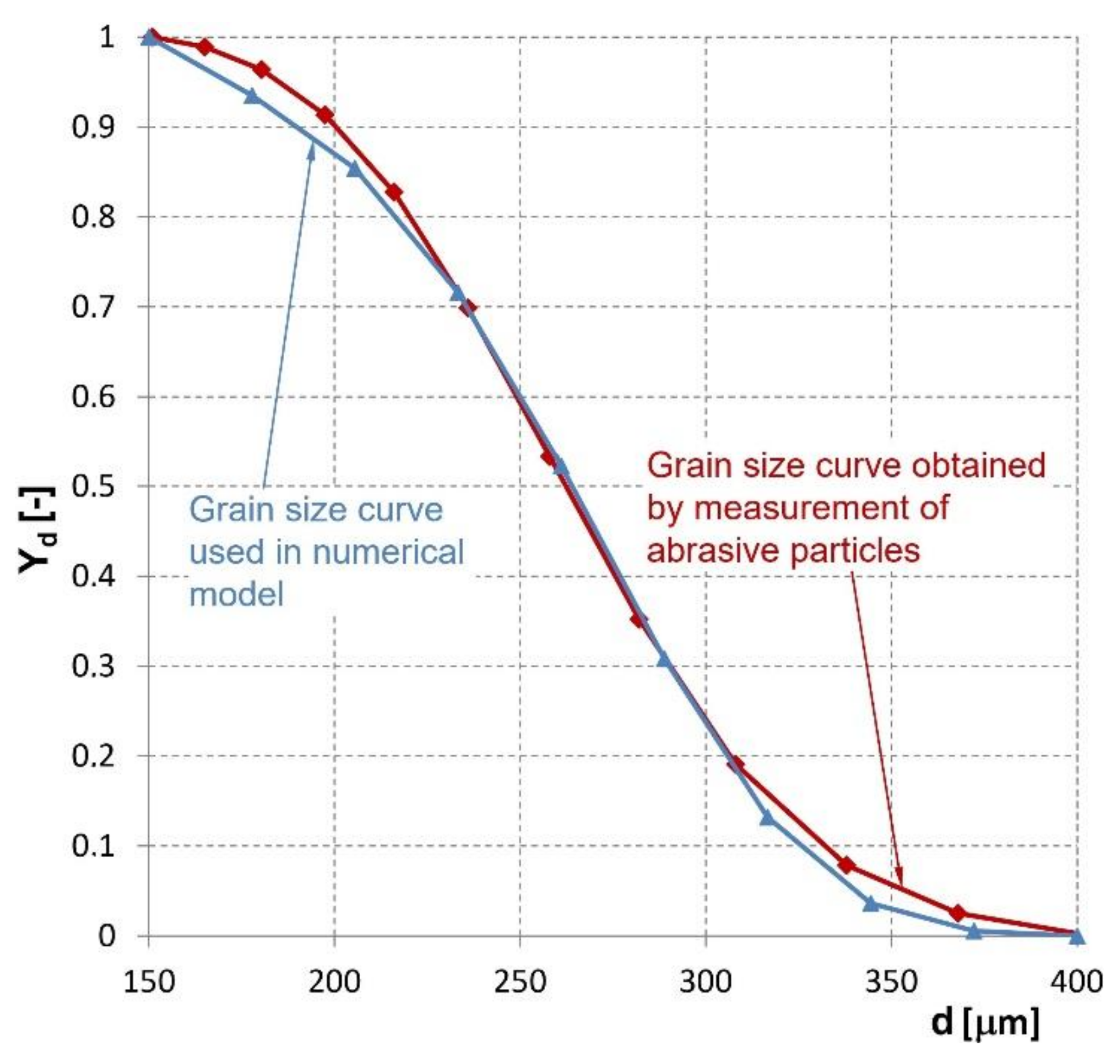
- At the outlet of the abrasive head, a very good conformity of the abrasive particle velocity in measurements and calculations was reached due to the detailed description of abrasive particle diameters (from 150 to 400 μm) based on the function of the Rosin-Rammler particle size distribution used in calculations. For both measurements and calculations, the increase in the abrasive mass flow rate caused a decrease in the velocity of abrasive particles at the outlet of the abrasive head;
- A numerical model enabling a 3D multiphase steady-state turbulent visualisation of the flow in the space around the abrasive cutting head was developed. The numerical model provided stable and sufficiently accurate simulations in a short time without requiring extreme computing power.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
- All authors have participated in the conception and design or analysis and interpretation of the data;
- This manuscript has not been submitted to, nor is under review at, another journal or other publishing venue;
- The authors have no affiliation with any organisation with a direct financial interest in the subject matter discussed in the manuscript.
References
- Momber, A.W.; Kovacevic, R. Principles of Abrasive Water Jet Machining; Springer Science and Business Media LLC.: Berlin, Germany, 1998. [Google Scholar] [CrossRef]
- Liu, X.; Liang, Z.; Wen, G.; Yuan, X. Waterjet machining and research developments: A review. Int. J. Adv. Manuf. Technol. 2019, 102, 1257–1335. [Google Scholar] [CrossRef]
- Summers, D.A. Waterjetting Technology; CRC Press: Boca Raton, FL, USA, 1995. [Google Scholar] [CrossRef]
- Sitek, L.; Hlaváček, P.; Bodnarova, L. Use of High-Speed Water Flows for Accelerated Mechanical Modelling of Erosive Wear of Concrete Surfaces. In MATEC Web of Conferences; EDP Sciences: Les Sulis, France, 2018; Volume 244. [Google Scholar] [CrossRef]
- Hlaváček, P.; Sitek, L.; Hela, R.; Bodnarova, L. Erosion Test with High-speed Water Jet Applied on Surface of Concrete Treated with Solution of Modified Lithium Silicates. In Lecture Notes in Mechanical Engineering; Springer Science and Business Media LLC.: Berlin, Germany, 2019. [Google Scholar] [CrossRef]
- Cárach, J.; Hloch, S.; Hlaváček, P.; Ščučka, J.; Martinec, P.; Petrů, J.; Zlámal, T.; Zeleňák, M.; Monka, P.; Lehocká, D.; et al. Tangential turning of Incoloy alloy 925 using abrasive water jet technology. Int. J. Adv. Manuf. Technol. 2015, 82, 1747–1752. [Google Scholar] [CrossRef]
- Hreha, P.; Radvanská, A.; Hloch, S.; Peržel, V.; Królczyk, G.; Monková, K. Determination of vibration frequency depending on abrasive mass flow rate during abrasive water jet cutting. Int. J. Adv. Manuf. Technol. 2015, 77, 763–774. [Google Scholar] [CrossRef]
- Mohyla, P.; Kubon, Z.; Cep, R.; Samardzic, I. Evaluation of Creep Properties of Steel P92 and Its Welded Joint. Metalurgija 2014, 53, 175–178. [Google Scholar]
- Zeleňák, M.; Říha, Z.; Jandačka, P. Visualization and velocity analysis of a high-speed modulated water jet generated by a hydrodynamic nozzle. Measurement 2020, 159, 107753. [Google Scholar] [CrossRef]
- Liu, H.; Wang, J.; Brown, R.J.; Kelson, N. Computational Fluid Dynamics (CFD) Simulation of Ultrahigh Velocity Abrasive Waterjet. Key Eng. Mater. 2003, 233–236, 477–482. [Google Scholar] [CrossRef]
- Liu, H.; Wang, J.; Kelson, N.; Brown, R.J. A study of abrasive waterjet characteristics by CFD simulation. J. Mater. Process. Technol. 2004, 153–154, 488–493. [Google Scholar] [CrossRef] [Green Version]
- Thongkaew, K.; Wang, J.; Yeoh, G.H. Impact characteristics and stagnation formation on a solid surface by a supersonic abrasive waterjet. Int. J. Extreme Manuf. 2019, 1, 045004. [Google Scholar] [CrossRef]
- Prisco, U.; D’Onofrio, M.C. Three-Dimensional CFD Simulation of Two-Phase Flow Inside the Abrasive Water Jet Cutting Head. Int. J. Comput. Methods Eng. Sci. Mech. 2008, 9, 300–319. [Google Scholar] [CrossRef]
- Yanaida, K. Flow Characteristics of Water Jets: Proceedings of the Second International Symposium on Jet Cutting Technology; Paper A2; BHRA Fluid Engineering: Cranfield, UK, 1974; pp. 19–32. [Google Scholar]
- Qiang, Z.; Wu, M.; Miao, X.; Sawhney, R. CFD Research on Particle Movement and Nozzle Wear in the Abrasive Water Jet Cutting Head. Int. J. Adv. Manuf. Technol. 2018, 95, 9–12. [Google Scholar] [CrossRef]
- Tazibt, A.; Parsy, F.; Abriak, N. Theoretical analysis of the particle acceleration process in abrasive water jet cutting. Comput. Mater. Sci. 1996, 5, 243–254. [Google Scholar] [CrossRef]
- Momber, A.W. Energy transfer during the mixing of air and solid particles into a high-speed waterjet: An impact-force study. Exp. Therm. Fluid Sci. 2001, 25, 31–41. [Google Scholar] [CrossRef]
- Narayanan, C.; Balz, R.; Weiss, D.A.; Heiniger, K.C. Modelling of abrasive particle energy in water jet machining. J. Mater. Process. Technol. 2013, 213, 2201–2210. [Google Scholar] [CrossRef]
- Swanson, R.K.; Kilman, M.; Cerwin, S.; Tarver, W.; Wellman, R. Study of particle velocities in water driven abrasive jet cutting. In Proceedings of the 4th U.S. Water Jet Conference, Berkeley, CA, USA, 26–28 August 1987; The American Society of Mechanical Engineers: New York, NY, USA; pp. 103–108. [Google Scholar]
- Isobe, T.; Yoshida, H.; Nish, I.K. Distribution of abrasive particles in abrasive water jet and acceleration mechanism. In Proceedings of the 9th International Symposium on Jet Cutting Technology, 4–6 October 1988; BHRA Fluid Engineering Centre: Sendai, Japan; pp. 217–223. [Google Scholar]
- Li, H.Y.; Geskin, E.S.; Chen, W.L. Investigation of Forces Exerted by an Abrasive Water Jet on a Workpiece. In Proceedings of the 5 th American Water Jet Conference, Toronto, ON, Canada, 29–31 August 1989. [Google Scholar]
- Haghbin, N.; Khakpour, A.; Schwartzentruber, J.; Papini, M. Measurement of abrasive particle velocity and size distribution in high pressure abrasive slurry and water micro-jets using a modified dual disc anemometer. J. Mater. Process. Technol. 2019, 263, 164–175. [Google Scholar] [CrossRef]
- Neusen, F.K.; Gores, T.J.; Amano, R.S. Axial variation of article and drop velocities downstream from an abrasive water jet mixing tube. In Proceedings of the 12th International Conference on Jet Cutting Technology, Rouen, France, 25–27 October 1994. [Google Scholar]
- Neusen, K.F.; Gores, T.J.; Labus, T.J. Measurement of Particle and Drop Velocities in a Mixed Abrasive Water Jet Using a Forward-Scatter LDV System. In Jet Cutting Technology; Springer: Dordrecht, The Netherlands, 1992. [Google Scholar]
- Chen, W.L.; Geskin, E.S. Correlation between particle velocity and conditions of abrasive waterjet formation. In Proceedings of the 6th American Water Jet Conference, Dearborn, Michigan, 23–26 August 1997; pp. 305–313. [Google Scholar]
- Roth, P.; Looser, H.; Heiniger, K.C.; Bühler, S. Determination of Abrasive Particle Velocity Using La-ser-Induced Fluorescence and Particle Tracking Methods in Abrasive Water Jets. In WTJA American Waterjet Conference; WTJA: Houston, TX, USA, 2005. [Google Scholar]
- Balz, R.; Heiniger, K.C. Determination of spatial distributions of abrasive particles in abrasive water jets using laser-induced fluorescence under real conditions. In WJTA-IMCA Conference and Expo; WTJA: Houston, TX, USA, 2011. [Google Scholar]
- Zeleňák, M.; Foldyna, J.; Linde, M.; Pude, F.; Rentsch, T.; Fernolendt, J.; Poort, H. Measurement and Analysis of Abrasive Particles Velocities in AWSJ. Procedia Eng. 2016, 149, 77–86. [Google Scholar] [CrossRef] [Green Version]
- Jerman, M.; Zeleňák, M.; Lebar, A.; Foldyna, V.; Foldyna, J.; Valentinčič, J. Observation of cryogenically cooled ice particles inside the high-speed water jet. J. Mater. Process. Technol. 2021, 289, 116947. [Google Scholar] [CrossRef]
- ANSYS Inc.: ANSYS Fluent Theory Guide (Release-15.0). Available online: http://www.pmt.usp.br/academic/martoran/notasmodelosgrad/ANSYS%20Fluent%20Theory%20Guide%2015.pdf, (accessed on 13 July 2021).
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef] [Green Version]
- Axisa, F.; Antunes, J. Modelling of Mechanical System: Fluid-Structure Interaction, Volume 3; Butter-worth-Heinemann: London, UK, 2007. [Google Scholar]
- Lefebvre, A.H.; McDonell, V.G. Atomization and Sprays. In Atomization and Sprays; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Long, X.; Liu, Q.; Chen, Z.; Xue, S. Numerical study of the particle movement in the abrasive entrained waterjet nozzle at 300 MPa. In Proceedings of the 14th Asian International Conference on Fluid Machinery, Zhenjiang, China, 10–13 November 2017. [Google Scholar]
- Long, X.; Ruan, X.; Liu, Q.; Chen, Z.; Xue, S.; Wu, Z. Numerical investigation on the internal flow and the particle movement in the abrasive waterjet nozzle. Powder Technol. 2017, 314, 635–640. [Google Scholar] [CrossRef]
- Long, X.; Liu, Q.; Ruan, X.; Chen, Z.; Xue, S.; Wu, Z. Numerical Analysis of Internal Flow of Abrasive En-trained Waterjet Nozzle. Paiguan Jixie Gongcheng Xuebao J. Drain. Irrig. Mach. Eng. 2016, 34. [Google Scholar] [CrossRef]
- Osman, A.; Mabrouki, T.; Théry, B.; Buisine, D. Experimental analysis of high-speed air–water jet flow in an abrasive water jet mixing tube. Flow Meas. Instrum. 2004, 15, 37–48. [Google Scholar] [CrossRef]
- Kim, T.J.; Labus, T.J. Influence of Basic Jet Parameters and Physics of Abrasive Water Jet Cutting. In Fluid Jet Technology: Fundamentals and Applications; WJTA: St. Louis, MI, USA, 1995; pp. 3.1.–3.45. [Google Scholar]
- Hashish, M. Precision Machining with Abrasive–Waterjets. In Proceedings of the 6th American Water Jet Conference, Houston, TX, USA, 24–27 August 1991; Volume 179. [Google Scholar]
- Foldyna, J.; Zeleňák, M.; Klich, J.; Hlavacek, P.; Sitek, L.; Říha, Z. The measurement of the velocity of abrasive particles at the suction part of cutting head. Teh. Vjesn. Tech. Gaz. 2015, 22, 1441–1446. [Google Scholar] [CrossRef]
- Hlavacek, P.; Sitek, L.; Foldyna, J. Evaluation of Erosion Performance of Abrasive Particles in Abrasive Water Jet Cutting Process. MM Sci. J. 2020, 2020, 3869–3872. [Google Scholar] [CrossRef]
- Onderová, I.; Šooš, L. Analysis of Parameters Affecting the Quality of a Cutting Machine. Acta Polytech. 2014, 54, 63–67. [Google Scholar] [CrossRef]


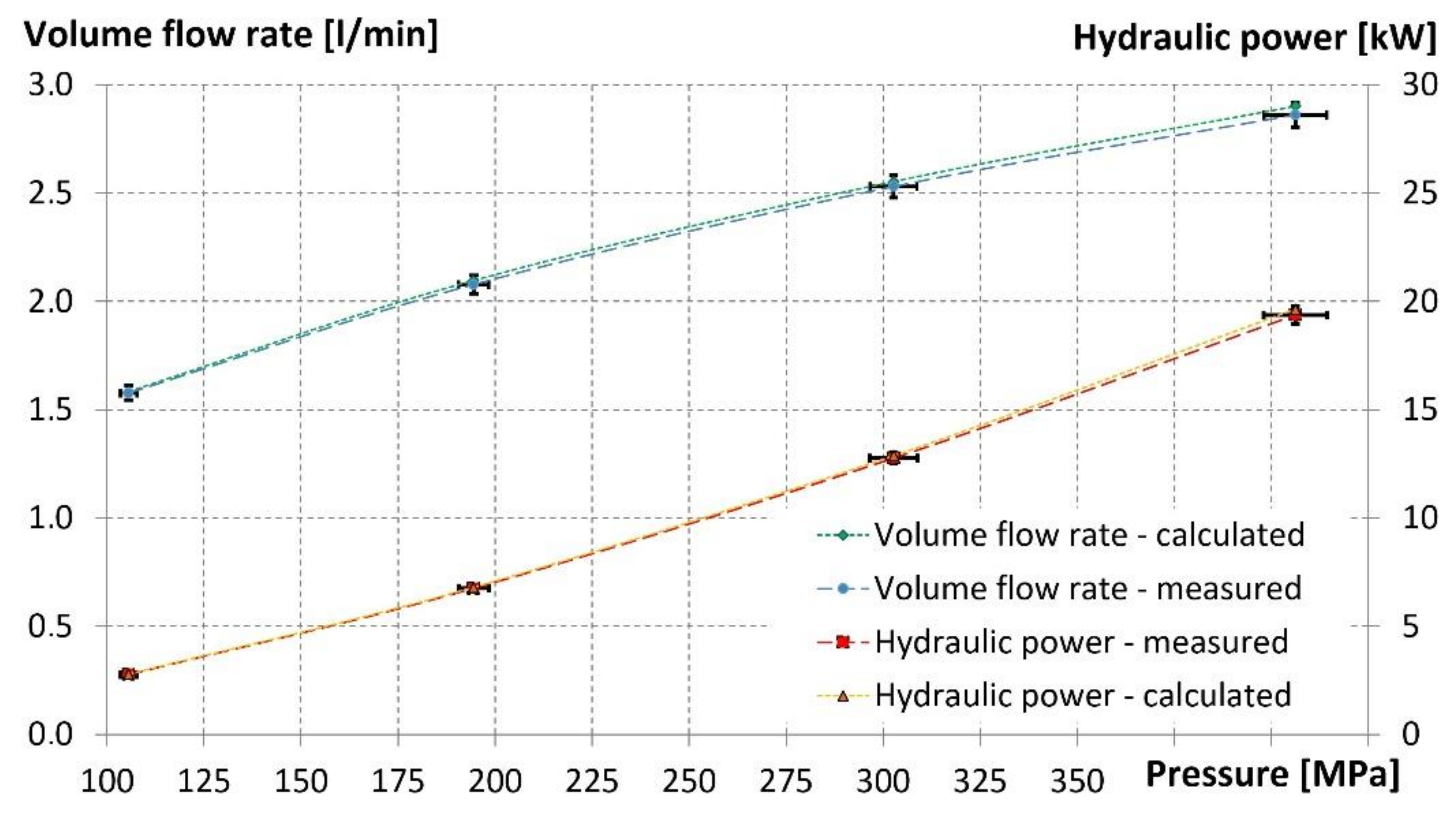


| pavg (MPa) | SD (MPa) | SEM (MPa) | 95% CI (MPa) | Qavg (L/min) | SD (L/min) | SEM (L/min) | 95% CI (L/min) | Pavg (kW) | SD (kW) | SEM (kW) | 95% CI (kW) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 105.56 | 1.68 | 0.22 | 105.98 105.14 | 1.58 | 0.01 | 0.001 | 1.56 1.57 | 2.77 | 0.05 | 0.006 | 2.79 2.76 |
| 194.46 | 15.27 | 1.95 | 198.29 190.64 | 2.08 | 0.08 | 0.010 | 2.10 2.06 | 6.75 | 0.75 | 0.095 | 6.94 6.56 |
| 302.72 | 2.13 | 0.27 | 303.26 302.19 | 2.53 | 0.02 | 0.001 | 2.53 2.52 | 12.76 | 0.16 | 0.019 | 12.80 12.72 |
| 406.17 | 3.22 | 0.41 | 406.98 405.36 | 2.86 | 0.02 | 0.002 | 2.75 2.74 | 19.36 | 0.17 | 0.002 | 19.41 19.32 |
| CFD Calculations | PTV Measurement | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| p (MPa) | N | vavg (m/s) | SD (m/s) | SEM (m/s) | 95%CI (m/s) | N | vavg (m/s) | SD (m/s) | SEM (m/s) | 95%CI (m/s) |
| 105.56 | 3059 | 296.07 | 113.79 | 2.05 | 300.10 292.04 | 1565 | 329.34 | 59.45 | 1.50 | 332.28 326.39 |
| 194.46 | 3060 | 400.09 | 159.71 | 2.89 | 405.75 394.42 | 2650 | 455.36 | 69.62 | 1.35 | 458.01 452.70 |
| 302.72 | 3054 | 493.39 | 205.39 | 3.72 | 500.76 486.19 | 1489 | 579.71 | 75.85 | 1.97 | 583.57 575.86 |
| 406.17 | 3056 | 566.06 | 242.27 | 4.38 | 574.65 557.47 | 2421 | 690.38 | 70.55 | 1.43 | 693.20 687.57 |
| CFD Calculations | PTV Measurement | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| p (MPa) | N | vavg (m/s) | SD (m/s) | SEM (m/s) | 95% CI m/s] | N | vavg (m/s) | SD (m/s) | SEM (m/s) | 95% CI (m/s) |
| 105.56 | 3060 | 285.01 | 107.33 | 1.94 | 288.81 281.21 | 3329 | 281.19 | 66.51 | 1.15 | 283.45 278.94 |
| 194.46 | 3058 | 388.61 | 153.81 | 2.78 | 394.07 383.16 | 3742 | 395.23 | 85.72 | 1.40 | 397.48 392.48 |
| 302.72 | 3059 | 488.95 | 193.68 | 3.50 | 495.81 565.62 | 3318 | 528.87 | 76.43 | 1.33 | 531.48 526.28 |
| 406.17 | 3059 | 557.36 | 233.34 | 4.22 | 565.63 549.07 | 4830 | 641.75 | 76.65 | 1.10 | 643.91 639.58 |
| CFD Calculations | PTV Measurement | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| p (MPa) | N | vavg (m/s) | SD (m/s) | SEM (m/s) | 95% CI (m/s) | N | vavg (m/s) | SD (m/s) | SEM (m/s) | 95% CI (m/s) |
| 105.56 | 3055 | 276.86 | 99.28 | 1.80 | 280.38 273.34 | 6483 | 251.81 | 63.55 | 0.79 | 253.36 250.27 |
| 194.46 | 3057 | 379.18 | 146.07 | 2.64 | 384.36 374.00 | 3350 | 365.40 | 82.14 | 1.42 | 368.18 362.62 |
| 302.72 | 3059 | 475.18 | 188.74 | 3.41 | 482.27 468.89 | 2218 | 479.52 | 86.59 | 1.84 | 483.13 475.92 |
| 406.17 | 3055 | 553.22 | 200.29 | 3.99 | 561.03 545.41 | 6372 | 601.70 | 80.28 | 1.01 | 603.68 599.73 |
| CFD Calculations | PTV Measurement | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| p (MPa) | N | Vavg (m/s) | SD (m/s) | SEM (m/s) | 95% CI(m/s) | N | Vavg (m/s) | SD (m/s) | SEM (m/s) | 95% CI (m/s) |
| 105.56 | 3055 | 269.31 | 92.54 | 1.67 | 272.59 266.02 | 5205 | 237.42 | 57.46 | 0.80 | 238.98 235.86 |
| 194.46 | 3059 | 375.86 | 133.85 | 2.42 | 380.60 371.12 | 4655 | 333.54 | 83.26 | 1.22 | 335.94 331.15 |
| 302.72 | 3056 | 473.57 | 174.53 | 3.15 | 479.75 467.38 | 2777 | 433.15 | 103.73 | 1.97 | 437.01 429.29 |
| 406.17 | 3055 | 549.16 | 208.90 | 3.78 | 556.57 541.76 | 6920 | 562.12 | 82.40 | 0.99 | 564.06 560.18 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Riha, Z.; Zelenak, M.; Soucek, K.; Hlavacek, A. Flow Field Analysis Inside and at the Outlet of the Abrasive Head. Materials 2021, 14, 3919. https://doi.org/10.3390/ma14143919
Riha Z, Zelenak M, Soucek K, Hlavacek A. Flow Field Analysis Inside and at the Outlet of the Abrasive Head. Materials. 2021; 14(14):3919. https://doi.org/10.3390/ma14143919
Chicago/Turabian StyleRiha, Zdenek, Michal Zelenak, Kamil Soucek, and Antonin Hlavacek. 2021. "Flow Field Analysis Inside and at the Outlet of the Abrasive Head" Materials 14, no. 14: 3919. https://doi.org/10.3390/ma14143919
APA StyleRiha, Z., Zelenak, M., Soucek, K., & Hlavacek, A. (2021). Flow Field Analysis Inside and at the Outlet of the Abrasive Head. Materials, 14(14), 3919. https://doi.org/10.3390/ma14143919





