Mechanical Properties of Cemented Particulate Composite: A 3D Micromechanical Model
Abstract
:1. Introduction
2. 3D Micromechanical Model
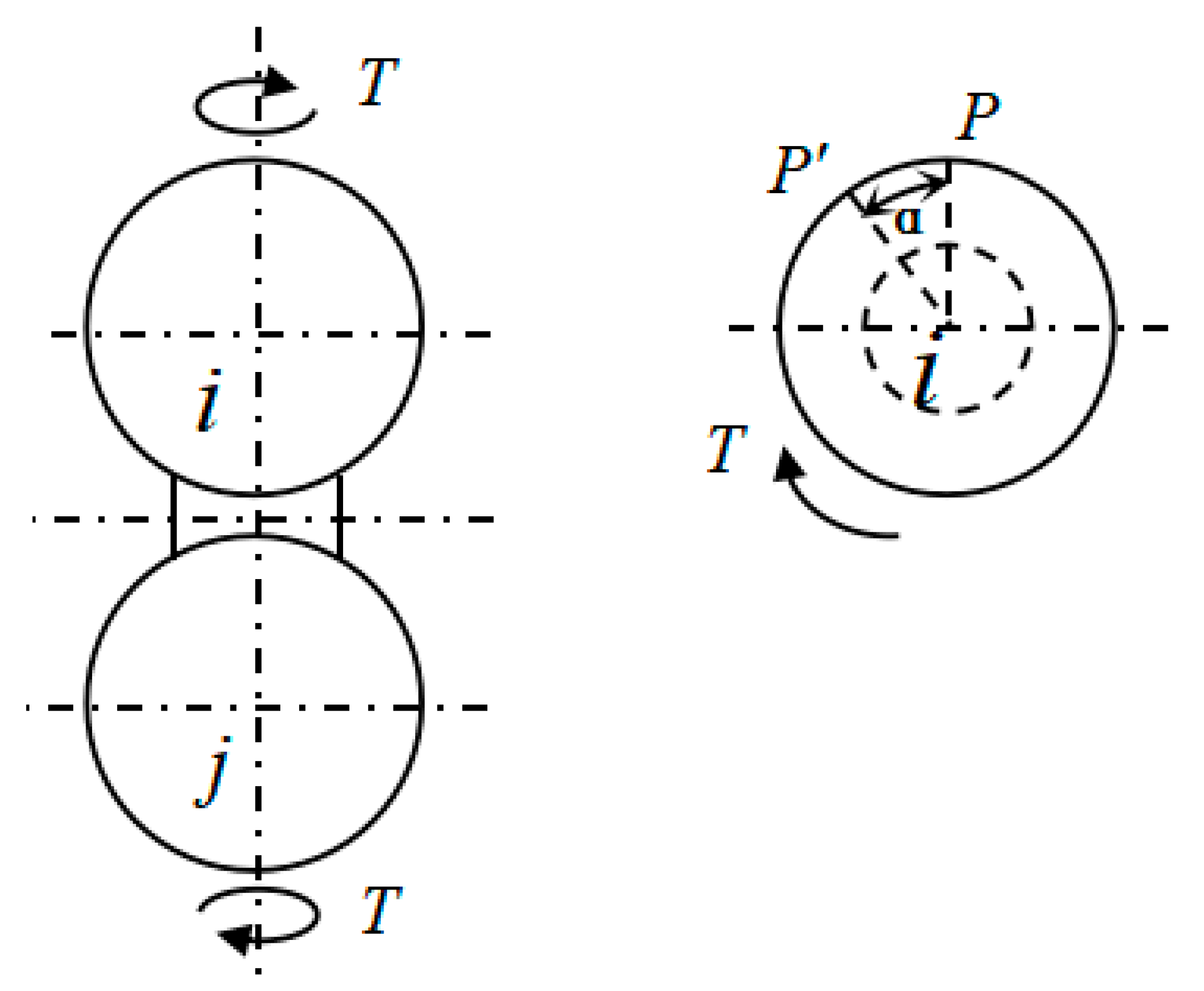
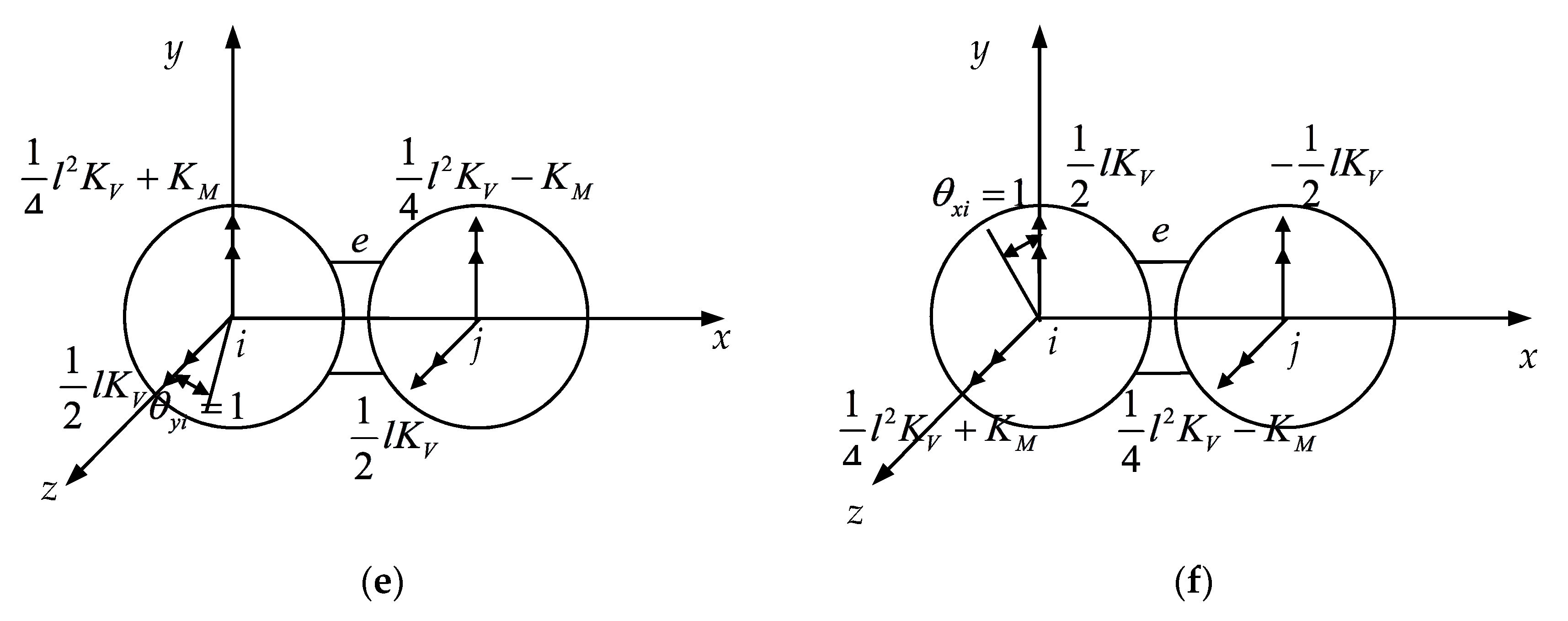
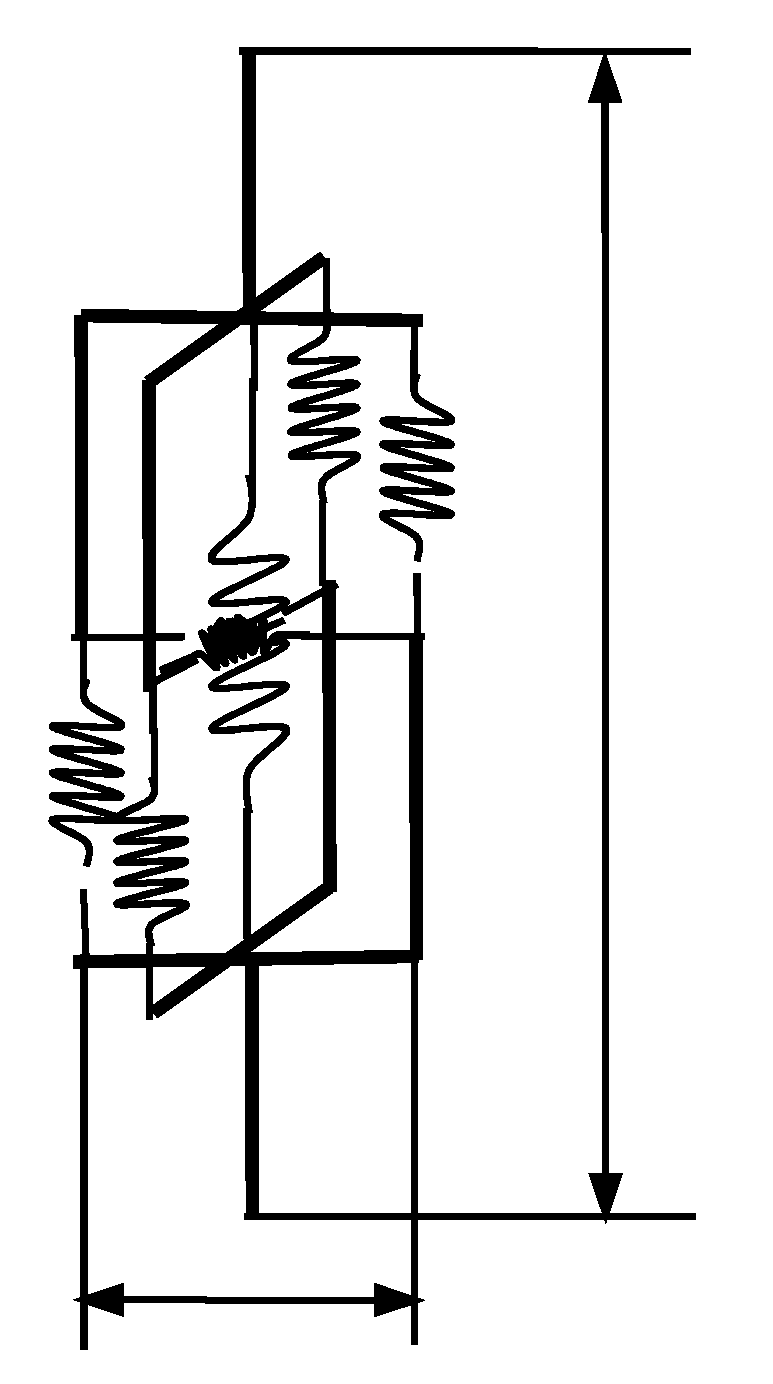
2.1. Calculation of Torsional Stiffness of CSE
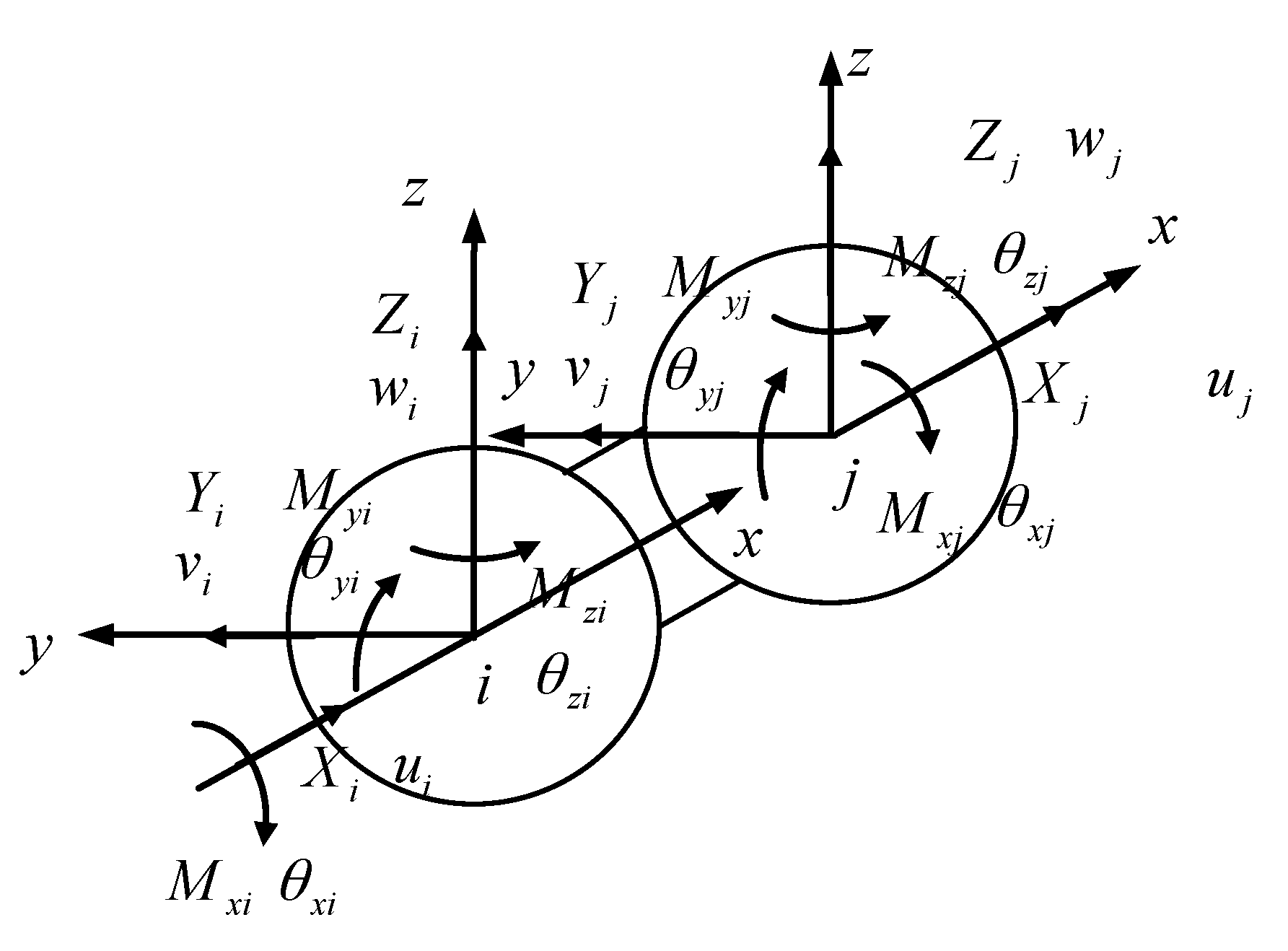
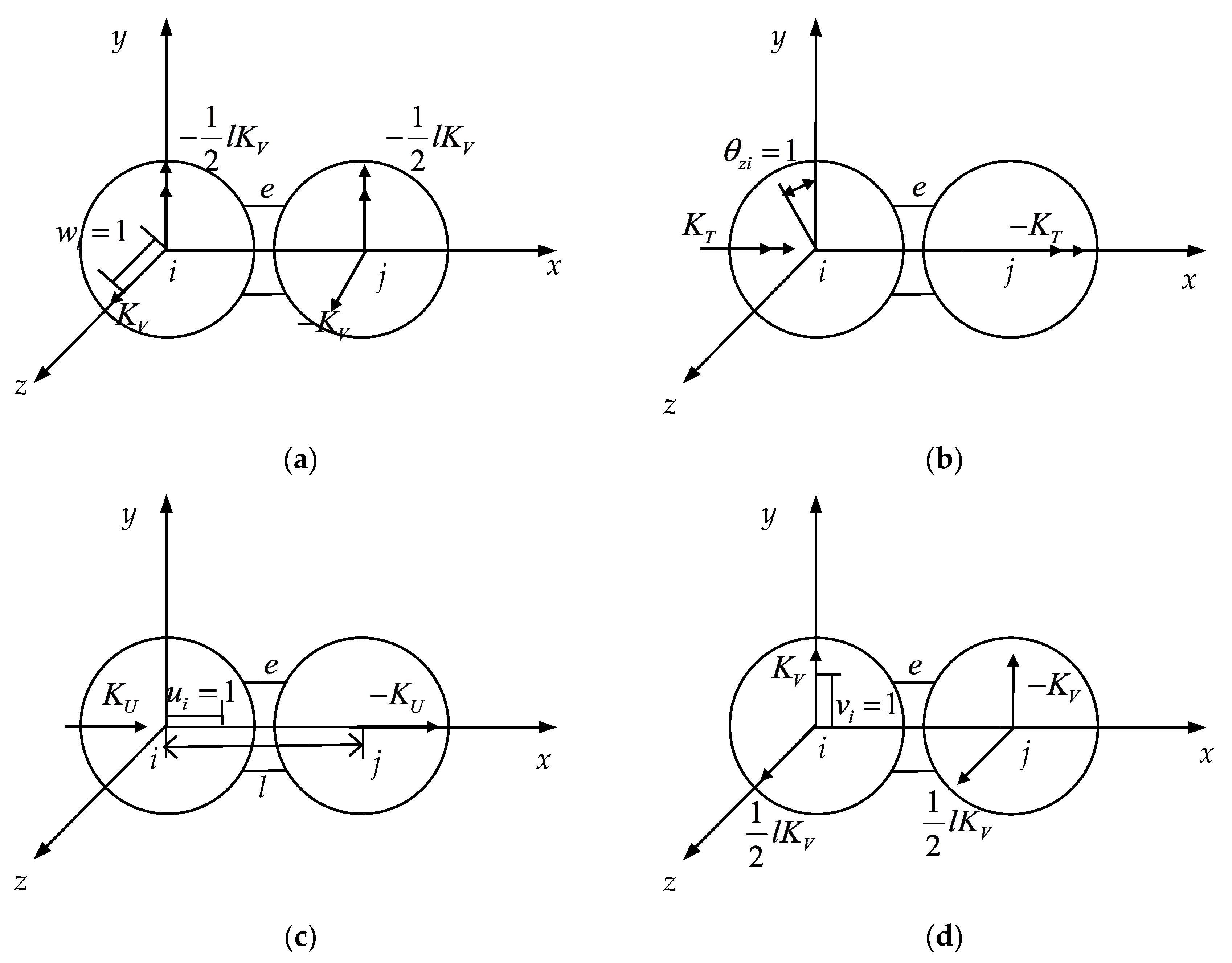
2.2. Establishment of CSE Stiffness Matrix
2.3. 3D Rigid Beam-Spring Equivalent Model
3. Epoxy Resin Glass Beads Mechanical Properties
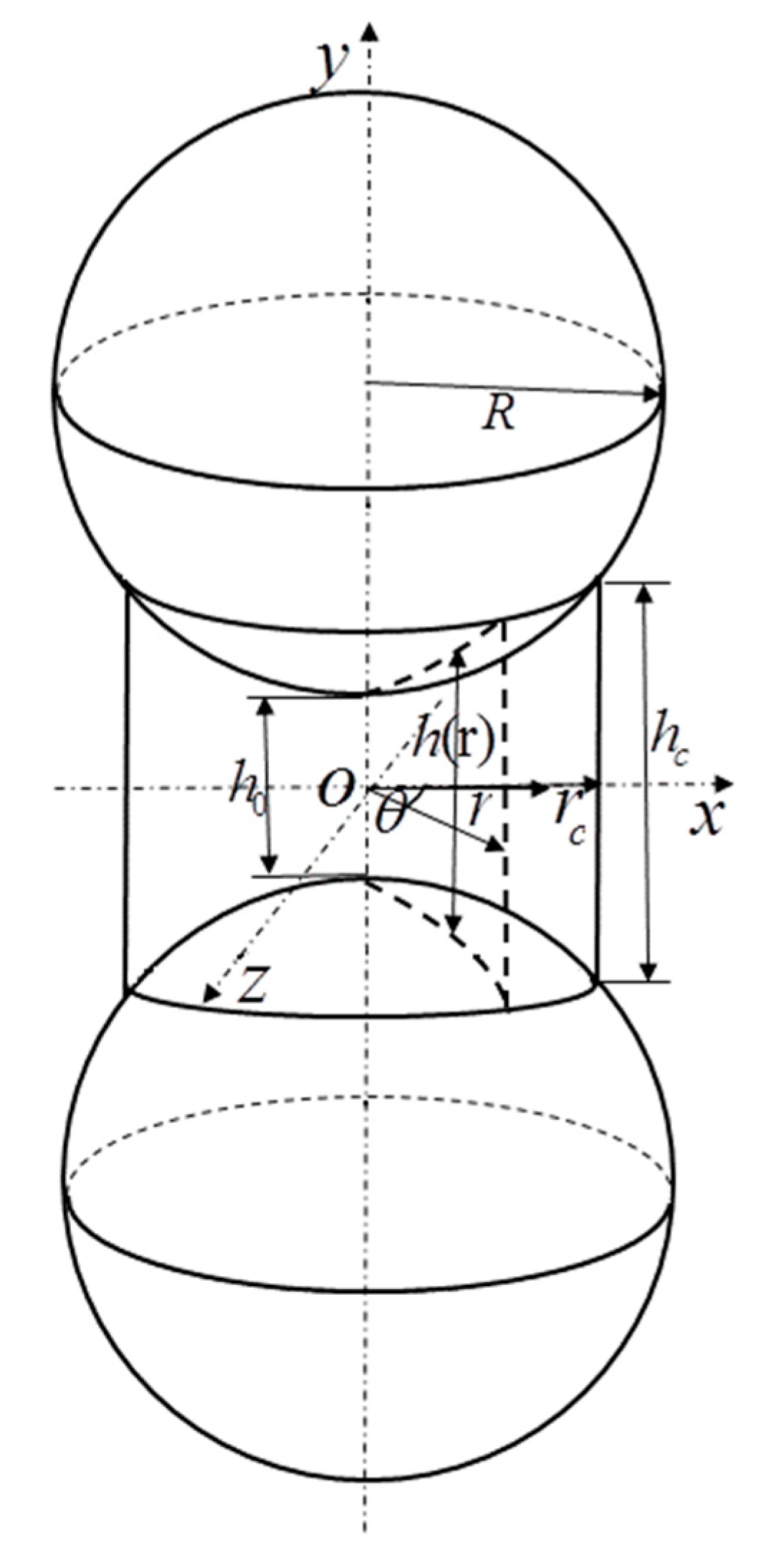
3.1. Materials and Methods
3.2. Results and Discussion
3.3. Damage Evolution Process of Materials with Defects
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dastgerdi, J.N.; Miettinen, A.; Parkkonen, J.; Remes, H. Multiscale microstructural characterization of particulate-reinforced composite with non-destructive X-ray micro-and nanotomography. Compos. Struct. 2018, 194, 292–301. [Google Scholar] [CrossRef]
- Chen, G.; Bezold, A.; Broeckmann, C. Influence of the size and boundary conditions on the predicted effective strengths of particulate reinforced metal matrix composites (PRMMCs). Compos. Struct. 2018, 189, 330–339. [Google Scholar] [CrossRef]
- Melo, A.B.L.; Panzera, T.H.; Freire, R.T.S.; Scarpa, F. The effect of Portland cement inclusions in hybrid glass fibre reinforced composites based on a full factorial design. Compos. Struct. 2018, 202, 233–240. [Google Scholar] [CrossRef] [Green Version]
- Dastgerdi, J.N.; Anbarlooie, B.; Marzban, S.; Marquis, G. Mechanical and real microstructure behavior analysis of particulate-reinforced nanocomposite considering debonding damage based on cohesive finite element method. Compos. Struct. 2015, 122, 518–525. [Google Scholar] [CrossRef]
- Spring, D.W.; Paulino, G.H. Computational homogenization of the debonding of particle reinforced composites: The role of interphases in interfaces. Comput. Mater. Sci. 2015, 109, 209–224. [Google Scholar] [CrossRef]
- Gautam, G.; Kumar, N.; Mohan, A.; Gautam, R.K.; Mohan, S. Synthesis and characterization of tri-aluminide in situ composites. J. Mater. Sci. 2016, 51, 8055–8074. [Google Scholar] [CrossRef]
- Wang, L.; Lau, J.; Thomas, E.L.; Boyce, M.C. Co-continuous composite mate-rials for stiffness, strength, and energy dissipation. Adv. Mater. 2011, 23, 1524–1529. [Google Scholar] [CrossRef]
- Bennett, K.C.; Luscher, D.J.; Buechler, M.A.; Yeager, J.D. A micromechanical framework and modified self-consistent homogenization scheme for the thermoelasticity of porous bonded-particle assemblies. Int. J. Solids Struct. 2018, 139, 224–237. [Google Scholar] [CrossRef]
- Lurie, S.; Solyaev, Y.; Shramko, K. Comparison between the Mori-Tanaka and generalized self-consistent methods in the framework of anti-plane strain inclusion problem in strain gradient elasticity. Mech. Mater. 2018, 122, 133–144. [Google Scholar] [CrossRef]
- Cho, Y.J.; Lee, W.J.; Park, Y.H. Effect of boundary conditions on plasticity and creep behavior analysis of particle reinforced composites by representative volume element approach. Comput. Mater. Sci. 2015, 100, 67–75. [Google Scholar] [CrossRef]
- Pal, R. Modeling viscoelastic behavior of particulate composites with high volume fraction of filler. Mater. Sci. Eng. A 2005, 412, 71–77. [Google Scholar] [CrossRef]
- Zhou, Q.; Jin, X.; Wang, Z.; Yang, Y.; Wang, J.; Keer, L.M.; Wang, Q. A mesh differential refinement scheme for solving elastic fields of half-space inclusion problems. Tribol. Int. 2016, 93, 124–136. [Google Scholar] [CrossRef]
- Zhou, C.; Wang, X. Elastoplastic Analysis of Particle Reinforced Composites Based on Meso Mechanical Method. J. Nanjing Univ. Aeronaut. Astronaut. 2001, 33, 512–515. [Google Scholar]
- Han, S.C.; Choi, J.M.; Liu, G.; Kang, K. A microscopic shell structure with Schwarz’s D-surface. Sci. Rep. 2017, 1, 13405. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhou, C. Micromechanical model for composites reinforced by large volume fraction of particles II: Elastoplastic and damage analysis. Acta Mater. Compos. Sin. 2005, 22, 131–135. [Google Scholar]
- Van Mier, J.G.M.; van Vliet, M.R.A.; Wang, T.K. Fracture mechanisms in particle composites: Statistical aspects in lattice type analysis. Mech. Mater. 2002, 34, 705–724. [Google Scholar] [CrossRef]
- Pompe, W.; Herrmann, H.J.; Roux, S. Statistical models for the fracture of disordered media. North-Holland, 1990, 353 p. ISBN 0444 88551x (hardbound), 0444 885501 (paperback) US $ 41.00. Cryst. Res. Technol. 2010, 26, 1076. [Google Scholar] [CrossRef]
- Karihaloo, B.L.; Shao, P.F.; Xiao, Q.Z. Lattice modelling of the failure of particle composites. Eng. Fract. Mech. 2003, 70, 2385–2406. [Google Scholar] [CrossRef]
- Hrennikoff, A. Solution of problems of elasticity by the framework method. J. Appl. Mech. 1941, 8, A169–A175. [Google Scholar] [CrossRef]
- Liu, J.; Deng, S.; Zhang, J. Beam mesh model for fracture of granular composites. Eng. Mech. 2008, 25, 33–37. (In Chinese) [Google Scholar]
- Eckschlager, A.; Han, W.; Böhm, H.J. A unit cell model for brittle fracture of particles embedded in a ductile matrix. Comput. Mater. Sci. 2002, 25, 85–91. [Google Scholar] [CrossRef]
- Chawla, N.; Sidhu, R.S.; Ganesh, V.V. Three-dimensional visualization and microstructure-based modeling of deformation in particle-reinforced composites. Acta Mater. 2006, 54, 1541–1548. [Google Scholar] [CrossRef]
- Hu, C.; Zeng, L.; Hu, B. Research on the Application of Hollow Glass Microspheres in Composite Materials. Chem. Build. Mater. 2008, 24, 46–48. [Google Scholar]
- Li, C.; Wang, Z.; Wen, W.; He, P. Curing of epoxy resin/polyamide/glass bead system. Chin. J. Compos. 2000, 17, 11–14. [Google Scholar]
- Zhou, J. Preparation and Properties of Hollow Glass Beads/Epoxy Resin Composites; Ocean University of China: Qingdao, China, 2013; pp. 15–52. [Google Scholar]
- Yang, Q. Study on the Curing Reaction Mechanism of Epoxy Resin/Cyanamide Resin and the Mechanical Properties of Epoxy Resin/Glass Cloth/Glass Beads System; Beijing University of Chemical Technology: Beijing, China, 2003; pp. 21–62. [Google Scholar]
- Wang, J.; Guo, Y.; Gao, Y.; Ge, R. Properties and applications of hollow glass beads/epoxy resin composites. Spec. Top. Compos. Mater. 2011, 9, 52–54. [Google Scholar]
- Yang, Z. Research on the Structure and Properties of Lightweight and High-Strength Hollow Microbeads/Nanotubes/Epoxy Composites; Tianjin University: Tianjin, China, 2011; pp. 21–43. [Google Scholar]
- Yang, Q.; Wang, J.; Yang, X.; Duan, H. Performance and structure of epoxy resin filled with hollow glass beads. J. Yunnan Univ. 2007, 29, 194–199. [Google Scholar]
- Hu, C.; Zeng, L.; Zhou, J. Study on the mechanical properties of modified hollow glass beads/epoxy resin composites. Thermosetting Resins 2008, 23, 21–23. [Google Scholar]
- Liang, X.; Li, H.; Yu, W.; Yang, X.; Zhang, Y.; Wang, X. Application of combinational sphere element in meso-mechanical analysis of cemented particulate composite. Compos. Struct. 2015, 131, 720–730. [Google Scholar] [CrossRef]
- Böhm, H.J.; Han, W. Comparisons between three-dimensional and two-dimensional multi-particle unit cell models for particle reinforced metal matrix composites. Model. Simul. Mater. Sci. Eng. 2001, 9, 47. [Google Scholar] [CrossRef]
- Iung, T.; Grange, M. Mechanical behaviour of two-phase materials investigated by the finite element method: Necessity of three-dimensional modeling. Mater. Sci. Eng. A 1995, 201, L8–L11. [Google Scholar] [CrossRef]
- Han, W.; Eckschlager, A.; Böhm, H.J. The effects of three-dimensional multi-particle arrangements on the mechanical behavior and damage initiation of particle-reinforced MMCs. Compos. Sci. Technol. 2001, 61, 1581–1590. [Google Scholar] [CrossRef]
- Pierard, O.; LLorca, J.; Segurado, J.; Doghri, I. Micromechanics of particle-reinforced elasto-viscoplastic composites: Finite element simulations versus affine homogenization. Int. J. Plast. 2007, 23, 1041–1060. [Google Scholar] [CrossRef]


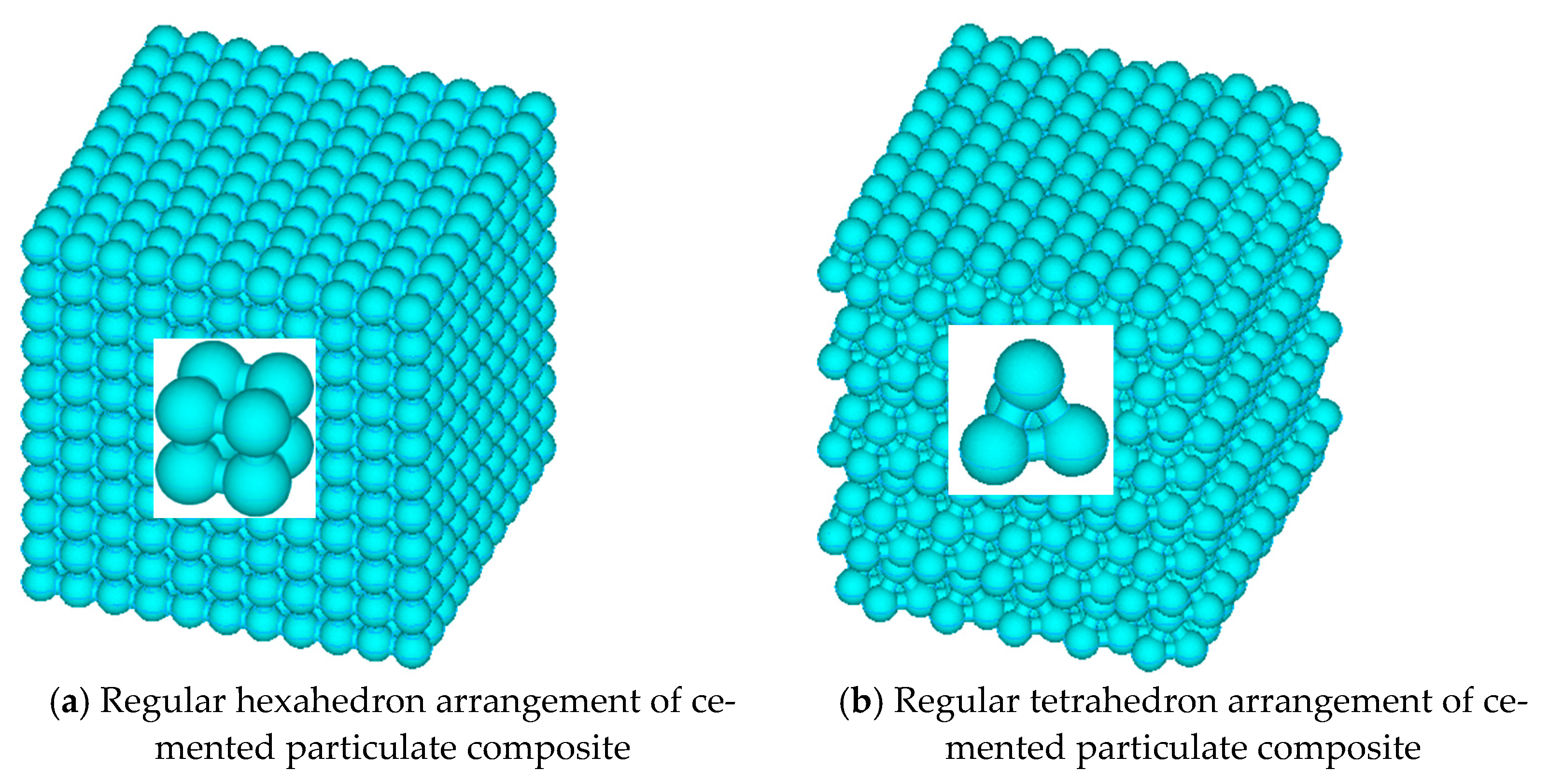
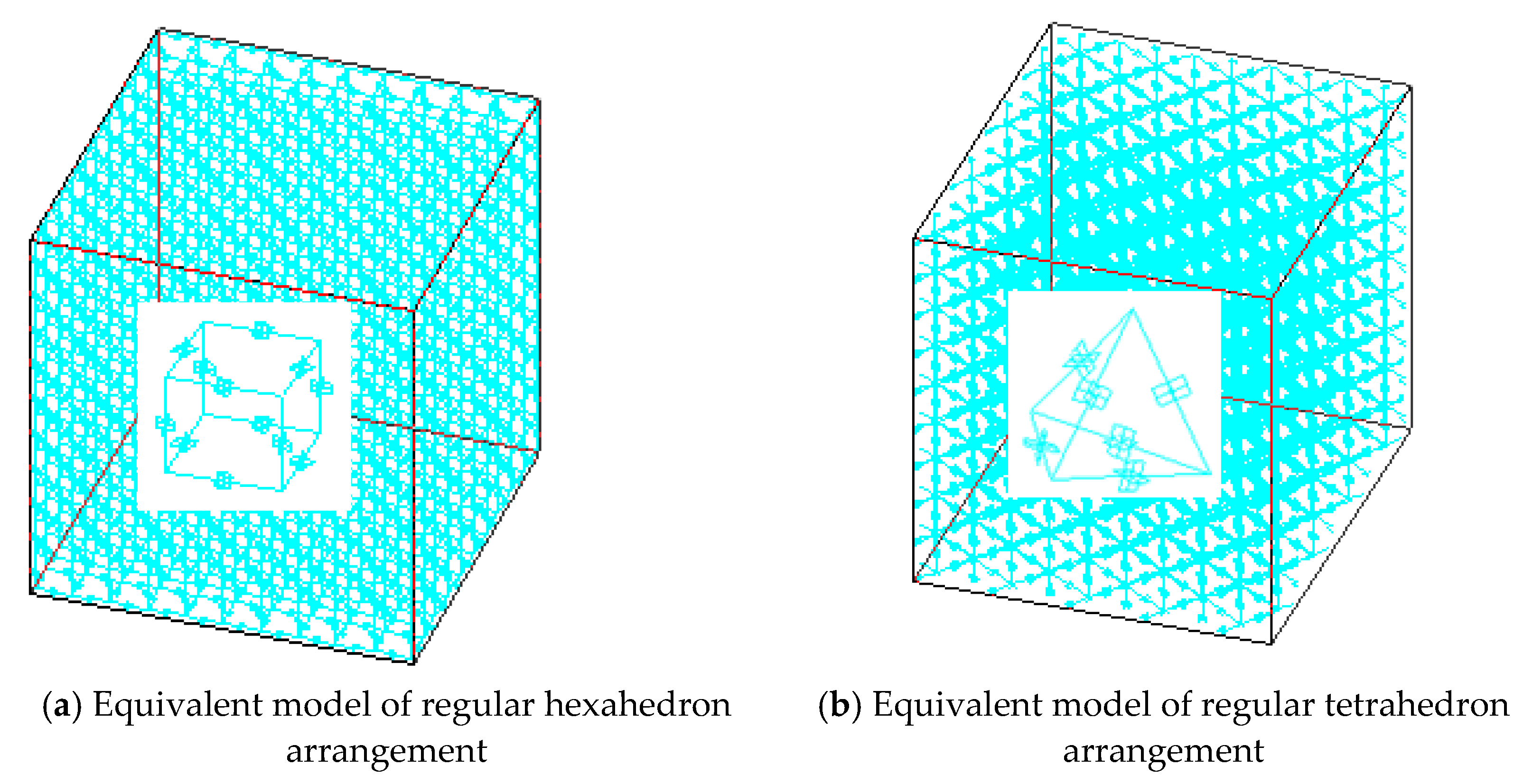
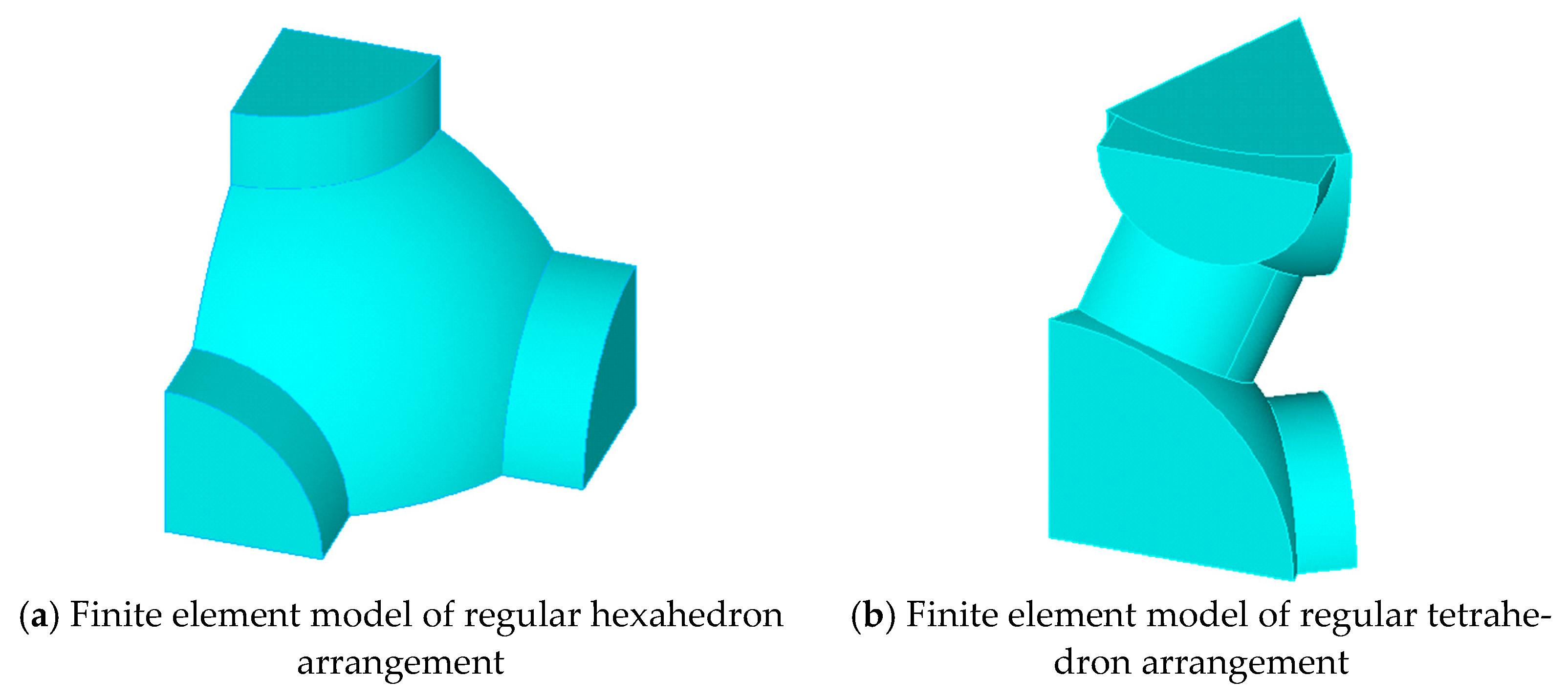
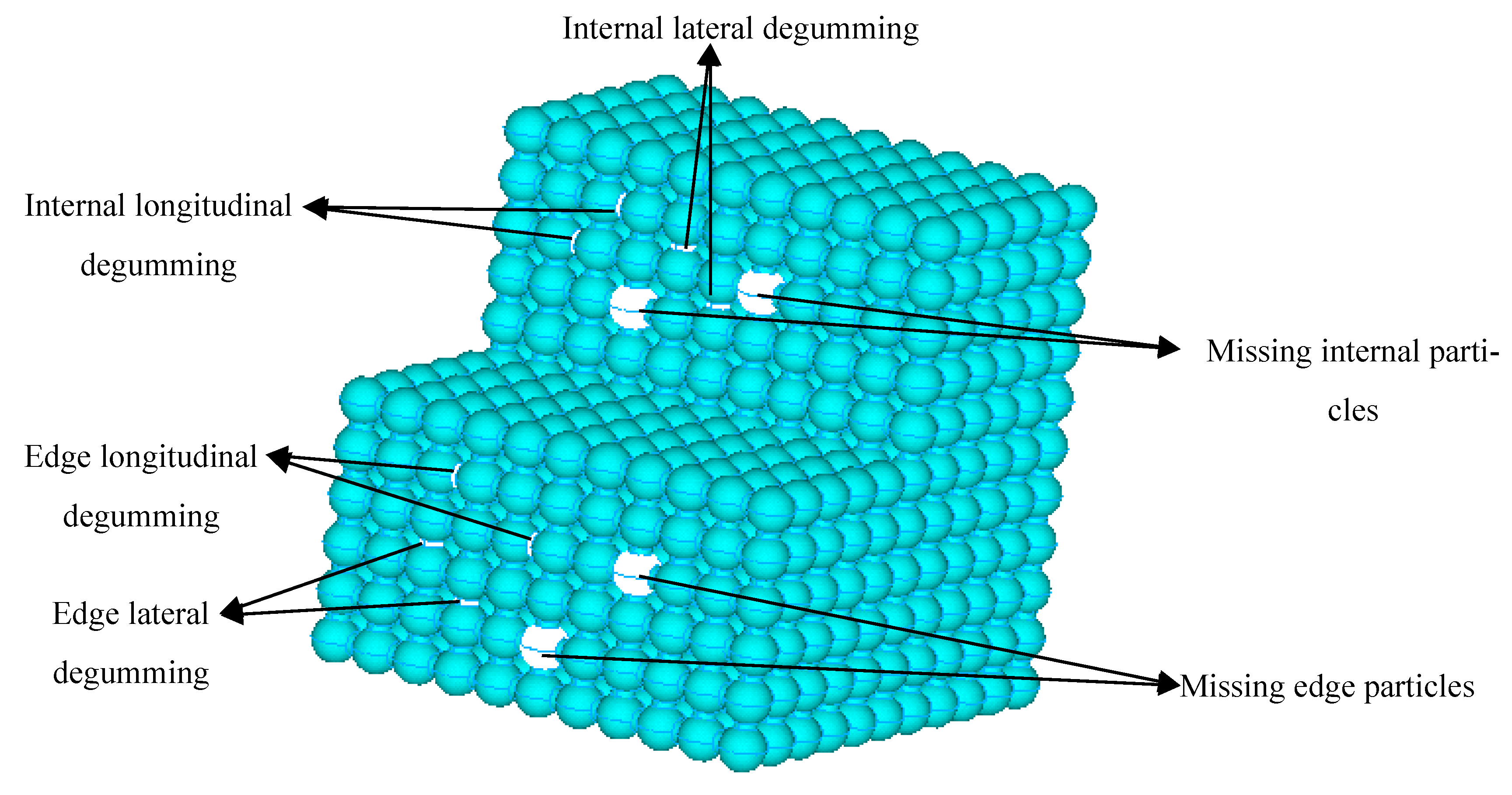
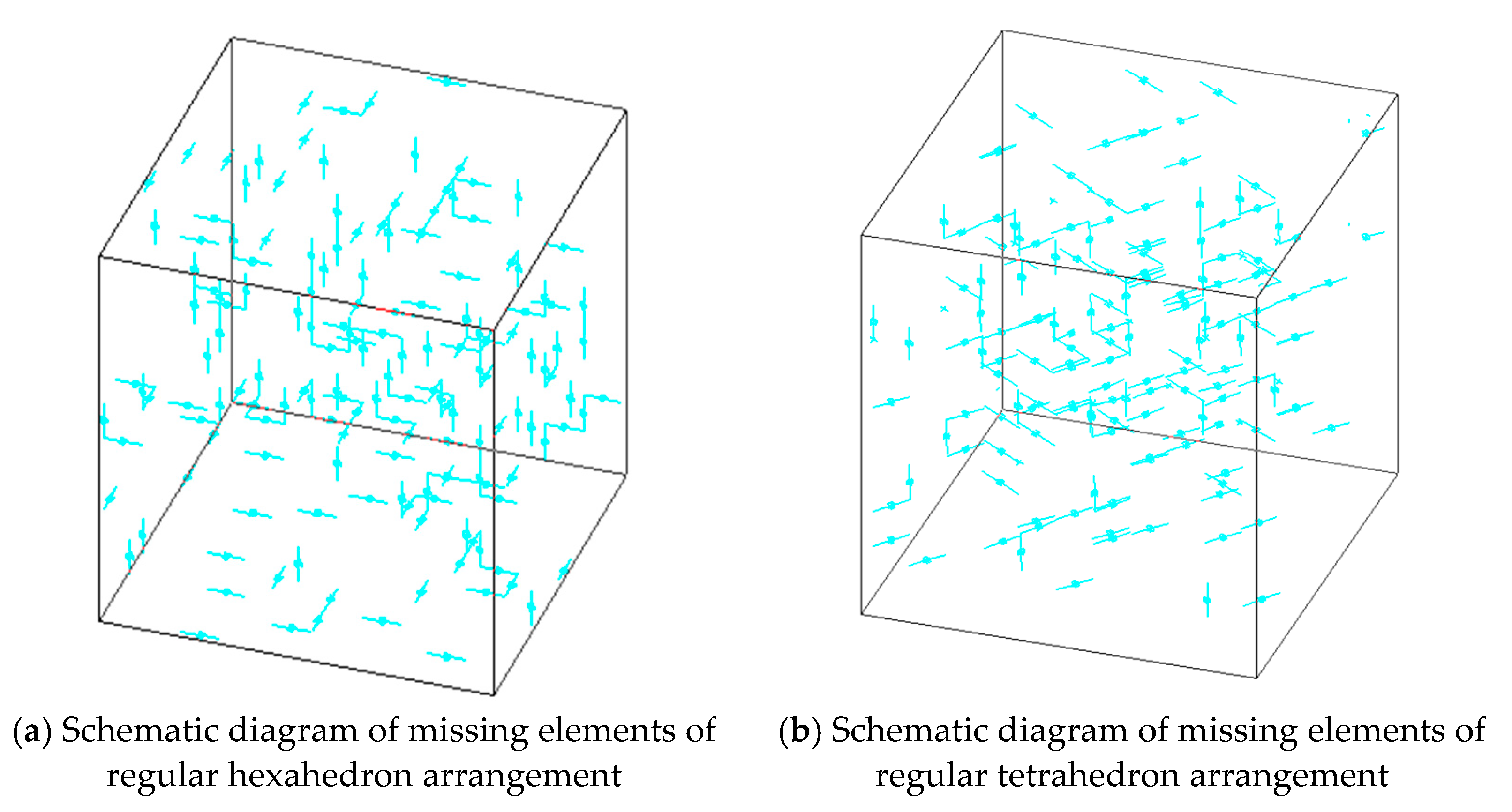


| Arrangement | E (GPa) | u |
|---|---|---|
| Tetrahedron arrangement (CSE) | 5.11 | 0.25 |
| Hexahedron arrangement (CSE) | 4.81 | 0.27 |
| Tetrahedron arrangement (RVE) | 5.05 | 0.26 |
| Hexahedron arrangement (RVE) | 4.75 | 0.28 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tao, C.; Liang, X.; Bi, X.; Liu, Z.; Li, H. Mechanical Properties of Cemented Particulate Composite: A 3D Micromechanical Model. Materials 2021, 14, 3875. https://doi.org/10.3390/ma14143875
Tao C, Liang X, Bi X, Liu Z, Li H. Mechanical Properties of Cemented Particulate Composite: A 3D Micromechanical Model. Materials. 2021; 14(14):3875. https://doi.org/10.3390/ma14143875
Chicago/Turabian StyleTao, Chenglin, Xi Liang, Xiaoxue Bi, Zeliang Liu, and Huijian Li. 2021. "Mechanical Properties of Cemented Particulate Composite: A 3D Micromechanical Model" Materials 14, no. 14: 3875. https://doi.org/10.3390/ma14143875
APA StyleTao, C., Liang, X., Bi, X., Liu, Z., & Li, H. (2021). Mechanical Properties of Cemented Particulate Composite: A 3D Micromechanical Model. Materials, 14(14), 3875. https://doi.org/10.3390/ma14143875





