Evaluating Elastic-Plastic Wavy and Spherical Asperity-Based Statistical and Multi-Scale Rough Surface Contact Models with Deterministic Results
Abstract
:1. Introduction
2. Methodology
2.1. Applying the JG Asperity Model to the GW Model
2.2. Sinusoidal Asperities in the GW Model
2.3. Multi-Scale Model
2.4. Deterministic Modeling
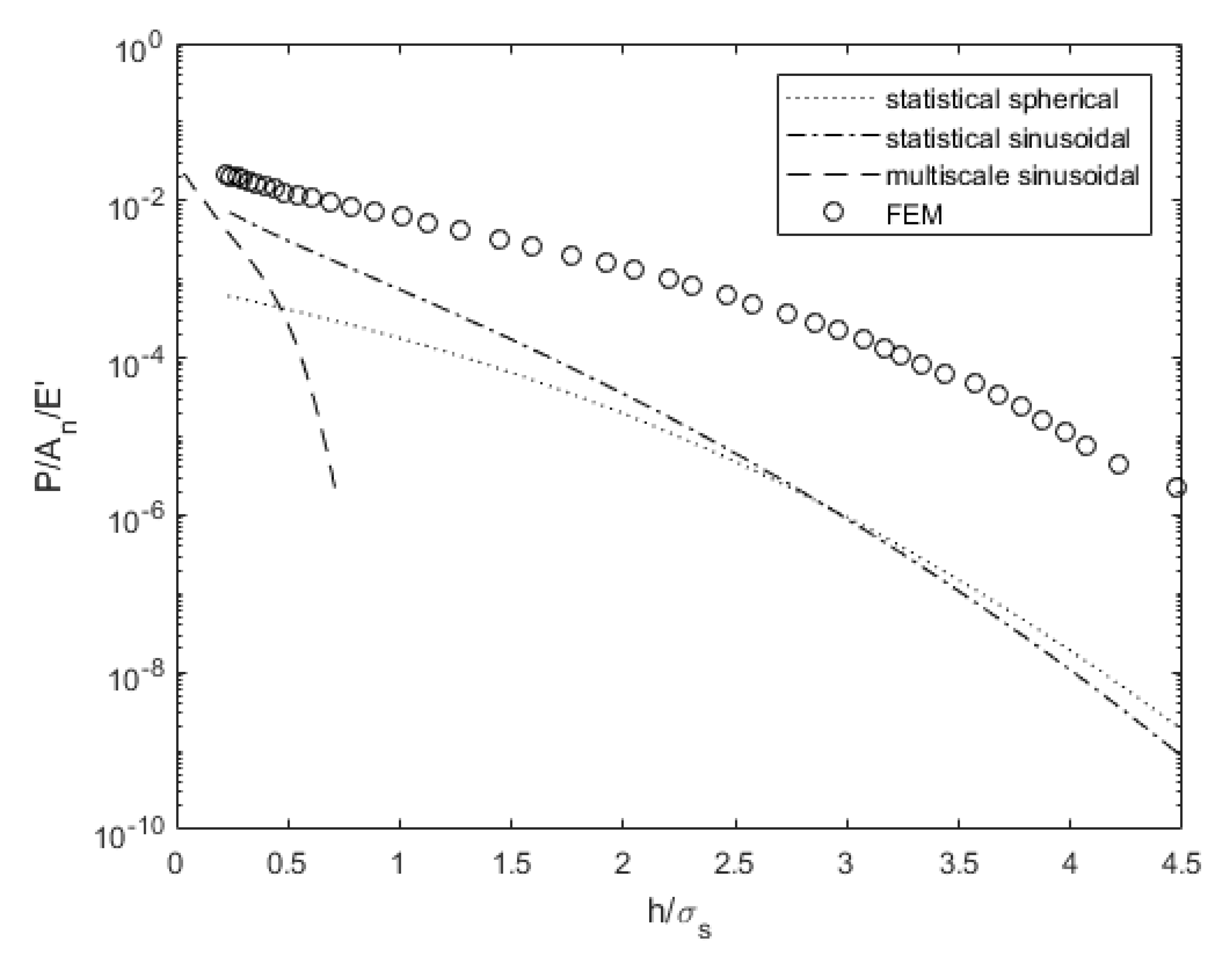
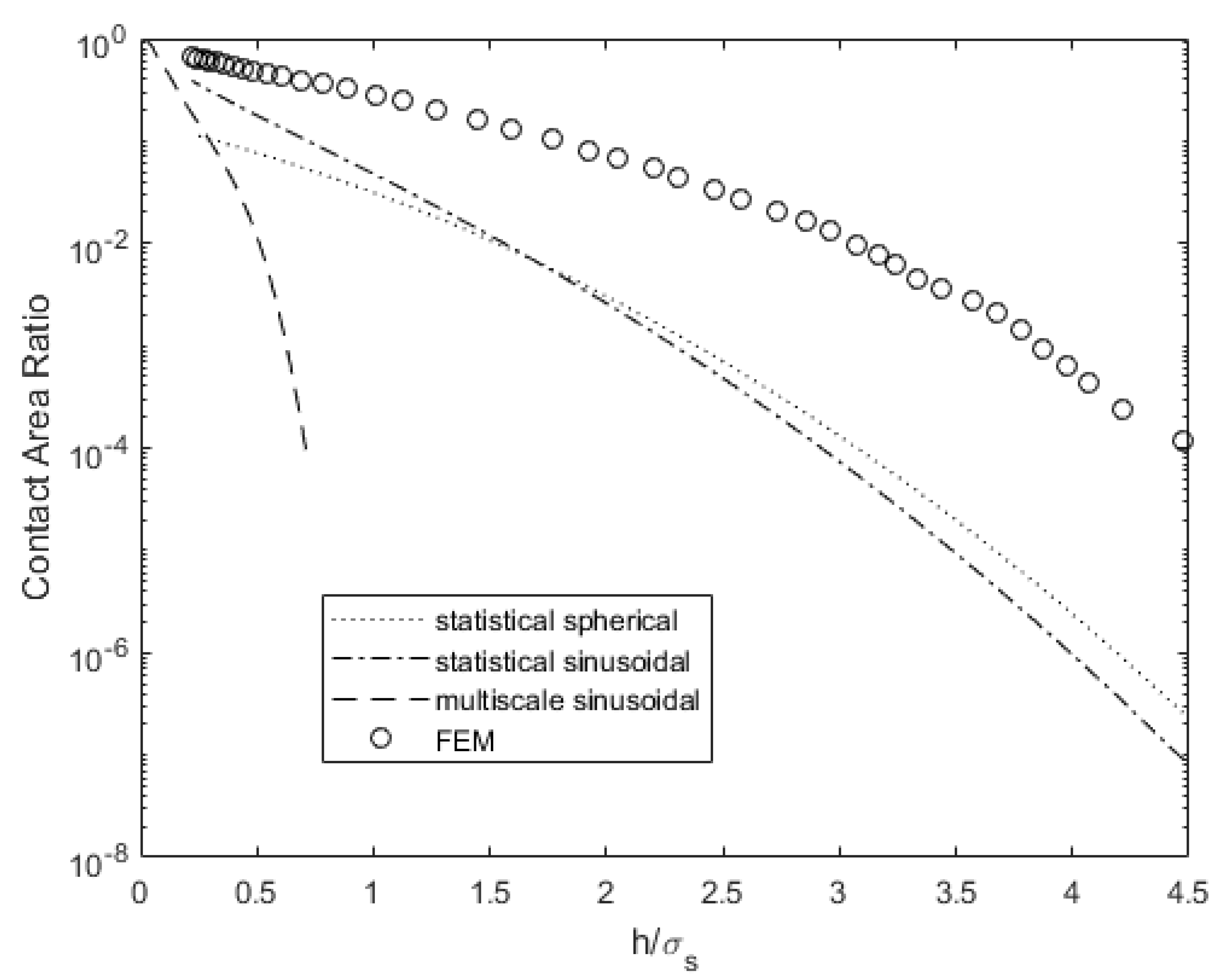
3. Results
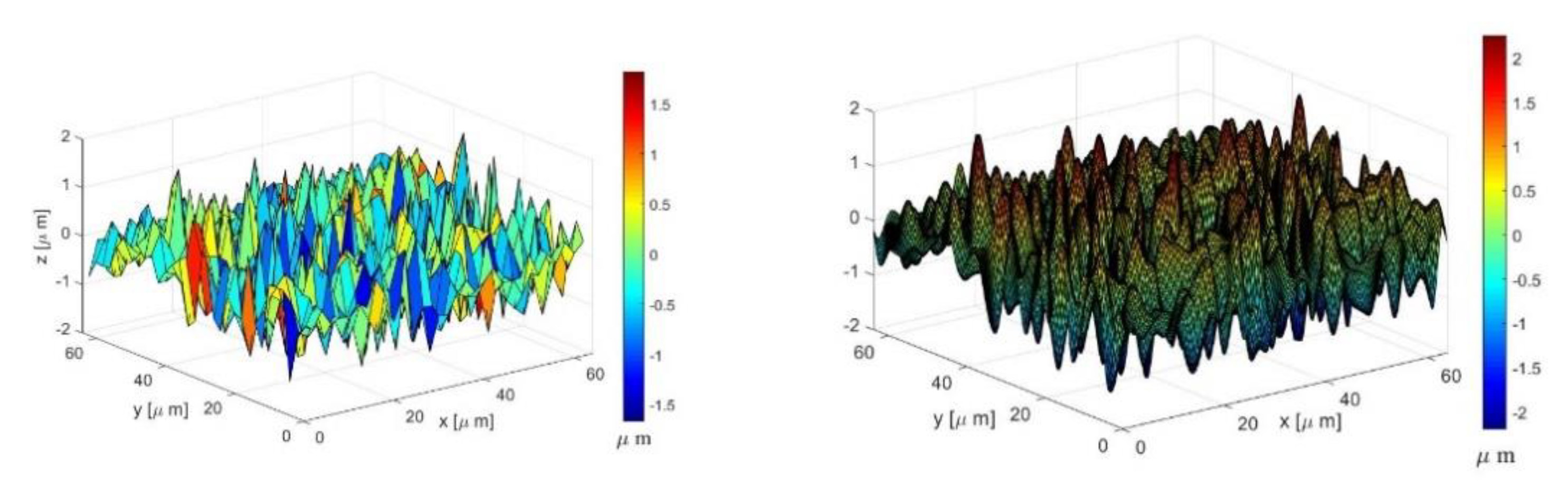
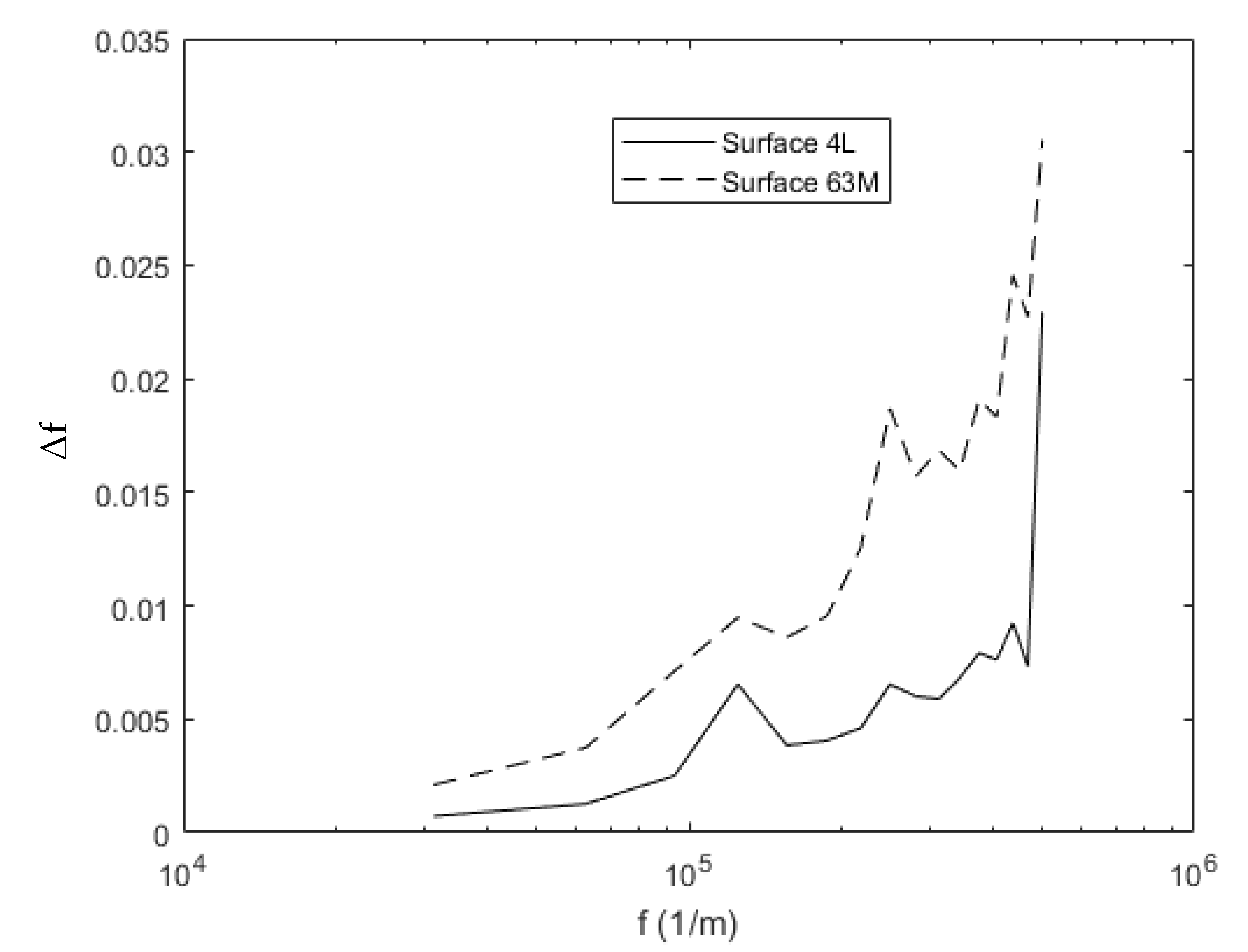
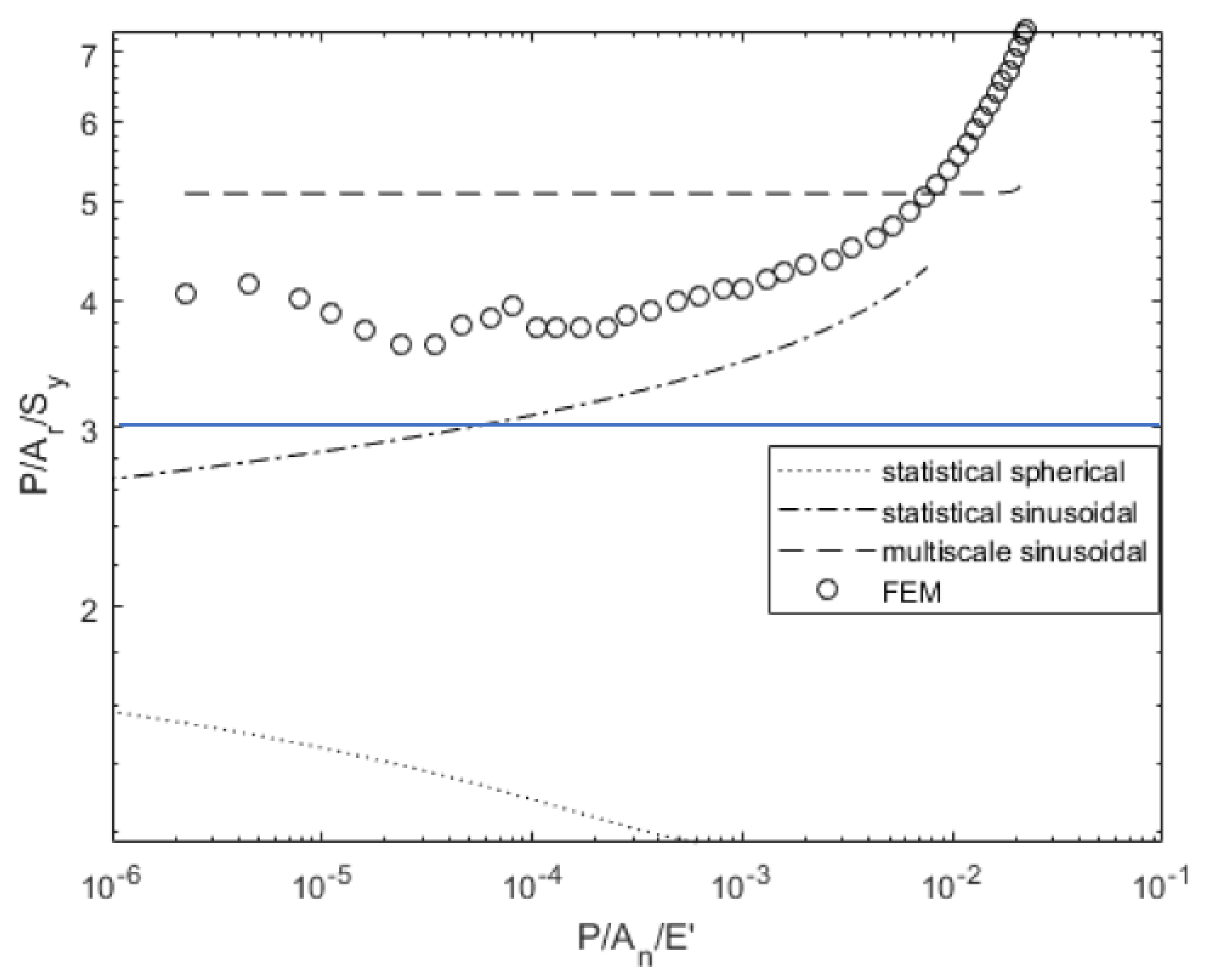
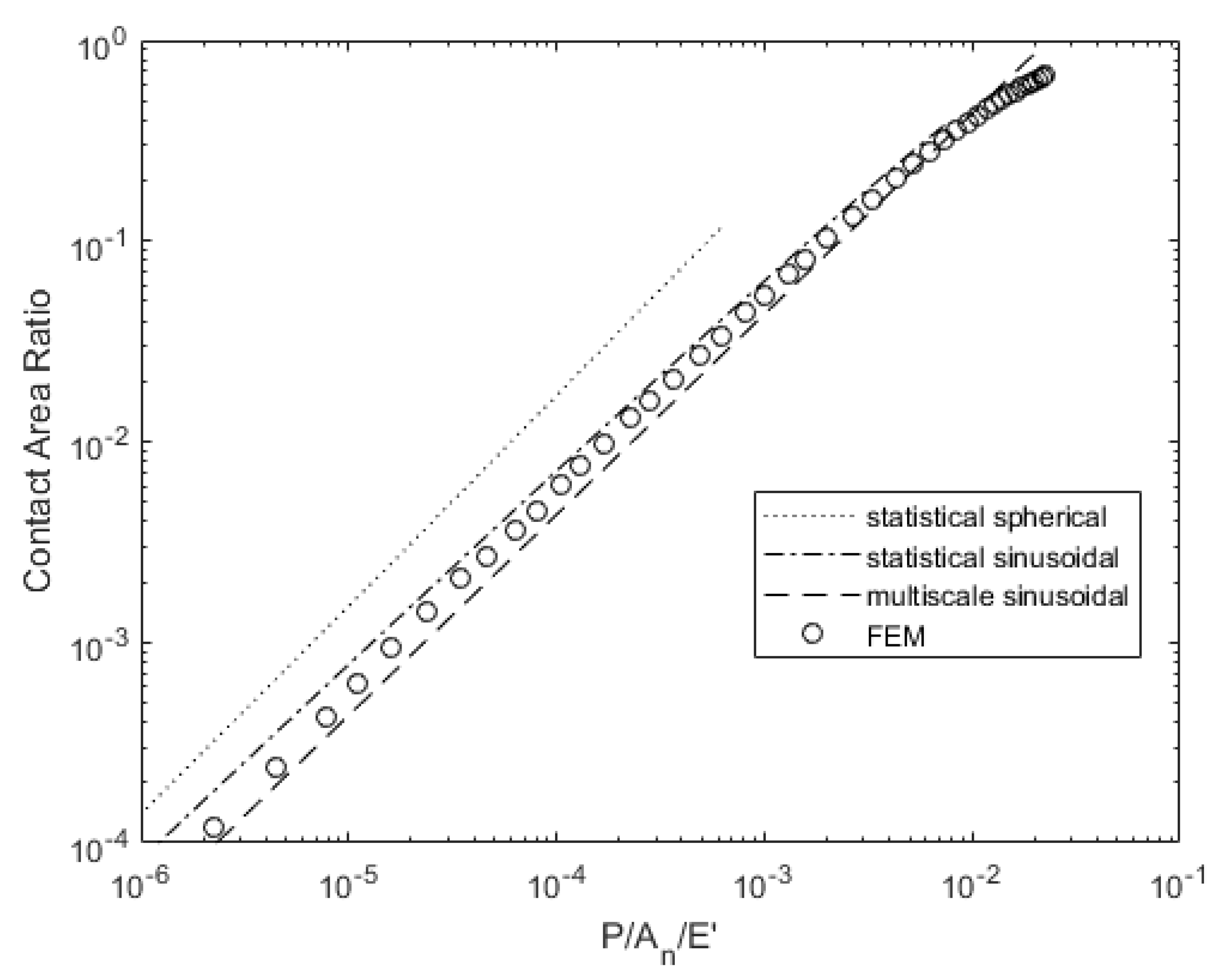
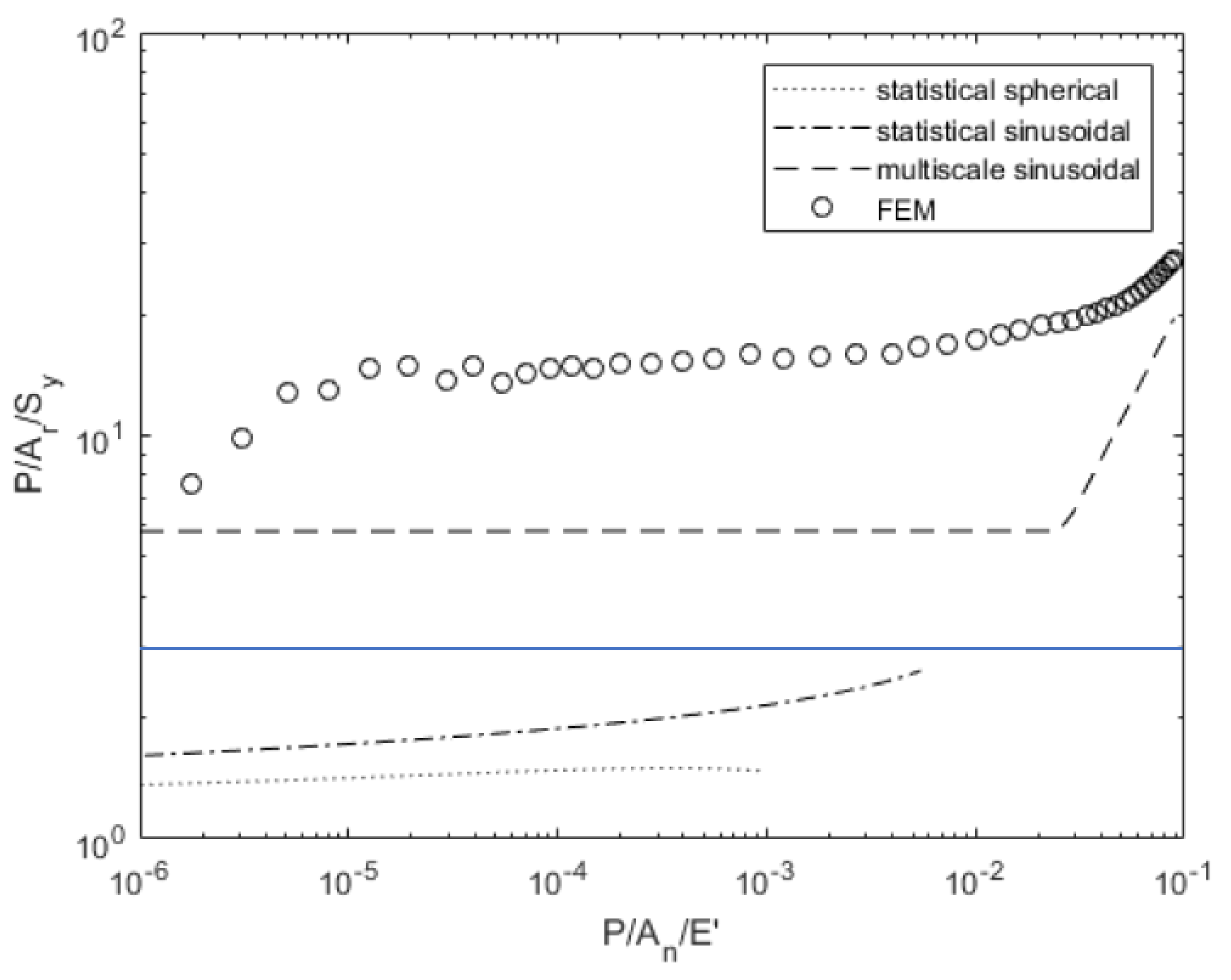
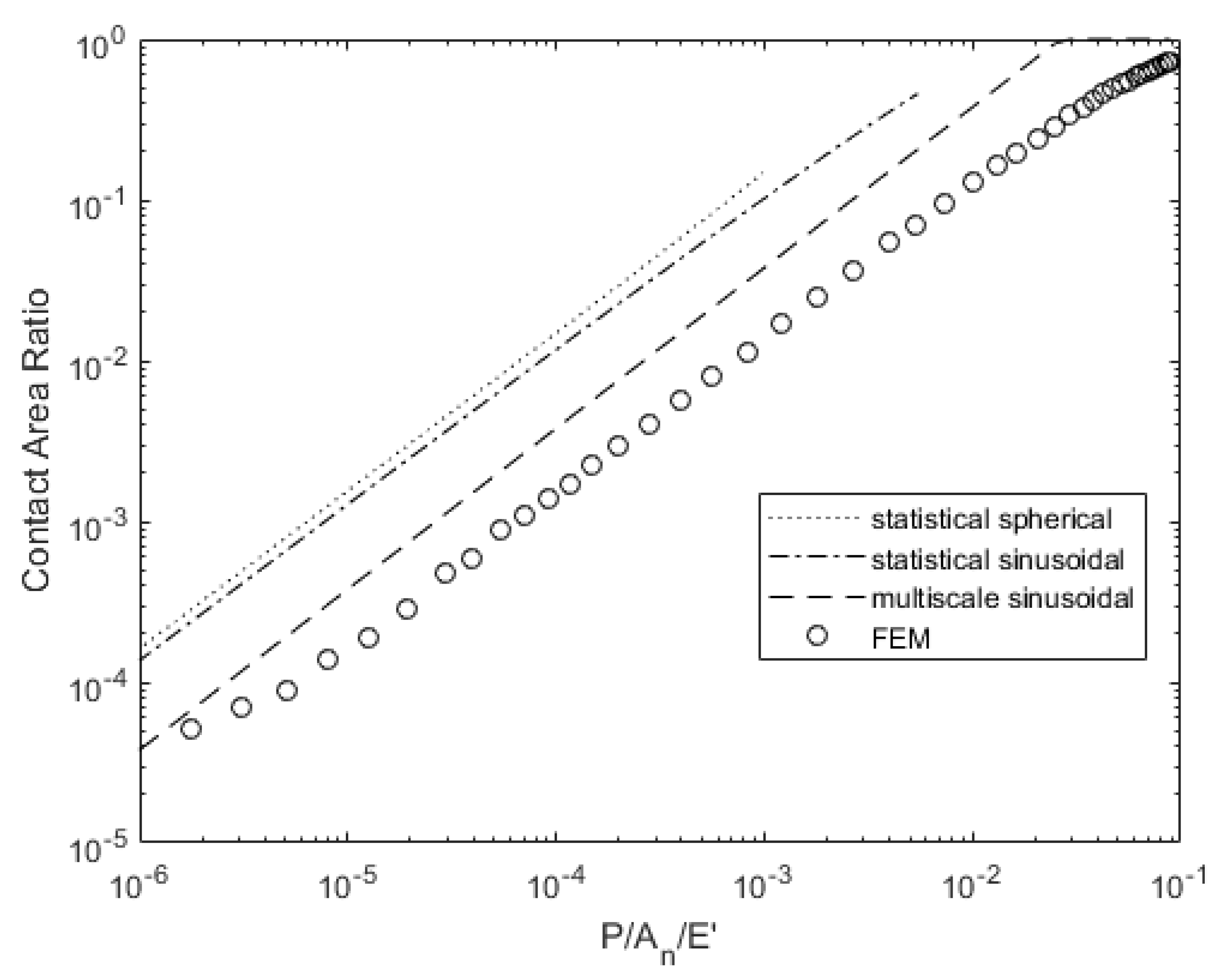
3.1. Surface 4L Analysis
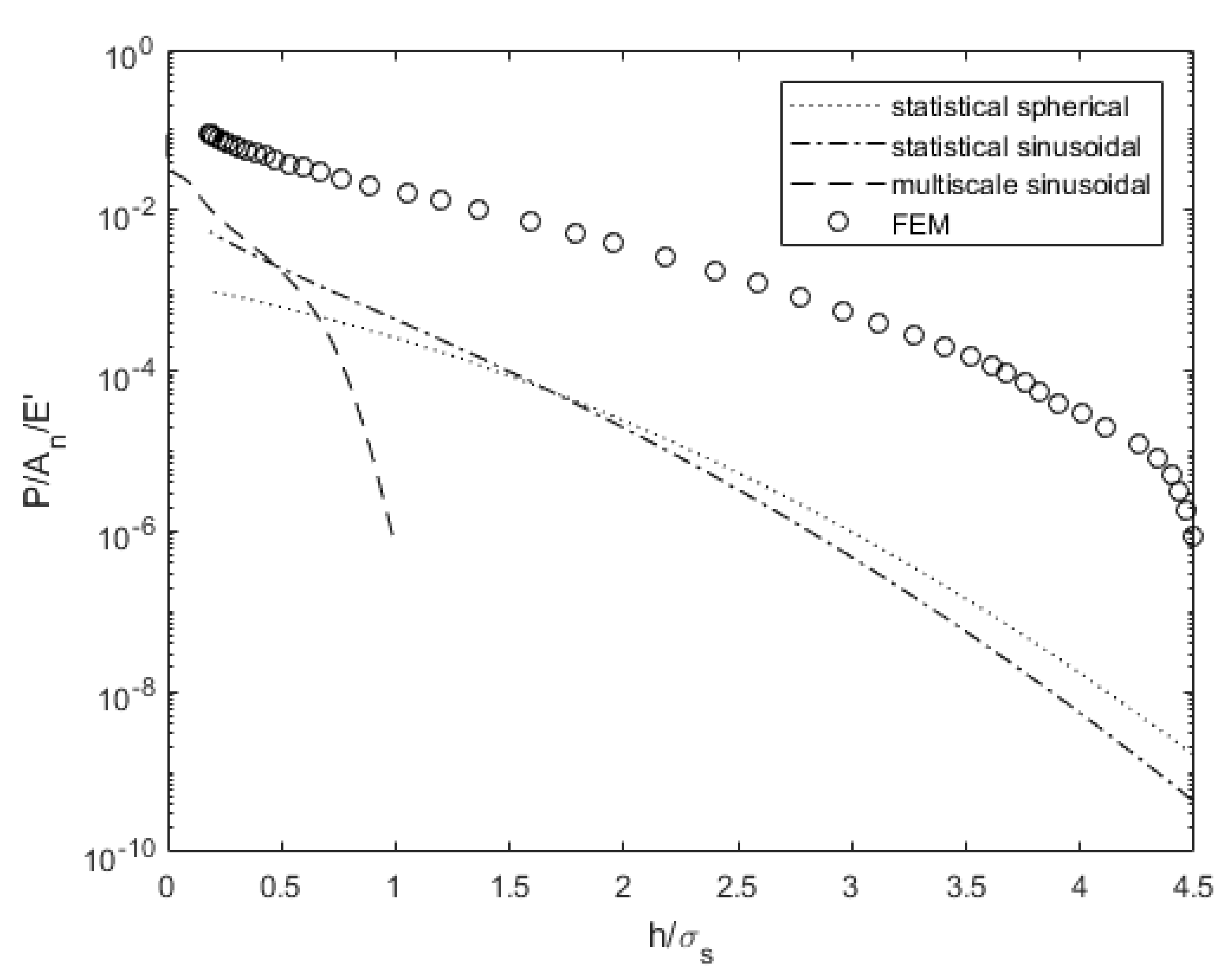
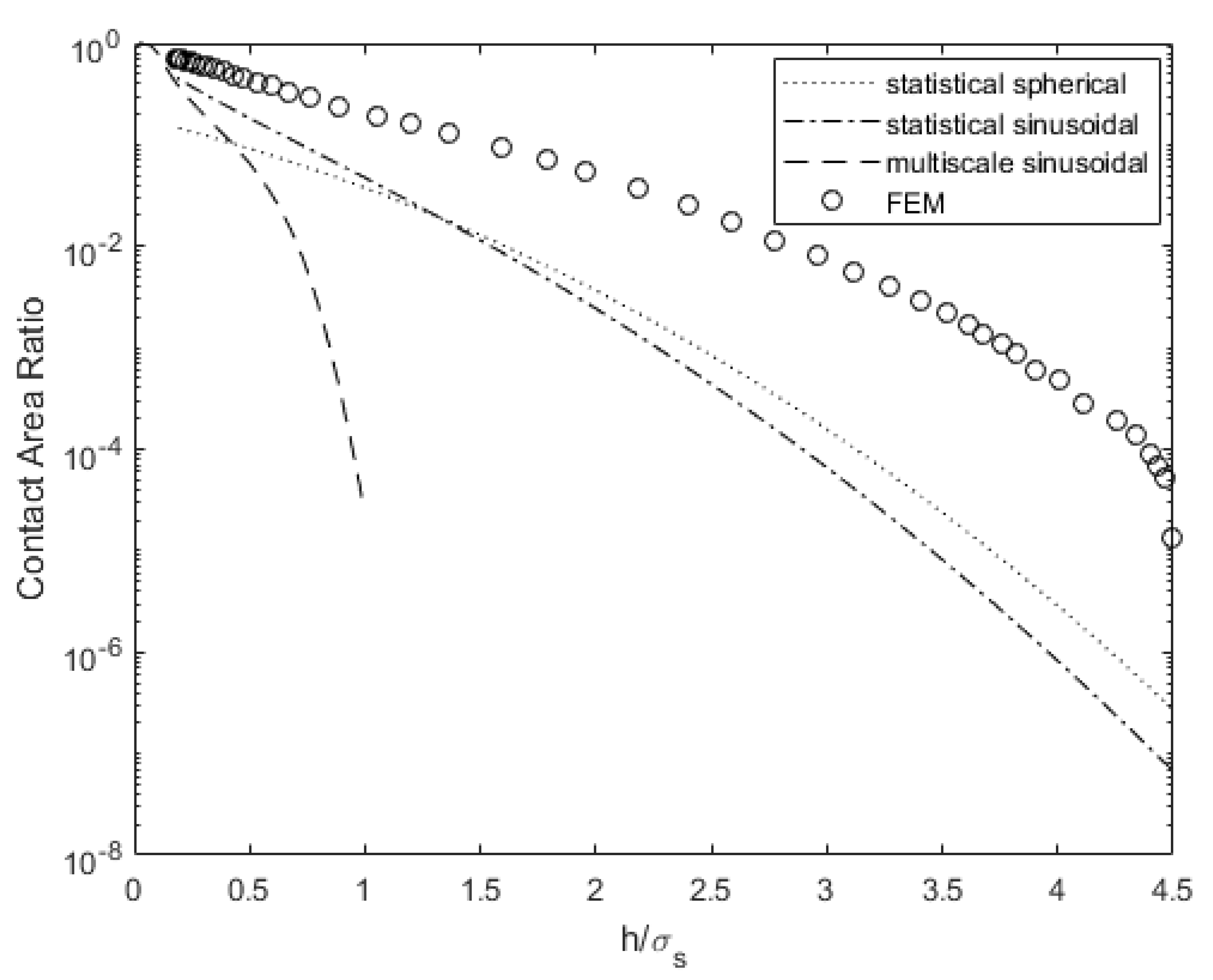
3.2. Surface 63M Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| An | Nominal contact area |
| Ar | Real contact area |
| Single asperity contact area | |
| ω | Interference between surfaces |
| ωc | Critical interference |
| Sy | Yield strength |
| E | Elastic modulus |
| ν | Poisson’s ratio |
| E’ | Effective elastic modulus, E/(1 − ν2) |
| Single asperity contact force | |
| η | Asperity density |
| R | Asperity radius |
| σs | RMS Asperity Height |
| f | Spatial frequency |
| Wavelength of sinusoidal surface (1/f) | |
| Δ | Amplitude of sinusoidal surface |
| Average pressure over surface | |
| p* | Average pressure for complete elastic contact |
| p*ep | Average pressure for complete elastic-plastic contact |
Appendix A. Summary of the JG Model
Appendix B. Contact Area and Load for the Sinusoidal Asperity Model
References
- Greenwood, J.A.; Williamson, J.B.P. Contact of nominally flat surfaces. Proc. R. Soc. London. Ser. A Math. Phys. Sci. 1966, 295, 300–319. [Google Scholar] [CrossRef]
- Chang, W.-R.; Etsion, I.; Bogy, D.B. An Elastic-Plastic Model for the Contact of Rough Surfaces. J. Tribol. 1987, 109, 257–263. [Google Scholar] [CrossRef]
- Jackson, R.L.; Green, I. A Statistical model of Elastic-Plastic Asperity Contact between Rough Surfaces. Trib. Int. 2006, 39, 906–914. [Google Scholar] [CrossRef]
- Kogut, L.; Etsion, I. A Finite Element Based Elastic-Plastic Model for the Contact of Rough Surfaces. Tribol. Trans. 2003, 46, 383–390. [Google Scholar] [CrossRef]
- Majumdar, A.; Bhushan, B. Fractal Model of Elastic-Plastic Contact between Rough Surfaces. J. Tribol. 1991, 113, 1–11. [Google Scholar] [CrossRef]
- Jackson, R.L.; Streator, J.L. A multi-scale model for contact between rough surfaces. Wear 2006, 261, 1337–1347. [Google Scholar] [CrossRef]
- Wadwalkar, S.S.; Jackson, R.; Kogut, L. A study of the elastic—plastic deformation of heavily deformed spherical contacts. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2010, 224, 1091–1102. [Google Scholar] [CrossRef]
- Ciavarella, M.; Greenwood, J.; Paggi, M. Inclusion of “interaction” in the Greenwood and Williamson contact theory. Wear 2008, 265, 729–734. [Google Scholar] [CrossRef]
- Afferrante, L.; Carbone, G.; Demelio, G. Interacting and coalescing Hertzian asperities: A new multiasperity contact model. Wear 2012, 278–279, 28–33. [Google Scholar] [CrossRef]
- Song, H.; van der Giessen, E.; Vakis, A. Asperity Interaction and Substrate Deformation in Statistical Summation Models of Contact between Rough Surfaces. J. Appl. Mech. 2016, 81, 041012. [Google Scholar]
- Ciavarella, M.; Demelio, G.; Barber, J.; Jang, Y.H. Linear elastic contact of the Weierstrass profile. Proc. R. Soc. A Math. Phys. Eng. Sci. 2000, 456, 387–405. [Google Scholar] [CrossRef] [Green Version]
- Johnson, K.; Greenwood, J.; Higginson, J. The contact of elastic regular wavy surfaces. Int. J. Mech. Sci. 1985, 27, 383–396. [Google Scholar] [CrossRef]
- Ciavarella, M.; Demelio, G. Elastic Multiscale Contact of Rough Surfaces: Archard’s Model Revisited and Comparisons with Modern Fractal Models. J. Appl. Mech. 2000, 68, 496–498. [Google Scholar] [CrossRef] [Green Version]
- Morag, Y.; Etsion, I. Resolving the contradiction of asperities plastic to elastic mode transition in current contact models of fractal rough surfaces. Wear 2007, 262, 624–629. [Google Scholar] [CrossRef]
- Candela, T.; Renard, F.; Bouchon, M.; Brouste, A.; Marsan, D.; Schmittbuhl, J.; Voisin, C. Characterization of Fault Roughness at Various Scales: Implications of Three-Dimensional High Resolution Topography Measurements. Pure Appl. Geophys. Pageoph 2009, 166, 1817–1851. [Google Scholar] [CrossRef] [Green Version]
- Pavelescu, D.; Tudor, A. On the Roughness Fractal Character, the Tribological Parameters and the Error Factors. Proc. Rom. Acad. 2004, 5, 1–6. [Google Scholar]
- Wu, J.-J. Characterization of fractal surfaces. Wear 2000, 239, 36–47. [Google Scholar] [CrossRef]
- Wu, J.-J. Spectral Analysis for the Effects of Stylus Tip Curvature on Measuring Fractal Profiles. Meas. Sci. Technol. 2000, 11, 1369–1376. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, Y.; Jackson, R.L. An analysis of generated fractal and measured rough surfaces in regards to their multi-scale structure and fractal dimension. Tribol. Int. 2017, 105, 94–101. [Google Scholar] [CrossRef]
- Zhang, X.; Jackson, R. An Analysis of the Multiscale Structure of Surfaces with Various Finishes. Tribol. Trans. 2017, 60, 121–134. [Google Scholar] [CrossRef]
- Whitehouse, D. Fractal or fiction. Wear 2001, 249, 345–353. [Google Scholar] [CrossRef]
- Jackson, R.L. An Analytical Solution to an Archard-Type Fractal Rough Surface Contact Model. Tribol. Trans. 2010, 53, 543–553. [Google Scholar] [CrossRef]
- Archard, J.F. Elastic deformation and the laws of friction. Proc. R. Soc. London. Ser. A Math. Phys. Sci. 1957, 243, 190–205. [Google Scholar] [CrossRef]
- Krithivasan, V.; Jackson, R.L. An analysis of three-dimensional elasto-plastic sinusoidal contact. Tribol. Lett. 2007, 27, 31–43. [Google Scholar] [CrossRef] [Green Version]
- Chen, Z.; Etsion, I. The elastic-plastic contact behavior of rough surfaces with hard coatings. Tribol. Int. 2019, 134, 435–442. [Google Scholar] [CrossRef]
- Song, H.; Vakis, A.; Liu, X.; van der Giessen, E. Statistical model of rough surface contact accounting for size-dependent plasticity and asperity interaction. J. Mech. Phys. Solids 2017, 106, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Li, L.; Etsion, I.; Talke, F.E. Contact Area and Static Friction of Rough Surfaces with High Plasticity Index. J. Tribol. 2010, 132, 031401-10. [Google Scholar] [CrossRef]
- Wang, X.; An, B.; Xu, Y.; Jackson, R.L. The effect of resolution on the deterministic finite element elastic-plastic rough surface contact under combined normal and tangential loading. Tribol. Int. 2020, 144, 106141. [Google Scholar] [CrossRef]
- Zhang, H.; Etsion, I. A Coupled Eulerian–Lagrangian Model for Sliding Inception of Elastic–Plastic Spherical Contact. J. Tribol. 2021, 143, 014501. [Google Scholar] [CrossRef]
- Zhang, H.; Etsion, I. Evolution of adhesive wear and friction in elastic-plastic spherical contact. Wear 2021, 478–479, 203915. [Google Scholar] [CrossRef]
- Liu, G.; Wang, Q.; Lin, C. A Survey of Current Models for Simulating the Contact between Rough Surfaces. Tribol. Trans. 1999, 42, 581–591. [Google Scholar] [CrossRef]
- Liu, G.; Zhu, J.; Yu, L.; Wang, Q.J. Elasto-Plastic Contact of Rough Surfaces. Tribol. Trans. 2001, 44, 437–443. [Google Scholar] [CrossRef]
- Jacq, C.; Ne´lias, D.; Lormand, G.; Girodin, D. Development of a Three-Dimensional Semi-Analytical Elastic-Plastic Contact Code. J. Tribol. 2002, 124, 653–667. [Google Scholar] [CrossRef]
- Sainsot, P.; Jacq, C.; Nélias, D. A Numerical Model for Elastoplastic Rough Contact. Comput. Modeling Eng. Sci. 2002, 3, 497–506. [Google Scholar]
- Wang, Z.; Wang, W.; Hu, Y.; Wang, H. A Simplified Numerical Elastic-Plastic Contact Model for Rough Surfaces. Adv. Tribol. 2009, 53, 159–166. [Google Scholar] [CrossRef]
- Pei, L.; Hyun, S.; Molinari, J.F.; Robbins, M.O. Finite Element Modeling of Elasto-Plastic Countact between Rough Surfaces. J. Mech. Phys. Solids 2005, 53, 2385–2409. [Google Scholar] [CrossRef]
- Sahoo, P.; Ghosh, N. Finite element contact analysis of fractal surfaces. J. Phys. D Appl. Phys. 2007, 40, 4245–4252. [Google Scholar] [CrossRef]
- Liu, H.; Leray, D.; Colin, S.; Pons, P.; Broué, A. Finite Element Based Sourface Roughness Study for Ohmic Contact of Microswitches. In Proceedings of the IEEE 58th Holm Conference on Electrical Contacts (Holm), Portland, OR, USA, 23–26 September 2012; pp. 1–10. [Google Scholar]
- Thompson, M.K.; Thompson, J.M. Considerations for the incorporation of measured surfaces in finite element models. Scanning 2010, 32, 183–198. [Google Scholar] [CrossRef]
- Thompson, M.K. A Comparions of Methods to Evaluate the Behavior of Finite Element Models with Rough Surfaces. Scanning 2011, 33, 353–369. [Google Scholar] [CrossRef]
- Megalingam, A.; Mayuram, M.M. Comparative Contact Analysis Study of Finite Element Method Based Deterministic, Simplified Multi-Asperity and Modified Statistical Contact Models. J. Tribol. 2012, 134, 014503. [Google Scholar] [CrossRef]
- Wang, X.; Xu, Y.; Jackson, R.L. Theoretical and Finite Element Analysis of Static Friction between Multi-Scale Rough Surfaces. Tribol. Lett. 2018, 66, 146. [Google Scholar] [CrossRef]
- An, B.; Wang, X.; Xu, Y.; Jackson, R.L. Deterministic Elastic-Plastic Modelling of Rough Surface Contact Including Spectral Interpolation and Comparison to Theoretical Models. Tribol. Int. 2019, 135, 246–258. [Google Scholar] [CrossRef]
- Jackson, R.L.; Saha, S.; Xu, Y. The Influence of Single Asperity Models on Predicting Contact Between Elastic Rough Surfaces Using Statistical Methods. In Proceedings of the STLE Tribology Frontiers Conference, Denver, CO, USA, 25–27 October 2015. [Google Scholar]
- Rostami, A.; Jackson, R.L. Predictions of the average surface separation and stiffness between contacting elastic and elastic–plastic sinusoidal surfaces. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2013, 227, 1376–1385. [Google Scholar] [CrossRef]
- Wang, X. Static Friction and Junction Growth of Contacting Three-Dimensional Sinusoidal Asperities and Rough Surfaces; Auburn University: Auburn, AL, USA, 2017. [Google Scholar]
- Wilson, W.E.; Angadi, S.; Jackson, R. Surface separation and contact resistance considering sinusoidal elastic–plastic multi-scale rough surface contact. Wear 2010, 268, 190–201. [Google Scholar] [CrossRef]
- Meier, D.; Schroder, D. Contact resistance: Its measurement and relative importance to power loss in a solar cell. IEEE Trans. Electron Devices 1984, 31, 647–653. [Google Scholar] [CrossRef]
- Wang, A.; Zhao, J. Review of prediction for thermal contact resistance. Sci. China Ser. E Technol. Sci. 2010, 53, 1798–1808. [Google Scholar] [CrossRef]
- Williamson, J.B.P.; Hunt, R.T. Asperity persistence and the real area of contact between rough surfaces. Proc. R. Soc. London. Ser. A Math. Phys. Sci. 1972, 327, 147–157. [Google Scholar] [CrossRef]
- Jackson, R.L. The Effect of Scale-Dependent Hardness on Elasto-Plastic Asperity Contact between Rough Surfaces. Tribol. Trans. 2006, 49, 135–150. [Google Scholar] [CrossRef]
- Jackson, R.L.; Crandall, E.R.; Bozack, M.J. Rough surface electrical contact resistance considering scale dependent properties and quantum effects. J. Appl. Phys. 2015, 117, 195101. [Google Scholar] [CrossRef]
- Jackson, R.L.; Krithivasan, V.; Wilson, W.E. The pressure to cause complete contact between elastic—plastic sinusoidal surfaces. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2008, 222, 857–863. [Google Scholar] [CrossRef]
- Manners, W. Plastic deformation of a sinusoidal surface. Wear 2008, 264, 60–68. [Google Scholar] [CrossRef]
- Tiwari, A.; Almqvist, A.; Persson, B.N.J. Plastic Deformation of Rough Metallic Surfaces. Tribol. Lett. 2020, 68, 129. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, W.; Zhao, Z. The effect of surface roughness characteristics on the elastic–plastic contact performance. Tribol. Int. 2014, 79, 59–73. [Google Scholar] [CrossRef]


| 32 × 32 | 64 × 64 | 128 × 128 | 256 × 256 | |
|---|---|---|---|---|
| R (µm) | 6.9 | 1.335 | 0.989 | 0.958 |
| η (1/µm2) | 0.0234 | 0.1074 | 0.1523 | 0.168 |
| σs (μm) | 0.1615 | 0.223 | 0.246 | 0.261 |
| Skewness | 0.1 | 0.086 | 0.086 | 0.0864 |
| Kurtosis | 2.38 | 2.59 | 2.54 | 2.53 |
| 32 × 32 | 64 × 64 | 128 × 128 | 256 × 256 | |
|---|---|---|---|---|
| R (µm) | 2.75 | 0.8 | 0.567 | 0.518 |
| η (1/µm2) | 0.0327 | 0.11 | 0.1494 | 0.16 |
| σs (μm) | 0.413 | 0.476 | 0.495 | 0.501 |
| Skewness | 0.137 | 0.114 | 0.1134 | 0.113 |
| Kurtosis | 3.32 | 3.46 | 3.423 | 3.42 |
| Property | Value |
|---|---|
| E | 200 GPa |
| ν | 0.3 |
| Sy | 1 GPa |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chu, N.R.; Jackson, R.L.; Wang, X.; Gangopadhyay, A.; Ghaednia, H. Evaluating Elastic-Plastic Wavy and Spherical Asperity-Based Statistical and Multi-Scale Rough Surface Contact Models with Deterministic Results. Materials 2021, 14, 3864. https://doi.org/10.3390/ma14143864
Chu NR, Jackson RL, Wang X, Gangopadhyay A, Ghaednia H. Evaluating Elastic-Plastic Wavy and Spherical Asperity-Based Statistical and Multi-Scale Rough Surface Contact Models with Deterministic Results. Materials. 2021; 14(14):3864. https://doi.org/10.3390/ma14143864
Chicago/Turabian StyleChu, Nolan Ryan, Robert L. Jackson, Xianzhang Wang, Arup Gangopadhyay, and Hamed Ghaednia. 2021. "Evaluating Elastic-Plastic Wavy and Spherical Asperity-Based Statistical and Multi-Scale Rough Surface Contact Models with Deterministic Results" Materials 14, no. 14: 3864. https://doi.org/10.3390/ma14143864
APA StyleChu, N. R., Jackson, R. L., Wang, X., Gangopadhyay, A., & Ghaednia, H. (2021). Evaluating Elastic-Plastic Wavy and Spherical Asperity-Based Statistical and Multi-Scale Rough Surface Contact Models with Deterministic Results. Materials, 14(14), 3864. https://doi.org/10.3390/ma14143864







