Use of the AE Effect to Determine the Stresses State in AAC Masonry Walls under Compression
Abstract
:1. Introduction
2. Theoretical Bases of the AE Method
3. Program of Own Research
4. Test Results
4.1. Stage I-Determination of Acoustoelastic Constant
4.1.1. Physical and Mechanical Properties of Autoclaved Aerated Concrete AAC
4.1.2. Test Stand and Procedure
- Hydraulic systems “A” (Zwick Roell Company Group, Ulm, Germany) and “B” (Hydac International GmbH, Sulzbach/Saar, Germany),
- Electrical system: developed by authors’ of the tests
- Peripheral devices: the model P30 pressure transmitters (WIKA SE & Co. KG, Klingenberg, Germany), the draw-wire displacement converters of SWH-1-B-FK-01 type with the TRA50-SA1800WSC01 encoder (TWK-ELEKTRONIK GmbH, Düsseldorf, Germany), the Digital Image Correlation System ARAMIS 6M ((GOM GmbH, Braunschweig, Germany), the PUNDITLAB+ instrument for reading and recording ultrasonic waves (Proceq Europe, Schwerzenbach, Switzerland),
- The measurement and control interface: based on the NIcRIO 9022, NIcRIO 9056 controller (National Instruments, Austin, TX, USA),
- IT system: developed by the authors in the LABVIEW 2020 software (National Instruments, Austin, TX, USA) [41].
4.1.3. Test Results
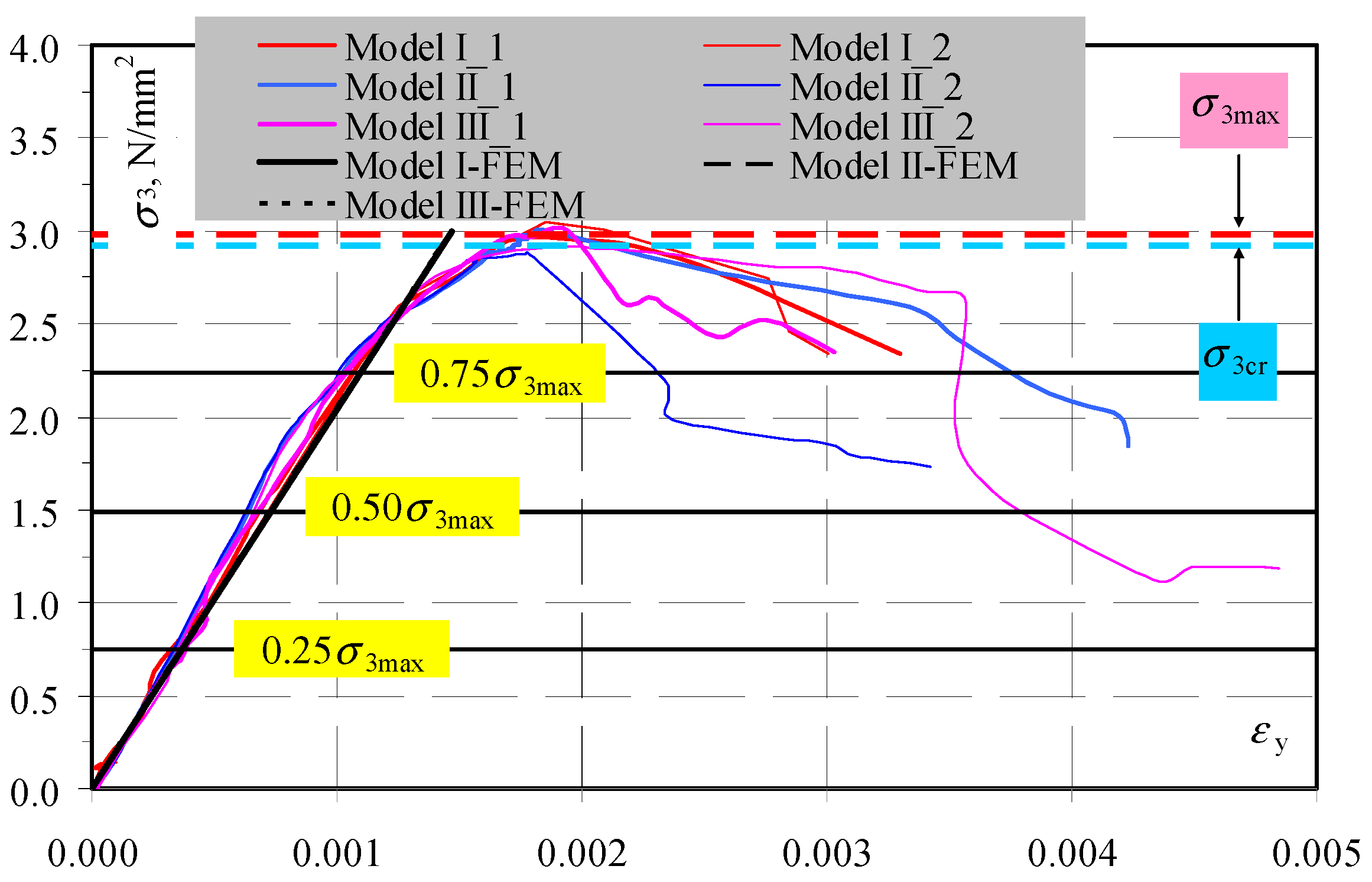
4.2. Stage II-Testing Models under Compression
5. Analysis of Test Results
5.1. Components of Stress State Based on the AE Effect
5.2. Numerical FEM Model
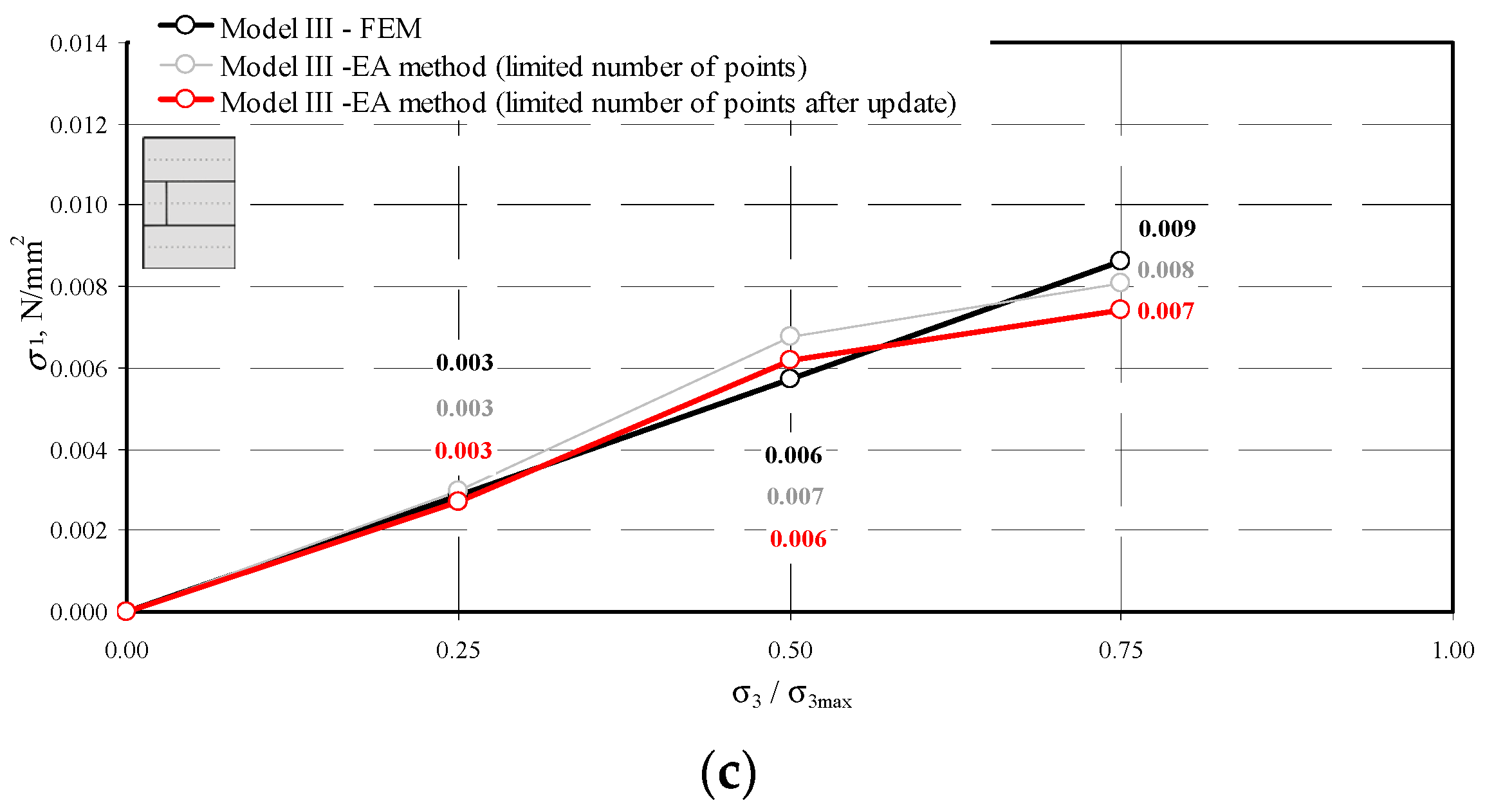
5.3. Model Update
- the general population had the normal distribution N(μ, σ),
- the variance σ of the general population was unknown at the known standard deviation for the small sample, which was taken as (νtest = 15%—the coefficient of variation corresponding to the results from the in-situ tests),
- α = 0.05—the confidence level,
- the relative error was defined at the level 0.5α = 0.0025. The absolute value was taken as d = 0.5α ,
- the minimum number of samples [53] were determined from the relationship , where tα,n−1 = 2.017—the parameter of a two-tailed T distribution at n − 1 degrees of freedom, n = 44—the number of samples to determine the number of samples.
6. Conclusions
- the acoustoelastic (AE) method was confirmed to be applied to mean hydrostatic stresses in AAC,
- the relationships between the acoustoelastic coefficient δP and AAC density and moisture content AAC were established,
- the performed measurements of the velocity of ultrasonic wave propagation were used to quite precisely determine the mean hydrostatic stresses in the wall (when compared to the FEM calculations) when the number of measuring points was high,
- a reduction in the measuring points significantly underestimated the mean hydrostatic stresses,
- the method validation considerably diminished differences between the experimentally obtained results and the calculations. The maximum overestimation of stress values did not exceed 15%, and the underestimation was at the level of 6%.
- an empirical nature of the employed method constraints possible applications to the complete range of standard stresses in the masonry. The reliable estimation of the mean stresses for the model validated can be used even to the level of <0.75σ3max.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Auld, B.A. Acoustic Fields an Waves in Solid; John Wiley and Sons: New York, NY, USA; London, UK; Sydney, NSW, Australia; Toronto, ON, Canada, 1973. [Google Scholar]
- Bayer, R.T.; Letcher, S.V. Phisical Ultarsonics; Academic Press: New York, NY, USA; London, UK, 1969. [Google Scholar]
- Malhotra, V.M.; Carino, N.J. Handbook on Nondestructive Testing of Concrete; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Huan, H.; Liu, L.; Mandelis, A.; Peng, C.; Chen, X.; Zhan, J. Mechanical Strength Evaluation of Elastic Materials by Multiphysical Nondestructive Methods: A Review. Appl. Sci. 2020, 10, 1588. [Google Scholar] [CrossRef] [Green Version]
- Hola, J.; Schabowicz, K. State-of-the-art non-destructive methods for diagnostic testing of building structures—Anticipated development trends. Arch. Civ. Mech. Eng. 2010, 10, 5–18. [Google Scholar] [CrossRef]
- Breysse, D. Nondestructive evaluation of concrete strength: An historical review and a new perspective by combining NDT methods. Constr. Build. Mater. 2012, 33, 139–163. [Google Scholar] [CrossRef]
- Reda, H.; Karathanasopoulos, N.; Elnady, K.; Ganghoffer, J.F.; Lakiss, H. The role of anisotropy on the static and wave propagation characteristics of two-dimensional architectured materials under finite strains. Mater. Des. 2018, 147, 134–145. [Google Scholar] [CrossRef]
- Reda, H.; Elnady, K.; Ganghoffer, J.F.; Lakiss, H. Wave propagation in pre-deformed periodic network materials based on large strains homogenization. Compos. Struct. 2018, 184, 860–871. [Google Scholar] [CrossRef]
- Srikantha Phani, A.; Woodhouse, J.; Fleck, N.A. Wave propagation in two-dimensional periodic lattices. J. Acoust. Soc. Am. 2006, 119, 1995–2005. [Google Scholar] [CrossRef] [Green Version]
- Gonella, S.; Ruzzene, M. Analysis of in-plane wave propagation in hexagonal and re-entrant lattices. J. Sound Vib. 2008, 312, 125–139. [Google Scholar] [CrossRef]
- Jasiński, R. Identification of Stress States in Compressed Masonry Walls Using a Non-Destructive Technique (NDT). Materials 2020, 13, 2852. [Google Scholar] [CrossRef]
- Gennisson, J.; Renier, M.; Catheline, S. Acoustoelasticity in soft solids: Assessment of the nonlinear shear modulus with the acoustic radiation force. J. Acoust. Soc. Am. 2007, 122, 3211–3219. [Google Scholar] [CrossRef]
- Homann, M. Porenbeton Handbuch. Planen und bauen Mit system, 6. In Auflage Hannover; Bauverlag: Gütersloh, Germany, 2008; ISBN 978-3-7625-3626-0. [Google Scholar]
- Jasiński, R.; Drobiec, Ł.; Mazur, W. Validation of Selected Non-Destructive Methods for Determining the Compressive Strength of Masonry Units Made of Autoclaved Aerated Concrete. Materials 2019, 12, 389. [Google Scholar] [CrossRef] [Green Version]
- Jasiński, R. Determination of AAC masonry compressive strength by semi destructive method. Nondestruct. Test. Diagn. 2018, 3, 81–85. [Google Scholar] [CrossRef] [Green Version]
- Biot, M.A. The influence of initial stress on elastic waves. J. Appl. Phys. 1940, 11, 522–530. [Google Scholar] [CrossRef]
- Huges, D.S.; Kelly, J.L. Second Order Elastic Deformation of Solids. Phys. Rev. 1953, 1145–1149. [Google Scholar] [CrossRef]
- Bergman, R.H.; Shahbender, R.A. Effect of statically applied stresses on the velocity of propagation of ultrasonic waves. J. Appl. Phys. 1958, 29, 1736–1738. [Google Scholar] [CrossRef]
- Tokuoka, T.; Saito, M. Elastic wave propagations and acoustical birefringence in stressed crystals. J. Acoust. Soc. Am. 1968, 45, 1241–1246. [Google Scholar] [CrossRef]
- Husson, D.; Kino., G.S. A perturbation theory for acoustoelastic effects. J. Appl. Phys. 1982, 53, 7250–7258. [Google Scholar] [CrossRef]
- Benson, R.W.; Raelson, V.J. Acoustoelasticity. Prod. Eng. 1959, 20, 56–59. [Google Scholar]
- Nikitina, N.Y.; Ostrovsky, L.A. An ultrasonic method for measuring stresses in engineering materials. Ultrasonics 1998, 35, 605–610. [Google Scholar] [CrossRef]
- Dorfi, H.R.; Busby, H.R.; Janssen, M. Ultrasonic stress measurements based on the generalized acoustic ratio technique. Int. J. Solids Struct. 1996, 33, 1157–1174. [Google Scholar] [CrossRef]
- Man, C.; Lu, W.Y. Towards an acoustoelastic theory for measurement of residual stress. J. Elast. 1987, 17, 159–182. [Google Scholar] [CrossRef]
- Murnaghan, F.D. Finite Deformation of an Elastic Solid; Wiley: New York, NY, USA, 1951. [Google Scholar]
- Murnaghan, F.D. Finite deformations of an elastic solid. Am. J. Math. 1937, 59, 235–260. Available online: https://www.jstor.org/stable/2371405 (accessed on 10 April 2020). [CrossRef]
- Tylczyński, Z.; Mróz, B. The influence of uniaxial stress on ultrasonic wave propagation in ferroelastic (NH4)4LiH3(SO4)4. Solid State Commun. 1997, 101, 653–656. [Google Scholar] [CrossRef]
- Takahashi, S.; Motegi, R. Measurement of third-order elastic constants and applications to loaded structural materials. SpringerPlus 2015, 4, 1–20. [Google Scholar] [CrossRef] [Green Version]
- Takahashi, S. Measurement of third-order elastic constants and stress dependent coefficients for steels. Mech. Adv. Mater. Mod. Process. 2018, 4. [Google Scholar] [CrossRef] [Green Version]
- Egle, D.M.; Bray, D.E. Measurement of acoustoelastic and third-order elastic constants for rail steel. J. Acoust. Soc. Am. 1976, 60, 741–744. [Google Scholar] [CrossRef]
- Takahashi, S. Stress Measurement Method and its Apparatus. U.S. Patent 7299138, 10 December 2007. [Google Scholar]
- Deputat, J. Properties and Use of the Elastoacoustic Phenomenon to Measure Self-Stress; Institute of Fundamental Technological Research Polish Academy of Sciences: Warsaw, Poland, 1987. (In Polish) [Google Scholar]
- EN 771-4:2011. Specification for Masonry Units—Part 4: Autoclaved Aerated Concrete Masonry Units; CEN: Brussels, Belgium, 2012. [Google Scholar]
- Bartlett, F.M.; Macgregor, J.G. Effect of Moisture Condition on Concrete Core Strengths. ACI Mater. J. 1993, 91, 227–236. [Google Scholar]
- Suprenant, B.A.; Schuller, M.P. Nondestructive Evaluation & Testing of Masonry Structures; Hanley Wood Inc.: San Antonio, TX, USA, 1994; ISBN 978-0924659577. [Google Scholar]
- McCann, D.M.; Forde, M.C. Review of NDT methods in the assessment of concrete and masonry structures. NDT E Int. 2001, 34, 71–84. [Google Scholar] [CrossRef]
- Jasiński, R.; Stebel, K.; Domin, J. Application of the DIC Technique to Remote Control of the Hydraulic Load System. Remote Sens. 2020, 12, 3667. [Google Scholar] [CrossRef]
- Polish Patent Office. The Testing Machine for Testing the Elements and Structures. Niepodległości 188/192, 00-950. Patent 432225, 16 December 2019. [Google Scholar]
- Klopot, T.; Skupin, P.; Grelewicz, P.; Czeczot, J. Practical PLC-based Implementation of Adaptive Dynamic Matrix Controller for Energy-Efficient Control of Heat Sources. IEEE Trans. Ind. Electron. 2020. [Google Scholar] [CrossRef]
- Nowak, P.; Stebel, K.; Klopot, J.; Czeczot, T.; Fratczak, M.; Laszczyk, P. Flexible function block for industrial applications of active disturbance rejection controller. Arch. Control. Sci. 2018, 28, 379–400. [Google Scholar] [CrossRef]
- Nocoń, W.; Polaków, G. LabVIEW Based Cooperative Design for Control System Implementation; CDVE 2011, LNCS; Luo, Y., Ed.; Springer: Berlin/Heidelberg, Germany, 2011; Volume 6874, pp. 137–140. [Google Scholar]
- Bolton, W. Mechatronics Electronic Control Systems in Mechanical and Electrical Engineering; Prentice Hall: Hoboken, NJ, USA, 2009; ISBN 978-0-13-240763-2. [Google Scholar]
- Rohner, P. Industrial Hydrualic Control; Willey: Hoboken, NJ, USA, 1995; ISBN 958149313. [Google Scholar]
- Bolton, W. Pneumatic and Hydraulic Systems; Butterworth-Heinemann: Oxford, UK, 1997; ISBN 750638362. [Google Scholar]
- Aciatore, D.G.; Histand, M.B. Introduction to Mechatronics and Measurement Systems; McGraw-Hill Companies: New York, NY, USA, 2012; ISBN 978-0072402414. [Google Scholar]
- EN 1015-11:2001/A1. Methods of Test for Mortar for Masonry. Part 11: Determination of Flexural and Compressive Strength of Hardened Mortar; CEN: Brussels, Belgium, 2007. [Google Scholar]
- EN 998-2. Specification for Mortar for Masonry. Masonry Mortar; CEN: Brussels, Belgium, 2003. [Google Scholar]
- Chu, T.C.; Ranson, W.F.; Sutton, M.A.; Peters, W.H. Application of digital-image-correlation techniques to experimental mechanics. Exp. Mech. 1985, 25, 232–244. [Google Scholar] [CrossRef]
- Lord, J.D. Digital Image Correlation (DIC), Modern Stress and Strain Analysis. A State of the Art Guide To Measurement Techniques, BSSM; Eaton Evans, J., Dulie-Barton, J.M., Burguete, R.L., Eds.; University of Southampton: Southampton, UK, 2009; pp. 14–15. [Google Scholar]
- Pan, K.; Yu, R.C.; Hang, X.; Ruiz, G.; Wu, Z. Propagation Speed of Dynamic Mode-I Cracks in Self-Compacting Steel Fiber-Reinforced Concrete. Materials 2020, 13, 4053. [Google Scholar] [CrossRef] [PubMed]
- Blenkinsopp, R.; Roberts, J.; Parland, A.; Sherratt, P.; Smith, P.; Lucas, T. A Method for Calibrating a Digital Image Correlation System for Full-Field Strain Measurements during Large Deformations. Appl. Sci. 2019, 9, 2828. [Google Scholar] [CrossRef] [Green Version]
- Jasiński, R. Research and Modelling of Masonry Shear. Walls; Silesian University of Technology: Gliwice, Poland, 2017; ISBN 978-83-7880-477-2. [Google Scholar]
- Volk, W. Applied Statistics for Engineers; Literary Licensing, LLC: Whitefish, MT, USA, 2013. [Google Scholar]
- Sundar, V.S.; Manohar, C.S. Updating reliability models of statically loaded instrumented structures. Struct. Saf. 2013, 40, 21–30. [Google Scholar] [CrossRef]
- Nowak, A.; Collins, K.R. Reliability of Structures, 2nd ed.; CRC Press: London, UK, 2013; ISBN 9780429107467. [Google Scholar] [CrossRef]






















| No. | Nominal Class of Density kg/m3 Acc. to [11] | Density Range of AAC, kg/m3 Acc. to [11] | Mean Density ρ0, kg/m3 (C.O.V) Acc. to [14] | Mean Modulus of Elasticity E, N/mm2 (C.O.V) Acc. to [11] | Mean Poisson’s Ratio ν, (C.O.V) Acc. to [11] | Compressive Strength of AAC fB, N/mm2 (C.O.V) Acc. to [14] |
|---|---|---|---|---|---|---|
| 1 | 400 | 375–446 | 397 (6%) | 1516 (9.6%) | 0.19 (7.9%) | 2.88 |
| 2 | 500 | 462–532 | 492 (3%) | 2039 (8.9%) | 0.21 (8.7%) | 3.59 |
| 3 | 600 | 562–619 | 599 (2%) | 2886 (10.5%) | 0.20 (8.5%) | 5.05 |
| 4 | 700 | 655–725 | 674 (3%) | 4778 (10.1%) | 0.19 (9.2%) | 8.11 |
| No. | Mean Density ρ, (Nominal Class of Density) kg/m3 | Mean Compressive Stress P, N/mm2 | Mean Relative Compressive Stress P/Pmax | Mean Path Length L, mm | Mean Passing Time of Wave t, µs | Mean Ultrasonic Velocity cp = L/t, m/s | COV, % | |
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | 397 (400) | 0 | 0 | 120.1 | 64.7 | obscp0 = 1875 | 0 | 1.7% |
| 2 | 0.51 | 0.23 | 70.6 | 1704 | −0.09 | 2.1% | ||
| 3 | 1.13 | 0.52 | 76.5 | 1572 | −0.16 | 1.4% | ||
| 4 | 1.65 | 0.75 | 87.0 | 1387 | −0.26 | 0.5% | ||
| 5 | 2.19 | 1 | 105.2 | 1145 | −0.39 | 2.3% | ||
| 6 | 492 (500) | 0 | 0 | 119.9 | 63.4 | obscp0 = 1893 | 0.00 | 2.1% |
| 7 | 0.62 | 0.23 | 69.3 | 1732 | −0.08 | 1.9% | ||
| 8 | 1.34 | 0.51 | 78.3 | 1534 | −0.19 | 1.6% | ||
| 9 | 2.01 | 0.76 | 82.8 | 1451 | −0.23 | 1.1% | ||
| 10 | 2.65 | 1 | 93.4 | 1286 | −0.32 | 1.7% | ||
| 11 | 599 (600) | 0 | 0 | 120.1 | 59.1 | obscp0 = 2031 | 0.00 | 1.9% |
| 12 | 0.98 | 0.24 | 61.3 | 1960 | −0.03 | 3.1% | ||
| 13 | 2.01 | 0.50 | 66.7 | 1800 | −0.11 | 2.7% | ||
| 14 | 3.03 | 0.76 | 70.8 | 1695 | −0.16 | 2.2% | ||
| 15 | 4.01 | 1 | 75.6 | 1588 | −0.22 | 2.4% | ||
| 11 | 674 (700) | 0 | 0 | 120.2 | 54.0 | obscp0 = 2225 | 0.00 | 2.1% |
| 12 | 1.54 | 0.25 | 57.7 | 2083 | −0.06 | 1.4% | ||
| 13 | 3.19 | 0.51 | 59.1 | 2032 | −0.09 | 1.8% | ||
| 14 | 4.73 | 0.75 | 62.0 | 1936 | −0.13 | 1.9% | ||
| 15 | 6.30 | 1 | 66.8 | 1799 | −0.19 | 3.1% |
| No. | Mean Density ρ, (Nominal Class of Density) kg/m3 | AE Coefficient δP, m3/kg | Relative Coefficient ηP |
|---|---|---|---|
| 1 | 2 | 3 | 4 |
| 1 | 397 (400) | −0.1632 | −0.3574 |
| 2 | 492 (500) | −0.1196 | −0.3168 |
| 3 | 599 (600) | −0.0530 | −0.2134 |
| 4 | 674 (700) | −0.0281 | −0.1772 |
| Series | Mean Density ρ0, kg/m3 | Moisture Content w, % | Maximum Moisture Content (17) wmax, % | Mean Compressive Stress Inducing Cracks σ3cr, N/mm2 (COV) | Maximum Mean Compressive Stress σ3max, N/mm2 (COV) |
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 |
| I | 592 | 5.20% | 61.2% | 2.89 | 3.01 |
| (0.43%) | (14.5%) | (0.57%) | (1.1%) | (1.3%) | |
| II | 595 | 5.63% | 61.1% | 2.95 | 2.96 |
| (0.34%) | (11.3%) | (0.90%) | (2.8%) | (2.6%) | |
| III | 590 | 5.33% | 61.4% | 2.90 | 2.97 |
| (0.59%) | (3.90%) | (0.73%) | (3.3%) | (1.9%) |
| Series | No. of Measuring Points in Each Loading Step, n | Time of Ultrasonic Wave Passing at Different Levels of Loading, tpmv, μs (COV) | |||
|---|---|---|---|---|---|
| 0 | 0.25σ3max | 0.50σ3max | 0.75σ3max | ||
| 1 | 2 | 3 | 4 | 5 | 6 |
| I-1 | 315 | 90.8 | 92.2 | 93.9 | 94.4 |
| (1.4%) | (1.3%) | (1.4%) | (1.4%) | ||
| 45 | 91.2 | 92.3 | 93.6 | 94.3 | |
| (1.3%) | (1.1%) | (1.3%) | (1.2%) | ||
| II-1 | 308 | 89.2 | 90.6 | 92.2 | 92.5 |
| (1.6%) | (1.2%) | (1.1%) | (1.1%) | ||
| 44 | 89.6 | 90.5 | 92.2 | 92.4 | |
| (1.5%) | (1.2%) | (0.9%) | (0.9%) | ||
| III-1 | 308 | 88.8 | 90.2 | 91.6 | 92.1 |
| (1.4%) | (1.2%) | (0.9%) | (0.9%) | ||
| 44 | 89.1 | 90.2 | 91.5 | 92.0 | |
| (1.2%) | (0.8%) | (0.7%) | (0.8%) | ||
| Model | Number of Measurements n | 0.25σ3max | 0.50σ3max | 0.75σ3max | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| δP (15) | (10) | δP (15) | (10) | δP (15) | (10) | |||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| I-1 | 315 | −0.0156 | −0.0640 | 0.247 | −0.0319 | −0.0640 | 0.502 | −0.0403 | −0.0640 | 0.634 |
| II-1 | 308 | −0.0151 | −0.0635 | 0.240 | −0.0333 | −0.0635 | 0.528 | −0.0372 | −0.0635 | 0.590 |
| III-1 | 308 | −0.0150 | −0.0640 | 0.240 | −0.0306 | −0.0640 | 0.495 | −0.0360 | −0.0640 | 0.587 |
| Model | Number of Measurements n | 0.25σ3max | 0.50σ3max | 0.75σ3max | |||
|---|---|---|---|---|---|---|---|
(10) | (10) | (10) | |||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| I-1 | 45 | −0.0115 | 0.181 | −0.0261 | 0.410 | −0.0337 | 0.528 |
| II-1 | 44 | −0.0104 | 0.166 | −0.0293 | 0.464 | −0.0316 | 0.501 |
| III-1 | 44 | −0.0119 | 0.187 | −0.0270 | 0.424 | −0.0324 | 0.509 |
| Model | Number of Measurements n | 0.25σ3max | 0.50σ3max | 0.75σ3max | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| σ3, N/mm2 [7] | P N/mm2 (Table 5 and Table 6) | σ1, N/mm2 (20) | σ3, N/mm2 [7] | P N/mm2 (Table 5 and Table 6) | σ1, N/mm2 (20) | σ3, N/mm2 [7] | P N/mm2 (Table 5 and Table 6) | σ1, N/mm2 (20) | ||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| I-1 | 315 | 0.737 | 0.247 | 0.004 | 1.499 | 0.502 | 0.008 | 1.892 | 0.634 | 0.010 |
| 45 | 0.540 | 0.181 | 0.003 | 1.224 | 0.410 | 0.007 | 1.577 | 0.528 | 0.008 | |
| II-1 | 308 | 0.714 | 0.240 | 0.005 | 1.573 | 0.528 | 0.011 | 1.757 | 0.590 | 0.012 |
| 44 | 0.493 | 0.166 | 0.003 | 1.383 | 0.464 | 0.009 | 1.493 | 0.501 | 0.010 | |
| III-1 | 308 | 0.716 | 0.240 | 0.004 | 1.478 | 0.495 | 0.008 | 1.750 | 0.587 | 0.009 |
| 44 | 0.557 | 0.187 | 0.003 | 1.265 | 0.424 | 0.007 | 1.518 | 0.509 | 0.008 | |
| Model | Number of Measurements n | 0.25σ3max | 0.50σ3max | 0.75σ3max | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| FEMσ3, N/mm2 | FEMP N/mm2 | FEMσ1, N/mm2 | FEMσ3, N/mm2 | FEMP N/mm2 | FEMσ1, N/mm2 | FEMσ3, N/mm2 | FEMP N/mm2 | FEMσ1, N/mm2 | ||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| I-1 | 315 | 0.752 | 0.251 | 0.003 | 1.503 | 0.503 | 0.006 | 2.255 | 0.754 | 0.008 |
| II-1 | 308 | 0.741 | 0.248 | 0.003 | 1.483 | 0.496 | 0.006 | 2.224 | 0.744 | 0.009 |
| III-1 | 308 | 0.743 | 0.249 | 0.003 | 1.486 | 0.497 | 0.006 | 2.229 | 0.746 | 0.009 |
| Model | Number of Measurements n | 0.25σ3max | 0.50σ3max | 0.75σ3max | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| I-1 | 315 | 0.98 | 0.98 | 1.33 | 1.00 | 1.00 | 1.33 | 0.84 | 0.84 | 1.25 |
| II-1 | 308 | 0.96 | 0.97 | 1.67 | 1.06 | 1.06 | 1.83 | 0.79 | 0.79 | 1.33 |
| III-1 | 308 | 0.96 | 0.96 | 1.33 | 0.99 | 1.00 | 1.33 | 0.79 | 0.79 | 1.00 |
| on average: | 0.97 | 0.97 | 1.44 | 1.02 | 1.02 | 1.50 | 0.81 | 0.81 | 1.19 | |
| I-1 | 45 | 0.72 | 0.72 | 1.00 | 0.81 | 0.82 | 1.17 | 0.70 | 0.70 | 1.00 |
| II-1 | 44 | 0.67 | 0.67 | 1.00 | 0.93 | 0.94 | 1.50 | 0.67 | 0.67 | 1.11 |
| III-1 | 44 | 0.75 | 0.75 | 1.00 | 0.85 | 0.85 | 1.17 | 0.68 | 0.68 | 0.89 |
| on average: | 0.71 | 0.71 | 1.00 | 0.87 | 0.87 | 1.28 | 0.68 | 0.69 | 1.00 | |
| Model | N/mm2 | N/mm2 | dσ3 = 0.5α σ3max N/mm2 | dP = 0.5α P N/mm2 | ||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| I-1 | 2.089 | 0.699 | 0.313 | 0.105 | 0.052 | 0.017 | 8 | 23 |
| II-1 | 1.978 | 0.663 | 0.297 | 0.099 | 0.049 | 0.017 | 7 | 22 |
| III-1 | 2.011 | 0.673 | 0.302 | 0.101 | 0.050 | 0.017 | 7 | 22 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jasiński, R.; Stebel, K.; Kielan, P. Use of the AE Effect to Determine the Stresses State in AAC Masonry Walls under Compression. Materials 2021, 14, 3459. https://doi.org/10.3390/ma14133459
Jasiński R, Stebel K, Kielan P. Use of the AE Effect to Determine the Stresses State in AAC Masonry Walls under Compression. Materials. 2021; 14(13):3459. https://doi.org/10.3390/ma14133459
Chicago/Turabian StyleJasiński, Radosław, Krzysztof Stebel, and Paweł Kielan. 2021. "Use of the AE Effect to Determine the Stresses State in AAC Masonry Walls under Compression" Materials 14, no. 13: 3459. https://doi.org/10.3390/ma14133459
APA StyleJasiński, R., Stebel, K., & Kielan, P. (2021). Use of the AE Effect to Determine the Stresses State in AAC Masonry Walls under Compression. Materials, 14(13), 3459. https://doi.org/10.3390/ma14133459







