Single-Station Coda Wave Interferometry: A Feasibility Study Using Machine Learning
Abstract
:1. Introduction
2. Numerical Setup and Machine-Learning Approach
2.1. Numerical Setup
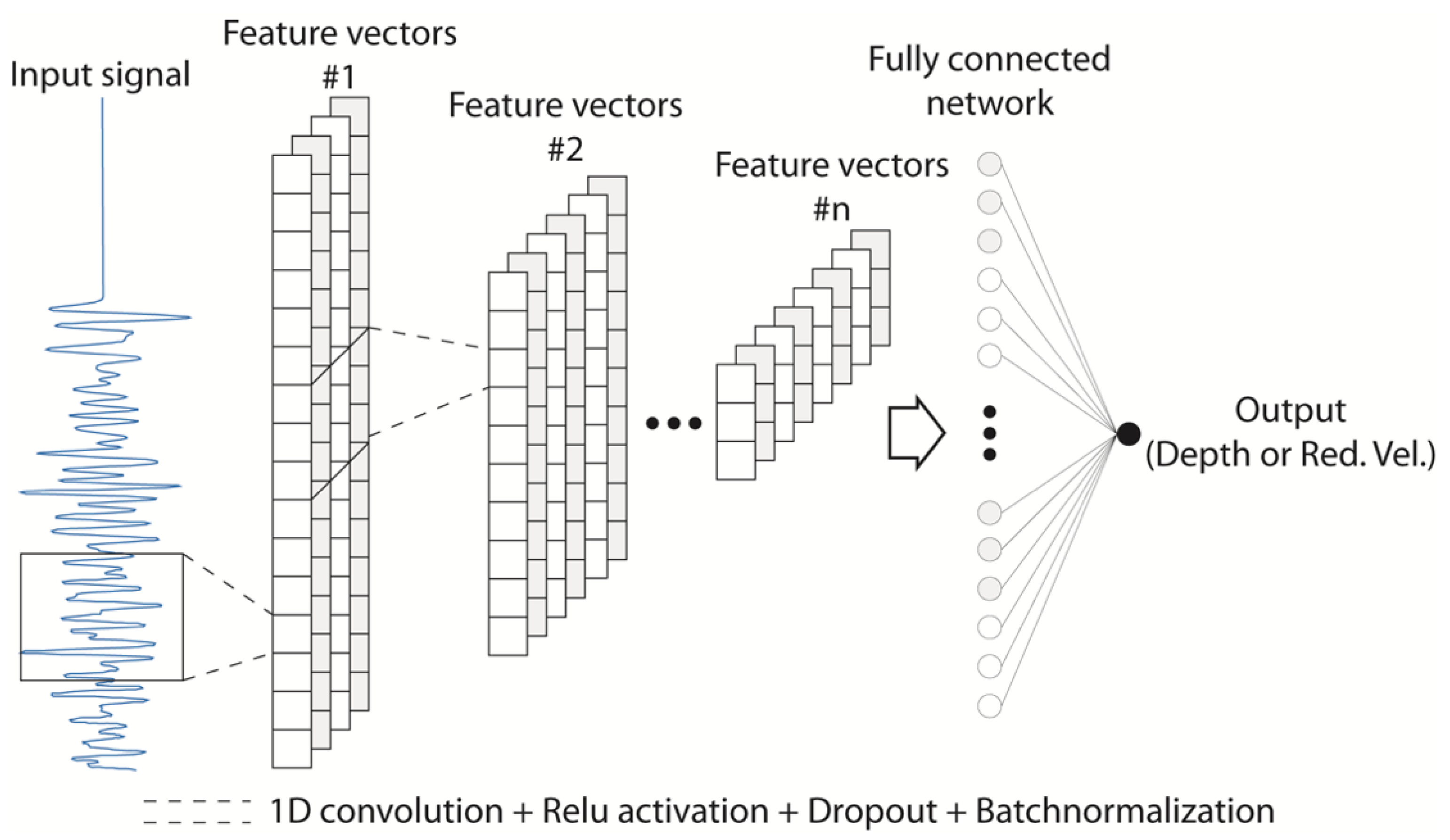
2.2. Machine Learning
3. Results
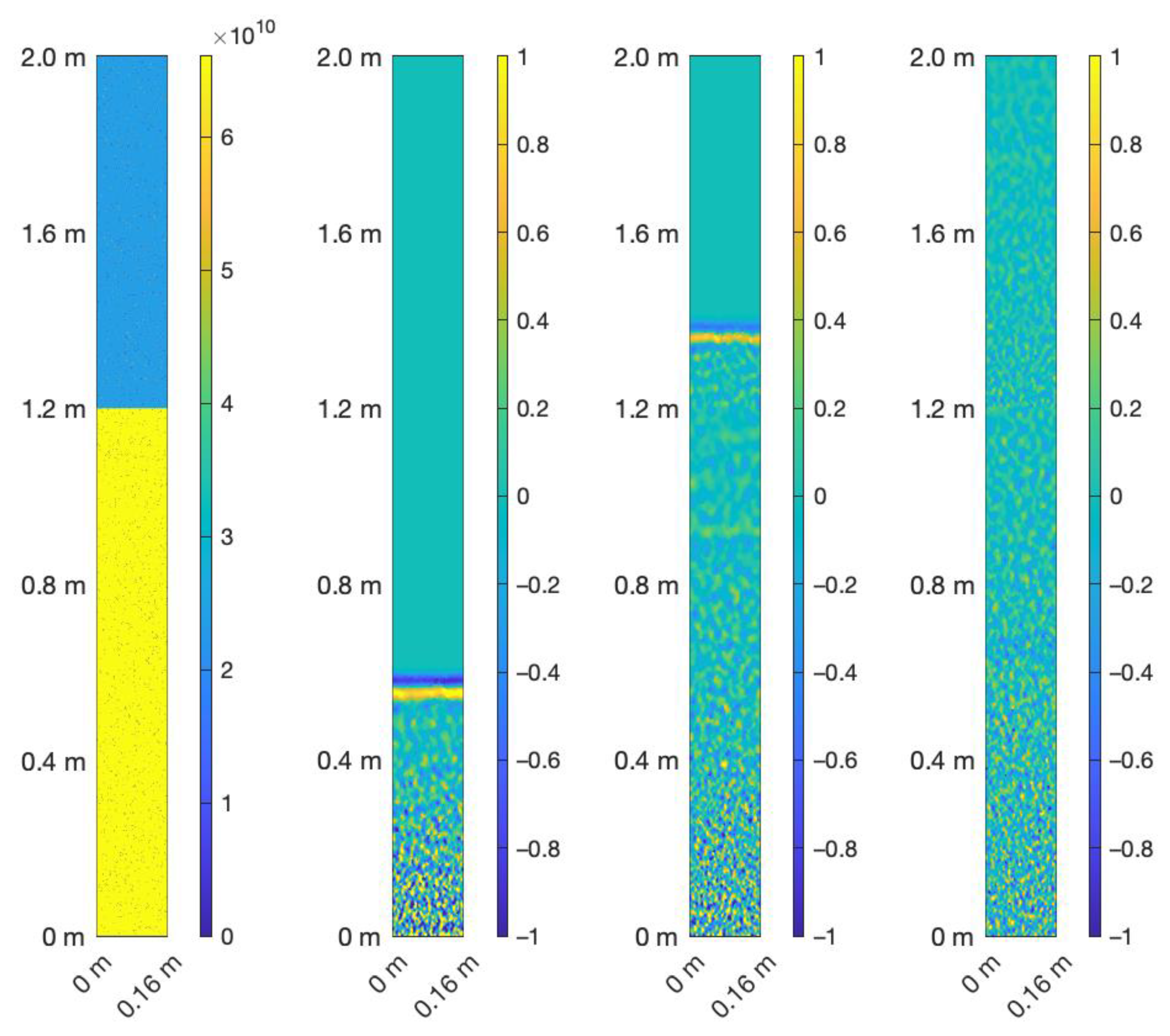
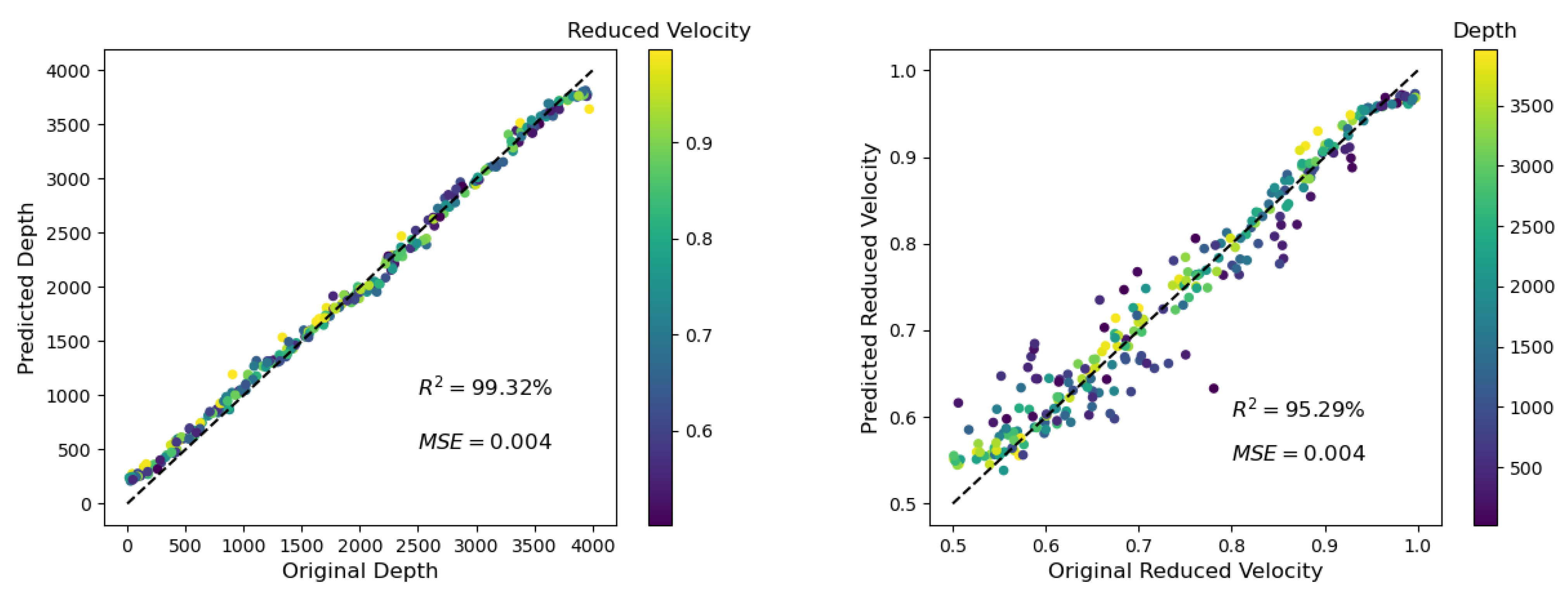
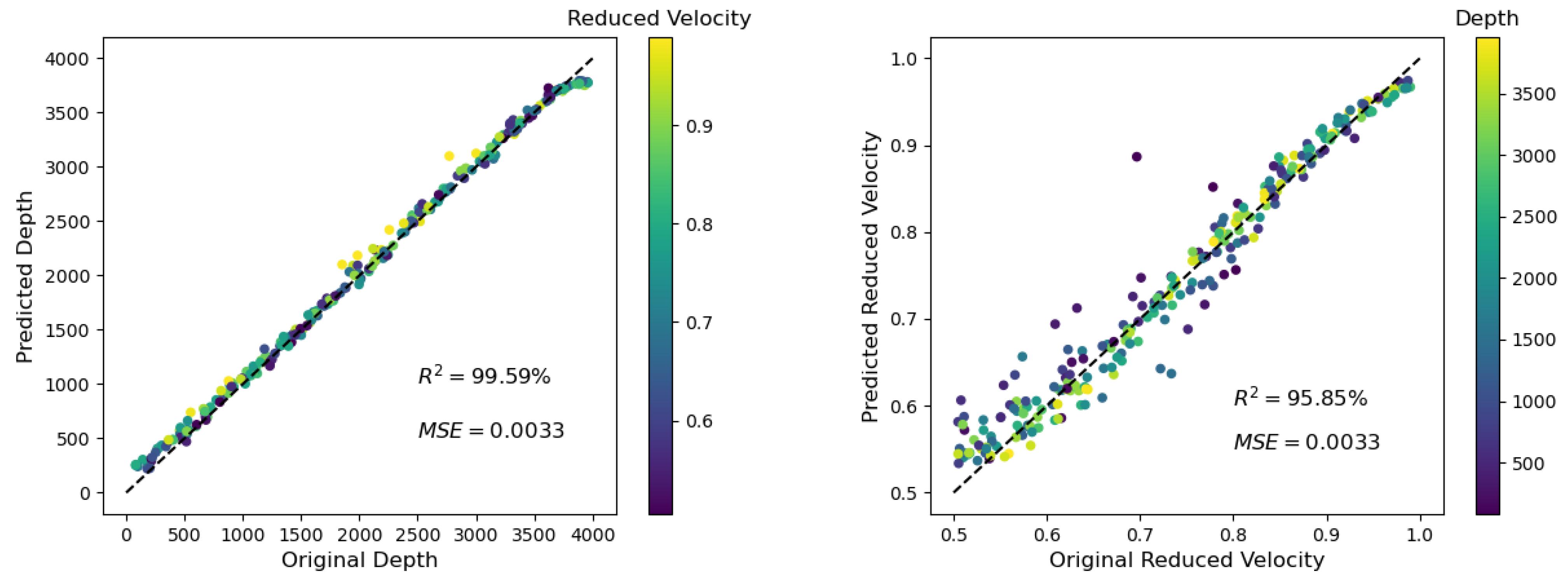
3.1. Case1: Basic Example (Average 100 Traces, No Noise, ρ = 0.1, L = 10)
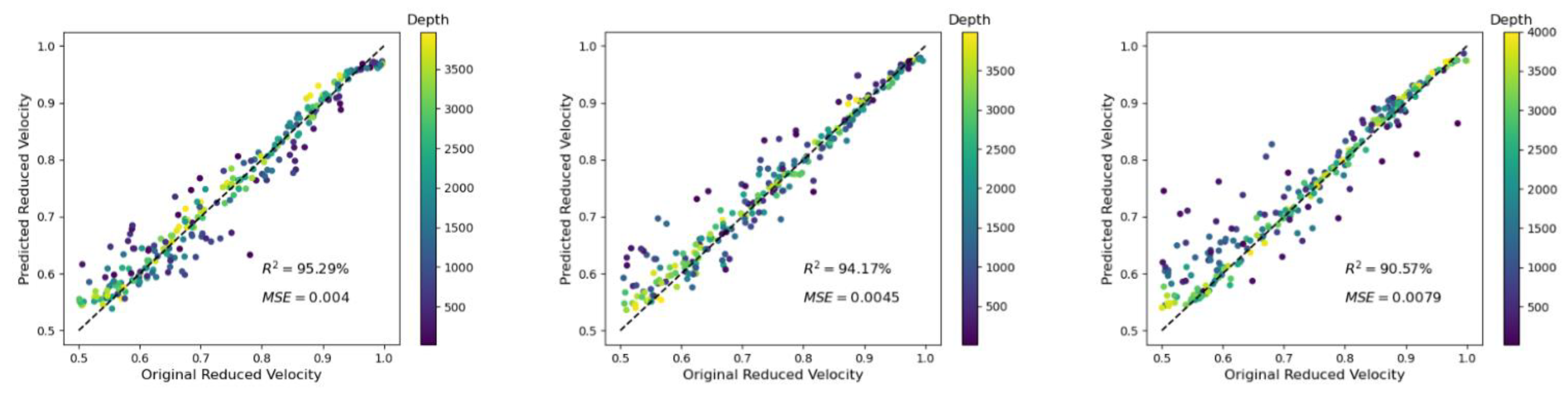
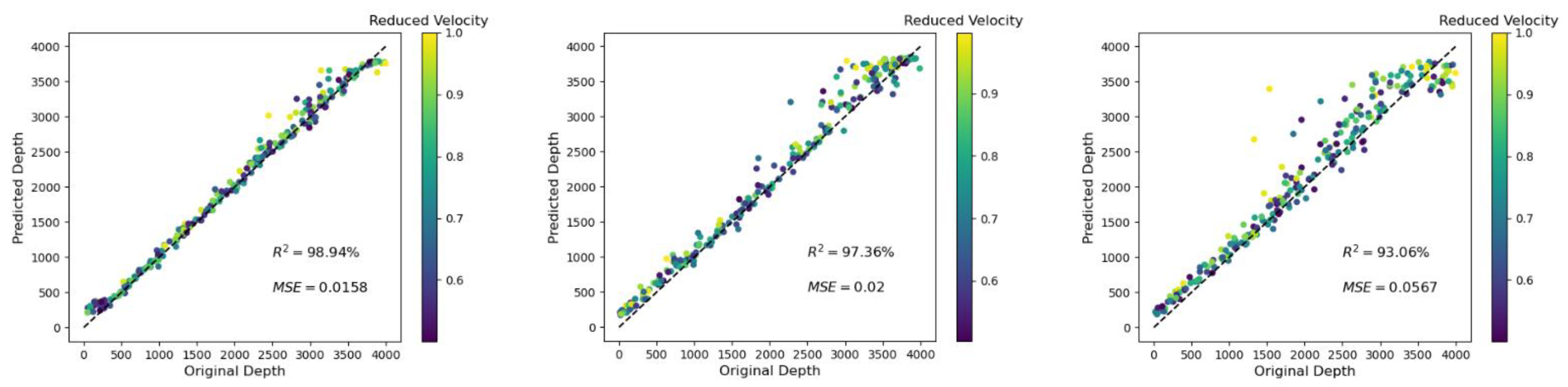
3.2. Case 2: Variation of the Crack Density
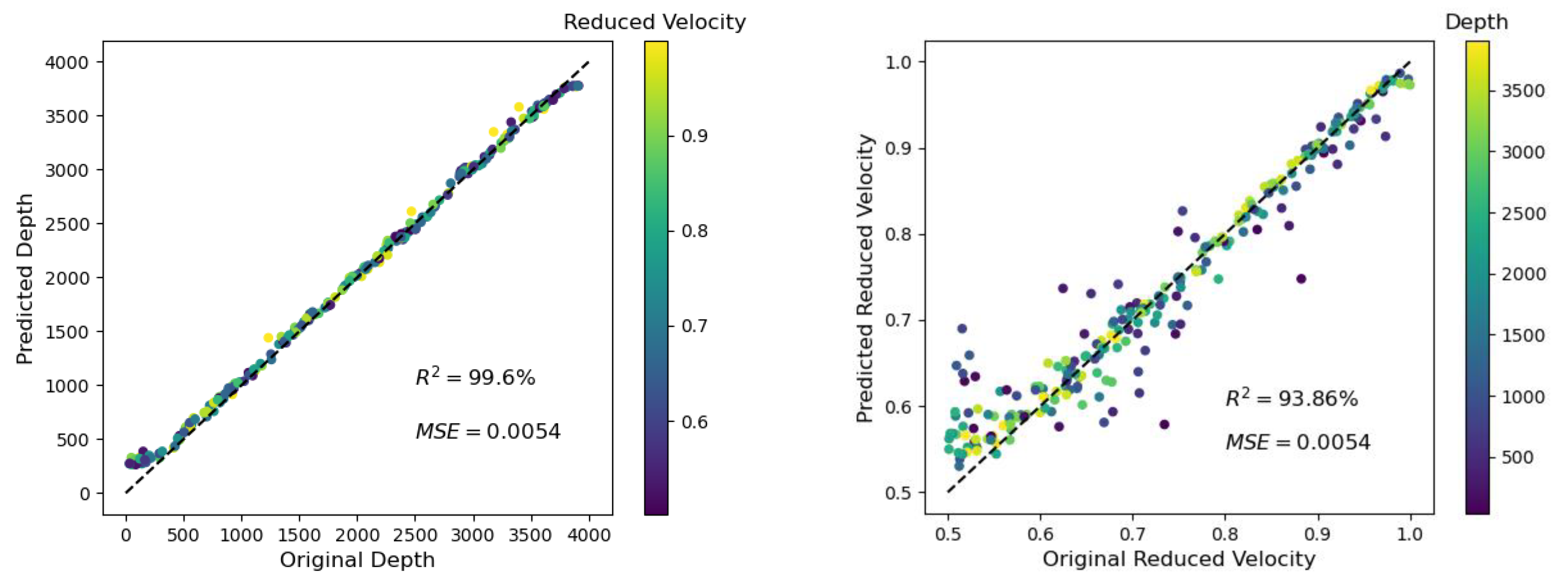
3.3. Case 3: Variation of Crack Length
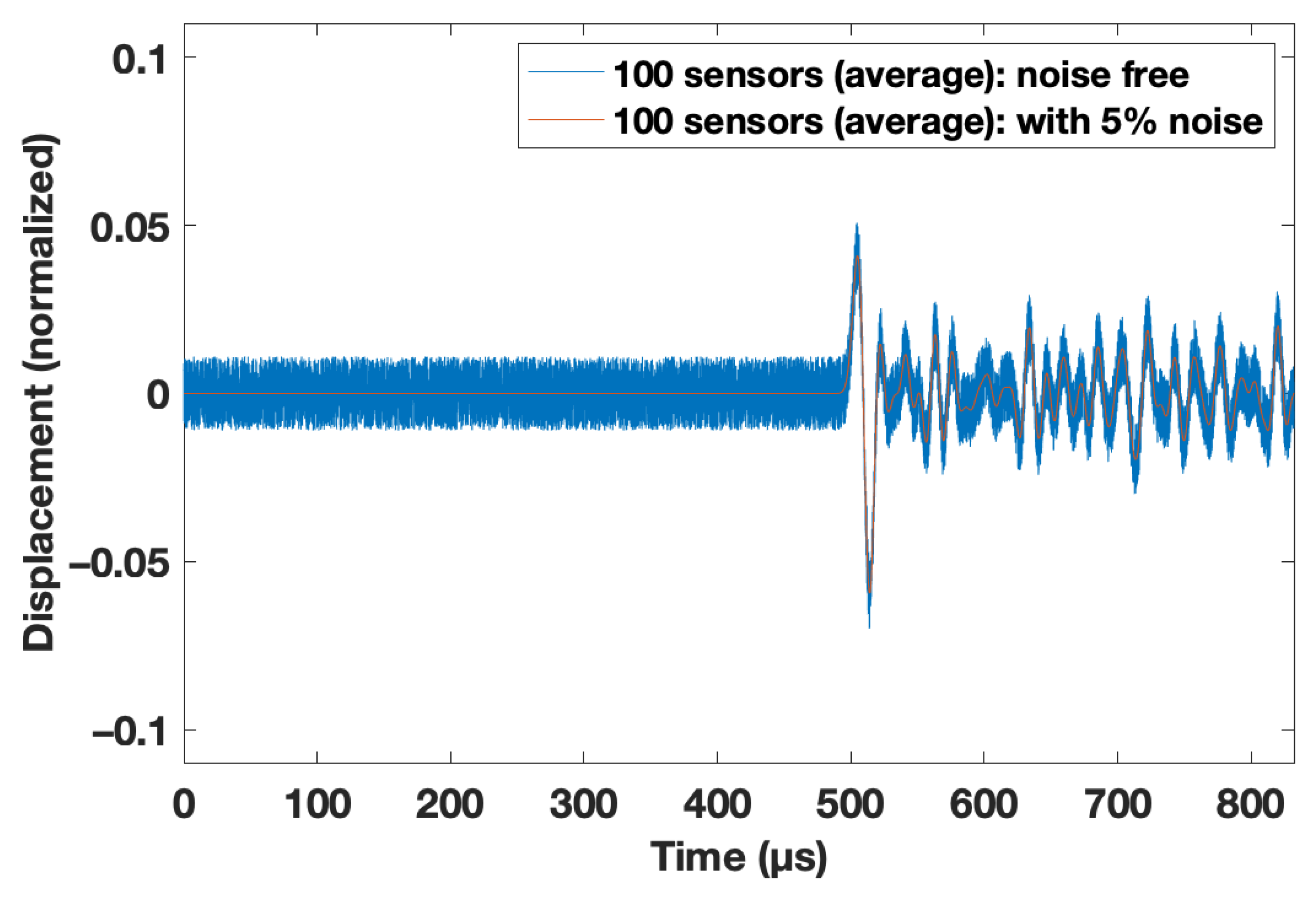
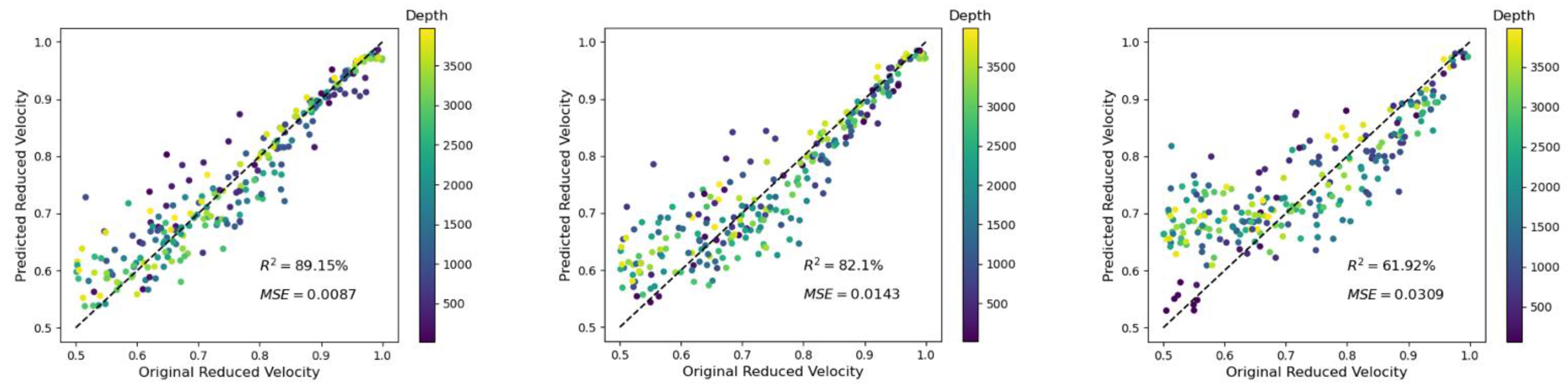
3.4. Case 4: Influence of Noise
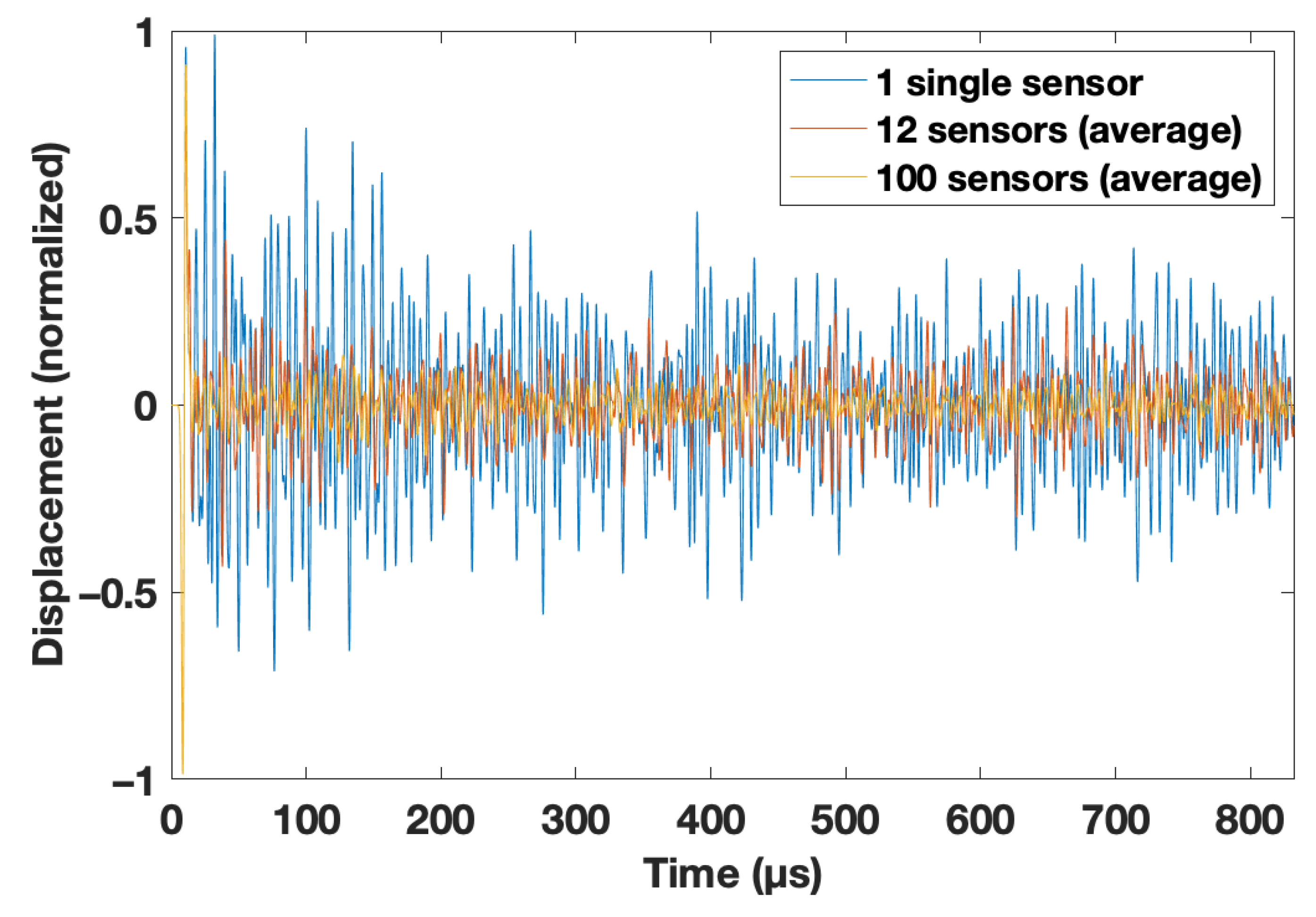
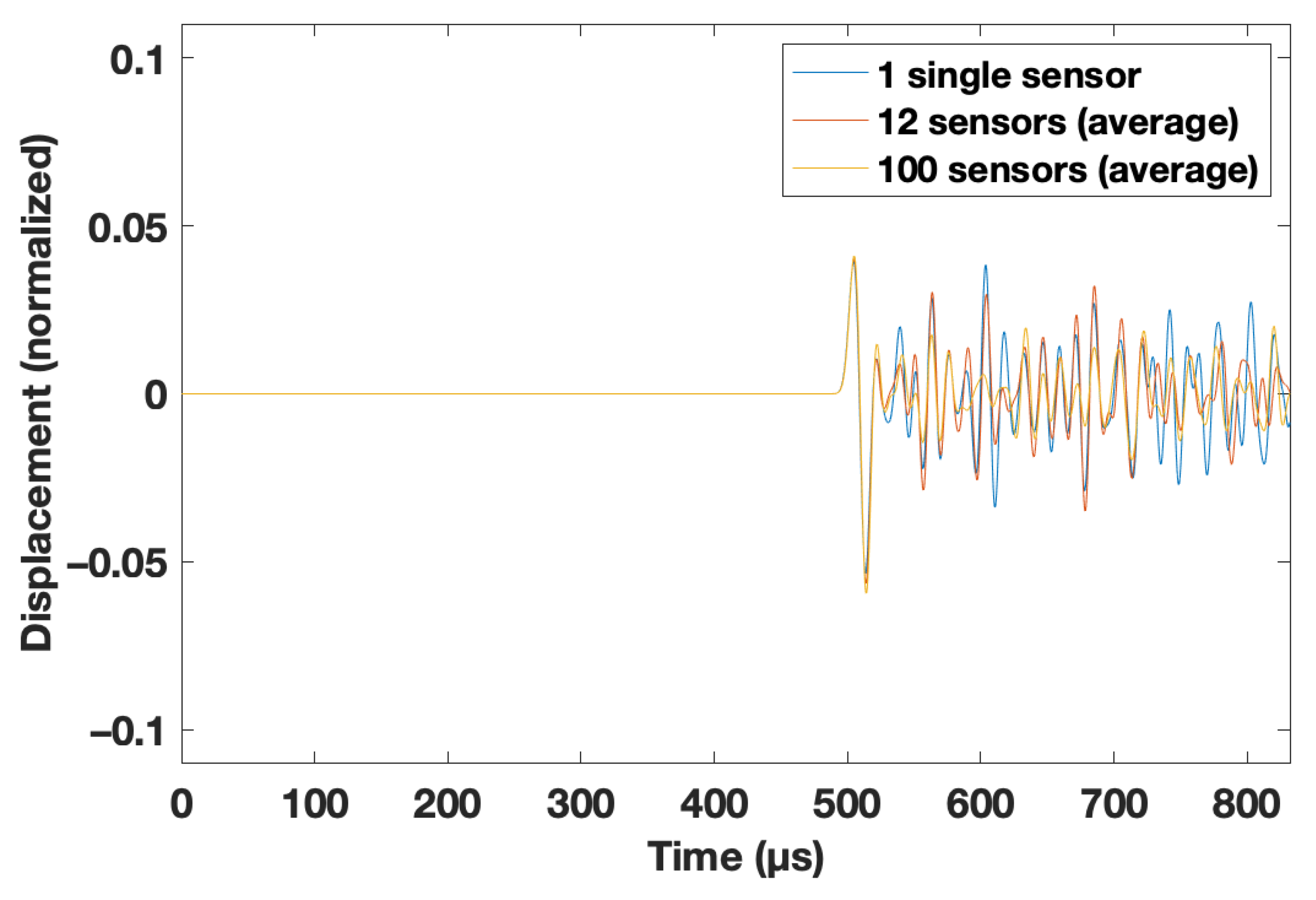
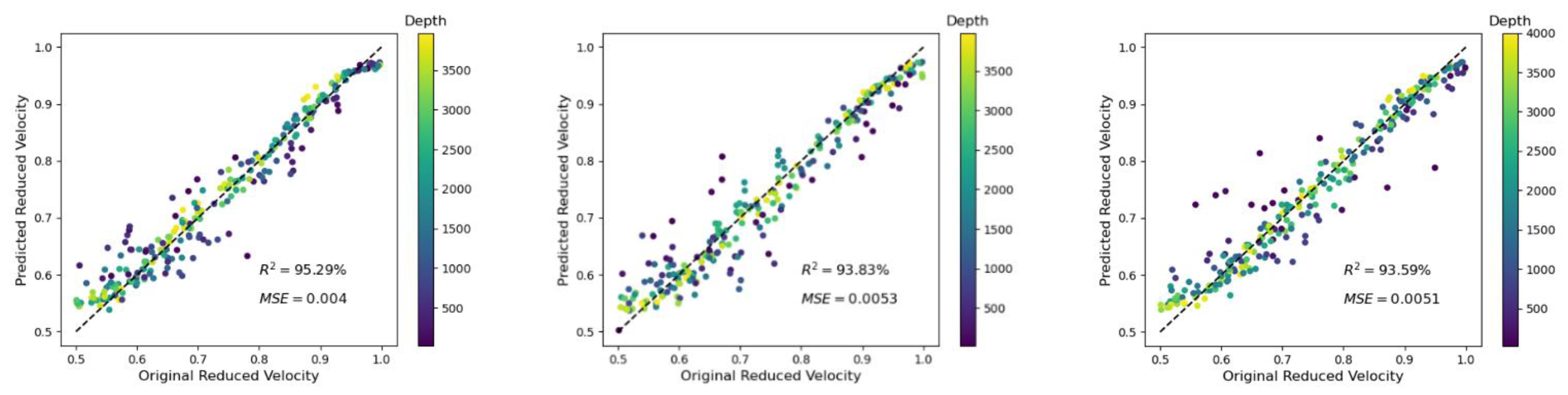
3.5. Case 5: Application of Different Averaging Techniques at the Bottom of the Model
3.6. Case 6: The Effect of Intrinsic Attenuation
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Herraiz, M.; Espinosa, A.F. Coda waves: A review. Pure Appl. Geophys. 1987. [Google Scholar] [CrossRef]
- Snieder, R. The Theory of Coda Wave Interferometry. Pure Appl. Geophys. 2006, 163, 455–473. [Google Scholar] [CrossRef]
- Margerin, L.; Planès, T.; Mayor, J.; Calvet, M. Sensitivity kernels for coda-wave interferometry and scattering tomography: Theory and numerical evaluation in two-dimensional anisotropically scattering media. Geophys. J. Int. 2016, 204, 650–666. [Google Scholar] [CrossRef] [Green Version]
- Karbhari, V.M.; Ansari, M. (Eds.) Structural Health Monitoring of Civil Infrastructure Systems; Woodhead Publishing: Cambridge, UK, 2009; ISBN 978-1-84569-392-3. [Google Scholar]
- Planès, T.; Larose, E. A Review of Ultrasonic Coda Wave Interferometry in Concrete. Cem. Concr. Res. 2013, 53, 248–255. [Google Scholar] [CrossRef]
- Niederleithinger, E.; Wang, X.; Herbrand, M.; Müller, M. Processing Ultrasonic Data by Coda Wave Interferometry to Monitor Load Tests of Concrete Beams. Sensors 2018, 18, 1971. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Karimpouli, S.; Tahmasebi, P. Image-based velocity estimation of rock using convolutional neural networks. Neural Netw. 2019, 111, 89–97. [Google Scholar] [CrossRef] [PubMed]
- Karimpouli, S.; Tahmasebi, P. Physics informed machine learning: Seismic wave equation. Geosci. Front. 2020, 11, 1993–2001. [Google Scholar] [CrossRef]
- Karimpouli, S.; Tahmasebi, P.; Saenger, E.H. Coal cleat/fracture segmentation using convolutional neural networks. Nat. Resour. Res. 2020, 29, 1675–1685. [Google Scholar] [CrossRef]
- Kamrava, S.; Tahmasebi, P.; Sahimi, M. Physics-and image-based prediction of fluid flow and transport in complex porous membranes and materials by deep learning. J. Membr. Sci. 2021, 622, 119050. [Google Scholar] [CrossRef]
- Saenger, E.H.; Gold, N.; Shapiro, S.A. Modeling the propagation of elastic waves using a modified finite-difference grid. Wave Motion 2000, 31, 77–92. [Google Scholar] [CrossRef]
- Saenger, E.H.; Bohlen, T. Finite-difference modeling of viscoelastic and anisotropic wave propagation using the rotated staggered grid. Geophysics 2004, 69, 583–591. [Google Scholar] [CrossRef]
- Kocur, G.K.; Saenger, E.H.; Vogel, T. Elastic wave propagation in a segmented X-ray computed tomography model of a concrete specimen. Constr. Build. Mater. 2010, 24, 2393–2400. [Google Scholar] [CrossRef]
- Saenger, E.H. Time reverse characterization of sources in heterogeneous media. NDT E Int. 2011, 44, 751–759. [Google Scholar] [CrossRef]
- Krüger, O.S.; Saenger, E.H.; Shapiro, S.A. Scattering and diffraction by a single crack: An accuracy analysis of the rotated staggered grid. Geophys. J. Int. 2005, 162, 25–31. [Google Scholar] [CrossRef]
- Kachanov, M. The elastic modulus of media containing strongly interacting antiplane cracks. Appl. Mech. Rev. 1992, 45, 304–335. [Google Scholar] [CrossRef]
- Saenger, E.H.; Shapiro, S.A.; Keehm, Y. Seismic effects of viscous Biot-coupling: Finite difference simulations on micro-scale. Geophys. Res. Lett. 2005, 32, L14310. [Google Scholar] [CrossRef]
- Mavko, G.; Mukerji, T.; Dvorkin, J. The Rock Physics Handbook; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Zhu, L.; Peng, Z.; McClellan, J.; Li, C.; Yao, D.; Li, Z.; Fang, L. Deep learning for seismic phase detection and picking in the aftershock zone of 2008 Mw7.9 Wenchuan Earthquake. Phys. Earth Planet. Inter. 2019, 293, 106261. [Google Scholar] [CrossRef] [Green Version]
- Owino, J.O.; Jacobs, L.J. Attenuation measurements in cement-based materials using laser ultrasonics. J. Eng. Mech. 1999, 125, 637–647. [Google Scholar] [CrossRef]
- Dix, C.H. Seismic Prospecting for Oil; Harper & Brothers: New York, NY, USA, 1952. [Google Scholar]
- Tsai, K.C.; Hu, W.; Wu, X.; Chen, J.; Han, Z. Automatic First Arrival Picking via Deep Learning with Human Interactive Learning. IEEE Trans. Geosci. Remote. Sens. 2020, 58, 1380–1391. [Google Scholar] [CrossRef]
| Fixed Properties | Random Properties | Number of Performed Simulations |
|---|---|---|
| ρ = 0.1, L = 10 GPs | Depth d = 5–4000 GPs; velocity reduction r = 0.5–1 | >1024 |
| ρ = 0.2; L = 10 GPs | Depth d = 5–4000 GPs; velocity reduction r = 0.5–1 | >1024 |
| ρ = 0.3; L = 10 GPs | Depth d = 5–4000 GPs; velocity reduction r = 0.5–1 | >1024 |
| ρ = 0.1; L = 40 GPs | Depth d = 5–4000 GPs; velocity reduction r = 0.5–1 | >1024 |
| ρ = 0.1, L = 10 GPs, Qmin = 33 | Depth d = 5–4000 GPs; velocity reduction r = 0.5–1 | >1024 |
| Output | Depth | Reduced Velocity | Inner Networks | |
|---|---|---|---|---|
| Layer | ||||
| Conv-1D | 16 ch, 3 k, ReLU | 128 ch, 3 k, ReLU | Feature vector #1 | |
| Maxpooling-1D | Pool size: 2 | |||
| Dropout | 10% | |||
| Batch-normalization | ||||
| Conv-1D | 32 ch, 3 k, ReLU | 128 ch, 3 k, ReLU | Feature vector #2 | |
| Maxpooling-1D | Pool size: 2 | |||
| Dropout | 10% | |||
| Batch-normalization | ||||
| Conv-1D | 64 ch, 3 k, ReLU | 256 ch, 3 k, ReLU | Feature vector #3 | |
| Maxpooling-1D | Pool size: 2 | |||
| Dropout | 10% | |||
| Batch-normalization | ||||
| Conv-1D | 128 ch, 3 k, ReLU | 256 ch, 3 k, ReLU | Feature vector #4 | |
| Maxpooling-1D | Pool size: 2 | |||
| Dropout | 10% | |||
| Batch-normalization | ||||
| Dense | 1024 ch, Tanh | 1024 ch, Tanh | Fully connected network | |
| Dropout | 30% | |||
| Batch-normalization | ||||
| Dense | 1 ch, Sigmoid | 1 ch, Sigmoid | Output | |
| Model Setup | Predicted Depth | Predicted Reduced Velocity | |||||
|---|---|---|---|---|---|---|---|
| Crack Density ρ | Crack Length L | Traces | Specifics | R2% | MSE | R2% | MSE |
| Training | Training | ||||||
| Validation/Test | Validation/Test | ||||||
| 0.1 | 10 GPs | 100 | - | 99.56 | 0.0028 | 97.36 | 0.0032 |
| 99.32 | 0.0040 | 95.29 | 0.0040 | ||||
| 0.1 | 10 GPs | 100 | 5% noise | 99.48 | 0.0018 | 97.06 | 0.0026 |
| 99.07 | 0.0033 | 96.04 | 0.0033 | ||||
| 0.1 | 10 GPs | 100 | 10% noise | 99.25 | 0.0043 | 92.04 | 0.0056 |
| 98.54 | 0.0079 | 90.12 | 0.0079 | ||||
| 0.1 | 10 GPs | 100 | 20% noise | 99.15 | 0.0096 | 86.38 | 0.0085 |
| 98.00 | 0.0132 | 84.57 | 0.0132 | ||||
| 0.2 | 10 GPs | 100 | - | 99.63 | 0.0035 | 96.34 | 0.0021 |
| 99.31 | 0.0045 | 94.17 | 0.0045 | ||||
| 0.2 | 10 GPs | 100 | 5% noise | 97.89 | 0.0111 | 85.73 | 0.0115 |
| 97.23 | 0.0127 | 84.68 | 0.0127 | ||||
| 0.2 | 10 GPs | 100 | 10% noise | 96.88 | 0.0114 | 76.12 | 0.0135 |
| 96.40 | 0.0205 | 74.42 | 0.0205 | ||||
| 0.2 | 10 GPs | 100 | 20% noise | 91.56 | 0.0223 | 59.35 | 0.0256 |
| 90.81 | 0.0372 | 56.19 | 0.0372 | ||||
| 0.3 | 10 GPs | 100 | - | 99.48 | 0.0062 | 92.03 | 0.0053 |
| 99.13 | 0.0079 | 90.57 | 0.0079 | ||||
| 0.3 | 10 GPs | 100 | 5% noise | 99.36 | 0.0125 | 80.95 | 0.0112 |
| 98.94 | 0.0158 | 80.65 | 0.0158 | ||||
| 0.3 | 10 GPs | 100 | 10% noise | 97.78 | 0.0165 | 76.98 | 0.0189 |
| 97.36 | 0.0200 | 74.37 | 0.0200 | ||||
| 0.3 | 10 GPs | 100 | 20% noise | 93.65 | 0.0428 | 35.37 | 0.0550 |
| 93.06 | 0.0567 | 32.30 | 0.0567 | ||||
| 0.1 | 40 GPs | 100 | - | 99.68 | 0.0048 | 94.50 | 0.0051 |
| 99.60 | 0.0054 | 93.86 | 0.0054 | ||||
| 0.1 | 40 GPs | 100 | 5% noise | 98.84 | 0.0068 | 90.28 | 0.0061 |
| 98.06 | 0.0087 | 89.15 | 0.0087 | ||||
| 0.1 | 40 GPs | 100 | 10% noise | 98.01 | 0.0095 | 84.45 | 0.0132 |
| 96.58 | 0.0143 | 82.10 | 0.0143 | ||||
| 0.1 | 40 GPs | 100 | 20% noise | 92.95 | 0.0268 | 65.08 | 0.0243 |
| 92.39 | 0.0309 | 61.92 | 0.0309 | ||||
| 0.1 | 10 GPs | 12 | - | 99.53 | 0.0019 | 94.57 | 0.0037 |
| 99.32 | 0.0053 | 93.83 | 0.0053 | ||||
| 0.1 | 10 GPs | 1 | - | 99.85 | 0.0032 | 93.86 | 0.0046 |
| 99.56 | 0.0051 | 93.59 | 0.0051 | ||||
| 0.1 | 10 GPs | 100 | Qmin = 33 | 99.68 | 0.0016 | 96.42 | 0.0030 |
| 99.59 | 0.0033 | 95.85 | 0.0033 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saenger, E.H.; Finger, C.; Karimpouli, S.; Tahmasebi, P. Single-Station Coda Wave Interferometry: A Feasibility Study Using Machine Learning. Materials 2021, 14, 3451. https://doi.org/10.3390/ma14133451
Saenger EH, Finger C, Karimpouli S, Tahmasebi P. Single-Station Coda Wave Interferometry: A Feasibility Study Using Machine Learning. Materials. 2021; 14(13):3451. https://doi.org/10.3390/ma14133451
Chicago/Turabian StyleSaenger, Erik H., Claudia Finger, Sadegh Karimpouli, and Pejman Tahmasebi. 2021. "Single-Station Coda Wave Interferometry: A Feasibility Study Using Machine Learning" Materials 14, no. 13: 3451. https://doi.org/10.3390/ma14133451
APA StyleSaenger, E. H., Finger, C., Karimpouli, S., & Tahmasebi, P. (2021). Single-Station Coda Wave Interferometry: A Feasibility Study Using Machine Learning. Materials, 14(13), 3451. https://doi.org/10.3390/ma14133451







