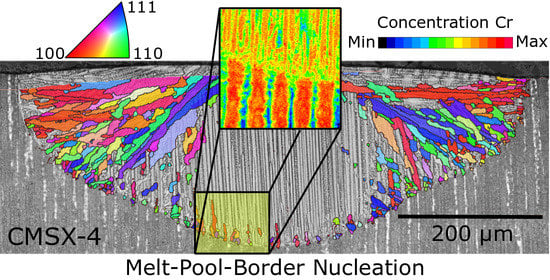
New Grain Formation Mechanisms during Powder Bed Fusion
Abstract
1. Introduction
2. Materials and Methods
2.1. Experiments
2.1.1. Feedstock Atomization and Powder Properties
2.1.2. SX Fabrication by EB-PBF
2.1.3. Heat Treatment of SX Samples
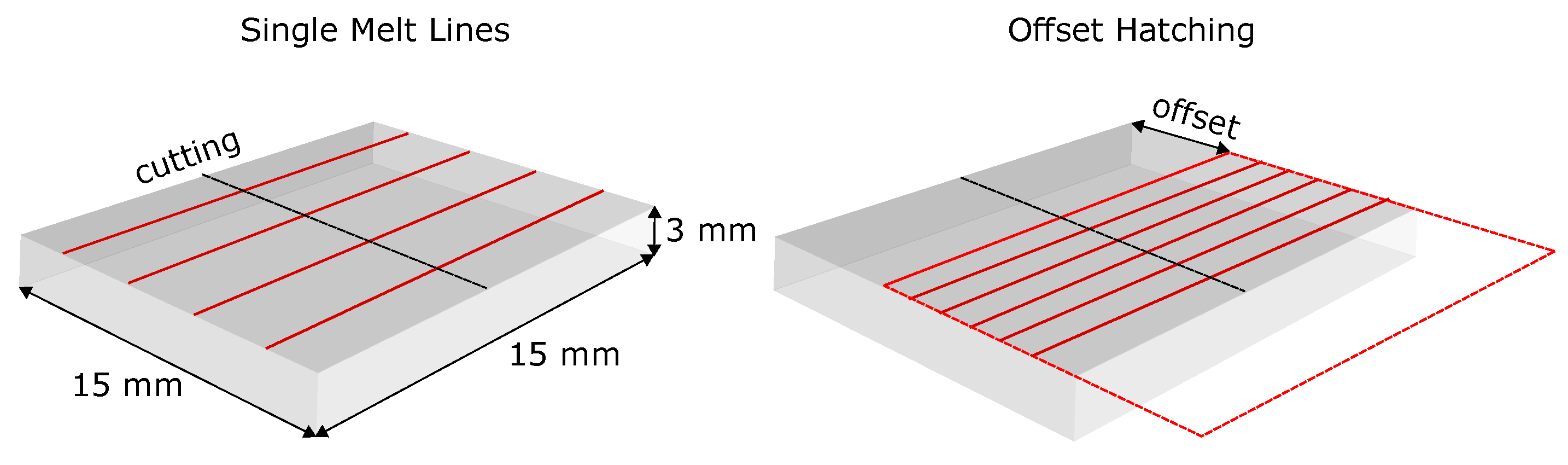
2.1.4. Single Line Remelting on SX Substrate
2.1.5. Offset Hatching on the SX Substrate
2.1.6. Metallographic Preparation and Microstructural Investigation
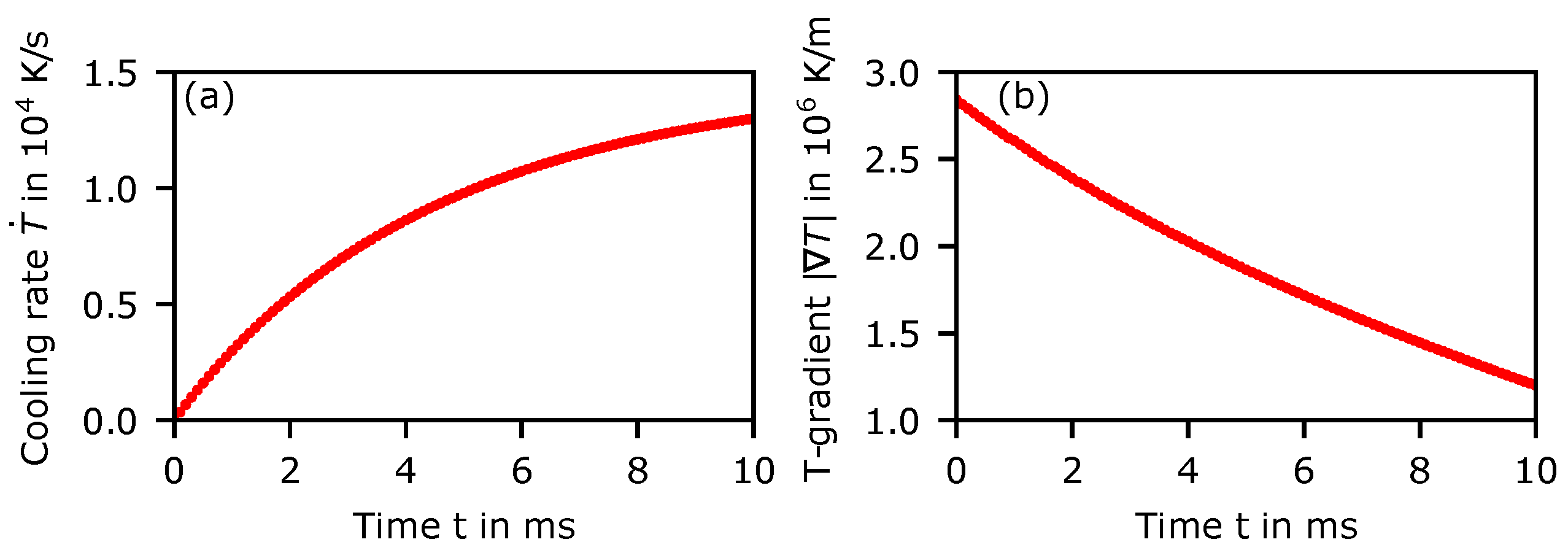
2.2. Calculation of the Temperature Evolution
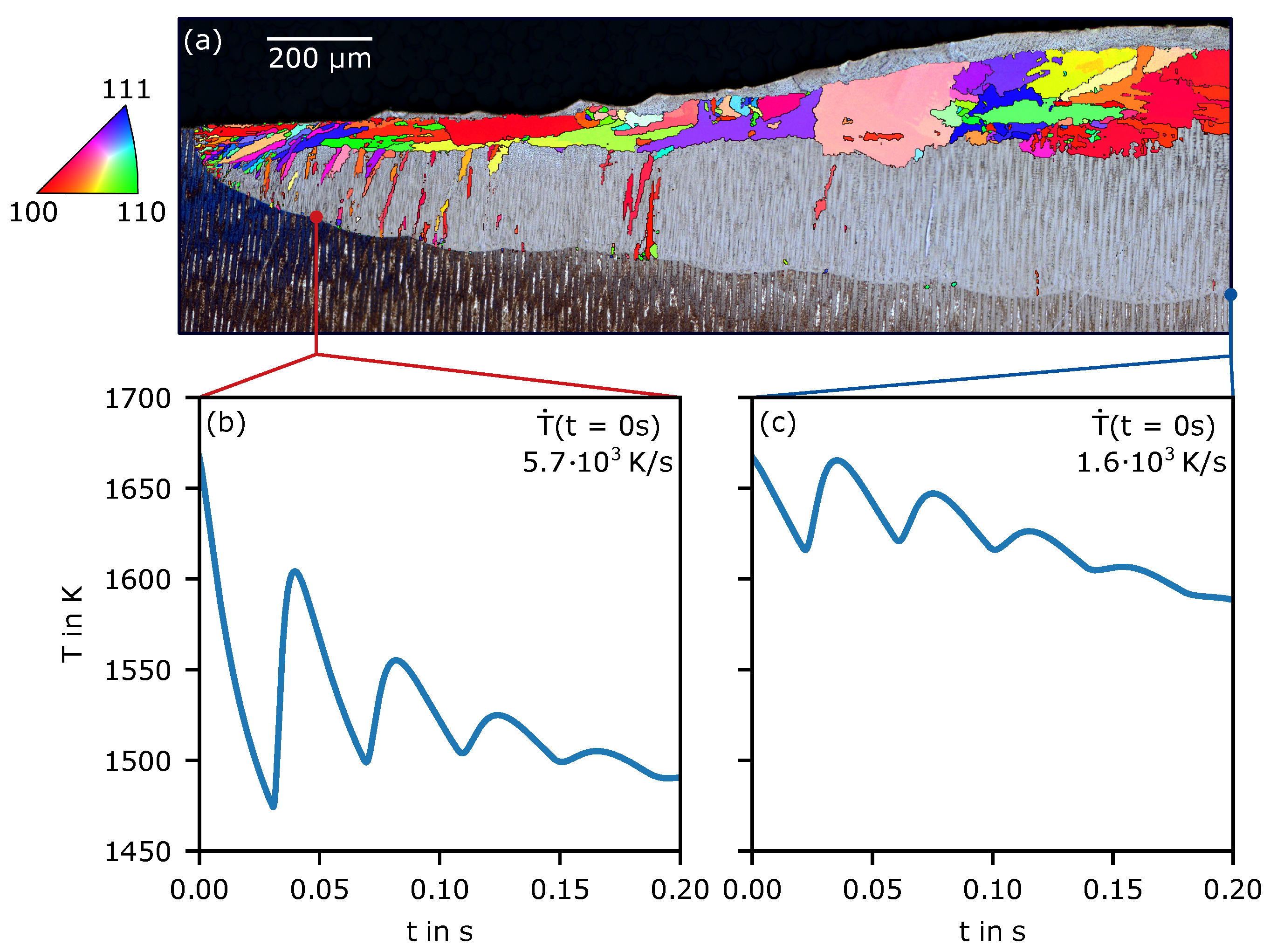
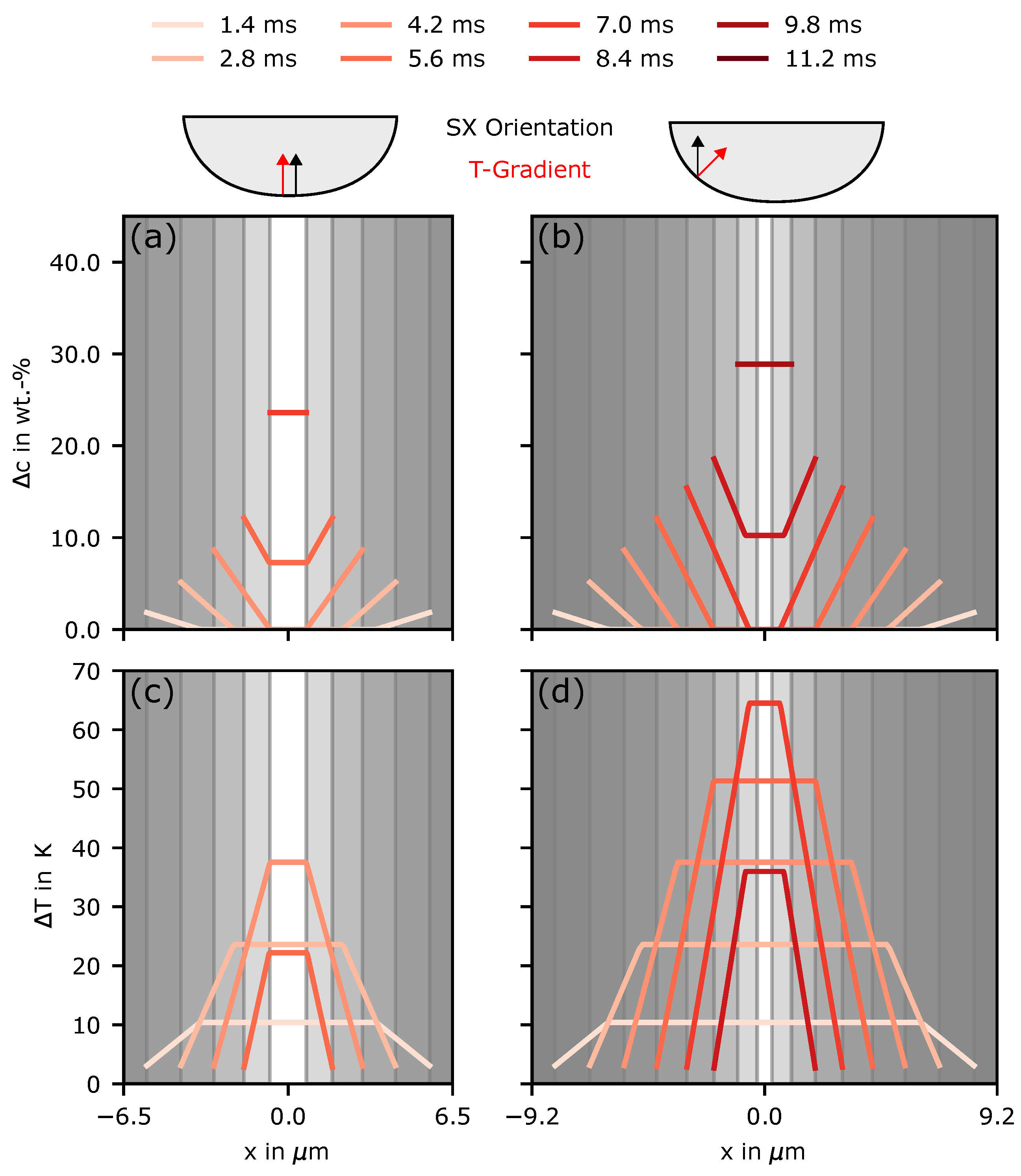
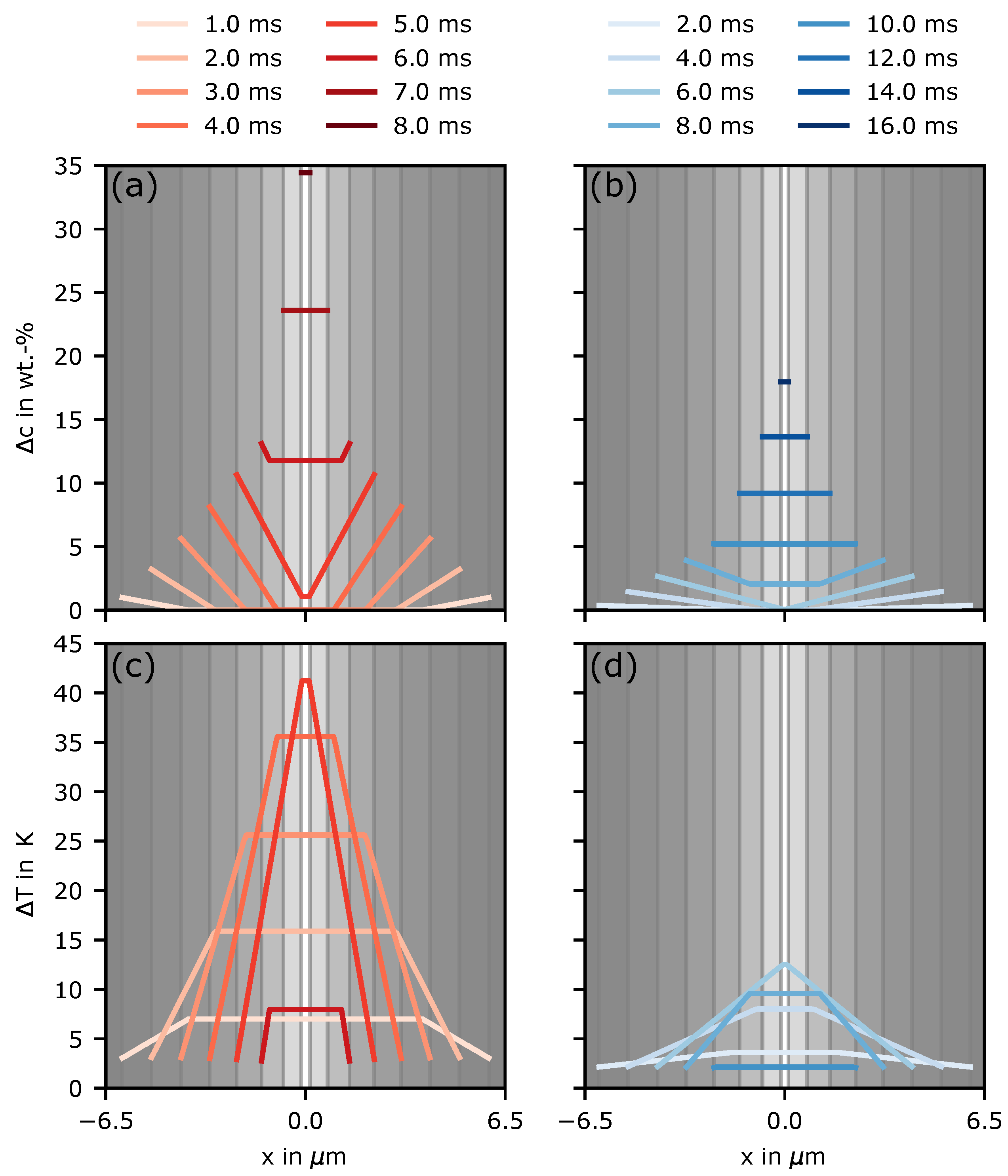
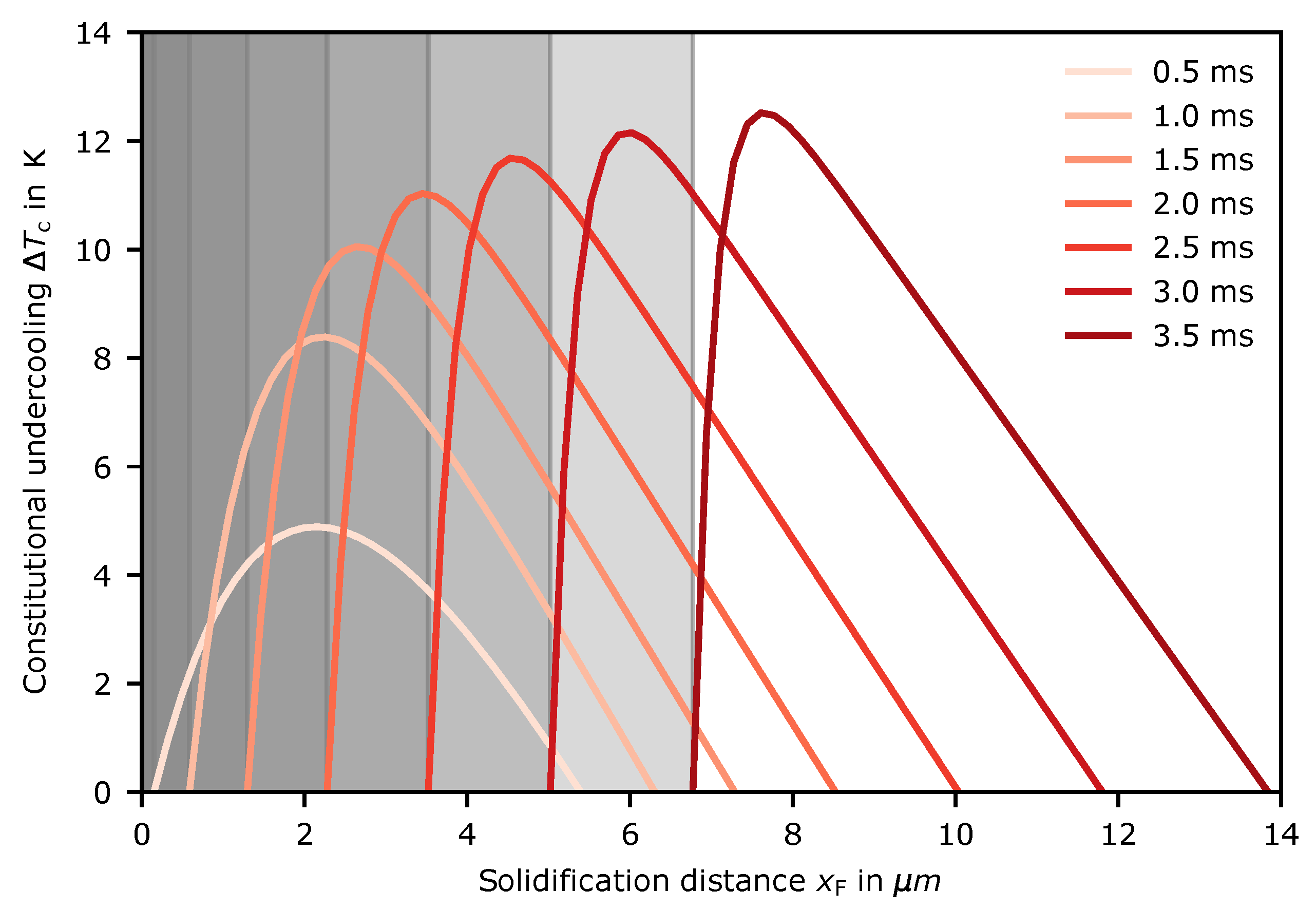
3. Results
4. Discussion
4.1. Grain Selection
4.2. Nucleation in As-Built Samples
4.3. Nucleation in Heat-Treated Samples
5. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Liquid Diffusion Coefficient
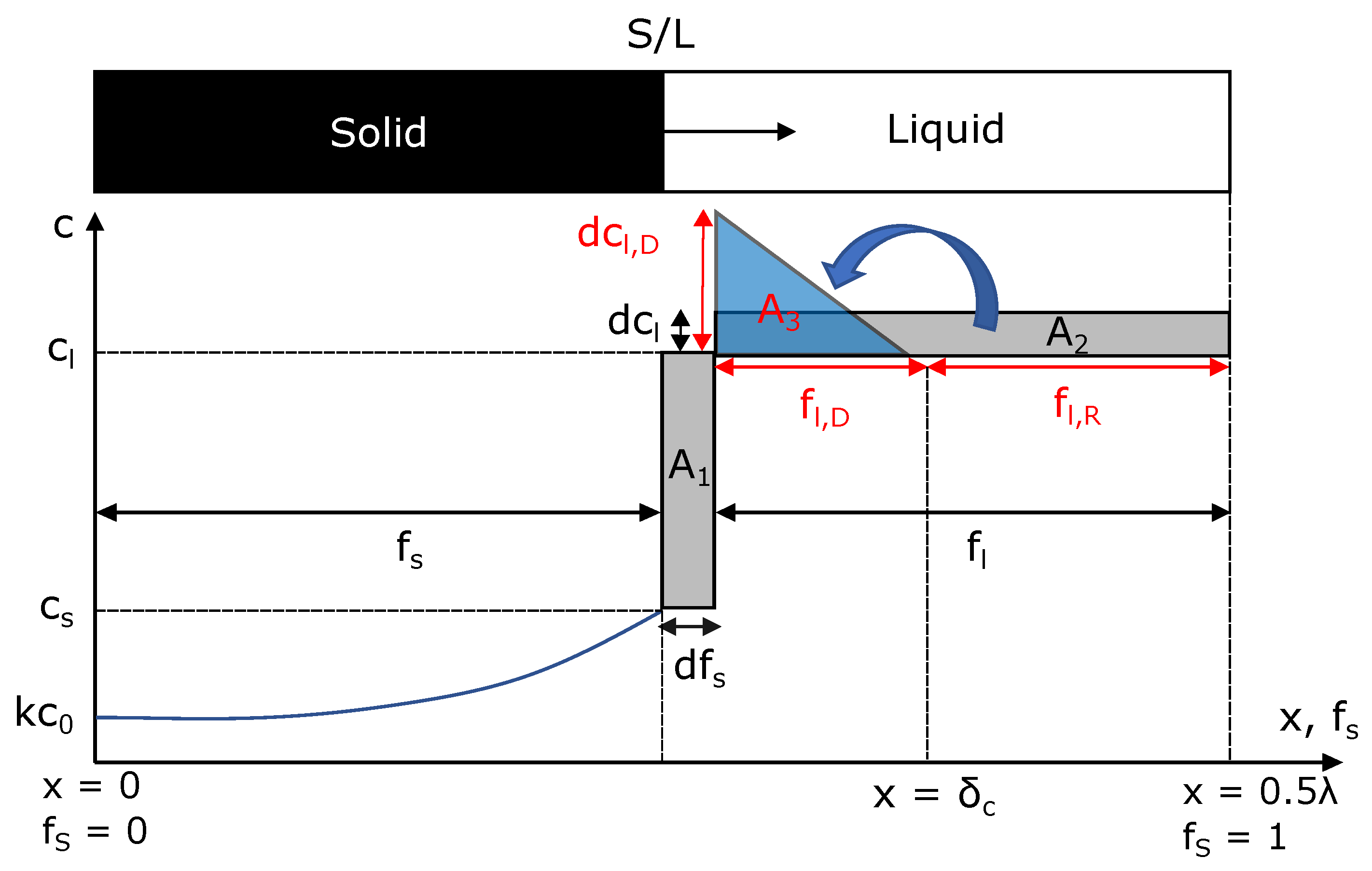
Appendix B. Derivation of the Advanced Scheil Model
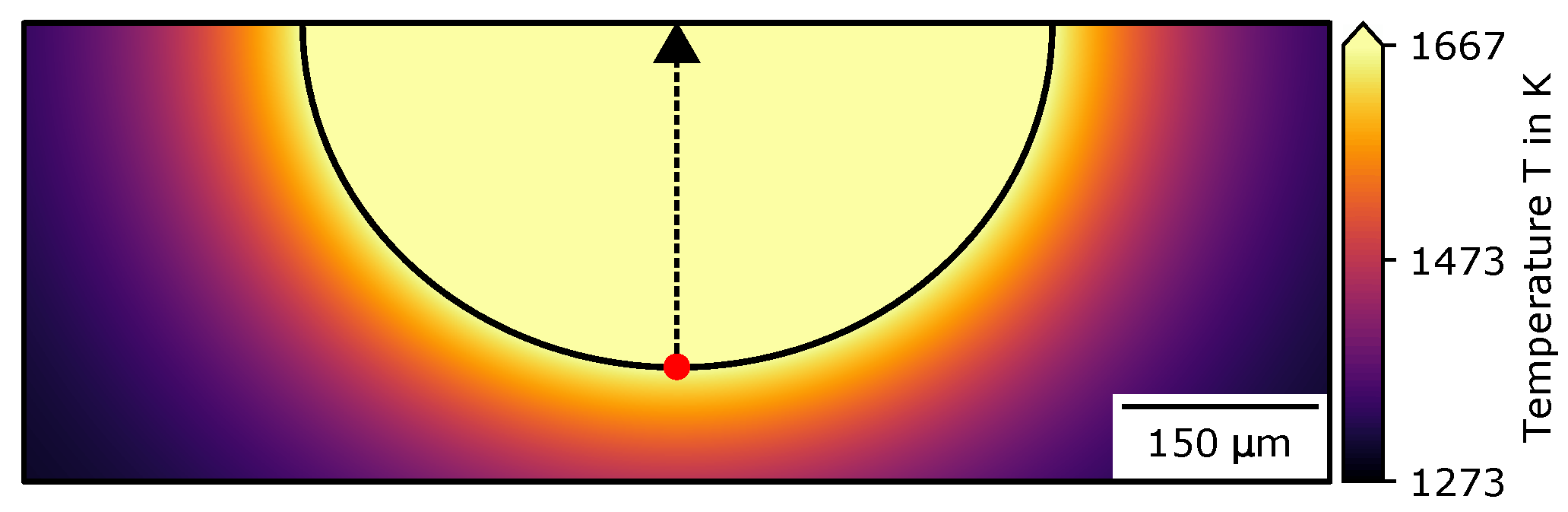
Appendix C. Simulation Overview
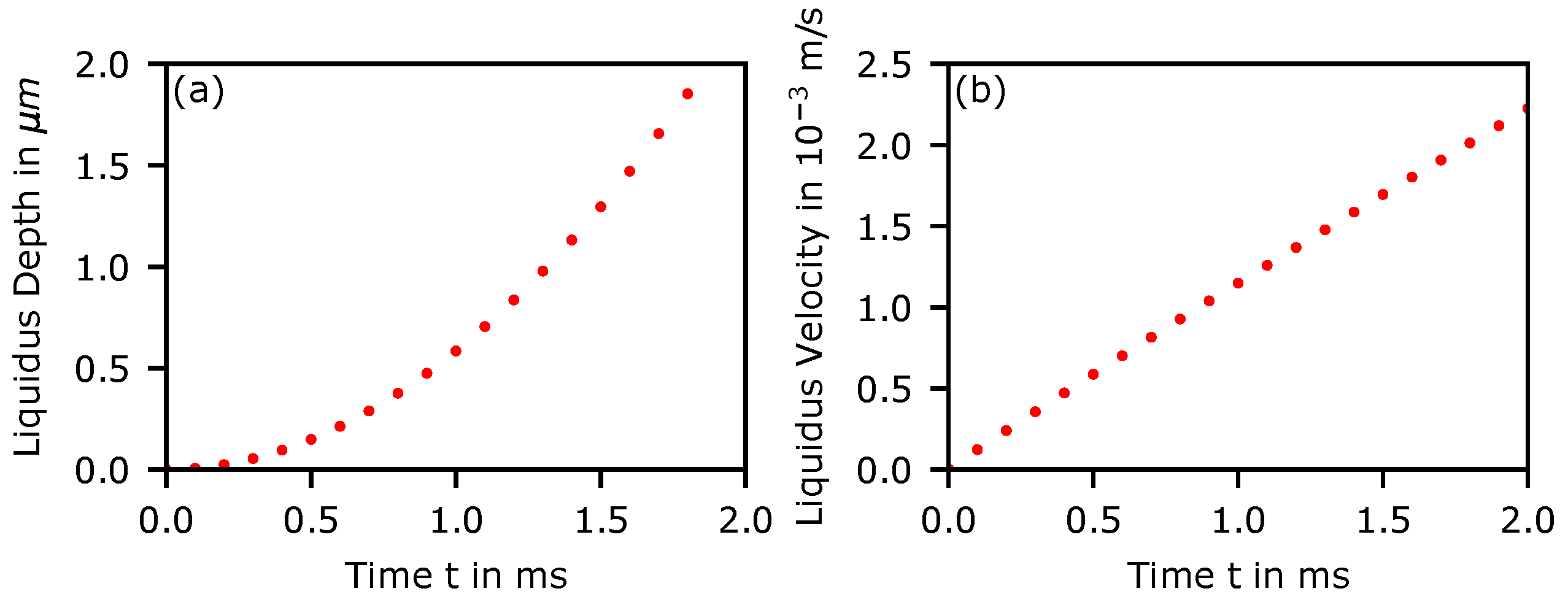
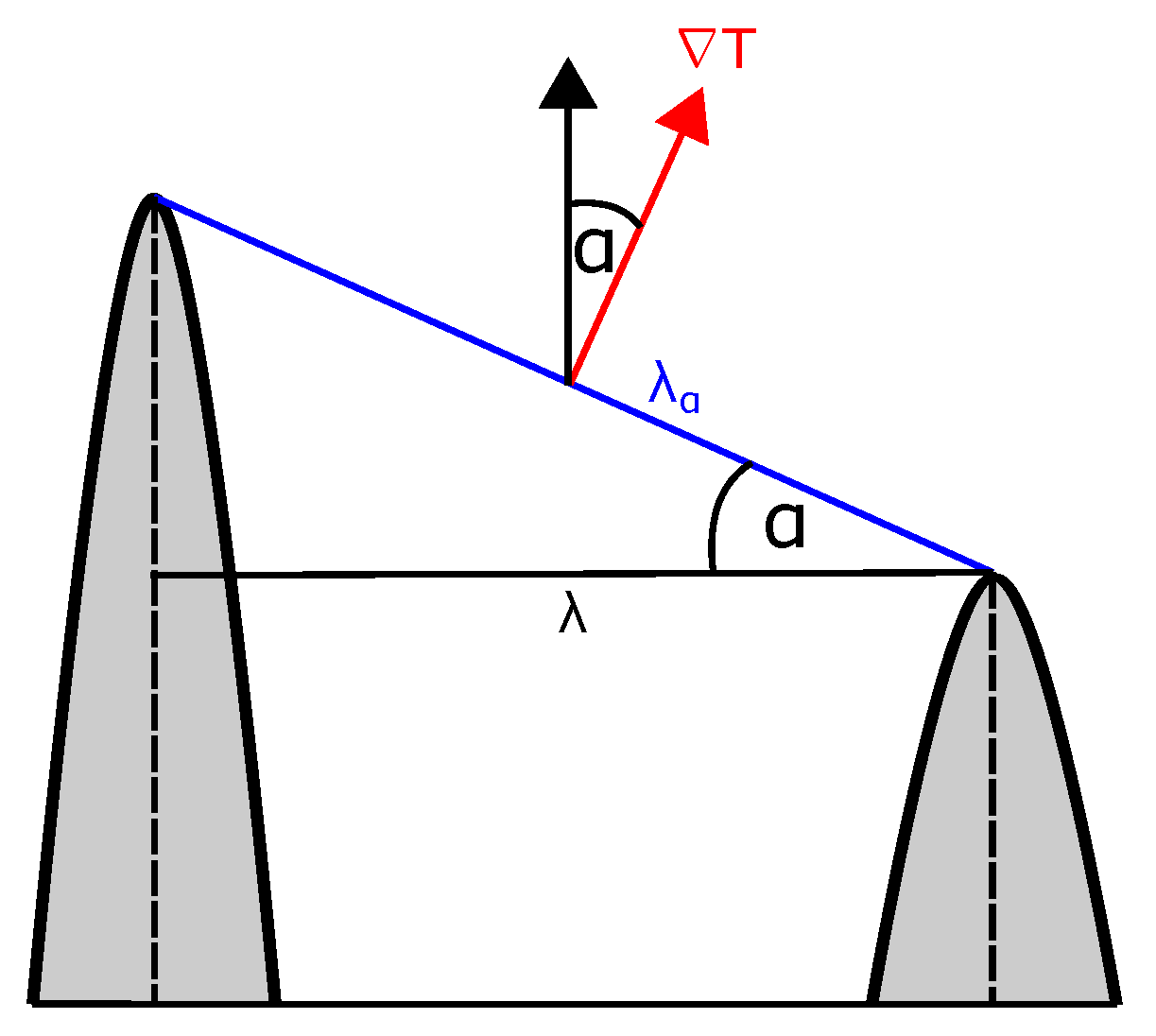
Appendix D. Angular Dependency
References
- Körner, C.; Helmer, H.; Bauereiß, A.; Singer, R.F. Tailoring the grain structure of IN718 during selective electron beam melting. MATEC Web Conf. 2014, 14, 08001. [Google Scholar] [CrossRef]
- Raghavan, N.; Dehoff, R.; Pannala, S.; Simunovic, S.; Kirka, M.; Turner, J.; Carlson, N.; Babu, S.S. Numerical modeling of heat-transfer and the influence of process parameters on tailoring the grain morphology of IN718 in electron beam additive manufacturing. Acta Mater. 2016, 112, 303–314. [Google Scholar] [CrossRef]
- Balachandramurthi, A.R.; Olsson, J.; Ålgårdh, J.; Snis, A.; Moverare, J.; Pederson, R. Microstructure tailoring in Electron Beam Powder Bed Fusion additive manufacturing and its potential consequences. Results Mater. 2019, 1, 100017. [Google Scholar] [CrossRef]
- Ding, X.; Koizumi, Y.; Aoyagi, K.; Kii, T.; Sasaki, N.; Hayasaka, Y.; Yamanaka, K.; Chiba, A. Microstructural control of alloy 718 fabricated by electron beam melting with expanded processing window by adaptive offset method. Mater. Sci. Eng. A 2019, 764, 138058. [Google Scholar] [CrossRef]
- Körner, C.; Ramsperger, M.; Meid, C.; Bürger, D.; Wollgramm, P.; Bartsch, M.; Eggeler, G. Microstructure and Mechanical Properties of CMSX-4 Single Crystals Prepared by Additive Manufacturing. Metall. Mater. Trans. A 2018, 49, 3781–3792. [Google Scholar] [CrossRef]
- Chauvet, E.; Tassin, C.; Blandin, J.J.; Dendievel, R.; Martin, G. Producing Ni-base superalloys single crystal by selective electron beam melting. Scr. Mater. 2018, 152, 15–19. [Google Scholar] [CrossRef]
- Gotterbarm, M.R.; Rausch, A.M.; Körner, C. Fabrication of Single Crystals through a µ-Helix Grain Selection Process during Electron Beam Metal Additive Manufacturing. Metals 2020, 10, 313. [Google Scholar] [CrossRef]
- Kirka, M.M.; Lee, Y.; Greeley, D.A.; Okello, A.; Goin, M.J.; Pearce, M.T.; Dehoff, R.R. Strategy for Texture Management in Metals Additive Manufacturing. JOM 2017, 69, 523–531. [Google Scholar] [CrossRef]
- Raghavan, N.; Simunovic, S.; Dehoff, R.; Plotkowski, A.; Turner, J.; Kirka, M.; Babu, S. Localized melt-scan strategy for site specific control of grain size and primary dendrite arm spacing in electron beam additive manufacturing. Acta Mater. 2017, 140, 375–387. [Google Scholar] [CrossRef]
- Helmer, H.; Bauereiß, A.; Singer, R.; Körner, C. Grain structure evolution in Inconel 718 during selective electron beam melting. Mater. Sci. Eng. A 2016, 668, 180–187. [Google Scholar] [CrossRef]
- Lee, Y.; Kirka, M.; Dinwiddie, R.; Raghavan, N.; Turner, J.; Dehoff, R.; Babu, S. Role of scan strategies on thermal gradient and solidification rate in electron beam powder bed fusion. Addit. Manuf. 2018, 22, 516–527. [Google Scholar] [CrossRef]
- Shimono, Y.; Oba, M.; Nomoto, S.; Koizumi, Y.; Akihiko, C. Numerical Investigation of Solidification in Additive Manufacturing of Ti Alloy by Multi-Phase Field Method. In Proceedings of the 28th Annual International Solid Freeform Fabrication Symposium, Austin, TX, USA, 7–9 August 2017. [Google Scholar]
- Yan, F.; Xiong, W.; Faierson, E.J. Grain Structure Control of Additively Manufactured Metallic Materials. Materials 2017, 10, 1260. [Google Scholar] [CrossRef]
- Gäumann, M.; Henry, S.; Cléton, F.; Wagnière, J.D.; Kurz, W. Epitaxial laser metal forming: Analysis of microstructure formation. Mater. Sci. Eng. A 1999, 271, 232–241. [Google Scholar] [CrossRef]
- Gäumann, M.; Bezençon, C.; Canalis, P.; Kurz, W. Single-crystal laser deposition of superalloys: Processing–microstructure maps. Acta Mater. 2001, 49, 1051–1062. [Google Scholar] [CrossRef]
- Gäumann, M.; Kurz, W. Why Is It so Difficult to Produce an Equiaxed Microstructure During Welding? CRC Press: Boca Raton, FL, USA, 1998; Volume 4, pp. 125–136. [Google Scholar]
- Zhang, D.; Qiu, D.; Gibson, M.A.; Zheng, Y.; Fraser, H.L.; StJohn, D.H.; Easton, M.A. Additive manufacturing of ultrafine-grained high-strength titanium alloys. Nature 2019, 576, 91–95. [Google Scholar] [CrossRef]
- Karimi, P.; Sadeghi, E.; Ålgårdh, J.; Andersson, J. EBM-manufactured single tracks of Alloy 718: Influence of energy input and focus offset on geometrical and microstructural characteristics. Mater. Charact. 2019, 148, 88–99. [Google Scholar] [CrossRef]
- Wang, X.; Liu, P.W.; Ji, Y.; Liu, Y.; Horstemeyer, M.H.; Chen, L. Investigation on Microsegregation of IN718 Alloy During Additive Manufacturing via Integrated Phase-Field and Finite-Element Modeling. J. Mater. Eng. Perform. 2019, 28, 657–665. [Google Scholar] [CrossRef]
- Dezfoli, A.; Ansari, R.; Hwang, W.S.; Huang, W.C.; Tsai, T.W. Determination and controlling of grain structure of metals after laser incidence: Theoretical approach. Sci. Rep. 2019, 7, 41527. [Google Scholar] [CrossRef]
- Thijs, L.; Kempen, K.; Kruth, J.P.; Humbeeck, J.V. Fine-structured aluminium products with controllable texture by selective laser melting of pre-alloyed AlSi10Mg powder. Acta Mater. 2013, 61, 1809–1819. [Google Scholar] [CrossRef]
- Drezet, J.M.; Mokadem, S. Marangoni Convection and Fragmentation in LASER Treatment. Mater. Sci. Forum 2006, 508, 257–262. [Google Scholar] [CrossRef]
- Liu, X.; Zhao, C.; Zhou, X.; Shen, Z.; Liu, W. Microstructure of selective laser melted AlSi10Mg alloy. Mater. Des. 2019, 168, 107677. [Google Scholar] [CrossRef]
- Rausch, A.M.; Gotterbarm, M.R.; Pistor, J.; Markl, M.; Körner, C. New Grain Formation by Constitutional Undercooling Due to Remelting of Segregated Microstructures during Powder Bed Fusion. Materials 2020, 13, 5517. [Google Scholar] [CrossRef]
- Gutierrez, A.; Lippold, J.C. A proposed mechanism for equiaxed grain formation along the fusion boundary in aluminum-copper-lithium alloys. Weld. J. 1998, 77, 123–132. [Google Scholar]
- Meid, C.; Dennstedt, A.; Ramsperger, M.; Pistor, J.; Ruttert, B.; Lopez-Galilea, I.; Theisen, W.; Körner, C.; Bartsch, M. Effect of heat treatment on the high temperature fatigue life of single crystalline nickel base superalloy additively manufactured by means of selective electron beam melting. Scr. Mater. 2019, 168, 124–128. [Google Scholar] [CrossRef]
- Pistor, J.; Körner, C. Formation of topologically closed packed phases within CMSX-4 single crystals produced by additive manufacturing. Mater. Lett. X 2019, 1, 100003. [Google Scholar] [CrossRef]
- Ramsperger, M.; Mújica Roncery, L.; Lopez-Galilea, I.; Singer, R.F.; Theisen, W.; Körner, C. Solution Heat Treatment of the Single Crystal Nickel-Base Superalloy CMSX-4 Fabricated by Selective Electron Beam Melting. Adv. Eng. Mater. 2015, 17, 1486–1493. [Google Scholar] [CrossRef]
- Plotkowski, A.; Kirka, M.; Babu, S. Verification and validation of a rapid heat transfer calculation methodology for transient melt pool solidification conditions in powder bed metal additive manufacturing. Addit. Manuf. 2017, 18, 256–268. [Google Scholar] [CrossRef]
- Forslund, R.; Snis, A.; Larsson, S. Analytical solution for heat conduction due to a moving Gaussian heat flux with piecewise constant parameters. Appl. Math. Model. 2019, 66, 227–240. [Google Scholar] [CrossRef]
- Schwalbach, E.J.; Donegan, S.P.; Chapman, M.G.; Chaput, K.J.; Groeber, M.A. A discrete source model of powder bed fusion additive manufacturing thermal history. Addit. Manuf. 2019, 25, 485–498. [Google Scholar] [CrossRef]
- Nguyen, N.; Ohta, A.; Matsuoka, K.; Suzuki, N.; Maeda, Y. Analytical solutions for transient temperature of semi-infinite body subjected to 3-D moving heat sources. Weld. J. 1999, 78, 265–274. [Google Scholar]
- Stump, B.; Plotkowski, A. An adaptive integration scheme for heat conduction in additive manufacturing. Appl. Math. Model. 2019, 75, 787–805. [Google Scholar] [CrossRef]
- Mills, K.C. (Ed.) Woodhead Publishing Series in Metals and Surface Engineering; Woodhead Publishing: Sawston, UK, 2002. [Google Scholar] [CrossRef]
- Parsa, A.B.; Ramsperger, M.; Kostka, A.; Somsen, C.; Körner, C.; Eggeler, G. Transmission Electron Microscopy of a CMSX-4 Ni-Base Superalloy Produced by Selective Electron Beam Melting. Metals 2016, 6, 258. [Google Scholar] [CrossRef]
- Karunaratne, M.; Cox, D.C.; Carter, P.; Reed, R.C. Modelling of the Microsegregation in CMSX-4 Superalloy and its Homogenisation During Heat Treatment. Superalloys 2000. [Google Scholar] [CrossRef]
- Szeliga, D.; Kubiak, K.; Burbelko, A.; Motyka, M.; Sieniawski, J. Modeling of Directional Solidification of Columnar Grain Structure in CMSX-4 Nickel-Based Superalloy Castings. J. Mater. Eng Perform 2014, 23, 1088–1095. [Google Scholar] [CrossRef]
- Walton, D.; Chalmers, B. The origin of the preferred orientation in the columnar zone of ingots. Trans. Metall. Soc. AIME 1959, 215, 447–457. [Google Scholar]
- Lippold, J.C.; Lin, W.M. Weldability of commercial AL-CU-LI Alloys. Mater. Sci. Forum 1996, 217, 1685–1690. [Google Scholar] [CrossRef]
- Ridgeway, C.D.; Gu, C.; Luo, A.A. Predicting primary dendrite arm spacing in Al–Si–Mg alloys: Effect of Mg alloying. J. Mater. Sci. 2019, 9907–9920. [Google Scholar] [CrossRef]
- Gulliver, G.H. The Quantitative Effect of Rapid Cooling Upon the Constitution of Binary Alloys. J. Inst. Met. 1913, 9, 120. [Google Scholar]
- Scheil, E. Bemerkungen zur Schichtkristallbildung. Z. Met. 1942, 34, 70. [Google Scholar]
- Kurz, W.; Fisher, D.J. Fundamentals of Solidification; Trans Tech Publications: Stäfa-Zürich, Switzerland, 1986; Volume 21. [Google Scholar] [CrossRef]
- Kurz, W.; Giovanola, B.; Trivedi, R. Theory of microstructural development during rapid solidification. Acta Metall. 1986, 34, 823–830. [Google Scholar] [CrossRef]
- Gandin, C.A.; Schäfer, R.; Rappax, M. Analytical and numerical predictions of dendritic grain envelopes. Acta Mater. 1996, 44, 3339–3347. [Google Scholar] [CrossRef]
- Koepf, J.A.; Gotterbarm, M.R.; Markl, M.; Körner, C. 3D multi-layer grain structure simulation of powder bed fusion additive manufacturing. Acta Mater. 2018, 152, 119–126. [Google Scholar] [CrossRef]
- Köpf, J.; Soldner, D.; Ramsperger, M.; Mergheim, J.; Markl, M.; Kö, C. Numerical microstructure prediction by a coupled finite element cellular automaton model for selective electron beam melting. Comput. Mater. Sci. 2019, 162, 148–155. [Google Scholar] [CrossRef]
- Verhoeven, J.; Gibson, E. Interface stability of the melting solid–liquid interface: I. Sn-Sb alloys. J. Cryst. Growth 1971, 11, 29–38. [Google Scholar] [CrossRef]
- Tiller, W.A.; Jackson, K.A.; Rutter, J.W.; Chalmers, B. The redistribution of solute atoms during the solidification of metals. Acta Metall. 1953, 1, 428–437. [Google Scholar] [CrossRef]
- Smith, V.G.; Tiller, W.A.; Rutter, J.W. A Mathematical Analysis of Solute Redistribution During Solidification. Can. J. Phys. 1955, 33, 723–745. [Google Scholar] [CrossRef]
- Einstein, A. Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen. Ann. Phys. 1905, 17, 549–560. [Google Scholar] [CrossRef]
- Sutherland, W. Dynamical theory of diffusion for non-electrolytes and the molecular mass of albumin. Phil. Mag. 1905, 9, 781–785. [Google Scholar] [CrossRef]
- Ricci, E.; Giuranno, D.; Novakovic, R.; Matsushita, R.; Seetharaman, S.; Brooks, R.; Chapman, L.A.; Quested, P.N. Density, Surface Tension, and Viscosity of CMSX-4® Superalloy. Int. J. Thermophys 2007, 28, 1304–1321. [Google Scholar] [CrossRef]




| Element | Al | Co | Cr | Hf | Mo | Re | Ta | Ti | W | Ni |
|---|---|---|---|---|---|---|---|---|---|---|
| wt.-% | 6.15 | 9.93 | 6.60 | 0.085 | 0.65 | 2.91 | 6.57 | 1.08 | 6.44 | Bal. |
| Heat Treatment | Ramp 1 | Ramp 2 | Target | Cooling |
|---|---|---|---|---|
| Solution | RT–1000 C | 1000–1310 C | 1310 C | water |
| Annealing | 20 K/min | 5 K/min | 35 min | |
| Ageing | RT–1000 C | 1000–1140 C | 1140 C | Argon |
| Annealing 1 | 20 K/min | 5 K/min | 2 h | |
| Ageing | RT–870 C | - | 870 C | Argon |
| Annealing 2 | 5 K/min | - | 20 h |
| Samples | Line Energy () | Beam Power P | Scan Speed v |
|---|---|---|---|
| 1–4 | 800–1400 J m‒1 | 200–350 | m s‒1 |
| 6–9 | 600–1400 J m‒1 | 300–700 | m s‒1 |
| Property | Value | Reference |
|---|---|---|
| Thermal diffusivity (m2 s−1) | [34] | |
| Density (kg m−3) | 8193 | [34] |
| Specific heat (J kg−1 K−1) | 925 | [34] |
| Absorption coefficient | ||
| Preheat temperature (C) | 1000 | - |
| Liquidus temperature (C) | 1394 | [28] |
| Parameter | Value | Reference |
|---|---|---|
| Nominal concentration (wt.-%) | Table 1 | |
| Partition coefficient k | [37] | |
| Diffusion coefficient (liquid) (m2 s−1) | Appendix A | |
| Diffusion coefficient (solid) (m2 s−1) | [36] | |
| Liquidus slope m (K wt.-%−1) | [37] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rausch, A.M.; Pistor, J.; Breuning, C.; Markl, M.; Körner, C. New Grain Formation Mechanisms during Powder Bed Fusion. Materials 2021, 14, 3324. https://doi.org/10.3390/ma14123324
Rausch AM, Pistor J, Breuning C, Markl M, Körner C. New Grain Formation Mechanisms during Powder Bed Fusion. Materials. 2021; 14(12):3324. https://doi.org/10.3390/ma14123324
Chicago/Turabian StyleRausch, Alexander M., Julian Pistor, Christoph Breuning, Matthias Markl, and Carolin Körner. 2021. "New Grain Formation Mechanisms during Powder Bed Fusion" Materials 14, no. 12: 3324. https://doi.org/10.3390/ma14123324
APA StyleRausch, A. M., Pistor, J., Breuning, C., Markl, M., & Körner, C. (2021). New Grain Formation Mechanisms during Powder Bed Fusion. Materials, 14(12), 3324. https://doi.org/10.3390/ma14123324