4.1. Compressibility Test
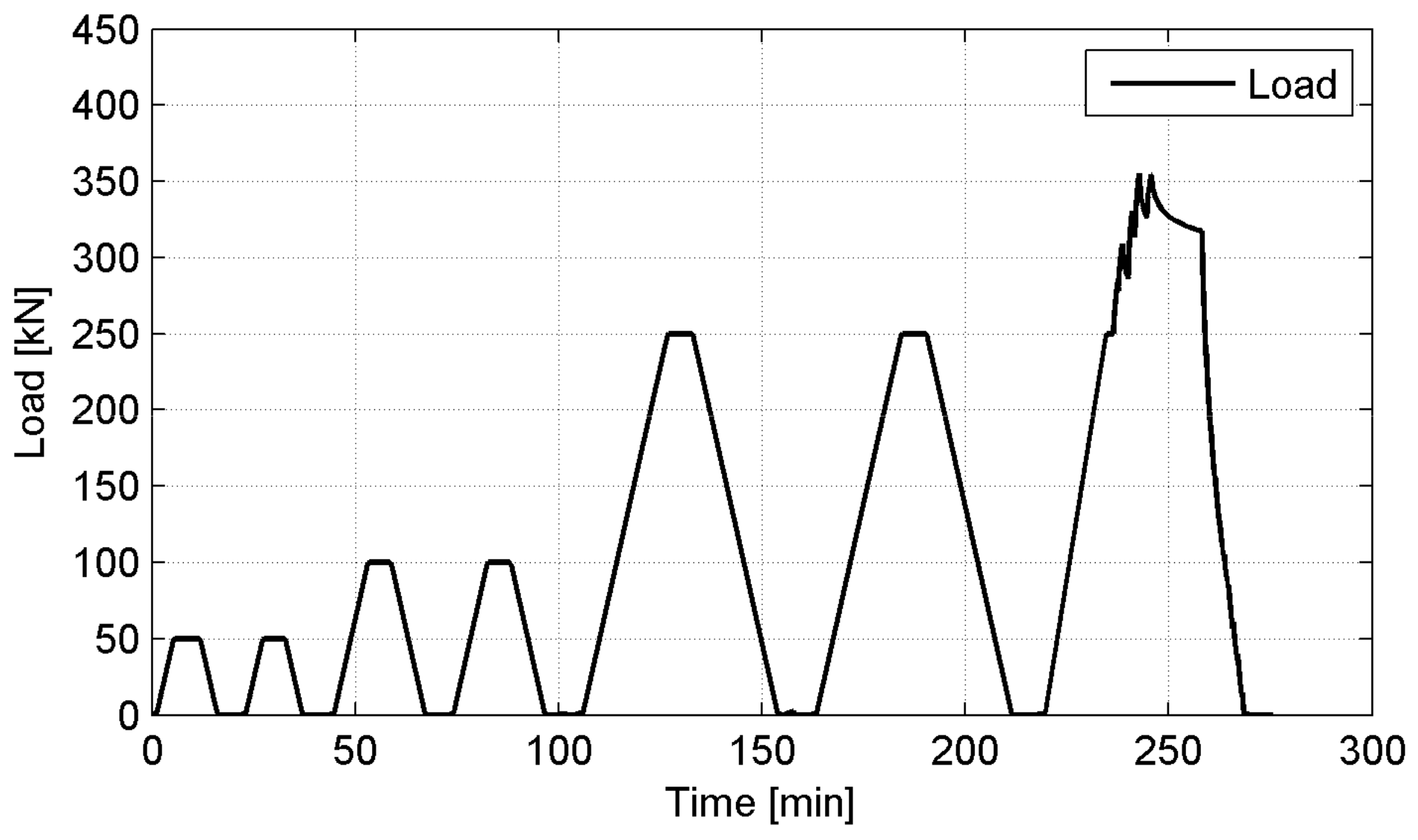
The load versus vertical and horizontal deformation plots are given to characterize the bales behavior under compression. In
Figure 11a,b the typical behavior of the exemplary P-4 bale is presented for vertical and horizontal deformations, respectively (the sixth cycle,
p = 250 kN). The considerable differences between displacement records for individual LVDTs are shown, particularly for horizontal ones. It is not due to uniform loading of a bale despite stiff platen applied as well as different structural homogeneity of the bales themselves. The summary average displacement plots for all bales are given in
Figure 12a,b, for vertical and horizontal deformations, respectively (the sixth cycle,
p = 250 kN).
The considerable differences in bale’s behavior under compression for individual bales are revealed. This was attributed to the variability of the bales’ structure and the fact that no two tests, although using the same type of bales, were the same. For all bales, the non-linear response of the tyre bale was revealed as well as a hysteretic unloading curve was obtained. The hysteretic curvature implies that the deformation remains in the tyre bale structure even after the applied load is removed, although the sixth load cycle was applied. This is evident by the apparent plastic deformation of the tyre bale after unloading, in which approximately 15 mm of deformation remain, most of which is fully recovered to a value of 2–3 mm after 5 min. The hysteretic curvature with approximately ten times smaller apparent plastic deformations was also observed in the horizontal direction.
The excessive platen incline was treated as a failure in each scheme (
Figure 13a). The reliable record of vertical displacements was impossible due to platen rotation and the applied force was recognized as a maximum (failure) load
Pmax. After reaching
Pmax the tyre bale was unloaded. Although no bale’s steel tie wires broke at failure load, the decrease of wire tension was observed (loose wires) after unloading (
Figure 13b).
The failure loads and average vertical and horizontal displacements at
p = 250 kN and at failure load, based on records of four vertical and three horizontal LVDTs, respectively, are collected together in
Table 3. The compressive strength of the tyre bales used in the current research was in the range of 355–436 kN and the average strength obtained was 382 kN. At this failure load, the average vertical displacement was 125 mm, which means 16.7% average vertical bale’s deformation. However, after unloading the bales had a permanent vertical deformation in the range of 25–30 mm only, which revealed their good elasticity under compression and the possibility of almost full recovering in several min after unloading.
The stress–strain curves for all bales obtained in the final (failure) cycle of loading are shown in
Figure 10. The relevant values of stresses and strains were calculated as follows:
and
where:
vavg–average vertical displacement at failure load (
Table 3);
A and
H–area and height of the bale (
Table 1).
The comparison of the five curves in
Figure 14 provides evidence of the effects of tyre bale structure and variability between bales. The test results indicated that the tyre bales did not have the ultimate strength at stress levels of less than 130 kPa, while the maximum ultimate strength obtained was 158 kPa. The higher strength was unable to obtain due to excessive platen inclination under ultimate loading. The vertical strain of the tyre bales was over 30% at the maximum test loads. However, at working stress levels (typically less than 50 kPa) strains are much lower and will be further reduced by filling and bale confinement. The ultimate strength of tyre bales can be enhanced due to sand infill (reduction of empty spaces in bales) and lateral constrains of a single bale, located always in a group of bales. The tests, which simulated both aforementioned conditions, revealed that the ultimate strength of tyre bales could be enhanced up to 815 kPa [
21].
The Young’s modulus (Ev) and the Poison’s ratio (ν) for a tyre bale are the basic design parameters of high importance, required for further site implementation. Therefore the evaluation of both parameters has been carried out based on compressibility test results. The non-linear deformation of the tyre bale can be represented by either an average linear modulus over the stress range of interest or a series of secant moduli with the applied load. The first approach was applied in the current research to assess the approximate modulus value and the latter was applied to show modulus variability under increasing load.
The Young’s modulus for each stress range considered was assessed according to the following formula:
where:
The values of the average Young’s moduli for the deformation curves of the tyre bales are presented in
Table 4. The approximate Young’s modulus for the tyre bale is in the range of 713.5 kPa to 904 kPa at a medium stress level of about 90 kPa (
p = 250 kN). However, the average
Ev value 826 kPa is close to the values reported in [
19,
21,
22] for a similar test setup (i.e., 914 kPa, 831 kPa, and 766 kPa, respectively). Moreover, including a predicted value of the tyre bale stiffness with sand infill, the determined modulus could be increased by 30% according to [
21]. To show Young’s modulus variability under increasing load a series of secant moduli with applied load was determined and graphically presented for P-5 bale in
Figure 15.
The Poisson’s ratio was defined as the horizontal strain divided by the total vertical strain of the tyre bale’s material. The equation for the Poisson’s ratio determination is as follows:
where:
The maximum horizontal strain
εh was calculated on the assumption of bales symmetry as the double horizontal deformation
2havg obtained at
Pmax (
Table 3), divided by the average bale length
L (
Table 1):
where:
—horizontal deformation (
Table 3);
It should be noted that horizontal strain was calculated only for the bale’s deformation in the length direction (
L), because the perpendicular deformation (
B-direction) was restrained from the wire ties. The horizontal deformation measurements indicated a relatively low Poison’s ratio on the order of 0.11 at the medium stress level of about 90 kPa (
p = 250 kN). Lateral movement at low and medium stress levels is likely restricted by the combination of compression during baling and vertical orientation of the tyres in the bale. Values reported in [
21] ranged from 0.1 to 0.2 for stresses less than 47.9 kPa, and increased up to 0.3–0.4 at higher stresses and those reported in [
22] ranged from 0.08 to 0.24 at maximum stress of 31.1 kPa. The Poisson’s ratio variability under increasing load in the range of 0–250 kN is graphically presented for P-5 bale in
Figure 16.
It should be noted that the asymptotic value of Poisson’s ratio was not determined yet, thus the values given in
Table 4 may be slightly underestimated. Finally, it should be underlined once again, that tyre bales used in the actual field applications will be surrounded by other tyre bales or soil, and therefore the effect of the confinement on the compressibility of the tyre bale needs to be taken into account.
4.3. Creep Test
The full creep curves for all tested specimens are shown in
Figure 23. In
Table 7 the deformation and time data are collected along with the regression analysis results (fitting curves and coefficient of determination R
2) estimated for all particular periods of creep loading. The following symbols were used in
Table 7:
h0—initial bale depth,
t—load time in h, Δ
hexp—the experimental measurement of creep deformation (an average of four records), R
2—coefficients of determination, Δ
h365—estimated 1-year creep deformation,
cα,365—estimated 1-year creep coefficient. The Δ
h365 values were estimated using the fitted regression lines given in
Table 7. The regression lines are very well fitted to testing results with the coefficients of determination R
2 > 0.94, except one case for specimen P-3 (load slab no.1), when test experienced accelerated movement on one corner after loading. Progressive deformation in different regions of the P-3 specimen resulted in variation in both deformation and load and made the determination of creep strain rate difficult.
The average creep deformation of three specimens under four-phase sustained load for the average sustain load period of 110 h was about 40 mm, which constitutes 6.1% of the average height of the bale. Approximately 95% of the deformation occurred on the first day and the maximum deformation appeared to occur within three days. The 1-year creep coefficients
cα,365 were estimated as 0.0048, 0.0042, and 0.0035 for P-1 to P-3 specimens, respectively, and the average
cα,365 value for the creep test as 0.0039 was obtained. This value is similar to those obtained by La Rocque [
19] and Zornberg et al. [
21]; the difference is less than 5%. The test indicates relatively little creep response at long-term stress levels. The post-3-day movement would roughly be the anticipated post-construction movement and could be reduced by preloading.