Performance Analysis of Radial Basis Function Metamodels for Predictive Modelling of Laminated Composites
Abstract
1. Introduction
2. Objectives and Problem Description
2.1. Problem 1: Low-Dimensional (LD) Problem
2.2. Problem 2: High-Dimensional (HD) Problem
3. Methodology
3.1. Sampling Schemes
3.1.1. Random Sampling
3.1.2. Latin Hypercube Sampling
3.1.3. Hammersley Sequence Sampling
3.2. Finite Element Method
3.3. Radial Basis Function
4. Results and Discussion
4.1. Low-Dimensional Problem
4.2. High-Dimensional Problem
5. Conclusions
- (a)
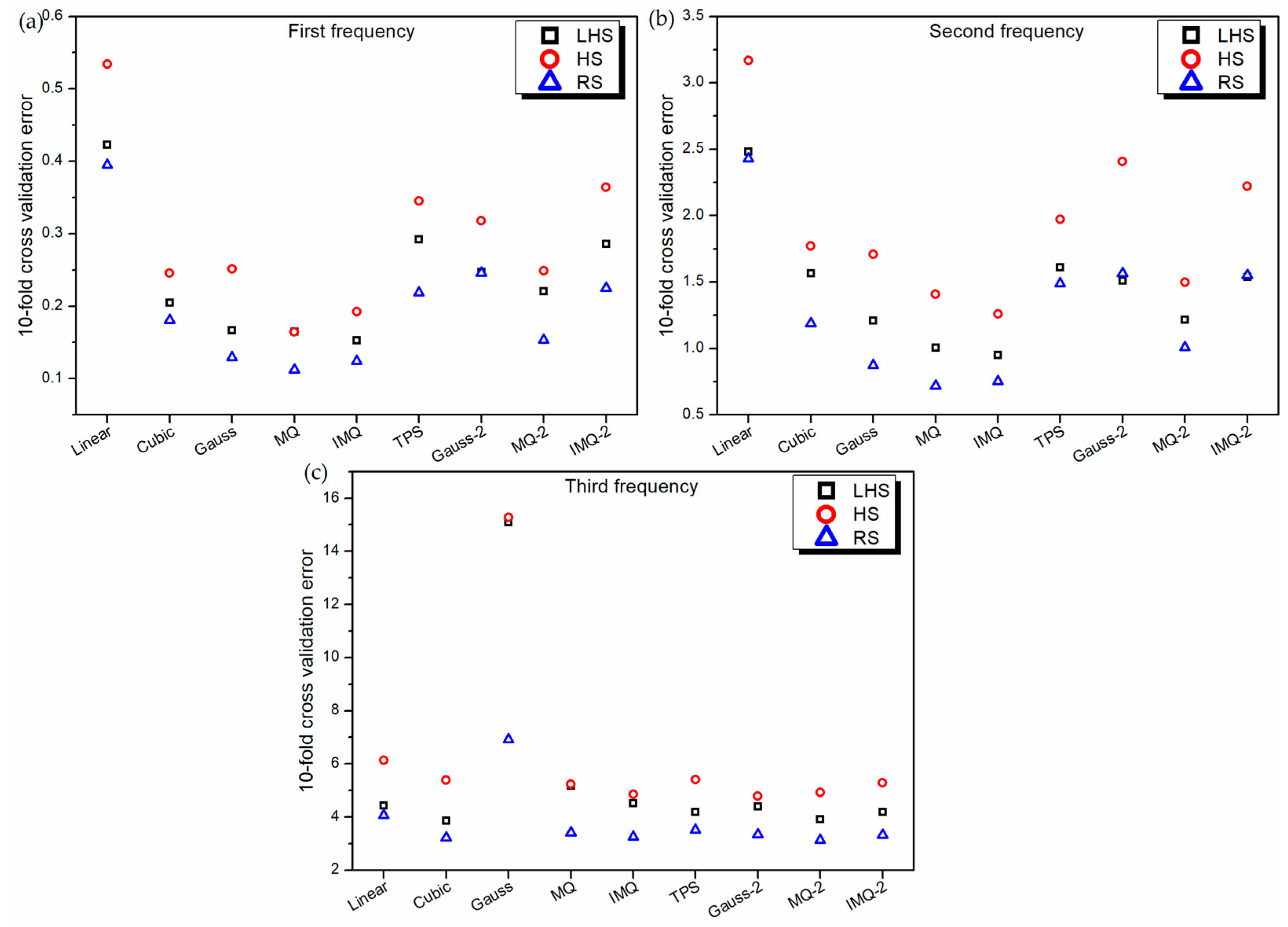
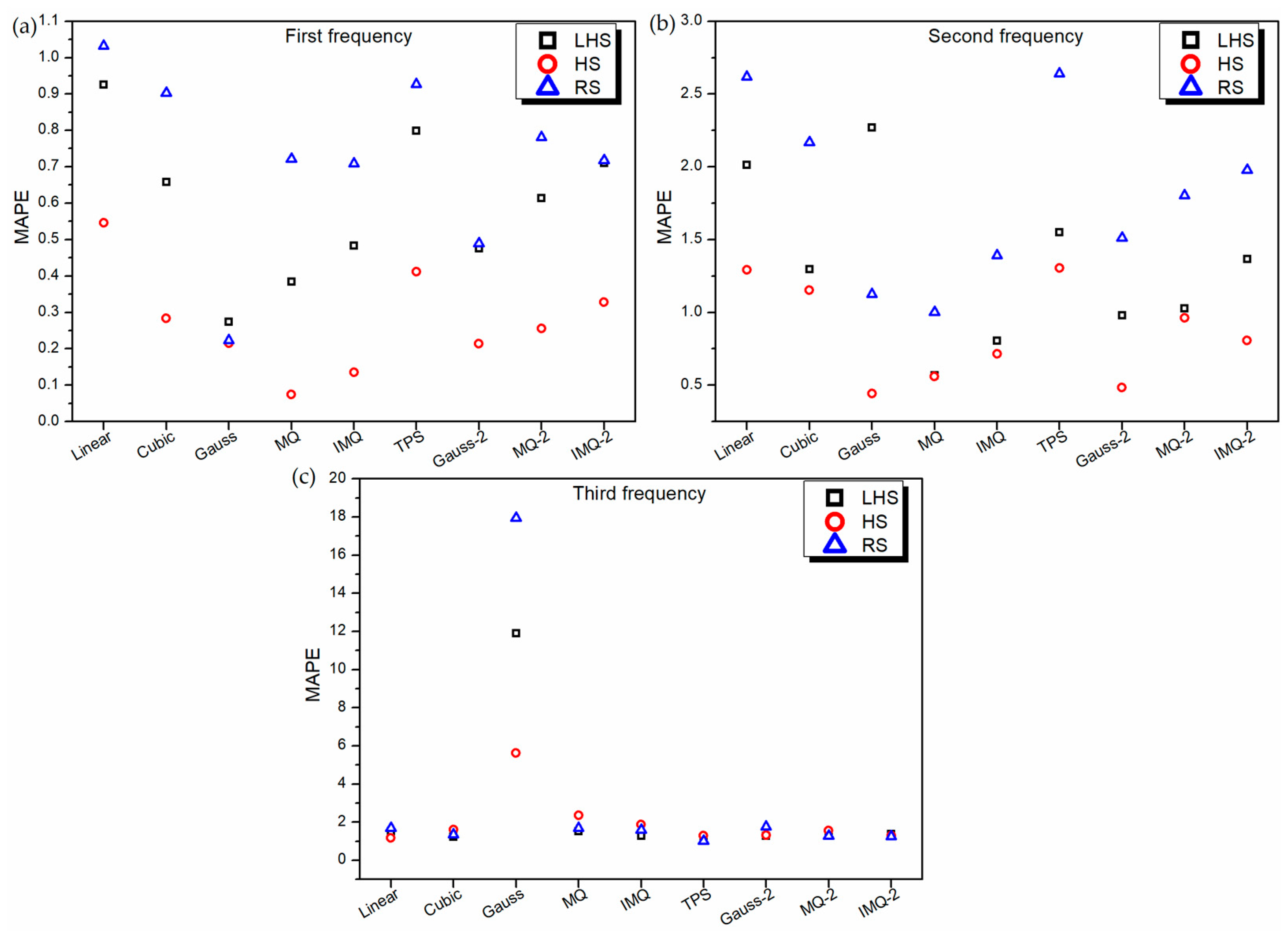
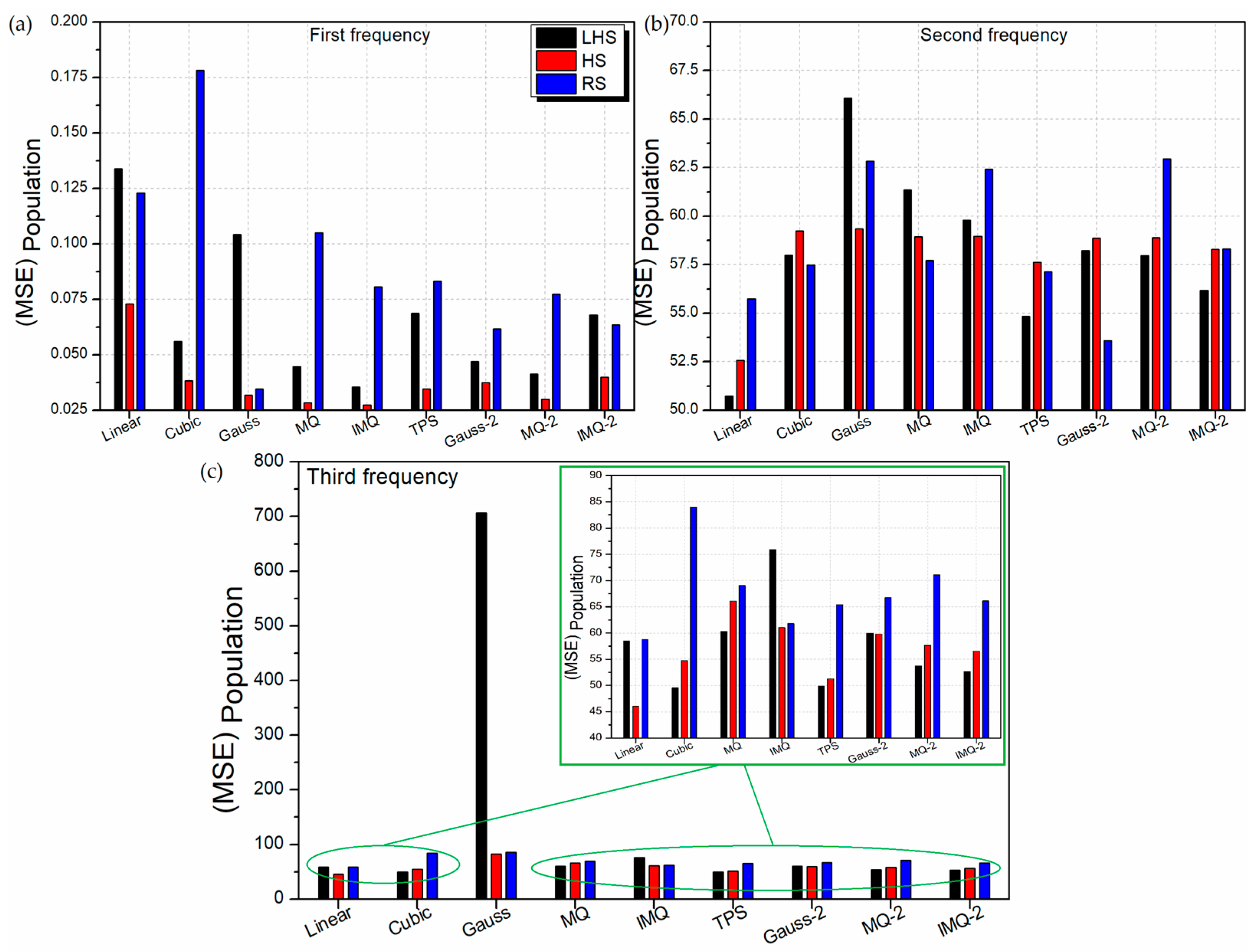
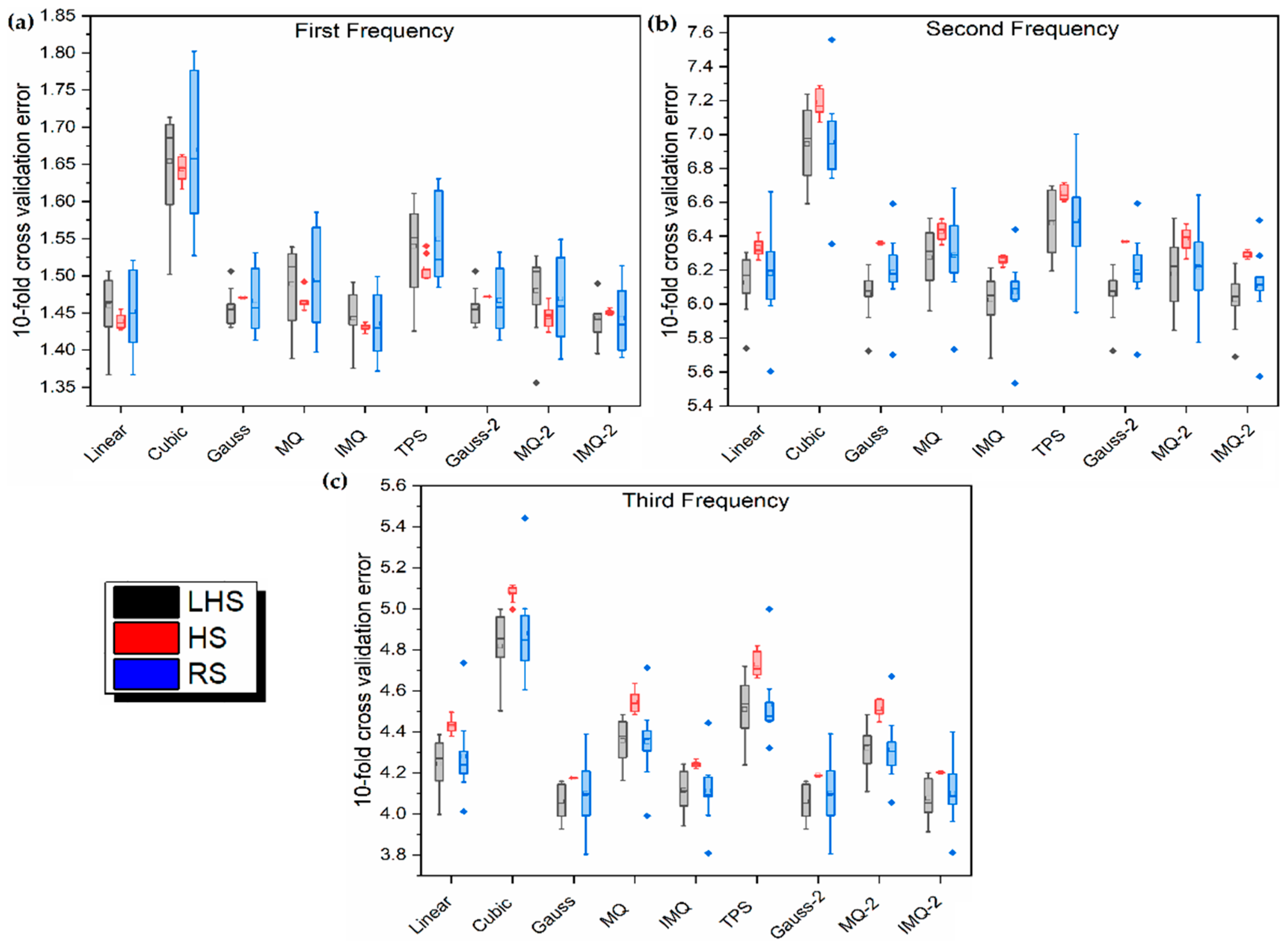
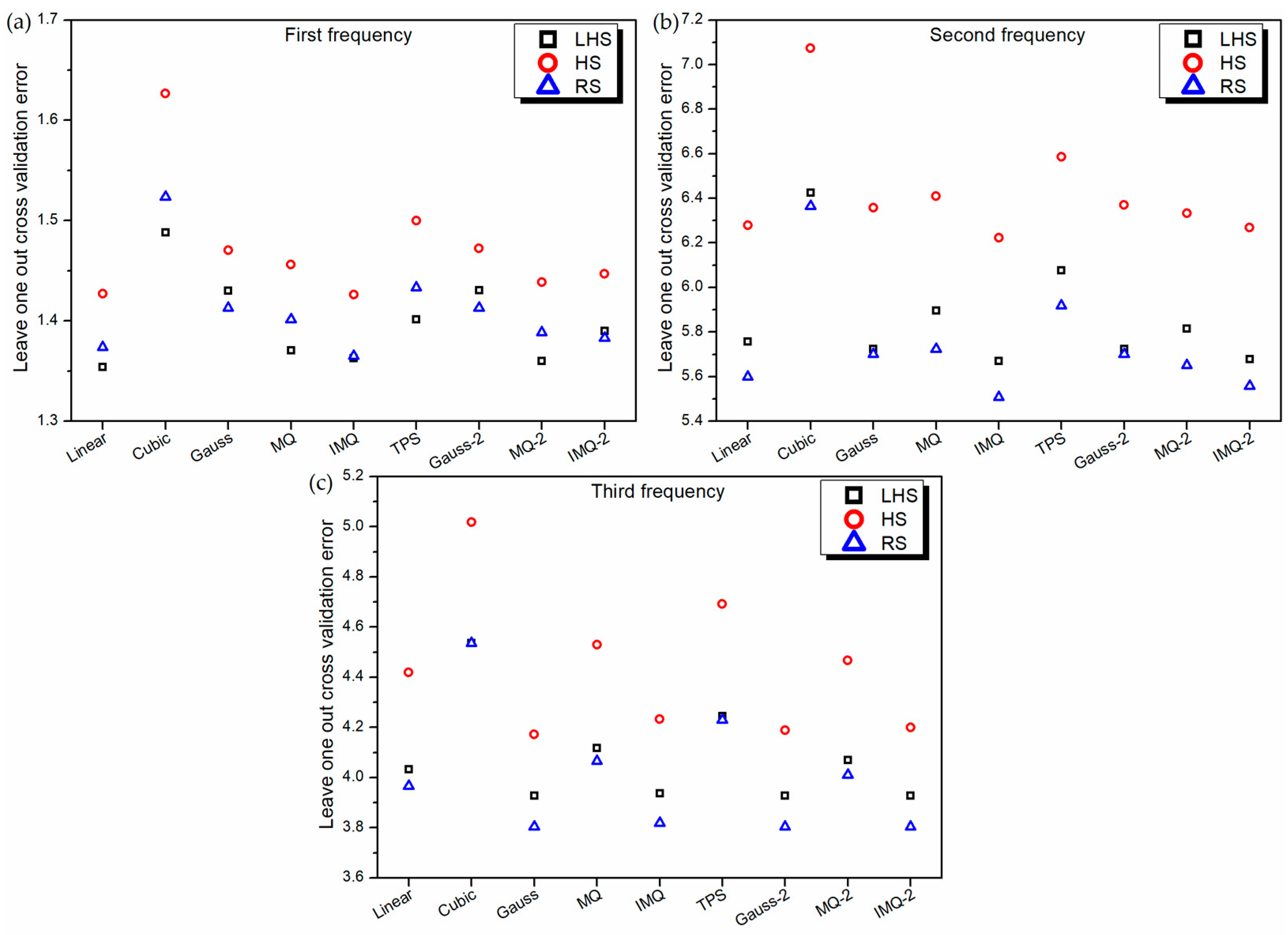
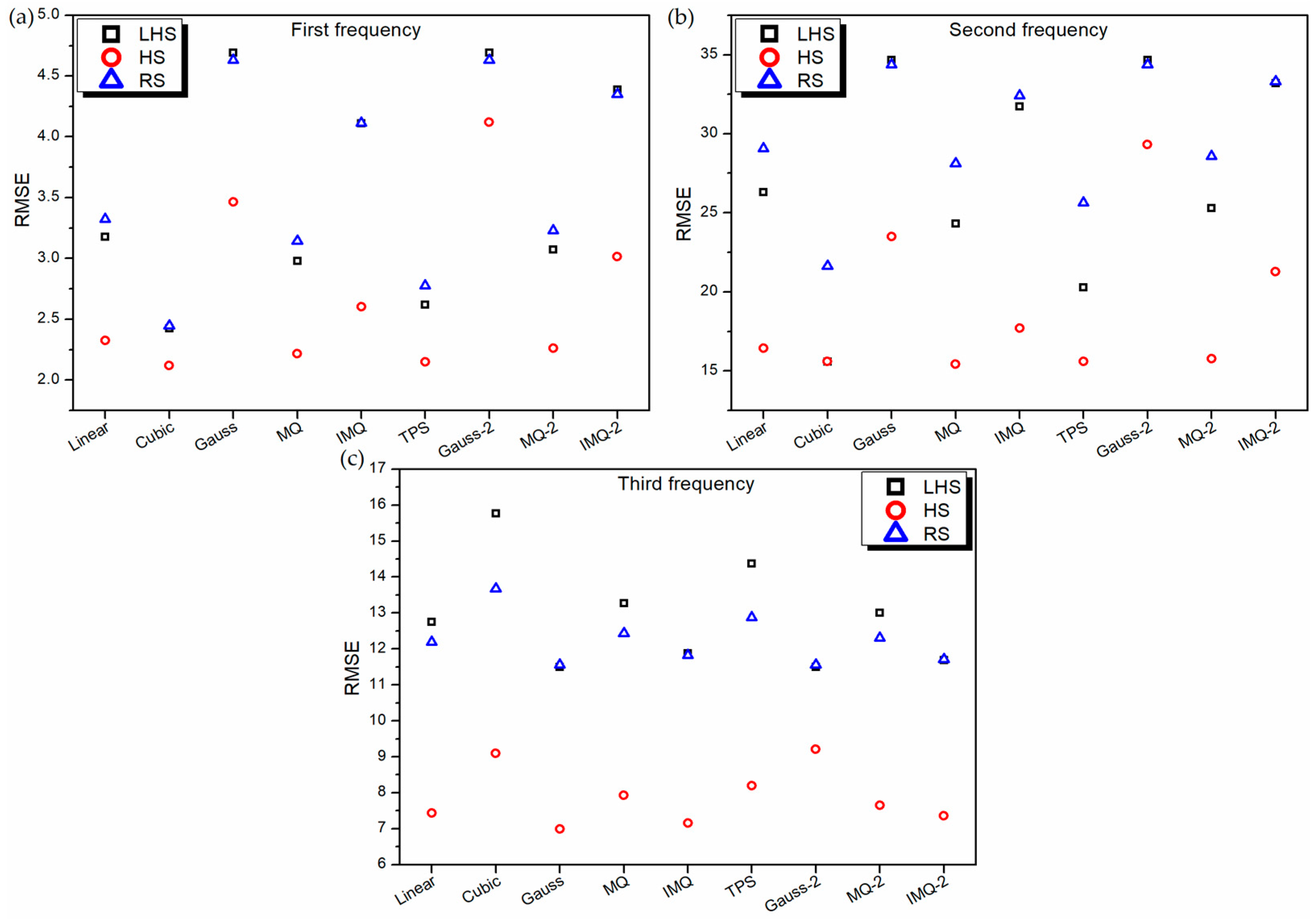
- The RBF metamodels trained on RS datasets have the best 10-fold cross-validation error and leave-one-out cross-validation error. However, this excellent prediction on training data does not necessarily correspond to excellent prediction (in terms of MAPE and RMSE) on independent test data. In fact, in all the three responses of LD problem, the worst MAPE and RMSE values are recorded for RBFs trained on the RS dataset.
- (b)
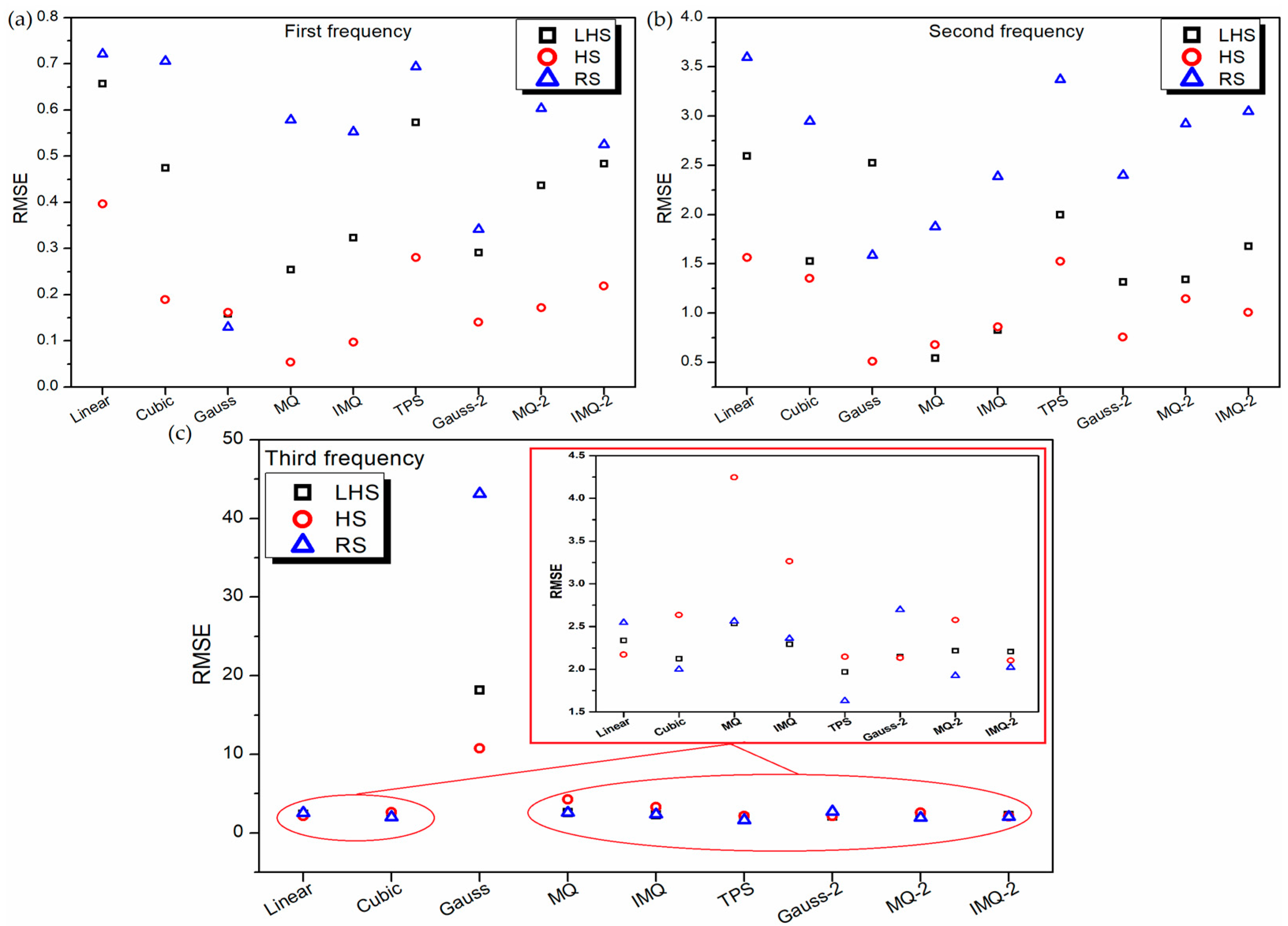
- The RBF metamodels trained on HS datasets have the best prediction with respect to MAPE and RMSE on independent test data. However, for all the three responses of both LD and HD problems, HS-data-trained RBFs show the worst 10-fold cross-validation error and leave-one-out cross-validation error. Nevertheless, in case of the LD problem, for the best (in terms of MAPE and RMSE) HS-data-trained RBF metamodels, the 10-fold cross-validation error is 47% (first frequency), 138% (second frequency) and 95% (third frequency) worst as compared to the overall best RBF metamodels. In case of the HD problem, these deviations are much lower, i.e., 19% (first frequency), 15% (second frequency) and 11% (third frequency). Thus, despite using metrics, like 10-fold cross-validation error and leave-one-out cross-validation error, performance measurement of metamodels on independent test data should be encouraged.
- (c)
- In general, irrespective of the sampling strategy and basis function, all RBF metamodels show better performance on the HD problem as compared to the corresponding metamodels for the LD problem. It should be noted that in terms of design variables, the HD problem is 8 times more complex than the LD problem, whereas the training datasets used have a ratio of 8.5:1 for HD and LD problems. Thus, the size of the training dataset has more influence on the metamodel’s predictive performance as compared to the number of variables.
- (d)
- Using TOPSIS, it can be observed that in general, MQ basis functions perform well for LD problem, whereas, for HD-problem, linear and MQ basis functions perform with high reliability.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
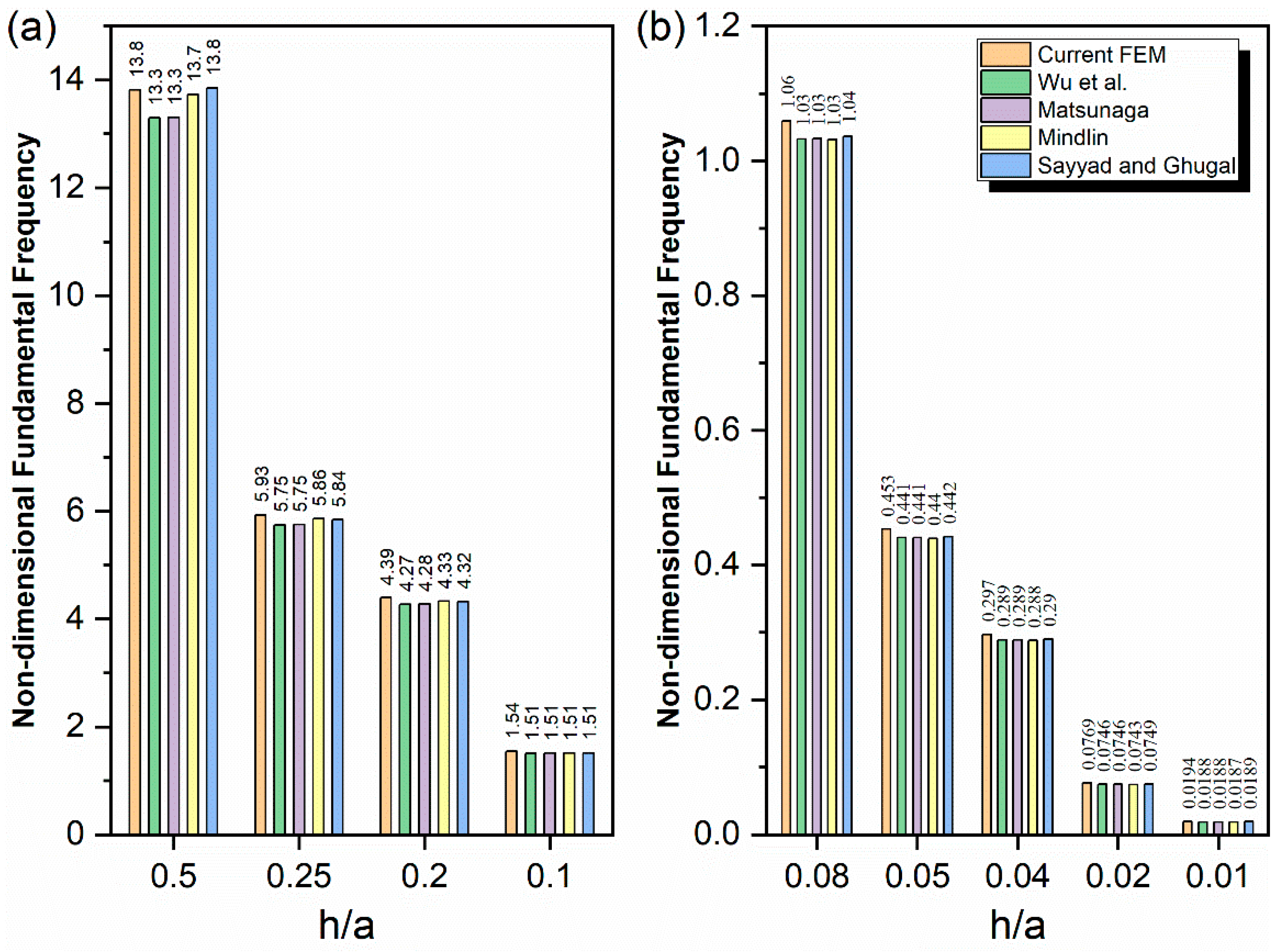
Appendix A. Validation of the FEM Formulation
Appendix B. Predictive Performance of the RBF Metamodels
| Metamodel | LD Problem | HD Problem | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| L10O CV 1 | LOOCV 2 | MAE | MAPE | MSE | L10O CV | LOOCV | MAE | MAPE | MSE | |
| Linear (LHS) | 0.4230 | 0.3996 | 0.4201 | 0.9253 | 0.4310 | 1.3667 | 1.3542 3 | 2.7372 | 6.2076 | 10.0952 |
| Cubic (LHS) | 0.2050 | 0.1997 | 0.2988 | 0.6584 | 0.2251 | 1.5018 | 1.4881 | 1.5735 | 3.5190 | 5.8822 |
| Gauss (LHS) | 0.1669 | 0.1830 | 0.1231 | 0.2742 | 0.0252 | 1.4303 | 1.4303 | 4.1653 | 9.4792 | 22.0251 |
| MQ (LHS) | 0.1646 | 0.1256 | 0.1739 | 0.3847 | 0.0647 | 1.3886 | 1.3705 | 2.5087 | 5.6825 | 8.8845 |
| IMQ (LHS) | 0.1527 | 0.1308 | 0.2188 | 0.4833 | 0.1045 | 1.3754 | 1.3630 | 3.6361 | 8.2695 | 16.8776 |
| TPS (LHS) | 0.2921 | 0.2488 | 0.3628 | 0.7991 | 0.3278 | 1.4256 | 1.4016 | 2.0118 | 4.5406 | 6.8539 |
| Gauss-2 (LHS) | 0.2469 | 0.2234 | 0.2144 | 0.4752 | 0.0848 | 1.4304 | 1.4304 | 4.1655 | 9.4794 | 22.0243 |
| MQ-2 (LHS) | 0.2205 | 0.1784 | 0.2783 | 0.6133 | 0.1909 | 1.3562 | 1.3602 | 2.6208 | 5.9402 | 9.4500 |
| IMQ-2 (LHS) | 0.2858 | 0.2483 | 0.3220 | 0.7104 | 0.2343 | 1.3953 | 1.3899 | 3.8974 | 8.8659 | 19.2459 |
| Linear (HS) | 0.5337 | 0.5264 | 0.2478 | 0.5454 | 0.1575 | 1.4274 | 1.4272 | 1.5109 | 3.4106 | 5.4063 |
| Cubic (HS) | 0.2455 | 0.2470 | 0.1286 | 0.2837 | 0.0357 | 1.6169 | 1.6264 | 1.3604 | 3.0373 | 4.4954 |
| Gauss (HS) | 0.2513 | 0.2619 | 0.0967 | 0.2146 | 0.0261 | 1.4704 | 1.4706 | 2.7284 | 6.1930 | 12.0072 |
| MQ (HS) | 0.1644 | 0.1552 | 0.0338 | 0.0748 | 0.0029 | 1.4535 | 1.4562 | 1.3976 | 3.1444 | 4.9146 |
| IMQ (HS) | 0.1921 | 0.1775 | 0.0616 | 0.1358 | 0.0094 | 1.4221 | 1.4262 | 1.7868 | 4.0455 | 6.7669 |
| TPS (HS) | 0.3453 | 0.3271 | 0.1868 | 0.4119 | 0.0789 | 1.4970 | 1.4997 | 1.3861 | 3.1114 | 4.6152 |
| Gauss-2 (HS) | 0.3176 | 0.3113 | 0.0966 | 0.2133 | 0.0196 | 1.4721 | 1.4721 | 3.4685 | 7.8823 | 16.9645 |
| MQ-2 (HS) | 0.2487 | 0.2355 | 0.1157 | 0.2552 | 0.0295 | 1.4241 | 1.4386 | 1.4404 | 3.2457 | 5.1219 |
| IMQ-2 (HS) | 0.3640 | 0.3468 | 0.1484 | 0.3274 | 0.0478 | 1.4473 | 1.4469 | 2.3586 | 5.3527 | 9.0770 |
| Linear (RS) | 0.3947 | 0.3380 | 0.4685 | 1.0320 | 0.5203 | 1.3672 | 1.3736 | 2.9342 | 6.6511 | 11.0335 |
| Cubic (RS) | 0.1809 | 0.1720 | 0.4091 | 0.9032 | 0.4979 | 1.5272 | 1.5237 | 1.8202 | 4.0734 | 5.9839 |
| Gauss (RS) | 0.1291 | 0.1102 | 0.1005 | 0.2232 | 0.0168 | 1.4132 | 1.4132 | 4.1115 | 9.3557 | 21.4504 |
| MQ (RS) | 0.1120 | 0.0865 | 0.3262 | 0.7212 | 0.3351 | 1.3976 | 1.4015 | 2.7707 | 6.2682 | 9.8799 |
| IMQ (RS) | 0.1245 | 0.1156 | 0.3207 | 0.7084 | 0.3051 | 1.3718 | 1.3652 | 3.6583 | 8.3158 | 16.9313 |
| TPS (RS) | 0.2187 | 0.2203 | 0.4209 | 0.9268 | 0.4807 | 1.4848 | 1.4335 | 2.3665 | 5.3376 | 7.7091 |
| Gauss-2 (RS) | 0.2463 | 0.2325 | 0.2214 | 0.4889 | 0.1167 | 1.4132 | 1.4132 | 4.1114 | 9.3555 | 21.4514 |
| MQ-2 (RS) | 0.1531 | 0.1568 | 0.3540 | 0.7813 | 0.3638 | 1.3880 | 1.3887 | 2.8525 | 6.4599 | 10.4330 |
| IMQ-2 (RS) | 0.2253 | 0.2040 | 0.3258 | 0.7181 | 0.2761 | 1.3900 | 1.3831 | 3.8646 | 8.7897 | 18.9036 |
| Metamodel | LD Problem | HD Problem | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| L10O CV | LOOCV | MAE | MAPE | MSE | L10O CV | LOOCV | MAE | MAPE | MSE | |
| Linear (LHS) | 2.4798 | 2.4290 | 1.6727 | 2.0130 | 6.7348 | 5.7387 | 5.7572 | 23.1989 | 32.3538 | 691.9223 |
| Cubic (LHS) | 1.5656 | 1.1782 | 1.0318 | 1.2958 | 2.3316 | 6.5919 | 6.4240 | 12.8804 | 17.2615 | 243.1132 |
| Gauss (LHS) | 1.2103 | 1.1837 | 1.8135 | 2.2702 | 3898 | 5.7234 | 5.7233 | 30.4541 | 42.5952 | 1202.6393 |
| MQ (LHS) | 1.0065 | 0.6612 | 0.4568 | 0.5686 | 0.2936 | 5.9608 | 5.8960 | 21.4918 | 29.9017 | 590.7010 |
| IMQ (LHS) | 0.9518 | 0.7734 | 0.6413 | 0.8045 | 0.6841 | 5.6802 | 5.6711 | 27.7195 | 38.8525 | 1006.2652 |
| TPS (LHS) | 1.6116 | 1.5472 | 1.2711 | 1.5495 | 4.0019 | 6.1969 | 6.0759 | 17.9242 | 24.6904 | 411.5608 |
| Gauss-2 (LHS) | 1.5109 | 1.4530 | 0.7466 | 0.9779 | 1.7330 | 5.7239 | 5.7239 | 30.4567 | 42.5989 | 1202.8600 |
| MQ-2 (LHS) | 1.2158 | 1.0548 | 0.8331 | 1.0279 | 1.7965 | 5.8464 | 5.8157 | 22.3485 | 31.1340 | 640.3793 |
| IMQ-2 (LHS) | 1.5388 | 1.4738 | 1.0932 | 1.3653 | 2.8164 | 5.6904 | 5.6790 | 29.0572 | 40.6952 | 1101.3604 |
| Linear (HS) | 3.1686 | 3.1799 | 1.0593 | 1.2912 | 2.4418 | 6.2596 | 6.2791 | 12.2203 | 16.3708 | 270.1005 |
| Cubic (HS) | 1.7698 | 1.8154 | 0.8917 | 1.1526 | 1.8309 | 7.0733 | 7.0739 | 12.4824 | 16.4916 | 243.5307 |
| Gauss (HS) | 1.7095 | 2.9085 | 0.3440 | 0.4432 | 0.2594 | 6.3550 | 6.3566 | 18.7299 | 25.3252 | 552.5873 |
| MQ (HS) | 1.4067 | 1.3765 | 0.4381 | 0.5602 | 0.4624 | 6.3493 | 6.4100 | 10.9620 | 14.5482 | 237.6996 |
| IMQ (HS) | 1.2609 | 1.2194 | 0.5584 | 0.7144 | 0.7371 | 6.2169 | 6.2224 | 13.1118 | 17.5664 | 313.6982 |
| TPS (HS) | 1.9730 | 1.9347 | 1.0212 | 1.3030 | 2.3211 | 6.6053 | 6.5867 | 11.6785 | 15.5172 | 243.9042 |
| Gauss-2 (HS) | 2.4066 | 2.3104 | 0.3956 | 0.4845 | 0.5706 | 6.3696 | 6.3696 | 24.5857 | 33.8412 | 859.1787 |
| MQ-2 (HS) | 1.4986 | 1.4456 | 0.7525 | 0.9632 | 1.3083 | 6.2661 | 6.3321 | 11.3002 | 15.0440 | 249.1558 |
| IMQ-2 (HS) | 2.2214 | 2.1980 | 0.6456 | 0.8079 | 1.0117 | 6.2652 | 6.2675 | 17.2876 | 23.4843 | 452.8401 |
| Linear (RS) | 2.4286 | 2.3346 | 2.2050 | 2.6185 | 12.9425 | 5.6040 | 5.6002 | 25.6846 | 35.8118 | 845.2555 |
| Cubic (RS) | 1.1874 | 1.0802 | 1.7935 | 2.1677 | 8.6909 | 6.3547 | 6.3643 | 19.3016 | 26.5988 | 468.7819 |
| Gauss (RS) | 0.8751 | 0.7927 | 0.9232 | 1.1250 | 2.5222 | 5.7013 | 5.7013 | 30.1709 | 42.2127 | 1182.6153 |
| MQ (RS) | 0.7173 | 0.5487 | 0.8503 | 1.0024 | 3.5183 | 5.7319 | 5.7249 | 24.8646 | 34.6374 | 790.1790 |
| IMQ (RS) | 0.7523 | 0.6464 | 1.1646 | 1.3907 | 5.6984 | 5.5327 | 5.5092 | 28.4928 | 39.8291 | 1051.2330 |
| TPS (RS) | 1.4883 | 1.3626 | 2.1791 | 2.6399 | 11.3841 | 5.9504 | 5.9193 | 22.7879 | 31.6445 | 658.0262 |
| Gauss-2 (RS) | 1.5656 | 1.2460 | 1.2379 | 1.5113 | 5.7580 | 5.7018 | 5.7018 | 30.1719 | 42.2150 | 1182.8340 |
| MQ-2 (RS) | 1.0100 | 0.8575 | 1.5162 | 1.8034 | 8.5495 | 5.7739 | 5.6515 | 25.2775 | 35.2279 | 817.4594 |
| IMQ-2 (RS) | 1.5527 | 1.4264 | 1.6484 | 1.9778 | 9.3007 | 5.5730 | 5.5584 | 29.2269 | 40.8789 | 1108.6229 |
| Metamodel | LD Problem | HD Problem | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| L10O CV | LOOCV | MAE | MAPE | MSE | L10O CV | LOOCV | MAE | MAPE | MSE | |
| Linear (LHS) | 4.4359 | 4.3846 | 1.8338 | 1.4141 | 5.4576 | 3.9984 | 4.0324 | 10.5484 | 9.1509 | 162.5176 |
| Cubic (LHS) | 3.8595 | 3.5830 | 1.6243 | 1.2218 | 4.5104 | 4.5029 | 4.5363 | 12.5952 | 10.9869 | 248.5740 |
| Gauss (LHS) | 15.098 | 15.524 | 15.132 | 11.9124 | 328.71 | 3.9279 | 3.9279 | 9.8104 | 8.4642 | 132.2075 |
| MQ (LHS) | 5.1684 | 5.0520 | 2.0034 | 1.5251 | 6.4269 | 4.1635 | 4.1168 | 10.8483 | 9.4278 | 176.0082 |
| IMQ (LHS) | 4.5200 | 4.2339 | 1.7250 | 1.2837 | 5.2536 | 3.9417 | 3.9364 | 10.0116 | 8.6562 | 141.2009 |
| TPS (LHS) | 4.1874 | 4.0146 | 1.4996 | 1.1313 | 3.8723 | 4.2397 | 4.2453 | 11.6407 | 10.1345 | 206.4641 |
| Gauss-2 (LHS) | 4.3990 | 3.9991 | 1.6313 | 1.2787 | 4.5993 | 3.9280 | 3.9280 | 9.8088 | 8.4627 | 132.1455 |
| MQ-2 (LHS) | 3.9172 | 3.6769 | 1.7275 | 1.2960 | 4.9123 | 4.1093 | 4.0687 | 10.7004 | 9.2909 | 169.1815 |
| IMQ-2 (LHS) | 4.1892 | 3.8021 | 1.7909 | 1.3845 | 4.8665 | 3.9141 | 3.9273 | 9.9243 | 8.5706 | 136.4878 |
| Linear (HS) | 6.1278 | 6.0542 | 1.5412 | 1.1644 | 4.7204 | 4.3780 | 4.4194 | 4.5329 | 3.7792 | 55.2910 |
| Cubic (HS) | 5.3936 | 5.5210 | 2.0704 | 1.6000 | 6.9511 | 4.9966 | 5.0183 | 5.6291 | 4.6959 | 82.7652 |
| Gauss (HS) | 15.269 | 20.293 | 7.1762 | 5.6193 | 115.2787 | 4.1733 | 4.1727 | 5.3265 | 4.4659 | 48.9555 |
| MQ (HS) | 5.2290 | 5.6424 | 3.0226 | 2.3622 | 18.0381 | 4.4855 | 4.5286 | 4.6683 | 3.8869 | 62.8607 |
| IMQ (HS) | 4.8501 | 5.0505 | 2.4151 | 1.8799 | 10.6604 | 4.2210 | 4.2333 | 4.3438 | 3.6220 | 51.1284 |
| TPS (HS) | 5.4072 | 5.5296 | 1.6889 | 1.2851 | 4.6118 | 4.6630 | 4.6910 | 4.9165 | 4.0963 | 67.2636 |
| Gauss-2 (HS) | 4.7843 | 5.2010 | 1.7273 | 1.3218 | 4.5502 | 4.1880 | 4.1880 | 7.6788 | 6.5332 | 84.7080 |
| MQ-2 (HS) | 4.9174 | 5.0753 | 2.0255 | 1.5656 | 6.6438 | 4.4495 | 4.4672 | 4.4864 | 3.7317 | 58.5835 |
| IMQ-2 (HS) | 5.2947 | 5.3882 | 1.7069 | 1.3019 | 4.4239 | 4.1954 | 4.2004 | 5.4790 | 4.6158 | 54.0921 |
| Linear (RS) | 4.0657 | 3.4502 | 2.1022 | 1.7004 | 6.4889 | 4.0126 | 3.9669 | 10.3277 | 8.9190 | 148.5799 |
| Cubic (RS) | 3.2289 | 2.7843 | 1.7475 | 1.3601 | 4.0009 | 4.6060 | 4.5358 | 11.2713 | 9.7666 | 187.0106 |
| Gauss (RS) | 6.9129 | 5.8174 | 23.052 | 17.9454 | 1861.08 | 3.8045 | 3.8045 | 9.8617 | 8.5103 | 133.5786 |
| MQ (RS) | 3.4044 | 3.0009 | 2.1841 | 1.6952 | 6.5737 | 3.9907 | 4.0656 | 10.4481 | 9.0285 | 154.6638 |
| IMQ (RS) | 3.2568 | 2.8318 | 2.0606 | 1.6001 | 5.5758 | 3.8090 | 3.8185 | 10.0666 | 8.6880 | 139.9123 |
| TPS (RS) | 3.5139 | 2.7862 | 1.3141 | 1.0169 | 2.6578 | 4.3219 | 4.2296 | 10.7681 | 9.3128 | 165.8049 |
| Gauss-2 (RS) | 3.3497 | 3.2682 | 2.2501 | 1.7746 | 7.2793 | 3.8048 | 3.8048 | 9.8591 | 8.5082 | 133.5162 |
| MQ-2 (RS) | 3.1444 | 3.0117 | 1.6420 | 1.2693 | 3.7105 | 4.0568 | 4.0108 | 10.3911 | 8.9765 | 151.6385 |
| IMQ-2 (RS) | 3.3308 | 2.7371 | 1.5944 | 1.2601 | 4.0925 | 3.8119 | 3.8043 | 9.9933 | 8.6236 | 137.0649 |
| RBF Metamodel | LD Problem | HD Problem | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| First, Frequency | Second, Frequency | Third, Frequency | First, Frequency | Second, Frequency | Third, Frequency | |||||||
| CCi 4 | Rank | CCi | Rank | CCi | Rank | CCi | Rank | CCi | Rank | CCi | Rank | |
| Linear (LHS) | 0.2003 | 27 | 0.3678 | 25 | 0.9568 | 15 | 0.5947 | 14 | 0.4680 | 15 | 0.3786 | 21 |
| Cubic (LHS) | 0.5723 | 16 | 0.7213 | 10 | 0.9767 | 6 | 0.8977 | 5 | 0.8652 | 6 | 0.0773 | 27 |
| Gauss (LHS) | 0.8362 | 4 | 0.4981 | 22 | 0.5098 | 26 | 0.0894 | 26 | 0.1522 | 26 | 0.4933 | 11 |
| MQ (LHS) | 0.7969 | 5 | 0.9427 | 1 | 0.9377 | 18 | 0.6659 | 12 | 0.5521 | 12 | 0.3240 | 24 |
| IMQ (LHS) | 0.7366 | 9 | 0.8965 | 2 | 0.9590 | 14 | 0.2664 | 20 | 0.2347 | 20 | 0.4607 | 17 |
| TPS (LHS) | 0.4229 | 22 | 0.6138 | 18 | 0.9677 | 10 | 0.8091 | 9 | 0.7169 | 8 | 0.2080 | 26 |
| Gauss-2 (LHS) | 0.6855 | 11 | 0.7678 | 9 | 0.9640 | 13 | 0.0894 | 27 | 0.1522 | 27 | 0.4935 | 10 |
| MQ-2 (LHS) | 0.6090 | 15 | 0.8039 | 5 | 0.9736 | 7 | 0.6320 | 13 | 0.5103 | 13 | 0.3510 | 22 |
| IMQ-2 (LHS) | 0.5010 | 20 | 0.6826 | 14 | 0.9675 | 11 | 0.1668 | 23 | 0.1836 | 23 | 0.4774 | 14 |
| Linear (HS) | 0.4072 | 24 | 0.5020 | 21 | 0.9160 | 23 | 0.9356 | 3 | 0.8952 | 3 | 0.9018 | 3 |
| Cubic (HS) | 0.7601 | 8 | 0.6963 | 11 | 0.9283 | 22 | 0.8796 | 6 | 0.8186 | 7 | 0.7611 | 8 |
| Gauss (HS) | 0.7697 | 7 | 0.6826 | 13 | 0.6257 | 25 | 0.5406 | 17 | 0.6330 | 11 | 0.9053 | 2 |
| MQ (HS) | 0.9157 | 1 | 0.8397 | 4 | 0.9147 | 24 | 0.9472 | 2 | 0.8978 | 2 | 0.8758 | 6 |
| IMQ (HS) | 0.8761 | 3 | 0.8527 | 3 | 0.9358 | 19 | 0.8543 | 7 | 0.8731 | 4 | 0.9317 | 1 |
| TPS (HS) | 0.6188 | 14 | 0.6449 | 17 | 0.9311 | 21 | 0.9306 | 4 | 0.8711 | 5 | 0.8430 | 7 |
| Gauss-2 (HS) | 0.7104 | 10 | 0.6854 | 12 | 0.9426 | 16 | 0.2753 | 19 | 0.3376 | 19 | 0.7094 | 9 |
| MQ-2 (HS) | 0.7756 | 6 | 0.7771 | 8 | 0.9400 | 17 | 0.9497 | 1 | 0.9044 | 1 | 0.8907 | 5 |
| IMQ-2 (HS) | 0.6362 | 13 | 0.6813 | 15 | 0.9342 | 20 | 0.6861 | 11 | 0.7155 | 9 | 0.8907 | 4 |
| Linear (RS) | 0.2128 | 26 | 0.1610 | 27 | 0.9660 | 12 | 0.5355 | 18 | 0.3474 | 18 | 0.4263 | 18 |
| Cubic (RS) | 0.4117 | 23 | 0.4563 | 23 | 0.9867 | 4 | 0.8479 | 8 | 0.6516 | 10 | 0.2562 | 25 |
| Gauss (RS) | 0.9059 | 2 | 0.7960 | 6 | 0.2621 | 27 | 0.1017 | 25 | 0.1573 | 24 | 0.4915 | 13 |
| MQ (RS) | 0.5617 | 18 | 0.7940 | 7 | 0.9729 | 8 | 0.5923 | 15 | 0.3853 | 16 | 0.4037 | 20 |
| IMQ (RS) | 0.5678 | 17 | 0.6676 | 16 | 0.9774 | 5 | 0.2622 | 21 | 0.2194 | 21 | 0.4664 | 16 |
| TPS (RS) | 0.3774 | 25 | 0.3318 | 26 | 0.9924 | 1 | 0.7157 | 10 | 0.4899 | 14 | 0.3496 | 23 |
| Gauss-2 (RS) | 0.6627 | 12 | 0.5901 | 19 | 0.9693 | 9 | 0.1017 | 24 | 0.1572 | 25 | 0.4918 | 12 |
| MQ-2 (RS) | 0.5004 | 21 | 0.5186 | 20 | 0.9889 | 3 | 0.5643 | 16 | 0.3642 | 17 | 0.4138 | 19 |
| IMQ-2 (RS) | 0.5180 | 19 | 0.4188 | 24 | 0.9903 | 2 | 0.1805 | 22 | 0.1906 | 22 | 0.4769 | 15 |
References
- Kalita, K.; Dey, P.; Haldar, S. Search for accurate RSM metamodels for structural engineering. J. Reinf. Plast. Compos. 2019, 38, 995–1013. [Google Scholar] [CrossRef]
- Ganguli, R. Optimum design of a helicopter rotor for low vibration using aeroelastic analysis and response surface methods. J. Sound Vib. 2002, 258, 327–344. [Google Scholar] [CrossRef]
- Kalita, K.; Mukhopadhyay, T.; Dey, P.; Haldar, S. Genetic programming-assisted multi-scale optimization for multi-objective dynamic performance of laminated composites: The advantage of more elementary-level analyses. Neural Comput. Appl. 2019, 32, 7969–7993. [Google Scholar] [CrossRef]
- Koide, R.M.; Ferreira, A.P.C.S.; Luersen, M.A. Laminated Composites Buckling Analysis Using Lamination Parameters, Neural Networks and Support Vector Regression. Lat. Am. J. Solids Struct. 2015, 12, 271–294. [Google Scholar] [CrossRef]
- Reddy, M.R.S.; Reddy, B.S.; Reddy, V.N.; Sreenivasulu, S. Prediction of Natural Frequency of Laminated Composite Plates Using Artificial Neural Networks. Engineering 2012, 04, 329–337. [Google Scholar] [CrossRef]
- García-Macías, E.; Triguero, R.C.; Friswell, M.; Adhikari, S.; Saez, A. Metamodel-based approach for stochastic free vibration analysis of functionally graded carbon nanotube reinforced plates. Compos. Struct. 2016, 152, 183–198. [Google Scholar] [CrossRef]
- Mukhopadhyay, T.; Naskar, S.; Dey, S.; Adhikari, S. On quantifying the effect of noise in surrogate based stochastic free vibration analysis of laminated composite shallow shells. Compos. Struct. 2016, 140, 798–805. [Google Scholar] [CrossRef]
- Ju, S.; Shenoi, R.; Jiang, D.; Sobey, A. Multi-parameter optimization of lightweight composite triangular truss structure based on response surface methodology. Compos. Struct. 2013, 97, 107–116. [Google Scholar] [CrossRef]
- Heinonen, O.; Pajunen, S. Optimal design of stiffened plate using metamodeling techniques. J. Struct. Mech. 2011, 44, 218–230. [Google Scholar]
- Dutra, T.A.; de Almeida, S.F.M. Composite plate stiffness multicriteria optimization using lamination parameters. Compos. Struct. 2015, 133, 166–177. [Google Scholar] [CrossRef]
- Passos, A.G.; Luersen, M.A. Multiobjective optimization of laminated composite parts with curvilinear fibers using Kriging-based approaches. Struct. Multidiscip. Optim. 2017, 57, 1115–1127. [Google Scholar] [CrossRef]
- Dey, S.; Mukhopadhyay, T.; Khodaparast, H.H.; Adhikari, S. A Response Surface Modelling Approach for Resonance Driven Reliability Based Optimization of Composite Shells. Period. Polytech. Civ. Eng. 2016, 60, 103–111. [Google Scholar] [CrossRef]
- Jafari, R.; Yousefi, P.; Hosseini-Hashemi, S. Vibration optimization of skew Composite plates Using the Rayleigh-Ritz & response surface methods. In Proceedings of the International Conference on Smart Technologies for Mechanical Engineering, New Delhi, India, 25–26 October 2013; pp. 26–33. [Google Scholar]
- Todoroki, A.; Sasai, M. Stacking sequence optimizations using GA with zoomed response surface on lamination parameters. Adv. Compos. Mater. 2002, 11, 299–318. [Google Scholar] [CrossRef]
- Todoroki, A.; Ozawa, T.; Mizutani, Y.; Suzuki, Y. Thermal deformation constraint using response surfaces for optimization of stacking sequences of composite laminates. Adv. Compos. Mater. 2013, 22, 265–279. [Google Scholar] [CrossRef]
- Todoroki, A.; Ishikawa, T. Design of experiments for stacking sequence optimizations with genetic algorithm using response surface approximation. Compos. Struct. 2004, 64, 349–357. [Google Scholar] [CrossRef]
- Rouhi, M.; Ghayoor, H.; Hoa, S.V.; Hojjati, M. Computational efficiency and accuracy of multi-step design optimization method for variable stiffness composite structures. Thin Walled Struct. 2017, 113, 136–143. [Google Scholar] [CrossRef]
- Kaveh, A.; Malek, N.G.; Eslamlou, A.D.; Azimi, M. An open-source framework for the FE modeling and optimal design of fiber-steered variable-stiffness composite cylinders using water strider algorithm. Mech. Based Des. Struct. Mach. 2020, 1–21. [Google Scholar] [CrossRef]
- Nguyen, D.H.; Wang, H.; Ye, F.; Hu, W. Investigation and multi-scale optimization design of woven composite cut-out structures. Eng. Comput. 2020. [Google Scholar] [CrossRef]
- Kalniņš, K.; Rikards, R.; Auzins, J.; Bisagni, C.; Abramovich, H.; Degenhardt, R. Metamodeling methodology for postbuckling simulation of damaged composite stiffened structures with physical validation. Int. J. Struct. Stab. Dyn. 2010, 10, 705–716. [Google Scholar] [CrossRef]
- Lanzi, L.; Giavotto, V. Post-buckling optimization of composite stiffened panels: Computations and experiments. Compos. Struct. 2006, 73, 208–220. [Google Scholar] [CrossRef]
- Jing, Z.; Chen, J.; Li, X. RBF-GA: An adaptive radial basis function metamodeling with genetic algorithm for structural reliability analysis. Reliab. Eng. Syst. Saf. 2019, 189, 42–57. [Google Scholar] [CrossRef]
- Joy, E.J.; Biju, N.; Menon, A.S. Delamination detection in composite laminates using ensemble of surrogates. Mater. Today Proc. 2020. [Google Scholar] [CrossRef]
- Raturi, H.P.; Kushari, S.; Dey, S. Radial Basis Function-Based Probabilistic First-Ply Failure Analyses of Composite Spherical Shells. In Recent Advances in Computational Mechanics and Simulations; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2021; pp. 667–675. [Google Scholar]
- Kumar, R.R.; Pandey, K.M.; Dey, S. Stochastic free vibration analysis of sandwich plates: A radial basis function approach. In Reliability, Safety and Hazard Assessment for Risk-Based Technologies; Springer: Berlin/Heidelberg, Germany, 2020; pp. 449–458. [Google Scholar]
- Kumar, R.R.; Pandey, K.M.; Dey, S. Probabilistic assessment on buckling behavior of sandwich panel: A radial basis function approach. Struct. Eng. Mech. 2019, 71, 197–210. [Google Scholar]
- Dey, S.; Mukhopadhyay, T.; Adhikari, S. Metamodel based high-fidelity stochastic analysis of composite laminates: A concise review with critical comparative assessment. Compos. Struct. 2017, 171, 227–250. [Google Scholar] [CrossRef]
- Amouzgar, K.; Strömberg, N. Radial basis functions as surrogate models with a priori bias in comparison with a posteriori bias. Struct. Multidiscip. Optim. 2017, 55, 1453–1469. [Google Scholar] [CrossRef]
- Jones, R.M. Mechanics of Composite Materials; Scripta Book Company: Washington, DC, USA, 1975; Volume 193. [Google Scholar]
- Kalita, K.; Haldar, S. Eigen frequencies of simply supported taper plates with cut-outs. Struct. Eng. Mech. 2017, 63, 103–113. [Google Scholar]
- Kalita, K.; Dey, P.; Haldar, S. Robust genetically optimized skew laminates. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2018, 233, 146–159. [Google Scholar] [CrossRef]
- Kalita, K.; Dey, P.; Haldar, S.; Gao, X.-Z. Optimizing frequencies of skew composite laminates with metaheuristic algorithms. Eng. Comput. 2019, 36, 741–761. [Google Scholar] [CrossRef]
- Jin, R.; Chen, W.; Simpson, T. Comparative studies of metamodeling techniques under multiple modeling criteria. Struct. Multidiscip. Optim. 2000, 23, 1–13. [Google Scholar] [CrossRef]
- Zhao, D.; Xue, D. A comparative study of metamodeling methods considering sample quality merits. Struct. Multidiscip. Optim. 2010, 42, 923–938. [Google Scholar] [CrossRef]
- McKay, M.D.; Beckman, R.J.; Conover, W.J. A Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output from a Computer Code. Technometrics 2000, 42, 55. [Google Scholar] [CrossRef]
- Hammersley, J.M. Monte carlo methods for solving multivariable problems. Ann. N. Y. Acad. Sci. 2006, 86, 844–874. [Google Scholar] [CrossRef]
- Funari, M.F.; Greco, F.; Lonetti, P. A coupled ALE-Cohesive formulation for layered structural systems. Procedia Struct. Integr. 2017, 3, 362–369. [Google Scholar] [CrossRef]
- Martin, E.; Leguillon, D. A strain energy density criterion for the initiation of edge debonding. Theor. Appl. Fract. Mech. 2015, 79, 58–61. [Google Scholar] [CrossRef]
- Hardy, R.L. Multiquadric equations of topography and other irregular surfaces. J. Geophys. Res. Space Phys. 1971, 76, 1905–1915. [Google Scholar] [CrossRef]
- Naskar, S.; Mukhopadhyay, T.; Sriramula, S.; Adhikari, S. Stochastic natural frequency analysis of damaged thin-walled laminated composite beams with uncertainty in micromechanical properties. Compos. Struct. 2017, 160, 312–334. [Google Scholar] [CrossRef]
- Hussain, M.F.; Barton, R.R.; Joshi, S.B. Metamodeling: Radial basis functions, versus polynomials. Eur. J. Oper. Res. 2002, 138, 142–154. [Google Scholar] [CrossRef]
- Fasshauer, G.E.; Zhang, J.G. On choosing “optimal” shape parameters for RBF approximation. Numer. Algorithms 2007, 45, 345–368. [Google Scholar] [CrossRef]
- Wu, C.-P.; Chen, W.-Y. Vibration and stability of laminated plates based on a local high order plate theory. J. Sound Vib. 1994, 177, 503–520. [Google Scholar] [CrossRef]
- Matsunaga, H. Vibration and stability of cross-ply laminated composite plates according to a global higher-order plate theory. Compos. Struct. 2000, 48, 231–244. [Google Scholar] [CrossRef]
- Mindlin, R.D. Influence of rotatory inertia and shear on flexural motions of isotropic, elastic plates. J. Appl. Mech. 1951, 18, 31–38. [Google Scholar] [CrossRef]
- Sayyad, A.S.; Ghugal, Y.M. On the free vibration analysis of laminated composite and sandwich plates: A review of recent literature with some numerical results. Compos. Struct. 2015, 129, 177–201. [Google Scholar] [CrossRef]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kalita, K.; Chakraborty, S.; Madhu, S.; Ramachandran, M.; Gao, X.-Z. Performance Analysis of Radial Basis Function Metamodels for Predictive Modelling of Laminated Composites. Materials 2021, 14, 3306. https://doi.org/10.3390/ma14123306
Kalita K, Chakraborty S, Madhu S, Ramachandran M, Gao X-Z. Performance Analysis of Radial Basis Function Metamodels for Predictive Modelling of Laminated Composites. Materials. 2021; 14(12):3306. https://doi.org/10.3390/ma14123306
Chicago/Turabian StyleKalita, Kanak, Shankar Chakraborty, S Madhu, Manickam Ramachandran, and Xiao-Zhi Gao. 2021. "Performance Analysis of Radial Basis Function Metamodels for Predictive Modelling of Laminated Composites" Materials 14, no. 12: 3306. https://doi.org/10.3390/ma14123306
APA StyleKalita, K., Chakraborty, S., Madhu, S., Ramachandran, M., & Gao, X.-Z. (2021). Performance Analysis of Radial Basis Function Metamodels for Predictive Modelling of Laminated Composites. Materials, 14(12), 3306. https://doi.org/10.3390/ma14123306