Breakage Strength of Wood Sawdust Pellets: Measurements and Modelling
Abstract
1. Introduction
2. Experiments
2.1. Materials and Methods
2.1.1. Materials
2.1.2. Pellets Preparation
2.1.3. Determination of Solid-Phase and Bulk Densities
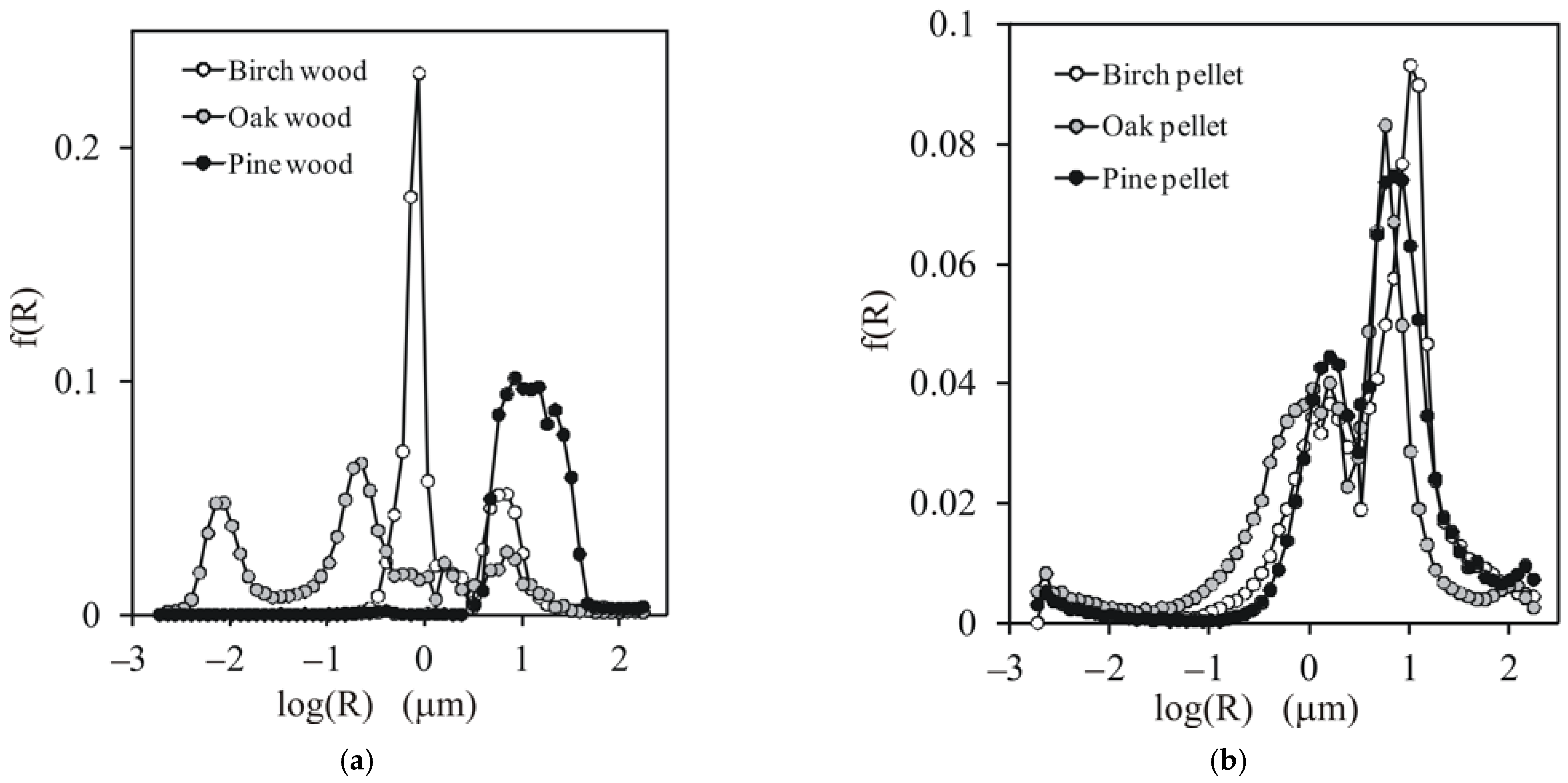
2.1.4. Estimation of Porosity and Pore Size Distribution
2.1.5. Scanning Electron Microscopy
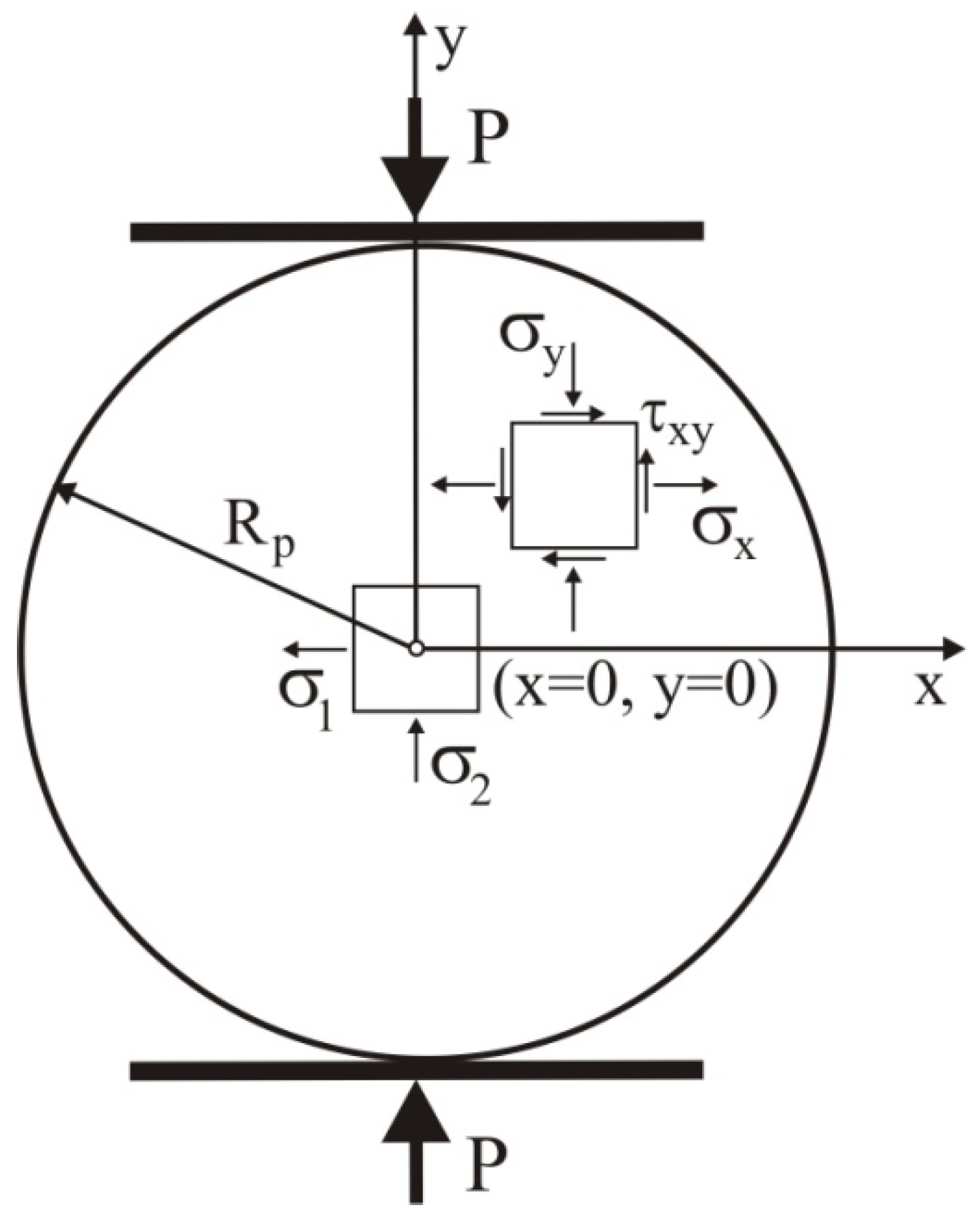
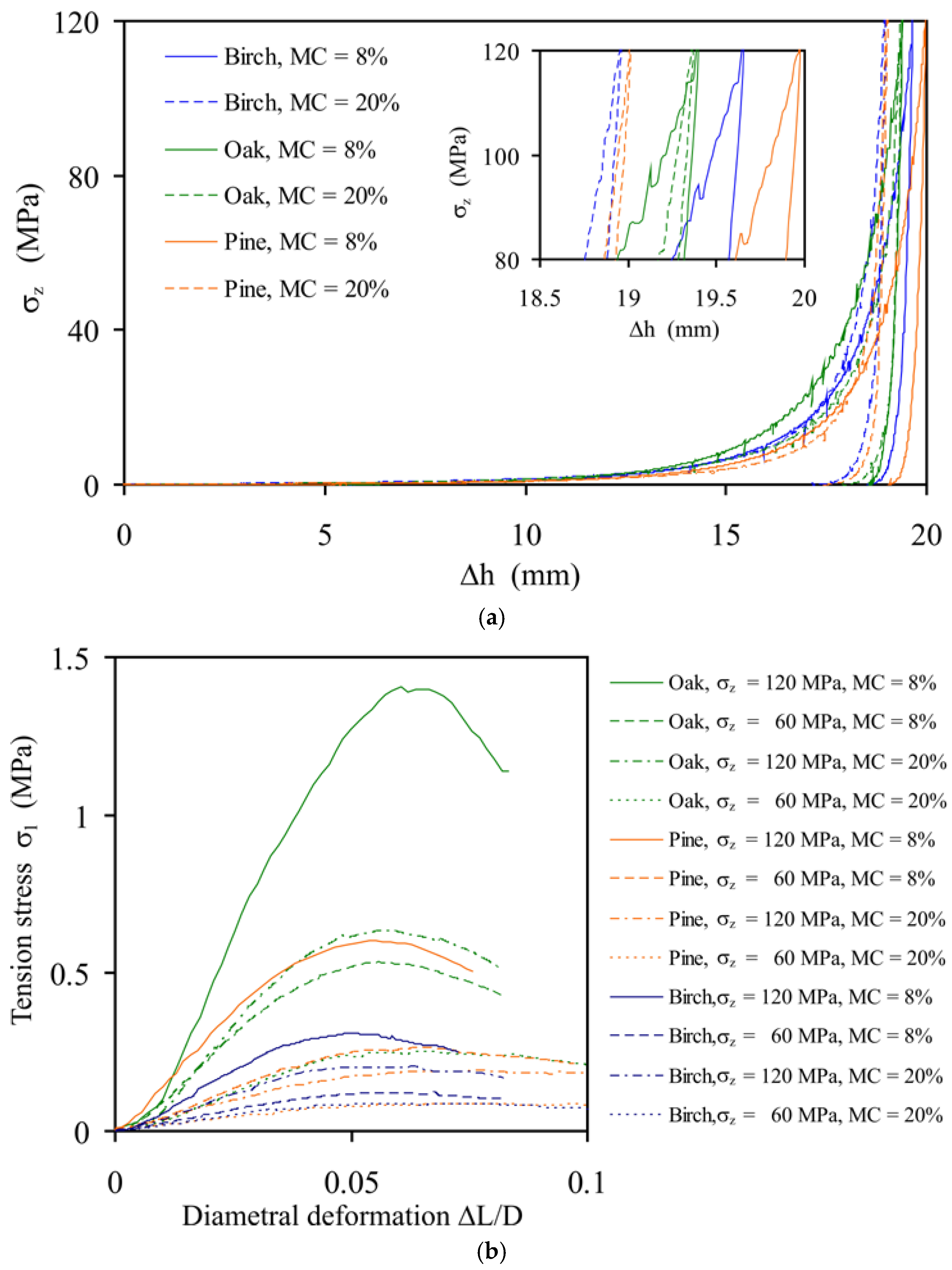
2.1.6. Diametral Compression Test
2.1.7. Statistics
2.2. Experimental Results
3. Modelling
3.1. DEM Setup
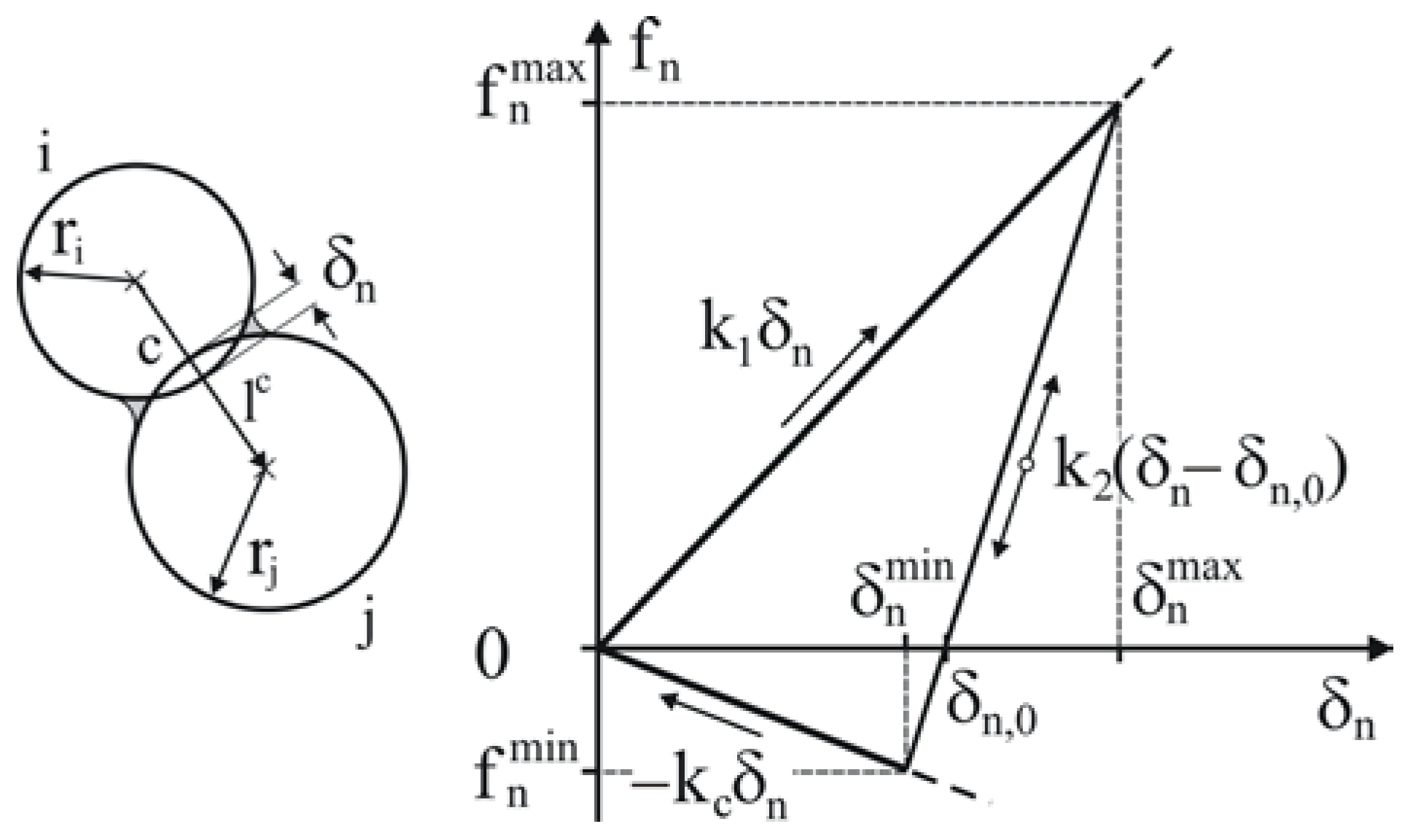
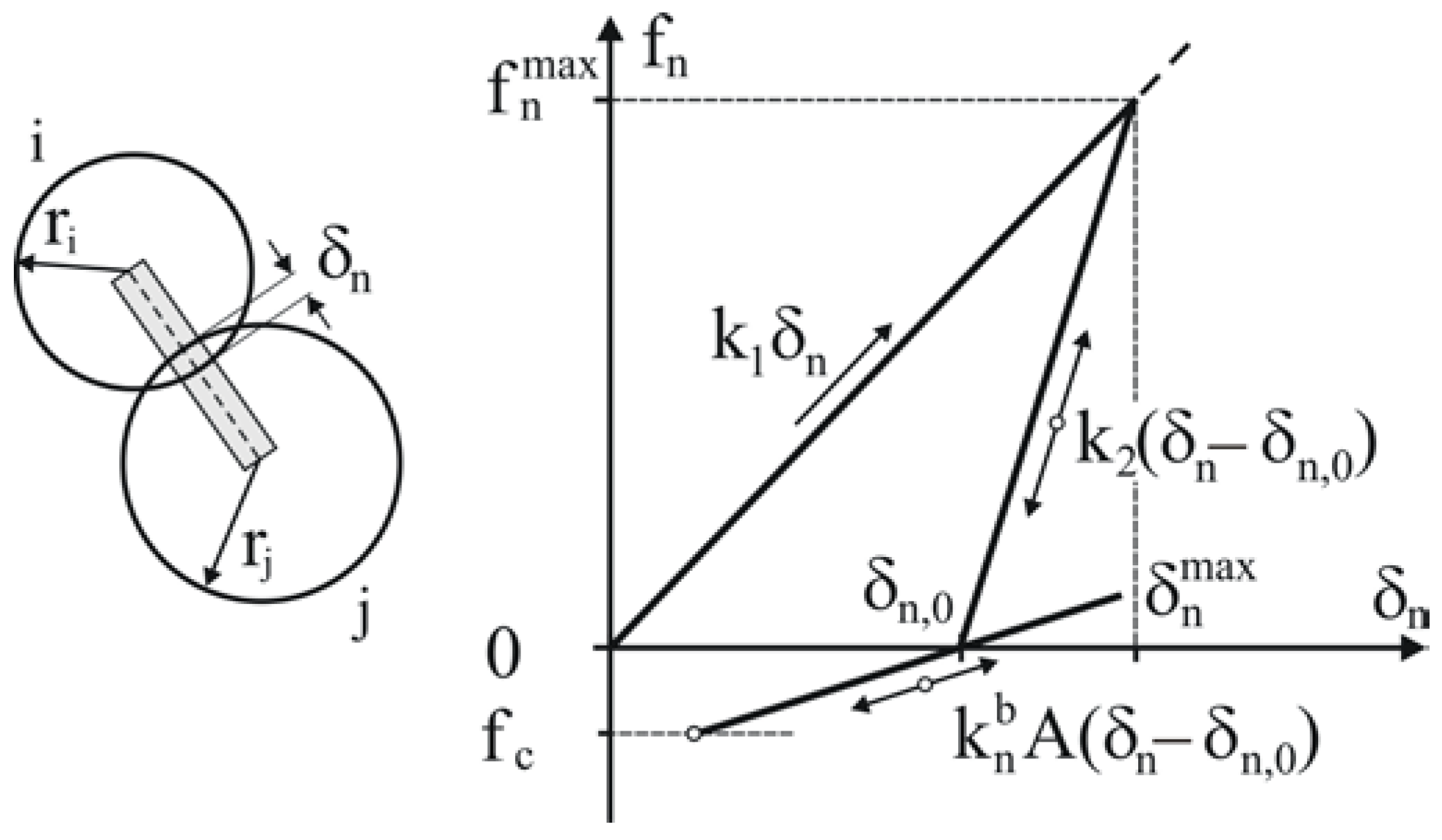
3.1.1. Contact Model
3.1.2. DEM Modelling Parameters
3.1.3. Stages of DEM Simulations
3.1.4. Fit Quality
3.1.5. Calibration of Material Parameters for DEM Modelling
3.2. DEM Run
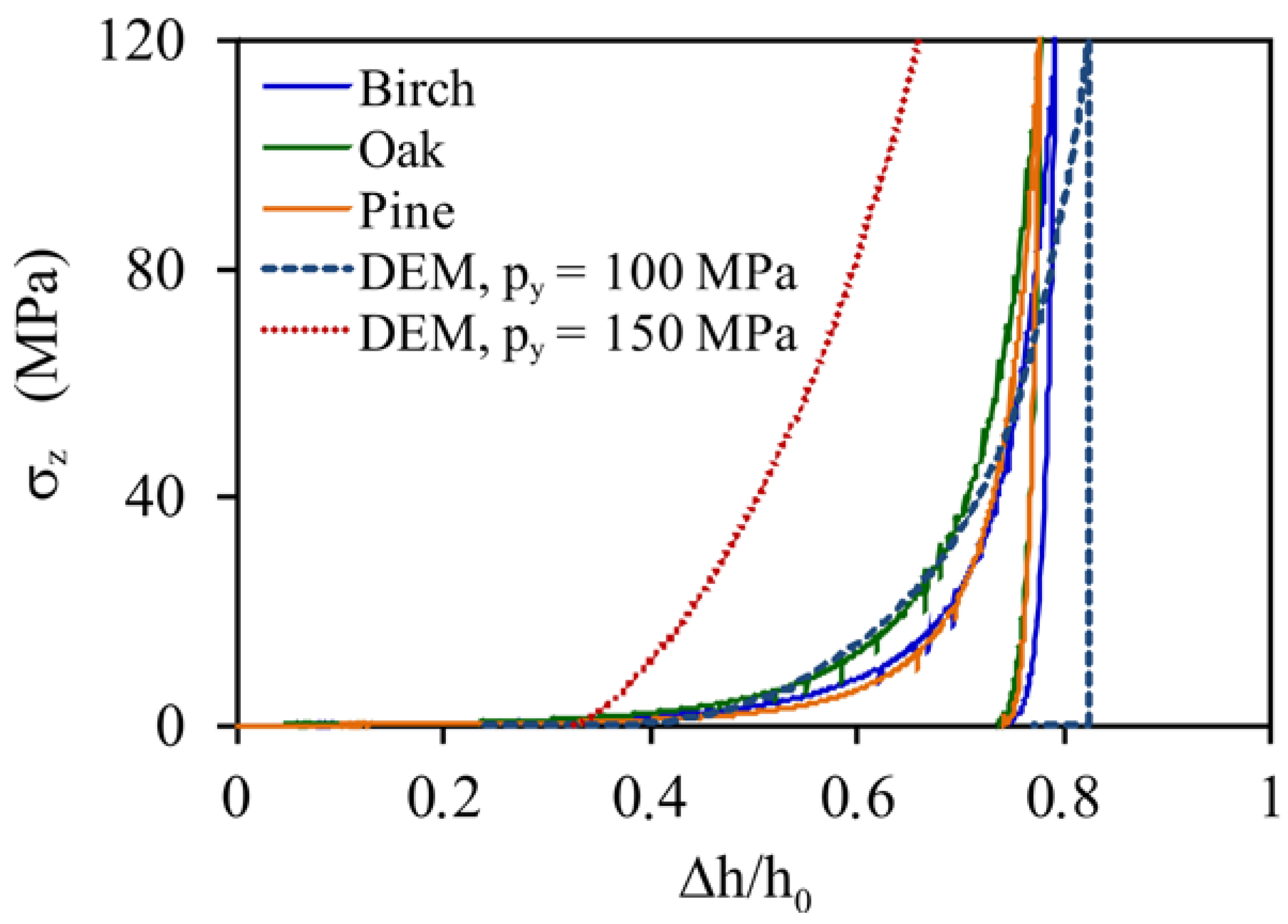
3.2.1. Compaction of Sawdust: Plastic and Elastic Stiffness of Particles
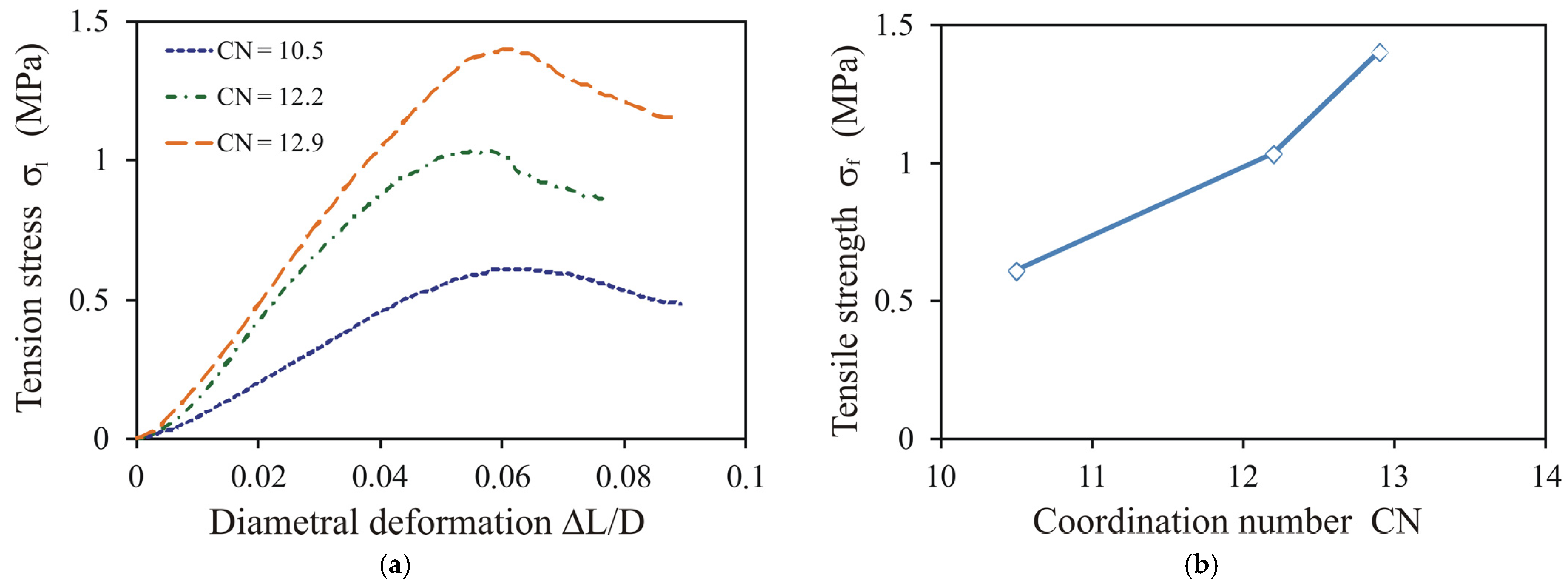
3.2.2. Coordination Number
3.2.3. Bond Radius Estimation
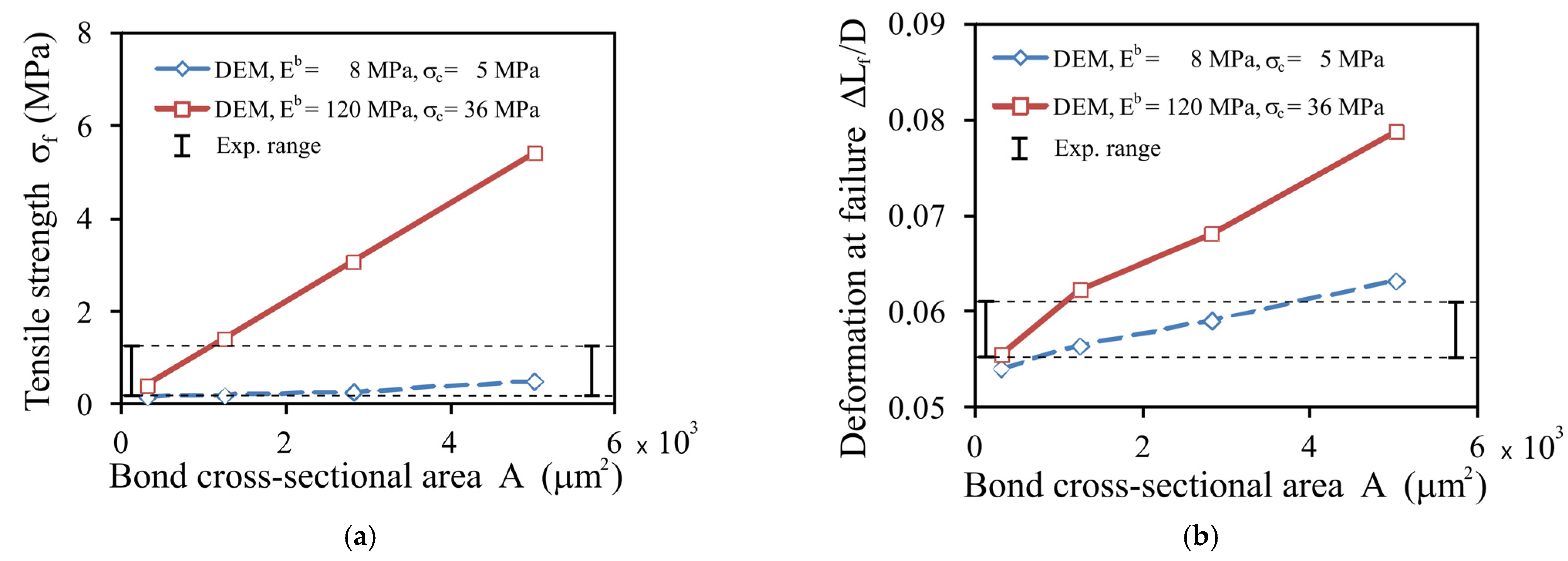
3.2.4. Bond Elasticity and Strength
4. Simulation Results
5. General Remarks
6. Conclusions
- The stress–deformation relationship during pelletisation of wood sawdust comprising a large range of particle deformations was successfully modelled using a DEM equipped with a linear hysteretic contact model. Good agreement between the simulated range of change in the bulk density during pelletisation with experimental data was obtained because of the application density of the intact wood as the input density of particles in the DEM simulations;
- The highest tensile strength was obtained for oak and the lowest for birch pellets. For all materials, the tensile strength was the highest for MC = 8% of sawdust compacted under a pressure of 120 MPa and the lowest for MC = 20% of sawdust compacted under a pressure of 60 MPa;
- The breakage processes of pellets of all tested materials were successfully simulated using the DEM with the BPM;
- All pellets exhibited a ductile breakage mode characterised by a smooth and round stress–deformation relationship without any sudden drops. Cracks were initiated in locations close to the centre of the pellet, and progressive deformation developed in the direction of loading and toward the interior of the pellet;
- Applying values of the bond elasticity modulus Eb and the tensile strength σc fulfilling the condition σc/Eb > 0.25 in the DEM simulations allowed the stress–deformation relationship and crack formation to be reproduced well for all studied pellets.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kaliyan, N.; Morey, R.V. Natural binders and solid bridge type binding mechanisms in briquettes and pellets made from corn stover and switchgrass. Bioresour. Technol. 2010, 101, 1082–1090. [Google Scholar] [CrossRef]
- Whittaker, C.; Shield, I. Factors affecting wood, energy grass and straw pellet durability—A review. Renew. Sustain. Energy Rev. 2017, 71, 1–11. [Google Scholar] [CrossRef]
- Adapa, P.K.; Tabil, L.G.; Schoenau, G.J. Factors affecting the quality of biomass pellet for biofuel and energy analysis of pelleting process. Int. J. Agric. Biol. Eng. 2013, 6, 1–12. [Google Scholar] [CrossRef]
- Stasiak, M.; Molenda, M.; Bańda, M.; Wiącek, J.; Parafiniuk, P.; Gondek, E. Mechanical and combustion properties of sawdust—Straw pellets blended in different proportions. Fuel Process. Technol. 2017, 156, 366–375. [Google Scholar] [CrossRef]
- Hehar, G.; Fasina, O.; Adhikari, S.; Fulton, J. Ignition and volatilization behavior of dust from loblolly pine wood. Fuel Process. Technol. 2014, 127, 117–123. [Google Scholar] [CrossRef]
- Shaw, M.D.; Karunakaran, C.; Tabil, L.G. Physicochemical characteristics of densified untreated and steam exploded poplar wood and wheat straw grinds. Biosyst. Eng. 2009, 103, 198–207. [Google Scholar] [CrossRef]
- Kretschmann, D.E. Mechanical Properties of Wood. In Wood Handbook: Wood as Engineering Material, 2nd ed.; U.S. Department of Agriculture: Madison, WI, USA, 2010; pp. 5.1–5.46. [Google Scholar]
- Carone, M.T.; Pantaleo, A.; Pellerano, A. Influence of process parameters and biomass characteristics on the durability of pellets from the pruning residues of Olea europaea L. Biomass Bioenergy 2011, 35, 402–410. [Google Scholar] [CrossRef]
- Li, Y.; Liu, H. High-pressure densification of wood residues to form an upgraded fuel. Biomass Bioenergy 2000, 19, 177–186. [Google Scholar] [CrossRef]
- EN ISO 17831-1:2015. Solid Biofuels-Determination of Mechanical Durability of Pellets and Briquettes—Part 1: Pellets; International Organization for Standardization: Geneva, Switzerland, 2015. [Google Scholar]
- Larsson, S.H.; Samuelsson, R. Prediction of ISO 17831-1:2015 mechanical biofuel pellet durability from single pellet characterization. Fuel Process. Technol. 2017, 163, 8–15. [Google Scholar] [CrossRef]
- Oveisi, E.; Lau, A.; Sokhansanj, S.; Lim, C.J.; Bi, X.; Larsson, S.H.; Melin, S. Breakage behavior of wood pellets due to free fall. Powder Technol. 2013, 235, 493–499. [Google Scholar] [CrossRef]
- Jonsén, P.; Häggblad, H.-Å.; Sommer, K. Tensile strength and fracture energy of pressed metal powder by diametral compression test. Powder Technol. 2007, 176, 148–155. [Google Scholar] [CrossRef]
- Timoshenko, S.P.; Goodier, J.N. Theory of Elasticity, 3rd ed.; McGraw-Hill: New York, NY, USA, 1970. [Google Scholar]
- Andreev, G. A review of the Brazilian test for rock tensile strength determination. Part I: Calculation formula. Min. Sci. Technol. 1991, 13, 445–456. [Google Scholar] [CrossRef]
- Labuz, J.F.; Cattaneo, S.; Chen, L.-H. Acoustic emission at failure in quasi-brittle materials. Constr. Build. Mater. 2001, 15, 225–233. [Google Scholar] [CrossRef]
- Alderborn, G. A Novel Approach to Derive a Compression Parameter Indicating Effective Particle Deformability. Pharm. Dev. Technol. 2003, 8, 367–377. [Google Scholar] [CrossRef]
- Nordström, J.; Persson, A.-S.; Lazorova, L.; Frenning, G.; Alderborn, G. The degree of compression of spherical granular solids controls the evolution of microstructure and bond probability during compaction. Int. J. Pharm. 2013, 442, 3–12. [Google Scholar] [CrossRef]
- Pai, D.A.; Hayes, A.A.; Okos, M.R. Modeling pharmaceutical compacts tensile strength based on viscoelastic properties. Powder Technol. 2013, 239, 441–450. [Google Scholar] [CrossRef]
- Han, L.; Elliott, J.; Bentham, A.; Mills, A.; Amidon, G.; Hancock, B. A modified Drucker-Prager Cap model for die compaction simulation of pharmaceutical powders. Int. J. Solids Struct. 2008, 45, 3088–3106. [Google Scholar] [CrossRef]
- Okot, D.K.; Bilsborrow, P.E.; Phan, A.N. Effects of operating parameters on maize COB briquette quality. Biomass Bioenergy 2018, 112, 61–72. [Google Scholar] [CrossRef]
- Song, X.; Zhang, S.; Wu, Y.; Cao, Z. Investigation on the properties of the bio-briquette fuel prepared from hydrothermal pretreated cotton stalk and wood sawdust. Renew. Energy 2020, 151, 184–191. [Google Scholar] [CrossRef]
- Ahmad, M.Z.; Akhter, S.; Anwar, M.; Rahman, M.; Siddiqui, M.A.; Ahmad, F.J. Compatibility and compressibility studies of Assam Bora rice starch. Powder Technol. 2012, 224, 281–286. [Google Scholar] [CrossRef]
- Mitchell, W.R.; Forny, L.; Althaus, T.; Dopfer, D.; Niederreiter, G.; Palzer, S. Compaction of food powders: The influence of material properties and process parameters on product structure, strength, and dissolution. Chem. Eng. Sci. 2017, 167, 29–41. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Géotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Azéma, E.; Sánchez, P.; Scheeres, D.J. Scaling behavior of cohesive self-gravitating aggregates. Phys. Rev. E 2018, 98, 030901. [Google Scholar] [CrossRef]
- Nordström, J.; Alderborn, G.; Frenning, G. Compressibility and tablet forming ability of bimodal granule mixtures: Experiments and DEM simulations. Int. J. Pharm. 2018, 540, 120–131. [Google Scholar] [CrossRef] [PubMed]
- Balevičius, R.; Sielamowicz, I.; Mróz, Z.; Kačianauskas, R. Effect of rolling friction on wall pressure, discharge velocity and outflow of granular material from a flat-bottomed bin. Particuology 2012, 10, 672–682. [Google Scholar] [CrossRef]
- Horabik, J.; Wiącek, J.; Parafiniuk, P.; Stasiak, M.; Bańda, M.; Molenda, M. Tensile strength of pressure-agglomerated potato starch determined via diametral compression test: Discrete element method simulations and experiments. Biosyst. Eng. 2019, 183, 95–109. [Google Scholar] [CrossRef]
- Rackl, M.; Top, F.; Molhoek, C.P.; Schott, D.L. Feeding system for wood chips: A DEM study to improve equipment performance. Biomass Bioenergy 2017, 98, 43–52. [Google Scholar] [CrossRef]
- Xia, Y.; Stickel, J.J.; Jin, W.; Klinger, J. A Review of Computational Models for the Flow of Milled Biomass Part I: Discrete-Particle Models. ACS Sustain. Chem. Eng. 2020, 8, 6142–6156. [Google Scholar] [CrossRef]
- Pachón-Morales, J.; Perré, P.; Casalinho, J.; Do, H.; Schott, D.; Puel, F.; Colin, J. Potential of DEM for investigation of non-consolidated flow of cohesive and elongated biomass particles. Adv. Powder Technol. 2020, 31, 1500–1515. [Google Scholar] [CrossRef]
- Ilic, D.; Williams, K.; Ellis, D. Assessment of biomass bulk elastic response to consolidation. Chem. Eng. Res. Des. 2018, 135, 185–196. [Google Scholar] [CrossRef]
- Guo, Y.; Chen, Q.; Xia, Y.; Westover, T.; Eksioglu, S.; Roni, M. Discrete element modeling of switchgrass particles under compression and rotational shear. Biomass Bioenergy 2020, 141, 105649. [Google Scholar] [CrossRef]
- Potyondy, D.O.; Cundall, P.A. A bonded-particle model for rock. Int. J. Rock Mech. Min. Sci. 2004, 41, 1329–1364. [Google Scholar] [CrossRef]
- Jiménez-Herrera, N.; Barrios, G.K.P.; Tavares, L.M. Comparison of breakage models in DEM in simulating impact on particle beds. Adv. Powder Technol. 2018, 29, 692–706. [Google Scholar] [CrossRef]
- Langston, P.; Kennedy, A.; Constantin, H. Discrete element modelling of flexible fibre packing. Comput. Mater. Sci. 2015, 96, 108–116. [Google Scholar] [CrossRef]
- Xia, Y.; Lai, Z.; Westover, T.; Klinger, J.; Huang, H.; Chen, Q. Discrete element modeling of deformable pinewood chips in cyclic loading test. Powder Technol. 2019, 345, 1–14. [Google Scholar] [CrossRef]
- Mahajan, A.; Dafnomilis, I.; Hancock, V.; Lodewijks, G.; Schott, D. Assessing the representativeness of durability tests for wood pellets by DEM Simulation—Comparing conditions in a durability test with transfer chutes. EPJ Web Conf. 2017, 140, 15004. [Google Scholar] [CrossRef]
- Gilvari, H.; De Jong, W.; Schott, D.L. Breakage behavior of biomass pellets: An experimental and numerical study. Comput. Part. Mech. 2020, 1–14. [Google Scholar] [CrossRef]
- Xia, Y.; Chen, F.; Klinger, J.L.; Kane, J.J.; Bhattacharjee, T.; Seifert, R.; Ajayi, O.O.; Chen, Q. Assessment of a tomography-informed polyhedral discrete element modelling approach for complex-shaped granular woody biomass in stress consolidation. Biosyst. Eng. 2021, 205, 187–211. [Google Scholar] [CrossRef]
- Molenda, M.; Horabik, J.; Parafiniuk, P.; Oniszczuk, A.; Bańda, M.; Wajs, J.; Gondek, E.; Chutkowski, M.; Lisowski, A.; Wiącek, J.; et al. Mechanical and Combustion Properties of Agglomerates of Wood of Popular Eastern European Species. Materials 2021, 14, 2728. [Google Scholar] [CrossRef] [PubMed]
- Sridharan, A.; Rao., G.V. Pore Size Distributions of Soils From Mercury Intrusion Porosimeter Data. Soil Sci. Soc. Am. J. 1972, 36, 980–981. [Google Scholar] [CrossRef]
- PubChem—National Center for Biotechnology Information, U.S. National Library of Medicine. Available online: https://pubchem.ncbi.nlm.nih.gov/compound/5988#section=Density (accessed on 10 June 2021).
- Walton, O.R.; Braun, R.L. Viscosity, granular-temperature, and stress calculations for shearing assemblies of inelastic, frictional disks. J. Rheol. 1986, 30, 949–980. [Google Scholar] [CrossRef]
- Luding, S. Shear flow modeling of cohesive and frictional fine powder. Powder Technol. 2005, 158, 45–50. [Google Scholar] [CrossRef]
- Thornton, C.; Ning, Z. A theoretical model for the stick/bounce behaviour of adhesive, elastic-plastic spheres. Powder Technol. 1998, 99, 154–162. [Google Scholar] [CrossRef]
- EDEM Solutions. EDEM 2018.2 Documentation; EDEM: Edinburgh, UK, 2018. [Google Scholar]
- Tsuji, Y.; Tanaka, T.; Ishida, T. Lagrangian numerical simulation of plug flow of cohesionless particles in a horizontal pipe. Powder Technol. 1992, 71, 239–250. [Google Scholar] [CrossRef]
- Huang, Y.J.; Nydal, O.J.; Yao, B. Time step criterions for nonlinear dense packed granular materials in time-driven method simulations. Powder Technol. 2014, 253, 80–88. [Google Scholar] [CrossRef]
- Gallego, E.; Fuentes, J.M.; Ruiz, Á.; Hernández-Rodrigo, G.; Aguado, P.; Ayuga, F. Determination of mechanical properties for wood pellets used in DEM simulations. Int. Agrophysics 2020, 34, 485–494. [Google Scholar] [CrossRef]
- Kocsis, Z.; Csanády, E. Investigation on the Mechanics of Wood Pellet Production from Sawdust and Chips; University of West: Sopron, Hungary, 2017; pp. 1–31. [Google Scholar]
- Graham, S.; Eastwick, C.; Snape, C.; Quick, W. Mechanical degradation of biomass wood pellets during long term stockpile storage. Fuel Process. Technol. 2017, 160, 143–151. [Google Scholar] [CrossRef]
- Horabik, J.; Wiącek, J.; Parafiniuk, P.; Stasiak, M.; Bańda, M.; Kobyłka, R.; Molenda, M. Discrete Element Method Modelling of the Diametral Compression of Starch Agglomerates. Materials 2020, 13, 932. [Google Scholar] [CrossRef]





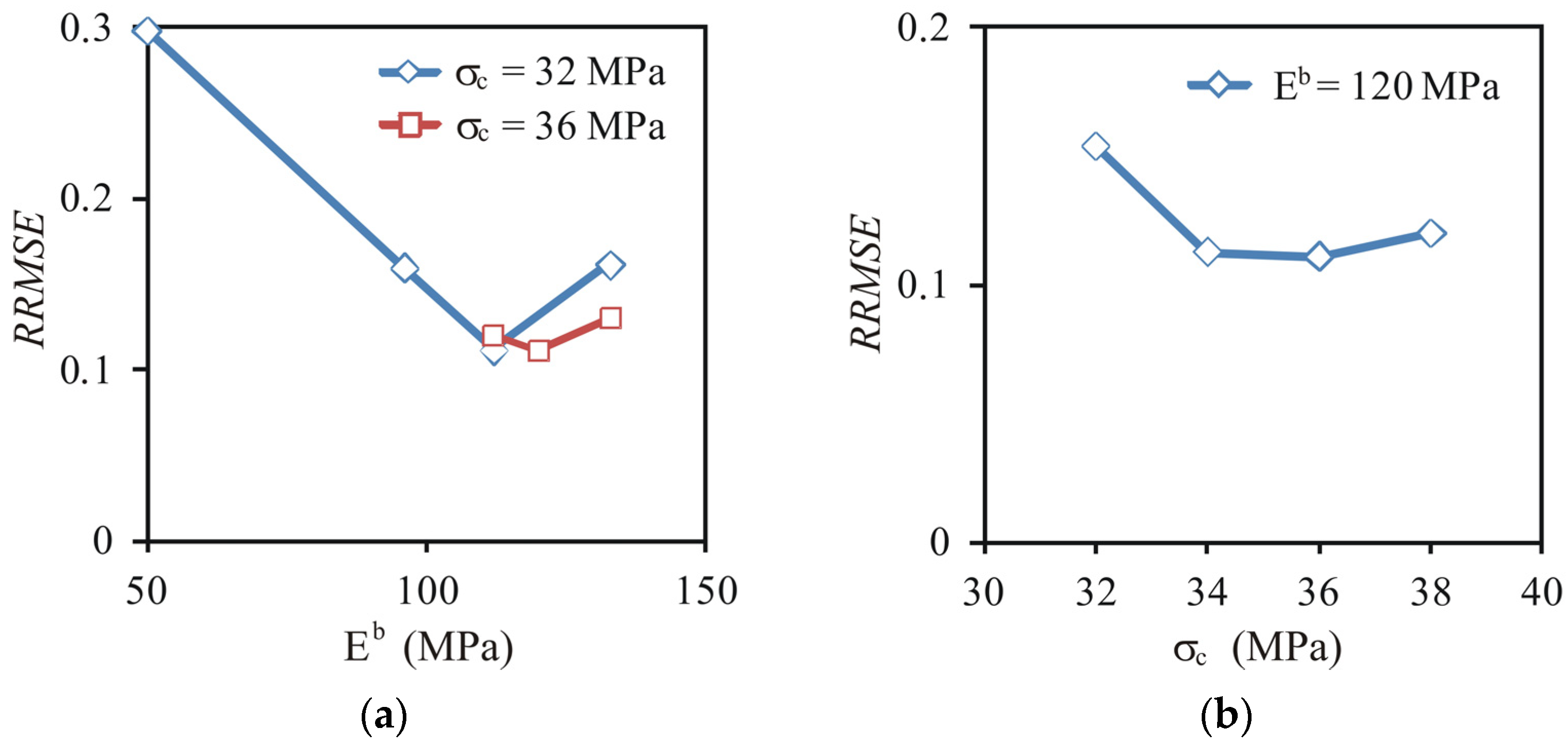
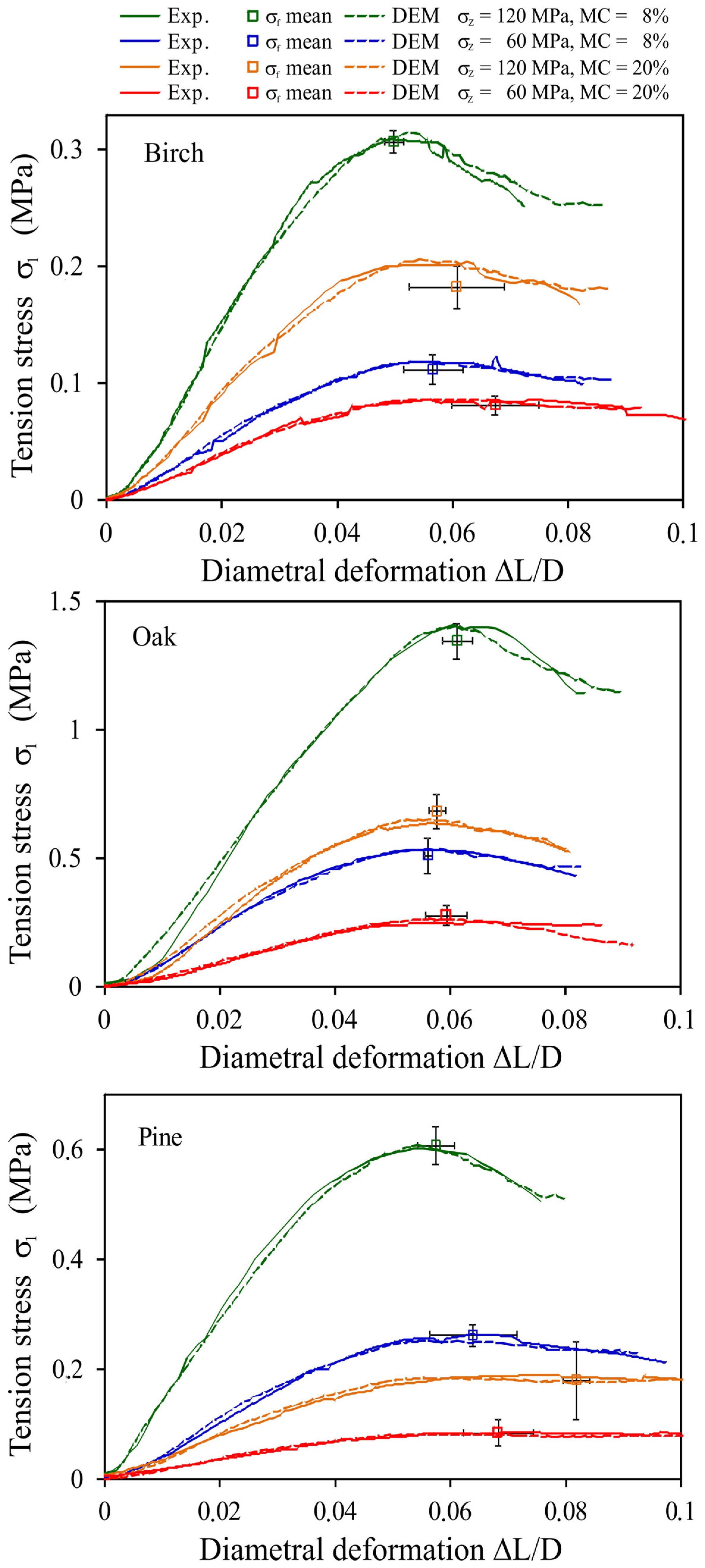
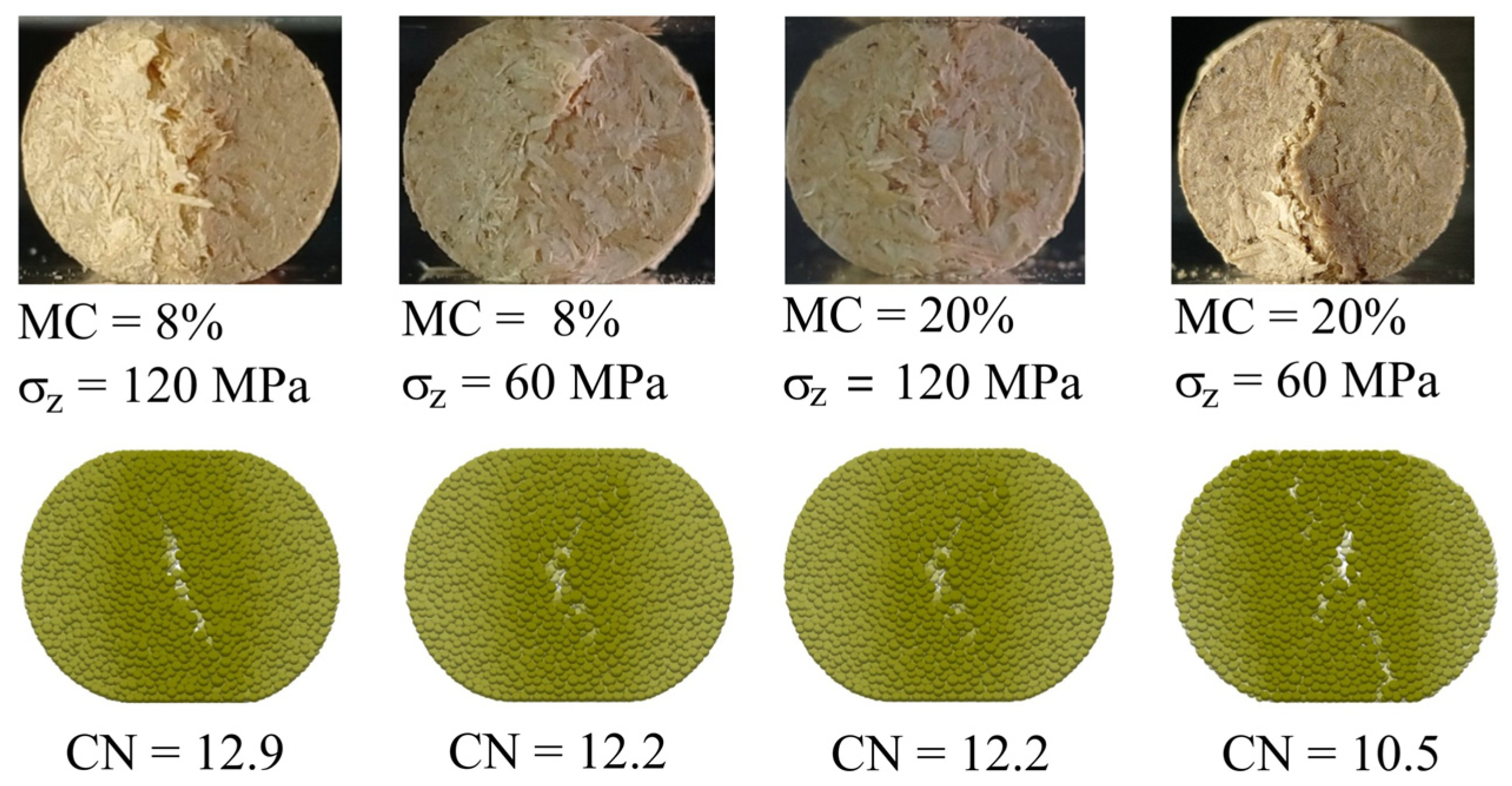
| Material | Wood Solid Phase (Including Closed Pores) | Sawdust |
|---|---|---|
| Density ρw (kg m−3) | Density ρs (kg m−3) | |
| Birch | 1369.8 ± 0.3 a | 1465.3 ± 0.8 a |
| Oak | 1068.4 ± 1.6 b | 1459.9 ± 1.1 b |
| Pine | 1426.6 ± 0.3 c | 1468.7 ± 0.6 c |
| MC (%) | Intact Wood | Sawdust (Initial) | Pellets | ||||||
|---|---|---|---|---|---|---|---|---|---|
| BDw (kg m−3) | pw (%) | BDs (kg m−3) | ps (%) | Compacted to 60 MPa | Compacted to 120 MPa | ||||
| BDp (kg m−3) | pp (%) | BDp (kg m−3) | pp (%) | ||||||
| Birch | 8 | 550 ± 2 a | 62.5 ± 0.2 a | 301.7 ± 6.4 a | 79.4 ± 1.7 a | 701.2 ± 9.9 a | 52.1 ± 0.7 a | 843.9 ± 4.8 a | 42.4 ± 0.2 a |
| Birch | 20 | 272.1 ± 9.7 b | 81.4 ± 2.9 b | 634.6 ± 6.7 b | 56.7 ± 0.6 b | 781.9 ± 22 b | 46.6 ± 1.3 b | ||
| Oak | 8 | 675 ± 3 b | 53.8 ± 0.2 b | 312.6 ± 5.4 a | 78.6 ± 1.4 a | 824.5 ± 10.4 c | 43.5 ± 0.5 c | 1005.8 ± 11.8 c | 31.1 ± 0.4 c |
| Oak | 20 | 267.8 ± 6.3 b | 81.6 ± 1.9 b | 700.3 ± 25.5 a | 52.0 ± 1.9 a | 826.4 ± 35.5 a | 43.3 ± 1.9 a | ||
| Pine | 8 | 510 ± 2 c | 65.2 ± 0.2 c | 267.9 ± 6.7 b | 81.8 ± 2.0 b | 779.6 ± 12.9 d | 46.9 ± 0.8 d | 937.8 ± 17.8 d | 36.2 ± 0.7 d |
| Pine | 20 | 250.9 ± 3.4 c | 82.9 ± 1.1 c | 610.9 ± 44.2 ab | 58.4 ± 4.2 ab | 673.1 ± 33.3 b | 54.2 ± 2.7 e | ||
| Material | σz (MPa) | MC (%) | ΔLf/D | σf (MPa) |
|---|---|---|---|---|
| Birch | 60 | 8 | 0.056 ± 0.005 a | 0.112 ± 0.012 a |
| Birch | 120 | 8 | 0.056 ± 0.003 a | 0.307 ± 0.009 b |
| Birch | 60 | 20 | 0.057 ± 0.005 a | 0.081 ± 0.008 a |
| Birch | 120 | 20 | 0.061 ± 0.008 b | 0.183 ± 0.018 c |
| Oak | 60 | 8 | 0.056 ± 0.001 a | 0.511 ± 0.069 d |
| Oak | 120 | 8 | 0.061 ± 0.003 b | 1.346 ± 0.068 e |
| Oak | 60 | 20 | 0.059 ± 0.004 c | 0.277 ± 0.039 b |
| Oak | 120 | 20 | 0.058 ± 0.002 c | 0.683 ± 0.067 d |
| Pine | 60 | 8 | 0.064 ± 0.008 b | 0.262 ± 0.019 b |
| Pine | 120 | 8 | 0.057 ± 0.003 a | 0.608 ± 0.034 d |
| Pine | 60 | 20 | 0.068 ± 0.006 d | 0.085 ± 0.025 a |
| Pine | 120 | 20 | 0.082 ± 0.002 e | 0.182 ± 0.071 c |
| Parameter | Symbol | Value |
|---|---|---|
| Container: | ||
| Diameter (mm) | Dc | 10 |
| Height (mm) | Hc | 25 |
| Solid density (kg m–3) | ρ | 7800 |
| Young’s modulus (MPa) | E | 1.561 × 106 |
| Poisson’s ratio | ν | 0.3 |
| Particles: | ||
| Number | 40,000 | |
| Mean particle radius (mm) | r | 0.2 |
| SD of particle radius (mm) | rsd | 0.02 |
| Particle radius range (mm) | 0.14–0.26 | |
| Particle solid density (kg m–3) | ρ | 680 |
| Young’s modulus (MPa) | E | 1.57 × 104 |
| Poisson’s ratio | ν | 0.35 |
| Yield strength (MPa) | py | 100; 150 |
| Mean loading (plastic) stiffness (N m–1) | k1 | 1 × 105 |
| Mean unloading (elastic) stiffness (N m–1) | k2 | 4 × 105 |
| Mean adhesion stiffness (N m–1) | kc | 0; 600 |
| Restitution coefficient | e | 0.5 |
| Particle–particle friction coefficient | μp-p | 0.5 |
| Particle–wall friction coefficient | μp-w | 0.15 |
| Rolling friction coefficient | mr | 0.01 |
| Bond radius (μm) | rb | 10; 20; 30; 40 |
| Bond tension strength (MPa) | σc | 3–40 |
| Bond shear strength (MPa) | τc | 3–40 |
| Bond Young’s modulus (MPa) | Eb | 5–120 |
| Material | σz (MPa) | MC (%) | CN | Eb (MPa) | σc (MPa) | RRMSE |
|---|---|---|---|---|---|---|
| Birch | 60 | 8 | 12.2 | 12.8 | 4.6 | 0.027 |
| Birch | 120 | 8 | 12.2 | 36.6 | 10.1 | 0.039 |
| Birch | 60 | 20 | 12.2 | 9.2 | 4 | 0.037 |
| Birch | 120 | 20 | 12.2 | 22.4 | 8.05 | 0.039 |
| Oak | 60 | 8 | 12.2 | 60 | 20 | 0.027 |
| Oak | 120 | 8 | 12.9 | 120 | 36 | 0.111 |
| Oak | 60 | 20 | 10.5 | 52.8 | 13 | 0.089 |
| Oak | 120 | 20 | 12.2 | 73.2 | 24 | 0.116 |
| Pine | 60 | 8 | 12.2 | 27.2 | 13.5 | 0.052 |
| Pine | 120 | 8 | 12.9 | 50.4 | 13.5 | 0.028 |
| Pine | 60 | 20 | 12.2 | 8.6 | 4.3 | 0.053 |
| Pine | 120 | 20 | 12.2 | 19.7 | 9.9 | 0.049 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Horabik, J.; Bańda, M.; Józefaciuk, G.; Adamczuk, A.; Polakowski, C.; Stasiak, M.; Parafiniuk, P.; Wiącek, J.; Kobyłka, R.; Molenda, M. Breakage Strength of Wood Sawdust Pellets: Measurements and Modelling. Materials 2021, 14, 3273. https://doi.org/10.3390/ma14123273
Horabik J, Bańda M, Józefaciuk G, Adamczuk A, Polakowski C, Stasiak M, Parafiniuk P, Wiącek J, Kobyłka R, Molenda M. Breakage Strength of Wood Sawdust Pellets: Measurements and Modelling. Materials. 2021; 14(12):3273. https://doi.org/10.3390/ma14123273
Chicago/Turabian StyleHorabik, Józef, Maciej Bańda, Grzegorz Józefaciuk, Agnieszka Adamczuk, Cezary Polakowski, Mateusz Stasiak, Piotr Parafiniuk, Joanna Wiącek, Rafał Kobyłka, and Marek Molenda. 2021. "Breakage Strength of Wood Sawdust Pellets: Measurements and Modelling" Materials 14, no. 12: 3273. https://doi.org/10.3390/ma14123273
APA StyleHorabik, J., Bańda, M., Józefaciuk, G., Adamczuk, A., Polakowski, C., Stasiak, M., Parafiniuk, P., Wiącek, J., Kobyłka, R., & Molenda, M. (2021). Breakage Strength of Wood Sawdust Pellets: Measurements and Modelling. Materials, 14(12), 3273. https://doi.org/10.3390/ma14123273








