Ultrafast Third-Order Nonlinear Optical Response Excited by fs Laser Pulses at 1550 nm in GaN Crystals
Abstract
1. Introduction
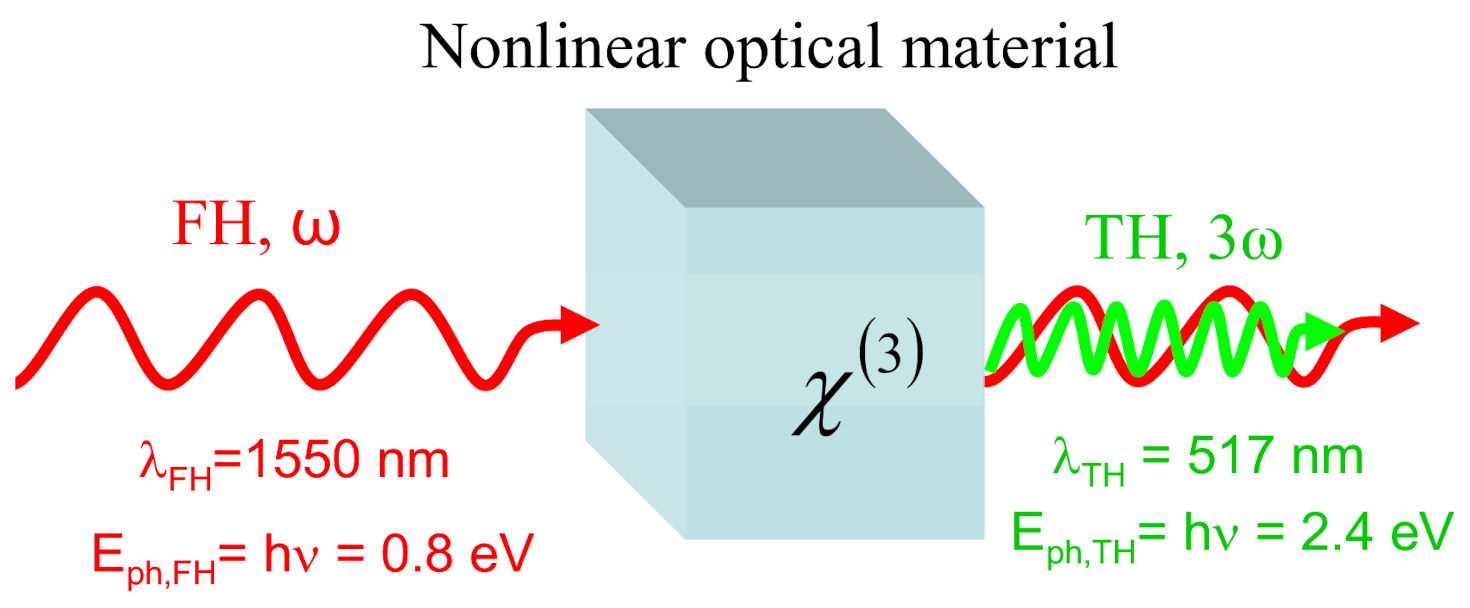
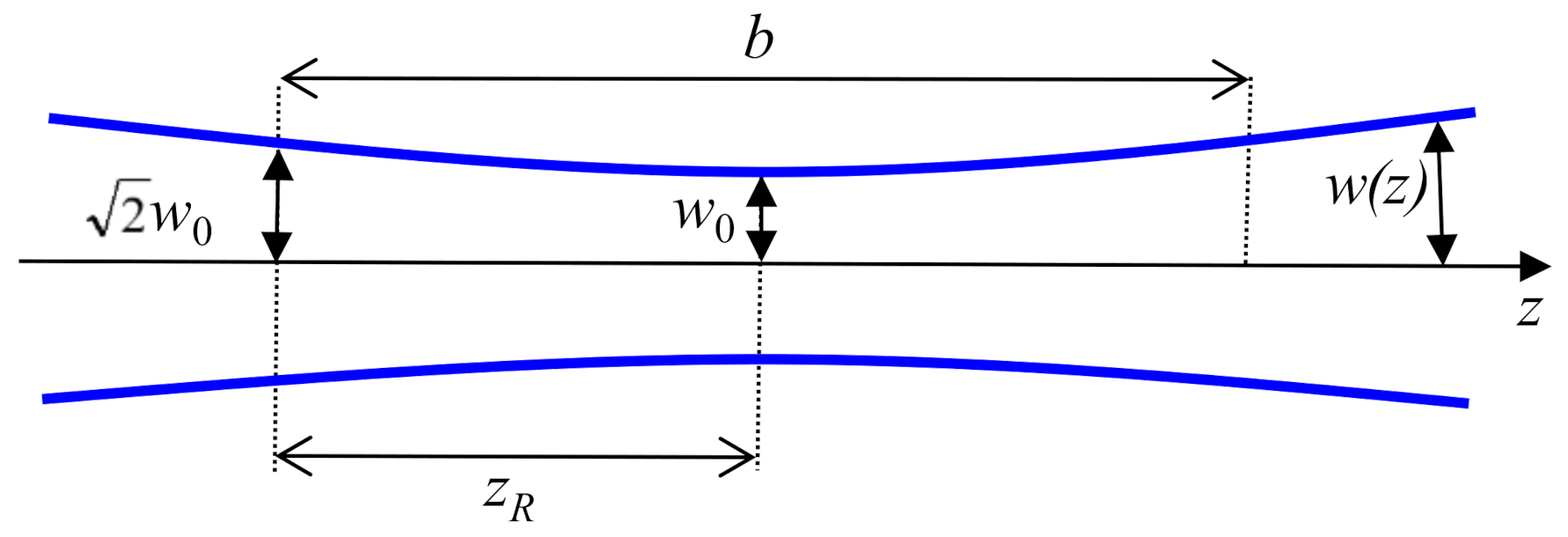
2. Direct Extraction of the Third-Order Nonlinear Optical Susceptibility from the Third-Harmonic Generation
3. Experimental Details of the Third-Harmonic Generation in GaN Crystal
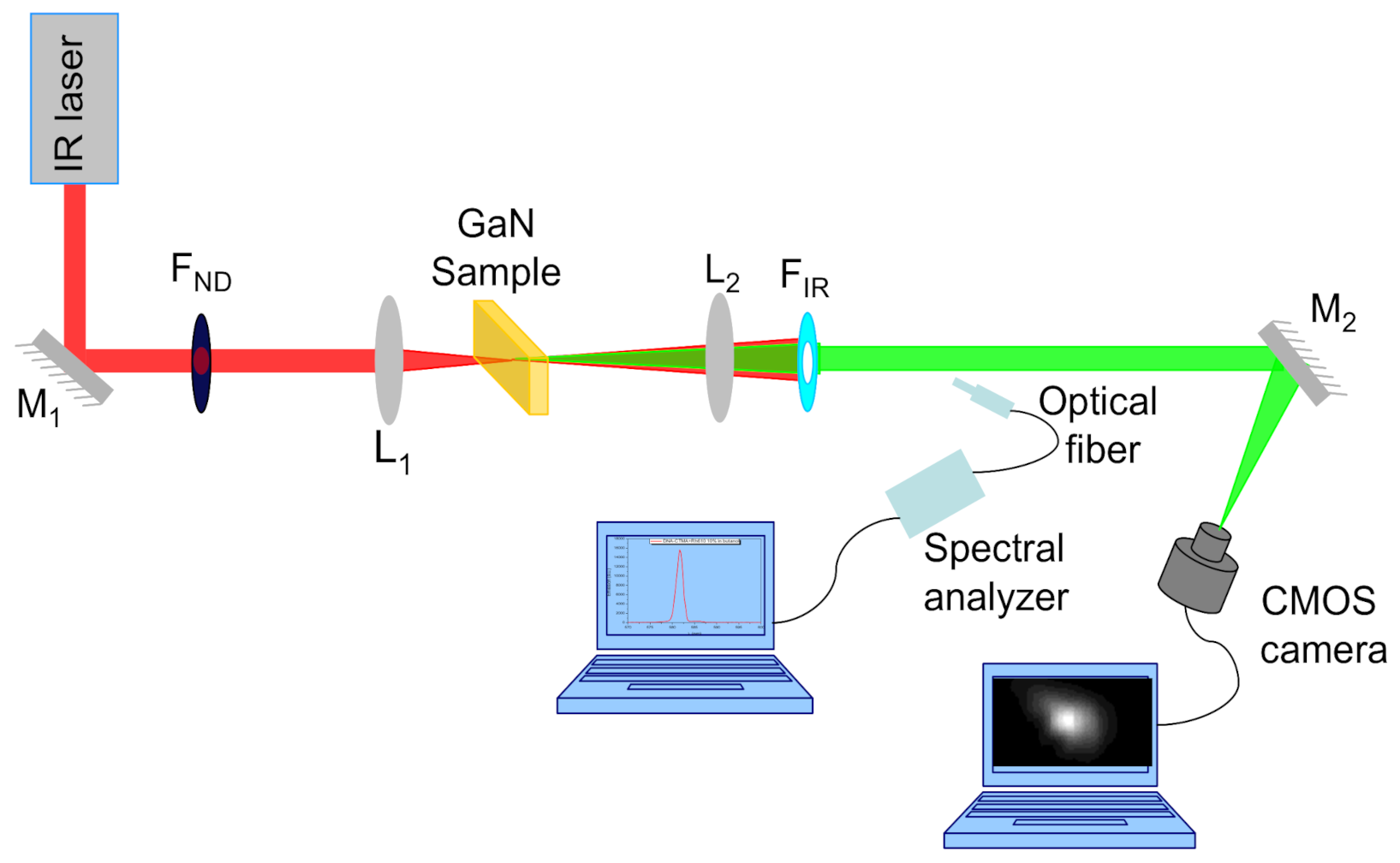
3.1. Experimental Setup
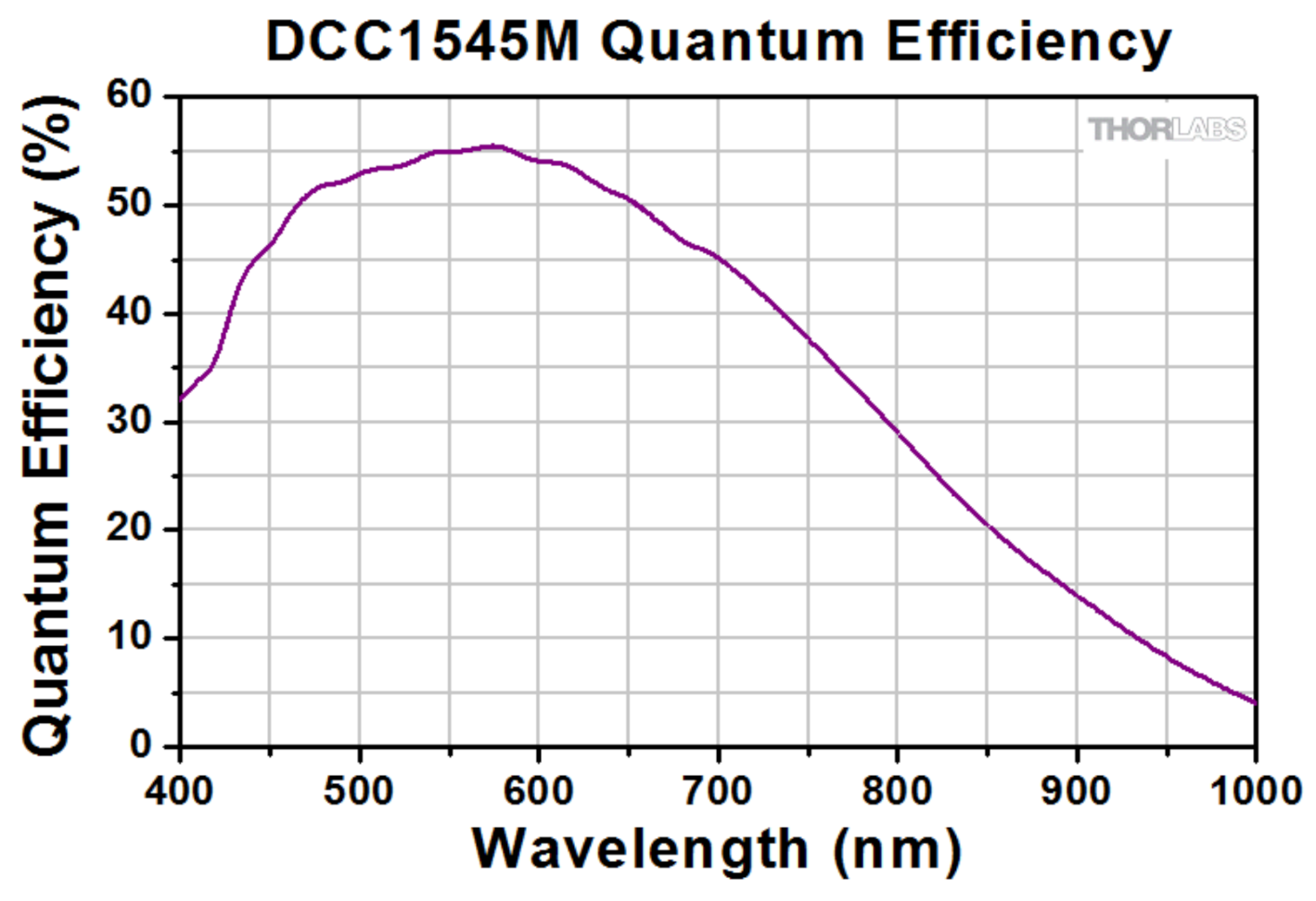
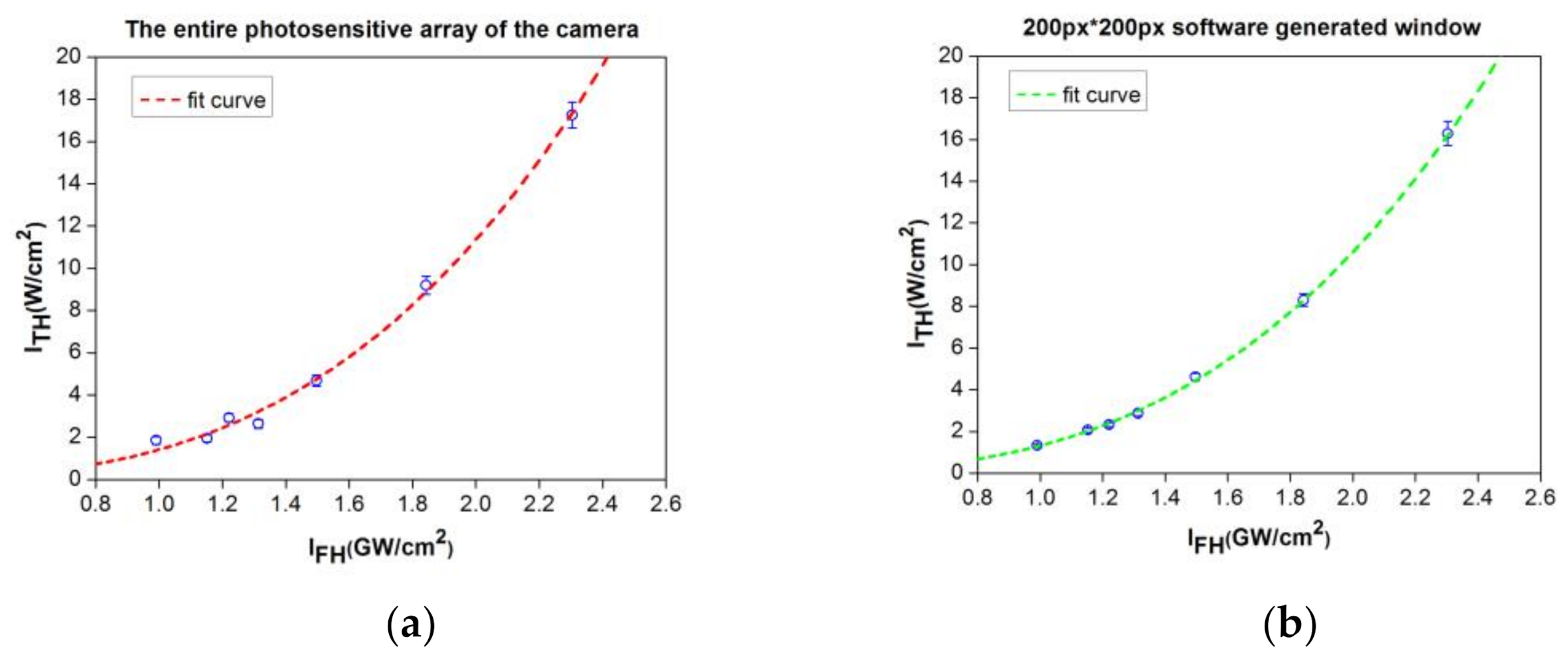
3.2. Measurement of Very Low Optical Powers Using a Camera as Power-Meter
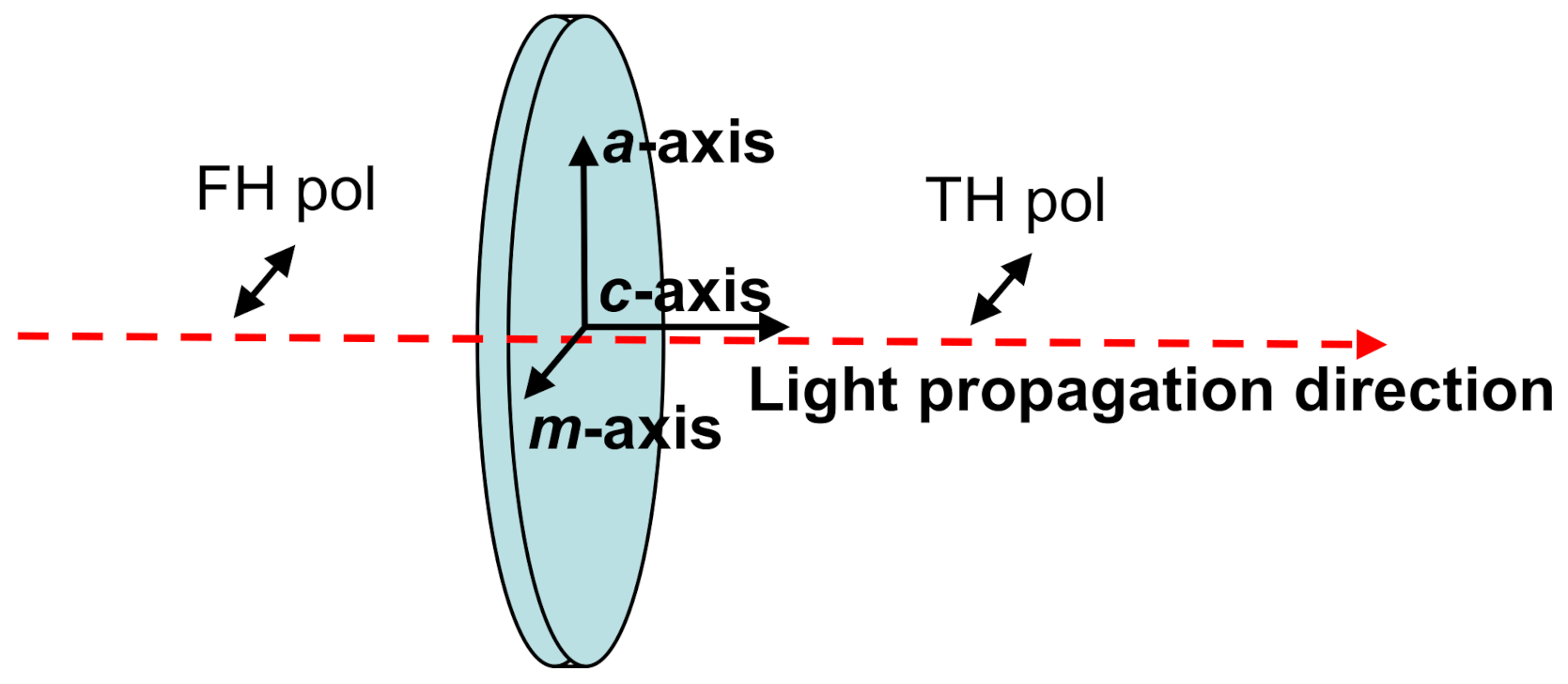
3.3. The Investigated Sample
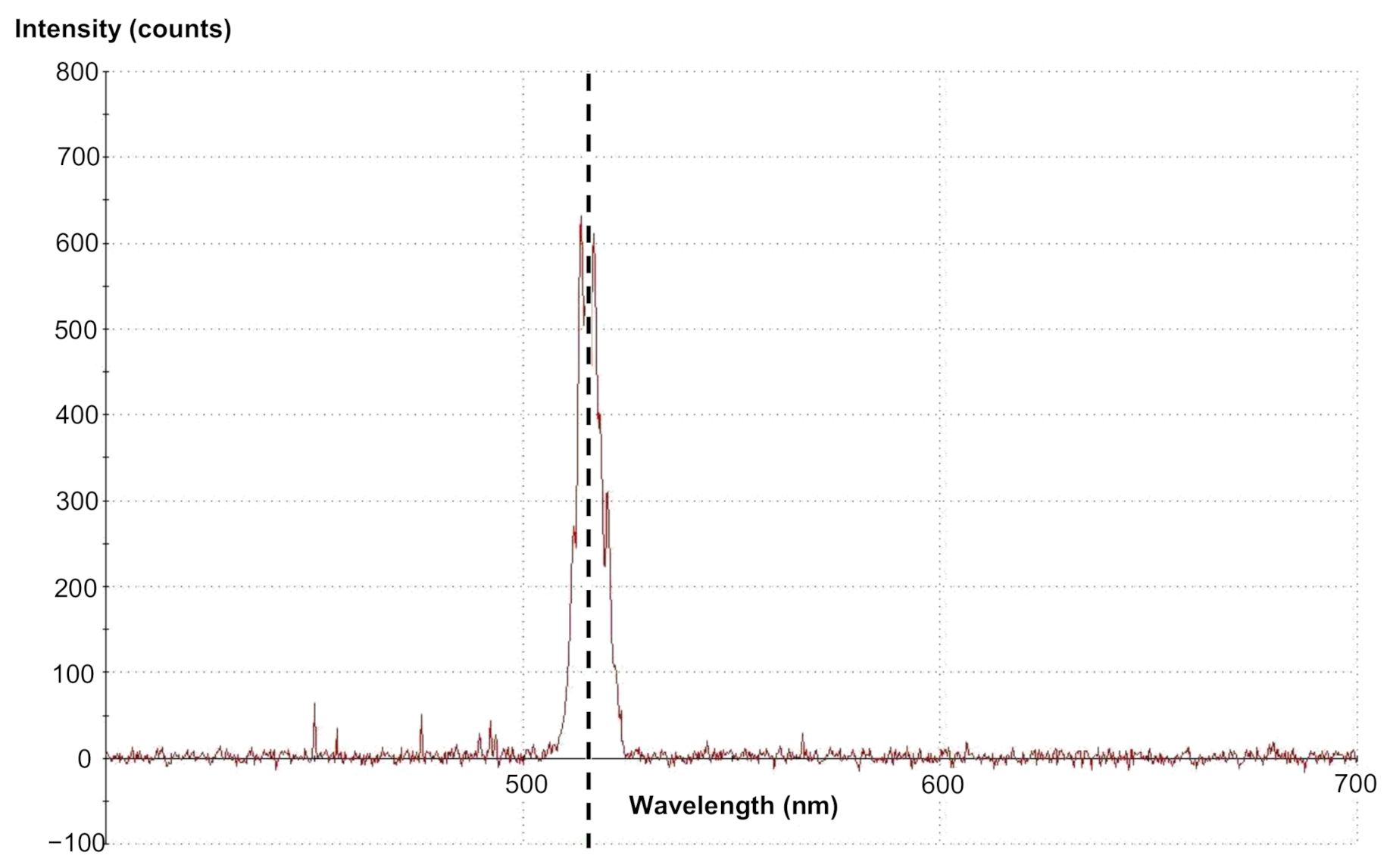
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Flack, T.J.; Pushpakaran, B.N.; Bayne, S.B. GaN Technology for Power Electronic Applications: A Review. J. Electron. Mater. 2016, 45, 2673–2682. [Google Scholar] [CrossRef]
- Yamahara, K.; Mannan, A.; Kawayama, I.; Nakanishi, H.; Tonouchi, M. Ultrafast spatiotemporal photocarrier dynamics near GaN surfaces studied by terahertz emission spectroscopy. Sci. Rep. 2020, 10, 14633. [Google Scholar] [CrossRef] [PubMed]
- Chu, R. GaN power switches on the rise: Demonstrated benefits and unrealized potentials. Appl. Phys. Lett. 2020, 116, 090502. [Google Scholar] [CrossRef]
- Amano, H.; Baines, Y.; Beam, E.; Borga, M.; Bouchet, T.; Chalker, P.R.; Charles, M.; Chen, K.J.; Chowdhury, N.; Chu, R.; et al. The 2018 GaN power electronics roadmap. J. Phys. D. Appl. Phys. 2018, 51, 163001. [Google Scholar] [CrossRef]
- Nakamura, S.; Senoh, M.; Mukai, T. High-power InGaN/GaN double-heterostructure violet light emitting diodes. Appl. Phys. Lett. 1993, 62, 2390. [Google Scholar] [CrossRef]
- Nakamura, S.; Pearton, S.; Fasol, G. The Blue Laser Diode—The Complete Story; Springer: Berlin/Heidelberg, Germany, 2000; ISBN 3-540-66505-6. [Google Scholar]
- Xu, G.Y.; Salvador, A.; Kim, W.; Fan, Z.; Lu, C.; Tang, H.; Morkoç, H.; Smith, G.; Estes, M.; Goldenberg, B.; et al. High speed, low noise ultraviolet photodetectors based on GaN p-i-n and AlGaN(p)-GaN(i)-GaN(n)structures. Appl. Phys. Lett. 1997, 71, 2154. [Google Scholar] [CrossRef]
- Pezzagna, S.; Brault, J.; De Micheli, M.; Vennéguès, P.; Wieck, A.; Massies, J. GaN, a new material for integrated nonlinear optics. In Proceedings of the European Conference on Integrated Optics ECIO 2007, Eindhoven, The Netherlands, 25–27 April 2007; pp. 25–27. [Google Scholar]
- Vico Triviño, N.; Dharanipathy, U.; Carlin, J.F.; Diao, Z.; Houdré, R.; Grandjean, N. Integrated photonics on silicon with wide bandgap GaN semiconductor. Appl. Phys. Lett. 2013, 102, 081120. [Google Scholar] [CrossRef]
- Dragoman, M.; Braniste, T.; Iordanescu, S.; Aldrigo, M.; Raevschi, S.; Shree, S.; Adelung, R.; Tiginyanu, I. Electromagnetic interference shielding in X-band with aero-GaN. Nanotechnology 2019, 30. [Google Scholar] [CrossRef] [PubMed]
- Braniste, T.; Zhukov, S.; Dragoman, M.; Alyabyeva, L.; Ciobanu, V.; Aldrigo, M.; Dragoman, D.; Iordanescu, S.; Shree, S.; Raevschi, S.; et al. Terahertz shielding properties of aero-GaN. Semicond. Sci. Technol. 2019, 34, 12LT02. [Google Scholar] [CrossRef]
- Wolff, N.; Ciobanu, V.; Enachi, M.; Kamp, M.; Braniste, T.; Duppel, V.; Shree, S.; Raevschi, S.; Medina-Sánchez, M.; Adelung, R.; et al. Advanced Hybrid GaN/ZnO Nanoarchitectured Microtubes for Fluorescent Micromotors Driven by UV Light. Small 2020, 16. [Google Scholar] [CrossRef]
- Tiginyanu, I.; Braniste, T.; Smazna, D.; Deng, M.; Schütt, F.; Schuchardt, A.; Stevens-Kalceff, M.A.; Raevschi, S.; Schürmann, U.; Kienle, L.; et al. Self-organized and self-propelled aero-GaN with dual hydrophilic-hydrophobic behaviour. Nano Energy 2019, 56, 759–769. [Google Scholar] [CrossRef]
- Braniste, T.; Ciers, J.; Monaico, E.; Martin, D.; Carlin, J.-F.; Ursaki, V.V.; Sergentu, V.V.; Tiginyanu, I.M.; Grandjean, N. Multilayer porous structures of HVPE and MOCVD grown GaN for photonic applications. Superlattices Microstruct. 2017, 102, 221–234. [Google Scholar] [CrossRef]
- Monaico, E.; Tiginyanu, I.; Ursaki, V. Porous Semiconductor Compounds. Semicond. Sci. Technol. 2020, 35, 103001. [Google Scholar] [CrossRef]
- Roland, I.; Gromovyi, M.; Zeng, Y.; El Kurdi, M.; Sauvage, S.; Brimont, C.; Guillet, T.; Gayral, B.; Semond, F.; Duboz, J.Y.; et al. Phase-matched second harmonic generation with on-chip GaN-on-Si microdisks. Sci. Rep. 2016, 6, 34191. [Google Scholar] [CrossRef] [PubMed]
- Hahn, D.N.; Kiehne, G.T.; Ketterson, J.B.; Wong, G.K.L.; Kung, P.; Saxler, A.; Razeghi, M. Phase-matched optical second-harmonic generation in GaN and AlN slab waveguides. J. Appl. Phys. 1999, 85, 2497. [Google Scholar] [CrossRef]
- Rigler, M.; Troha, T.; Guo, W.; Kirste, R.; Bryan, I.; Collazo, R.; Sitar, Z.; Zgonik, M. Second-harmonic generation of blue light in GaN waveguides. Appl. Sci. 2018, 8, 1218. [Google Scholar] [CrossRef]
- Xiong, C.; Pernice, W.; Ryu, K.K.; Schuck, C.; Fong, K.Y.; Palacios, T.; Tang, H.X. Integrated GaN photonic circuits on silicon (100) for second harmonic generation. Opt. Express 2011, 19, 10462–10470. [Google Scholar] [CrossRef] [PubMed]
- Pačebutas, V.; Stalnionis, A.; Krotkus, A.; Suski, T.; Perlin, P.; Leszczynski, M. Picosecond Z-scan measurements on bulk GaN crystals. Appl. Phys. Lett. 2001, 78, 4118. [Google Scholar] [CrossRef]
- Taheri, B.; Hays, J.; Song, J.J.; Goldenberg, B. Picosecond four-wave-mixing in GaN epilayers at 532 nm. Appl. Phys. Lett. 1996, 68, 587. [Google Scholar] [CrossRef]
- Fazio, E.; Passaseo, A.; Alonzo, M.; Belardini, A.; Sibilia, C.; Larciprete, M.C.; Bertolotti, M. Measurement of pure Kerr nonlinearity in GaN thin films at 800 nm by means of eclipsing Z-scan experiments. J. Opt. A Pure Appl. Opt. 2007, 9, L3. [Google Scholar] [CrossRef]
- Munk, D.; Katzman, M.; Westreich, O.; Bin Nun, M.; Lior, Y.; Sicron, N.; Paltiel, Y.; Zadok, A. Four-wave mixing and nonlinear parameter measurement in a gallium-nitride ridge waveguide. Opt. Mater. Express 2018, 8, 66–72. [Google Scholar] [CrossRef]
- Martins, R.J.; Siqueira, J.P.; Manglano Clavero, I.; Margenfeld, C.; Fündling, S.; Vogt, A.; Waag, A.; Voss, T.; Mendonca, C.R. Carrier dynamics and optical nonlinearities in a GaN epitaxial thin film under three-photon absorption. J. Appl. Phys. 2018, 123, 243101. [Google Scholar] [CrossRef]
- Almeida, G.F.B.; Santos, S.N.C.; Siqueira, J.P.; Dipold, J.; Voss, T.; Mendonça, C.R. Third-order nonlinear spectrum of GaN under femtosecond-pulse excitation from the visible to the near infrared. Photonics 2019, 6, 69. [Google Scholar] [CrossRef]
- Sun, C.K.; Huang, Y.L.; Liang, J.C.; Wang, J.C.; Gan, K.G.; Kao, F.J.; Keller, S.; Mack, M.P.; Mishra, U.; Denbaars, S.P. Large near resonance third order nonlinearity in GaN. Opt. Quantum Electron. 2000, 32, 619–640. [Google Scholar] [CrossRef]
- Huang, Y.L.; Sun, C.K.; Liang, J.C.; Keller, S.; Mack, M.P.; Mishra, U.K.; DenBaars, S.P. Femtosecond Z-scan measurement of GaN. Appl. Phys. Lett. 1999, 75, 3524. [Google Scholar] [CrossRef]
- Chen, H.; Huang, X.; Fu, H.; Lu, Z.; Zhang, X.; Montes, J.A.; Zhao, Y. Characterizations of nonlinear optical properties on GaN crystals in polar, nonpolar, and semipolar orientations. Appl. Phys. Lett. 2017, 110, 181110. [Google Scholar] [CrossRef]
- Fang, Y.; Xiao, Z.; Wu, X.; Zhou, F.; Yang, J.; Yang, Y.; Song, Y. Optical nonlinearities and ultrafast all-optical switching of m-plane GaN in the near-infrared. Appl. Phys. Lett. 2015, 106, 251903. [Google Scholar] [CrossRef]
- Zhang, F.; Han, X. Large third-order nonlinearity of nonpolar A -plane GaN film at 800 nm determined by Z-scan technology. J. Mod. Opt. 2014, 61, 1360–1363. [Google Scholar] [CrossRef]
- Rau, I.; Kajzar, F.; Luc, J.; Sahraoui, B.; Boudebs, G. Comparison of Z-scan and THG derived nonlinear index of refraction in selected organic solvents. J. Opt. Soc. Am. B 2008, 25, 1738–1747. [Google Scholar] [CrossRef]
- Butcher, P.; Cotter, D. The Elements of Nonlinear Optics; Cambridge University Press: Cambridge, UK, 1990; ISBN 0-521-34183-3. [Google Scholar]
- Boyd, R.W. Nonlinear Optics, 3rd ed.; Academic Press: London, UK, 2008; ISBN 978-0-12-369470-6. [Google Scholar]
- Fuentes-Hernandez, C.; Tseng, S.Y.; Owens, D.; Kippelen, B. Ultrafast optical image processing based on third-harmonic generation in organic thin films. Appl. Phys. Lett. 2007, 91, 131110. [Google Scholar] [CrossRef]
- Popescu, S.T.; Gheorghe, P.S.; Petris, A. Measuring very low optical powers with a common camera. Appl. Opt. 2014, 53, 5460–5464. [Google Scholar] [CrossRef] [PubMed]
- Petris, A.; Gheorghe, P.S.; Vlad, V.I.; Rusu, E.; Ursaki, V.V.; Tiginyanu, I.M. Ultrafast third-order optical nonlinearity in SnS2 layered compound for photonic applications. Opt. Mater. 2018, 76, 69–74. [Google Scholar] [CrossRef]
- Paschotta, R. RP Photonics Encyclopedia. Available online: www.rp-photonics.com (accessed on 4 January 2021).
- Tiginyanu, I.; Stevens-Kalceff, M.A.; Sarua, A.; Braniste, T.; Monaico, E.; Popa, V.; Andrade, H.D.; Thomas, J.O.; Raevschi, S.; Schulte, K.; et al. Self-Organized Three-Dimensional Nanostructured Architectures in Bulk GaN Generated by Spatial Modulation of Doping. ECS J. Solid State Sci. Technol. 2016, 5, P218–P227. [Google Scholar] [CrossRef]
- Wolff, N.; Jordt, P.; Braniste, T.; Popa, V.; Monaico, E.; Ursaki, V.; Petraru, A.; Adelung, R.; Murphy, B.M.; Kienle, L.; et al. Modulation of Electrical Conductivity and Lattice Distortions in Bulk HVPE-Grown GaN. ECS J. Solid State Sci. Technol. 2019, 8, Q141–Q146. [Google Scholar] [CrossRef]
- Ghosh, S.; Waltereit, P.; Brandt, O.; Grahn, H.T.; Ploog, K.H. Polarization-dependent spectroscopic study of M-plane GaN on γ-LiAlO2. Appl. Phys. Lett. 2002, 80, 413–415. [Google Scholar] [CrossRef]
- Gębski, M.; Dems, M.; Szerling, A.; Motyka, M.; Marona, L.; Kruszka, R.; Urbańczyk, D.; Walczakowski, M.; Pałka, N.; Wójcik-Jedlińska, A.; et al. Monolithic high-index contrast grating: A material independent high-reflectance VCSEL mirror. Opt. Express 2015, 23, 11674. [Google Scholar] [CrossRef]
- Liu, M.; Li, K.; Kong, F.; Zhao, J.; Ding, Q.; Zhang, M. Electrical-optical analysis of photonic crystals GaN-based high power light emitting diodes. Opt. Quantum Electron. 2016, 48, 274. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Petris, A.; Gheorghe, P.; Braniste, T.; Tiginyanu, I. Ultrafast Third-Order Nonlinear Optical Response Excited by fs Laser Pulses at 1550 nm in GaN Crystals. Materials 2021, 14, 3194. https://doi.org/10.3390/ma14123194
Petris A, Gheorghe P, Braniste T, Tiginyanu I. Ultrafast Third-Order Nonlinear Optical Response Excited by fs Laser Pulses at 1550 nm in GaN Crystals. Materials. 2021; 14(12):3194. https://doi.org/10.3390/ma14123194
Chicago/Turabian StylePetris, Adrian, Petronela Gheorghe, Tudor Braniste, and Ion Tiginyanu. 2021. "Ultrafast Third-Order Nonlinear Optical Response Excited by fs Laser Pulses at 1550 nm in GaN Crystals" Materials 14, no. 12: 3194. https://doi.org/10.3390/ma14123194
APA StylePetris, A., Gheorghe, P., Braniste, T., & Tiginyanu, I. (2021). Ultrafast Third-Order Nonlinear Optical Response Excited by fs Laser Pulses at 1550 nm in GaN Crystals. Materials, 14(12), 3194. https://doi.org/10.3390/ma14123194





