Injection Molding of 3-3 Hydroxyapatite Composites
Abstract
1. Introduction
2. Material and Methods
2.1. Injection Molding of Porous Hydroxyapatite Ceramics
2.2. Fabrication of HAp/UDMA Composites
2.3. Characterization
3. Results and Discussion
3.1. Microstructural and Mechanical Properties of the Porous Injection Molded HAp
3.2. Microstructural and Mechanical Properties of the Interpenetrating HAp/UDMA Composites
3.3. Potentials and Future Perspectives of the Porous HAp Ceramics and HAp/UDMA Composites
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- White, A.A.; Best, S.M.; Kinloch, I.A. Hydroxyapatite—Carbon Nanotube Composites for Biomedical Applications: A Review. Int. J. Appl. Ceram. Technol. 2007, 4, 1–13. [Google Scholar] [CrossRef]
- Giannoudis, P.V.; Dinopoulos, H.; Tsiridis, E. Bone substitutes: An update. Injury 2005, 36 (Suppl. 3), 20–27. [Google Scholar] [CrossRef]
- Schmitz, J.P.; Hollinger, J.O. The Critical Size Defect as an Experimental Model for Craniomandibulofacial Nonunions. Clin. Orthop. Relat. Res. 1986, 299–308. [Google Scholar] [CrossRef]
- de Long, W.G.; Einhorn, T.A.; Koval, K.; McKee, M.; Smith, W.; Sanders, R.; Watson, T. Bone grafts and bone graft substitutes in orthopaedic trauma surgery. A critical analysis. J. Bone Jt. Surg. 2007, 89, 649–658. [Google Scholar] [CrossRef]
- Dimitriou, R.; Jones, E.; McGonagle, D.; Giannoudis, P.V. Bone regeneration: Current concepts and future directions. BMC Med. 2011, 9, 66. [Google Scholar] [CrossRef] [PubMed]
- Salgado, A.J.; Coutinho, O.P.; Reis, R.L. Bone tissue engineering: State of the art and future trends. Macromol. Biosci. 2004, 4, 743–765. [Google Scholar] [CrossRef] [PubMed]
- Deville, S.; Saiz, E.; Tomsia, A.P. Freeze casting of hydroxyapatite scaffolds for bone tissue engineering. Biomaterials 2006, 27, 5480–5489. [Google Scholar] [CrossRef]
- Feng, P.; Niu, M.; Gao, C.; Peng, S.; Shuai, C. A novel two-step sintering for nano-hydroxyapatite scaffolds for bone tissue engineering. Sci. Rep. 2014, 4, 5599. [Google Scholar] [CrossRef]
- Teixeira, S.; Rodriguez, M.A.; Pena, P.; De Aza, A.H.; De Aza, S.; Ferraz, M.P.; Monteiro, F.J. Physical characterization of hydroxyapatite porous scaffolds for tissue engineering. Mater. Sci. Eng. C 2009, 29, 1510–1514. [Google Scholar] [CrossRef]
- Ramay, H.R.; Zhang, M. Preparation of porous hydroxyapatite scaffolds by combination of the gel-casting and polymer sponge methods. Biomaterials 2003, 24, 3293–3302. [Google Scholar] [CrossRef]
- Milosevski, M.; Bossert, J.; Milosevski, D.; Gruevska, N. Preparation and properties of dense and porous calcium phosphate. Ceram. Int. 1999, 25, 693–696. [Google Scholar] [CrossRef]
- Lett, J.A.; Sundareswari, M.; Ravichandran, K. Porous hydroxyapatite scaffolds for orthopedic and dental applications—The role of binders. Mater. Today Proc. 2016, 3, 1672–1677. [Google Scholar] [CrossRef]
- Yasuda, H.Y.; Mahara, S.; Terashita, N.; Umakoshi, Y. Preparation of Porous Hydroxyapatite/α-Tricalcium Phosphate Composites by a Colloidal Process. Mater. Trans. 2002, 43, 1332–1335. [Google Scholar] [CrossRef][Green Version]
- Woottichaiwat, S.; Puajindanetr, S.; Best, S.M. Fabrication of Porous Hydroxyapatite through Combination of Sacrificial Template and Direct Foaming Techniques. Eng. J. 2011, 15, 1–16. [Google Scholar] [CrossRef]
- Kawata, M.; Uchida, H.; Itatani, K.; Okada, I.; Koda, S.; Aizawa, M. Development of porous ceramics with well-controlled porosities and pore sizes from apatite fibers and their evaluations. J. Mater. Sci. Mater. Med. 2004, 15, 817–823. [Google Scholar] [CrossRef] [PubMed]
- Montufar, E.B.; Traykova, T.; Gil, C.; Harr, I.; Almirall, A.; Aguirre, A.; Engel, E.; Planell, J.A.; Ginebra, M.P. Foamed surfactant solution as a template for self-setting injectable hydroxyapatite scaffolds for bone regeneration. Acta Biomater. 2010, 6, 876–885. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.; Jang, T.-S.; Song, J.; Kim, H.-E.; Jung, H.-D. The Production of Porous Hydroxyapatite Scaffolds with Graded Porosity by Sequential Freeze-Casting. Materials 2017, 10, 367. [Google Scholar] [CrossRef]
- Jang, D.-W.; Franco, R.A.; Sarkar, S.K.; Lee, B.-T. Fabrication of Porous Hydroxyapatite Scaffolds as Artificial Bone Preform and its Biocompatibility Evaluation. ASAIO J. 2014, 60, 216–223. [Google Scholar] [CrossRef]
- Shao, H.; He, J.; Lin, T.; Zhang, Z.; Zhang, Y.; Liu, S. 3D gel-printing of hydroxyapatite scaffold for bone tissue engineering. Ceram. Int. 2019, 45, 1163–1170. [Google Scholar] [CrossRef]
- Liu, Z.; Liang, H.; Shi, T.; Xie, D.; Chen, R.; Han, X.; Shen, L.; Wang, C.; Tian, Z. Additive manufacturing of hydroxyapatite bone scaffolds via digital light processing and in vitro compatibility. Ceram. Int. 2019, 45, 11079–11086. [Google Scholar] [CrossRef]
- Leukers, B.; Gülkan, H.; Irsen, S.H.; Milz, S.; Tille, C.; Schieker, M.; Seitz, H. Hydroxyapatite scaffolds for bone tissue engineering made by 3D printing. J. Mater. Sci. Mater. Med. 2005, 16, 1121–1124. [Google Scholar] [CrossRef] [PubMed]
- Dellinger, J.G.; Eurell, J.A.C.; Stewart, M.; Jamison, R.D. Bone response to 3D periodic hydroxyapatite scaffolds with and without tailored microporosity to deliver bone morphogenetic protein 2. J. Biomed. Mater. Res. A 2006, 76, 366–376. [Google Scholar] [CrossRef]
- Han, J.; Zhao, J.; Shen, Z. Zirconia ceramics in metal-free implant dentistry. Adv. Appl. Ceram. 2017, 116, 138–150. [Google Scholar] [CrossRef]
- Hu, C.Y.; Yoon, T.-R. Recent updates for biomaterials used in total hip arthroplasty. Biomater. Res. 2018, 22, 33. [Google Scholar] [CrossRef] [PubMed]
- Lacefield, W.R. Hydroxyapatite coatings. Ann. N. Y. Acad. Sci. 1988, 523, 72–80. [Google Scholar] [CrossRef] [PubMed]
- Matula, G.; Krysteczko, J. Porous material produced by ceramic injection molding. J. Achiev. Mater. Manuf. Eng. 2015, 71, 14–21. [Google Scholar]
- Surawatthana, J.; Chuankrerkkul, N.; Buggakupta, W. Properties of Porous Alumina Fabricated by Ceramic Injection Moulding Using Environmentally Friendly Binder. AMR 2012, 506, 238–241. [Google Scholar] [CrossRef]
- Zhang, S.X.; Ong, Z.Y.; Li, T.; Li, Q.F.; Pook, S.F. Ceramic composite components with gradient porosity by powder injection moulding. Mater. Des. 2010, 31, 2897–2903. [Google Scholar] [CrossRef]
- Biggemann, J.; Pezoldt, M.; Stumpf, M.; Greil, P.; Fey, T. Modular ceramic scaffolds for individual implants. Acta Biomater. 2018, 80, 390–400. [Google Scholar] [CrossRef]
- Chuankrerkkul, N.; Chauoon, S.; Meepho, M.; Pornprasertsuk, R. Characterisation of NiO-YSZ Porous Anode-Support for Solid Oxide Fuel Cells Fabricated by Ceramic Injection Moulding. KEM 2017, 751, 467–470. [Google Scholar] [CrossRef]
- Cihlář, J.; Tranec, M. Injection moulded hydroxyapatite ceramics. Biomaterials 1996, 17, 1905–1911. [Google Scholar] [CrossRef]
- Vivanco, J.; Aiyangar, A.; Araneda, A.; Ploeg, H.-L. Mechanical characterization of injection-molded macro porous bioceramic bone scaffolds. J. Mech. Behav. Biomed. Mater. 2012, 9, 137–152. [Google Scholar] [CrossRef] [PubMed]
- Eom, J.-H.; Kim, Y.-W.; Park, C.B.; Wang, C. Effect of forming methods on porosity and compressive strength of polysiloxane-derived porous silicon carbide ceramics. J. Ceram. Soc. Jpn. 2012, 120, 199–203. [Google Scholar] [CrossRef][Green Version]
- Barbosa, A.P.C.; Bram, M.; Stöver, D.; Buchkremer, H.P. Realization of a Titanium Spinal Implant with a Gradient in Porosity by 2-Component-Metal Injection Moulding. Adv. Eng. Mater. 2013, 15, 510–521. [Google Scholar] [CrossRef]
- Chen, L.-J.; Li, T.; Li, Y.-M.; He, H.; Hu, Y.-H. Porous titanium implants fabricated by metal injection molding. Trans. Nonferrous Metal. Soc. 2009, 19, 1174–1179. [Google Scholar] [CrossRef]
- Gülsoy, H.Ö.; German, R.M. Production of micro-porous austenitic stainless steel by powder injection molding. Scr. Mater. 2008, 58, 295–298. [Google Scholar] [CrossRef]
- Studart, A.R.; Gonzenbach, U.T.; Tervoort, E.; Gauckler, L.J. Processing Routes to Macroporous Ceramics: A Review. J. Am. Ceram. Soc. 2006, 89, 1771–1789. [Google Scholar] [CrossRef]
- Biggemann, J.; Diepold, B.; Pezoldt, M.; Stumpf, M.; Greil, P.; Fey, T. Automated 3D assembly of periodic alumina-epoxy composite structures. J. Am. Ceram. Soc. 2018, 101, 3864–3873. [Google Scholar] [CrossRef]
- European Committee for Standardization. Advanced Technical Ceramics; Monolithic Ceramics; General and Textural Properties; Part 2: Determination of Density and Porosity, German version EN 623-2:1993; Beuth Verlag GmbH: Berlin, Germany, 1993. [Google Scholar]
- E28 Committee. Test Method for Dynamic Youngs Modulus, Shear Modulus, and Poissons Ratio by Impulse Excitation of Vibration; ASTM International: West Conshohocken, PA, USA, 2015. [Google Scholar]
- European Committee for Standardization. Advanced Technical Ceramics—Mechanical Properties of Monolithic Ceramics at Room Temperature—Part 2: Determination of Young’s Modulus, Shear Modulus and Poisson’s Ratio; German Version EN 843-2:2006; Beuth Verlag GmbH: Berlin, Germany, 2007. [Google Scholar]
- European Committee for Standardization. Advanced Technical Ceramics—Mechanical Properties of Monolithic Ceramics at Room Temperature—Part 1: Determination of Flexural Strength; German Version EN 843-1:2006; Beuth Verlag GmbH: Berlin, Germany, 2008. [Google Scholar]
- Hench, L.L. An Introduction to Bioceramics, 2nd ed.; Imperial College Press: London, UK, 2013; ISBN 978-1-908977-15-1. [Google Scholar]
- Jones, J.R.; Hench, L.L. Regeneration of trabecular bone using porous ceramics. Curr. Opin. Solid State Mater. Sci. 2003, 7, 301–307. [Google Scholar] [CrossRef]
- Ziff, R.M.; Torquato, S. Percolation of disordered jammed sphere packings. J. Phys. A Math. Theor. 2017, 50, 85001. [Google Scholar] [CrossRef]
- Xu, W.; Jiao, Y. Theoretical framework for percolation threshold, tortuosity and transport properties of porous materials containing 3D non-spherical pores. Int. J. Eng. Sci. 2019, 134, 31–46. [Google Scholar] [CrossRef]
- Xu, W.; Jia, M.; Gong, Z. Thermal conductivity and tortuosity of porous composites considering percolation of porous network: From spherical to polyhedral pores. Compos. Sci. Technol. 2018, 167, 134–140. [Google Scholar] [CrossRef]
- Jing, X.; Zhao, W.; Lan, L. The effect of particle size on electric conducting percolation threshold in polymer/conducting particle composites. J. Mater. Sci. Lett. 2000, 19, 377–379. [Google Scholar] [CrossRef]
- Scher, H.; Zallen, R. Critical Density in Percolation Processes. J. Chem. Phys. 1970, 53, 3759–3761. [Google Scholar] [CrossRef]
- Erk, K.A.; Dunand, D.C.; Shull, K.R. Titanium with controllable pore fractions by thermoreversible gelcasting of TiH2. Acta Mater. 2008, 56, 5147–5157. [Google Scholar] [CrossRef]
- Liu, Z.; Li, Y.; Kowk, K. Mean interparticle distances between hard particles in one to three dimensions. Polymer 2001, 42, 2701–2706. [Google Scholar] [CrossRef]
- Phani, K.K.; Niyogi, S.K. Young’s modulus of porous brittle solids. J. Mater. Sci. 1987, 22, 257–263. [Google Scholar] [CrossRef]
- Spriggs, R.M. Expression for Effect of Porosity on Elastic Modulus of Polycrystalline Refractory Materials, Particularly Aluminum Oxide. J. Am. Ceram. Soc. 1961, 44, 628–629. [Google Scholar] [CrossRef]
- Orlovskii, V.P.; Komlev, V.S.; Barinov, S.M. Hydroxyapatite and Hydroxyapatite-Based Ceramics. Inorg. Mater. 2002, 38, 973–984. [Google Scholar] [CrossRef]
- He, L.-H.; Standard, O.C.; Huang, T.T.Y.; Latella, B.A.; Swain, M.V. Mechanical behaviour of porous hydroxyapatite. Acta Biomater. 2008, 4, 577–586. [Google Scholar] [CrossRef]
- Akao, M.; Aoki, H.; Kato, K. Mechanical properties of sintered hydroxyapatite for prosthetic applications. J. Mater. Sci. 1981, 16, 809–812. [Google Scholar] [CrossRef]
- Pabst, W.; Gregorová, E. Young’s modulus of isotropic porous materials with spheroidal pores. J. Eur. Ceram. Soc. 2014, 34, 3195–3207. [Google Scholar] [CrossRef]
- Andersson, C.A. Derivation of the Exponential Relation for the Effect of Ellipsoidal Porosity on Elastic Modulus. J. Am. Ceram. Soc. 1996, 79, 2181–2184. [Google Scholar] [CrossRef]
- Ridzwan, M.; Shuib, S.; Hassan, A.Y.; Shokri, A.A.; Ibrahim, M. Problem of Stress Shielding and Improvement to the Hip Implant Designs: A Review. J. Med. Sci. 2007, 7, 460–467. [Google Scholar] [CrossRef]
- Clarke, D.R. Interpenetrating Phase Composites. J. Am. Ceram. Soc. 1992, 75, 739–758. [Google Scholar] [CrossRef]
- Feng, X.-Q.; Mai, Y.-W.; Qin, Q.-H. A micromechanical model for interpenetrating multiphase composites. Comput. Mater. Sci. 2003, 28, 486–493. [Google Scholar] [CrossRef]
- O’Brien, D.J.; Parquette, B. Polymer toughness transfer in a transparent interpenetrating glass–polymer composite. Compos. Sci. Technol. 2012, 73, 57–63. [Google Scholar] [CrossRef]
- Franco Steier, V.; Koplin, C.; Kailer, A. Influence of pressure-assisted polymerization on the microstructure and strength of polymer-infiltrated ceramics. J. Mater. Sci. 2013, 48, 3239–3247. [Google Scholar] [CrossRef]
- Chung, C.-M.; Kim, J.-G.; Kim, M.-S.; Kim, K.-M.; Kim, K.-N. Development of a new photocurable composite resin with reduced curing shrinkage. Dent. Mater. 2002, 18, 174–178. [Google Scholar] [CrossRef]
- Coldea, A.; Swain, M.V.; Thiel, N. Mechanical properties of polymer-infiltrated-ceramic-network materials. Dent. Mater. 2013, 29, 419–426. [Google Scholar] [CrossRef]
- Li, W.; Sun, J. Effects of Ceramic Density and Sintering Temperature on the Mechanical Properties of a Novel Polymer-Infiltrated Ceramic-Network Zirconia Dental Restorative (Filling) Material. Med. Sci. Monit. 2018, 24, 3068–3076. [Google Scholar] [CrossRef] [PubMed]
- Sutera, S.P.; Skalak, R. The History of Poiseuille’s Law. Ann. Rev. Fluid Mech. 1993, 25, 1–20. [Google Scholar] [CrossRef]
- Reuss, A. Berechnung der Fließgrenze von Mischkristallen auf Grund der Plastizitätsbedingung für Einkristalle. ZAMM J. Appl. Math. Mech. 1929, 9, 49–58. [Google Scholar] [CrossRef]
- Voigt, W. Ueber die Beziehung zwischen den beiden Elasticitätsconstanten isotroper Körper. Ann. Phys. 1889, 274, 573–587. [Google Scholar] [CrossRef]
- Huang, L.J.; Geng, L.; Peng, H.-X. Microstructurally inhomogeneous composites: Is a homogeneous reinforcement distribution optimal? Prog. Mater. Sci. 2015, 71, 93–168. [Google Scholar] [CrossRef]
- Hashin, Z.; Shtrikman, S. A variational approach to the theory of the elastic behaviour of multiphase materials. J. Mech. Phys. Solids 1963, 11, 127–140. [Google Scholar] [CrossRef]
- Evans, A.G. Perspective on the Development of High-Toughness Ceramics. J. Am. Ceram. Soc. 1990, 73, 187–206. [Google Scholar] [CrossRef]
- Dunlop, J.W.; Fratzl, P. Biological Composites. Ann. Rev. Mater. Res. 2010, 40, 1–24. [Google Scholar] [CrossRef]
- Suchanek, W.; Yoshimura, M. Processing and properties of hydroxyapatite-based biomaterials for use as hard tissue replacement implants. J. Mater. Res. 1998, 13, 94–117. [Google Scholar] [CrossRef]
- Imbeni, V.; Kruzic, J.J.; Marshall, G.W.; Marshall, S.J.; Ritchie, R.O. The dentin-enamel junction and the fracture of human teeth. Nat. Mater. 2005, 4, 229–232. [Google Scholar] [CrossRef]
- Di Luca, A.; Ostrowska, B.; Lorenzo-Moldero, I.; Lepedda, A.; Swieszkowski, W.; van Blitterswijk, C.; Moroni, L. Gradients in pore size enhance the osteogenic differentiation of human mesenchymal stromal cells in three-dimensional scaffolds. Sci. Rep. 2016, 6, 22898. [Google Scholar] [CrossRef] [PubMed]
- Miao, X.; Sun, D. Graded/Gradient Porous Biomaterials. Materials 2010, 3, 26–47. [Google Scholar] [CrossRef]
- Werner, J.; Linner-Krčmar, B.; Friess, W.; Greil, P. Mechanical properties and in vitro cell compatibility of hydroxyapatite ceramics with graded pore structure. Biomaterials 2002, 23, 4285–4294. [Google Scholar] [CrossRef]

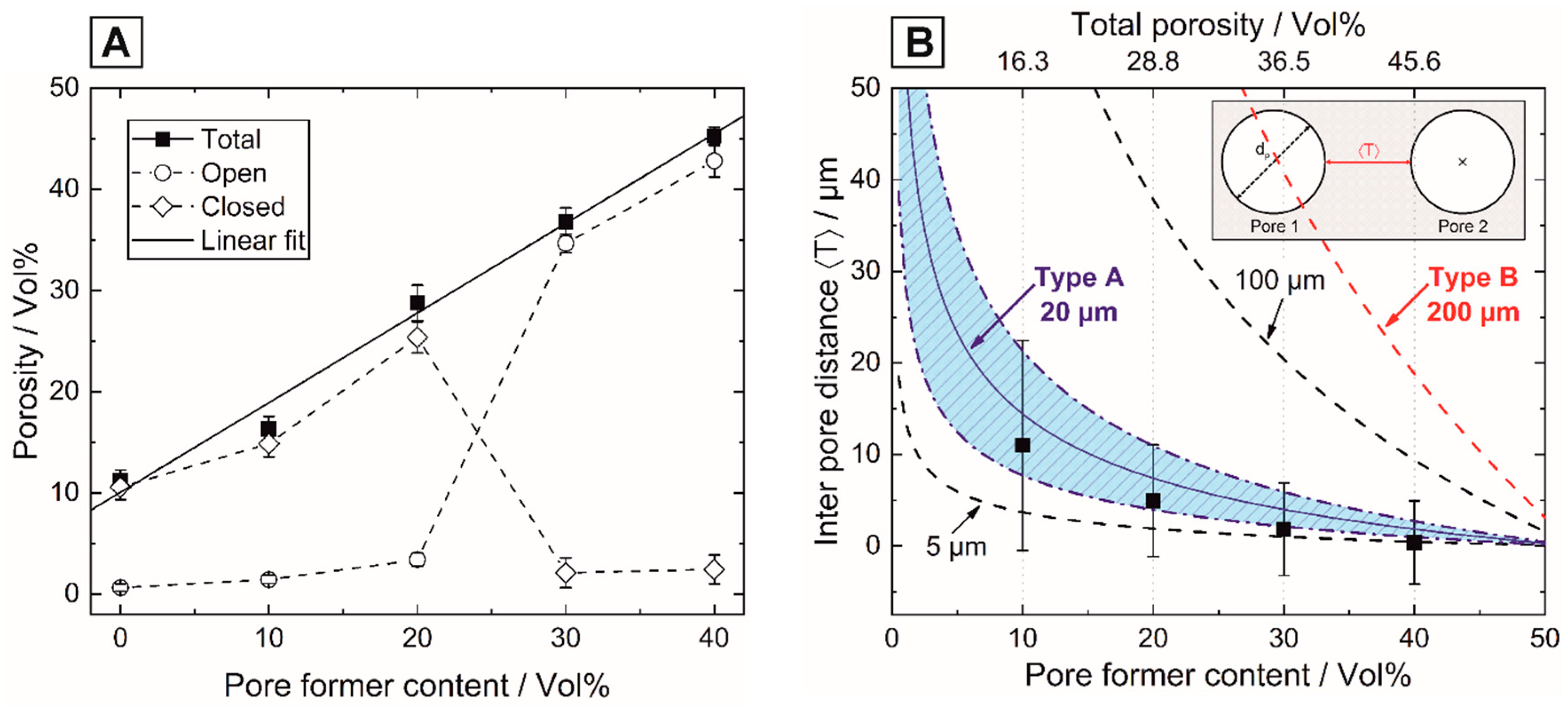
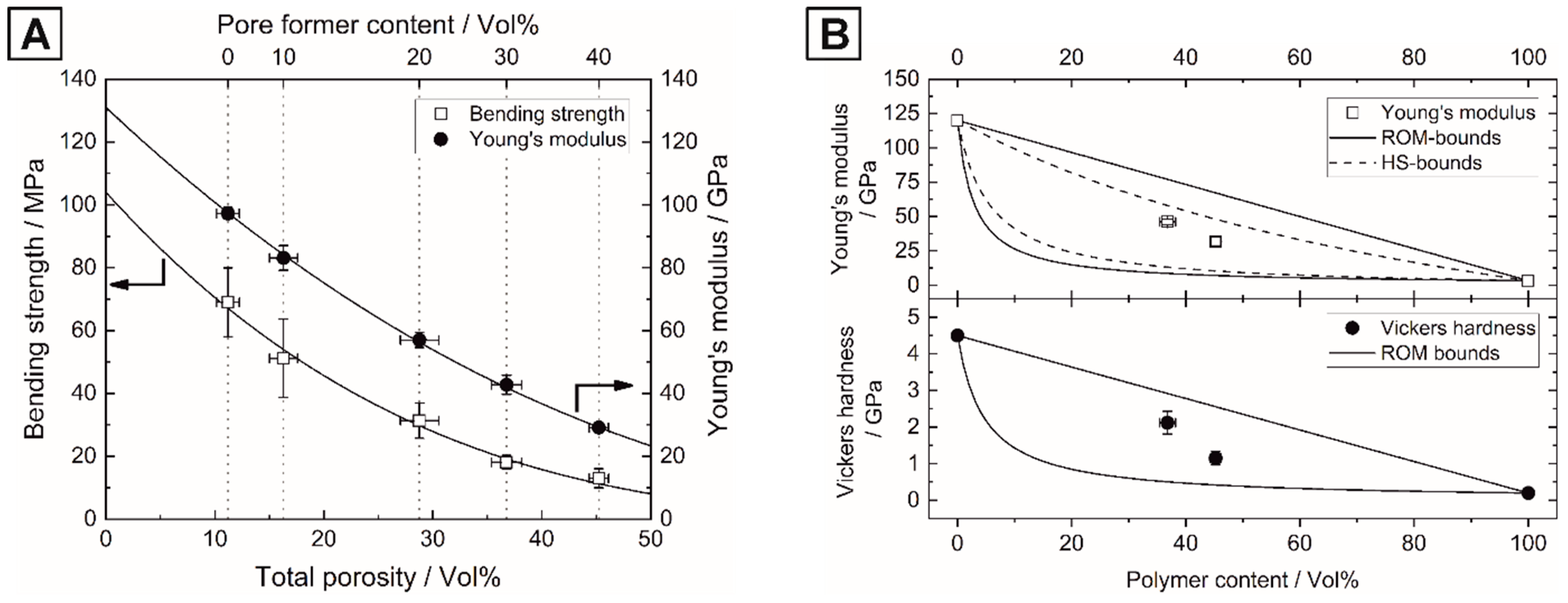
| Pore Former Content /Vol% | Open /Vol% | Porosity (Φp) Closed /Vol% | Total /Vol% | Interpore Distance 〈T〉 /µm | Young’s Modulus (E) /GPa | Flexural Strength (σf) /MPa |
|---|---|---|---|---|---|---|
| 0 | 0.6 ± 0.4 | 10.6 ± 1.2 | 11.2 ± 1.0 | - | 97.3 ± 1.9 | 69.0 ± 10.9 |
| 10 | 1.4 ± 0.4 | 14.9 ± 1.3 | 16.3 ± 1.3 | 11 | 83.1 ± 3.9 | 51.1 ± 12.5 |
| 20 | 3.4 ± 0.7 | 25.4 ± 1.5 | 28.8 ± 1.7 | 4.9 | 57.0 ± 2.5 | 31.4 ± 5.6 |
| 30 | 34.7 ± 0.9 | 2.1 ± 1.5 | 36.8 ± 1.4 | 1.8 | 42.8 ± 3.1 | 18.1 ± 2.3 |
| 40 | 42.8 ± 1.6 | 2.4 ± 1.4 | 45.2 ± 0.9 | 0.4 | 29.1 ± 0.9 | 13.0 ± 3.0 |
| Samples | Preform Porosity | Geometric Density | Theoretical Density | Vickers Hardness | Young’s Modulus | Flexural Strength |
|---|---|---|---|---|---|---|
| /Vol% | /g·cm−3 | /% | HV1/GPa | /GPa | /MPa | |
| Pure HAp | - | 2.81 ± 0.05 | 88.8 | 4.5* | 131** | 104** |
| 30 Vol% Inf. | 36.8 ± 1.4 | 2.29 ± 0.05 | 97.6 | 2.12 ± 0.31 | 46.1 ± 2.1 | 29.6 ± 5.5 |
| 40 Vol% Inf. | 45.2 ± 0.9 | 2.10 ± 0.04 | 94.9 | 1.15 ± 0.18 | 31.8 ± 3.3 | 19.7 ± 3.9 |
| Pure UDMA/TEGDMA | - | 1.20 ± 0.01 | - | 0.2 ± 0.04 | 3.9 ± 0.3 | 97.3 ± 21.4 |
| Monolithic Ceramic | Material | Porosity | Young’s Modulus | Vickers Hardness | Flexural Strength | Reference |
|---|---|---|---|---|---|---|
| /Vol% | /GPa | /GPa | /MPa | |||
| Bone restoration | Cortical Bone | 5–10 | 7–30 | - | 50–150 | [8,43,74] |
| Trabecular bone | 75–95 | 0.05–0.5 | - | 10–20 | [43,74] | |
| Porous HAp | 11.2–45.2 | 29–97 | - | 13–69 | This work | |
| PICN | Material | Polymer Content | Young’s Modulus | Vickers Hardness | Flexural Strength | Reference |
| /Vol% | /GPa | /GPa | /MPa | |||
| Dental restoration | Enamel | - | 48–105 | 3–5.3 | 76 | [74,75] |
| Dentin | - | 11–20.3 | 0.5–1.0 | 245–268 | [74,75] | |
| HAp/UDMA*,a | 37–45 | 32–46 | 1.2–2.1 | 20–30 | This work | |
| Feldspar/UDMA**,a | 28–41 | 16–28 | 1.1–2.1 | 131–160 | [65] | |
| ZrO2/UDMA**,a | 8–42 | 15–101 | 0.4–10.8 | 58–212 | [66] |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Biggemann, J.; Hoffmann, P.; Hristov, I.; Simon, S.; Müller, P.; Fey, T. Injection Molding of 3-3 Hydroxyapatite Composites. Materials 2020, 13, 1907. https://doi.org/10.3390/ma13081907
Biggemann J, Hoffmann P, Hristov I, Simon S, Müller P, Fey T. Injection Molding of 3-3 Hydroxyapatite Composites. Materials. 2020; 13(8):1907. https://doi.org/10.3390/ma13081907
Chicago/Turabian StyleBiggemann, Jonas, Patrizia Hoffmann, Ivaylo Hristov, Swantje Simon, Philipp Müller, and Tobias Fey. 2020. "Injection Molding of 3-3 Hydroxyapatite Composites" Materials 13, no. 8: 1907. https://doi.org/10.3390/ma13081907
APA StyleBiggemann, J., Hoffmann, P., Hristov, I., Simon, S., Müller, P., & Fey, T. (2020). Injection Molding of 3-3 Hydroxyapatite Composites. Materials, 13(8), 1907. https://doi.org/10.3390/ma13081907






