An RVE-Based Study of the Effect of Martensite Banding on Damage Evolution in Dual Phase Steels
Abstract
1. Introduction
2. Constitutive Model
2.1. Crystal Plasticity
2.1.1. Kinematics
2.1.2. Flow Rule
2.1.3. Hardening Rule
2.2. Geometrically Necessary Dislocations (GND) Density: Strain Gradient Enhancement
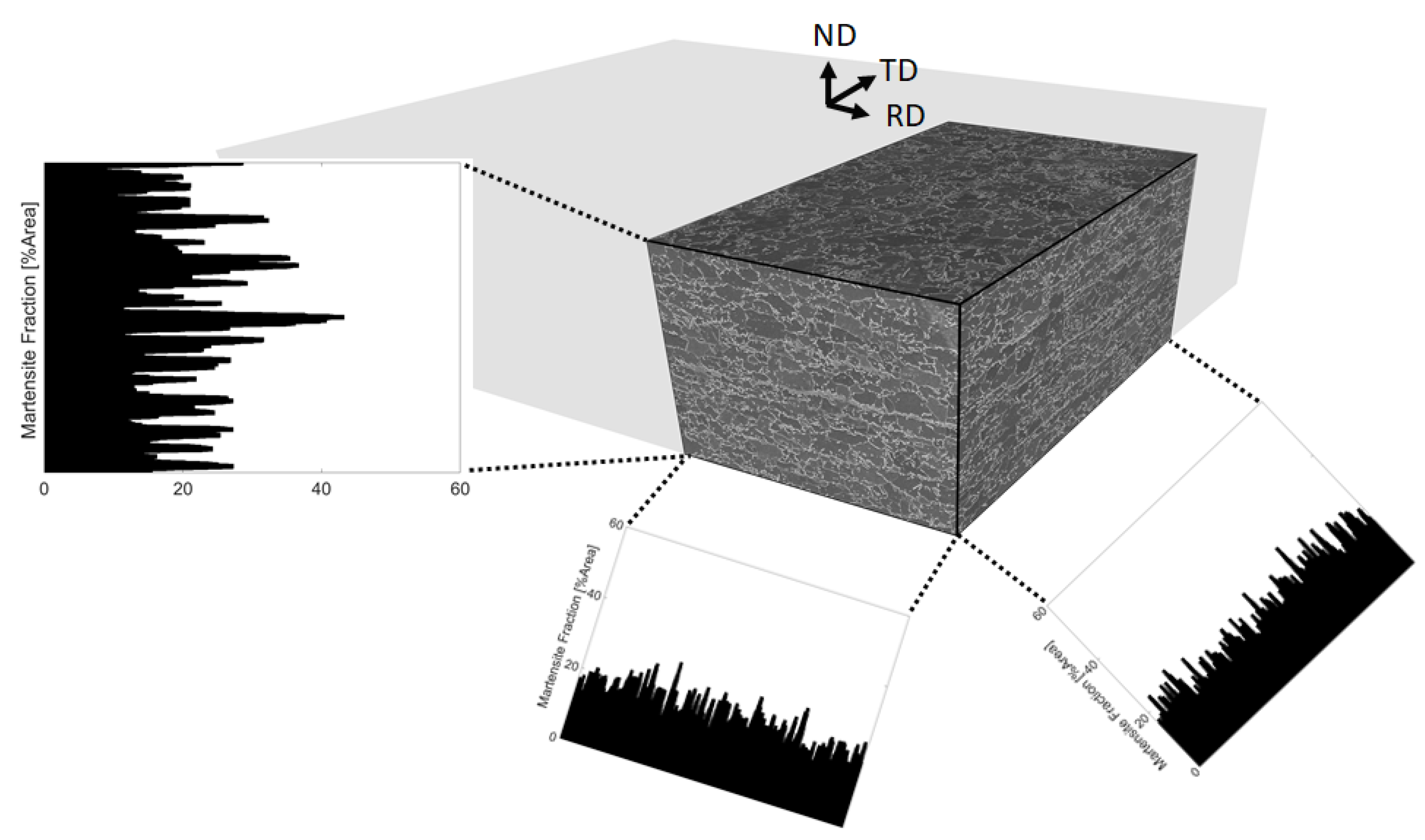
3. Microstructure
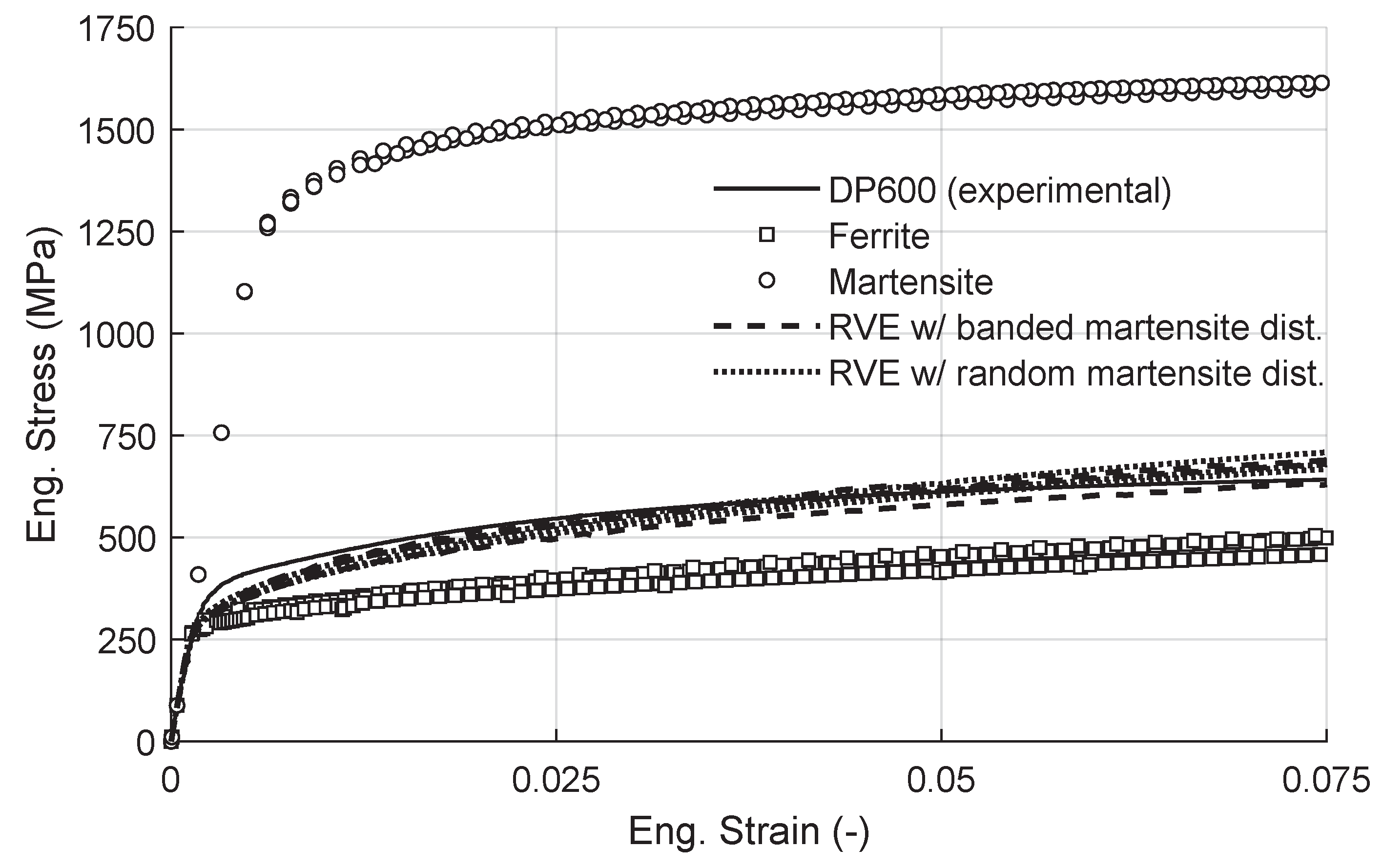
Parameter Identification
4. Results and Discussion
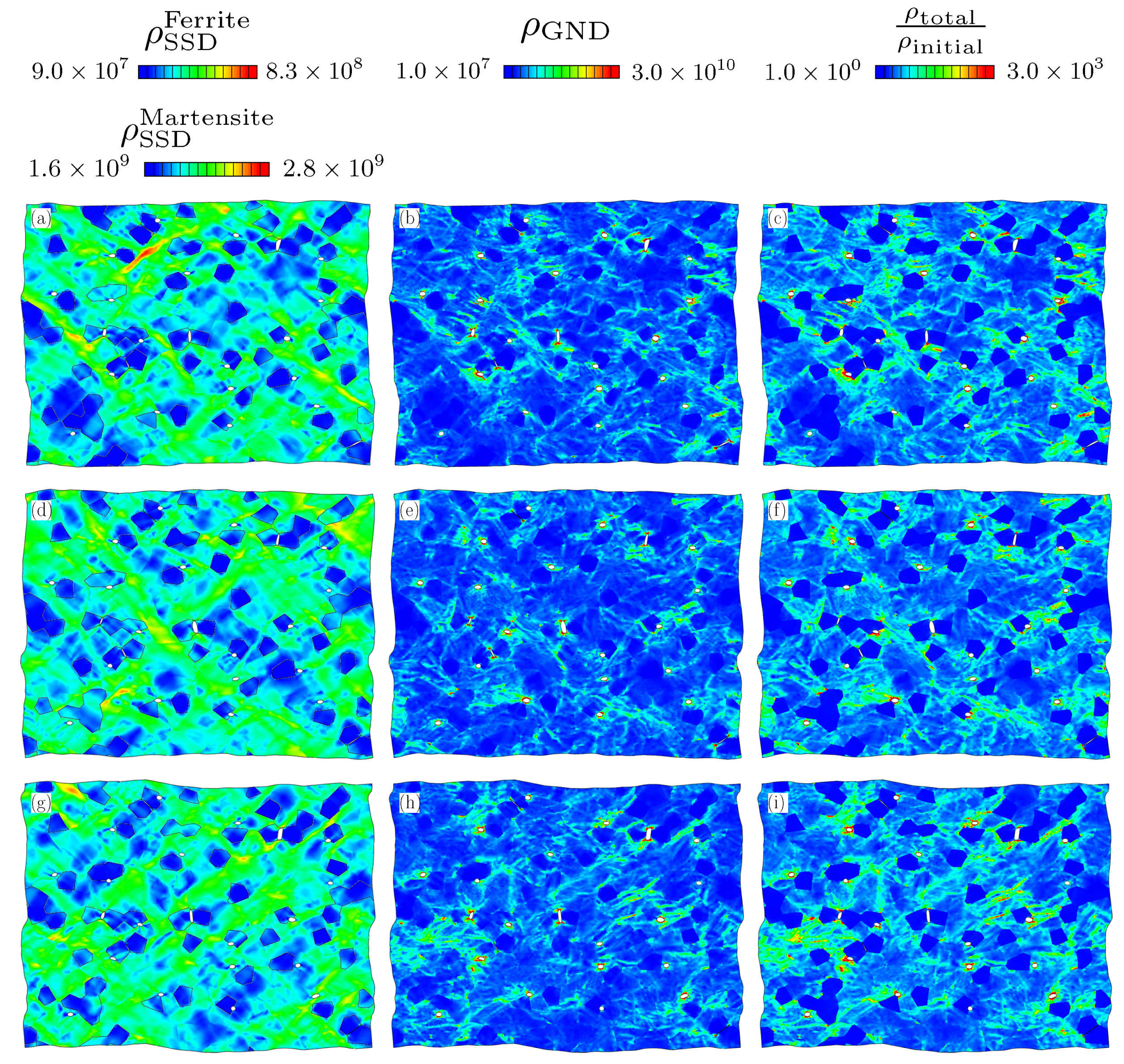
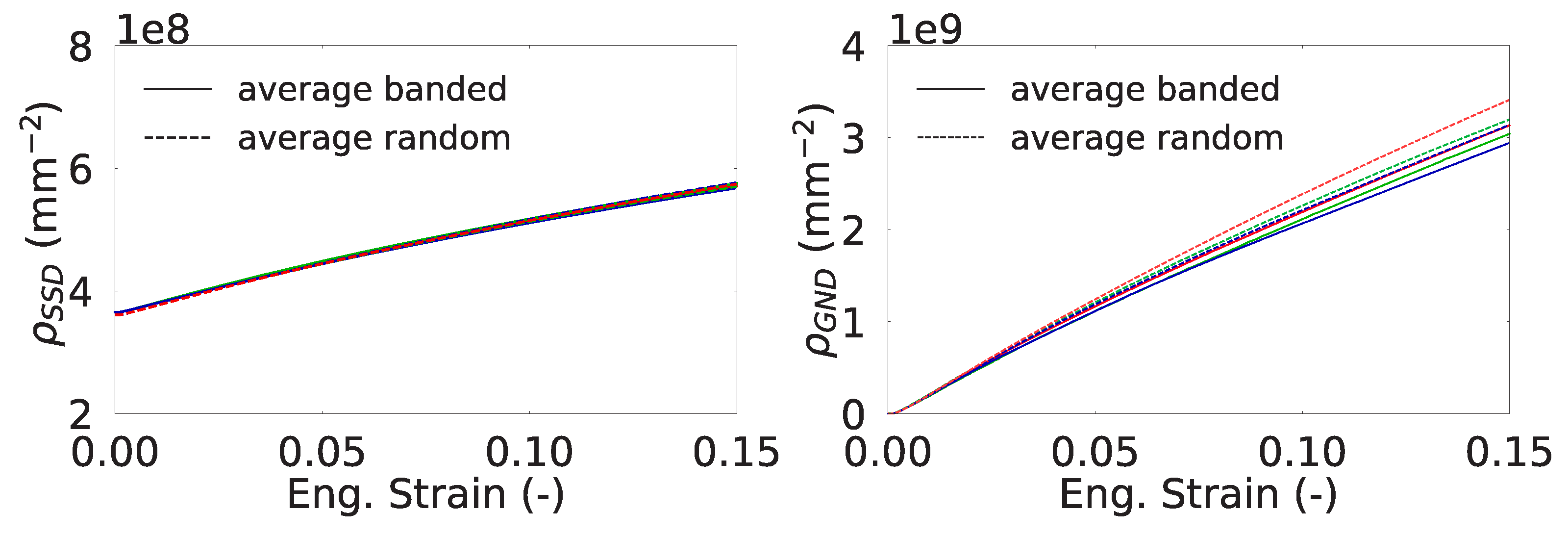
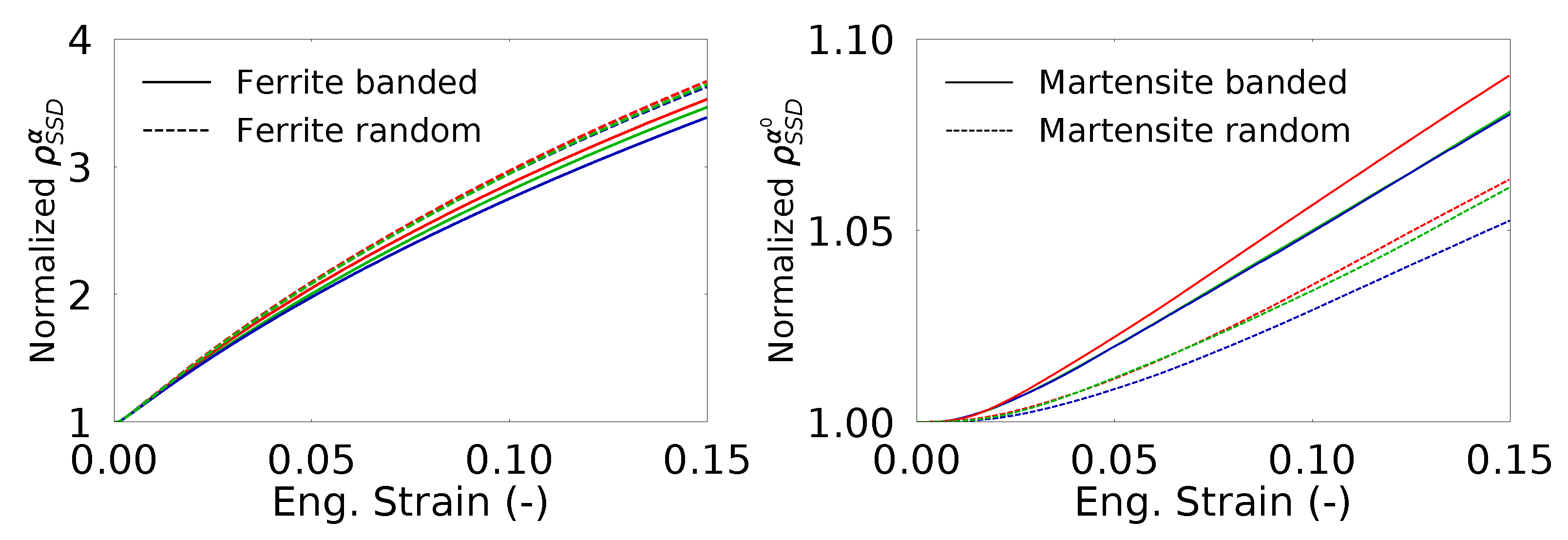
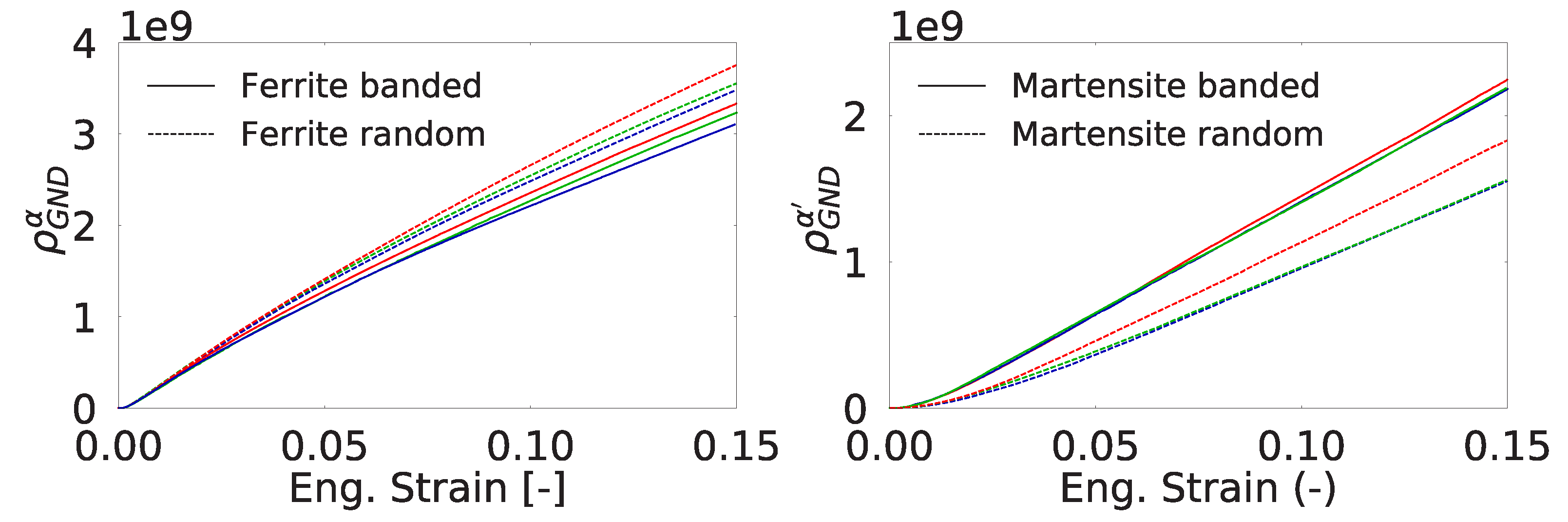
4.1. Evolution of Dislocation Densities
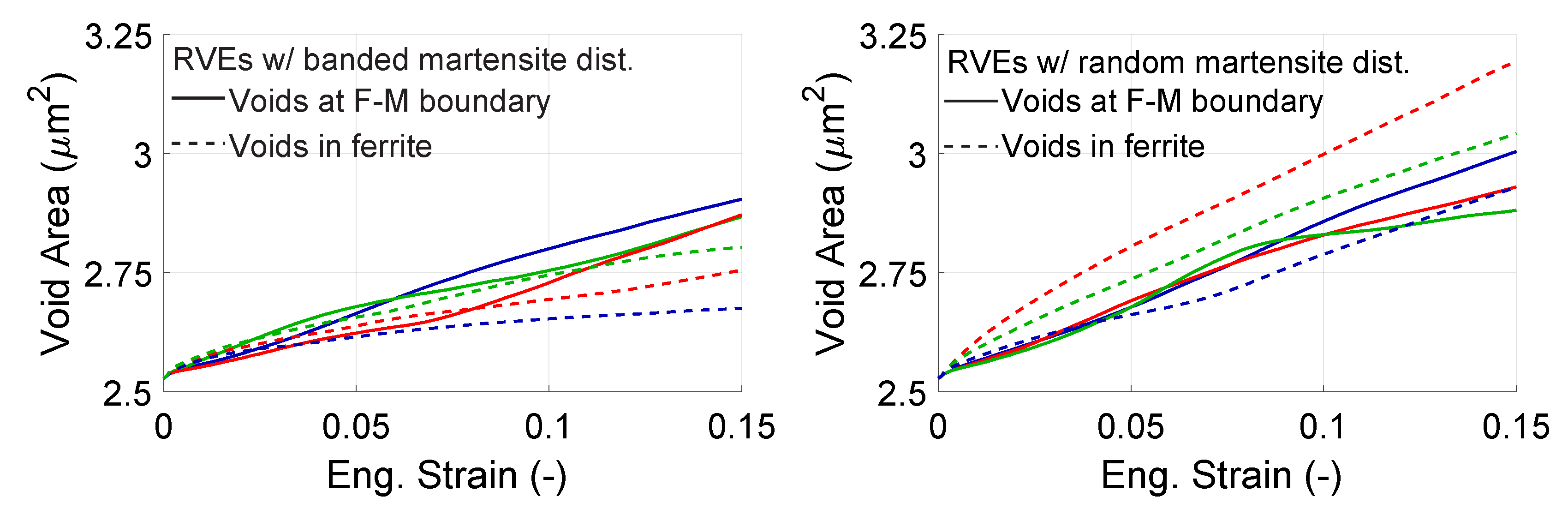
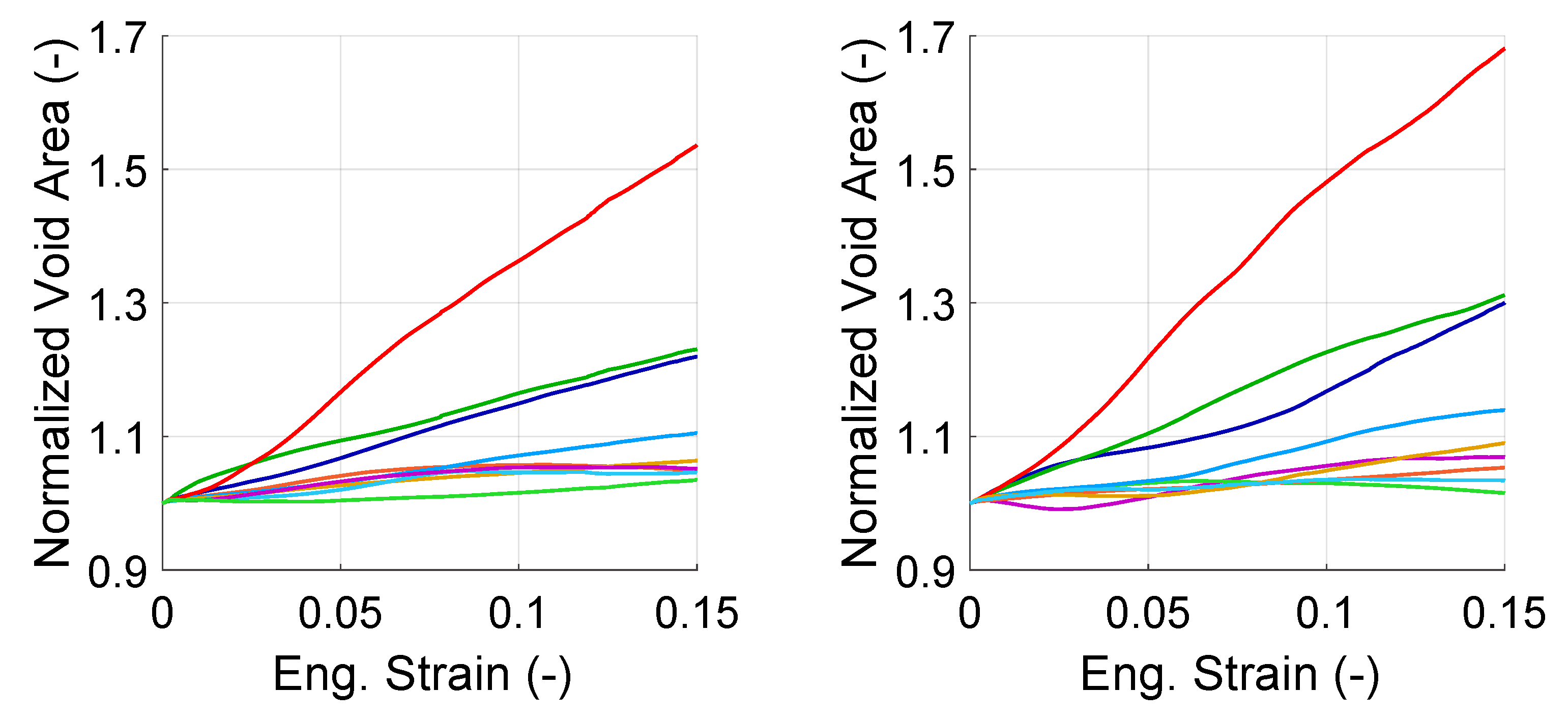
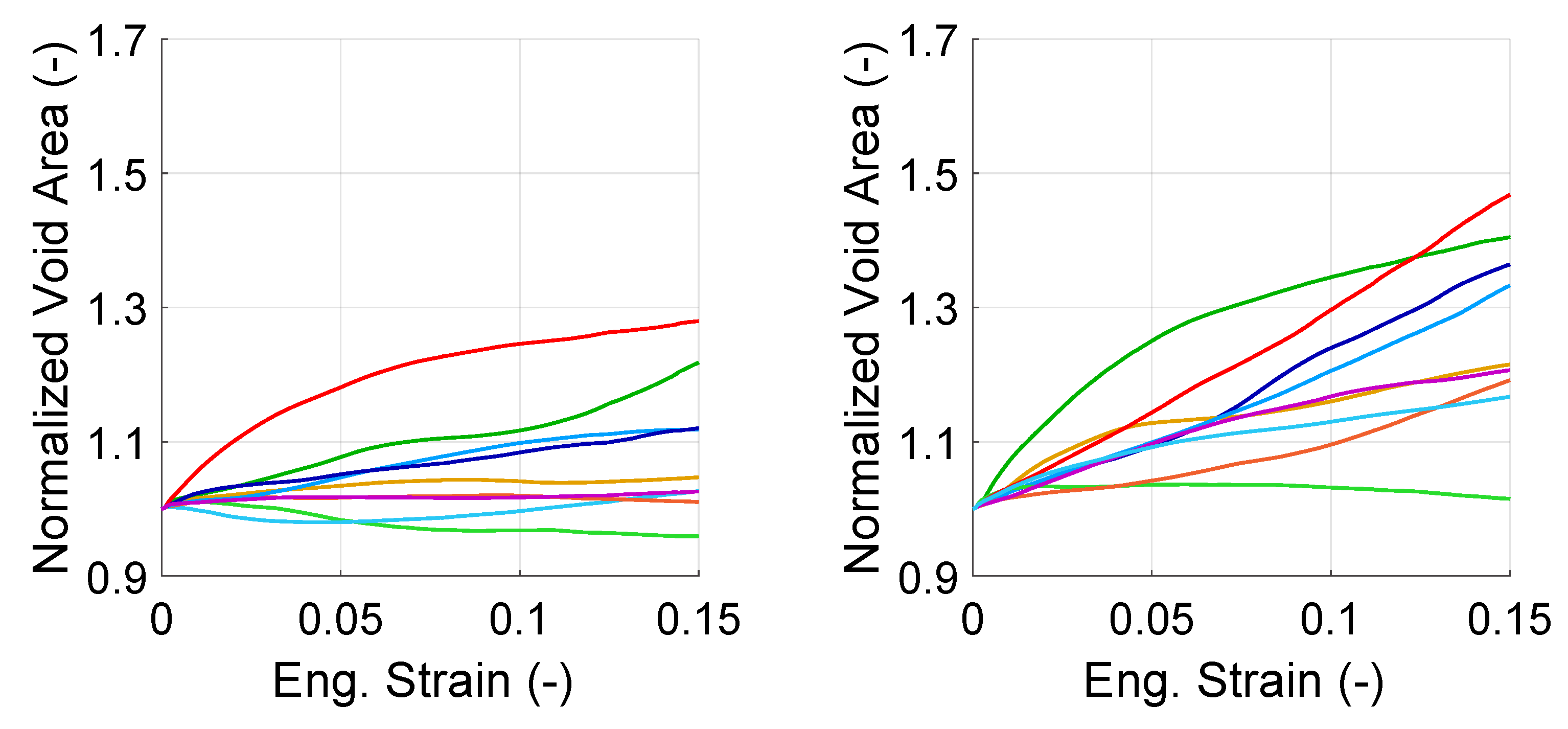
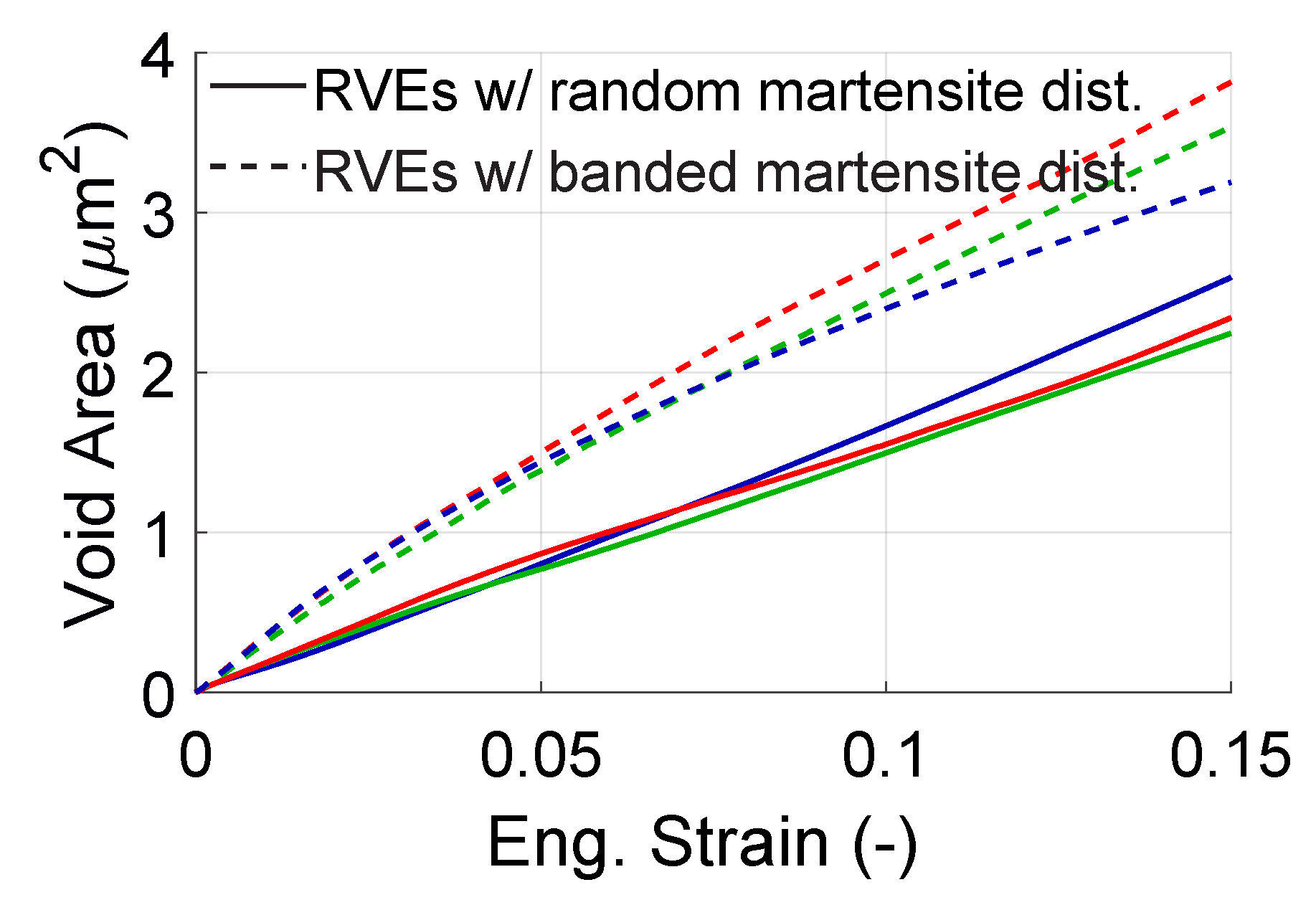
4.2. Evolution of Voids
4.3. Evolution of Voids Formed by Cracking of Martensite
5. Summary and Conclusions
- The morphology of the martensite phase in dual phase steels has a direct effect on the stress and plastic strain distribution among the phases.
- The size of the observed shear bands is strongly influenced by the average spacing between martensite islands.
- An accurate prediction of the local stress state is necessary to capture the evolution of individual voids.
- The heterogeneity of the plastic strain within an RVE results in significant GND densities which can be captured using a gradient enhanced crystal plasticity model.
- Local stress state around a void varies significantly from the applied average stress state and it evolves considerably during deformation.
- The change of stress state around a void during large plastic deformation may lead to closure of the void.
- Voids that are formed by cracking of martensite exhibit the highest growth rates, thus they are considered as the most severe damage mechanism.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| b | Burgers vector length. |
| BCC | Body Centered Cubic crystal structure. |
| Elasticity tensor. | |
| Elastic rate of deformation between the lattice and the deformed configurations, defined in the deformed configuration. | |
| Inelastic rate of deformation between the reference and lattice configurations, defined in the deformed configuration. | |
| Rate of deformation that is the symmetric part of the velocity gradient and a measure of the rate of strain between the reference and the deformed configurations, defined in the deformed configuration. | |
| Deformation gradient that describes elastic stretching and lattice rotation of the plastically deformed material point at an intermediate configuration (#). | |
| Deformation gradient that takes a line element of the material from an undeformed, reference configuration to in the final deformed configuration as . | |
| Deformation gradient that describes the inelastic deformation caused by glide of dislocations and takes a line element from the reference configuration to an intermediate (lattice) configuration. | |
| FCC | Face Centered Cubic crystal structure. |
| Shear rate on slip system . | |
| Phenomenological constant that controls the rate of saturation of the Statistically Stored Dislocation density. | |
| Burgers tensor. | |
| Plastically convected rate of the Burgers tensor. | |
| GND | Geometrically Necessary Dislocations. |
| Velocity gradient that gives the gradient of the velocity field (between the lattice and deformed configuration) at the final deformed configuration. | |
| Velocity gradient that gives the gradient of the velocity field (between the reference and lattice configuration) at the final deformed configuration. | |
| Velocity gradient that gives the gradient of the velocity field (between the reference and deformed configuration) at the final deformed configuration. | |
| A lattice vector that is orthogonal to both and . | |
| Slip plane normal vector on slip system given at the deformed configuration. | |
| Normal to the non-glide plane on slip system observed in BCC crystals. | |
| Slip plane normal vector on slip system given at the reference configuration. | |
| Shear modulus. | |
| Gradient operator in the reference configuration. | |
| Gradient operator in the lattice configuration. | |
| Contribution of non-Schmid effects seen in BCC crystals to the total Schmid tensor. | |
| Schmid tensor on slip system , i.e., | |
| Flow criterion for slip system . | |
| Physically based interaction matrix relating the hardening of slip system to the dislocation density on slip system . | |
| Scalar distance between the points used in the computation of shear gradients. | |
| Rotation resulting from the elastic deformation between the lattice and the deformed configuration as well as rigid rotation. | |
| Total rotation of a line element of the material from the reference configuration to the deformed configuration, calculated using Polar Decomposition. | |
| Position vector that is used for the computation shear rate gradients. | |
| Density of Geometrically Necessary Dislocations on slip system . | |
| Density of Statistically Stored Dislocations on slip system . | |
| Total dislocation density of the slip system . | |
| Phenomenological constant that controls the saturation level of Statistically Stored Dislocation density. | |
| Cauchy stress, defined in the deformed configuration. | |
| Slip direction vector on slip system given at the deformed configuration. | |
| Slip direction vector on slip system given at the reference configuration. | |
| An objective rate of the Cauchy stress tensor, in Abaqus/Standard it is updated using the corotational formulation. | |
| SSD | Statistically Stored Dislocations. |
| Resolved shear stress on slip system . | |
| Critical resolved shear stress on slip system . | |
| Strain independent lattice friction. | |
| Spin resulting from the elastic deformation between the lattice and the deformed configurations and rigid rotation, defined in the deformed configuration. | |
| Spin resulting from the inelastic deformation between the reference and lattice configurations, defined in the deformed configuration. | |
| Spin tensor that is the skew-symmetric part of the velocity gradient and a measure of the rate of rotation between the reference and the deformed configurations, defined in the deformed configuration. | |
| Numerically calculated gradient of the shear rates. |
Appendix A. Large Deformation Implementation of Crystal Plasticity
Appendix B. Large Deformation Implementation of Strain Gradient Enhancement
References
- Besson, J. Continuum models of ductile fracture: A review. Int. J. Damage Mech. 2010, 19, 3–52. [Google Scholar] [CrossRef]
- Garrison, W.; Moody, N. Ductile fracture. J. Phys. Chem. Solids 1987, 48, 1035–1074. [Google Scholar] [CrossRef]
- Stone, R.V.; Cox, T.; Low, J.; Psioda, J. Microstructural aspects of fracture by dimpled rupture. Int. Met. Rev. 1985, 30, 157–180. [Google Scholar] [CrossRef]
- Su, Y.; Gurland, J. Strain partition, uniform elongation and fracture strain in dual-phase steels. Mater. Sci. Eng. 1987, 95, 151–165. [Google Scholar] [CrossRef]
- Avramovic-Cingara, G.; Ososkov, Y.; Jain, M.; Wilkinson, D. Effect of martensite distribution on damage behaviour in DP600 dual phase steels. Mater. Sci. Eng. A 2009, 516, 7–16. [Google Scholar] [CrossRef]
- Calcagnotto, M.; Adachi, Y.; Ponge, D.; Raabe, D. Deformation and fracture mechanisms in fine- and ultrafine-grained ferrite/martensite dual-phase steels and the effect of aging. Acta Mater. 2011, 59, 658–670. [Google Scholar] [CrossRef]
- Ghadbeigi, H.; Pinna, C.; Celotto, S. Failure mechanisms in DP600 steel: Initiation, evolution and fracture. Mater. Sci. Eng. A 2013, 588, 420–431. [Google Scholar] [CrossRef]
- Kadkhodapour, J.; Butz, A.; Rad, S.Z. Mechanisms of void formation during tensile testing in a commercial, dual-phase steel. Acta Mater. 2011, 59, 2575–2588. [Google Scholar] [CrossRef]
- Aşık, E.; Perdahcıoğlu, E.; van den Boogaard, A. Microscopic investigation of damage mechanisms and anisotropic evolution of damage in DP600. Mater. Sci. Eng. A 2019, 739, 348–356. [Google Scholar] [CrossRef]
- Tasan, C.; Diehl, M.; Yan, D.; Bechtold, M.; Roters, F.; Schemmann, L.; Zheng, C.; Peranio, N.; Ponge, D.; Koyama, M.; et al. An Overview of Dual-Phase Steels: Advances in Microstructure-Oriented Processing and Micromechanically Guided Design. Annu. Rev. Mater. Res. 2015, 45, 391–431. [Google Scholar] [CrossRef]
- McClintock, F. A criterion for ductile fracture by the growth of holes. J. Appl. Mech. 1968, 35, 363–371. [Google Scholar] [CrossRef]
- Rice, J.R.; Tracey, D.M. On the ductile enlargement of voids in triaxial stress fields. J. Mech. Phys. Solids 1969, 17, 201–217. [Google Scholar] [CrossRef]
- Gurson, A. Continuum Theory of Ductile Rupture by Void Nucleation and Growth: Part I—Yield Criteria and Flow Rules for Porous Ductile Media. J. Eng. Mater. Technol. 1977, 99, 2–15. [Google Scholar] [CrossRef]
- Koplik, J.; Needleman, A. Void growth and coalescence in porous plastic solids. Int. J. Solids Struct. 1988, 24, 835–853. [Google Scholar] [CrossRef]
- Monchiet, V.; Cazacu, O.; Charkaluk, E.; Kondo, D. Macroscopic yield criteria for plastic anisotropic materials containing spheroidal voids. Int. J. Plast. 2008, 24, 1158–1189. [Google Scholar] [CrossRef]
- Schacht, T.; Untermann, N.; Steck, E. The influence of crystallographic orientation on the deformation behaviour of single crystals containing microvoids. Int. J. Plast. 2003, 19, 1605–1626. [Google Scholar] [CrossRef]
- O’regan, T.; Quinn, D.; Howe, M.; McHugh, P. Void growth simulations in single crystals. Comput. Mech. 1997, 20, 115–121. [Google Scholar] [CrossRef]
- Han, X.; Besson, J.; Forest, S.; Tanguy, B.; Bugat, S. A yield function for single crystals containing voids. Int. J. Solids Struct. 2013, 50, 2115–2131. [Google Scholar] [CrossRef]
- Yerra, S.; Tekog, C.; Scheyvaerts, F.; Delannay, L.; Van Houtte, P.; Pardoen, T. Void growth and coalescence in single crystals. Int. J. Solids Struct. 2010, 47, 1016–1029. [Google Scholar] [CrossRef]
- Lebensohn, R.A.; Escobedo, J.P.; Cerreta, E.K.; Dennis-Koller, D.; Bronkhorst, C.A.; Bingert, J.F. Modeling void growth in polycrystalline materials. Acta Mater. 2013, 61, 6918–6932. [Google Scholar] [CrossRef]
- Shu, J.Y. Scale-dependent deformation of porous single crystals. Int. J. Plast. 1998, 14, 1085–1107. [Google Scholar] [CrossRef]
- Ling, C.; Besson, J.; Forest, S.; Tanguy, B.; Latourte, F.; Bosso, E. An elastoviscoplastic model for porous single crystals at finite strains and its assessment based on unit cell simulations. Int. J. Plast. 2016, 84, 58–87. [Google Scholar] [CrossRef]
- Borg, U.; Niordson, C.F.; Kysar, J.W. Size effects on void growth in single crystals with distributed voids. Int. J. Plast. 2008, 24, 688–701. [Google Scholar] [CrossRef]
- Tvergaard, V.; Niordson, C. Nonlocal plasticity effects on interaction of different size voids. Int. J. Plast. 2004, 20, 107–120. [Google Scholar] [CrossRef]
- Segurado, J.; LLorca, J. Discrete dislocation dynamics analysis of the effect of lattice orientation on void growth in single crystals. Int. J. Plast. 2010, 26, 806–819. [Google Scholar] [CrossRef]
- Tang, T.; Kim, S.; Horstemeyer, M. Molecular dynamics simulations of void growth and coalescence in single crystal magnesium. Acta Mater. 2010, 58, 4742–4759. [Google Scholar] [CrossRef]
- Potirniche, G.; Horstemeyer, M.; Wagner, G.; Gullett, P. A molecular dynamics study of void growth and coalescence in single crystal nickel. Int. J. Plast. 2006, 22, 257–278. [Google Scholar] [CrossRef]
- Hoefnagels, J.P.M.; Tasan, C.C.; Maresca, F.; Peters, F.J.; Kouznetsova, V.G. Retardation of plastic instability via damage-enabled microstrain delocalization. J. Mater. Sci. 2015, 50, 6882–6897. [Google Scholar] [CrossRef]
- Grange, R.A. Effect of microstructural banding in steel. Metall. Trans. 1971, 2, 417–426. [Google Scholar] [CrossRef]
- Perdahcıoğlu, E.; Soyarslan, C.; Aşık, E.; van den Boogaard, T.; Bargmann, S. A class of rate-independent lower-order gradient plasticity theories: Implementation and application to disc torsion problem. Materials 2018, 11, 1425. [Google Scholar] [CrossRef]
- Soyarslan, C.; Perdahcıoğlu, E.; Aşık, E.; Van Den Boogaard, A.; Bargmann, S. Implementation and application of a gradient enhanced crystal plasticity model. In Proceedings of the ESAFORM conference, Dublin, Ireland, 26–28 April 2017; Volume 1896, p. 160008. [Google Scholar]
- Mandel, J. Généralisation de la théorie de plasticité de WT Koiter. Int. J. Solids Struct. 1965, 1, 273–295. [Google Scholar] [CrossRef]
- Rice, J.R. Inelastic constitutive relations for solids: An internal-variable theory and its application to metal plasticity. J. Mech. Phys. Solids 1971, 19, 433–455. [Google Scholar] [CrossRef]
- Miehe, C.; Schröder, J. A comparative study of stress update algorithms for rate-independent and rate-dependent crystal plasticity. Int. J. Numer. Methods Eng. 2001, 50, 273–298. [Google Scholar] [CrossRef]
- Abaqus Analysis User’s Manual; Version 6.12; Dassault Systèmes Simulia Corp.: Providence, RI, USA, 2012.
- Zecevic, M.; McCabe, R.J.; Knezevic, M. A new implementation of the spectral crystal plasticity framework in implicit finite elements. Mech. Mater. 2015, 84, 114–126. [Google Scholar] [CrossRef]
- Gröger, R.; Racherla, V.; Bassani, J.; Vitek, V. Multiscale modeling of plastic deformation of molybdenum and tungsten: II. Yield criterion for single crystals based on atomistic studies of glide of 1/2<111> screw dislocations. Acta Mater. 2008, 56, 5412–5425. [Google Scholar]
- Patra, A.; Zhu, T.; McDowell, D.L. Constitutive equations for modeling non-Schmid effects in single crystal bcc-Fe at low and ambient temperatures. Int. J. Plast. 2014, 59, 1–14. [Google Scholar] [CrossRef]
- Po, G.; Cui, Y.; Rivera, D.; Cereceda, D.; Swinburne, T.D.; Marian, J.; Ghoniem, N. A phenomenological dislocation mobility law for bcc metals. Acta Mater. 2016, 119, 123–135. [Google Scholar] [CrossRef]
- Lee, Y.J.; Subhash, G.; Ravichandran, G. Constitutive modeling of textured body-centered-cubic (bcc) polycrystals. Int. J. Plast. 1999, 15, 625–645. [Google Scholar] [CrossRef]
- Cereceda, D.; Diehl, M.; Roters, F.; Raabe, D.; Perlado, J.M.; Marian, J. Unraveling the temperature dependence of the yield strength in single-crystal tungsten using atomistically-informed crystal plasticity calculations. Int. J. Plast. 2016, 78, 242–265. [Google Scholar] [CrossRef]
- Yalcinkaya, T.; Brekelmans, W.; Geers, M. BCC single crystal plasticity modeling and its experimental identification. Model. Simul. Mater. Sci. Eng. 2008, 16, 085007. [Google Scholar] [CrossRef]
- Duesbery, M.A.S.; Vitek, V. Plastic anisotropy in bcc transition metals. Acta Mater. 1998, 46, 1481–1492. [Google Scholar] [CrossRef]
- Gröger, R.; Bailey, A.; Vitek, V. Multiscale modeling of plastic deformation of molybdenum and tungsten: I. Atomistic studies of the core structure and glide of 1/2<111> screw dislocations at 0 K. Acta Mater. 2008, 56, 5401–5411. [Google Scholar]
- Koester, A.; Ma, A.; Hartmaier, A. Atomistically informed crystal plasticity model for body-centered cubic iron. Acta Mater. 2012, 60, 3894–3901. [Google Scholar] [CrossRef]
- Mapar, A.; Ghassemi-Armaki, H.; Pourboghrat, F.; Kumar, K. A differential-exponential hardening law for non-Schmid crystal plasticity finite element modeling of ferrite single crystals. Int. J. Plast. 2017, 91, 268–299. [Google Scholar] [CrossRef]
- Maruyama, N.; Tabata, S.; Kawata, H. Excess Solute Carbon and Tetragonality in As-Quenched Fe-1Mn-C (C:0.07 to 0.8 Mass Pct) Martensite. Metall. Mater. Trans. 2020, 51, 1085–1097. [Google Scholar] [CrossRef]
- Taylor, G.I. The mechanism of plastic deformation of crystals. Part I.—Theoretical. Proc. R. Soc. Lond. A 1934, 145, 362–387. [Google Scholar]
- Franciosi, P. Glide mechanisms in bcc crystals: An investigation of the case of α-iron through multislip and latent hardening tests. Acta Metall. 1983, 31, 1331–1342. [Google Scholar] [CrossRef]
- Madec, R.; Kubin, L. Dislocation interactions and symmetries in bcc crystals. In IUTAM Symposium on Mesoscopic Dynamics of Fracture Process and Materials Strength; Springer: Dordrecht, The Netherlands, 2004; pp. 69–78. [Google Scholar]
- Queyreau, S.; Monnet, G.; Devincre, B. Slip systems interactions in α-iron determined by dislocation dynamics simulations. Int. J. Plast. 2009, 25, 361–377. [Google Scholar] [CrossRef]
- Ashby, M. The deformation of plastically non-homogeneous materials. Philos. Mag. 1970, 21, 399–424. [Google Scholar] [CrossRef]
- Becker, M. Incompatibility and Instability Based Size Effects in Crystals and Composites at Finite Elastoplastic Strains; University of Stuttgart: Stuttgart, Germany, 2006. [Google Scholar]
- Gurtin, M.E. The Burgers vector and the flow of screw and edge dislocations in finite-deformation single-crystal plasticity. J. Mech. Phys. Solids 2006, 54, 1882–1898. [Google Scholar] [CrossRef]
- Cermelli, P.; Gurtin, M.E. On the characterization of geometrically necessary dislocations in finite plasticity. J. Mech. Phys. Solids 2001, 49, 1539–1568. [Google Scholar] [CrossRef]
- Liszka, T.; Orkisz, J. The finite difference method at arbitrary irregular grids and its application in applied mechanics. Comput. Struct. 1980, 11, 83–95. [Google Scholar] [CrossRef]
- Kok, P.; Spanjer, W.; Vegter, H. A Microstructure Based Model for the Mechanical Behavior of Multiphase Steels. In Key Engineering Materials; Trans. Tech. Publications Ltd.: Stafa-Zurich, Switzerland, 2015; Volume 651, pp. 975–980. [Google Scholar]
- Yadegari, S.; Turteltaub, S.; Suiker, A.; Kok, P. Analysis of banded microstructures in multiphase steels assisted by transformation-induced plasticity. Comput. Mater. Sci. 2014, 84, 339–349. [Google Scholar] [CrossRef][Green Version]
- Ramazani, A.; Mukherjee, K.; Prahl, U.; Bleck, W. Modelling the effect of microstructural banding on the flow curve behaviour of dual-phase (DP) steels. Comput. Mater. Sci. 2012, 52, 46–54. [Google Scholar] [CrossRef]
- Charleux, M.; Poole, W.; Militzer, M.; Deschamps, A. Precipitation behavior and its effect on strengthening of an HSLA-Nb/Ti steel. Metall. Mater. Trans. A 2001, 32, 1635–1647. [Google Scholar] [CrossRef]
- Morito, S.; Nishikawa, J.; Maki, T. Dislocation density within lath martensite in Fe-C and Fe-Ni alloys. ISIJ Int. 2003, 43, 1475–1477. [Google Scholar] [CrossRef]
- Gurtin, M.E.; Reddy, B.D. Some issues associated with the intermediate space in single-crystal plasticity. J. Mech. Phys. Solids 2016, 95, 230–238. [Google Scholar] [CrossRef]
- Anand, L.; Kothari, M. A computational procedure for rate-independent crystal plasticity. J. Mech. Phys. Solids 1996, 44, 525–558. [Google Scholar] [CrossRef]
- Havner, K. Finite Plastic Deformation of Crystalline Solids; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Hughes, T.J.; Winget, J. Finite rotation effects in numerical integration of rate constitutive equations arising in large-deformation analysis. Int. J. Numer. Methods Eng. 1980, 15, 1862–1867. [Google Scholar] [CrossRef]
- Mathur, K.K.; Dawson, P.R. On modeling the development of crystallographic texture in bulk forming processes. Int. J. Plast. 1989, 5, 67–94. [Google Scholar] [CrossRef]
- Gurtin, M.E. A finite-deformation, gradient theory of single-crystal plasticity with free energy dependent on the accumulation of geometrically necessary dislocations. Int. J. Plast. 2010, 26, 1073–1096. [Google Scholar] [CrossRef]




| Self | Coplanar | Collinear | Orthogonal | Glissile | Sessile |
|---|---|---|---|---|---|
| 0.009 | 0.009 | 0.72 | 0.05 | 0.09 | 0.06 |
| C | Cr | Mn | Si | P & S |
|---|---|---|---|---|
| 0.09 | 0.5 | 1.9 | 0.06 | trace |
| Ferrite | Martensite | |
|---|---|---|
| E (GPa) | 212 | 212 |
| (-) | 0.3 | 0.3 |
| (MPa) | 40 | 250 |
| b (mm) | ||
| (mm) | ||
| (mm) | ||
| 0.4 | 0.3 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aşık, E.E.; Perdahcıoğlu, E.S.; van den Boogaard, T. An RVE-Based Study of the Effect of Martensite Banding on Damage Evolution in Dual Phase Steels. Materials 2020, 13, 1795. https://doi.org/10.3390/ma13071795
Aşık EE, Perdahcıoğlu ES, van den Boogaard T. An RVE-Based Study of the Effect of Martensite Banding on Damage Evolution in Dual Phase Steels. Materials. 2020; 13(7):1795. https://doi.org/10.3390/ma13071795
Chicago/Turabian StyleAşık, Emin Erkan, Emin Semih Perdahcıoğlu, and Ton van den Boogaard. 2020. "An RVE-Based Study of the Effect of Martensite Banding on Damage Evolution in Dual Phase Steels" Materials 13, no. 7: 1795. https://doi.org/10.3390/ma13071795
APA StyleAşık, E. E., Perdahcıoğlu, E. S., & van den Boogaard, T. (2020). An RVE-Based Study of the Effect of Martensite Banding on Damage Evolution in Dual Phase Steels. Materials, 13(7), 1795. https://doi.org/10.3390/ma13071795







