A Novel Algorithm for the Determination of Walker Damage in Loaded Disc Springs
Abstract
1. Introduction
2. Related Research
2.1. Mechanical Behavior of Disc Springs
2.2. The Walker Damage Parameter
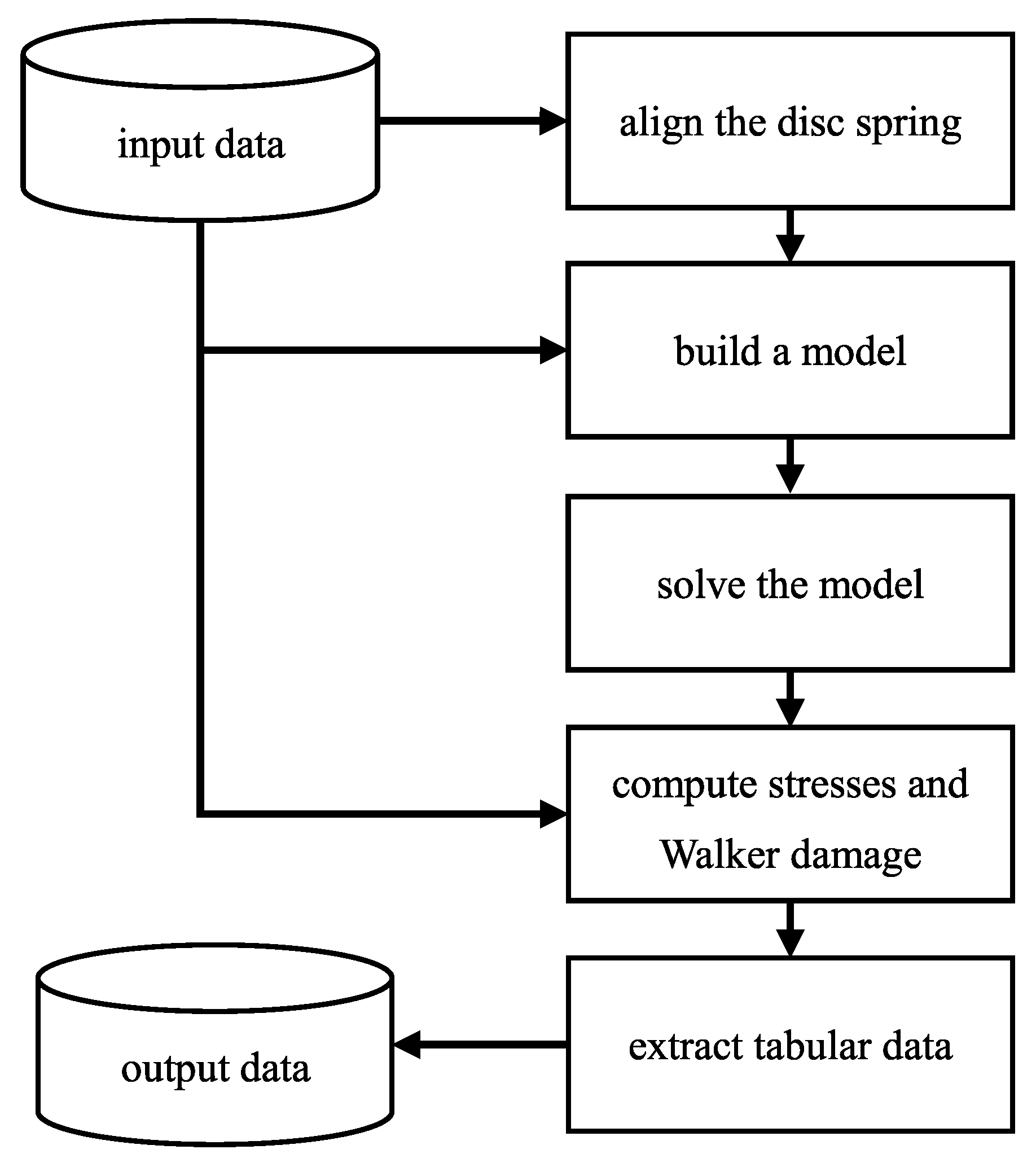
3. The Algorithm
3.1. General Concept
3.2. Architecture
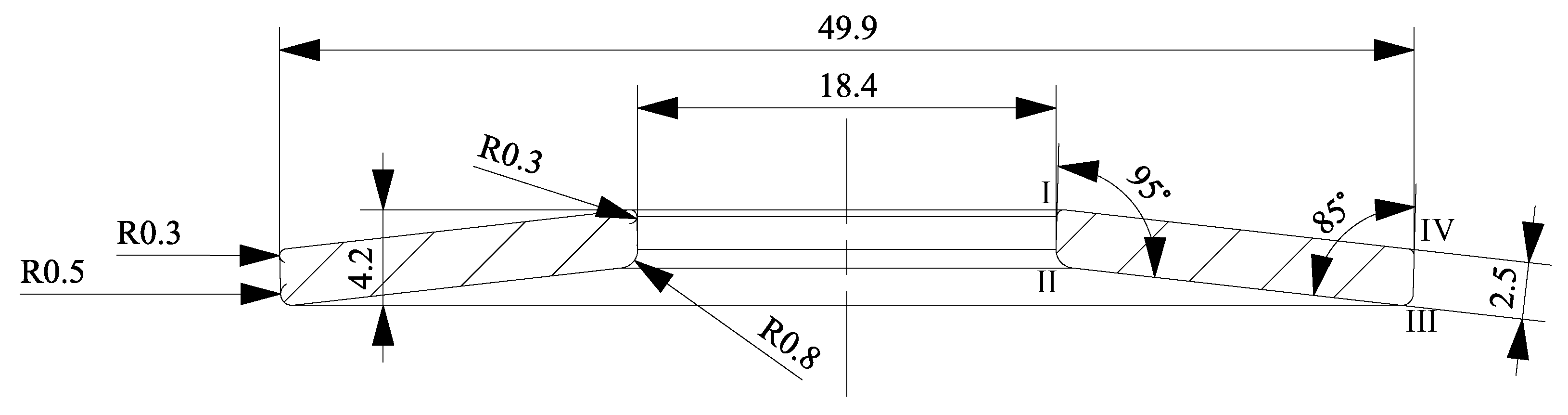
3.3. User-provided Inputs
4. Implementation
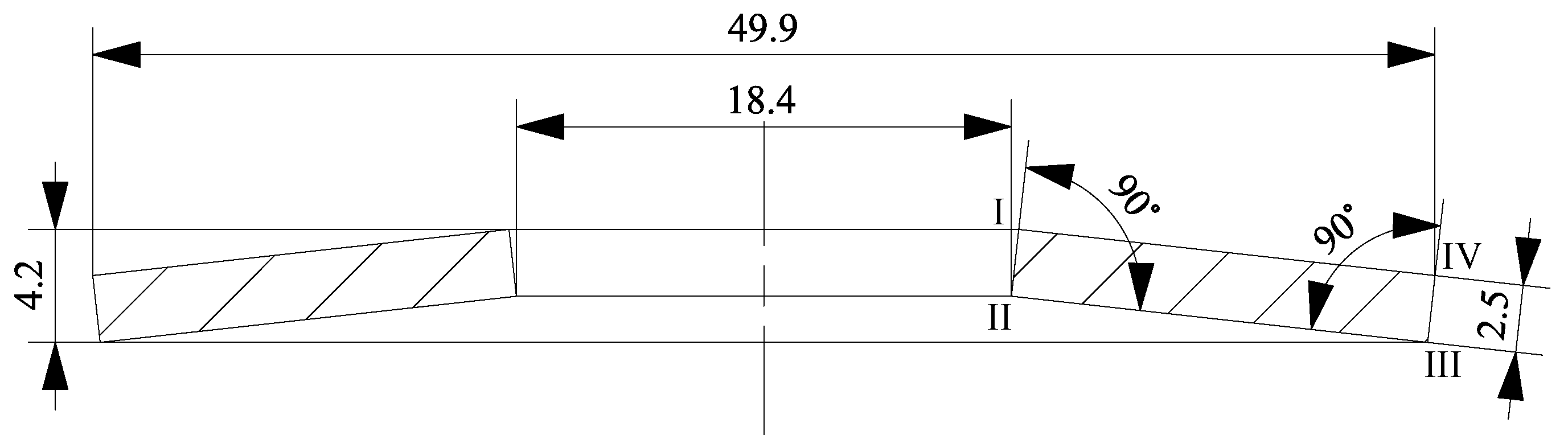
4.1. Aligning the Disc Spring
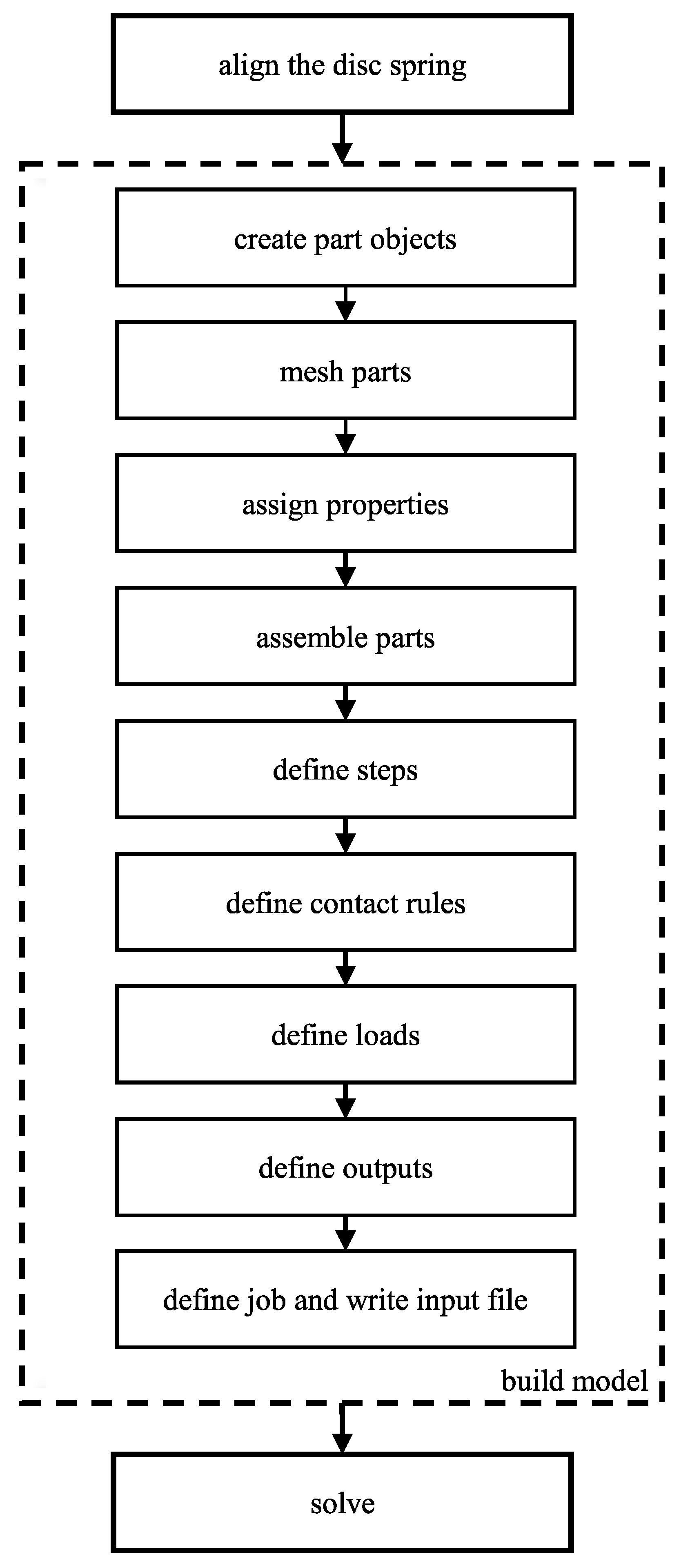
4.2. Building the Finite Element Model
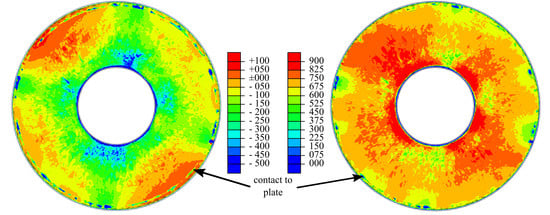
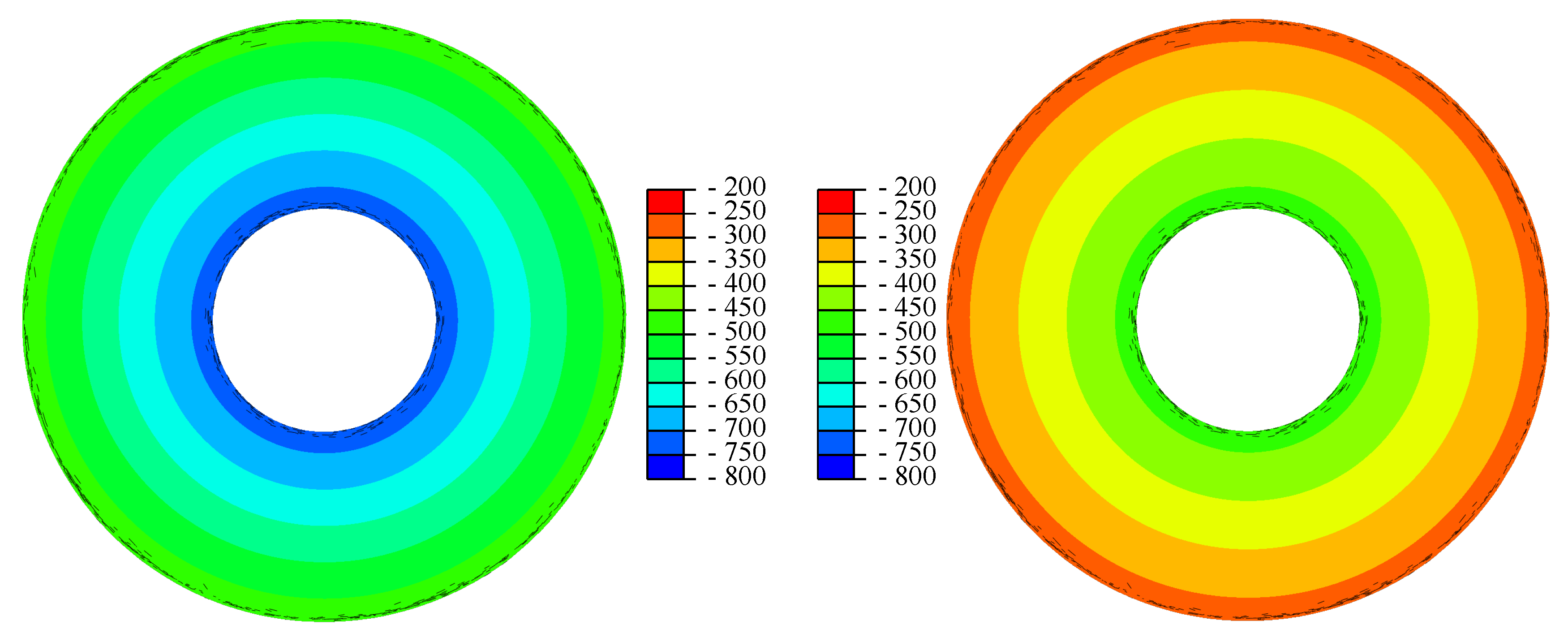
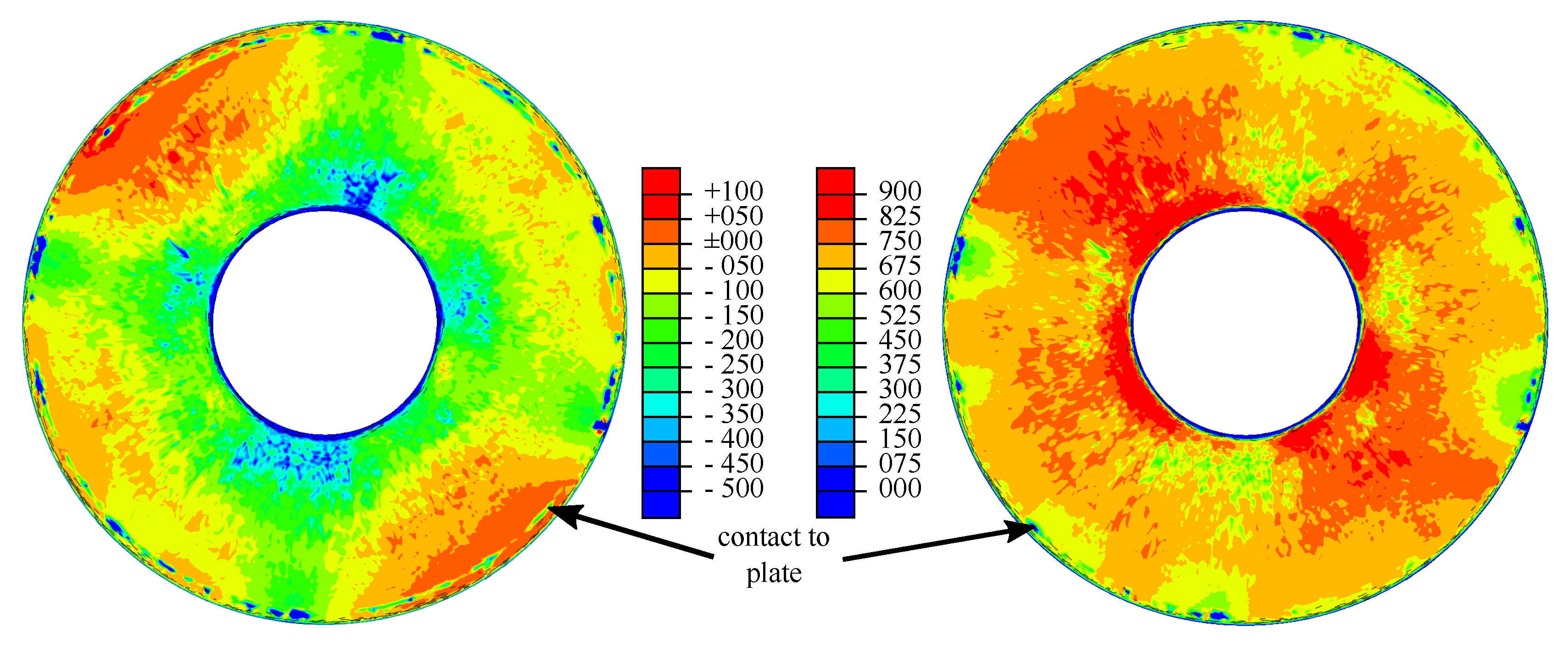
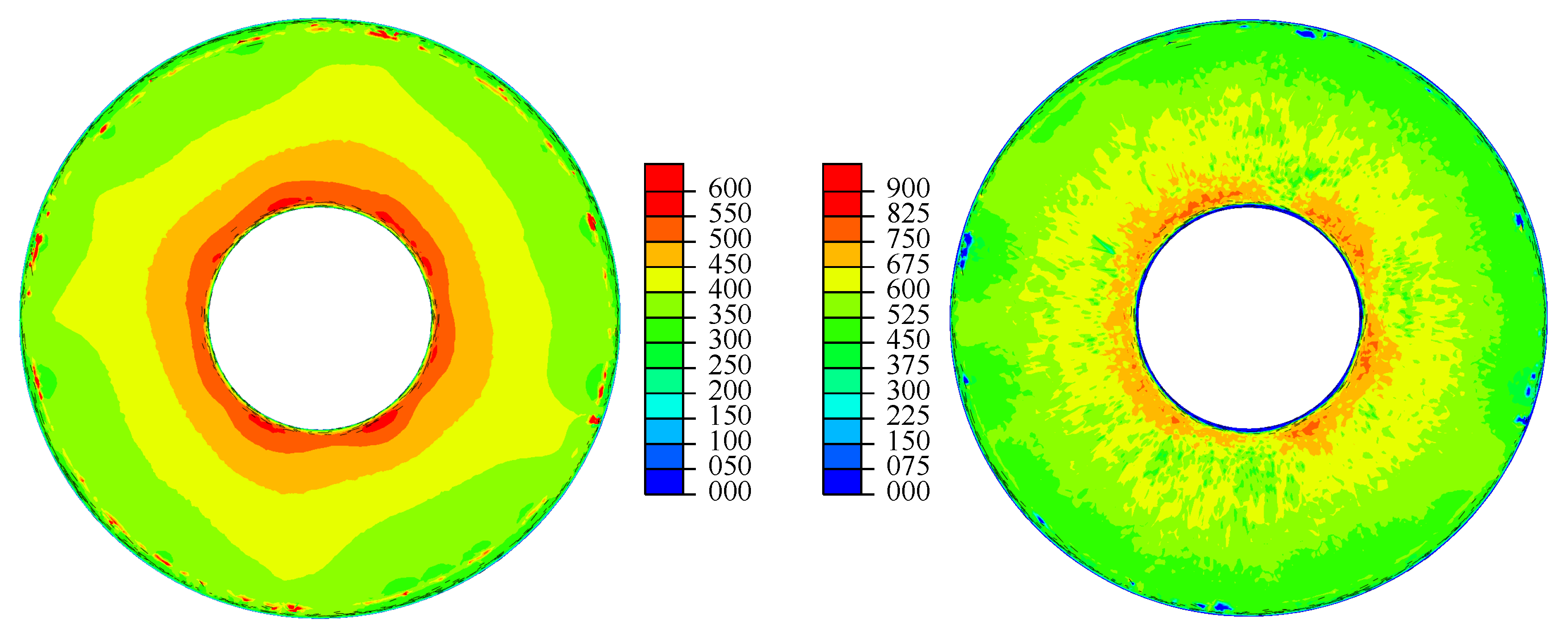
4.3. Computing Stresses and Walker Damage Parameters
4.4. Extracting Tabular Data
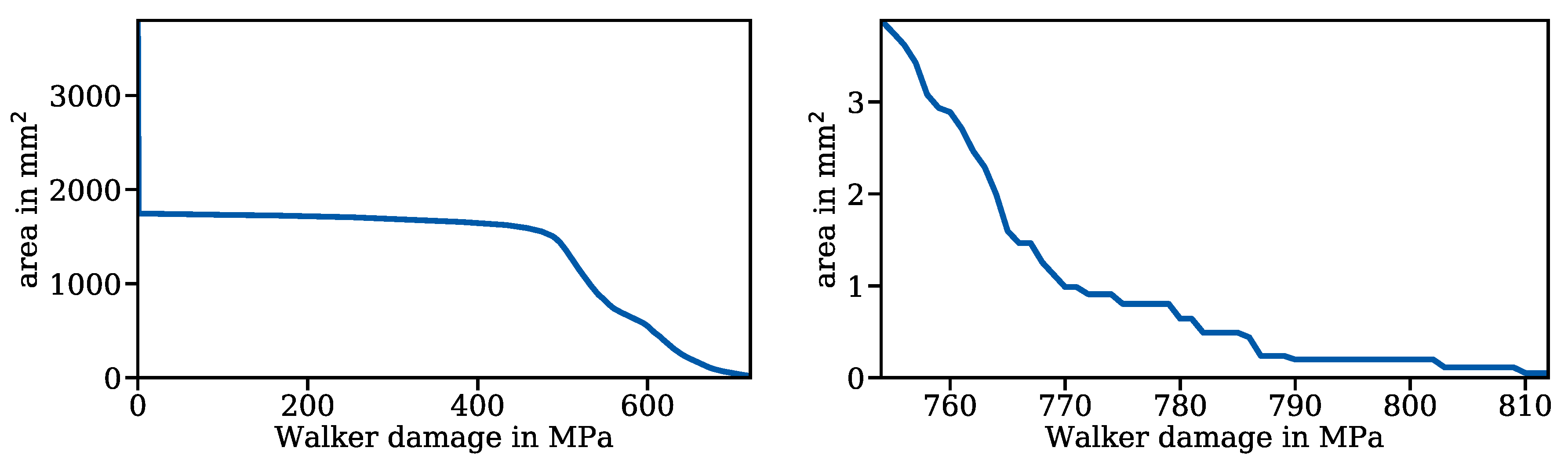
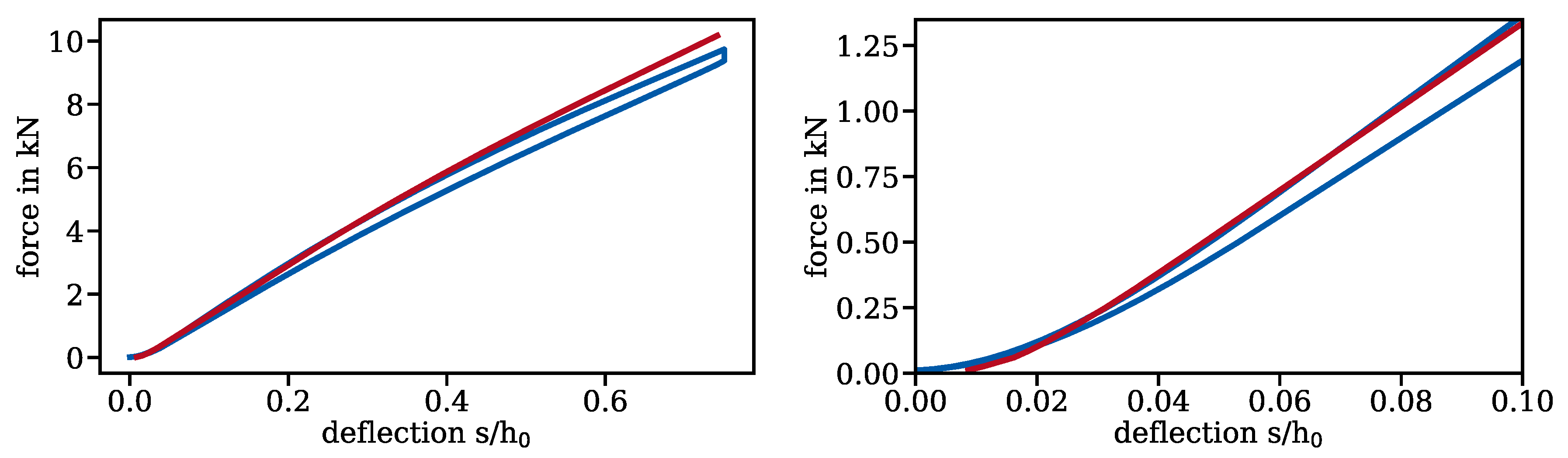
5. Example Application
6. Summary
Author Contributions
Funding
Conflicts of Interest
References
- DIN EN 16983. Tellerfedern–Qualitätsanforderungen–Maße; Beuth: Berlin, Germany, 2017. [Google Scholar]
- DIN EN 16984. Tellerfedern–Berechnung; Beuth: Berlin, Germany, 2017. [Google Scholar]
- Geilen, M.B.; Klein, M.; Oechsner, M. Building Models with 3D-Scanned Geometry using Abaqus Scripting—A Case Study on Disc Springs. In Proceedings of the 3DEXPERIENCE Conference–Design, Modeling & Simulation, Dassault Systemes, Darmstadt, Germany, 19–21 November 2019. [Google Scholar]
- Geilen, M.B.; Klein, M.; Oechsner, M. Spring_stack-ein Modul zur numerischen Simulation von Tellerfedern und Tellerfedersäulen. In Ilmenauer Federntag 2019—Neueste Erkenntnisse zu Funktion, Berechnung, Prüfung und Gestaltung von Federn und Werkstoffen; ISLE: Ilmenau, Germany, 2019; pp. 77–86. [Google Scholar]
- Mischke, C.R.; Shigley, J.E. Standard Handbook of Machine Design; McGraw-Hill: New York, NY, USA, 1996. [Google Scholar]
- Meissner, M.; Fischer, F.; Wanke, K.; Plitzko, M. Die Geschichte der Metallfedern und der Federntechnik in Deutschland; Universitätsverlag Ilmenau: Ilemanu, Germany, 2009. [Google Scholar]
- Bhandari, V.B. Design of Machine Elements; Tata McGraw-Hill Education: New York, NY, USA, 2010. [Google Scholar]
- Curti, G.; Montanini, R. On the influence of friction in the calculation of conical disk springs. J. Mech. Des. 1999, 121, 622–627. [Google Scholar] [CrossRef]
- Bühl, P. Zur Spannungsberechnung von Tellerfedern. Draht 1971, 22, 760–763. [Google Scholar]
- Curti, G.; Orlando, M. Ein neues Berechnungverfahren für Tellerfedern. Wire 1979, 29, 199–204. [Google Scholar]
- Fawazi, N.; Lee, J.Y. An improved load-displacement prediction for a coned disc spring using the energy method. ARPN J. Eng. Appl. Sci. 2006, 11, 833–836. [Google Scholar]
- Hübner, W. Deformationen und Spannungen bei Tellerfedern. Konstruktion 1982, 34, 387–392. [Google Scholar]
- Hübner, W.; Emmerling, F.A. Axialsymmetrische große Deformationen einer elastischen Kegelschale. ZAMM 1982, 62, 404–406. [Google Scholar] [CrossRef]
- Kobelev, V. Exact shell solutions for conical springs. Mech. Based Des. Struct. Mach. 2016, 44, 317–339. [Google Scholar] [CrossRef]
- Lutz, O. Zur Berechnung der Tellerfeder. Konstruktion 1960, 12, 57–59. [Google Scholar]
- Lutz, O.; Wernitz, W. Stülpen einer konischen Ringscheibe (Tellerfeder) unter Berücksichtigung der Mantellinienkrümmung. Forsch. Ingenieurwesen A 1967, 33, 77–84. [Google Scholar] [CrossRef]
- Mastricola, N.P.; Dreyer, J.T.; Singh, R. Analytical and experimental characterization of nonlinear coned disk springs with focus on edge friction contribution to force-deflection hysteresis. Mech. Syst. Signal Process. 2017, 91, 215–232. [Google Scholar] [CrossRef]
- Mastricola, N.P.; Singh, R. Nonlinear load-deflection and stiffness characteristics of coned springs in four primary configurations. Mech. Mach. Theory 2017, 116, 513–528. [Google Scholar] [CrossRef]
- Zheng, E.; Jia, F.; Zhou, X. Energy-based method for nonlinear characteristics analysis of Belleville springs. Thin-Walled Struct. 2014, 79, 52–61. [Google Scholar] [CrossRef]
- Curti, G. Vereinfachtes Verfahren zur Berechnung von Tellerfedern. Draht 1980, 31, 789–792. [Google Scholar]
- Curt, G.; Orlando, M. Geschlitzte Tellerfedern. Draht 1981, 32, 608–615. [Google Scholar]
- Fawazi, N.; Lee, J.Y.; Oh, J.E. A load–displacement prediction for a bended slotted disc using the energy method. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2012, 226, 2126–2137. [Google Scholar] [CrossRef]
- Fawazi, N.; Yang, I.H.; Kim, J.S.; Lee, J.Y.; Kim, H.S.; Oh, J.E. An inverse algorithm of nonlinear load-displacement for a slotted disc spring geometric design. Int. J. Precis. Eng. Manuf. 2013, 14, 137–145. [Google Scholar] [CrossRef]
- Ferrari, G. A new calculation method for belleville disc springs with contact flats and reduced thickness. Int. J. Manuf. Mater. Mech. Eng. 2013, 3, 63–73. [Google Scholar] [CrossRef][Green Version]
- La Rosa, G.; Messina, M.; Risitano, A. Stiffness of variable thickness Belleville springs. J. Mech. Des. 2001, 123, 294–299. [Google Scholar] [CrossRef]
- Muhr, K.H.; Niepage, P. Zur Berechnung von Tellerfedern mit rechteckigem Querschnitt und Auflageflächen. Konstruktion 1966, 18, 24–27. [Google Scholar]
- Saini, P.K.; Kumar, P.; Tandon, P. Design and analysis of radially tapered disc springs with parabolically varying thickness. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2007, 221, 151–158. [Google Scholar] [CrossRef]
- Schremmer, G. Die geschlitzte Tellerfeder. Konstruktion 1972, 24, 226–229. [Google Scholar]
- Boorboor Ajdari, M.; Jalili, S.; Jafari, M.; Zamani, J.; Shariyat, M. The analytical solution of the buckling of composite truncated conical shells under combined external pressure and axial compression. J. Mech. Sci. Technol. 2012, 26, 2783–2791. [Google Scholar] [CrossRef]
- Patangtalo, W.; Aimmanee, S.; Chutima, S. A unified analysis of isotropic and composite Belleville springs. Thin-Walled Struct. 2016, 109, 285–295. [Google Scholar] [CrossRef]
- Kobelev, V. Durability of Springs; Springer: Berlin, Germnay, 2018. [Google Scholar]
- Ozaki, S.; Tsuda, K.; Tominaga, J. Analyses of static and dynamic behavior of coned disk springs: Effects of friction boundaries. Thin-Walled Struct. 2012, 59, 132–143. [Google Scholar] [CrossRef]
- Schiffner, K.; Borchert, T. Schwingungen flacher Rotationsschalen unter statischer Vorlast. ZAMM 1988, 68, 250–255. [Google Scholar]
- Carfagni, M. A CAD program for the automated checkout and design of Belleville springs. J. Mech. Des. 2002, 124, 393–398. [Google Scholar] [CrossRef]
- Paredes, M.; Daidié, A. Optimal catalogue selection and custom design of belleville spring arrangements. Int. J. Interact. Des. Manuf. 2010, 4, 51–59. [Google Scholar] [CrossRef]
- Ha, S.H.; Seong, M.S.; Choi, S.B. Design and vibration control of military vehicle suspension system using magnetorheological damper and disc spring. Smart Mater. Struct. 2013, 22, 065006. [Google Scholar] [CrossRef]
- Wang, W.; Wang, X. Tests, model, and applications for coned-disc-spring vertical isolation bearings. Bull. Earthq. Eng. 2020, 18, 357–398. [Google Scholar] [CrossRef]
- Curti, G.; Appendino, D. Vergleich von Berechnungsverfahren fürTellerfedern. Draht 1982, 33, 38–40. [Google Scholar]
- Wagner, W.; Wetzel, M. Berechnung von Tellerfedern mit Hilfe der Methode der Finiten Elemente. Konstruktion 1987, 39, 147–150. [Google Scholar]
- Bagavathiperumal, P.; Chandrasekaran, K.; Manivasagam, S. Elastic load-displacement predictions for coned disc springs subjected to axial loading using the finite element method. J. Strain Anal. Eng. Des. 1991, 26, 147–152. [Google Scholar] [CrossRef]
- Schiffner, K.; Dietrich, M. Numerische Simulation der Entstehung von Eigenspannungen 1. Art an Tellerfedern. ZAMM 1987, 67, 235–237. [Google Scholar]
- Curti, G.; Raffa, F.A. Material nonlinearity effects in the stress analysis of conical disk springs. J. Mech. Des. 1992, 114, 238–244. [Google Scholar] [CrossRef]
- Yahata, N.; Watanabe, M.; Ishii, N. Analysis of coned disc spring by finite element method. Jpn. Soc. Mech. Eng. 1993, 59, 260–265. [Google Scholar]
- Veleva, D.; Kaiser, B.; Berger, C. Experimentelle Untersuchung und numerische Simulation des Relaxationsverhaltens von Tellerfedern. In Ilmenauer Federntag 2010—Neueste Erkenntnisse zu Funktion, Berechnung, Prüfung und Gestaltung von Federn und Werkstoffen; ISLE: Ilmenau, Germany, 2010; pp. 71–78. [Google Scholar]
- Veleva, D. Experimentelle Untersuchung und Numerische Simulation des Relaxationsverhaltens von Tellerfedern. Ph.D. Thesis, TU Darmstadt, Darmsatdt, Germnay, 2012. [Google Scholar]
- Maqbool, F.; Hajavifard, R.; Walther, F.; Bambach, M. Engineering the residual stress state of the metastable austenitic stainless steel (MASS) disc springs by incremental sheet forming (ISF). Prod. Eng. 2019, 13, 139–148. [Google Scholar] [CrossRef]
- Lee, C.Y.; Chae, Y.S.; Gwon, J.D.; Nam, U.H.; Kim, T.H. Finite element analysis and optimal design of automobile clutch diaphragm spring. Trans. Korean Soc. Mech. Eng. A 2000, 24, 1616–1623. [Google Scholar]
- Karakaya, Ş. Investigation of hybrid and different cross-section composite disc springs using finite element method. Trans. Can. Soc. Mech. Eng. 2012, 36, 399–412. [Google Scholar] [CrossRef]
- Sfarni, S.; Bellenger, E.; Fortin, J.; Malley, M. Numerical and experimental study of automotive riveted clutch discs with contact pressure analysis for the prediction of facing wear. Finite Elem. Anal. Des. 2011, 47, 129–141. [Google Scholar] [CrossRef]
- Yubing, G.; Defeng, Z. Mechanism for the Forced Strengthening on the Diaphragm Spring’s Load-Deflection Characteristic. Int. J. Eng. Technol. 2017, 9, 287–292. [Google Scholar] [CrossRef][Green Version]
- Zhu, D.; Ding, F.; Liu, H.; Zhao, S.; Liu, G. Mechanical property analysis of disc spring. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 230. [Google Scholar] [CrossRef]
- Chen, Y.S.; Chiu, C.C.; Cheng, Y.D. Dynamic analysis of disc spring effects on the contact pressure of the collet—Spindle interface in a high-speed spindle system. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2009, 223, 1191–1201. [Google Scholar] [CrossRef]
- Maletta, C.; Filice, L.; Furgiuele, F. NiTi Belleville washers: Design, manufacturing and testing. J. Intell. Mater. Syst. Struct. 2013, 24, 695–703. [Google Scholar] [CrossRef]
- Fang, C.; Zhou, X.; Osofero, A.I.; Shu, Z.; Corradi, M. Superelastic SMA Belleville washers for seismic resisting applications: Experimental study and modeling strategy. Smart Mater. Struct. 2016, 25, 105013. [Google Scholar] [CrossRef]
- Sgambitterra, E.; Maletta, C.; Furgiuele, F. Modeling and simulation of the thermo-mechanical response of NiTi-based Belleville springs. J. Intell. Mater. Syst. Struct. 2016, 27, 81–91. [Google Scholar] [CrossRef]
- Fang, C.; Yam, M.C.H.; Chan, T.M.; Wang, W.; Yang, X.; Lin, X. A study of hybrid self-centring connections equipped with shape memory alloy washers and bolts. Eng. Struct. 2018, 164, 155–168. [Google Scholar] [CrossRef]
- Koplin, C.; Schröder, C.; Becker, W.; Stockmann, J.; Kailer, A. Demonstration der Zuverlässigkeit von keramischen Schraubendruck-und Tellerfedern für korrosive Umgebungen und hohe Temperaturen. In Ilmenauer Federntag 2019—Neueste Erkenntnisse zu Funktion, Berechnung, Prüfung und Gestaltung von Federn und Werkstoffen; ISLE: Ilmenau, Germany, 2019; pp. 11–21. [Google Scholar]
- Jia, F.; Zhang, F.C. A Study on the Mechanical Properties of Disc Spring Vibration Isolator with Viscous Dampers. Adv. Mater. Res. 2014, 904, 454–459. [Google Scholar] [CrossRef]
- Lonkwic, P.; Różyło, P.; Usydus, I. Numerical Analysis and Experimental Investigation of Disk Spring Configurations with Regard to Load Capacity of Safety Progressive Gears. Appl. Comput. Sci. 2016, 12, 5–16. [Google Scholar]
- Zhou, J.; Zhang, C.; Wang, Z.; Mao, K. Study on Dynamic Characteristics of the Disc Spring System in Vibration Screen. Shock Vib. 2020, 2020, 3518037. [Google Scholar] [CrossRef]
- Kletzin, U. Finite Elemente basiertes Entwurfssystem für Federn und Federanordnungen. Ph.D. Thesis, TU Ilmenau, Ilmenau, Germany, 2000. [Google Scholar]
- Wehmann, C.; Neidnicht, M.; Nützel, F.; Roith, B.; Rieg, F. Finite Elemente Analysen zur Berechnung von Maschinenelementen mit nichtlinearem Verhalten. In 8. Gemeinsames Kolloquium Konstruktionstechnik— Herausforderungen für die Produkt-und Prozessinnovation; Docuprint: Barleben, Germany, 2010; pp. 47–52. [Google Scholar]
- Walker, K. The effect of stress ratio during crack propagation and fatigue for 2024-T3 and 7075-T6 aluminum. In Effects of Environment and Complex Load History on Fatigue Life; ASTM International: West Conshohocken, PA, USA, 1970. [Google Scholar]
- Goodman, J. Mechanics Applied to Engineering; Longmans, Green: Harlow, UK, 1919. [Google Scholar]
- Morrow, J. Fatigue properties of metals. In Fatigue Design Handbook; Society of Automotive Engineers: Warrendale, PA, USA, 1968; pp. 21–30. [Google Scholar]
- Smith, K.N.; Watson, P.; Topper, T.H. A Stress-Strain Function for the Fatigue of Metals. J. Mater. 1970, 5, 767–778. [Google Scholar]
- Dowling, N.E.; Calhoun, C.A.; Arcari, A. Mean stress effects in stress–life fatigue and the Walker equation. Fatigue Fract. Eng. Mater. Struct. 2009, 32, 163–179. [Google Scholar] [CrossRef]
- Dowling, N.E. Mechanical Behavior of Materials: Engineering Methods for Deformation, Fracture, and Fatigue; Pearson: London, UK, 2012. [Google Scholar]
- Gyekenyesi, J.Z.; Murthy, P.L.N.; Mital, S.K. NASALIFE-Component Fatigue and Creep Life Prediction Program; NASA Glenn Research Center: Cleveland, OH, USA, 2014. [Google Scholar]
- Dassault Systemes. Abaqus 2018 Scripting User’s Guide; Dassault Systemes: Vélizy-Villacoublay, France, 2018. [Google Scholar]
- Dassault Systemes. Abaqus 2018 Scripting User’s Reference Guide; Dassault Systemes: Vélizy-Villacoublay, France, 2018. [Google Scholar]
- Barber, C.B.; Dobkin, D.P.; Huhdanpaa, H. The quickhull algorithm for convex hulls. ACM Trans. Math. Softw. 1996, 22, 469–483. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J. SciPy 1.0–Fundamental Algorithms for Scientific Computing in Python. arXiv 2019, arXiv:1907.10121. [Google Scholar] [CrossRef] [PubMed]
- Byrd, R.H.; Lu, P.; Nocedal, J.; Zhu, C. A limited memory algorithm for bound constrained optimization. SIAM J. Sci. Comput. 1995, 16, 1190–1208. [Google Scholar] [CrossRef]
- Zhu, C.; Byrd, R.H.; Lu, P.; Nocedal, J. L-BFGS-B: Fortran subroutines for large-scale bound-constrained optimization. ACM Trans. Math. Softw. 1997, 23, 550–560. [Google Scholar] [CrossRef]
- Cignoni, P.; Callieri, M.; Corsini, M.; Dellepiane, M.; Ganovelli, F.; Ranzuglia, G. Meshlab: An open-source mesh processing tool. In Proceedings of the Eurographics Italian Chapter Conference, Salerno, Italy, 2–4 July 2008; pp. 129–136. [Google Scholar]
- Hunter, J.D. Matplotlib: A 2D graphics environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Dassault Systemes. Abaqus 2018 Analysis User’s Guide; Volume IV: Elements; Dassault Systemes: Vélizy-Villacoublay, France, 2018. [Google Scholar]
- Spies, A.; Beyer, J.; Oechsner, M. Ermittlung und Bewertung der Schwingfestigkeitseigenschaften von Tellerfedern aus verschiedenen Werkstoffen. In Ilmenauer Federntag 2015—Neueste Erkenntnisse zu Funktion, Berechnung, Prüfung und Gestaltung von Federn und Werkstoffen; ISLE: Ilmenau, Germany, 2015; pp. 121–130. [Google Scholar]
- Hertzer, K.H. Über die Dauerfestigkeit und das Setzen von Tellerfedern. Ph.D. Thesis, Technische Hoschschule Carolo-Wilhelmina, Braunschweig, Germany, 1959. [Google Scholar]
- Muhr, K.H.; Niepage, P.; Willwacher, H. Warmvorsetzen vermindert die Relaxation von Tellerfedern. Konstruktion 1975, 27, 468–471. [Google Scholar]
- Niepage, P.; Grahn, B.; Virnich, K.H. Der Einfluss des Eigenspannungszustandes auf die Schwingfestigkeit von Tellerfedern. Draht 1993, 44, 224–227. [Google Scholar]
- Buchfink, B.; Naue, K.C.; Wunderle, G. Tellerfedern: Funktion, Fertigung, Werkstoffe; Die Bibliothek der Technik, Verlag Moderne Industrie: Landsberg am Lech, Germany, 2015. [Google Scholar]
- Christian Bauer GmbH & Co. KG. Tellerfedern–Theorie und Praxis.
- Mubea Disc Scprings. Mubea Disc Springs Manual.




© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Geilen, M.B.; Klein, M.; Oechsner, M. A Novel Algorithm for the Determination of Walker Damage in Loaded Disc Springs. Materials 2020, 13, 1661. https://doi.org/10.3390/ma13071661
Geilen MB, Klein M, Oechsner M. A Novel Algorithm for the Determination of Walker Damage in Loaded Disc Springs. Materials. 2020; 13(7):1661. https://doi.org/10.3390/ma13071661
Chicago/Turabian StyleGeilen, Max Benedikt, Marcus Klein, and Matthias Oechsner. 2020. "A Novel Algorithm for the Determination of Walker Damage in Loaded Disc Springs" Materials 13, no. 7: 1661. https://doi.org/10.3390/ma13071661
APA StyleGeilen, M. B., Klein, M., & Oechsner, M. (2020). A Novel Algorithm for the Determination of Walker Damage in Loaded Disc Springs. Materials, 13(7), 1661. https://doi.org/10.3390/ma13071661