Abstract
A homogenization theory that can go beyond the regime of long wavelengths is proposed, namely, a theory that is still valid for vectors of waves near the edge of the first zone of Brillouin. In this paper, we consider that the displacement vector and the magnetic induction fields have averages in the volume of the cell associated with the values of the electric and magnetic fields in the edges of the cell, so they satisfy Maxwell’s equations. Applying Fourier formalism, explicit expressions were obtained for the case of a photonic crystal with arbitrary periodicity. In the case of one-dimensional (1D) photonic crystals, the expressions for the tensor of the effective bianisotropic response (effective permittivity, permeability and crossed magneto-electric tensors) are remarkably simplified. Specifically, the effective permittivity and permeability tensors are calculated for the case of 1D photonic crystals with isotropic and anisotropic magnetic inclusions. Through a numerical calculation, the dependence of these effective tensors upon the filling fraction of the magnetic inclusion is shown and analyzed. Our results show good correspondence with the approach solution of Rytov’s effective medium. The derived formulas can be very useful for the design of anisotropic systems with specific optical properties that exhibit metamaterial behavior.
1. Introduction
The concept of metamaterial was initially introduced to explain the striking physical properties of photonic crystals, composed of resonant elements or having a very large dielectric contrast. For example, recently in [1], the design of a bilayer device (1D photonic crystal) made of dielectric materials on a substrate was reported. This membrane-type device enhances the Faraday rotation in comparison with plasmonic or metal-dielectric periodic structures, as well as showing good efficiency as a waveguide for transverse magnetic and transverse electric polarizations. Staude and Schilling [2] reviewed the optical properties of metamaterial-inspired silicon nanostructures, to explain the resonant frequency dependence of the optical metamaterial parameters, e.g., three-dimensional metamaterial-inspired arrangements of silicon nanoparticles having Mie resonances at a low frequency and behaving as double-negative electromagnetic mediums with simultaneously negative effective dielectric permittivity and magnetic permeability. Moreover, there are photonic crystals made of materials that are stimuli-responsive (the materials, either soft or aggregate, respond to thermal, pH, chemical, mechanical, optical, electrical or magnetic stimuli). With the application of these external stimuli, the range of electromagnetic frequencies in which there are no allowed propagation modes for any direction of the crystal are principally controlled. This can be exploited for applications in liquid–crystalline structures, sensors, optical phenomena diffraction and emission of photoluminescent materials. However, in recent years, scientists have faced a new challenge in studying the optical properties of these stimuli-responsive artificial materials in the area of nanophotonics. One of the great advances in this area is the design and manufacture of stimuli-responsive optical nanostructures (see, e.g., [3] and references therein). Thus, the most recent reports on these extraordinary structures offer great challenges and research opportunities in both physics and materials engineering, ranging from manufacturing techniques to the development of approximations and useful theories for the calculation of their effective electromagnetic magnitudes that allow us to characterize the control of the propagation of electromagnetic waves in the medium.
Magneto-dielectric photonic crystals are an interesting kind of metamaterial because of their unusual optical anisotropy [4,5]. The homogenization theories suggested in [4] and [5] provide accurate calculations to determine the effective refractive index for dielectric and magneto-dielectric 2D photonic crystals, respectively. Nowadays, homogenization theories have been proposed in order to calculate the effective optical parameters of metallo-dielectric photonic crystals with magnetic components (see, for example, [6,7,8,9,10,11,12,13] and references therein). All these theories characterize the electromagnetic oscillations in bianisotropic media, defined by the effective permeability, permittivity, and crossed magneto-electric tensors. Unfortunately, although the expressions for the effective parameters, obtained by some of these theories [4,5,6,9,11,12], are valid for photonic crystals with any type of Bravais lattice, their application in the case of 3D periodicity turns out to be impractical.
The purpose of this work is to present a homogenization theory that allows us to calculate the effective electromagnetic response of magneto-dielectric photonic crystals valid beyond the regime of long wavelengths, i.e., for wave vectors near the edge of the first zone of Brillouin. Explicit expressions are obtained for the tensors of the effective bianisotropic responses in the case of a photonic crystal with arbitrary periodicity, which, in the case of 1D photonic crystals, are significantly simplified. In developing our theory, called Coherent Wave Homogenization theory, we consider that the displacement vector (D) and the magnetic induction (B) fields have averages in the volume of the cell associated with the values of the electric (E) and magnetic (H) fields in the edges of the cell, so that they satisfy Maxwell’s equations. Furthermore, to determine the effective optical properties, we will efficiently use the general formalism of homogenization theories (see [14] and its references), based on Fourier formalism, which provides explicit formulas to determining all the components of the bianisotropic response tensors. Unlike previous theories, we present an approach for accurate calculations of the effective tensors in terms of the parameters of permittivity and permeability of the inclusion in the unit cell. The numerical implementation of the formulas obtained will be applied to 1D magneto-dielectric photonic crystals to study how the effective response of permeability and permittivity tensors behave versus the filling fraction and with the variation in the material parameters of the isotropic or anisotropic magnetic inclusions.
2. Mathematical Formulation: Homogenization Theory of Coherent Wave
2.1. Finite Fourier Transform
In this section, we shall derive an expression for the effective tensors based on the principle of wavelengths comparable with the lattice period for characterizing the bulk optical response of a homogenized magneto-dielectric photonic crystal. The most general form for such a response is the so-called bianisotropic response, generally written in the EH- (or Tellegen) representation, using the permittivity and permeability tensors and two crossed magneto-electric dyadics, and , which depend on the position () in the photonic crystal. Such tensorial representation relates the electric E and magnetic H fields with the displacement vector D and the magnetic induction B:
The behavior of these fields is governed by Maxwell equations:
Now, with Equations (1) and (2), we rewrite the laws of Ampere–Maxwell (in Equations (3) and (4)) and Faraday in (Equations (5) and (6)) in matrix form:
In this latter equation, the dyadic unit and zero are introduced ( and , respectively), as well as the vectors EH and DB ( and , respectively), given by:
where is a 6 × 6 matrix defined by:
Due to the periodicity of the bianisotropic response tensors, we write the matrix in an expansion in Fourier series:
the summation extends over the vectors of the reciprocal lattice () of the photonic crystal.
Moreover, we can expand the vectors in Bloch waves due to the periodicity along the plane parallel to one of the surfaces of the photonic crystal:
where is a vector of the reciprocal lattice of the plane perpendicular to the z-direction.
Substituting Equation (11) into Equation (7), we get:
Now, we will apply the finite Fourier transform in an interval along the z-axis of length equal to the lattice constant a:
where , = . The inverse transform is given by the series:
From Equations (12) and (13), we obtain:
Rewriting this equation and considering that:
here, is the matrix of the bianisotropic response. Therefore, Equation (15) can be rewritten as:
where:
The amplitudes and in Equation (17) are defined by the expressions:
Using Equations (17)–(19), a homogeneous system is obtained for the amplitudes and . Therefore, the amplitudes for can be expressed in terms of one of them, for example, .
Now, let us determine the effective response. From Equations (17) and (19), we have:
This expression can be written as:
Evaluating this equation in , we obtain an equation for the coherent component:
In the bulk of the photonic crystal, the Bloch theorem must be satisfied, , so the term on the left side in Equation (23) can be written as:
Substituting this into Equation (23), we arrive at the equations for the coherent amplitude:
which correspond to the Maxwell equations for the amplitude of the field E–H, propagating in the z-direction, in a homogeneous medium:
where
is the effective field D–B. The effective matrix of the bianisotropic response is obtained directly from Equations (25) and (27), and the relationship between the coefficients and the coherent amplitude mentioned above (Equation (21)). Therefore, we have explicit expressions to calculate the effective tensors of the bianisotropic response of a homogenized photonic crystal without any restrictions on the wave vector .
2.2. 1D Photonic Crystals
Let us calculate the effective parameters for a homogenized binary (bilayer) 1D photonic crystal. The Fourier coefficients in Equation (16) are given by Equation (28); the crossed magnetoelectric tensors are assumed to be equal to 3 × 3 zero matrices:
where
effecting the integral on the unit cell, the following expression is obtained:
The matrix (Equation (18)), acquires the simplest form:
and it satisfies
On the other hand, the effective matrix takes the form:
Let us introduce
so, the effective matrix (Equation (33)) acquires the simplest form:
Note that this expression depends on , which in general is non-local, i.e., the effective parameters depend on both frequency ω and the wave vector .
3. Implementation and Results
In this section, we apply the Coherent Wave Homogenization theory developed in the previous section for calculating the effective permeability and permittivity tensors versus the filling-fraction of 1D magneto-dielectric photonic crystals. Here, it is convenient to indicate that in the case of alternating layers being sufficiently thin in comparison with the characteristic wavelength, we can treat the whole system as an anisotropic medium with effective response tensors (we consider that the Bloch wavelength is much greater than the lattice parameter of the photonic crystal, a << 1). As follows from Figure 1 and according to the previous conditions for wavelength frequencies in THz, a lattice parameter a = 0.15 µm is proposed, d is the thickness of the inclusion layer and for the case of a superlattice with two alternating layers, the filling fraction , and is valid for values of d in the range 0 ≤ d ≤ a. In this work, the interest in the THz regime becomes more attractive due to the huge technological applications, e.g., telecommunications, sensing and astronomy. In general, the periodicity of the photonic structure will be proportional to the wavelength of the electromagnetic radiation to be controlled. Therefore, for homogenized photonic crystals of arbitrary thickness, the effective electromagnetic magnitudes of magnetic permeability and dielectric permittivity that characterize the propagation of electromagnetic waves in the medium can always be determined. Here, we will study photonic crystals whose bilayer unitary cell is composed of a layer of dielectric material with inclusions of magnetic–isotropic and magnetic–anisotropic media. The constituents of the unit cell will be considered in a usual manner—that is, medium “A” will correspond to the inclusion and medium “B” to the background or host (see Figure 1).
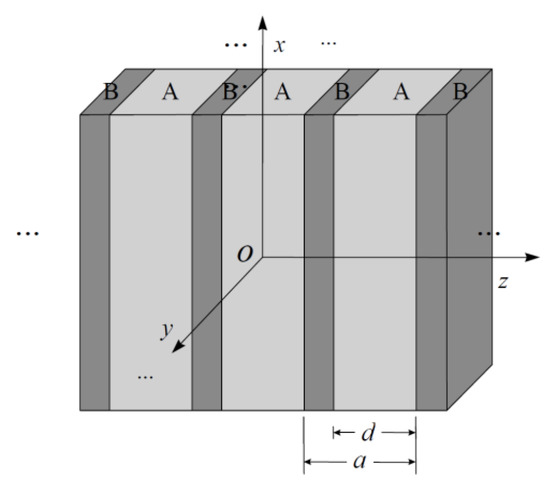
Figure 1.
One-dimensional (1D) photonic crystal or bilayer superlattice with periodicity in z-direction.
3.1. 1D Photonic Crystals with Isotropic Inclusion
Now, using Equation (35), we have numerically calculated the 6 × 6 matrix of the effective tensor of the bianisotropic response, in the local limit (→0) with a total number of nz = 101 waves. As an initial application, we consider photonic crystals composed of a homogeneous host and isotropic inclusions. Specifically, in Figure 2, we present the results for a superlattice whose unit cell is composed of a magnetic material, in this case isotropic ferrite, considered as medium “A”, and a dielectric material homogeneous to silicon, as medium “B”; the parameters considered for this calculation were: εA = 13ε0, μA = 8μ0 and εB = 12.25ε0, μB = μ0, respectively (ε0 and μ0 are the permittivity and permeability of the vacuum, respectively). In this figure we show the permittivity and the effective permeability as a function of the filling fraction f, note that εx = εy and μx = μy, since there is isotropy in the x − y plane. Figure 3 corresponds to a unit cell formed by ferrite in air; the parameters considered were: εA = 13ε0, μA = 8μ0 and εB = ε0, μB = μ0.
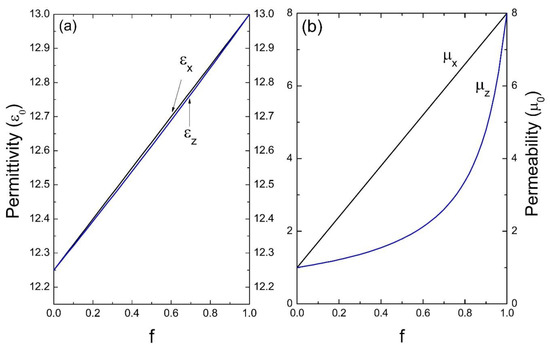
Figure 2.
Permittivity ε (a) and permeability μ (b) versus the filling fraction f (ε0 and μ0 are the units).
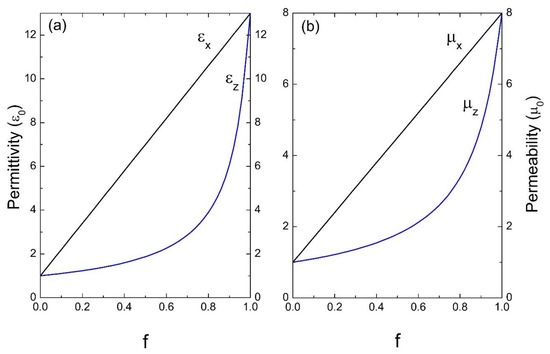
Figure 3.
Permittivity ε (a) and permeability μ (b) versus the filling fraction f (ε0 and μ0 are the units).
Next, we considered photonic crystals with high dielectric and magnetic contrast in their unit cell. Figure 4 corresponds to a system of common glass in a homogeneous dielectric as the host, the parameters used were: εA = 100ε0, μA = 200μ0 and εB = 2.25ε0, μB = μ0. Finally, in Figure 5, a medium of common glass in air is considered, whose parameters are: εA = 100ε0, μA = 200μ0 and εB = ε0, μB = μ0.
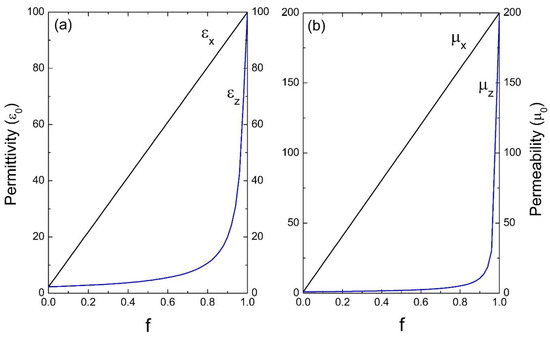
Figure 4.
Permittivity ε (a) and permeability μ (b) versus the filling fraction f (ε0 and μ0 are the units).
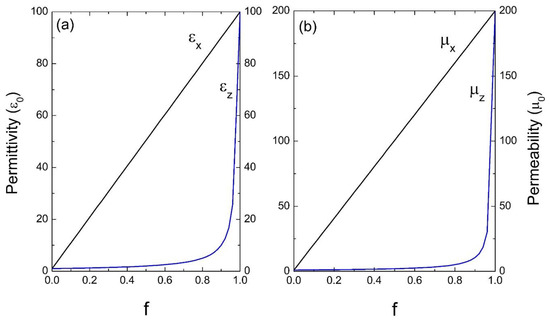
Figure 5.
Permittivity ε (a) and permeability μ (b) versus the filling fraction f (ε0 and μ0 are the units).
Figure 2, Figure 3, Figure 4 and Figure 5 indicate the averages of the permittivity and the permeability in the unit cell and it is observed that the increase in the values of εx (=εy) and μx (=μy), as well as in εz and μz in the function of the filling fraction present a linear and non-linear behavior, respectively. Therefore, our results describe the effective medium approach proposed by Rytov [15]—if the materials of the superlattice layers are local and isotropic, the permittivity tensor is diagonal with principal values [15]:
Here, the metal and dielectric layers are characterized by their permittivity, εm and εd; f is the metal filling fraction and z denotes the direction perpendicular to the planes of the layers in the superlattice. Equations similar to the previous ones are fulfilled for the magnetic media:
Evidently, when f →0, the medium “B” predominates and as the filling fraction increases, namely f →1, the material will correspond to the inclusion. On the other hand, in Figure 4 and Figure 5 it is observed how for the effective electric permittivity and the effective magnetic permeabilities in the z-component for filling fractions near 0.8, their values remain very close to the host, later ascending rapidly before reaching the value of inclusion. This is due to the high contrast dielectric and magnetic qualities of the materials in the unit cell, the contrast being defined as the ratio of medium “A” and medium “B”—that is, εA/εB and μA/μB, respectively. Note that this behavior is not presented in Figure 2 and Figure 3 due to the low dielectric and magnetic contrast between the host and the inclusion.
3.2. 1D Photonic Crystals with Anisotropic Inclusion
In the applications that follow, we calculate the effective parameters of a photonic crystal whose unit cell is formed by an anisotropic inclusion and isotropic background in the dielectric constant and magnetic permeability.
Figure 6a shows the results for a superlattice where the inclusion presents anisotropy in the dielectric constant; as can be observed, as the amount of the anisotropic medium increases (medium "A"), the effective response becomes anisotropic, creating three well-defined values—that is, when the filling fraction tends towards zero (f →0), the system is an isotropic homogenous medium with permittivity εB. In the opposite case, when f →1 the system is an anisotropic homogenous medium with permittivity εA. Note that εx and εy maintain a linear behavior determined by Equation (36), while the component εz is represented by a curve defined by the result of the inverse relationship of Equation (37). In the case of effective permeability (see Figure 6b), a linear behavior is observed, as determined by Equation (38), which indicates an isotropic behavior for any filling fraction of the inclusion. Moreover, from the inspection of Figure 6b, it is evident that μx = μy = μz, considering that both the inclusion and the host have a relative permeability approximately equal to one (vacuum permeability).
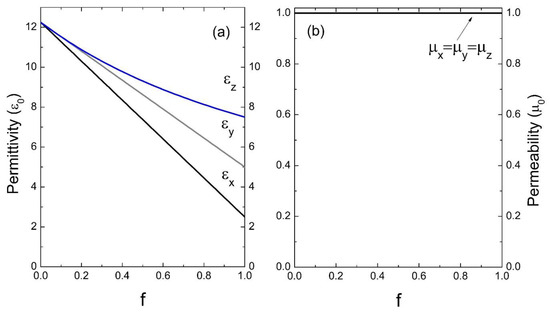
Figure 6.
Permittivity ε (a) and permeability μ (b) versus the filling fraction f (ε0 and μ0 are the units). The parameters used were: εAx = 2.5ε0, εAy = 5ε0, εAz = 7.5ε0, μA = μ0 (anisotropic media) and εB = 12.25ε0, μB = μ0 (isotropic media).
On the other hand, the effective parameters of a superlattice whose inclusion presents anisotropy in the magnetic permeability are determined. Therefore, the effective permittivity turns out to be isotropic throughout the filling fraction of the inclusion (see Figure 7a) and shows a linear behavior (εx = εy = εz), as determined in the first approximation by Equation (36). However, in Figure 7b, the situation is somewhat different because as the amount of the anisotropic medium increases, the effective response becomes anisotropic—that is, when f →0 the homogeneous medium is isotropic and when f →1 the homogeneous medium is clearly anisotropic. However, it should be noted that μx and μy maintain a linear behavior determined by Equation (38), while the μz component is represented by a curve which is defined by Equation (39).
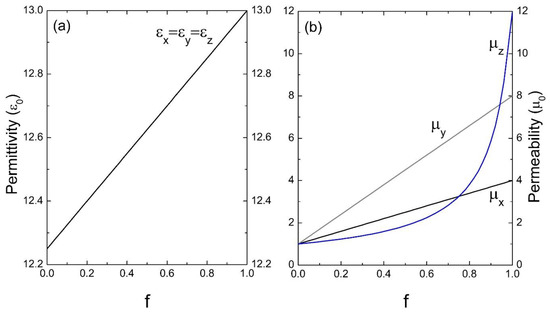
Figure 7.
Permittivity ε (a) and permeability μ (b) versus the filling fraction f (ε0 and μ0 are the units). The parameters used were: εA = 13ε0, μAx = 4μ0, μAy = 8μ0, μAz = 12μ0 and εB = 12.25ε0, μB = μ0.
Finally, Figure 8 shows the results of the effective response for a photonic crystal whose inclusion in its unit cell presents anisotropy in the dielectric permittivity and magnetic permeability. As can be seen in both graphs, the physical situation is similar to that already discussed in Figure 6a and Figure 7b for the effective permittivity and permeability, respectively, where it is basically noted that when increasing the filling fraction of the anisotropic medium, the effective response is anisotropic.
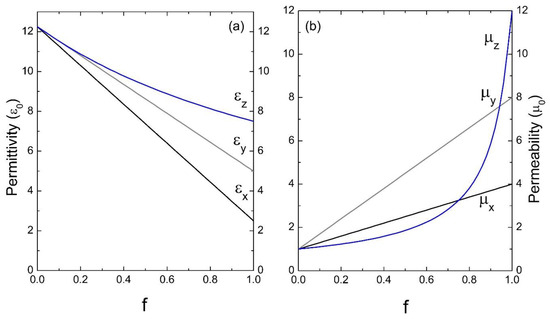
Figure 8.
Permittivity ε (a) and permeability μ (b) versus the filling fraction f (ε0 and μ0 are the units). The parameters used were: εAx = 2.5ε0, εAy = 5ε0, εAz = 7.5ε0, μAx = 4μ0, μAy = 8μ0, μAz = 12μ0 and εB = 12.25ε0, μB = μ0.
4. Conclusions
In this work, a homogenization theory for 1D magneto-dielectric photonic crystals was presented. The theory developed reports of analytical expressions that allow us to calculate the effective components of the permittivity and permeability tensors. In particular, we have analyzed the case of photonic crystals whose bilayer unitary cell is composed of a layer of dielectric material with inclusions of magnetic–isotropic and magnetic–anisotropic media, in the local limit, when the wavelength of the work frequency of the incident radiation on the medium is large compared to the period of the unit cell. The numerical implementation of the formulas provides results for new types of homogenized photonic metamaterials; in particular, we have studied theoretically the anisotropy of effective magnetic permeability and effective dielectric permittivity for homogenized magneto-dielectric binary superlattices versus the filling fraction. We demonstrated that the principal values for the components of the permeability and permittivity effective tensors describe a regime where Rytov’s formulas are valid. Our results may be useful for the better comprehension and design of metamaterials, due to the anisotropy that they present in electro-magnetic modes, which can be manufactured even with structures as simple superlattices.
Author Contributions
A.C.P.R., M.M.M., A.M.-S. and G.M.M. were in charge of the whole trial. J.F.M. kindly provided supervision to this project. R.C.A.L., H.V.L. and F.C.G. wrote the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
This work was partially supported by VIEP-BUAP. The authors also thank the support of PRODEP program.
Conflicts of Interest
The authors declare that they have no competing interests.
References
- Royer, F.; Varghese, B.; Gamet, E.; Neveu, S.; Jourlin, Y.; Jamon, D. Enhancement of Both Faraday and Kerr Effects with an All-Dielectric Grating Based on a Magneto-Optical Nanocomposite Material. ACS Omega 2020, 5, 2886–2892. [Google Scholar] [CrossRef] [PubMed]
- Staude, I.; Schilling, J. Metamaterial-inspired silicon nanophotonics. Nat. Photon. 2017, 11, 274–284. [Google Scholar] [CrossRef]
- Wang, L.; Li, Q. Stimuli-Directing Self-Organized 3D Liquid-Crystalline Nanostructures: From Materials Design to Photonic Applications. Adv. Funct. Mater. 2016, 26, 10–28. [Google Scholar] [CrossRef]
- Halevi, P.; Krokhin, A.; Arriaga, J. Photonic Crystal Optics and Homogenization of 2D Periodic Composites. Phys. Rev. Lett. 1999, 82, 719–726. [Google Scholar] [CrossRef]
- Krokhin, A.A.; Reyes, E. Homogenization of magnetodielectric photonic crystals. Phys. Rev. Lett. 2004, 93, 023904. [Google Scholar] [CrossRef] [PubMed]
- Silveirinha, M.G. Nonlocal homogenization model for a periodic array of ϵ-negative rods. Phys. Rev. E 2006, 73, 046612. [Google Scholar] [CrossRef] [PubMed]
- Smith, D.R.; Pendry, J.B. Homogenization of metamaterials by field averaging (invited paper). J. Opt. Soc. Am. B 2006, 23, 391–403. [Google Scholar] [CrossRef]
- Ouchetto, O.; Qiu, C.W.; Zouhdi, S.; Li, L.W.; Razek, A. Homogenization of 3-D periodic bianisotropic metamaterials. IEEE Trans. Microw. Theory Tech. 2006, 54, 3893–3898. [Google Scholar] [CrossRef]
- Reyes-Ayona, E.; Halevi, P. Mean field theory of metallo-dielectric photonic crystals with magnetic components: The long-wavelength limit. Proc. SPIE 2007, 6638, 1–7. [Google Scholar]
- Reyes-Avendaño, J.A.; Algredo-Badillo, U.; Halevi, P.; Pérez-Rodríguez, F. From photonic crystals to metamaterials: The bianisotropic response. New J. Phys. 2011, 13, 1–33. [Google Scholar] [CrossRef]
- Ciattoni, M.A.; Rizza, C. Nonlocal homogenization theory in metamaterials: Effective electromagnetic spatial dispersion and artificial chirality. Phys. Rev. B 2015, 91, 184207. [Google Scholar] [CrossRef]
- Krokhin, A.A.; Arriaga, J.; Gumen, L.N.; Drachev, V.P. High-frequency homogenization for layered hyperbolic metamaterials. Phys. Rev. B 2016, 93, 075418. [Google Scholar] [CrossRef]
- Maxim, A.; Gorlach, T.; Voytova, A.; Lapine, M.; Yuri, S.; Kivshar, P.; Belov, A. Nonlocal homogenization for nonlinear metamaterials. Phys. Rev. B 2016, 93, 165125. [Google Scholar]
- Konovalenko, A.; Pérez-Rodríguez, F. Nonlocal response of tunable photonic metamaterials with semiconductor inclusions. J. Opt. Soc. Am. B 2017, 34, 2031–2040. [Google Scholar] [CrossRef]
- Rytov, S.M. Electromagnetic properties of a finely stratified medium. Sov. Phys. JETP 1956, 2, 466–475. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).