Prediction of Strain Fatigue Life of HRB400 Steel Based on Meso-Deformation Inhomogeneity
Abstract
1. Introduction
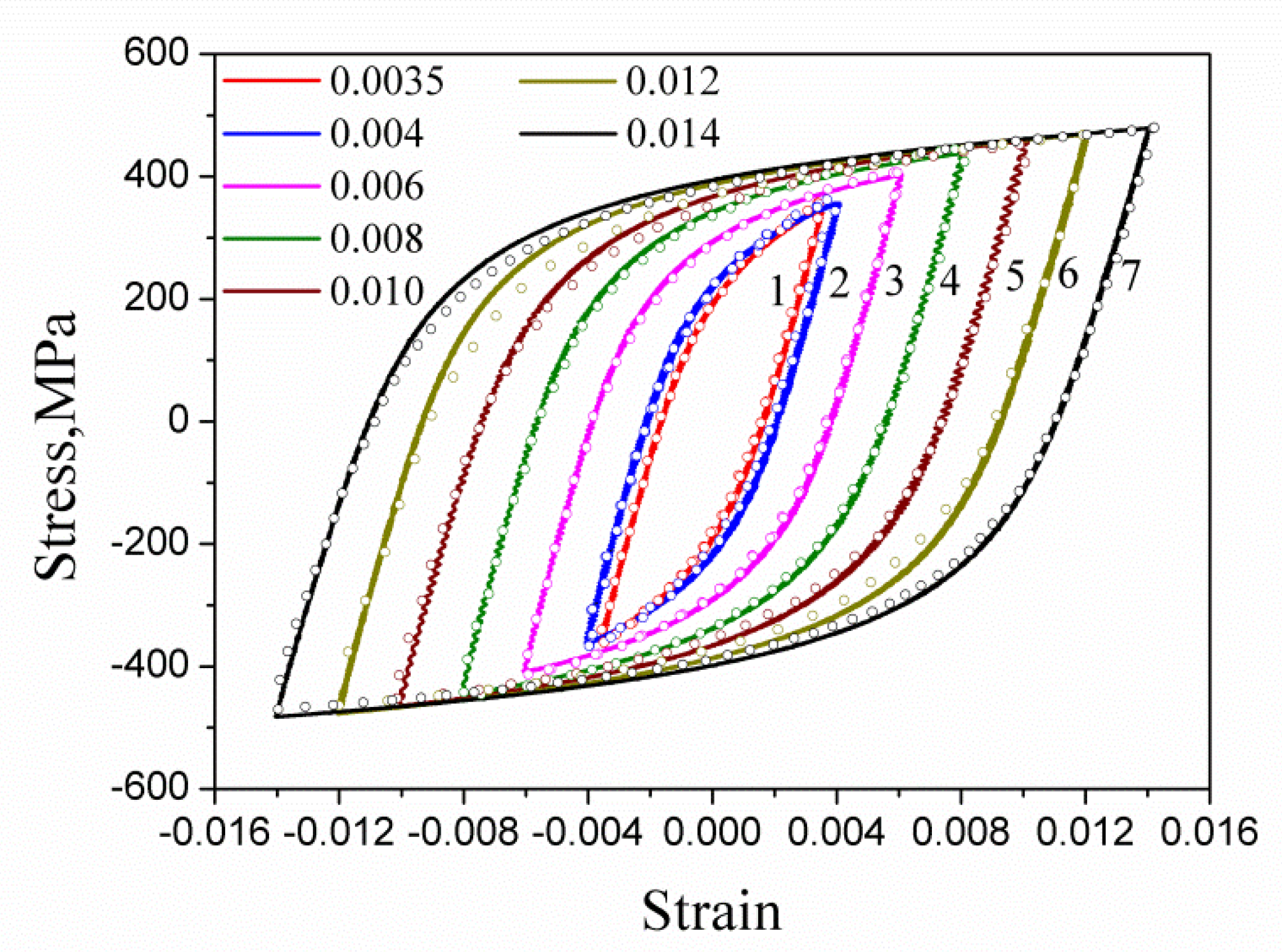
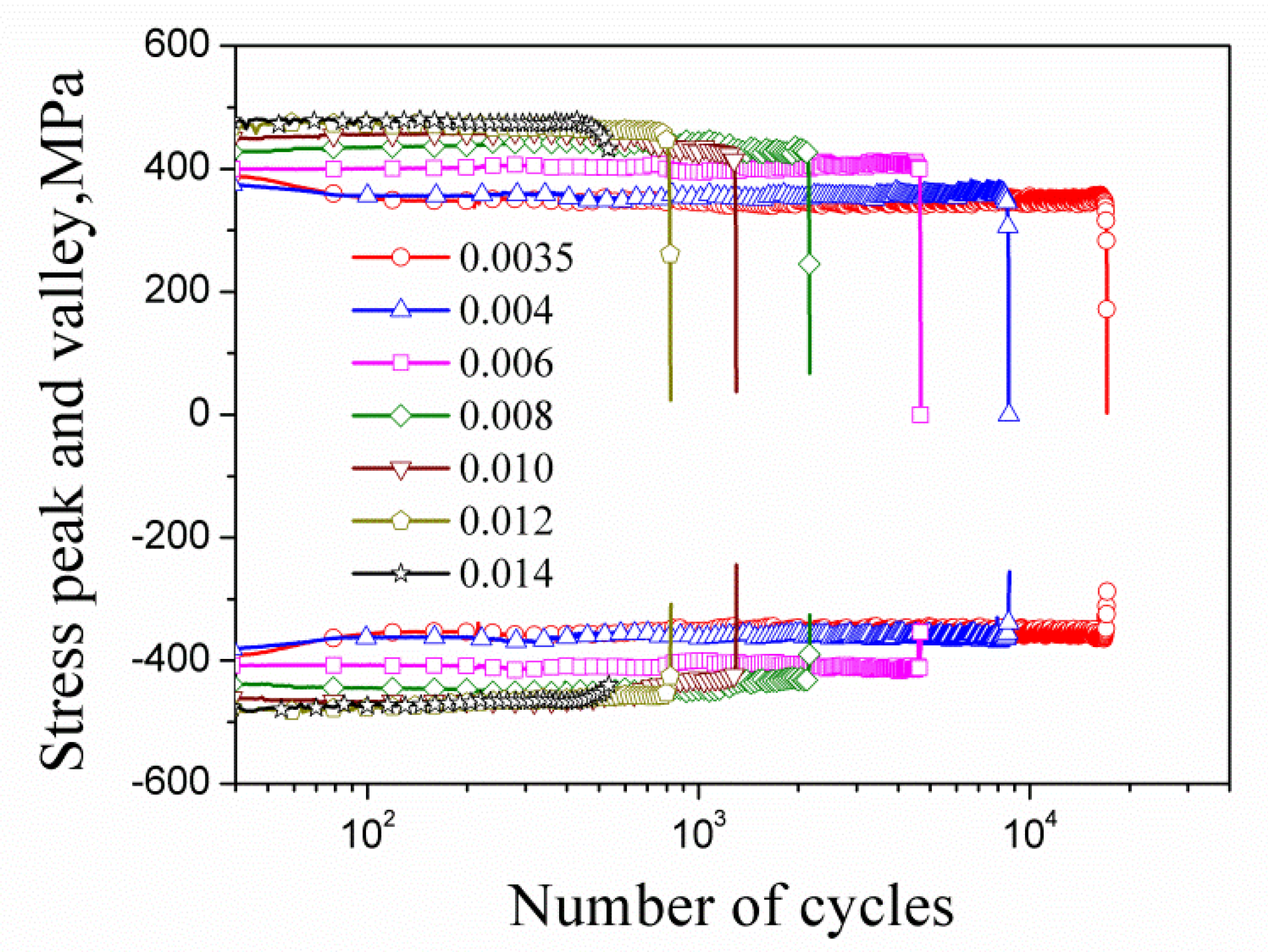
2. Material and Strain Fatigue Experiments
3. The Constitutive Model and the Material Model
3.1. The Crystal Plastic Constitutive Model
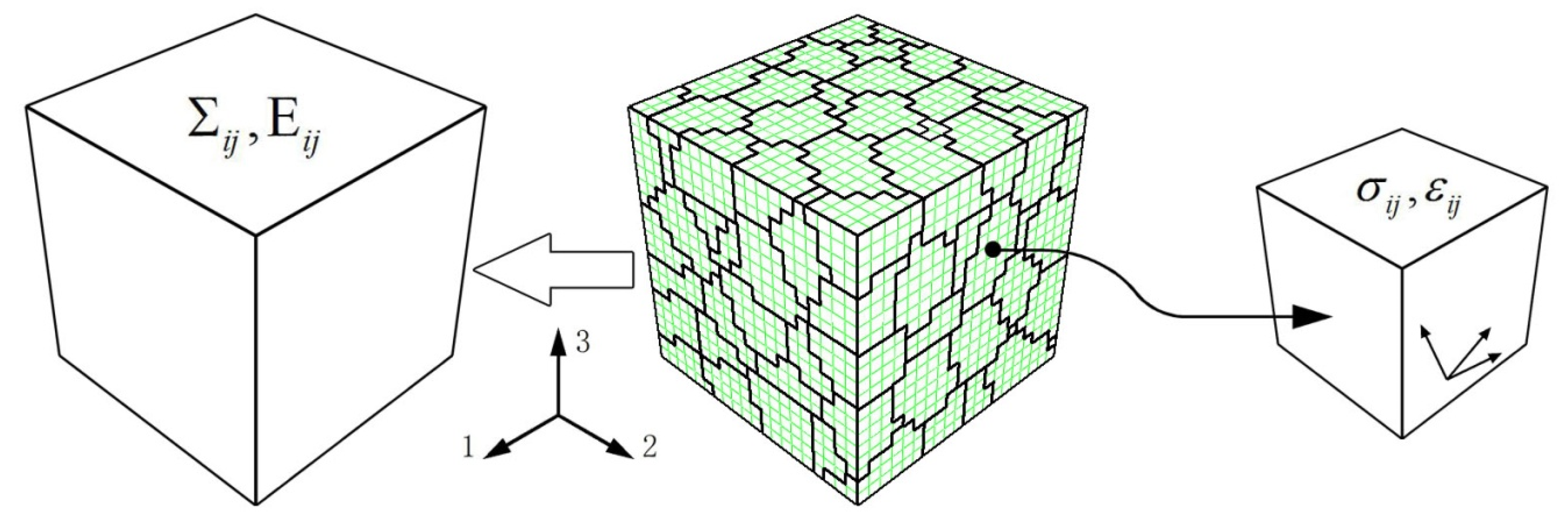
3.2. Polycrystalline RVE Material Model
3.3. Model Parameters of Crystal Plastic Constitutive Model
4. Low-Cycle Fatigue Life Prediction Based on Inhomogeneity of Material Deformation
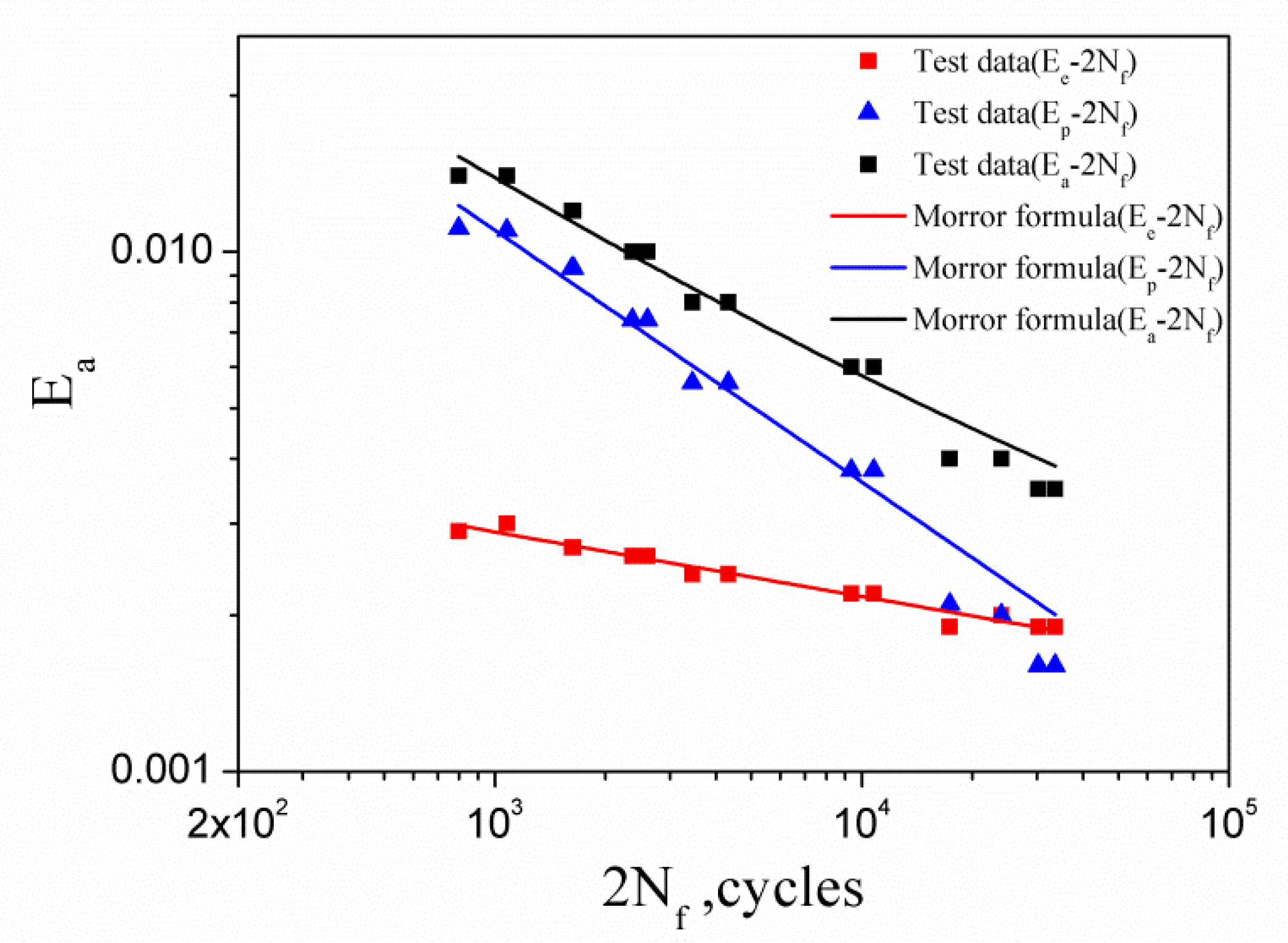
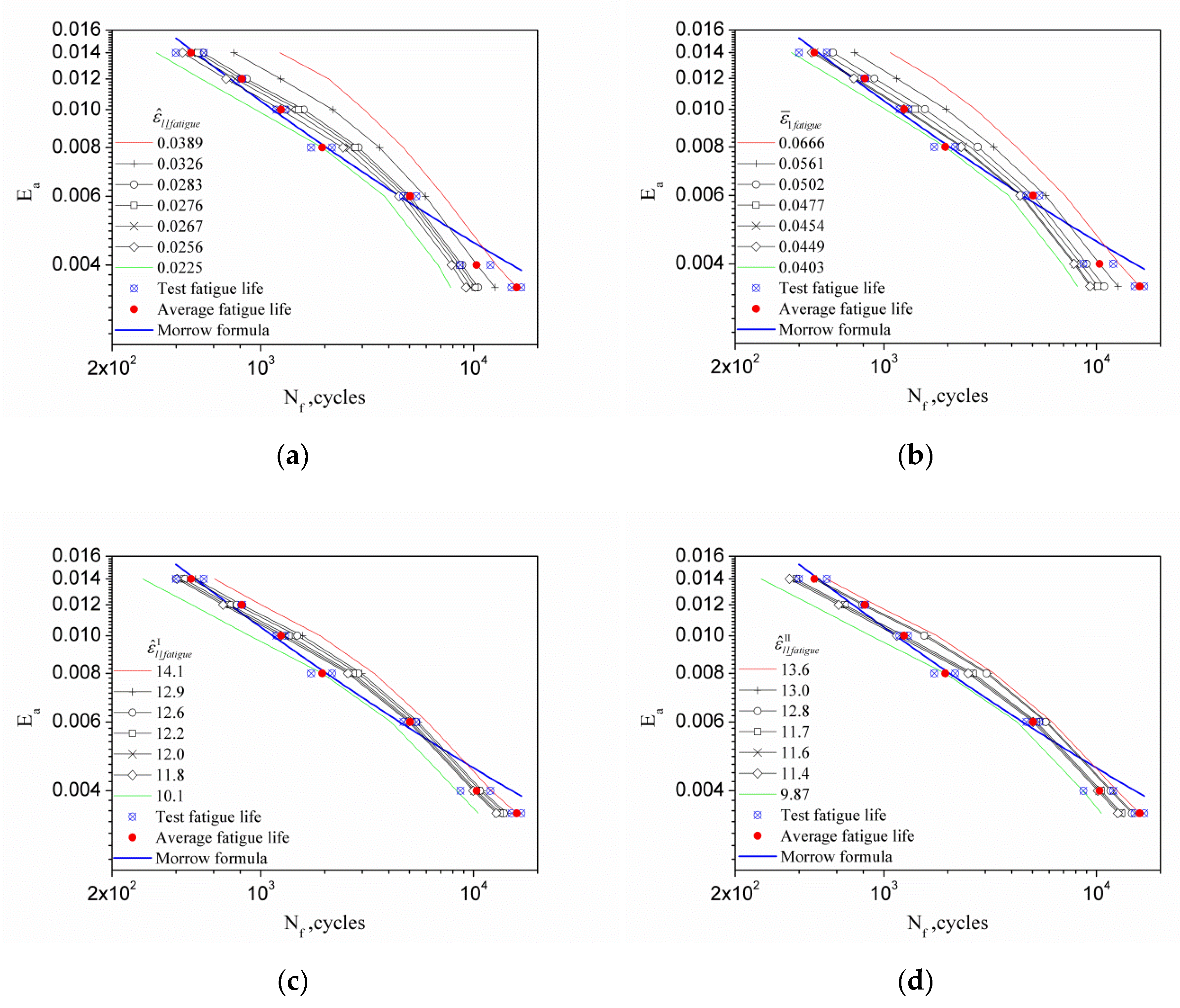
4.1. The Indicator Parameters of Material Deformation Inhomogeneity
4.2. The Parameters of Deformation Inhomogeneity Considering the Influence of Peak Stress
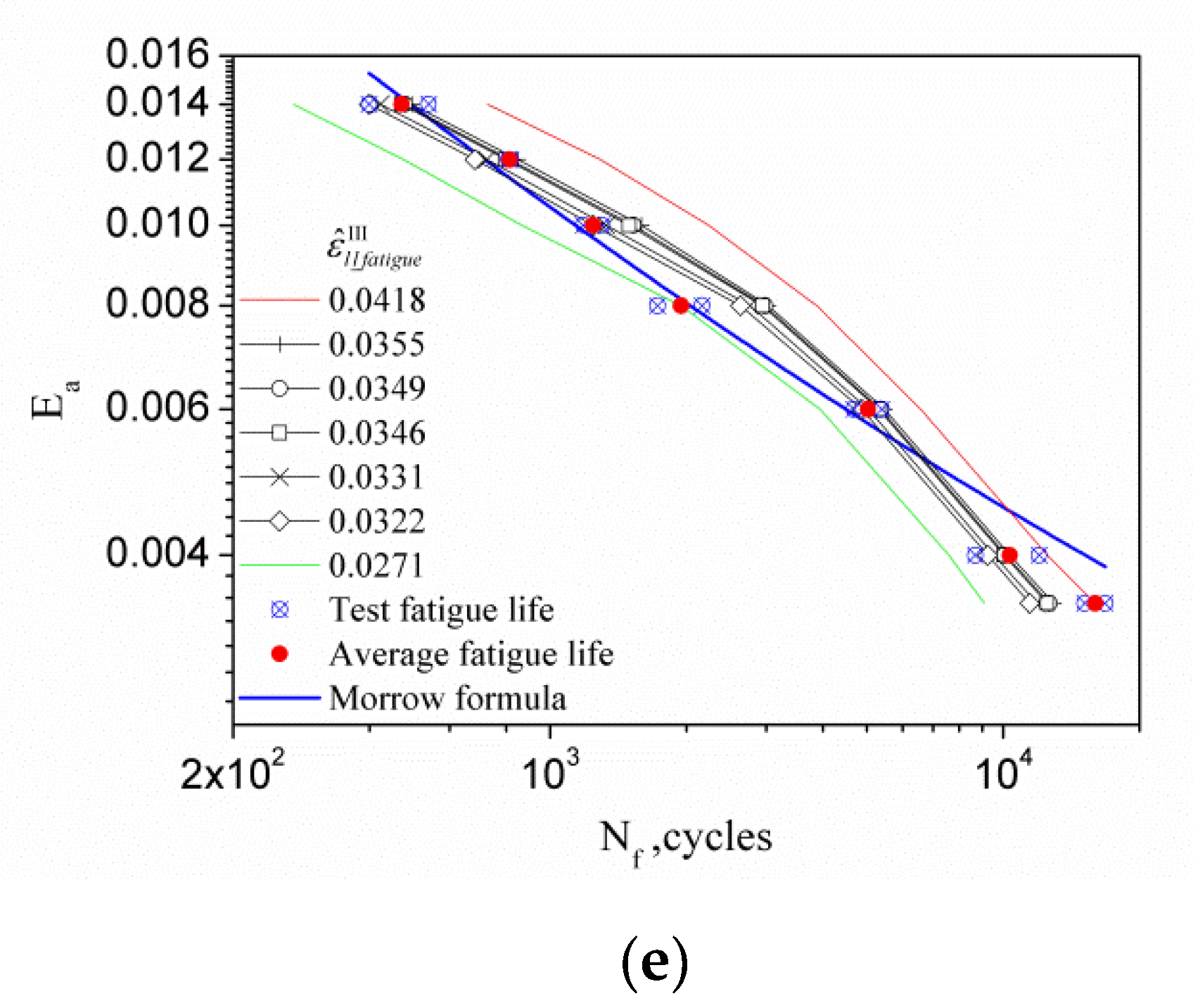
4.3. Prediction of Low Cycle Fatigue Life of Materials
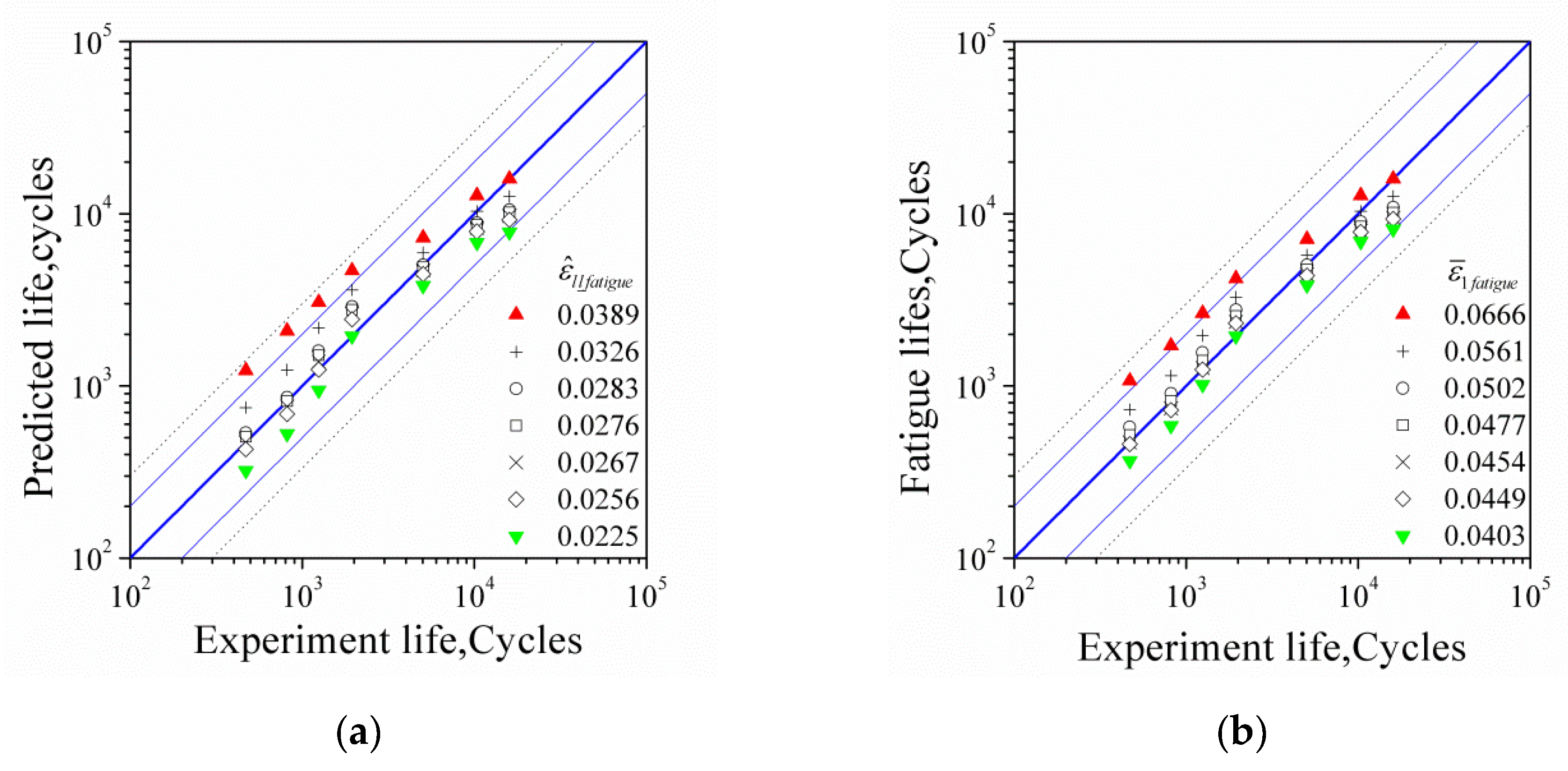
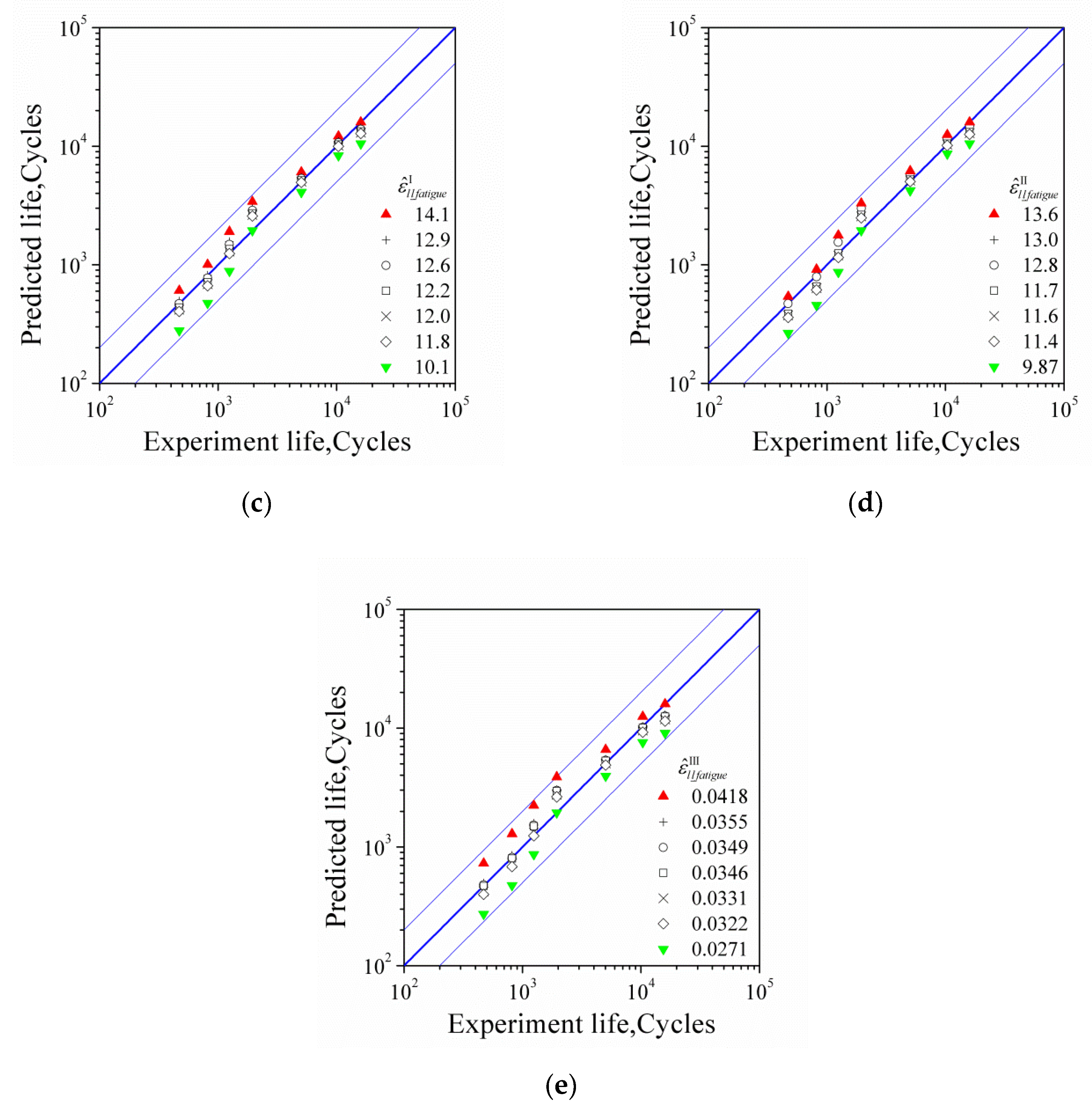
4.4. Error Test of Life Prediction
5. Conclusions
- (1)
- The fatigue life prediction method based on the parameter of meso-deformation inhomogeneity is also applicable for BCC materials.
- (2)
- Considering the influence of the stress peak, three improved FIPs are suggested on the basis of the indicator parameter . These new parameters are similar to each other in describing the evolution of the inhomogeneity of the meso-deformation along with the cycle.
- (3)
- More reasonable fatigue life prediction results can be obtained using the FIPs proposed in this paper, which means that the description of fatigue damage accumulation by the new indicator parameters is closer to the actual process.
Author Contributions
Funding
Conflicts of Interest
References
- Lee, Y.-L.; Pan, J.; Hathaway, R.; Barkey, M. Fatigue Testing and Analysis: Theory and Practice; Elsevier: Oxford, UK, 2005. [Google Scholar]
- Wang, Z.-Y.; Wang, Q.-Y.; Cao, M. Experimental study on fatigue behaviour of Shot-Peened Open-Hole steel plates. Materials 2017, 10, 996. [Google Scholar] [CrossRef] [PubMed]
- Ni, K.; Mahadevan, S. Strain-based probabilistic fatigue life prediction of spot-welded joints. Int. J. Fatigue 2004, 26, 763–772. [Google Scholar] [CrossRef]
- Ince, A.; Glinka, G. A generalized fatigue damage parameter for multiaxial fatigue life prediction under proportional and non-proportional loadings. Int. J. Fatigue 2014, 62, 34–41. [Google Scholar] [CrossRef]
- Wang, G.; Che, X.; Zhang, Z.; Zhang, H.; Zhang, S.; Li, Z.; Sun, J. Microstructure and Low-Cycle Fatigue Behavior of Al-9Si-4Cu-0.4Mg-0.3Sc Alloy with Different Casting States. Materials 2020, 13, 638. [Google Scholar] [CrossRef] [PubMed]
- Ahmadzadeh, G.R.; Varvani-Farahani, A. Fatigue damage and life evaluation of SS304 and Al 7050-T7541 alloys under various multiaxial strain paths by means of energy-based Fatigue damage models. Mech. Mater. 2016, 98, 59–70. [Google Scholar] [CrossRef]
- Radhakrishnan, V.M. An analysis of low cycle fatigue based on hysteresis energy. Fatigue Fract. Eng. Mater. Struct. 1980, 3, 75–84. [Google Scholar] [CrossRef]
- Jiang, Y.; Ott, W.; Baum, C.; Vormwald, M.; Nowack, H. Fatigue life predictions by integrating EVICD fatigue damage model and an advanced cyclic plasticity theory. Int. J. Plast. 2009, 25, 780–801. [Google Scholar] [CrossRef]
- Feng, E.S.; Wang, X.G.; Jiang, C. A new multiaxial fatigue model for life prediction based on energy dissipation evaluation. Int. J. Fatigue 2019, 122, 1–8. [Google Scholar] [CrossRef]
- Fan, Y.-N.; Shi, H.-J.; Tokuda, K. A generalized hysteresis energy method for fatigue and creep-fatigue life prediction of 316L (N). Mater. Sci. Eng. A 2015, 625, 205–212. [Google Scholar] [CrossRef]
- Ren, X.; Yang, S.; Wen, G.; Zhao, W. A Crystal-Plasticity Cyclic Constitutive Model for the Ratchetting of Polycrystalline Material Considering Dislocation Substructures. Acta Mech. Solida Sin. 2020, 33, 268–280. [Google Scholar] [CrossRef]
- Farooq, H.; Cailletaud, G.; Forest, S.; Ryckelynck, D. Crystal plasticity modeling of the cyclic behavior of polycrystalline aggregates under non-symmetric uniaxial loading: Global and local analyses. Int. J. Plast. 2020, 126, 102619. [Google Scholar] [CrossRef]
- Yuan, G.-J.; Zhang, X.-C.; Chen, B.; Tu, S.-T.; Zhang, C.-C. Low-cycle fatigue life prediction of a polycrystalline nickel-base superalloy using crystal plasticity modelling approach. J. Mater. Sci. Technol. 2020, 38, 28–38. [Google Scholar] [CrossRef]
- Li, D.-F.; Barrett, R.A.; O’Donoghue, P.E.; O’Dowd, N.P.; Leen, S.B. A multi-scale crystal plasticity model for cyclic plasticity and low-cycle fatigue in a precipitate-strengthened steel at elevated temperature. J. Mech. Phys. Solids 2017, 101, 44–62. [Google Scholar] [CrossRef]
- Cruzado, A.; Lucarini, S.; LLorca, J.; Segurado, J. Crystal plasticity simulation of the effect of grain size on the fatigue behavior of polycrystalline Inconel 718. Int. J. Fatigue 2018, 113, 236–245. [Google Scholar] [CrossRef]
- Cruzado, A.; Lucarini, S.; LLorca, J.; Segurado, J. Microstructure-based fatigue life model of metallic alloys with bilinear Coffin-Manson behavior. Int. J. Fatigue 2018, 107, 40–48. [Google Scholar] [CrossRef]
- Lucarini, S.; Segurado, J. An upscaling approach for micromechanics based fatigue: From RVEs to specimens and component life prediction. Int. J. Fract. 2019, 1–16. [Google Scholar] [CrossRef]
- Liu, L.; Wang, J.; Zeng, T.; Yao, Y. Crystal plasticity model to predict fatigue crack nucleation based on the phase transformation theory. Acta Mech. Sin. 2019, 35, 1033–1043. [Google Scholar] [CrossRef]
- Zhang, K.-S.; Shi, Y.-K.; Ju, J.W. Grain-level statistical plasticity analysis on strain cycle fatigue of a FCC metal. Mech. Mater. 2013, 64, 76–90. [Google Scholar] [CrossRef]
- Zhang, K.-S.; Ju, J.W.; Li, Z.; Bai, Y.-L.; Brocks, W. Micromechanics based fatigue life prediction of a polycrystalline metal applying crystal plasticity. Mech. Mater. 2015, 85, 16–37. [Google Scholar] [CrossRef]
- Zhang, M.-H.; Shen, X.-H.; He, L.; Zhang, K.-S. Application of differential entropy in characterizing the deformation inhomogeneity and life prediction of low-cycle fatigue of metals. Materials 2018, 11, 1917. [Google Scholar] [CrossRef] [PubMed]
- Liu, G.-L.; Zhang, K.-S.; Zhong, X.-C.; Ju, J.W. Analysis of meso-inhomogeneous deformation on a metal material surface under low-cycle fatigue. Acta Mech. Solida Sin. 2017, 30, 557–572. [Google Scholar] [CrossRef]
- Hutchinson, J.W. Bounds and self-consistent estimates for creep of polycrystalline materials. Proc. R. Soc. A Math. Phys. 1976, 348, 101–127. [Google Scholar]
- Chaboche, J.L. Constitutive equations for cyclic plasticity and cyclic viscoplasticity. Int. J. Plast. 1989, 5, 247–302. [Google Scholar] [CrossRef]
- Feng, L.; Zhang, G.; Zhang, K.-S. Discussion of cyclic plasticity and viscoplasticity of single crystal nickel-based superalloy in large strain analysis: Comparison of anisotropic macroscopic model and crystallographic model. Int. J. Mech. Sci. 2004, 46, 1157–1171. [Google Scholar]
- Zhang, K.S.; Shi, Y.K.; Xu, L.B.; Yu, D.K. Anisotropy of yielding/hardening and micro inhomogeneity of deforming/rotating for a polycrystalline metal under cyclic tension–compression. Acta Metall. Sin. 2011, 47, 1292–1300. [Google Scholar]
- Pan, J.; Rice, J.R. Rate sensitivity of plastic flow and implications for yield-surface vertices. Int. J. Solids Struct. 1983, 19, 973–987. [Google Scholar] [CrossRef]
- Hutchinson, J. Elastic-plastic behaviour of polycrystalline metals and composites. Proc. R. Soc. A Math. Phys. 1970, 319, 247–272. [Google Scholar]
- Chang, Y.W.; Asaro, R.J. An experimental study of shear localization in aluminum-copper single crystals. Acta Metall. 1981, 29, 241–257. [Google Scholar] [CrossRef]
- Hill, R.; Rice, J.R. Constitutive analysis of elastic-plastic crystals at arbitrary strain. J. Mech. Phys. Solids 1972, 20, 401–413. [Google Scholar] [CrossRef]
- Needleman, A.; Asaro, R.; Lemonds, J.; Peirce, D. Finite element analysis of crystalline solids. Comput. Methods Appl. Mech. Eng. 1985, 52, 689–708. [Google Scholar] [CrossRef]
- Asaro, R.J.; Rice, J.R. Strain localization in ductile single crystals. J. Mech. Phys. Solids 1977, 25, 309–338. [Google Scholar] [CrossRef]



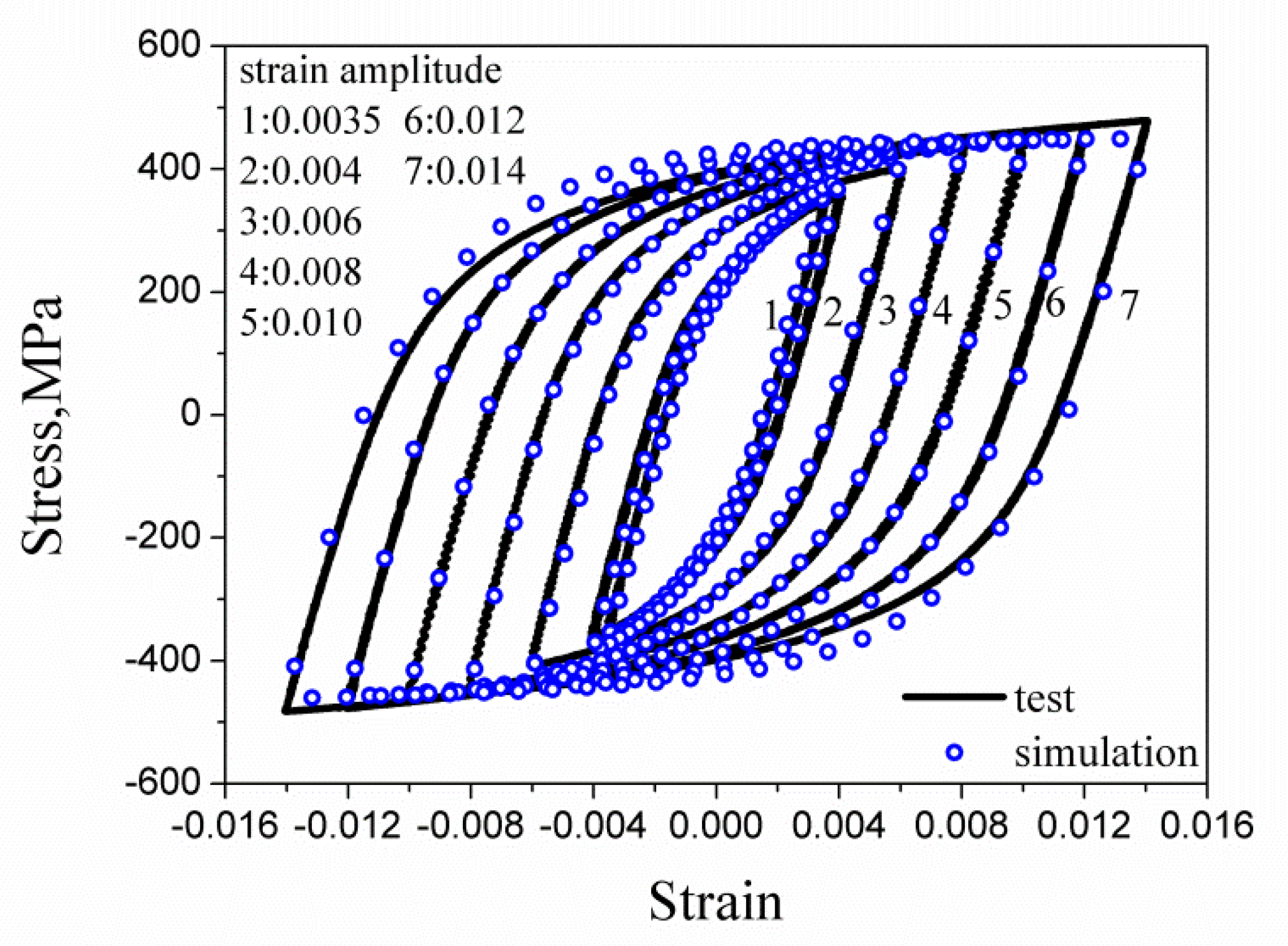
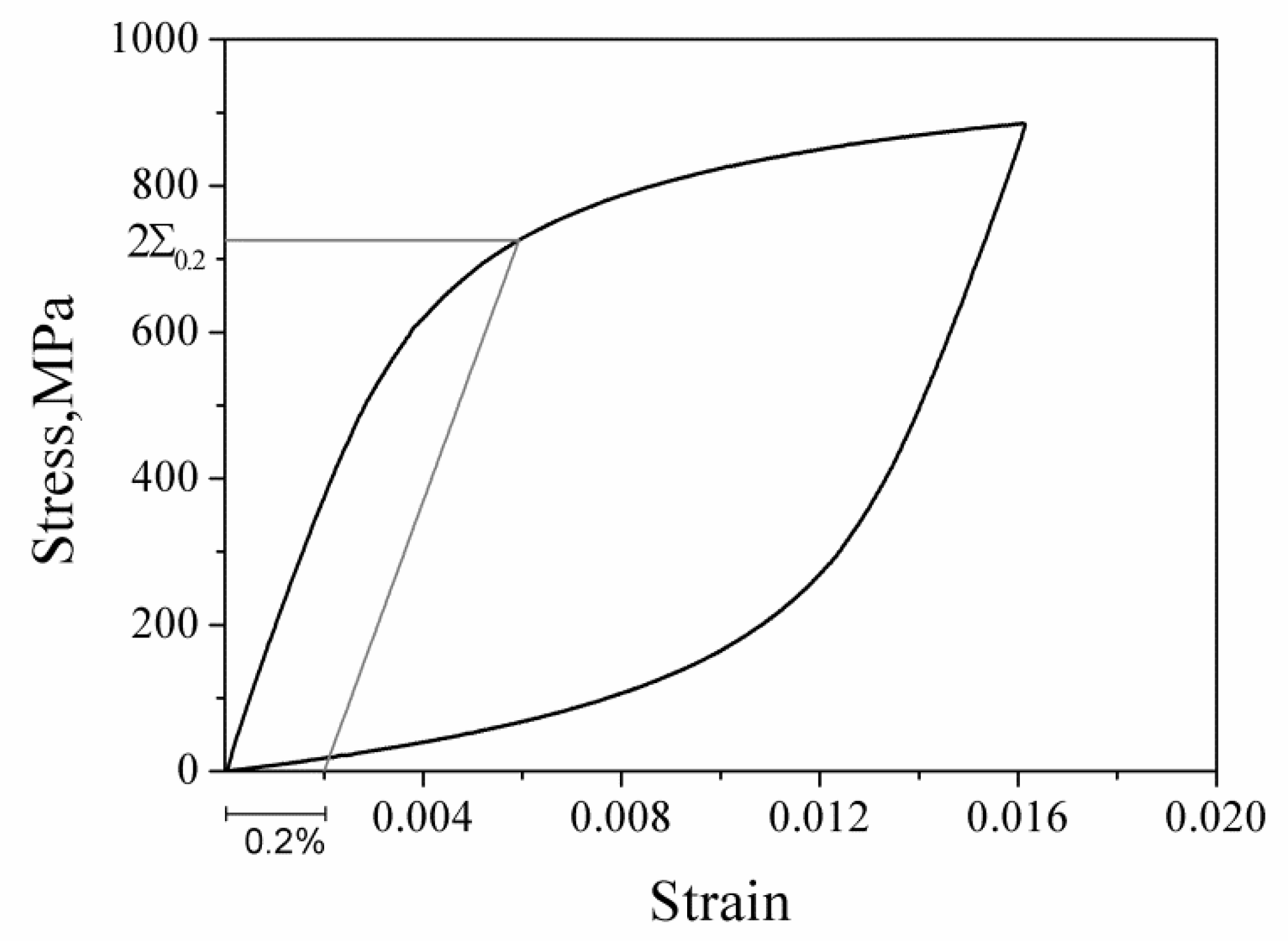
| C | Si | Mn | P | S | Ceq | Fe |
|---|---|---|---|---|---|---|
| 0.23 | 0.37 | 1.30 | 0.032 | 0.015 | 0.48 | rest |
| E/MPa | G/MPa | /% | /% | ||||
|---|---|---|---|---|---|---|---|
| 201,000 | 75,100 | 0.34 | 410 | 615 | 33.7 | 58.2 | 0.871 |
| 0.0035 | 0.004 | 0.006 | 0.008 | 0.010 | 0.012 | 0.014 | |
|---|---|---|---|---|---|---|---|
| 16,800/15,128 | 8681/12,009 | 4680/5392 | 2165/1727 | 1185/1302 | 810/820 | 399/540 | |
| 15964 | 10341 | 5036 | 1946 | 1244 | 815 | 470 |
| Elastic Constants | Material Parameters of the Crystal Viscoplastic Model | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| GPa | GPa | GPa | MPa | MPa | MPa | GPa | GPa | p | q | k | |||
| 293.4 | 158.0 | 67.6 | 103 | 109 | 40 | 31 | 0.42 | 0 | 0 | 0 | 0.001 | 1 | 200 |
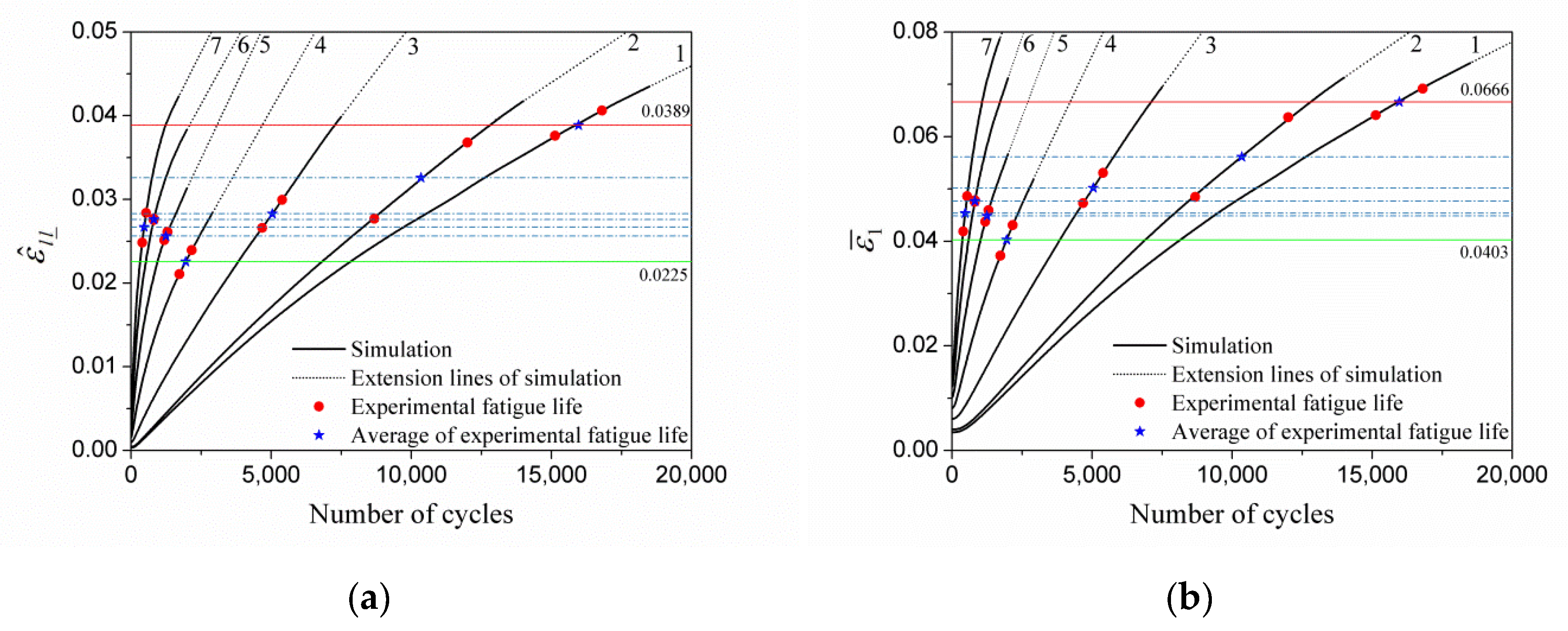
| Ea | Test Life (Average) | |||||
|---|---|---|---|---|---|---|
| 0.0035 | 15964 | 0.0389 | 0.0666 | 14.1 | 13.6 | 0.0418 |
| 0.004 | 10341 | 0.0326 | 0.0561 | 12.2 | 11.6 | 0.0355 |
| 0.006 | 5036 | 0.0283 | 0.0502 | 12.0 | 11.4 | 0.0331 |
| 0.008 | 1946 | 0.0225 | 0.0403 | 10.1 | 9.87 | 0.0271 |
| 0.010 | 1244 | 0.0256 | 0.0449 | 11.8 | 11.7 | 0.0322 |
| 0.012 | 815 | 0.0276 | 0.0477 | 12.9 | 13.0 | 0.0349 |
| 0.014 | 470 | 0.0267 | 0.0454 | 12.6 | 12.8 | 0.0346 |
| 0.0389 Ea = 0.0035 | 0.0326 Ea = 0.004 | 0.0283 Ea = 0.0.006 | 0.0225 Ea = 0.008 | 0.0256 Ea = 0.010 | 0.0276 Ea = 0.012 | 0.0267 Ea = 0.014 | Test Life (Average) | |
|---|---|---|---|---|---|---|---|---|
| 0.0035 | 15,964 | 12,611 | 10,526 | 7819 | 9210 | 10,187 | 9732 | 15,964 |
| 0.004 | 12,800 | 10,341 | 8844 | 6807 | 7892 | 8609 | 8286 | 10,341 |
| 0.006 | 7262 | 5939 | 5036 | 3822 | 4466 | 4894 | 4704 | 5036 |
| 0.008 | 4681 | 3615 | 2885 | 1946 | 2438 | 2772 | 2619 | 1946 |
| 0.010 | 3061 | 2176 | 1597 | 945 | 1244 | 1506 | 1385 | 1244 |
| 0.012 | 2083 | 1241 | 858 | 525 | 687 | 815 | 759 | 815 |
| 0.014 | 1230 | 748 | 534 | 322 | 429 | 506 | 470 | 470 |
| 0.0666 Ea = 0.0035 | 0.0561 Ea = 0.004 | 0.0502 Ea = 0.006 | 0.0403 Ea = 0.008 | 0.0449 Ea = 0.010 | 0.0477 Ea = 0.012 | 0.0454 Ea = 0.014 | Test life (Average) | |
|---|---|---|---|---|---|---|---|---|
| 0.0035 | 15,964 | 12,625 | 10,873 | 8148 | 9344 | 10,127 | 9480 | 15,964 |
| 0.004 | 12,802 | 10,341 | 8988 | 6898 | 7842 | 8443 | 7950 | 10,341 |
| 0.006 | 7109 | 5769 | 5036 | 3849 | 4382 | 4725 | 4444 | 5036 |
| 0.008 | 4212 | 3281 | 2765 | 1946 | 2312 | 2545 | 2354 | 1946 |
| 0.010 | 2699 | 1961 | 1562 | 1016 | 1244 | 1404 | 1271 | 1244 |
| 0.012 | 1712 | 1147 | 904 | 587 | 723 | 815 | 739 | 815 |
| 0.014 | 1071 | 728 | 577 | 367 | 458 | 518 | 470 | 470 |
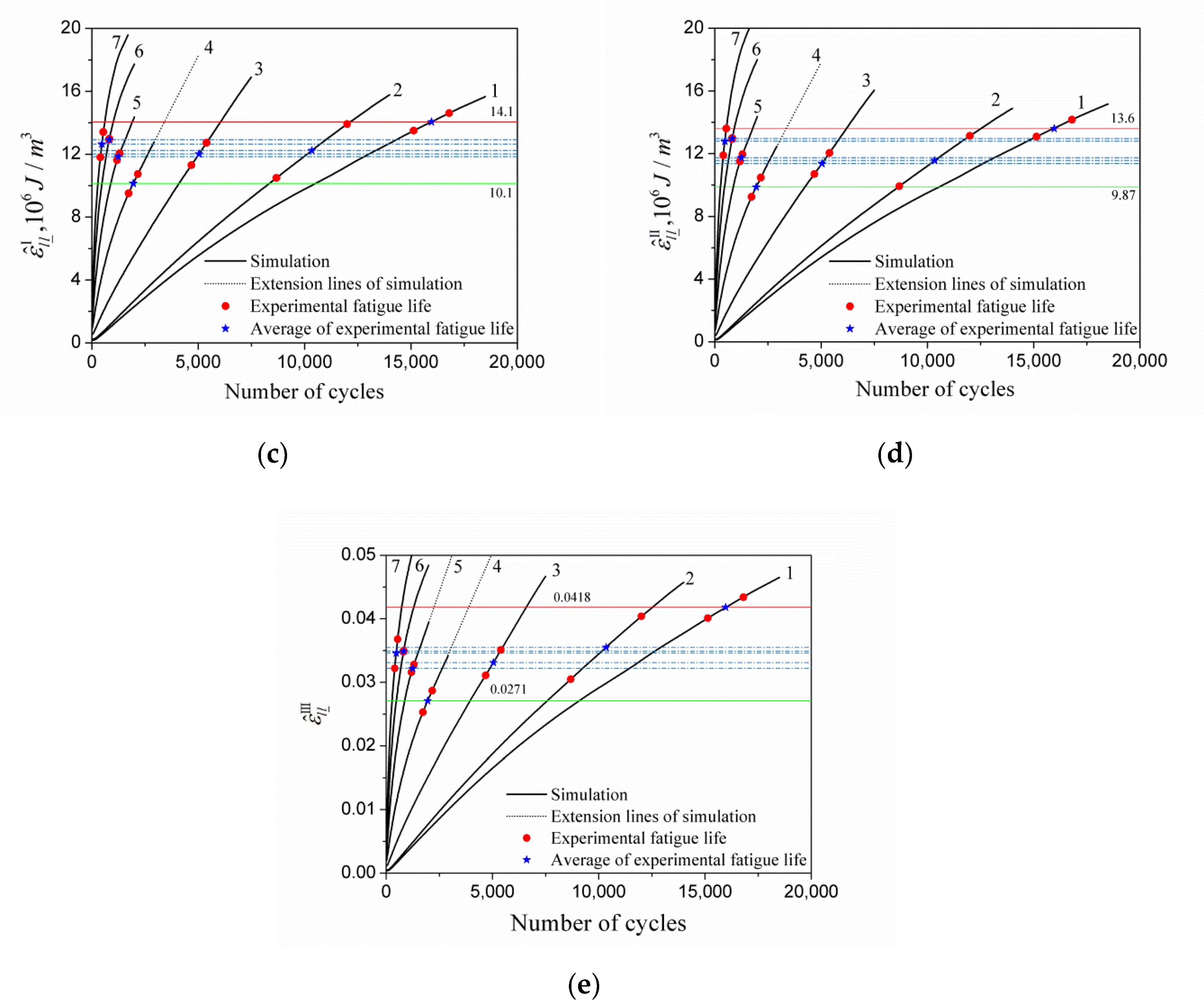
| 14.1 Ea = 0.0035 | 12.2 Ea = 0.004 | 12.0 Ea = 0.006 | 10.1 Ea = 0.008 | 11.8 Ea = 0.010 | 12.9 Ea = 0.012 | 12.6 Ea = 0.014 | Test Life (Average) | |
|---|---|---|---|---|---|---|---|---|
| 0.0035 | 15,964 | 13,345 | 13,031 | 10,514 | 12,801 | 14,322 | 13,931 | 15,964 |
| 0.004 | 12,147 | 10,341 | 10,133 | 8345 | 9974 | 11,005 | 10,733 | 10,341 |
| 0.006 | 6049 | 5147 | 5036 | 4094 | 4951 | 5491 | 5353 | 5036 |
| 0.008 | 3411 | 2718 | 2635 | 1946 | 2572 | 2981 | 2874 | 1946 |
| 0.010 | 1903 | 1356 | 1292 | 885 | 1244 | 1569 | 1483 | 1244 |
| 0.012 | 1005 | 714 | 687 | 475 | 665 | 815 | 772 | 815 |
| 0.014 | 606 | 436 | 418 | 279 | 404 | 494 | 470 | 470 |
| 13.6 Ea = 0.0035 | 11.6 Ea = 0.004 | 11.4 Ea = 0.006 | 9.87 Ea = 0.008 | 11.7 Ea = 0.010 | 13.0 Ea = 0.012 | 12.8 Ea = 0.014 | Test Life (Average) | |
|---|---|---|---|---|---|---|---|---|
| 0.0035 | 15,964 | 12,886 | 12,617 | 10,542 | 13,151 | 14,944 | 14,699 | 15,964 |
| 0.004 | 12,514 | 10,341 | 10,152 | 8633 | 10,527 | 11,805 | 11,627 | 10,341 |
| 0.006 | 6189 | 5137 | 5036 | 4235 | 5235 | 5864 | 5778 | 5036 |
| 0.008 | 3303 | 2565 | 2493 | 1946 | 2635 | 3109 | 3043 | 1946 |
| 0.010 | 1777 | 1197 | 1152 | 867 | 1244 | 1597 | 1549 | 1244 |
| 0.012 | 913 | 635 | 613 | 456 | 656 | 815 | 792 | 815 |
| 0.014 | 540 | 374 | 360 | 265 | 387 | 483 | 470 | 470 |
| 0.0418 Ea = 0.0035 | 0.0355 Ea = 0.004 | 0.0331 Ea = 0.006 | 0.0271 Ea = 0.008 | 0.0322 Ea = 0.010 | 0.0349 Ea = 0.012 | 0.0346 Ea = 0.014 | Test Life (Average) | |
|---|---|---|---|---|---|---|---|---|
| 0.0035 | 15,964 | 12,912 | 11,845 | 9084 | 11,447 | 12,635 | 12,499 | 15,964 |
| 0.004 | 12,520 | 10,341 | 9542 | 7580 | 9241 | 10,140 | 10,042 | 10,341 |
| 0.006 | 6584 | 5470 | 5036 | 3945 | 4876 | 5363 | 5310 | 5036 |
| 0.008 | 3874 | 3033 | 2762 | 1946 | 2634 | 2979 | 2940 | 1946 |
| 0.010 | 2242 | 1591 | 1331 | 867 | 1244 | 1527 | 1495 | 1244 |
| 0.012 | 1291 | 849 | 725 | 475 | 683 | 815 | 800 | 815 |
| 0.014 | 728 | 496 | 423 | 272 | 399 | 478 | 470 | 470 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, L.; Zeng, B.; Lu, D.; Gao, Y.; Zhang, K. Prediction of Strain Fatigue Life of HRB400 Steel Based on Meso-Deformation Inhomogeneity. Materials 2020, 13, 1464. https://doi.org/10.3390/ma13061464
Jin L, Zeng B, Lu D, Gao Y, Zhang K. Prediction of Strain Fatigue Life of HRB400 Steel Based on Meso-Deformation Inhomogeneity. Materials. 2020; 13(6):1464. https://doi.org/10.3390/ma13061464
Chicago/Turabian StyleJin, Lili, Bin Zeng, Damin Lu, Yingjun Gao, and Keshi Zhang. 2020. "Prediction of Strain Fatigue Life of HRB400 Steel Based on Meso-Deformation Inhomogeneity" Materials 13, no. 6: 1464. https://doi.org/10.3390/ma13061464
APA StyleJin, L., Zeng, B., Lu, D., Gao, Y., & Zhang, K. (2020). Prediction of Strain Fatigue Life of HRB400 Steel Based on Meso-Deformation Inhomogeneity. Materials, 13(6), 1464. https://doi.org/10.3390/ma13061464





