Experimental Evaluation of Mode II fracture Properties of Eucalyptus globulus L.
Abstract
1. Introduction
2. Materials and Methods
2.1. Raw Material
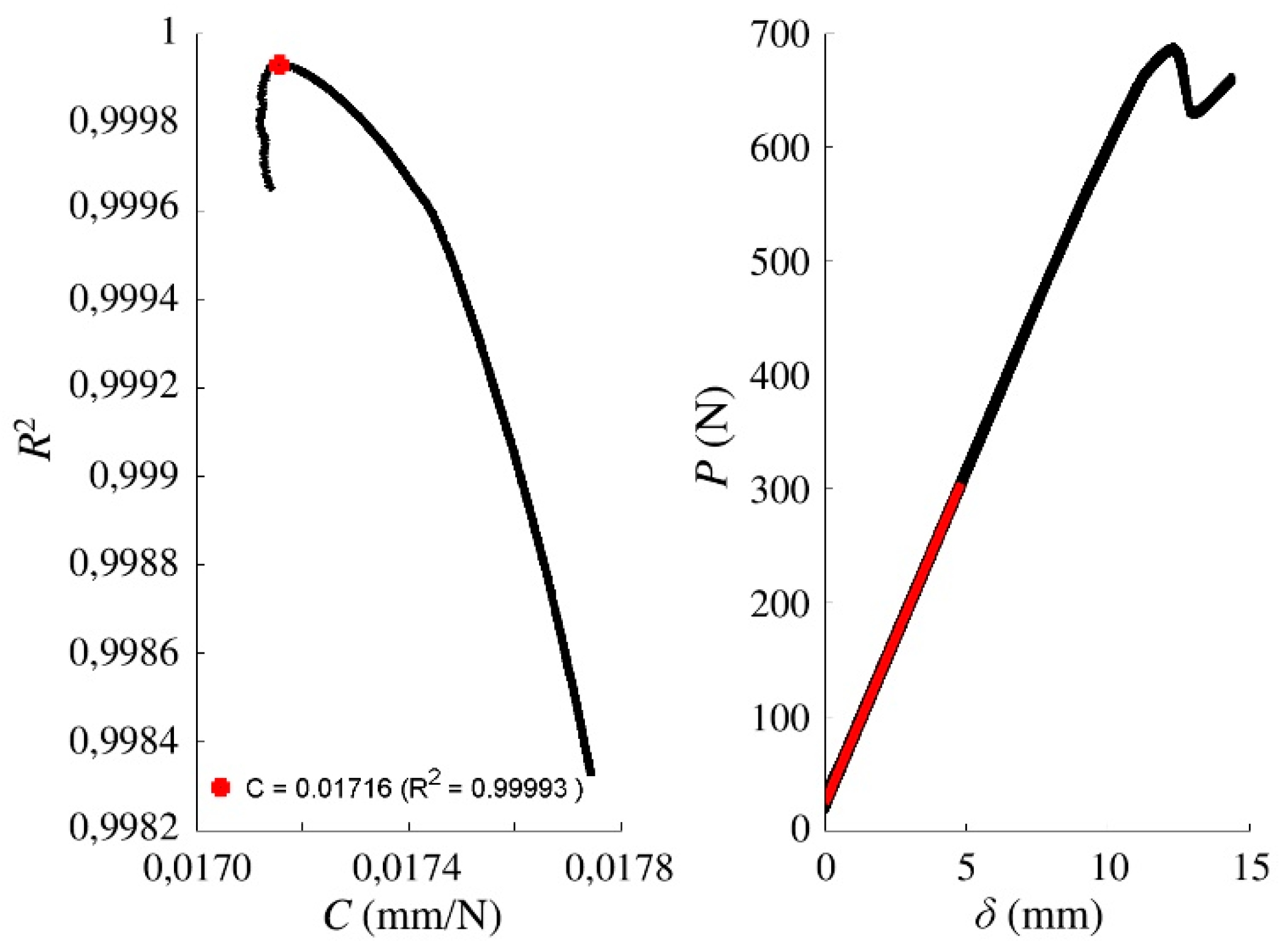
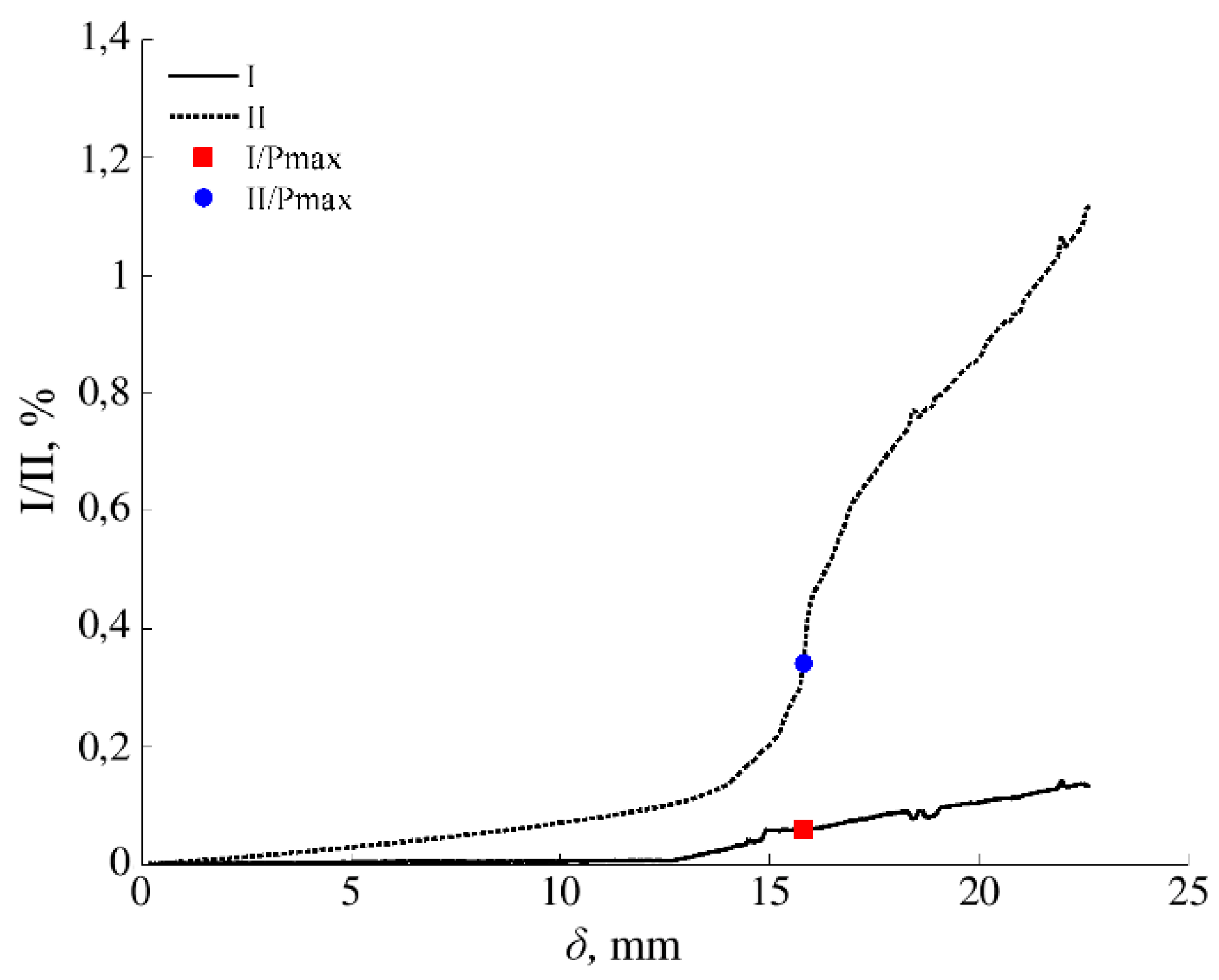
2.2. Data Reduction: Compliance-Based Beam Method (CBBM)
2.3. End-notched Flexure Tests
3. Results and Discussion
3.1. Resistance Curve
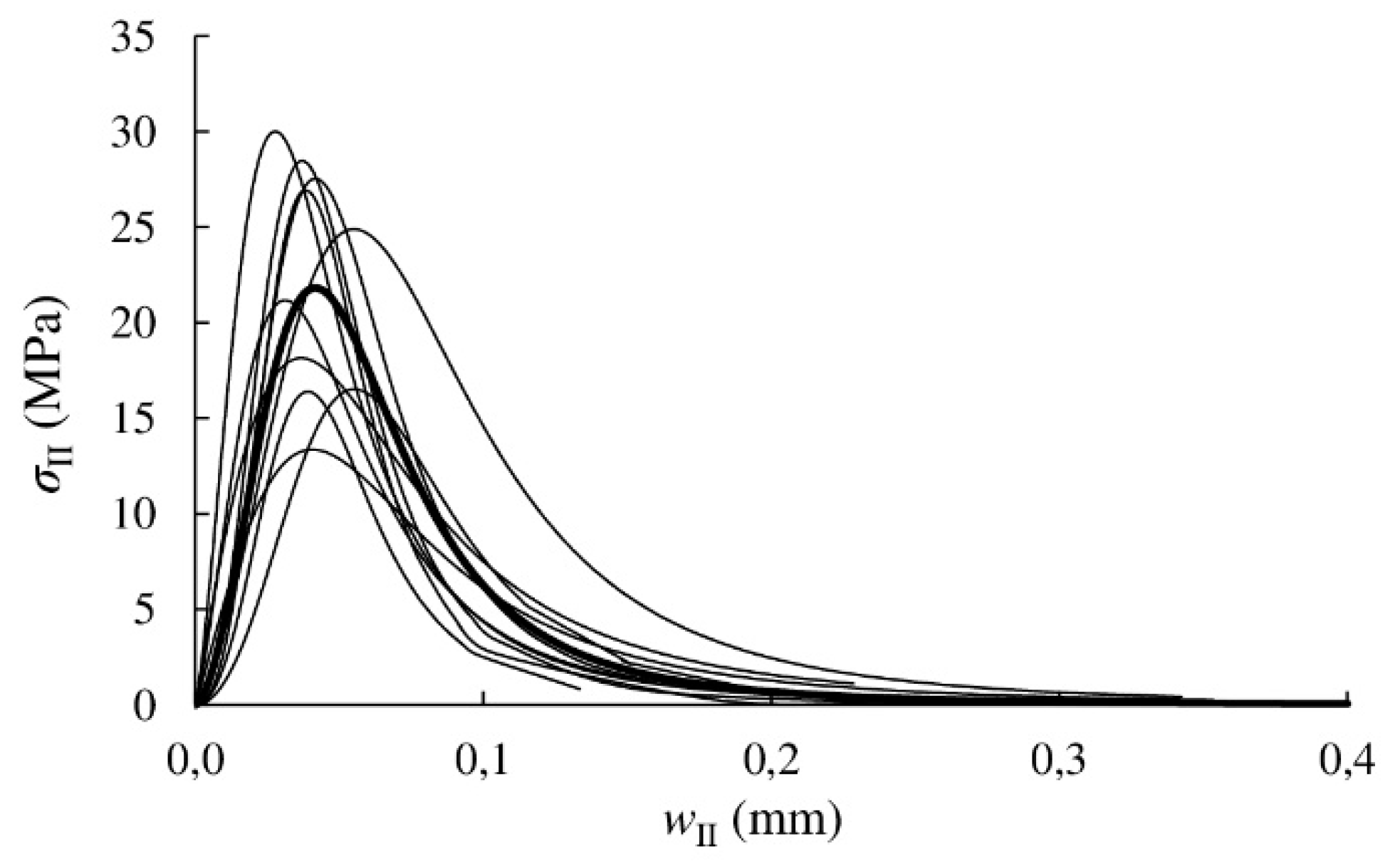
3.2. Cohesive Law
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- EN 1995-1-1:2016. Eurocode 5: Design of Timber Structures. Part 1-1: General. Common Rules and Rules for Buildings; The Spanish Association for Standardization and Certification (AENOR): Madrid, Spain, 2016. [Google Scholar]
- CSA. O86:2014 Engineering Design in Wood; Canadian Standards Association: Toronto, ON, Canada, 2014. [Google Scholar]
- de Moura, M.F.S.F.; Morais, J.J.L.; Dourado, N. A new data reduction scheme for mode I wood fracture characterization using the double cantilever beam test. Eng. Fract. Mech. 2008, 75, 3852–3865. [Google Scholar] [CrossRef]
- Fernberg, S.P.; Berglund, L.A. Bridging law and toughness characterisation of CSM and SMC composites. Compos. Sci. Technol. 2001, 61, 2445–2454. [Google Scholar] [CrossRef]
- Sousa, A.M.R.; Xavier, J.; Morais, J.J.L.; Filipe, V.M.J.; Vaz, M. Processing discontinuous displacement fields by a spatio-temporal derivative technique. Opt. Laser Eng. 2011, 49, 1402–1412. [Google Scholar] [CrossRef]
- Pan, B.; Qian, K.; Xie, H.; Asundi, A. Two-dimensional digital image correlation for in-plane displacement and strain measurement: A review. Meas. Sci. Technol. 2009, 20, 062001. [Google Scholar] [CrossRef]
- Sutton, M.; Orteu, J.J.; Schreier, H. Image Correlation for Shape, Motion and Deformation Measurements: Basic Concepts, Theory and Applications; Springer: Berlin, Germany, 2009. [Google Scholar]
- Franke, B.; Quenneville, P. Numerical modeling of the failure behavior of dowel connections in wood. J. Eng. Mech. 2011, 137, 186–195. [Google Scholar] [CrossRef]
- Caldeira, T.V.P.; Dourado, N.; de Jesus, A.M.P.; de Moura, M.F.S.F.; Morais, J.J.L. Quasi-static behavior of moment-carrying steel-wood doweled joints. Constr. Build. Mater. 2014, 53, 439–447. [Google Scholar] [CrossRef]
- EN 1912:2012. Structural Timber Strength Classes—Assignment of Visual Grades and Species; The Spanish Association for Standardization and Certification (AENOR): Madrid, Spain, 2012. [Google Scholar]
- Franke, S.; Marto, J. Investigation of Eucalyptus globulus wood for the use as an engineered material. In Proceedings of the World Conference on Timber Engineering, Quebec, QC, Canada, 10–14 August 2014. [Google Scholar]
- Lara-Bocanegra, A.J.; Majano-Majano, A.; Crespo, J.; Guaita, M. Finger-jointed Eucalyptus globulus with 1C-PUR adhesive for high performance engineered laminated products. Constr. Build. Mater. 2017, 135, 529–537. [Google Scholar] [CrossRef]
- Pangh, H.; Hosseinabadi, H.Z.; Kotlarewski, N.; Moradpour, P.; Lee, M.; Nolan, G. Flexural performance of cross-laminated timber constructed from fibre-managed plantation eucalyptus. Constr. Build. Mater. 2019, 208, 535–542. [Google Scholar] [CrossRef]
- Crespo, J.; Aira, J.R.; Vázquez, C.; Guaita, M. Comparative analysis of the elastic constants measured via conventional, ultrasound, and 3-D Digital Image Correlation methods in Eucalyptus globulus. Bioresources 2017, 12, 3728–3743. [Google Scholar] [CrossRef]
- Crespo, J.; Majano-Majano, A.; Xavier, J.; Guaita, M. Determination of the resistance-curve in Eucalyptus globulus through double cantilever beam tests. Mater. Struct. 2018, 51, 77. [Google Scholar] [CrossRef]
- Majano-Majano, A.; Lara-Bocanegra, A.J.; Xavier, J.; Morais, J. Measuring the cohesive law in mode I loading of Eucalyptus globulus. Materials 2019, 12, 23. [Google Scholar] [CrossRef] [PubMed]
- UNE 56546:2013. Visual Grading for Structural Sawn Timber: Hardwood Timber; The Spanish Association for Standardization and Certification (AENOR): Madrid, Spain, 2011. (In Spanish) [Google Scholar]
- EN 408:2011+A1. Timber Structures—Structural Timber and Glued Laminated Timber—Determination of Some Physical and Mechanical Properties; The Spanish Association for Standardization and Certification (AENOR): Madrid, Spain, 2011. [Google Scholar]
- Irwin, G.R.; Kies, J.A. Critical energy rate analysis of fracture strength. Weld. J. Res. Suppl. 1952, 33, 193–198. [Google Scholar]
- Davies, P.; Sims, G.D.; Blackman, B.R.K.; Brunner, A.J.; Kageyama, K.; Hojo, M.; Tanaka, K.; Murri, G.; Rousseau, C.; Gieseke, B.; et al. Comparison of test configurations for determination of mode II interlaminar fracture toughness results from international collaborative test programme. Plast. Rubber Compos. 1999, 28, 432–437. [Google Scholar] [CrossRef]
- Xavier, J.; Morais, J.; Dourado, N.; de Moura, M.F.S.F. Measurement of mode I and mode II fracture properties of wood-bonded joints. J. Adhes. Sci. Technol. 2011, 25, 2881–2895. [Google Scholar]
- Wang, Y.; Williams, J.G. Corrections for mode II fracture toughness specimens of composites materials. Compos. Sci. Technol. 1992, 43, 251–256. [Google Scholar] [CrossRef]
- de Moura, M.F.S.F.; Silva, M.A.L.; Morais, J.J.L.; de Morais, A.B.; Lousada, J.J.L. Data reduction scheme for measuring GIIc of wood in end-notched flexure (ENF) tests. Holzforschung 2009, 63, 99–106. [Google Scholar] [CrossRef]
- de Moura, M.F.S.F.; Silva, M.A.L.; de Morais, A.B.; Morais, J.J.L. Equivalent crack based mode II fracture characterization of wood. Eng. Fract. Mech. 2006, 73, 978–993. [Google Scholar] [CrossRef]
- Lancaster, P.; Salkauskas, K. Curve and Surface Fitting: An Introduction; Academic Press: San Diego, CA, USA, 1986. [Google Scholar]
- Xavier, J.; Oliveira, M.; Morais, J.J.L.; de Moura, M.F.S.F. Determining mode II cohesive law of Pinus pinaster by combining the end-notched flexure test with digital image correlation. Constr. Build. Mater. 2014, 71, 109–115. [Google Scholar] [CrossRef]
- GOM mbH. ARAMIS Commercial Software; ARAMIS 6.0.2; GOM mbH: Braunschweig, Germany, 2007. [Google Scholar]
- Pereira, J.L.; Xavier, J.; Ghiassi, B.; Lousada, J.; Morais, J. On the identification of earlywood and latewood radial elastic modulus of P. pinaster by digital image correlation: A parametric analysis. J. Strain Anal. Eng. Des. 2018, 53, 566–574. [Google Scholar] [CrossRef]
- Sousa, A.M.R.; Xavier, J.; Vaz, M.; Morais, J.J.L.; Filipe, V.M.J. Cross-correlation and differential technique combination to determine displacement fields. Strain 2011, 47, 87–98. [Google Scholar] [CrossRef]
- Xavier, J.; de Jesus, A.M.P.; Morais, J.J.L.; Pinto, J.M.T. Stereovision measurements on evaluating the modulus of elasticity of wood by compression tests parallel to the grain. Constr. Build. Mater. 2012, 26, 207–215. [Google Scholar] [CrossRef]
- Xavier, J.; Oliveira, M.; Monteiro, P.; Morais, J.J.L.; de Moura, M.F.S.F. Direct evaluation of cohesive law in Mode I of Pinus pinaster by Digital Image Correlation. Exp. Mech. 2014, 54, 829–840. [Google Scholar] [CrossRef]
- Yoshihara, H. Mode II initiation fracture toughness analysis for wood obtained by 3-ENF test. Compos. Sci. Technol. 2005, 65, 2198–2207. [Google Scholar] [CrossRef]
- Yoshihara, H.; Ohta, M. Measurement of mode II fracture toughness of wood by the end-notched flexure tests. J. Wood. Sci. 2000, 46, 273–278. [Google Scholar] [CrossRef]






| Board ref. | ρ (kg/m3) | EL (MPa) |
|---|---|---|
| 144 | 765 | 19234 |
| 161 | 867 | 19658 |
| 176 | 779 | 19359 |
| 189 | 748 | 19114 |
| 192 | 815 | 20612 |
| mean | 795 | 19595 |
| SD | 47 | 603 |
| CoV (%) | 6.0 | 3.1 |
| Settings | |
|---|---|
| CCD camera | |
| Model | Baumer Optronic FWX20 (8 bits, 1624 × 1236 pixels, 4.4 μm/pixel) |
| Shutter time | 0.7 ms |
| Acquisition frequency | 1 Hz |
| Lens | |
| Model | Opto Engineering Telecentric lens TC 23 36 |
| Magnification | 0.243 ± 3% |
| Field of view (1/1.8”) | 29.3 × 22.1 mm2 |
| Working distance | 103.5 ± 3 mm |
| Working F-number | f/8 |
| Field depth | 11 mm |
| Conversion factor | 0.018 mm/pixel |
| Lighting | Raylux 25 white-light LED |
| DIC measurements | |
| Subset size | 15 × 15 pixel2 (0.270 × 0.270 mm2) |
| Subset step | 13 × 13 pixel2 (0.234 × 0.234 mm2) |
| Resolution | 1–2 × 10−2 pixel (0.18 × 0.36 μm2) |
| Specimen Ref. | Ef (MPa) | Pmax (N) | C0 (mm/N) | GII,Pmax (N/mm) | GIIc (N/mm) |
|---|---|---|---|---|---|
| 144-1 | 17,576 | 888.32 | 0.014 | 2.42 | 2.50 |
| 144-2 | 14,440 | 701.23 | 0.018 | 1.79 | 1.84 |
| 144-3 | 14,180 | 618.65 | 0.017 | 1.37 | 1.38 |
| 161-2 | 16,346 | 767.78 | 0.015 | 1.63 | 1.70 |
| 176-1 | 14,703 | 683.96 | 0.016 | 1.29 | 1.32 |
| 176-3 | 14,286 | 688.20 | 0.017 | 1.46 | 1.50 |
| 189-2 | 16,380 | 690.00 | 0.015 | 1.22 | 1.24 |
| 189-3 | 15,837 | 581.88 | 0.015 | 0.89 | 0.90 |
| 192-1 | 17,032 | 684.18 | 0.015 | 1.24 | 1.28 |
| 192-2 | 16,714 | 761.13 | 0.015 | 1.51 | 1.70 |
| Mean | 15,749 | 706.53 | 0.016 | 1.65 | 1.54 |
| SD | 1251 | 84.78 | 0.001 | 0.41 | 0.44 |
| CoV (%) | 8 | 12 | 9 | 25 | 28 |
| Ref. | A1 (N/mm) | A2 (N/mm) | p | wII0 (mm) | Glaw,II (N/mm) | σIIu (MPa) | wIIu (mm) |
|---|---|---|---|---|---|---|---|
| 144-1 | 0.042 | 2.62 | 2.52 | 0.077 | 2.55 | 24.89 | 0.055 |
| 144-2 | 0.017 | 1.82 | 2.28 | 0.042 | 1.78 | 30.01 | 0.028 |
| 144-3 | 0.007 | 1.47 | 2.25 | 0.048 | 1.42 | 21.17 | 0.031 |
| 161-2 | 0.027 | 1.80 | 2.93 | 0.053 | 1.75 | 27.53 | 0.042 |
| 176-1 | 0.035 | 1.41 | 3.30 | 0.046 | 1.42 | 26.92 | 0.038 |
| 176-3 | 0.033 | 1.62 | 3.00 | 0.047 | 1.61 | 28.46 | 0.037 |
| 189-2 | 0.035 | 1.39 | 3.01 | 0.069 | 1.33 | 16.51 | 0.055 |
| 189-3 | 0.017 | 0.93 | 3.11 | 0.048 | 0.92 | 16.39 | 0.039 |
| 192-1 | 0.001 | 1.39 | 2.05 | 0.068 | 1.35 | 13.36 | 0.041 |
| 192-2 | 0.002 | 1.82 | 1.97 | 0.065 | 1.76 | 18.14 | 0.037 |
| Mean | 0.022 | 1.63 | 2.64 | 0.056 | 1.59 | 22.34 | 0.040 |
| SD | 0.015 | 0.44 | 0.48 | 0.012 | 0.43 | 5.96 | 0.008 |
| CoV (%) | 69 | 27 | 18 | 22 | 27 | 27 | 22 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Majano-Majano, A.; Lara-Bocanegra, A.J.; Xavier, J.; Morais, J. Experimental Evaluation of Mode II fracture Properties of Eucalyptus globulus L. Materials 2020, 13, 745. https://doi.org/10.3390/ma13030745
Majano-Majano A, Lara-Bocanegra AJ, Xavier J, Morais J. Experimental Evaluation of Mode II fracture Properties of Eucalyptus globulus L. Materials. 2020; 13(3):745. https://doi.org/10.3390/ma13030745
Chicago/Turabian StyleMajano-Majano, Almudena, Antonio José Lara-Bocanegra, José Xavier, and José Morais. 2020. "Experimental Evaluation of Mode II fracture Properties of Eucalyptus globulus L." Materials 13, no. 3: 745. https://doi.org/10.3390/ma13030745
APA StyleMajano-Majano, A., Lara-Bocanegra, A. J., Xavier, J., & Morais, J. (2020). Experimental Evaluation of Mode II fracture Properties of Eucalyptus globulus L. Materials, 13(3), 745. https://doi.org/10.3390/ma13030745








