Abstract
The structural, mechanical, electronic, and thermal properties, as well as the stability and elastic anisotropy, of XP (X = Al, Ga, or In) in the P6422 phase were studied via density functional theory (DFT) in this work. P6422-XP (X = Al, Ga, or In) are dynamically and thermodynamically stable via phonon spectra and enthalpy. At 0 GPa, P6422-XP (X = Al, Ga, or In) are more rigid than Fm-XP (X = Al, Ga, or In), of which P6422-XP (X = Al or Ga) are brittle and P6422-InP is ductile. In the same plane (except for (001)-plane), P6422-AlP and P6422-InP exhibit the smallest and the largest anisotropy, respectively, and P6422-XP (X = Al, Ga, or In) is isotropic in the (001)-plane. In addition, Al, Ga, In, and P bonds bring different electrical properties: P6422-InP exhibits a direct band gap (0.42 eV) with potential application for an infrared detector, whereas P6422-XP (X = Al or Ga) exhibit indirect band gap (1.55 eV and 0.86 eV). At high temperature (approaching the melting point), the theoretical minimum thermal conductivities of P6422-XP (X = Al, Ga, or In) are AlP (1.338 W∙m−1∙K−1) > GaP (1.058 W∙m−1∙K−1) > InP (0.669 W∙m−1∙K−1), and are larger than those of Fm-XP (X = Al, Ga, or In). Thus, P6422-XP (X = Al, Ga, or In) have high potential application at high temperature.
1. Introduction
GaP and InP, which are typical second-generation compound semiconductor materials, are primarily used to produce high-speed, high-frequency, high-power, and light-emitting electronic devices. These materials are also excellent materials for producing high-performance microwave and millimeter-wave devices and light-emitting devices. With the rise of the information highway and the Internet, these materials have also been widely used in the fields of satellite and mobile communications, solar power technology and GPS navigation [1]. AlP is an important material that is mainly used in light emitting diodes and infrared photo detectors [2,3] in industrial application. AlP, GaP, and InP have been given wide attention due to high thermal conductivities and wide energy band gap [4].
Computational chemistry is the subject of applying computer technology based on basic physicochemical theories (quantum chemistry, statistical thermodynamics, and classical mechanics) and a large number of numerical methods to study and predict the regularity of the relationship between the structure and properties of chemicals. The present direction of material research and development should combine computational chemistry with material design, apply the basic principle of computational chemistry, and carry out material design and simulation on molecule and atom level to provide reliable theoretical guidance. The first-principle electronic structure method is widely used in materials science, including Hartree–Fork equation, DFT and so on.
Increasingly many researchers have focused on the polymorphism of XP (X = Al, Ga, or In) compound semiconductors. Xu et al. [5] studied the polymorphs, mechanical, and thermodynamic properties of AlX (X = N, P, or As) compound in the wurtzite, zinc-blende, and NiAs structures via first-principle calculations, and summarized the relationships between the temperature and the thermodynamic properties of AlX (X = N, P, or As) compounds based on a quasi-harmonic approximation. The results demonstrated that in the same structure, the hardness and Debye temperature decrease: AlN > AlP > AlAs. Based on the advanced method of crystal structure prediction, three new metastable structures of AlAs were investigated by Liu et al. [6], namely, hP6-AlAs, oC12-AlAs, and cI24-AlAs, of which the space groups are P6422, C222, and Id, respectively. The mechanical and dynamic stabilities of these structures were evaluated by calculating the elastic constant and the phonon spectrum. According to first-principle calculations, the hardness of oC12- and hP6-AlAs are larger than that of cI24-AlAs under the same pressure. Under ambient pressure, oC12-, hP6-AlAs, and cI24-AlAs exhibit semiconductor properties and the first two show direct band gap properties (0.468 eV and 1.356 eV), whereas the last exhibits indirect band gap property (1.761 eV).
By utilizing a crystal structure prediction software (CALYPSO), Yang Ruike [7] proposed four possible phases of AlP (Pmn21-, Pbam-, Pbca-, and bct-AlP) and studied their structures, elastic constants, thermodynamics, and electrical properties based on first-principles. It was found that these four new phases all have semiconductor properties; Pmn21-AlP and Pbam-AlP show direct band gap properties with larger electronic advantages than wz-AlP and zb-AlP at ambient pressure; and Pmn21-AlP, Pbam-AlP, Pbca-AlP, and bct-AlP are ductile. Pmn21-AlP and Pbam-AlP are direct band gap semiconductors (3.22 eV and 3.27 eV), whereas Pbca-AlP and bct-AlP are indirect band gap semiconductors (3.47 eV and 3.04 eV). Based on density functional theory (DFT), A. Baida et al. [8] studied the structural, optical, and electronic properties of indium phosphide (InP) via the augmented plane wave (FP-LAPW) method. The results demonstrated that the phase transitions from zinc-blende phase to Imm2, NiAs, PbO, and CsCl phases are possible at low pressure.
Arbouche et al. [9] used the full-potential linearized augmented plane-wave (FP-LAPW+lo) method to calculate the phase transitions of zinc-blende (zb), sc16, cmcm, NaCl, CSCl, d-β-tin, Imm2, Immm, and NiAs of III-phosphide XP (X = Al, Ga, or In) under high pressure. The calculated physical parameters such as the lattice constants and bulk modulus demonstrated that zb-XP (X = Al, Ga, or In) are more stable than these phases and cmcm-XP (X = Al, Ga, or In) have the highest hardness, respectively. The results on pressure transitions demonstrated that GaP will transform from the zb phase to the NaCl phase at 22.19 GPa and into the Imm2 phase above 33.76 GPa. When the pressure changed, zb-AlP and zb-InP will transform into NaCl-AlP (at 11.78 GPa) and NaCl-InP (at 7.35 GPa), respectively, whereas CSCl-AlP and CSCl-InP transform into the NaCl-AlP (at 64.89 GPa) and NaCl-InP (at 71.79 GPa), respectively.
The physical properties of XP (X = Al, Ga, or In) in the P6422 phase have not been identified to date. Therefore, in this work, the initial geometries of P6422-XP (X = Al, Ga, or In) are constructed by atomic substitution base on the structure of hP6-AlAs [6]. The structural, mechanical, thermal, and electronic properties and the stability of P6422-XP (X = Al, Ga, or In) have been systematically studied via density functional theory. The results demonstrate that only P6422-InP is a direct band gap semiconductor material with potential application in an infrared detector.
2. Calculation Methods
The theoretical investigations on P6422-XP (X = Al, Ga, or In) were conducted by utilizing density functional theory (DFT) [10,11], which is one of the most commonly used methods for calculating the properties of condensed matter physics based on the CASTEP code [12]. The generalized gradient approximation (GGA) [13] and the Perdew–Burke–Ernzerhof (PBE) [14] exchange-correlation functional were used for geometry optimization and property prediction of the materials. To improve computational precision, the convergence analysis of cut-off energy and the k-point grid allocation in the Brillouin zone are completed in turn by keeping the cut-off energy and the k-point constant, respectively. As is shown in Figure 1, the plane-wave cut-off energies were finally chosen to be 320, 400, and 420 eV with ultrasoft pseudopotentials for P6422-AlP, P6422-GaP, and P6422-InP, respectively. The k-points in the first irreducible Brillouin zone were set to (11 × 11 × 5; 11 × 11 × 5; 11 × 11 × 5) [15] by using the Monkhorst–Pack scheme [16] for P6422-AlP, P6422-GaP, and P6422-InP. By using the Broyden–Fletcher–Goldfarb–Shenno (BFGS) algorithm [17], structural parameter optimizations were conducted with the following thresholds for the convergent structures: a maximum stress of less than 0.02 GPa, a maximum residual force of less than 0.01 eV/Å, a maximum energy change of less than 5 × 10−6 eV per atom, and a maximum displacement of atoms for geometry optimization of less than 5 × 10−4 Å. The phonon spectra were calculated via linear response theory (density functional perturbation theory (DFPT)) [18]. The accurate electronic band-gap structures of P6422-XP (X = Al, Ga, or In) were obtained via the Heyd–Scuseria–Ernzerhof (HSE06) [19,20] screened-exchange hybrid functional base on the previous geometry optimizations via GGA-PBE. The configurations of the valence electrons are 3s23p3 for P, 3s23p1 for Al, 3d104s24p1 for Ga, and 4d105s25p1 for In.
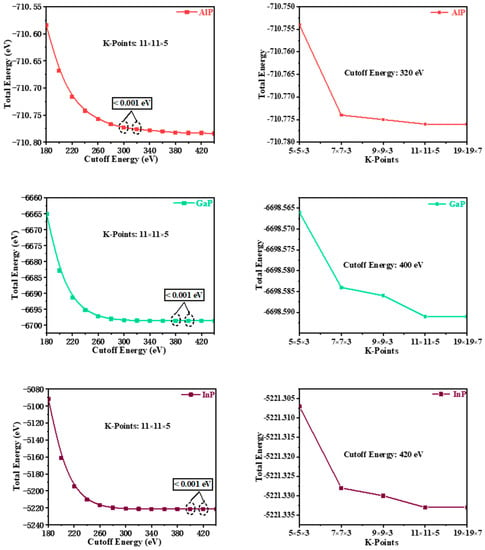
Figure 1.
The convergence analysis of cut-off energy and the k-point grid allocation in the Brillouin zone.
3. Results and Discussion
3.1. Structural Properties
The three-dimensional crystal structure of P6422-XP (X = Al, Ga, or In) is illustrated in Figure 2. The 3D crystal structure of P6422-XP (X = Al, Ga, or In) is composed of an sp3-bonded network. To evaluate the performance of the theoretical method that is used in this work, the related physical properties of Fm-XP (X = Al, Ga, or In) are also studied via the same method. The lattice parameters of XP (X = Al, Ga, or In) in the P6422 phase and in the Fm phase are listed in Table 1 via GGA-PBE. The lattice parameters and the crystal density of XP (X = Al, Ga, or In) in the Fm phase (sphalerite phase) are very close to other experimental results, namely, the optimization and calculation method that is utilized in this work can provide theoretical support for the results [21,22,23]. In addition, the lattice structure of P6422- and Fm-XP (X = Al, Ga, or In) are also optimized by using DFT-D2 (Grimme) on the basis of GGA-PBE to verify the effect of dispersion on the properties of the material. The results show that the errors between lattice constants a, b, and c of Fm-XP (X = Al, Ga, or In) and experimental values without (with) considering the dispersion action are 0.78% (0.46%), 0.99% (0.72%), 1.77% (0.26%), respectively, which proves our calculation method can provide theoretical support. For P6422-XP (X = Al, Ga, or In), the lattice constants a, b, and c of P6422-AlP change by ~1.53% (2.07% for P6422-GaP, 3% for P6422- InP), ~1.53% (2.07% for P6422-GaP, 3% for P6422-InP), and ~0.16% (0.2% for P6422-GaP, 1.25% for P6422-InP) with considering the dispersive action, indicating that P6422-XP (X = Al, Ga, or In) are insensitive to the dispersive action. Considering the computational cost and accuracy, we adopt the optimized lattice parameters via GGA-PBE for subsequent studies of physical properties. The investigated P6422-XP (X = Al, Ga, or In) has a hexagonal structure with the following equilibrium lattice parameters; a = b = 3.849 Å and c = 8.683 Å for AlP, a = b = 3.899 Å and c = 8.570 Å for GaP, and a = b = 4.190 Å and c = 9.416 Å for InP. For P6422-XP (X = Al, Ga, or In), the P–Al bond length is 2.408 Å, the P–Ga bond length is 2.419 Å, and the P–In bond length is 2.618 Å. As shown in Table 1, in the same crystal structure, the volume per molecule for P6422-XP (X = Al, Ga, or In) increases due to the long bond length and the large lattice constant. In the P6422 phase, the densities of AIP (ρ = 2.591 g/cm3), GaP (ρ = 4.446 g/cm3) and InP (ρ = 5.073 g/cm3) are larger than the corresponding densities in the Fm phase because the corresponding volume per molecule in the P6422 phase is smaller.
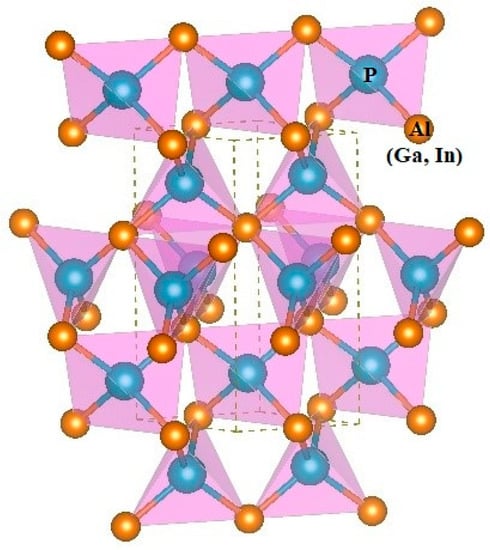
Figure 2.
The 3D crystal structure of P6422-XP (X = Al, Ga, or In).

Table 1.
The calculated (GGA-PBE and DFT-D2) lattice parameters and densities of P6422- and Fm-XP (X = Al, Ga, or In).
In Table 2, the equilibrium volume V0 and bulk modulus B0 of P6422-XP (X = Al, Ga, or In) are calculated via GGA-PBE. The calculated total energy (E) per primitive cell for each compound as a function of different cell volumes (V) over a range of 0.9V0–1.1V0 is fitted by the Murnaghan equation of state [EOS] [21,22].

Table 2.
The calculated elastic constants (C11, C12, C13, C33, C44, C66), bulk moduli B, shear moduli G, Young’s modulus E (GPa), Poisson’s ratios ʋ and universal anisotropic index AU for P6422-XP (X = Al, Ga, or In) when pressure P (GPa) increases from 0 to 35 GPa via the method of GGA-PBE.
Where B0 and B′ are the bulk modulus and their first pressure derivatives at 0 GPa, V0 is the unit-cell volume at 0 GPa, and E(V) is the total energy under the different cell volume V. The fitted energy vs. volume (E-V) curves are shown in Figure 3. The equation between pressure and volume (P-V in Figure 3) is obtained through the derivation of E(V).
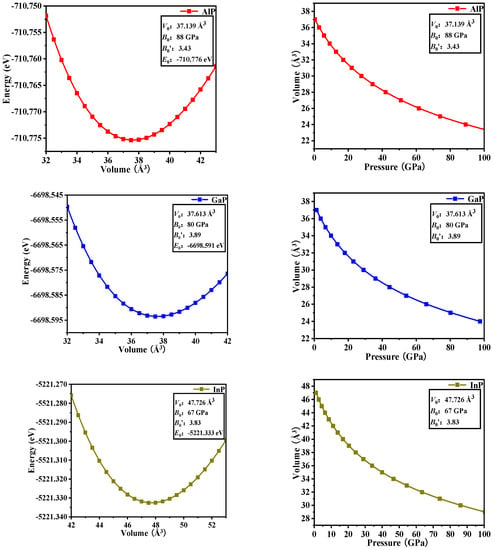
Figure 3.
Computed total energy versus unit-cell volume (left column) and the variation of the volume versus pressure (right column) for P6422-XP (X = Al, Ga, or In).
In the fitting curve (E–V), there is a minimum energy near the volume V0, and this minimum energy (−710.776 eV for AlP, −6698.591 eV for GaP, and −5221.333 eV for InP) is in good agreement with the simulation data in Figure 1 (cut-off energy: 320, 400, and 420 eV, K -Points: 11 × 11 × 5, 11 × 11 × 5, 11 × 11 × 5 for P6422-XP (X = Al, Ga, or In), respectively). It shows that P6422-GaP are more stable than P6422-XP (X = Al or In). Through the fitting P–V curve, InP-P6422 has the largest volume compressibility: 38.15% (36.55% for AlP and 35.80% for GaP).
3.2. Stability and Mechanical Properties
Dynamic stability is an important property for verifying the existence of new materials. The dynamic stability of P6422-XP (X = Al, Ga, or In) can be determined by studying the phonon spectra. The phonon spectra of P6422-XP (X = Al, Ga, or In) are shown in Figure 4. By observation, the P6422-XP (X = Al, Ga, or In) are dynamically stable because their phonon spectra have no imaginary frequencies in the Brillouin region. The highest vibrational frequencies of P6422-XP (X = Al, Ga, or In) are 13.596 THz at point G, 10.412 THz at point K and 11.298 THz at point K, respectively. The elastic constants and elastic moduli of P6422- and Fm-XP (X = Al, Ga, or In) are listed from 0 GPa to 35 GPa in Table 2. For XP (X = Al, Ga, or In) in the Fm phase, the calculated elastic constants are in good agreement with the reported experimental results, which proves the correctness of the theoretical calculation method. For a hexagonal system, the necessary and sufficient Born criteria for stability can be expressed as follows [26].
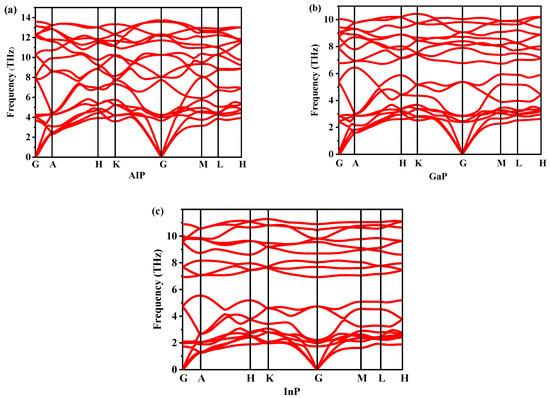
Figure 4.
The phonon spectra of P6422-XP (X = Al, Ga, or In): AlP (a), GaP (b), and InP (c).
In Table 2, all the elastic constants of P6422-XP (X = Al, Ga, or In) at 0 GPa satisfy the above stability criteria, namely, P6422-XP (X = Al, Ga, or In) are mechanically stable. The form ability and stability of the alloy can be characterized by the formation enthalpy and the cohesion energy [27]. To study the thermodynamic stability of P6422-XP (X = Al, Ga, or In), its formation enthalpy (ΔH) and cohesive energy (Ecoh) are also further investigated, and the corresponding formulas [28,29] are described as follows,
where is the total energy of P6422-XP (X = Al, Ga, or In) at the equilibrium lattice constant; and are the energies per atom of the pure constituents of X (X = Al, Ga, or In) and P, respectively, in the solid states; and are the energies from the free atoms of X (X = Al, Ga, or In) and P, respectively; and NX and Np refer to the numbers of X (X = Al, Ga, or In) and P atoms, respectively, in each conventional cell. The calculated formation enthalpies for P6422-AlP, P6422-GaP, and P6422-InP are −1.72, −0.82, and −1.17 eV, respectively. All the values of formation enthalpies are negative; therefore, the bond energies of P6422-XP (X = Al, Ga, or In) are very large and P6422-XP (X = Al, Ga, or In) are easier to form, where P6422-AlP > P6422-InP > P6422-GaP according to the stability of alloy formation. The cohesion energy is the energy that is needed for decomposing solid materials into isolated atoms. The smaller the value is, the higher the crystal structure stability. The results of Ecoh for XP (X = Al, Ga, or In) in the P6422 phase are −9.95, −8.21, and −8.74 eV, respectively. P6422-AlP has the highest thermodynamic stability followed by P6422-InP and, finally, P6422-GaP, in a high-temperature environment.
The elastic moduli can be obtained based on the elastic constant. The bulk moduli B and the shear moduli G can be estimated via the Voigt–Reus–Hill approximation [30]. , , and can be expressed via the following equations [31], where the subscripts V and R are the Voight and Reuss schemes:
Young’s modulus E and Poisson’s ratio ʋ are calculated from B and G as
According to Table 2, the elastic constants C11 (147 GPa, 152 GPa, 108 GPa), C22 = C11 (147 GPa, 152 GPa, 108 GPa), and C33 (174 GPa, 144 GPa, 117 GPa) for P6422-XP (X = Al, Ga, or In) are larger than C11 = C22 = C33 (123 GPa, 134 GPa, 96 GPa) of Fm-XP (X = Al, Ga, or In); therefore, P6422-XP (X = Al, Ga, or In) have stronger ability to resist elastic deformation along the X-, Y-, and Z- axes. The bulk moduli B and the shear moduli G of P6422-XP (X = Al or In) are larger than those of Fm-XP (X = Al or In); thus, the anti-compression and anti-shearing strain abilities of P6422-XP (X = Al or In) are stronger. Furthermore, the B/G ratios [32] of P6422- and Fm-XP (X = Al, Ga, or In) at ambient pressure are also shown in Table 2. In the P6422 phase, XP (X = Al or Ga) are brittle (B/G < 1.75) and InP are ductile (B/G > 1.75), and Fm-XP (X = Al, Ga, or In) are all brittle (B/G < 1.75).
The calculated Young’s modulus E of XP (X = Al, Ga, or In) in the P6422 phase at 0 GPa are 132, 140 and 94 GPa, respectively, which are larger than those (118, 131, and 88 GPa) in the Fm phase. Therefore, the stiffness of P6422-XP (X = Al, Ga, or In) are higher, and they are more difficult to deform, especially GaP. There are no significant changes in the calculated values of Poisson’s ratio ʋ of XP (X = Al, Ga, or In) between the P6422 phase and Fm phase at 0 GPa. The Poisson’s ratios ʋ of P6422-AlP and P6422-InP are 0.25 and 0.27, which are slightly larger than that of GaP (0.21) in the P6422 phase. All Poisson’s ratios ʋ of P6422-XP (X = Al, Ga, or In) are less than 1; thus, after the P6422-XP (X = Al, Ga, or In) are subjected to uniform longitudinal stress, the transverse deformations are smaller than the longitudinal deformations before plastic deformation occurs, especially for GaP.
Pressure is a significative physical parameter that has a momentous impact on the Brillouin zone. Enthalpy is an important state parameter in thermodynamics for characterizing the energy of a material system. The lower its energy of matter or a system, the less likely it is to undergo spontaneous processes; therefore, the more stable it is [33].
The relative formation enthalpy curves relative to Fm-XP (X = Al, Ga, or In) as functions of the pressure up to 35 GPa for P6422-XP (X = Al, Ga, or In) are plotted in Figure 5. At ambient pressure, Fm-XP (X = Al, Ga, or In) are more favorable than any other P6422-XP. Moreover, at 0 GPa, P6422-AlP, P6422-GaP, and P6422-InP have larger enthalpy than Fm-XP (X = Al, Ga, or In) (0.418, 0.436, and 0.345 eV per formula (f.u.), respectively). As the pressure increases, P6422-XP (X = Al, Ga, or In) become increasingly stable, and P6422-AlP, P6422-GaP, and P6422-InP become more stable than Fm-AlP, Fm-GaP, and Fm-InP at the pressures that exceed 11.42, 16.60, and 20.91 GPa, respectively. In addition, P6422-InP is the most stable, followed by P6422-AlP and, finally, P6422-GaP. According to the Table 2, the values of the elastic constant, Young’s modulus E (GPa), and Poisson’s ratio ʋ increase with the pressure.
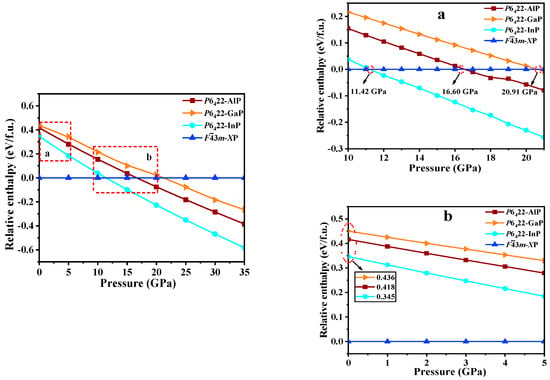
Figure 5.
The relative formation enthalpies curves (relative to Fm-XP) as a function of pressure (0 to 35 GPa) for P6422-XP (X = Al, Ga, or In); (a,b) are the zoomed in views of selected areas.
3.3. Mechanical Anisotropic Properties
The universal anisotropic index AU that present the elastic anisotropy of P6422-XP (X = Al, Ga, or In) also calculated for further investigation in this work. The relevant calculation formulas are given in [37]. In Table 2, the AU of P6422-XP (X = Al, Ga, or In) shows an increasing tendency with increasing atomic order (AI < Ga < In) at ambient pressure. The variation tendencies of AU for XP (X = Al, Ga, or In) in the P6422 phase differ from those of Young’s modulus E. For example, P6422-InP has the smallest Young’s modulus in the P6422-XP (X = Al, Ga, or In) but has the largest universal anisotropic index AU.
The 3D directional constructions and 2D representations of Young’s modulus E in the (001)-plane, (011)-plane, (100)-plane, (110)-plane, (010)-plane, and (111)-plane for P6422-XP (X = Al, Ga, or In) are shown in Figure 6. Through observation, along with XY-, XZ-, and YZ-plane, P6422-XP (X = Al, Ga, or In) exhibit strong anisotropy in various planes excluding XY-plane. Compared with the XY-plane, the three-dimensional surface structure in the XZ-plane deviates further from the shape of the sphere; therefore, the XZ- plane has stronger anisotropy than the XY-plane [38]. For P6422-XP (X = Al, Ga, or In), the maximum and minimum values of Young’s modulus E are attained in the XZ- and YZ-planes, whereas only the minimum value is attained in the XY-plane because they are isotropic in the (001)-plane. In Figure 6, as Young’s modulus has the same properties in the (100)-, (010)-, and (110)-plane, Figure 6 shows only the two-dimensional curve in the (110)-plane.
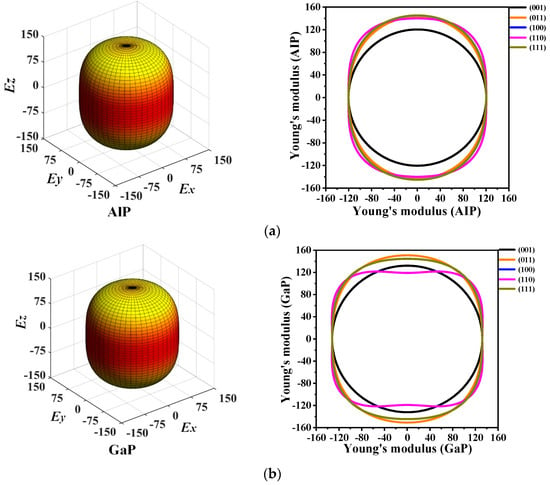
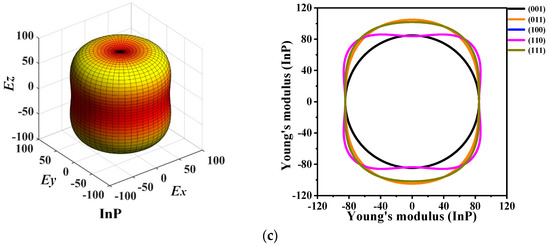
Figure 6.
The 3D directional constructions and 2D representation of Young’s modulus E in the (001)-, (011)-, (100)-, (110)-, and (111)- plane for P6422-AlP (a), P6422-GaP (b) and P6422-InP (c).
The calculated maximum values Emax, minimum values Emin, and ratios Emax/Emin of Young’s modulus E in each plane for P6422-XP (X = Al, Ga, or In) are listed in Table 3. It is found that, in the (001)-plane, the minimum values of Emax/Emin for P6422-XP (X = Al, Ga, or In) are all 1.000; thus, P6422-XP (X = Al, Ga, or In) are attained with the isotropy in the (001)-plane. The maximum ratio Emax/Emin of Young’s modulus E is 1.206, with the largest anisotropy occurring in the (100)-, (110)-, and (010)-plane for P6422-AlP. For P6422-GaP, the maximum value of Emax/Emin is 1.273, which is attained in the (100)-, (110)-, and (010)-plane with larger anisotropy. The ratios Emax/Emin for P6422-InP are all 1.251 in the (100)-, (110)-, and (010)-plane, which is larger than in the other planes. Therefore, the (100)-, (110)-, and (010)-plane of P6422-InP exhibit higher anisotropy. In the (100)-, (110)-, and (010)-plane for P6422-XP (X = Al, Ga, or In), the ratios Emax/Emin of Young’s modulus are 1.206, and 1.251, respectively. In the (100)-, (110)-, and (010)-plane, P6422-AlP exhibits the smallest anisotropy and P6422-GaP exhibits the largest anisotropy. From the (011)-plane to the (111)-plane, P6422-InP exhibits the largest anisotropy with Emax/Emin = 1.237, and P6422-GaP exhibits the smallest anisotropy with Emax/Emin = 1.147.

Table 3.
The calculated maximum values Emax, minimum values Emin and ratios Emax/Emin of XP (X = Al, Ga, or In) in the P6422 phase via the method of GGA-PBE.
3.4. Electrical and Thermal Properties
In solid-state physics, the electron band structure describes the energy that electrons are prohibited or allowed to carry, which is caused by quantum dynamic electron wave diffraction in periodic lattices [39]. The general characteristics of electron motion in crystals are qualitatively expounded by energy band theory. The orbital projection electronic band structures for P6422-XP (X = Al, Ga, or In) are plotted in Figure 7. The coordinates of high-symmetry points in the Brillouin zone for P6422-XP (X = Al, Ga, or In) are G (0.00, 0.00, 0.00), A (0.00, 0.00, 0.50), H (−0.33, 0.67, 0.50), K (0.33, 0.67, 0.00), G (−0.50, 0.50, 0.00), M (0.00, 0.50, 0.00), L (0.00, 0.50, 0.50), and H (−0.33, 0.67, 0.50). The band structures of P6422-XP (X = Al, Ga, or In) are calculated via the HSE06 hybrid functional [40]. In the P6422 phase, only InP is a direct band gap semiconductor, which has a band gap of 0.42 eV and the conduction band minimums and the valence band maximums are both located at point G (0.00, 0.00, 0.00). The band gap of P6422-InP corresponds to a wavelength of 2958.04 nm, which is in the infrared region. P6422-AlP and P6422-GaP show indirect band gap properties with band gaps of 1.55 and 0.86 eV, respectively. The conduction band minimums and the valence band maximums of P6422-AlP are located at point G (0.00, 0.00, 0.00) and point M (0.00, 0.50, 0.00), respectively, whereas the conduction band minimums and the valence band maximums of P6422-GaP are located at point G (0.00, 0.00, 0.00) and point K (0.33, 0.67, 0.00), respectively.
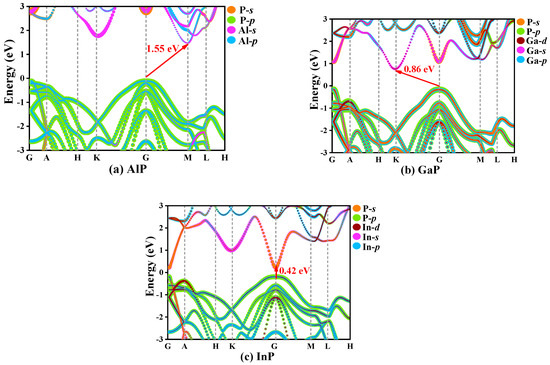
Figure 7.
The electronic band structure for P6422-XP (X = Al, Ga, or In), AlP (a), GaP (b), InP (c).
The calculated partial atomic site projected densities of states (PDOS) of P6422-XP (X = Al, Ga, or In), which are used to reflect elastic characteristics and the bonding properties and orbital distribution of electrons, are plotted in Figure 8. The main bonding peaks distribute in the range from −15 to 15 eV. Below 0 eV, the PDOS in the valence band consist of three parts: the first part ranges from −5 to −10 eV, where the −s orbital makes a larger contribution to electrical conductivity, and, in this part, the percentages of the −p orbital change minimally with increasing energy; the second part ranges from −10 to −5 eV, where the main contributions to conduct electricity are from the −p orbital for AlP, whereas the main contributions to conduct electricity are from the −s orbital for GaP and InP; and the last part consists of the −p orbital from −5 to 0 eV. Above 0 eV, the PDOS in the conduction band originate mainly consist of the −p orbital. From AlP to XP (X = Ga or In), due to the increase in the atomic volume, the contributions of the −s orbital increase substantially from the Al atom to the X (X = Ga or In) atoms in the range of −10 to −5 eV, and when the energy exceeds −5 eV, the contributions of the −p orbital increase substantially. In addition, in the vast majority of the energy range, the PDOS originate mainly from the −p orbital, namely, strong hybridization from the −p orbital of the P atom and the −p orbital of the X (X = Al, Ga, or In) atoms occurs. These PDOS peaks depend on the X–p/P–p (X = Al, Ga, or In) bonding orbital contribution. The results demonstrate that covalent bonds X–P (X = Al, Ga, or In) interactions occur.
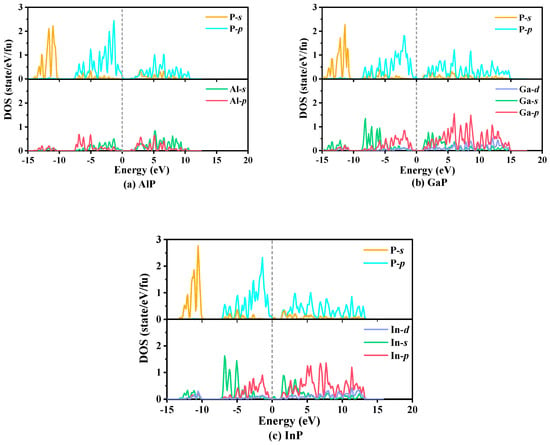
Figure 8.
The partial densities of states of P6422-XP (X = Al, Ga, or In): AlP (a), GaP (b), and InP (c).
Finally, we examine the theoretical minimum thermal conductivity under high temperature, representing the heat that is transferred through the phonon transmission in a temperature gradient, which depends not only on material thermal conductivity, but also on the temperature at which the material attains the lowest thermal conductivity, namely, the minimal thermal conductivity of the material. According to Clark, the main factors that affect it are the average relative atomic mass, the Young’s modulus, the density, the defects in the crystal, and the porosity. In addition, Cahill posits that the wave velocity of the acoustic wave is also closely related to the thermal conductivity of the material, and as the thermal conductivity decreases with the increase of the temperature under high-temperature conditions, its minimum value is of substantial significance to the application of the material under the high-temperature conditions. The theoretical minimum thermal conductivity is calculated via the Clark [41] model and the Cahill [42] model.
Clark model:
Cahill model:
In the Clark model, E and ρ represent the Young’s modulus and density of the crystal, respectively; kB represents the Boltzmann constant; and Ma = [M/(n ∙ NA)] represents the average mass of the atoms in the lattice, where M is the molar mass of the molecule, n is the number of atoms in the molecule, and NA represents Avogadro’s constant. In the Cahill model, p is the number of atoms per unit volume, and νl and νt [43] are the average acoustic longitudinal wave and acoustic shear wave, respectively, which can be calculated via the following formulas.
The calculation results are presented in Table 4, in accordance with Formulas (18) and (19), and the theoretical minimum thermal conductivities of P6422-AlP, P6422-GaP, and P6422-InP in the Clark model are 1.222 W∙m−1∙K−1, 0.972 W∙m−1∙K−1, and 0.610 W∙m−1∙K−1, respectively. In the Cahill model, the theoretical minimum thermal conductivities for P6422-XP (X = Al, Ga, or In) are 1.338 W∙m−1∙K−1, 1.058 W∙m−1∙K−1 and 0.669 W∙m−1∙K−1, respectively. According to the calculated values, the theoretical minimum values of the thermal conductivity that are calculated by the Clark model are slightly less than those by the Cahill model. As the contributions of the atomic number density and the phonon spectrum are considered in the Cahill model, whereas the Clark model does not calculate the contribution of the optical phonons [44], the Clark model underestimates the theoretical minimum thermal conductivity and the Cahill model yields a value that is closer to the actual value. The maximum of the theoretical minimum thermal conductivity of P6422-XP (X = Al, Ga, or In) corresponds to P6422-AlP and the minimum to P6422-InP, namely, according to the capacity of heat dissipation at high temperature (approaching the melting point), P6422-AlP > P6422-GaP > P6422-InP. The theoretical minimum thermal conductivities of Fm-XP (X = Al, Ga, or In) at high temperature are lower than those of P6422-XP (X = Al, Ga, or In); therefore, P6422-XP (X = Al, Ga, or In) have stronger thermal conductivity than Fm-XP (X = Al, Ga, or In) at high temperature.

Table 4.
Average mass per atom, Ma/g; the transverse and longitudinal sound velocities, νt, νl/(km∙s−1); the density of number of atom per volume, p; and the minimum thermal conductivity at high temperature, κmin/(W∙m−1∙K−1), of P6422- and Fm-XP (X = Al, Ga, or In) base on calculated (GGA-PBE) Young’s modulus E, density of the crystal ρ, bulk moduli B, and shear moduli G.
4. Conclusions
In this study, the related properties of P6422-XP (X = Al, Ga, or In) are investigated via the density functional method, which include structural, mechanical, anisotropy, electrical, and thermal properties. P6422-XP (X = Al, Ga, or In) are dynamically, mechanically, and thermodynamically stable, where P6422-XP (X = Al or In) show stronger anti-compression and anti-shearing strain abilities than Fm-XP (X = Al or In). In the P6422 phase, XP (X = Al or Ga) are brittle, and InP is ductile. The stiffness of P6422-XP (X = Al, Ga, or In) are higher, and they are more difficult to deform than Fm-XP (X = Al, Ga, or In), especially GaP. As the pressure increases, P6422-XP (X = Al, Ga, or In) become increasingly stable. P6422-XP (X = Al, Ga, or In) have the largest anisotropy in the (100)-plane and show isotropy in the (001)-plane. P6422-InP is a direct band gap semiconductor, which has a band gap of 0.42 eV and potential application as an infrared detector. P6422-XP (X = Al or Ga) exhibit indirect band gap properties with band gaps of 1.55 and 0.86 eV, respectively. At high temperature, P6422-XP (X = Al, Ga, or In) have stronger thermal conductivity than Fm-XP (X = Al, Ga, or In), where maximum and minimum thermal conductivities correspond P6422-AlP and P6422-InP, respectively. These properties provide a theoretical basis and new ideas for the application of P6422-XP (X = Al, Ga, or In) in optoelectronic devices and thermoelectric materials.
Author Contributions
W.Z. designed the project; W.Z., C.C., Y.S., and J.M. performed the calculations; J.M., W.Z., Y.S., Y.Y., and C.C. analyzed the results, J.M., C.C., and Y.S. wrote the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (No. 61974116).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Jiao, Z.-Y.; Ma, S.-H.; Guo, Y.-L. Simulation of optical function for phosphide crystals following the DFT band structure calculations. Comput. Theor. Chem. 2011, 970, 79–84. [Google Scholar] [CrossRef]
- Lakel, S.; Okbi, F.; Meradji, H. Optical and electronic properties of BxAl1−xP alloys: A first principles study. Optik 2016, 127, 3755–3761. [Google Scholar] [CrossRef]
- Zhang, W.; Wu, W.; Cheng, X. First-principles study of phase transition and thermodynamic properties of InP. Phys. B 2010, 405, 4536–4540. [Google Scholar] [CrossRef]
- Lin, L.; Woods, G.T.; Callcott, T.A. Soft-X-ray fluorescence spectra of III−V phosphides BP, GaP, and InP. Phys. Rev. B 2001, 63, 235107. [Google Scholar] [CrossRef]
- Xu, L.F.; Bu, W. Mechanical and thermodynamic properties of AlX (X = N, P, As) compounds. Int. J. Mod. Phys. B 2017, 31, 1750167. [Google Scholar] [CrossRef]
- Liu, C.; Ma, M.; Yuan, X.; Sun, H.; Ying, P.; Xu, B.; Zhao, Z.; He, J. Metastable phases, phase transformation and properties of AlAs based on first-principle study. Comput. Mater. Sci. 2017, 128, 337–342. [Google Scholar] [CrossRef]
- Yang, R.; Zhu, C.; Wei, Q.; Zhang, D. First-principles study on phases of AlP. Solid State Commun. 2017, 267, 23–28. [Google Scholar] [CrossRef]
- Baida, A.; Ghezali, M. Structural, electronic and optical properties of InP under pressure: An ab-initio study. Comput. Condens. Matter 2018, 17, e00333. [Google Scholar] [CrossRef]
- Arbouche, O.; Belgoumène, B.; Soudini, B.; Azzaz, Y.; Bendaoud, H.; Amara, K. First-principles study on structural properties and phase stability of III-phosphide (BP, GaP, AlP and InP). Comput. Mater. Sci. 2010, 47, 685–692. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Zhang, W.; Chai, C.; Fan, Q.; Song, Y.; Yang, Y. PBCF-graphene: A 2D sp2 hybridized honeycomb carbon allotrope with a direct band gap. ChemNanoMat 2020, 6, 139–147. [Google Scholar] [CrossRef]
- Clark, S.J.; Segall, M.D.; Pickard, C.J.; Hasnip, P.J.; Probert, M.J.; Refson, K.; Payne, M.C. First Principles Methods Using CASTEP. Z. Fuer Krist. 2005, 220, 567–570. [Google Scholar] [CrossRef]
- Zhang, W.; Chai, C.; Song, Y.; Fan, Q.; Yang, Y. Anisotropic, and Thermal Properties of AlAs in oC12 and hP6 Phases under Pressure. Materials 2018, 11, 740. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Fan, Q.; Niu, R.; Zhang, W.; Zhang, W.; Ding, Y.; Yun, S. t-Si64: A Novel Silicon Allotrope. ChemPhysChem 2019, 20, 128–133. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Pfrommer, B.G.; Côté, M.; Louie, S.G.; Cohen, M.L. Relaxation of Crystals with the Quasi-Newton Method. J. Comput. Phys. 1997, 131, 233. [Google Scholar] [CrossRef]
- Baroni, S.; de Gironcoli, S.; dal Corso, A.; Giannozzi, P. Phonons and related crystal properties from density-functional perturbation theory. Rev. Mod. Phys. 2001, 73, 515. [Google Scholar] [CrossRef]
- Krukau, A.V.; Vydrov, O.A.; Izmaylov, A.F.; Scuseria, G.E. Influence of the exchange screening parameter on the performance of screened hybrid functionals. J. Chem. Phys. 2006, 125, 224106. [Google Scholar] [CrossRef]
- Fan, Q.; Xu, J.; Zhang, W.; Song, Y.; Yun, S. Physical properties of group 14 semiconductor alloys in orthorhombic phase. J. Appl. Phys. 2019, 126, 045709. [Google Scholar] [CrossRef]
- Murnaghan, F.D. The compressibility of media under extreme pressures. Proc. Natl. Acad. Sci. USA 1944, 30, 244. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, R.; Hashemifar, S.J.; Akbarzadeh, H. First-principles study of the structural and electronic properties of III-phosphides. Phys. B Condens. Matter. 2008, 403, 1876–1881. [Google Scholar] [CrossRef]
- Giesecke, G.; Pfister, H. Präzisionsbestimmung der Gitterkonstanten von AIIIBv-Verbindungen. Acta Crystallogr. 1958, 11, 369–371. [Google Scholar] [CrossRef]
- Kishino, S. Improved Techniques of Lattice Parameter Measurements Using two X-ray Beams. Adv. X-ray Anal. 1972, 16, 367–378. [Google Scholar] [CrossRef]
- Wang, C.C.; Zaheeruddin, M.; Spinar, L.H. Preparation and properties of aluminum phosphide. J. Inorg. Nucl. Chem. 1963, 25, 326. [Google Scholar] [CrossRef]
- Wu, Z.J.; Zhao, E.J.; Xiang, H.P.; Hao, X.F.; Liu, X.J.; Meng, J. Crystal structures and elastic properties of superhard IrN2 and IrN3 from first principles. Phys. Rev. B 2007, 76, 054115. [Google Scholar] [CrossRef]
- Fan, Q.; Zhang, W.; Yun, S.; Xu, J.; Song, Y. III-Nitride Polymorphs: XN (X = Al, Ga, In) in the Pnma Phase. Chem. Eur. J. 2018, 24, 17280–17287. [Google Scholar] [CrossRef]
- Zhang, X.D.; Ying, C.H.; Li, Z.J.; Shi, G.M. First-principles calculations of structural stability, elastic, dynamical and thermodynamic properties of SiGe, SiSn, GeSn. Superlattices Microstruct. 2012, 52, 459–469. [Google Scholar] [CrossRef]
- Zhang, W.; Chai, C.; Fan, Q.; Weng, K.; Yang, Y. Theoretical investigations of Ge1−xSnx alloys (x = 0, 0.333, 0.667, 1) in P42/ncm phase. J. Mater. Sci. 2018, 53, 9611–9626. [Google Scholar] [CrossRef]
- Hill, R. The Elastic Behaviour of a Crystalline Aggregate. Proc. Phys. Soc. Lond. 1952, 65, 349. [Google Scholar] [CrossRef]
- Yang, R.K.; Zhu, C.S.; Wei, Q.; Du, Z. Investigations on structural, elastic, thermodynamic and electronic properties of TiN, Ti2N and Ti3N2 under high pressure by first-principles. J. Phys. Chem. Solids 2016, 98, 10–19. [Google Scholar] [CrossRef]
- Zhang, W.; Chai, C.; Fan, Q.; Song, Y.; Yang, Y. Two novel superhard carbon allotropes with honeycomb structures. J. Appl. Phys. 2019, 126, 145704. [Google Scholar] [CrossRef]
- Ishii, I.; Fujiwara, T. Electronic structures and cohesion mechanism of Cd-based quasicrystals. J. Noncryst. Solids. 2002, 312, 494–497. [Google Scholar] [CrossRef]
- Muramatsu, S.; Kitahara, M. Simple expressions for elastic constants c11, c12, and c44 and internal displacements of semiconductors. J. Appl. Phys. 1993, 73, 4270. [Google Scholar] [CrossRef]
- Weil, R.; Groves, W.O. The Elastic Constants of Gallium Phosphide. J. Appl. Phys. 1968, 39, 4049. [Google Scholar] [CrossRef]
- Borcherds, P.H.; Kunc, K. The lattice dynamics of indium pnictides. J. Phys. C Solid State Phys. 1978, 11, 4145. [Google Scholar] [CrossRef]
- Fan, Q.Y.; Wei, Q.; Yan, H.Y.; Zhang, M.G.; Zhang, Z.X.; Zhang, J.Q.; Zhang, D.Y. Elastic and electronic properties of Pbca-BN: First-principles calculations. Comput. Mater. Sci. 2014, 85, 80. [Google Scholar] [CrossRef]
- Hu, W.C.; Liu, Y.; Li, D.J.; Zeng, X.Q.; Xu, C.S. First-principles study of structural and electronic properties of C14-type Laves phase Al2Zr and Al2Hf. Comput. Mater. Sci. 2014, 83, 27–34. [Google Scholar] [CrossRef]
- Deng, R.P.; Ozsdolay, B.D.; Zheng, P.Y.; Khare, S.V.; Gall, D. Optical and transport measurement and first-principles determination of the ScN band gap. Phys. Rev. B 2015, 91, 045104. [Google Scholar] [CrossRef]
- Li, X.Z.; Xing, M.J. Prediction of a novel carbon allotrope from first-principle calculations: A potential superhard material in monoclinic symmetry. Mater. Chem. Phys. 2020, 242, 122480. [Google Scholar] [CrossRef]
- Clarke, D.R. Materials selection guidelines for low thermal conductivity thermal barrier coatings. Surf. Coat. Technol. 2003, 163, 67–74. [Google Scholar] [CrossRef]
- Cahill, D.G.; Watson, S.K.; Pohl, R.O. Lower limit to the thermal conductivity of disordered crystals. Phys. Rev. B 1992, 46, 6131–6140. [Google Scholar] [CrossRef] [PubMed]
- Schreiber, E.; Anderson, O.L.; Soga, N. Elastic Constants and Their Measurements; McGraw-Hill: New York, NY, USA, 1974. [Google Scholar]
- Li, C.X.; Duan, Y.H.; Hu, W.C. Electronic structures, elastic anisotropy, thermal conductivity and optical properties of calcium apatite Ca5(PO4)3X (X = F, Cl or Br). J. Alloys Compd. 2015, 619, 66–77. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).