Parameter Identification of Cutting Forces in Crankshaft Grinding Using Artificial Neural Networks
Abstract
1. Introduction
2. Literature Review
3. Materials and Methods
3.1. General Formulation of the Problem
- creating a method for conducting a virtual experiment to determine the cutting force depending on an array of m parameters of formula (1):
- creating a table of input data for the variation range of parameters that affect the cutting force;
- generating an array of experimental data as a sample of a sufficiently large number of n random arrays of input parameters:
- creating a subroutine for determining the total number of each input parameter;
- generating a set of n combinations of values of m input parameters with a predetermined relative error δ;
- calculation of n values of cutting forces as a result of a virtual experiment;
- determining the maximum values of each input parameter and the cutting force ;
- using artificial intelligence tools to identify parameters of a mathematical model based on experimental data:
- normalization of input and output parameters;
- creating an artificial neural network and configuring its parameters;
- training an artificial neural network based on an array of normalized experimental data;
- determining the accuracy of estimating the cutting-force value for an arbitrary set of input parameters;
- creating a reliable generalized mathematical model for estimating (m + 1) parameters that determine the cutting force using multi-parameter quasi-linear regression analysis:
- creating a matrix relation for determining the cutting force based on experimental data;
- formation of the stiffness matrix and the column vector of external influence:
- formation of column sub-vectors of external influence and local stiffness parameters;
- formation of the stiffness submatrix;
- globalization of submatrix and column sub-vectors to a common stiffness matrix;
- using the inverse matrix method to evaluate (m + 1) unknown parameters;
- forming a ratio for calculating the cutting force based on a specific coefficient and indices of power, and comparing the obtained dependence with the empirical formula (1);
- determination of relative errors in determining unknown coefficients of the regression model.
3.2. Virtual Experiment on the Cutting Force
4. Results
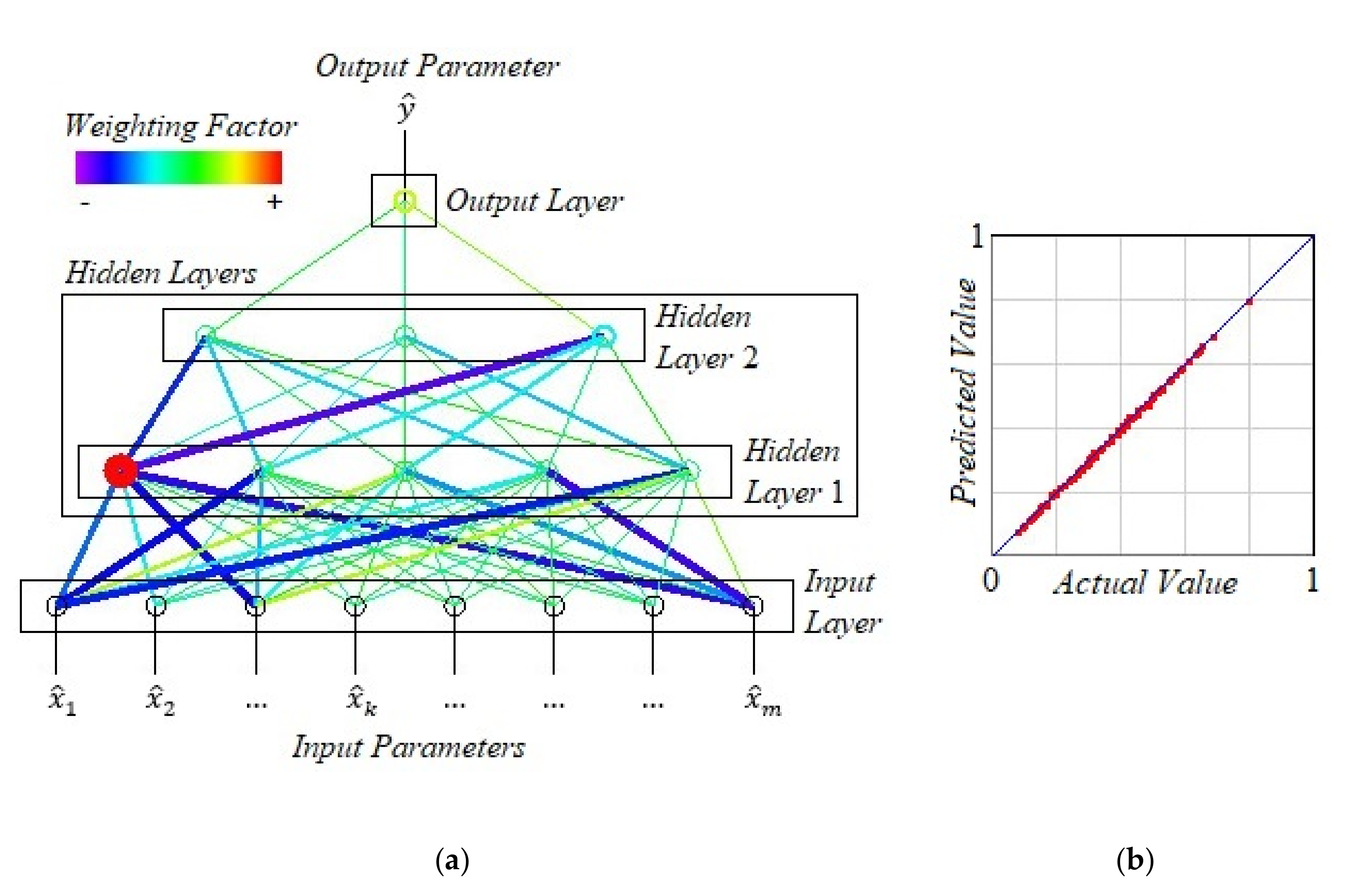
4.1. Application of Artificial Intelligence Systems
4.2. Multi-Parameter Quasi-Linear Regression Procedure
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ivanov, V.; Dehtiarov, I.; Pavlenko, I.; Kosov, I.; Kosov, M. Technology for complex parts machining in multiproduct manufacturing. Manag. Prod. Eng. Rev. 2019, 10, 25–36. [Google Scholar] [CrossRef]
- Karpus, V.; Ivanov, V.; Dehtiarov, I.; Zajac, J.; Kurichkina, V. Technological assurance of complex parts manufacturing. In Advances in Design, Simulation and Manufacturing: DSMIE-2018; Lecture Notes in Mechanical Engineering; Ivanov, V., Rong, Y., Trojanowska, J., Venus, J., Liaposhchenko, O., Zajac, J., Pavlenko, I., Edl, M., Perakovic, D., Eds.; Springer: Cham, Switzerland, 2019; pp. 51–61. [Google Scholar] [CrossRef]
- Denysenko, Y.; Dynnyk, O.; Yashyna, T.; Malovana, N.; Zaloga, V. Implementation of CALS-Technologies in quality management of product life cycle processes. In Advances in Design, Simulation and Manufacturing: DSMIE-2018; Lecture Notes in Mechanical Engineering; Ivanov, V., Rong, Y., Trojanowska, J., Venus, J., Liaposhchenko, O., Zajac, J., Pavlenko, I., Edl, M., Perakovic, D., Eds.; Springer: Cham, Switzerland, 2019; pp. 3–12. [Google Scholar] [CrossRef]
- Dynnyk, O.; Denysenko, Y.; Zaloga, V.; Ivchenko, O.; Yashyna, T. Information support for the quality management system assessment of engineering enterprises. In Advances in Design, Simulation and Manufacturing II: DSMIE-2019; Lecture Notes in Mechanical Engineering; Ivanov, V., Trojanowska, J., Machado, J., Liaposhchenko, O., Zajac, J., Pavlenko, I., Edl, M., Perakovic, D., Eds.; Springer: Cham, Switzerland, 2020; pp. 65–74. [Google Scholar] [CrossRef]
- Yarovyi, Y.; Yarova, I. Energy criterion for metal machining methods. In Advances in Design, Simulation and Manufacturing II: DSMIE-2019; Lecture Notes in Mechanical Engineering; Ivanov, V., Trojanowska, J., Machado, J., Liaposhchenko, O., Zajac, J., Pavlenko, I., Edl, M., Perakovic, D., Eds.; Springer: Cham, Switzerland, 2020; pp. 378–387. [Google Scholar] [CrossRef]
- Fesenko, A.; Basova, Y.; Ivanov, V.; Ivanova, M.; Yevsiukova, F.; Gasanov, M. Increasing of equipment efficiency by intensification of technological processes. Period. Polytech. Mech. Eng. 2019, 63, 67–73. [Google Scholar] [CrossRef]
- Krol, O.; Sokolov, V. Development of models and research into tooling for machining centers. East. Eur. J. Enterp. Technol. 2018, 3, 12–22. [Google Scholar] [CrossRef]
- Sokolov, V.; Krol, O.; Baturin, Y. Dynamics research and automatic control of technological equipment with electrohydraulic drive. In Proceedings of the IEEE International Russian Automation Conference, RusAutoCon 2019, Sochi, Russia, 8–14 September 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Basova, Y.; Nutsubidze, K.; Ivanova, M.; Slipchenko, S.; Kotliar, A. Design and numerical simulation of the new design of the gripper for manipulating of the rotational parts. Diagnostyka 2018, 19, 11–18. [Google Scholar] [CrossRef]
- Karpus, V.E.; Ivanov, V.A. Locating accuracy of shafts in V-blocks. Russ. Eng. Res. 2012, 32, 144–150. [Google Scholar] [CrossRef][Green Version]
- Denkena, B.; Gümmer, O. Active tailstock for precise alignment of precision forged crankshafts during grinding. Procedia CIRP 2013, 12, 121–126. [Google Scholar] [CrossRef][Green Version]
- Dražumerič, R.; Roininen, R.; Badger, J.; Krajnik, P. Temperature-based method for determination of feed increments in crankshaft grinding. J. Mater. Process. Technol. 2018, 259, 228–234. [Google Scholar] [CrossRef]
- Aliakbari, K. Failure analysis of four-cylinder diesel engine crankshaft. J. Braz. Soc. Mech. Sci. Eng. 2019, 41. [Google Scholar] [CrossRef]
- Xu, X.L.; Yu, Z.W. Failure analysis of a truck diesel engine crankshaft. Eng. Fail. Anal. 2018, 92, 84–94. [Google Scholar] [CrossRef]
- Belkhode, P.N. Optimum choice of the front suspension of an automobile. J. Eng. Sci. 2019, 6, E21–E24. [Google Scholar] [CrossRef]
- Citti, P.; Giorgetti, A.; Millefanti, U. Current challenges in material choice for high-performance engine crankshaft. Procedia Structural Integrity 2018, 8, 486–500. [Google Scholar] [CrossRef]
- Kostyuk, G. Prediction of the microhardness characteristics, the removable material volume for the durability period, cutting tools durability and processing productivity depending on the grain size of the coating or cutting tool base material. In Advances in Manufacturing II: MANUFACTURING 2019; Lecture Notes in Mechanical Engineering; Gapinski, B., Szostak, M., Ivanov, V., Eds.; Springer: Cham, Switzerland, 2019; Volume 4, pp. 300–316. [Google Scholar] [CrossRef]
- Kostyuk, G.; Nechyporuk, M.; Kostyk, K. Determination of technological parameters for obtaining nanostructures under pulse laser radiation on steel of drone engine parts. In Proceedings of the 10th International Conference on Dependable Systems, Services and Technologies, DESSERT 2019, Leeds, UK, 5–7 June 2019; pp. 208–212. [Google Scholar] [CrossRef]
- Martsynkovskyy, V.; Tarelnyk, V.; Konoplianchenko, I.; Gaponova, O.; Dumanchuk, M. Technology support for protecting contacting surfaces of half-coupling—Shaft press joints against fretting wear. In Advances in Design, Simulation and Manufacturing II: DSMIE-2019; Lecture Notes in Mechanical Engineering; Ivanov, V., Trojanowska, J., Machado, J., Liaposhchenko, O., Zajac, J., Pavlenko, I., Edl, M., Perakovic, D., Eds.; Springer: Cham, Switzerland, 2020; pp. 216–225. [Google Scholar] [CrossRef]
- Tarelnyk, V.; Konoplianchenko, I.; Tarelnyk, N.; Kozachenko, A. Modeling technological parameters for producing combined electrospark deposition coatings. In Proceedings of the International Conference on Actual Problems of Engineering Mechanics, APEM 2019, Odessa, Ukraine, 20–24 May 2019; Surianinov, M., Ed.; Trans Tech Publications Ltd.: Baech, Switzerland, 2019; pp. 131–142. [Google Scholar] [CrossRef]
- Da Silva, S.P.; Da Silva, E.J.; Coelho, R.T.; Rossi, M.A. Finding dimensional stability considering deflection effects in cylindrical plunge grinding. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 555. [Google Scholar] [CrossRef]
- Stepanov, M.; Ivanova, L.; Litovchenko, P.; Ivanova, M.; Basova, Y. Model of thermal state of the system of application of coolant in grinding machine. In Advances in Design, Simulation and Manufacturing: DSMIE-2018; Lecture Notes in Mechanical Engineering; Ivanov, V., Rong, Y., Trojanowska, J., Venus, J., Liaposhchenko, O., Zajac, J., Pavlenko, I., Edl, M., Perakovic, D., Eds.; Springer: Cham, Switzerland, 2019; pp. 156–165. [Google Scholar] [CrossRef]
- Patel, A.; Bauer, R.J.; Warkentin, A. Investigation of the effect of speed ratio on workpiece surface topography and grinding power in cylindrical plunge grinding using grooved and non-grooved grinding wheels. Int. J. Adv. Manuf. Technol. 2019, 105, 2977–2987. [Google Scholar] [CrossRef]
- Lezanski, P. A data-driven predictive model of the grinding wheel wear using the neural network approach. J. Mach. Eng. 2017, 17, 69–82. [Google Scholar] [CrossRef]
- Shapovalova, M.; Vodka, O. Image microstructure estimation algorithm of heterogeneous materials for identification their chemical composition. In Proceedings of the 2nd IEEE Ukraine Conference on Electrical and Computer Engineering, UKRCON 2019, Lviv, Ukraine, 2–6 July 2019. [Google Scholar] [CrossRef]
- Lipiński, D.; Kacalak, W.; Bałasz, B. Optimization of sequential grinding process in a fuzzy environment using genetic algorithms. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 96. [Google Scholar] [CrossRef]
- Boaron, A.; Weingaertner, W.L. Dynamic in-process characterization method based on acoustic emission for topographic assessment of conventional grinding wheels. Wear 2018, 406, 218–229. [Google Scholar] [CrossRef]
- Botcha, B.; Rajagopal, V.; Bukkapatnam, S.T. Process-machine interactions and a multi-sensor fusion approach to predict surface roughness in cylindrical plunge grinding process. Procedia Manuf. 2018, 26, 700–711. [Google Scholar] [CrossRef]
- Steffan, M.; Haas, F.; Pierer, A.; Gentzen, J. Adaptive grinding process-prevention of thermal damage using OPC-UA technique and in situ metrology. J. Manuf. Sci. Eng. Trans. ASME 2017, 139. [Google Scholar] [CrossRef]
- Bordin, F.M.; Weingaertner, W.L. Steel subsurface damage on plunge cylindrical grinding with sol-gel aluminum oxide grinding wheels. Int. J. Adv. Manuf. Technol. 2019, 105, 2907–2917. [Google Scholar] [CrossRef]
- Kotliar, A.; Basova, Y.; Ivanova, M.; Gasanov, M.; Sazhniev, I. Technological assurance of machining accuracy of crankshaft. In Advances in Manufacturing II: MANUFACTURING 2019; Lecture Notes in Mechanical Engineering; Diering, M., Wieczorowski, M., Brown, C., Eds.; Springer: Cham, Switzerland, 2019; Volume 2, pp. 37–51. [Google Scholar] [CrossRef]
- Kotliar, A.; Gasanov, M.; Basova, Y.; Panamariova, O.; Gubskyi, S. Ensuring the reliability and performance criterias of crankshafts. Diagnostyka 2019, 20, 23–32. [Google Scholar] [CrossRef]
- Kundrák, J.; Fedorenko, D.O.; Fedorovich, V.A.; Fedorenko, E.Y.; Ostroverkh, E.V. Porous diamond grinding wheels on ceramic binders: Design and manufacturing. Manuf. Technol. 2019, 19, 446–454. [Google Scholar] [CrossRef]
- Sokhan’, S.V.; Maystrenko, A.L.; Kulich, V.H.; Sorochenko, V.H.; Voznyy, V.V.; Gamaniuk, M.P.; Zubaniev, Y.M. Diamond grinding the ceramic balls from silicon carbide. J. Eng. Sci. 2018, 5, A12–A20. [Google Scholar] [CrossRef]
- Kundrák, J.; Mamalis, A.G.; Fedorovich, V.; Pyzhov, I.; Kryukova, N. Evaluation of the characteristics of diamond grinding wheels at their production and operation stages. Int. J. Adv. Manuf. Technol. 2018, 94, 1131–1137. [Google Scholar] [CrossRef]
- Mamalis, A.G.; Grabchenko, A.I.; Mitsyk, A.V.; Fedorovich, V.A.; Kundrak, J. Mathematical simulation of motion of working medium at finishing-grinding treatment in the oscillating reservoir. Int. J. Adv. Manuf. Technol. 2014, 70, 263–276. [Google Scholar] [CrossRef]
- Maier, M.; Rupenyan, A.; Bobst, C.; Wegener, K. Self-optimizing grinding machines using Gaussian process models and constrained Bayesian optimization. Int. J. Adv. Manuf. Technol. 2020, 108, 539–552. [Google Scholar] [CrossRef]
- Hernández-Becerro, P.; Purtschert, J.; Konvicka, J.; Buesser, C.; Schranz, D.; Mayr, J.; Wegener, K. Reduced-order model of the environmental variation error of a precision five-axis machine tool. J. Manuf. Sci. Eng. Trans. ASME 2021, 143, 021005. [Google Scholar] [CrossRef]
- Pavlenko, I.V.; Simonovskiy, V.I.; Demianenko, M.M. Dynamic analysis of centrifugal machines rotors supported on ball bearings by combined application of 3D and beam finite element models. In Proceedings of the 15th International Scientific and Engineering Conference Hermetic Sealing, Vibration Reliability and Ecological Safety of Pump and Compressor Machinery, HERVICON+PUMPS 2017, Sumy, Ukraine, 5–8 September 2017; Institute of Physics Publishing: Bristol, UK, 2017. [Google Scholar] [CrossRef]
- Pavlenko, I.; Ivanov, V.; Kuric, I.; Gusak, O.; Liaposhchenko, O. Ensuring vibration reliability of turbopump units using artificial neural networks. In Advances in Manufacturing II: MANUFACTURING 2019; Lecture Notes in Mechanical Engineering; Trojanowska, J., Ciszak, O., Machado, J., Pavlenko, I., Eds.; Springer: Cham, Switzerland, 2019; Volume 1, pp. 166–175. [Google Scholar] [CrossRef]
- Pavlenko, I.; Trojanowska, J.; Ivanov, V.; Liaposhchenko, O. Parameter identification of hydro-mechanical processes using artificial intelligence systems. Int. J. Mechatron. Appl. Mech. 2019, 2019, 19–26. [Google Scholar]
- Sacks, J.; Welch, W.J.; Mitchell, T.J.; Wynn, H.P. Design and analysis of computer experiments. Stat. Sci. 1989, 4, 409–423. [Google Scholar] [CrossRef]
- Ye, Y.; Wang, Z.; Zhang, X. An optimal pointwise weighted ensemble of surrogates based on minimization of local mean square error. Struct. Multidiscip. Optim. 2020, 62, 529–542. [Google Scholar] [CrossRef]
- Filelis-Papadopoulos, C.K.; Gravvanis, G.A. Generic approximate sparse inverse matrix techniques. Int. J. Comput. Methods 2014, 11, 1350084. [Google Scholar] [CrossRef]
| Parameter | σt | H | Vp | Z | S | Spr | tpr | B |
|---|---|---|---|---|---|---|---|---|
| Measurement units | kgf/mm2 | – | mm/min | μm | m/min | mm/min | mm | mm |
| Minimum value | 20 | 1.38 | 0.10 | 16 | 20 | 60 | 0.01 | 20 |
| Maximum value | 120 | 1.60 | 0.15 | 40 | 100 | 300 | 0.03 | 120 |
| Parameter change increment | 10 | 0.02 | 0.01 | 8 | 5 | 10 | 0.01 | 2 |
| σt | H | Vp | Z | S | Spr | tpr | B | Pz |
|---|---|---|---|---|---|---|---|---|
| kgf/mm2 | – | mm/min | μm | m/min | mm/min | mm | mm | H |
| 20 | 1.40 | 0.11 | 25 | 65 | 190 | 0.01 | 110 | 45 |
| 60 | 1.46 | 0.14 | 16 | 35 | 260 | 0.01 | 30 | 24 |
| 40 | 1.54 | 0.13 | 32 | 100 | 300 | 0.02 | 100 | 57 |
| 80 | 1.56 | 0.11 | 40 | 95 | 60 | 0.02 | 120 | 83 |
| 20 | 1.52 | 0.13 | 16 | 35 | 60 | 0.03 | 30 | 17 |
| Unitless Parameters | ||||||||
| 0.167 | 0.875 | 0.733 | 0.625 | 0.650 | 0.633 | 0.333 | 0.917 | 0.294 |
| 0.500 | 0.913 | 0.933 | 0.400 | 0.350 | 0.867 | 0.333 | 0.250 | 0.157 |
| 0.333 | 0.963 | 0.867 | 0.800 | 1.000 | 1.000 | 0.667 | 0.833 | 0.373 |
| 0.667 | 0.975 | 0.733 | 1.000 | 0.950 | 0.200 | 0.667 | 1.000 | 0.542 |
| 0.167 | 0.950 | 0.867 | 0.400 | 0.350 | 0.200 | 1.000 | 0.250 | 0.111 |
| Parameter | α | β1 | β1 | β1 | β1 | β1 | β1 | β1 | β1 |
|---|---|---|---|---|---|---|---|---|---|
| Predicted value | 2.315 | 0.337 | 0.256 | 0.932 | −0.051 | −0.072 | −0.072 | −0.025 | 0.985 |
| Actual value | 2.254 | 0.342 | 0.258 | 0.945 | −0.051 | −0.072 | −0.072 | −0.026 | 1.000 |
| Relative error, % | 2.7 | 1.4 | 0.9 | 1.4 | 0.8 | 1.2 | 1.5 | 2.0 | 1.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pavlenko, I.; Saga, M.; Kuric, I.; Kotliar, A.; Basova, Y.; Trojanowska, J.; Ivanov, V. Parameter Identification of Cutting Forces in Crankshaft Grinding Using Artificial Neural Networks. Materials 2020, 13, 5357. https://doi.org/10.3390/ma13235357
Pavlenko I, Saga M, Kuric I, Kotliar A, Basova Y, Trojanowska J, Ivanov V. Parameter Identification of Cutting Forces in Crankshaft Grinding Using Artificial Neural Networks. Materials. 2020; 13(23):5357. https://doi.org/10.3390/ma13235357
Chicago/Turabian StylePavlenko, Ivan, Milan Saga, Ivan Kuric, Alexey Kotliar, Yevheniia Basova, Justyna Trojanowska, and Vitalii Ivanov. 2020. "Parameter Identification of Cutting Forces in Crankshaft Grinding Using Artificial Neural Networks" Materials 13, no. 23: 5357. https://doi.org/10.3390/ma13235357
APA StylePavlenko, I., Saga, M., Kuric, I., Kotliar, A., Basova, Y., Trojanowska, J., & Ivanov, V. (2020). Parameter Identification of Cutting Forces in Crankshaft Grinding Using Artificial Neural Networks. Materials, 13(23), 5357. https://doi.org/10.3390/ma13235357









