Base-Pairs’ Correlated Oscillation Effects on the Charge Transfer in Double-Helix B-DNA Molecules
Abstract
1. Introduction
2. DNA Model Hamiltonian
2.1. Lattice Hamiltonian
2.2. The - Electronic Coupling
2.3. Electronic Hamiltonian
3. Dynamical Equations of Motion
3.1. General Expressions
3.2. Dynamics of Homopolymer dsDNA Macromolecules
4. Charge Transfer through dsDNA Homopolymers
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| dsDNA | double-stranded DNA |
| bp | base pair |
| CT | charge transfer |
| A | adenine |
| C | cytosine |
| G | guanine |
| T | thymine |
| PDB | Peyrard–Dauxois–Bishop |
| HOMO | highest occupied molecular orbital |
| LUMO | lowest occupied molecular orbital |
| LCAO | linear combination of atomic orbitals |
References
- Eley, D.D.; Spivey, D.I. Semiconductivity of organic substances. Part 9. Nucleic Acid in the Dry State. Trans. Faraday Soc. 1962, 58, 411–415. [Google Scholar] [CrossRef]
- Starikov, E.B.; Fujita, T.; Wanatabe, H.; Sengoku, Y.; Tanaka, S.; Wenzel, W. Effects of molecular motion on charge transfer/transport through DNA duplexes with and without base pair mismatch. Mol. Simul. 2006, 32, 759–764. [Google Scholar] [CrossRef]
- Berlin, Y.A.; Grozema, F.C.; Siebbeles, L.D.A.; Ratner, M.A. Charge transfer in donor-bridge-acceptor systems: Static disorder, dynamic fluctuations, and complex kinetics. J. Phys. Chem. C 2008, 112, 10988–11000. [Google Scholar] [CrossRef]
- Starikov, E.B.; Quintilla, A.; Nganou, C.; Lee, K.H.; Cuniberti, G.; Wenzel, W. Single-molecule DNA conductance in water solutions: Role of DNA low-frequency dynamics. Chem. Phys. Lett. 2009, 467, 369–374. [Google Scholar] [CrossRef]
- Bruinsma, R.; Grüner, G.; D’Orsogna, M.R.; Rudnick, J. Fluctuation-facilitated charge migration along DNA. Phys. Rev. Lett. 2000, 85, 4393–4396. [Google Scholar] [CrossRef] [PubMed]
- Roche, S. Sequence Dependent DNA-Mediated Conduction. Phys. Rev. Lett. 2003, 91, 108101. [Google Scholar] [CrossRef]
- Zhu, Y.; Kaun, C.C.; Guo, H. Contact, charging, and disorder effects on charge transport through a model DNA molecule. Phys. Rev. B 2004, 69, 245112. [Google Scholar] [CrossRef]
- Ren, W.; Wang, J.; Ma, Z.; Guo, H. Effect of thermal fluctuations of twist angles on charge transport in DNA: A model calculation. Phys. Rev. B 2005, 72, 035456. [Google Scholar] [CrossRef]
- Guo, A.M.; Xu, H. Sequence dependent charge transport through DNA molecules: The role of periodicity and long-range correlations. Physica B 2007, 391, 292–298. [Google Scholar] [CrossRef]
- Gutiérrez, R.; Mandal, S.; Cuniberti, G. Dissipative effects in the electronic transport through DNA molecular wires. Phys. Rev. B 2005, 71, 235116. [Google Scholar] [CrossRef]
- Gutiérrez, R.; Mohapatra, S.; Cohen, H.; Porath, D.; Cuniberti, G. Inelastic quantum transport in a ladder model: Implications for DNA conduction and comparison to experiments on suspended DNA oligomers. Phys. Rev. B 2006, 74, 235105. [Google Scholar] [CrossRef]
- Lemaur, V.; da Silva Filho, D.A.; Coropceanu, V.; Lehmann, M.; Geerts, Y.; Piris, J.; Debije, M.G.; van de Craats, A.M.; Senthilkumar, K.; Siebbeles, L.D.A.; et al. Charge transport properties in discotic liquid crystals: A quantum-chemical insight into structure-property relationships. J. Am. Chem. Soc. 2004, 126, 3271–3279. [Google Scholar] [CrossRef] [PubMed]
- Gutiérrez, R.; Caetano, R.; B Woiczikowski, P.B.; Kubar, T.; Elstner, M.; Cuniberti, G. Structural fluctuations and quantum transport through DNA molecular wires: A combined molecular dynamics and model Hamiltonian approach. New J. Phys. 2010, 12, 023022. [Google Scholar] [CrossRef]
- Maciá, E. Electrical conductance in duplex DNA: Helical effects and low-frequency vibrational coupling. Phys. Rev. B 2007, 76, 245123. [Google Scholar] [CrossRef]
- Maciá, E. π-π orbital resonance in twisting douplex DNA: Dynamical phyllotaxis and electronic structure effects. Phys. Rev. B 2009, 80, 125102. [Google Scholar] [CrossRef]
- Torrellas, G.; Maciá, E. Twist–radial normal mode analysis in double-stranded DNA chains. Phys. Lett. A 2012, 376, 3407–3410. [Google Scholar] [CrossRef]
- Peyrard, M. Nonlinear dynamics and statistical physics of DNA. Nonlinearity 2004, 17, R1–R40. [Google Scholar] [CrossRef]
- Peyrard, M.; Bishop, A.R. Statistical mechanics of a nonlinear model for DNA denaturation. Phys. Rev. Lett. 1989, 62, 2755–2758. [Google Scholar] [CrossRef]
- Dauxois, T.; Peyrard, M. Entropy-driven transition in a one-dimensional system. Phys. Rev. E 1995, 51, 4027–4040. [Google Scholar] [CrossRef]
- Peyrard, M.; Cuesta-López, S.; Angelov, D. Experimental and theoretical studies of sequence effects on the fluctuation and melting of short DNA molecule. J. Phys. Condens. Matter 2009, 21, 034103. [Google Scholar] [CrossRef][Green Version]
- Maciá-Barber, E. Aperiodic Structures in Condensed Matter: Fundamentals and Applications; Taylor and Francis, CRC Press: Boca Raton, FL, USA, 2009; pp. 209–297. [Google Scholar]
- Shinwari, W.; Deen, M.J.; Starikov, E.B.; Cuniberti, G. Electrical Conductance in Biological Molecules. Adv. Funct. Mater. 2010, 20, 1865–1883. [Google Scholar] [CrossRef]
- Artacho, E.; Machado, M.; Sánchez-Portal, D.; Ordejón, P.; Soler, J.M. Electrons in dry DNA from density functional calculations. Mol. Phys. 2003, 101, 1587–1594. [Google Scholar] [CrossRef][Green Version]
- Barbi, M.; Cocco, S.; Peyrard, M. Helicoidal model for DNA opening. Phys. Lett. A 1999, 253, 358–369. [Google Scholar] [CrossRef]
- Cocco, S.; Monasson, R. Statistical mechanics of torque induced denaturation of DNA. Phys. Rev. Lett. 1999, 83, 5178–5181. [Google Scholar] [CrossRef]
- Agarwal, J.; Hennig, D. Breather solutions of a nonlinear DNA model including a longitudinal degree of freedom. Physica A 2003, 323, 519–533. [Google Scholar] [CrossRef]
- Krisch, M.; Mermet, A.; Grimm, H.; Forsyth, V.T.; Rupprecht, A. Phonon dispersion of oriented DNA by inelastic x-ray scattering. Phys. Rev. E 2006, 73, 061909. [Google Scholar] [CrossRef]
- Dauxois, T.; Peyrard, M.; Bishop, A.R. Entropy-driven DNA denaturation. Phys. Rev. E 1993, 47, R44–R47. [Google Scholar] [CrossRef]
- Zhu, J.X.; Rasmussen, K.O.; Balatsky, A.V.; Bishop, A.R. Local electronic structure in the Peyrard–Bishop–Holstein model. J. Phys. Condens. Matter 2007, 19, 136203. [Google Scholar] [CrossRef]
- Cocco, S.; Monasson, R. Theoretical study of collective modes in DNA at ambient temperature. J. Chem. Phys. 2000, 112, 10017–10033. [Google Scholar] [CrossRef]
- Campa, A.; Giansanti, A. Experimental tests of the Peyrard-Bishop model applied to the melting of very short DNA chains. Phys. Rev. E 1998, 58, 3585–3588. [Google Scholar] [CrossRef]
- Cule, D.; Hwa, T. Denaturation of Heterogeneous DNA. Phys. Rev. Lett. 1997, 79, 2375–2378. [Google Scholar] [CrossRef]
- Endres, R.G.; Cox, D.L.; Singh, R.R.P. Colloquium: The quest for high-conductance DNA. Rev. Mod. Phys. 2004, 76, 195–214. [Google Scholar] [CrossRef]
- Hawke, L.G.D.; Kalosakas, G.; Simserides, C. Empirical LCAO parameters for π molecular orbitals in planar organic molecules. Mol. Phys. 2009, 107, 1755–1771. [Google Scholar] [CrossRef]
- Endres, R.G.; Cox, D.L.; Singh, R.R.P. Electronic properties of DNA: Structural and chemical influence on the quest for high conductance and charge transfer. arXiv 2002, arXiv:cond-mat/0201404. [Google Scholar]
- Maciá, E.; Roche, S. Backbone-induced effects in the charge transport efficiency of synthetic DNA molecules. Nanotechnology 2006, 17, 3002–3007. [Google Scholar] [CrossRef]
- De Almeida, M.L.; Ourique, G.S.; Fulco, U.L.; Albuquerque, E.L.; de Moura, F.A.B.F.; Lyra, M.L. Charge transport properties of a twisted DNA molecule: A renormalization approach. Chem. Phys. 2016, 478, 48–54. [Google Scholar] [CrossRef]
- Hawke, L.G.D.; Kalosakas, G.; Simserides, C. Electronic parameters for charge transfer along DNA. Eur. Phys. J. E 2010, 32, 291–305. [Google Scholar] [CrossRef]
- Maciá, E. Electronic structure and transport properties of double-stranded Fibonacci DNA. Phys. Rev. B 2006, 74, 245105. [Google Scholar] [CrossRef]
- Cuniberti, G.; Craco, L.; Porath, D.; Dekker, C. Backbone-induced semiconducting behavior in short DNA wires. Phys. Rev. B 2002, 65, 241314. [Google Scholar] [CrossRef]
- Cuniberti, G.; Maciá, E.; Rodríguez, A.; Römer, R.A. Charge Migration in DNA: Physics, Chemistry and Biology Perspectives; Chakraborty, T., Ed.; Springer: Berlin, Germany, 2007. [Google Scholar]
- Sarmento, R.G.; Fulco, U.L.; Albuquerque, E.L.; Caetano, E.W.S.; Freire, V.N. A renormalization approach to describe charge transport in quasiperiodic dangling backbone ladder (DBL)-DNA molecules. Phys. Lett. A 2011, 375, 3993–3996. [Google Scholar] [CrossRef]
- De Moura, F.A.B.F.; Lyra, M.L.; de Almeida, M.L.; Ourique, G.S.; Fulco, U.L.; Albuquerque, E.L. Methylation effect on the ohmic resistance of a poly-GC DNA-like chain. Phys. Lett. A 2016, 380, 3559–3563. [Google Scholar] [CrossRef]
- De Almeida, M.L.; Oliveira, J.I.N.; Lima Neto, J.X.; Gomes, C.E.M.; Fulco, U.L.; Albuquerque, E.L.; Freire, V.N.; Caetano, E.W.S.; de Moura, F.A.B.F.; Lyra, M.L. Electronic transport in methylated fragments of DNA. Appl. Phys. Lett. 2015, 107, 203701. [Google Scholar] [CrossRef]
- Qi, J.; Govind, N.; Anantram, M.P. The role of cytosine methylation on charge transport through a DNA strand. J. Phys. Lett. 2015, 143, 094306. [Google Scholar] [CrossRef] [PubMed]
- Maciá, E. Charge transfer in DNA: Effective Hamiltonian approaches. Z. Kristallogr. 2009, 224, 91–95. [Google Scholar] [CrossRef]
- Mantela, M.; Lambropoulos, K.; Theodorakou, M.; Simserides, C. Quasi-Periodic and Fractal Polymers: Energy Structure and Carrier Transfer. Materials 2019, 12, 2177. [Google Scholar] [CrossRef]
- Lambropoulos, K.; Simserides, C. Periodic, quasiperiodic, fractal, Kolakoski, and random binary polymers: Energy structure and carrier transport. Phys. Rev. E 2019, 99, 032415. [Google Scholar] [CrossRef]
- Lambropoulos, K.; Simserides, C. Tight-Binding Modeling of Nucleic Acid Sequences: Interplay between Various Types of Order or Disorder and Charge Transport. Symmetry 2019, 11, 968. [Google Scholar] [CrossRef]
- Lee, O.; Jeon, J.H.; Sung, W. How double-stranded DNA breathing enhances its flexibility and instability on short length scales. Phys. Rev. E 2010, 81, 021906. [Google Scholar] [CrossRef]
- Michoel, T.; Van de Peer, Y. Helicoidal transfer matrix model for inhomogeneous DNA melting. Phys. Rev. E 2006, 73, 011908. [Google Scholar] [CrossRef]
- Okonogi, T.M.; Alley, S.C.; Harwood, E.A.; Hopkins, P.B.; BHRobinson, B.H. Phosphate backbone neutralization increases duplex DNA flexibility. Proc. Natl. Acad. Sci. USA 2002, 99, 4156–4160. [Google Scholar] [CrossRef]
- Duduială, C.I.; Wattis, J.A.D.; Dryden, I.L.; Laughton, C.A. Nonlinear breathing modes at a defect site in DNA. Phys. Rev. E 2009, 80, 061906. [Google Scholar] [CrossRef] [PubMed]
- Zdravković, S.; Satarixcx, M.V. Single-molecule unzippering experiments on DNA and Peyrard-Bishop-Dauxois model. Phys. Rev. E 2006, 73, 021905. [Google Scholar] [CrossRef] [PubMed]
- Ghorbani, M.; Rafiee, F.M. Geometrical correlations in the nucleosomal DNA conformation and the role of the covalent bonds rigidity. Nucleic Acids Res. 2011, 39, 1220–1230. [Google Scholar] [CrossRef] [PubMed]
- Barbi, M.; Lepri, S.; Peyrard, M.; Theodorakopoulos, N. Thermal denaturation of a helicoidal DNA model. Phys. Rev. E 2003, 68, 061909. [Google Scholar] [CrossRef] [PubMed]
- Voityuk, A.A. Fluctuation of the electronic coupling in DNA: Multistate versus two-state model. Chem. Phys. Lett. 2007, 439, 162–165. [Google Scholar] [CrossRef]
- Mehrez, H.; Anantram, M.P. Interbase electronic coupling for transport through DNA. Phys. Rev. B 2005, 71, 115405. [Google Scholar] [CrossRef]
- Peluso, A.; Caruso, T.; Landi, A.; Capobianco, A. The dynamics of hole transfer in DNA. Molecules 2019, 24, 4044. [Google Scholar] [CrossRef]
- Leal, M.R.; Weber, G. Sharp DNA denaturation in a helicoidal mesoscopic model. Chem. Phys. Lett. 2020, 755, 137781. [Google Scholar] [CrossRef]
- Blancafort, L.; Voityuk, A.A. CASSCF/CAS-PT2 Study of Hole Transfer in Stacked DNA Nucleobases. J. Phys. Chem. A 2006, 110, 6426–6432. [Google Scholar] [CrossRef]
- Iguchi, K. π-Electrons in a single strand of DNA: A phenomenological approach. Int. J. Mod. Phys. B 2004, 18, 1845–1910. [Google Scholar] [CrossRef]
- Landi, A.; Borrelli, R.; Capobianco, A.; Peluso, A. Transient and enduring electronic resonances drive coherent long distance charge transport in molecular wires. J. Phys. Chem. Lett. 2019, 10, 1845–1851. [Google Scholar] [CrossRef] [PubMed]
- Behnia, S.; Fathizadeh, S.; Javanshour, E.; Nemati, F. Light-driven modulation of electrical current through DNA sequences: Engineering of a molecular optical switch. J. Phys. Chem.B 2020, 124, 3261–3270. [Google Scholar] [CrossRef] [PubMed]
- González-Jiménez, M.; Ramakrishnan, G.; Harwood, T.; Lapthorn, A.J.; Kelly, S.M.; Ellis, E.M.; Wynne, K. LESS Observation of coherent delocalized phonon-like modes in DNA under physiological conditions. Nat. Commun. 2016, 7, 11799. [Google Scholar] [CrossRef] [PubMed]
- Hithell, G.; González-Jiménez, M.; Greetham, G.M.; Donaldson, P.M.; Towrie, M.; Parker, A.W.; Burley, G.A.; Wynne, K.; Hunt, N.T. Ultrafast 2D-IR and optical Kerr effect spectroscopy reveal the impact of duplex melting on the structural dynamics of DNA. Phys. Chem. Chem. Phys. 2017, 19, 10333–10342. [Google Scholar] [CrossRef] [PubMed]
- Paez, C.J.; Schulz, P.A. Delocalization of vibrational normal modes in double chains: Application to DNA systems. Microelectron. J. 2008, 39, 1222–1223. [Google Scholar] [CrossRef]
- Young, M.A.; Ravishanker, G.; Beveridge, D.L. A 5-nanosecond molecular dynamics trajectory for B-DNA: Analysis of structure, motions, and solvation. Biophys. J. 1997, 73, 2313–2336. [Google Scholar] [CrossRef]
- Paciaroni, A.; Comez, L.; Longo, M.; Sebastiani, F.; Bianchi, F.; Orecchini, A.; Zanatta, M.; Verbeni, R.; Bosak, A.; Sacchetti, F.; et al. Terahertz collective dynamics of DNA as affected by hydration and counterions. J. Mol. Liq. 2020, 318, 113956. [Google Scholar] [CrossRef]
- Andresen, K.; Das, R.; Park, H.Y.; Smith, H.; Kwok, L.W.; Lamb, J.S.; Kirkl, E.J.; Herschlag, D.; Finkelstein, K.D.; Pollack, L. Spatial Distribution of Competing Ions around DNA in Solution. Phys. Rev. Lett. 2004, 93, 248103. [Google Scholar] [CrossRef]
- Iguchi, K. The Huckel theoretical calculation for the electronic structure of DNA. In DNA Engineering: Properties and Applications; Mizoguch, K., Sakamoto, H., Eds.; Pan Stanford: New York, NY, USA, 2016. [Google Scholar]
- Lakhno, V.D.; Sultanov, V.B. Band structure of the spectra of Hamiltonians of regular polynucleotide duplexes. Theor. Math. Phys. 2013, 176, 1194–1206. [Google Scholar] [CrossRef]
- Yamada, H.; Iguchi, K. Some effective tight-binding models for electrons in DNA conduction: A review. Adv. Cond. Mat. Phys. 2010, 380710. [Google Scholar] [CrossRef][Green Version]
- Hennig, D.; Starikov, E.B.; Archilla, J.F.R.; Palmero, F. Charge Transport in Poly(dG)–Poly(dC) and Poly(dA)–Poly(dT) DNA Polymers. J. Biol. Phys. 2004, 30, 227–238. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Govorov, A.O.; Ulloa, S.E. Polarons with a twist. Phys. Rev. B 2002, 66, 060303(R). [Google Scholar] [CrossRef]
- Iguchi, K. Semiconductivity and band gap of a double strand of DNA. J. Phys. Soc. Jpn. 2001, 70, 593–597. [Google Scholar] [CrossRef]
- Available online: http://telomerase.asu.edu/sequences_telomere.html (accessed on 20 August 2020).
- A Tandem Repeat Is a Sequence of Two or More DNA Base Pairs That Is Repeated in Such a Way that the Repeats Lie Adjacent to Each Other on the Chromosome. Tandem Repeats are Generally Associated with Non-coding DNA. In Some Instances, the Number of Times the DNA Sequence Is Repeated Is Variable. Such Variable Tandem Repeats Are Used in DNA Fingerprinting Procedures. Available online: https://www.genome.gov/genetics-glossary/Tandem-Repeat (accessed on 20 August 2020).
- Lopes Cardoso, I.; Marques, V. Trinucleotide repeat diseases—Antecipation diseases. J. Clin. Gen. Genom. 2018, 1, 4–9. [Google Scholar]
- Beeker, D.; Adhikary, A.; Sevilla, M.D. Charge Migration in DNA. Perspectives from Physics, Chemistry and Biology; Chakraborty, T., Ed.; Springer: Berlin, Germany, 2007; p. 139. [Google Scholar]
- Braun, E.; Eichen, Y.; Sivan, U.; Ben-Yoseph, G. DNA-templated assembly and electrode attachment of a conducting silver wire. Nature 1998, 391, 775–779. [Google Scholar] [CrossRef]
- Treadway, C.; Hill, M.G.; Barton, J.K. Charge Transport Through a Molecular Pi-stack: Double Helical DNA. Chem. Phys. 2002, 281, 409–428. [Google Scholar] [CrossRef]
- Zwang, T.J.; Tse, E.C.M.; Barton, J.K. Sensing DNA through DNA Charge Transport. ACS Chem. Biol. 2018, 13, 1799–1809. [Google Scholar] [CrossRef]
- Di Felice, R.; Calzolari, A.; Zhang, H. Towards metalated DNA-based structures. Nanotechnology 2004, 15, 1256–1263. [Google Scholar] [CrossRef]
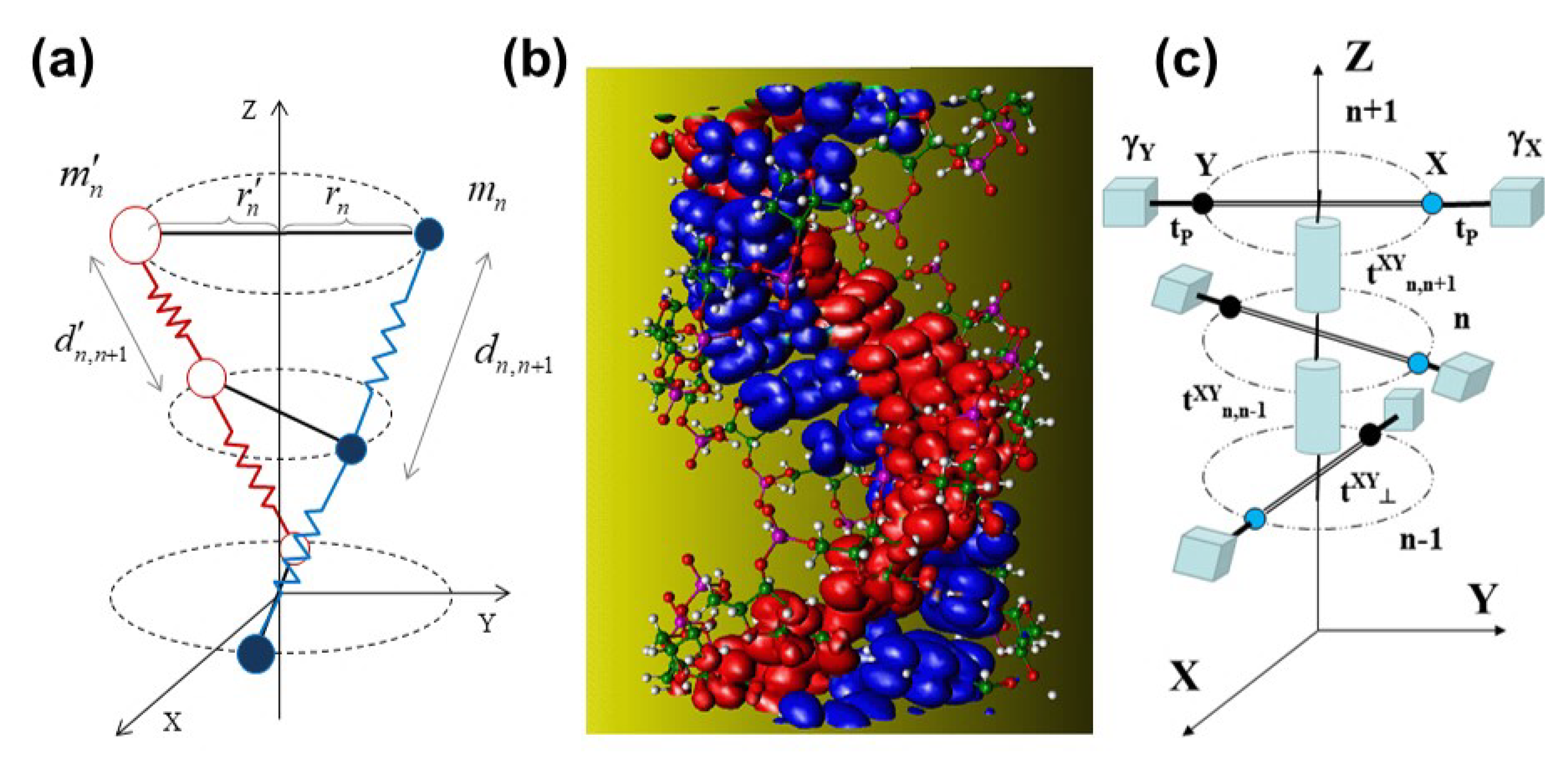
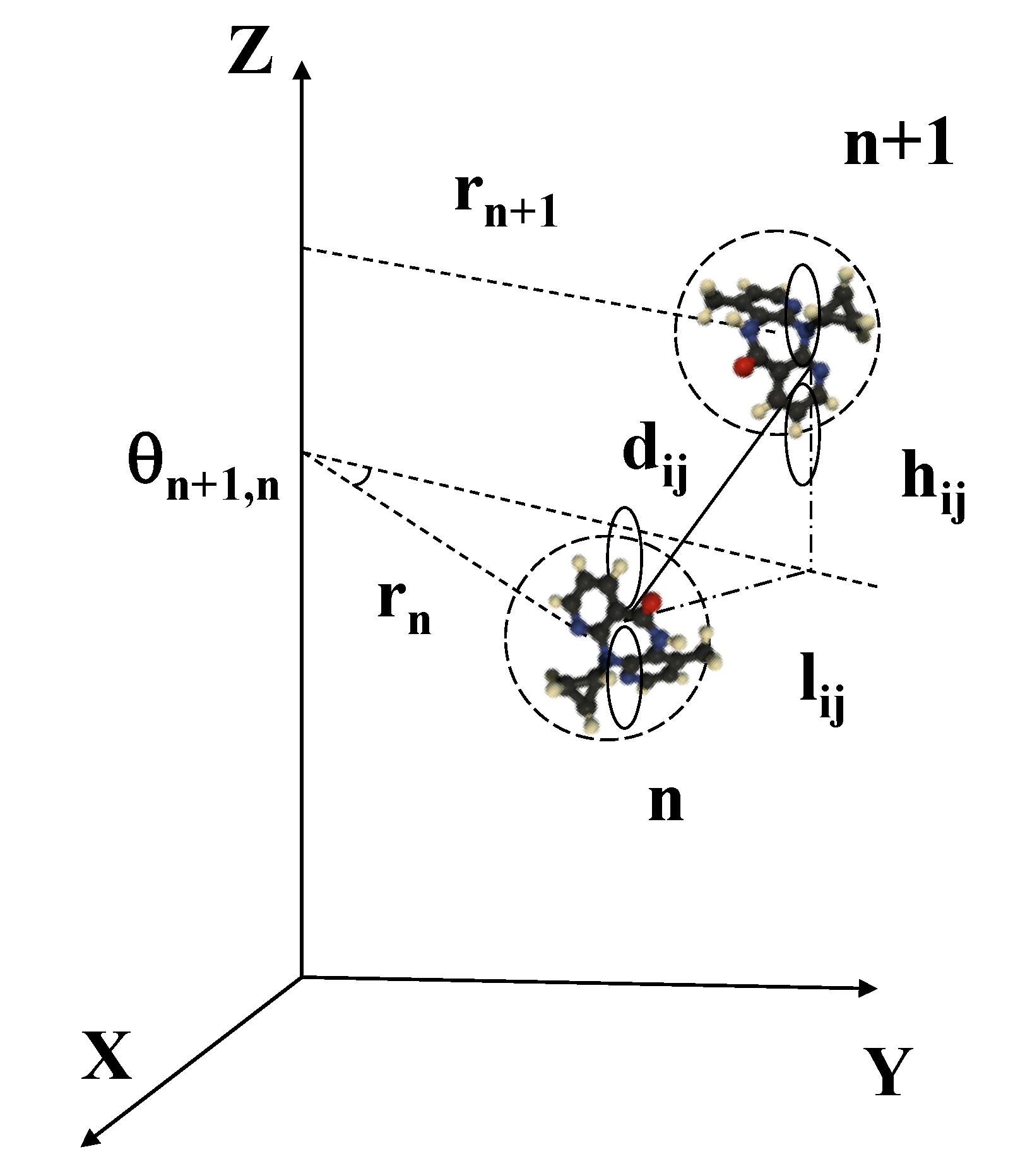
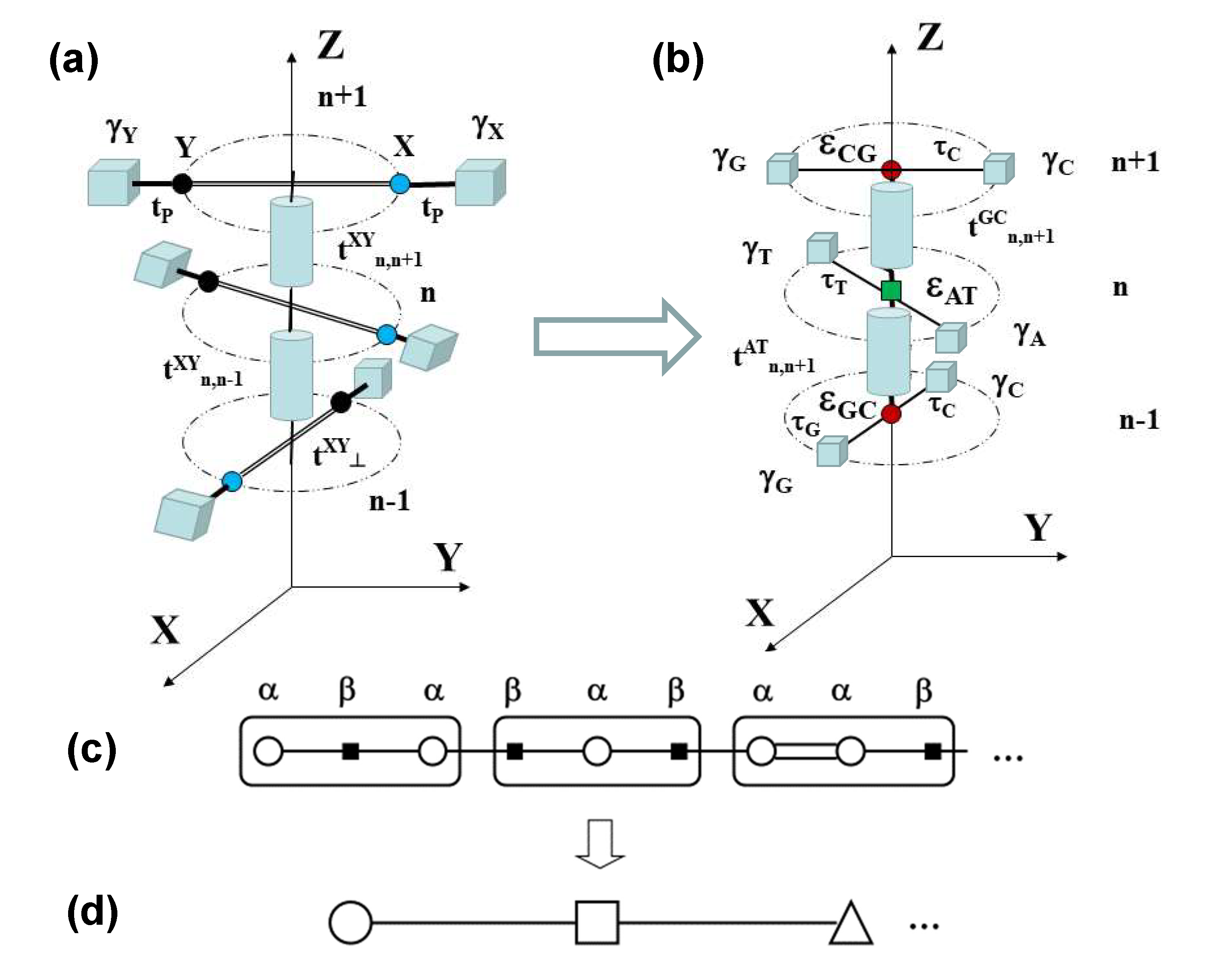

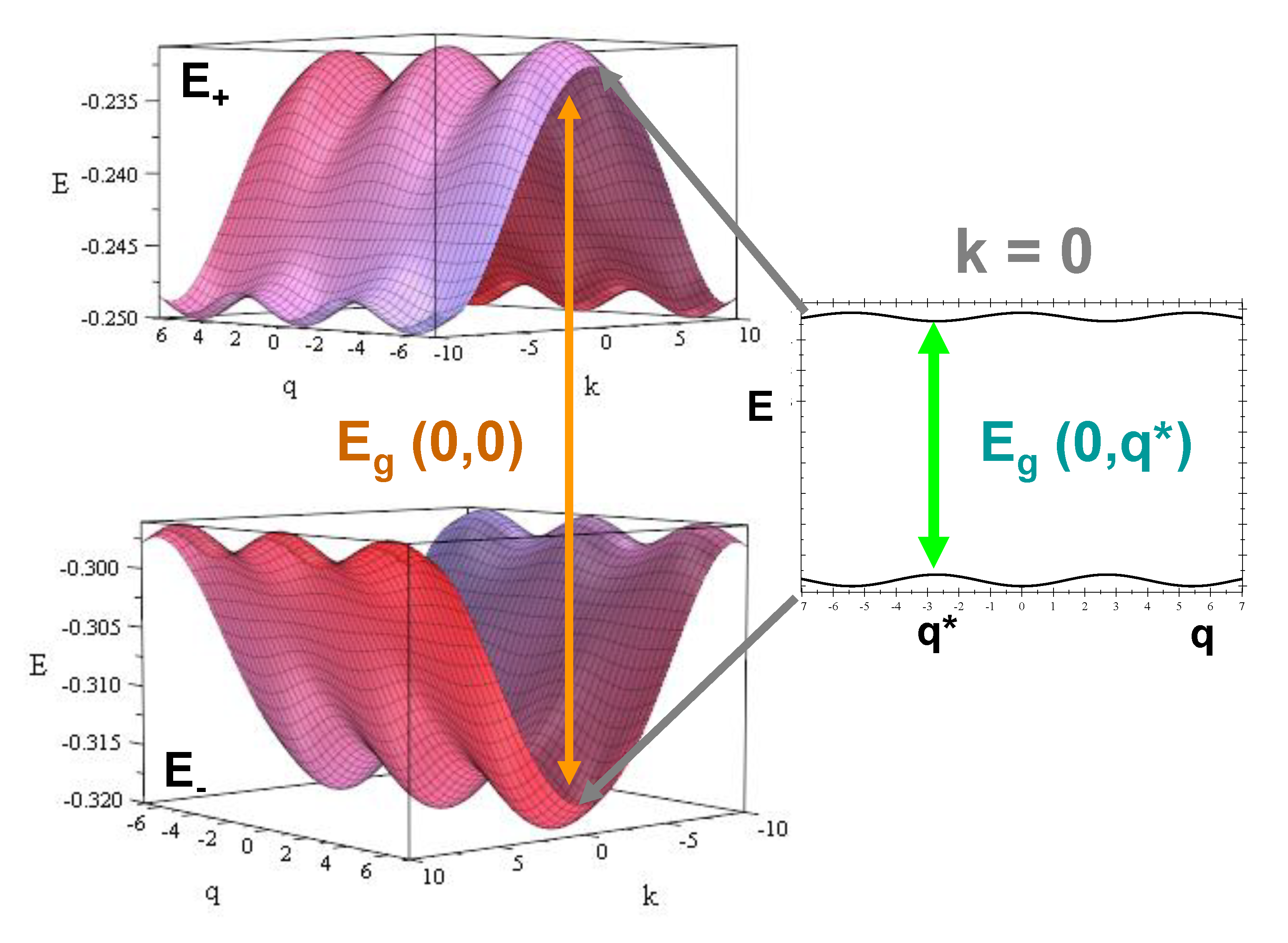
| Geometrical | Dynamical | Lattice | Electronic (eV) | Electronic (eV) |
|---|---|---|---|---|
| rad | amu | Å [25,56] | [38,57,58] | [39,59] |
| nm | Å [24,56,60] | [38] | [59] | |
| nm | eV [30,56,60] | [38,59,61] | [59] | |
| nm | eV Å [30] | [38,58,59] | [39,59] | |
| nm | eV Å [56] | [62] | [14,62] |
| Oscillation | ( rad s) | (THz) | (ps) | |
|---|---|---|---|---|
| Twist | ||||
| Stacking | ||||
| H-Bonding | ||||
| Twist-Stacking | ||||
| Twist-Radial | ||||
| Stretch-Stacking |
| Homopolymer | ||||
|---|---|---|---|---|
| PolyG-PolyC | ||||
| PolyA-PolyT |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maciá, E. Base-Pairs’ Correlated Oscillation Effects on the Charge Transfer in Double-Helix B-DNA Molecules. Materials 2020, 13, 5119. https://doi.org/10.3390/ma13225119
Maciá E. Base-Pairs’ Correlated Oscillation Effects on the Charge Transfer in Double-Helix B-DNA Molecules. Materials. 2020; 13(22):5119. https://doi.org/10.3390/ma13225119
Chicago/Turabian StyleMaciá, Enrique. 2020. "Base-Pairs’ Correlated Oscillation Effects on the Charge Transfer in Double-Helix B-DNA Molecules" Materials 13, no. 22: 5119. https://doi.org/10.3390/ma13225119
APA StyleMaciá, E. (2020). Base-Pairs’ Correlated Oscillation Effects on the Charge Transfer in Double-Helix B-DNA Molecules. Materials, 13(22), 5119. https://doi.org/10.3390/ma13225119





