Magnetorheological Elastomer Stress Relaxation Behaviour during Compression: Experiment and Modelling
Abstract
1. Introduction
2. Materials and Methods
2.1. Sample Preparation
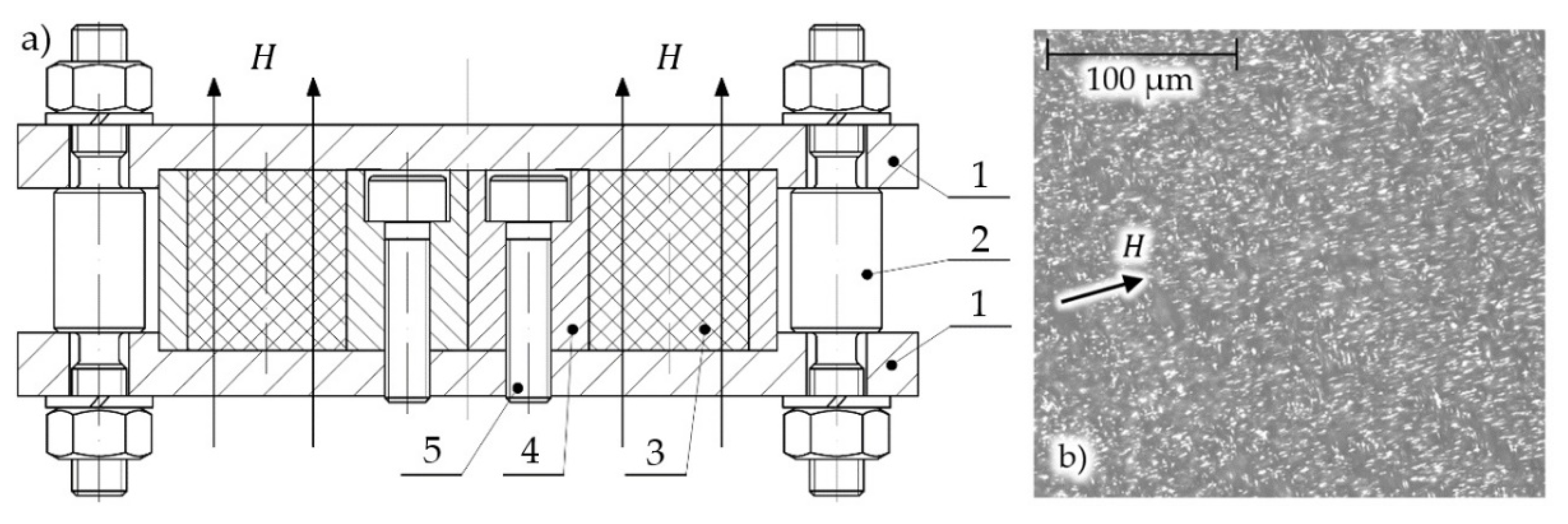
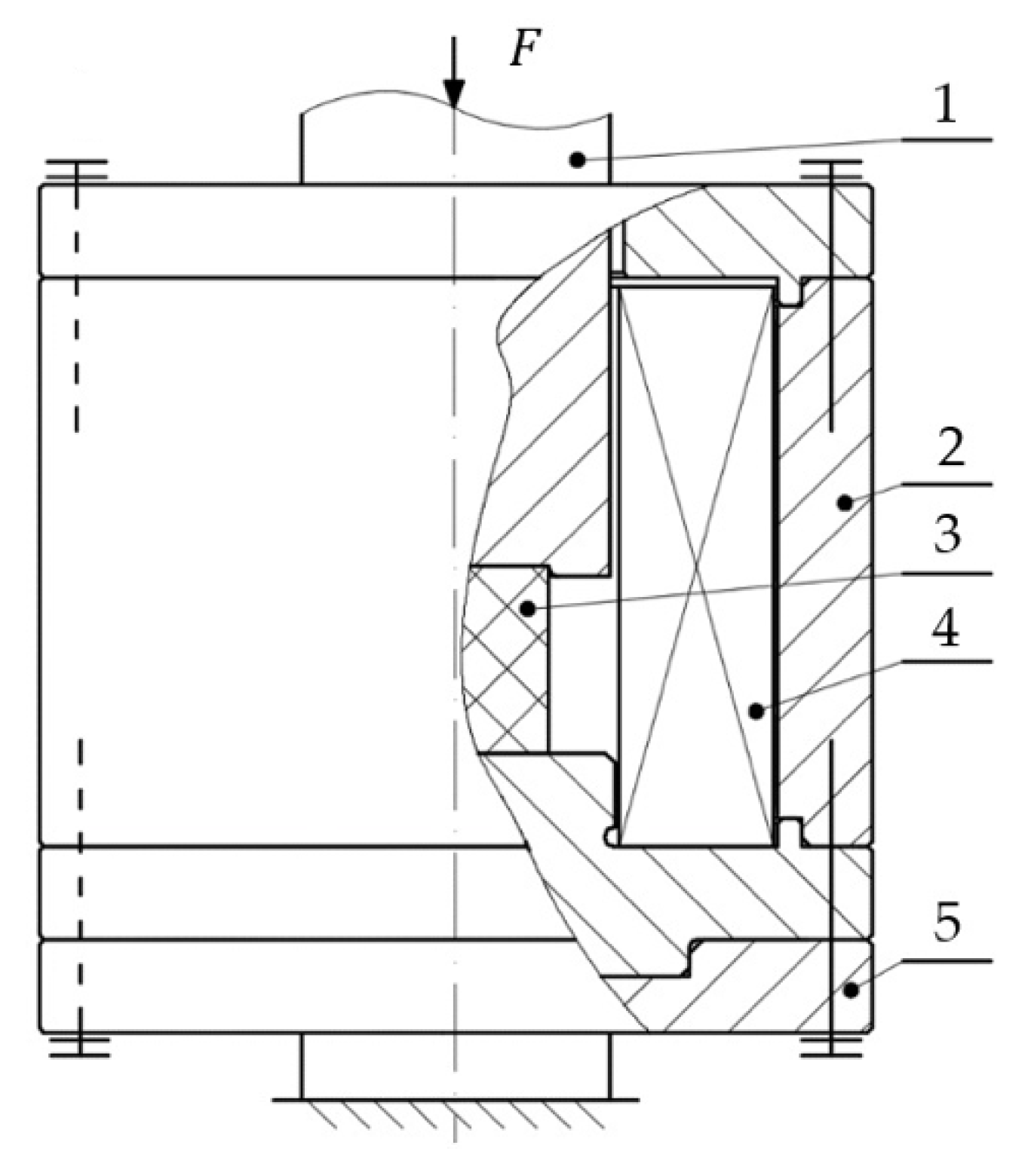
2.2. Experiment Detalis
3. Results and Discussion
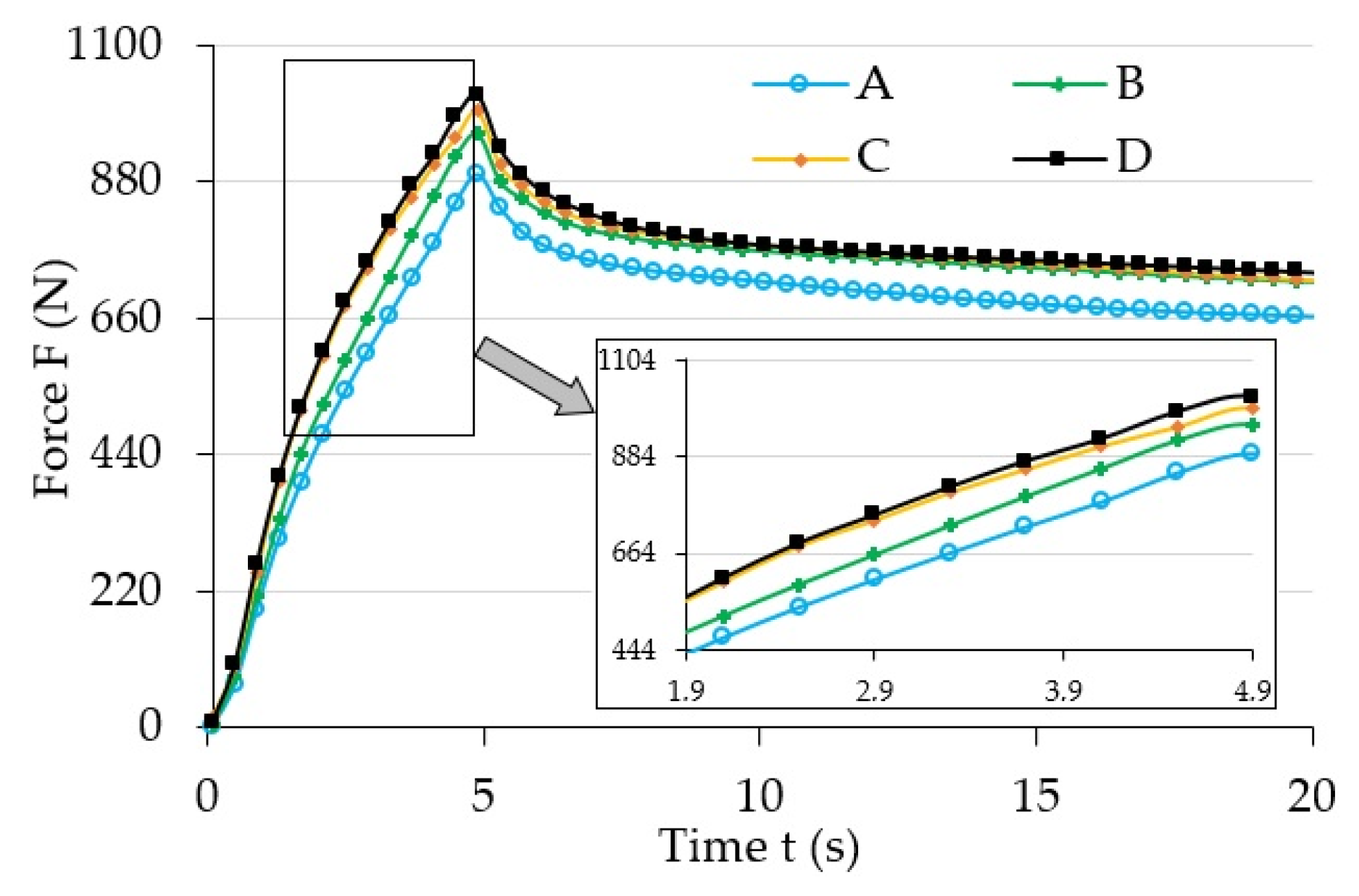
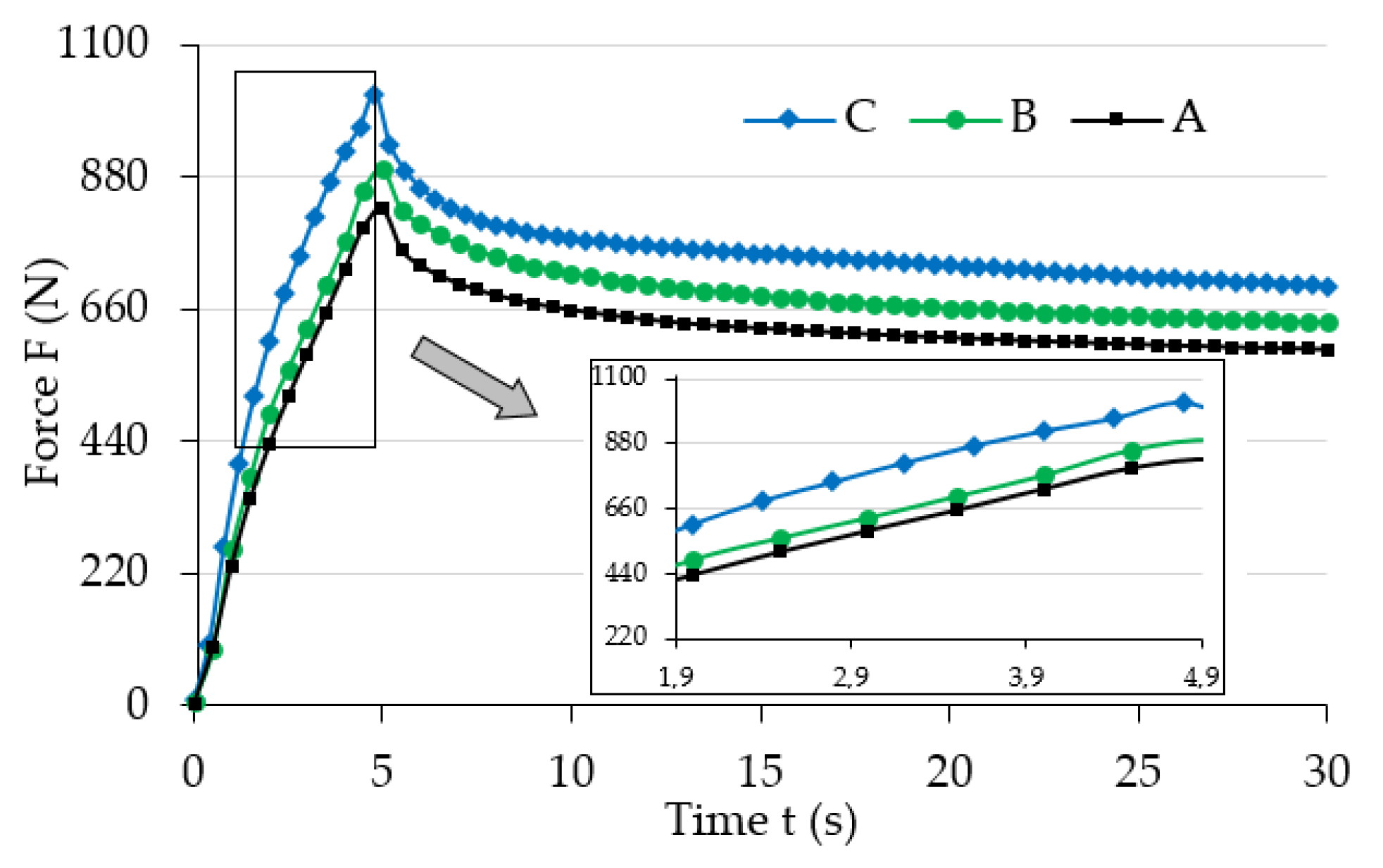
3.1. Experimental Research
3.2. Mathematical Model
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lewandowski, D. Modeling of Magnetorheological Elastomers Using the Elastic–Plastic Model with Kinematic Hardening. Materials 2019, 12, 892. [Google Scholar] [CrossRef]
- Samal, S.; Kolinova, M.; Blanco, I. The Magneto-Mechanical Behavior of Active Components in Iron-Elastomer Composite. J. Compos. Sci. 2018, 2, 54. [Google Scholar] [CrossRef]
- Samal, S.; Škodová, M.; Abate, L.; Blanco, I. Magneto-Rheological Elastomer Composites. A Review. Appl. Sci. 2020, 10, 4899. [Google Scholar] [CrossRef]
- Li, T.; El-Aty, A.A.; Cheng, C.; Shen, Y.; Wu, C.; Yang, Q.; Hu, S.; Xu, Y.; Tao, J.; Guo, X. Investigate the Effect of the Magnetic Field on the Mechanical Properties of Silicone Rubber-Based Anisotropic Magnetorheological Elastomer during Curing Process. J. Renew. Mater. 2020, 8, 1411–1427. [Google Scholar] [CrossRef]
- Miedzińska, D.; Boczkowska, A.; Zubko, K. Numerical verification of three points bending experiment of magnetorheological elastomer (MRE) in magnetic field. J. Phys. Conf. Ser. 2010, 240, 012158. [Google Scholar] [CrossRef]
- Bica, I.; Bunoiu, O.M. Magnetorheological Hybrid Elastomers Based on Silicone Rubber and Magnetorheological Suspensions with Graphene Nanoparticles: Effects of the Magnetic Field on the Relative Dielectric Permittivity and Electric Conductivity. Int. J. Mol. Sci. 2019, 20, 4201. [Google Scholar] [CrossRef]
- Samal, S.; Kolinova, M.; Blanco, I.; Poggetto, G.D.; Catauro, M. Magnetorheological Elastomer Composites: The Influence of Iron Particle Distribution on the Surface Morphology. Macromol. Symp. 2020, 389, 1900053. [Google Scholar] [CrossRef]
- Samal, S.; Škodová, M.; Blanco, I. Effects of Filler Distribution on Magnetorheological Silicon-Based Composites. Materials 2019, 12, 3017. [Google Scholar] [CrossRef]
- Choi, W.J. Dynamic Analysis of Magnetorheological Elastomer Configured Sandwich Structures. Ph.D. Thesis, University of Southampton, Southampton, UK, 2009. [Google Scholar]
- Liao, G.; Gong, X.; Xuan, S.; Guo, C.; Zong, L. Magnetic-field-induced normal force of magnetorheological elastomer under compression status. Ind. Eng. Chem. Res. 2012, 51, 3322–3328. [Google Scholar] [CrossRef]
- Hoang, N.; Zhang, N.; Du, H. An adaptive tunable vibration absorber using a new magnetorheological elastomer for vehicular powertrain transient vibration reduction. Smart Mater. Struct. 2010, 20, 1–11. [Google Scholar] [CrossRef]
- Hoang, N.; Zhang, N.; Li, W.H.; Du, H. Development of a torsional dynamic absorber using a magnetorheological elastomer for vibration reduction of a powertrain test rig. J. Intell. Mater. Syst. Struct. 2013, 24, 2036–2044. [Google Scholar] [CrossRef]
- Mitsumata, T.; Ohori, S. Magnetic Polyurethane Elastomers with Wide Range Modulation of Elasticity. Polym. Chem. 2011, 2, 1063–1067. [Google Scholar] [CrossRef]
- Sun, S.S.; Chen, Y.; Yang, J.; Tian, T.F.; Deng, H.X.; Li, W.H.; Du, H.; Alici, G. The development of an adaptive tuned magnetorheological elastomer absorber working in squeeze mode. Smart Mater. Struct. 2014, 23, 1–8. [Google Scholar] [CrossRef]
- Bica, I. Electroconductive magnetorheological suspensions: Production and physical processes. J. Ind. Eng. Chem. 2009, 15, 233–237. [Google Scholar] [CrossRef]
- Pavlenko, A.V.; Turik, A.V.; Reznichenko, L.A.; Shilkina, L.A.; Konstantinov, G.M. The magnetodielectric effect in Bi1/2 La1/2 MnO3 cramics. Tech. Phys. Lett. 2013, 39, 78–80. [Google Scholar] [CrossRef]
- Mouritz, A.P.; Gardiner, C.P. Compression properties of fire-damaged polymer sandwich composites. Compos. Part A Appl. Sci. Manuf. 2002, 33, 609–620. [Google Scholar] [CrossRef]
- Zhang, W.; Gong, X.L.; Jiang, W.Q.; Fan, Y.C. Investigation of the durability of anisotropic magnetorheological elastomers based on mixed rubber. Smart Mater. Struct. 2010, 19, 085008. [Google Scholar] [CrossRef]
- Blanco, I. Lifetime Prediction of Polymers: To Bet, or Not to Bet-Is This the Question? Materials 2018, 11, 1383. [Google Scholar] [CrossRef]
- Zhang, W.; Gong, X.; Xuan, S.; Jiang, W. Temperature-dependent mechanical properties and model of magnetorheological elastomers. Ind. Eng. Chem. Res. 2011, 50, 6704–6712. [Google Scholar] [CrossRef]
- Yu, M.; Zhao, L.; Fu, J.; Zhu, M. Thermal effects on the laminated magnetorheological elastomer isolator. Smart Mater. Struct. 2016, 25, 115039. [Google Scholar] [CrossRef]
- Wan, Y.; Xiong, Y.; Zhang, S. Temperature dependent dynamic mechanical properties of Magnetorheological elastomers: Experiment and modeling. Compos. Struct. 2018, 202, 768–773. [Google Scholar] [CrossRef]
- Wargula, Ł.; Waluś, K.J.; Krawiec, P. The problems of measuring the temperature of the small engines (SI) on the example of a drive for non-road mobile machines. In MATEC Web of Conferences, Proceedings of the XXIII Polish-Slovak Scientific Conference on Machine Modelling and Simulations, Rydzyna, Poland, 4–7 September 2019; EDP Sciences: Lez Ili, France, 2019; Volume 254. [Google Scholar]
- Krawiec, P.; Różański, L.; Czarnecka-Komorowska, D.; Warguła, Ł. Evaluation of the Thermal Stability and Surface Characteristics of Thermoplastic Polyurethane V-Belt. Materials 2020, 13, 1502. [Google Scholar] [CrossRef]
- Yashiro, T.; Ogawa, T.; Sasahara, H. Temperature measurement of cutting tool and machined surface layer in milling of CFRP. Int. J. Mach. Tools Manuf. 2013, 70, 63–69. [Google Scholar] [CrossRef]
- Kchit, N.; Lancon, P.; Bossis, G. Thermoresistance and giant magnetoresistance of magnetorheological elastomers. J. Phys. D Appl. Phys. 2009, 42, 105506. [Google Scholar] [CrossRef]
- Li, W.; Zhou, Y.; Tian, T.; Alici, G. Creep and recovery behaviors of magnetorheological elastomers. Front. Mech. Eng. China 2010, 5, 341–346. [Google Scholar] [CrossRef]
- Qi, S.; Yu, M.; Fu, J.; Zhu, M. Stress relaxation behavior of magnetorheological elastomer: Experimental and modeling study. J. Intell. Mater. Syst. Struct. 2018, 29, 205–213. [Google Scholar] [CrossRef]
- Yu, G.J.; Lin, X.G.; Guo, F. Modeling and Verification of Relaxation Behavior for Magnetorheological Elastomers with Applied Magnetic Field. Key Eng. Mater. 2017, 730, 527–532. [Google Scholar] [CrossRef]
- Xu, Y.; Liu, T.; Liao, G.J.; Lubineau, G. Magneto-dependentstress relaxation of magnetorheological gels. Smart Mater. Struct. 2017, 26, 115005. [Google Scholar] [CrossRef]
- Meharthaj, H.; Srinivasan, S.M.; Arockiarajan, A. Creep behavior of magnetorheological gels. Mech. Adv. Mater. Struct. 2020, 27, 1031–1039. [Google Scholar] [CrossRef]
- Puente-Córdova, J.G.; Reyes-Melo, M.E.; Palacios-Pineda, L.M.; Martínez-Perales, I.A.; Martínez-Romero, O.; Elías-Zúñiga, A. Fabrication and Characterization of Isotropic and Anisotropic Magnetorheological Elastomers, Based on Silicone Rubber and Carbonyl Iron Microparticles. Polymers 2018, 10, 1343. [Google Scholar] [CrossRef]
- Carlson, J.; Jolly, M. MR fluid, foam and elastomer devices. Mechatronics 2000, 10, 429–594. [Google Scholar] [CrossRef]
- Bocian, M.; Kaleta, J.; Lewandowski, D.; Przybylski, M. Tunable Absorption System based on magnetorheological elastomers and Halbach array: Design and testing. J. Magn. Magn. Mater. 2017, 435, 46–57. [Google Scholar] [CrossRef]
- Xu, X.; Hou, J. A stress relaxation model for the viscoelastic solids based on the steady-state creep equation. Mech. Time Depend. Mater. 2011, 15, 29–39. [Google Scholar] [CrossRef]


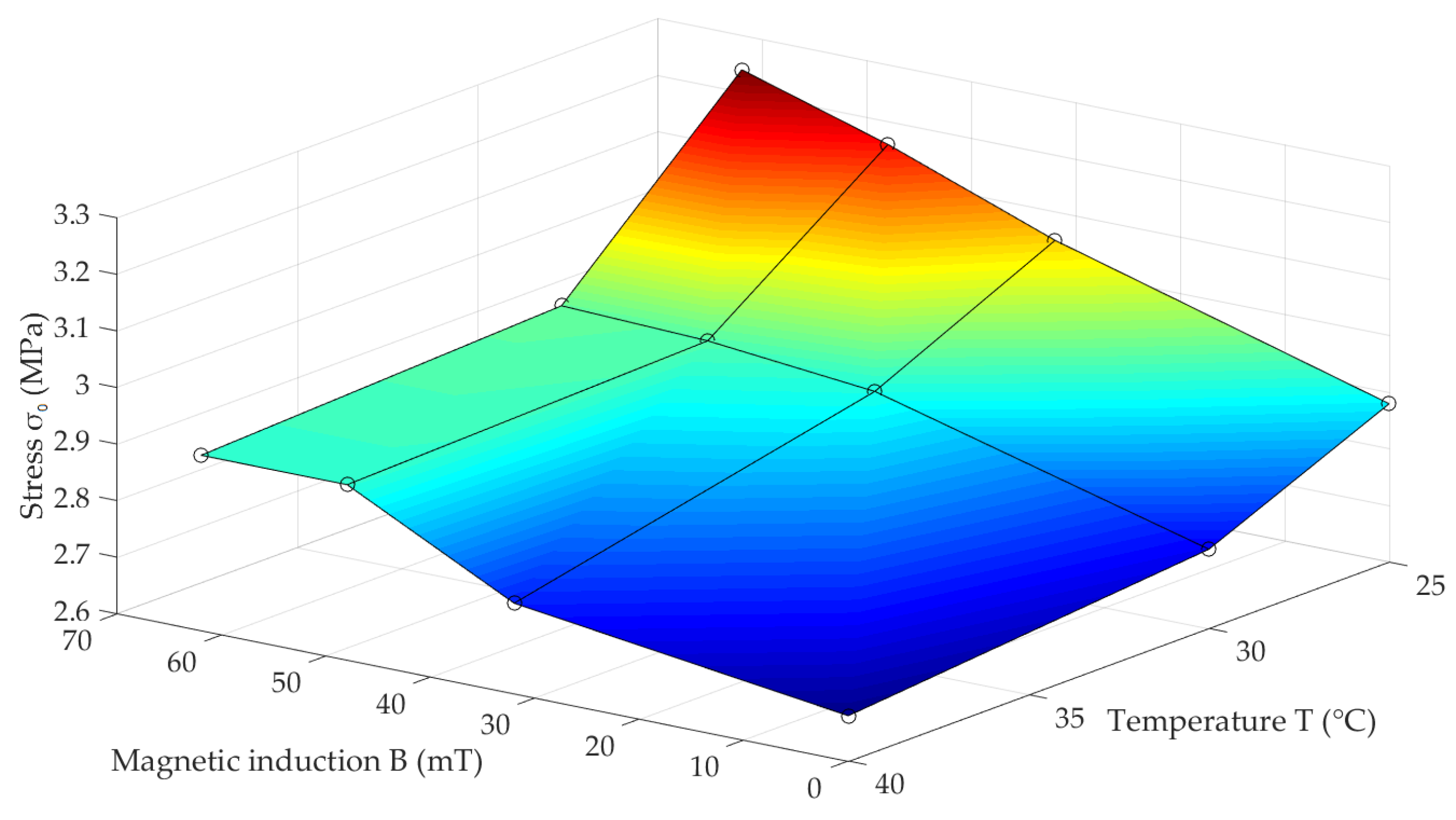
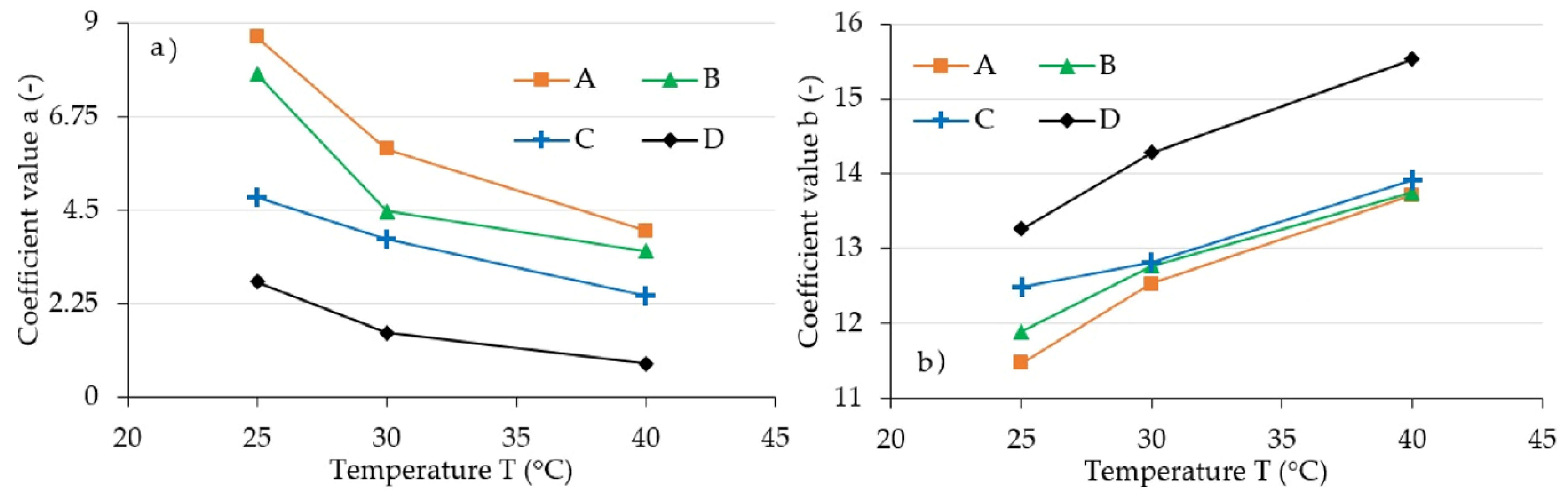
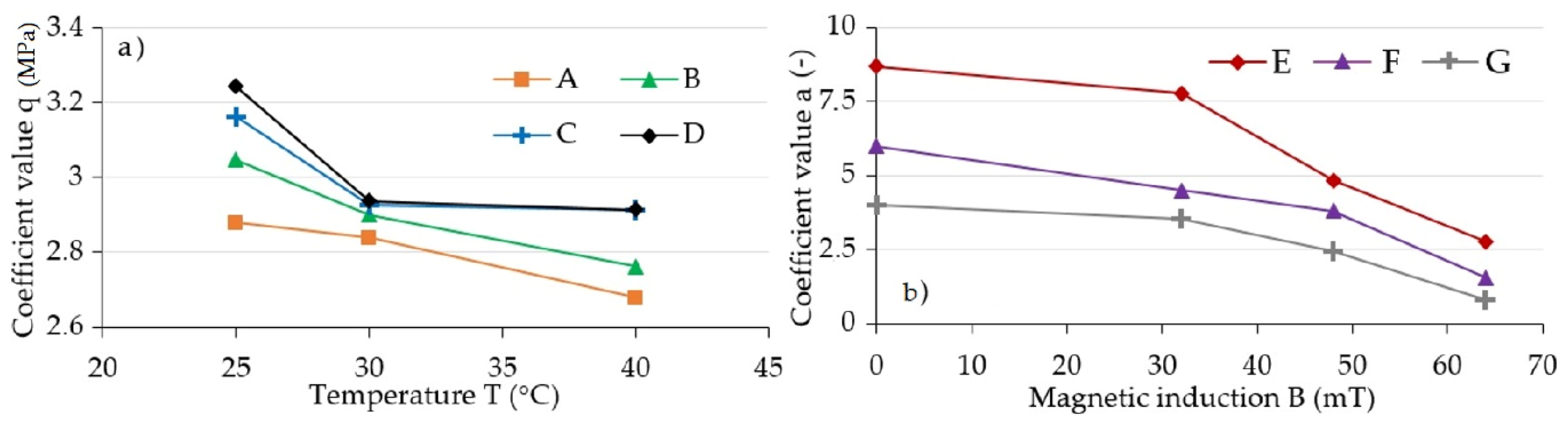
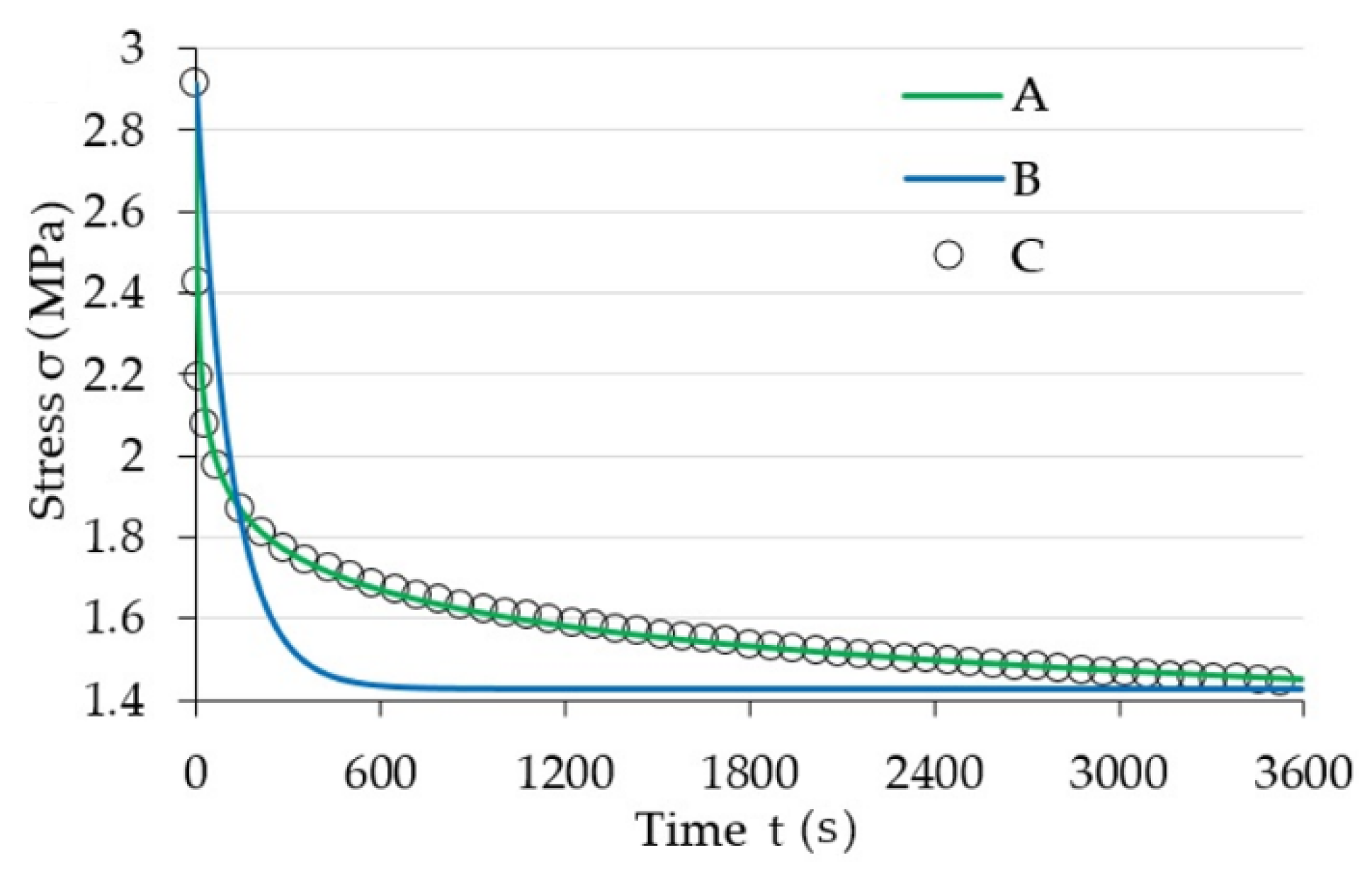
| Magnetic Induction (mT) | ||||||
|---|---|---|---|---|---|---|
| 0 | 32 | 48 | 64 | |||
| Stress Amplitude (MPa) | ||||||
| Temperature (°C) | 25 | 2.88 | 3.05 | 3.16 | 3.24 | 12.7 |
| 30 | 2.74 | 2.90 | 2.93 | 2.94 | 7.2 | |
| 40 | 2.68 | 2.76 | 2.91 | 2.92 | 8.8 | |
| (%) | 7.5 | 10.3 | 8.6 | 11.3 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kukla, M.; Warguła, Ł.; Talaśka, K.; Wojtkowiak, D. Magnetorheological Elastomer Stress Relaxation Behaviour during Compression: Experiment and Modelling. Materials 2020, 13, 4795. https://doi.org/10.3390/ma13214795
Kukla M, Warguła Ł, Talaśka K, Wojtkowiak D. Magnetorheological Elastomer Stress Relaxation Behaviour during Compression: Experiment and Modelling. Materials. 2020; 13(21):4795. https://doi.org/10.3390/ma13214795
Chicago/Turabian StyleKukla, Mateusz, Łukasz Warguła, Krzysztof Talaśka, and Dominik Wojtkowiak. 2020. "Magnetorheological Elastomer Stress Relaxation Behaviour during Compression: Experiment and Modelling" Materials 13, no. 21: 4795. https://doi.org/10.3390/ma13214795
APA StyleKukla, M., Warguła, Ł., Talaśka, K., & Wojtkowiak, D. (2020). Magnetorheological Elastomer Stress Relaxation Behaviour during Compression: Experiment and Modelling. Materials, 13(21), 4795. https://doi.org/10.3390/ma13214795







