Creep Testing of Thermoplastic Fiber-Reinforced Polymer Composite Tubular Coupons
Abstract
1. Introduction
2. Materials and Methods
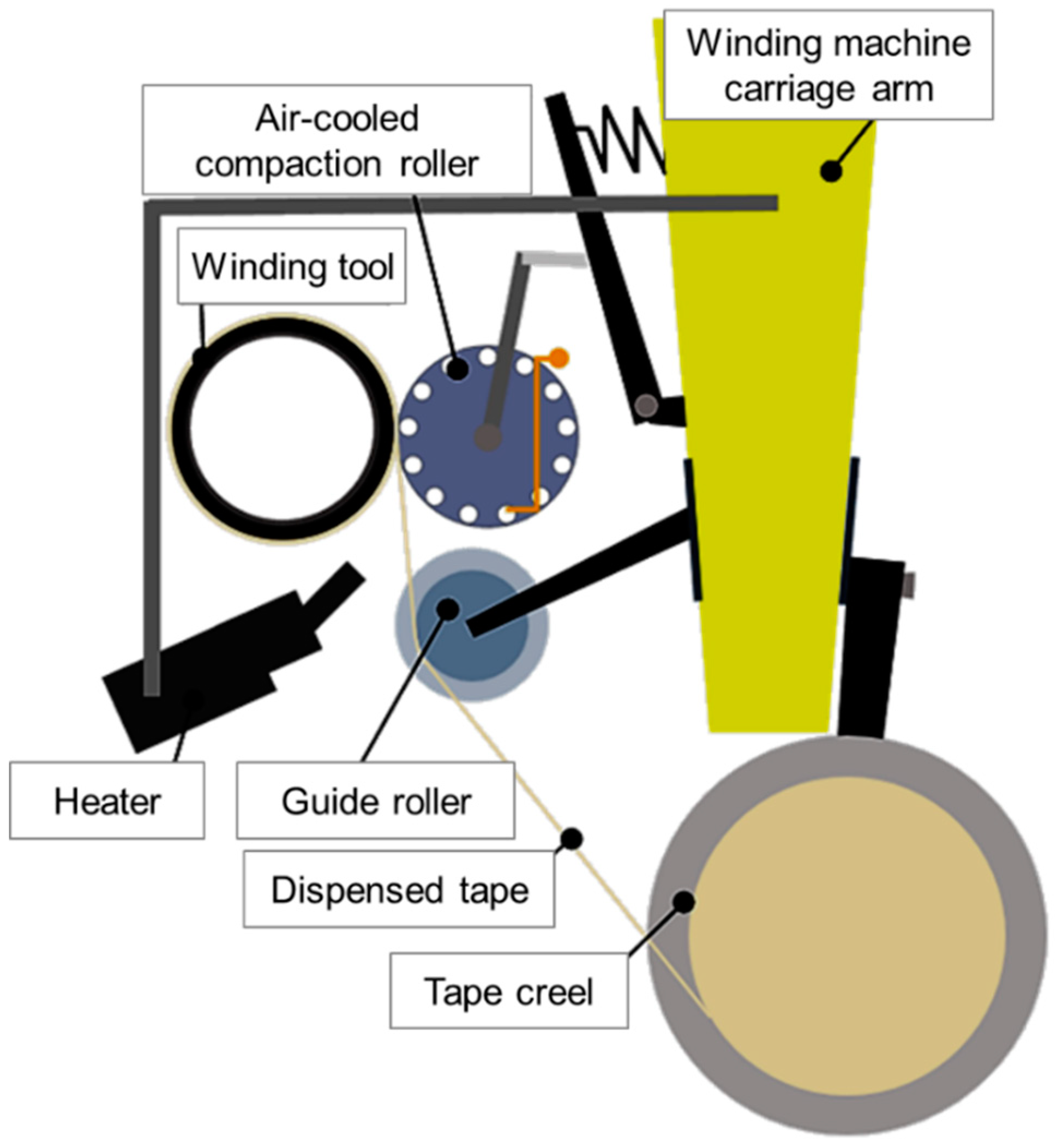
2.1. Fabrication of TP-FRPC Tubular Coupons
2.2. Preparation of Tubular Coupons
2.3. Testing Procedure and Data Acquisition
3. Results and Discussion
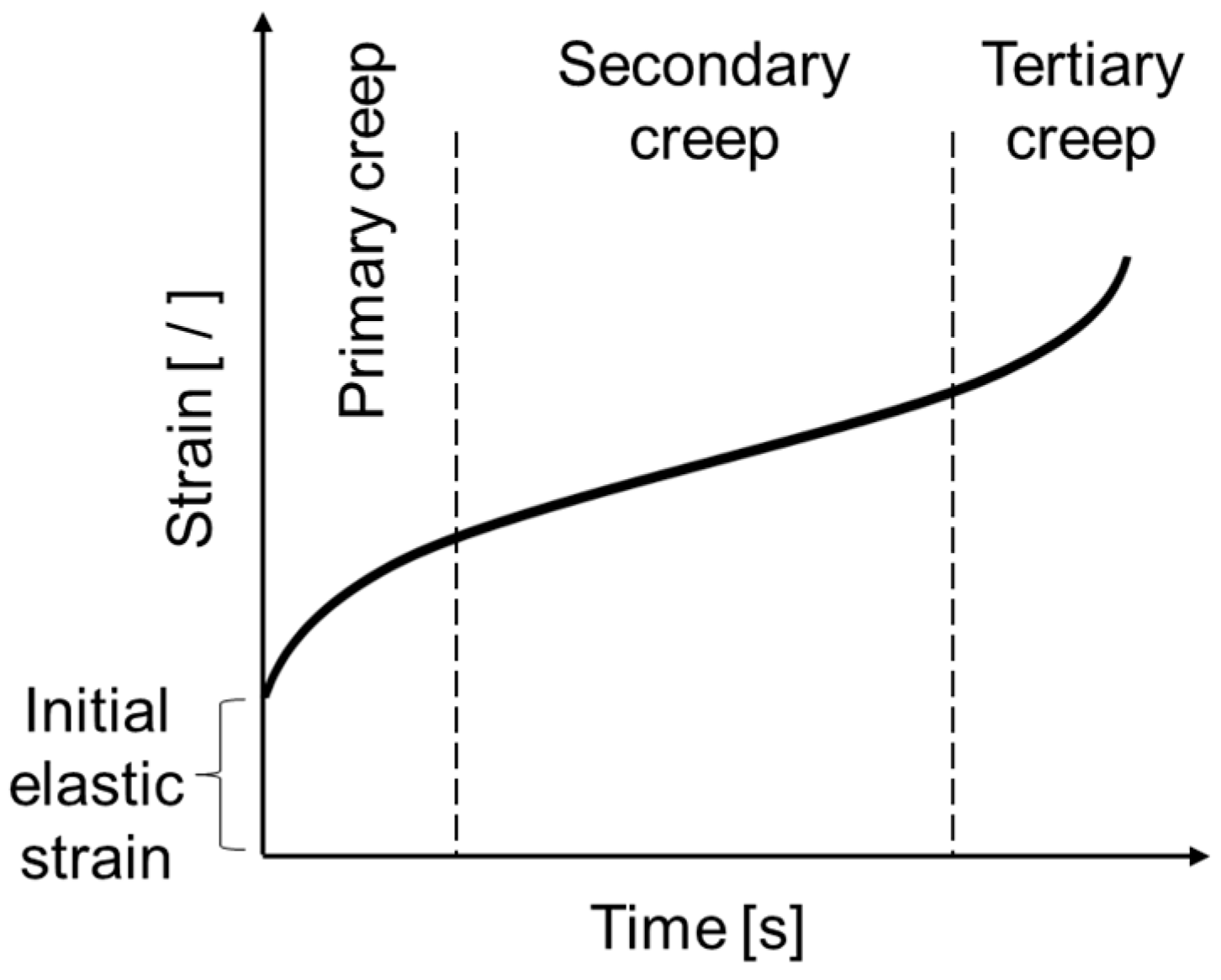
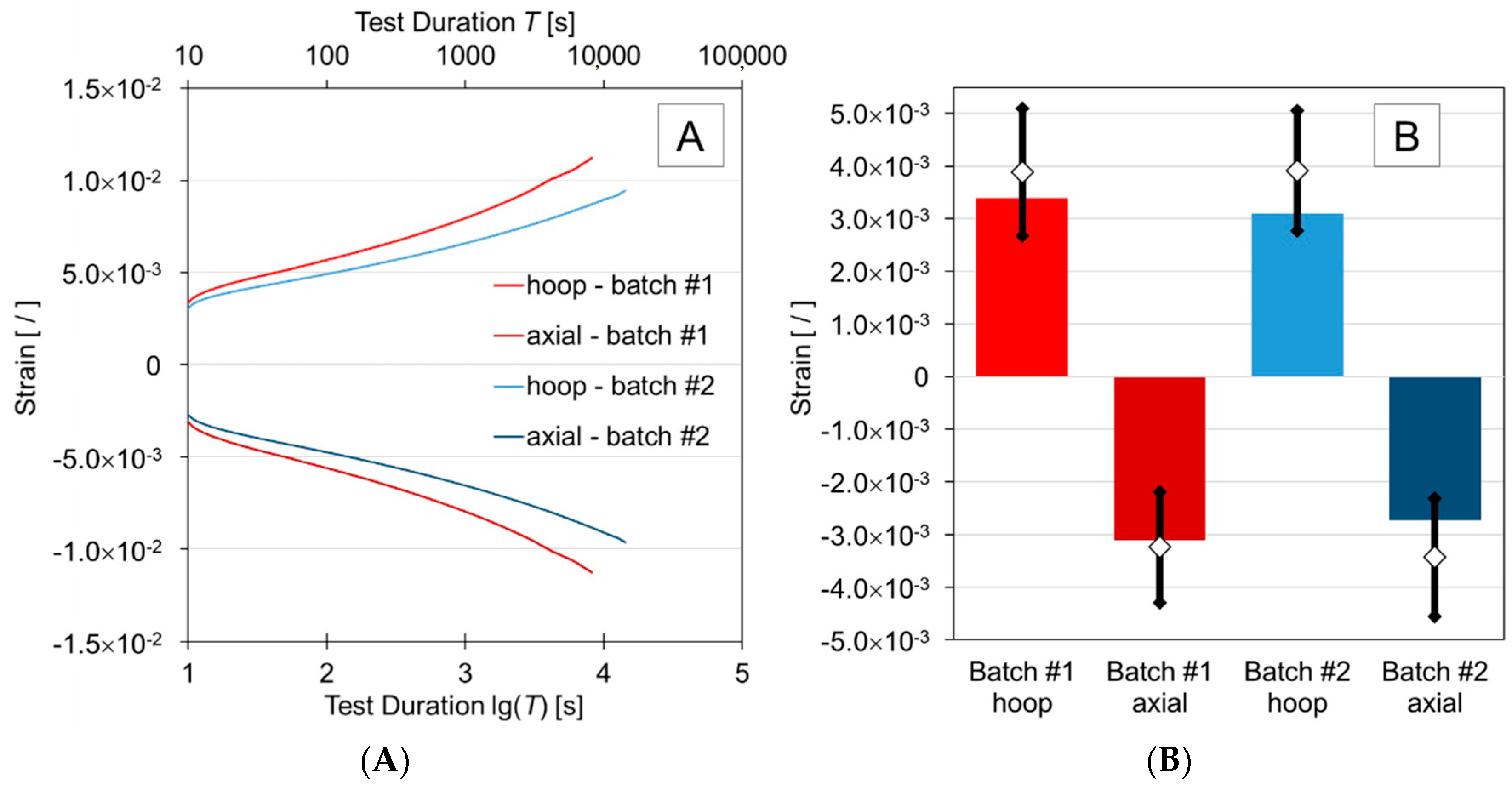
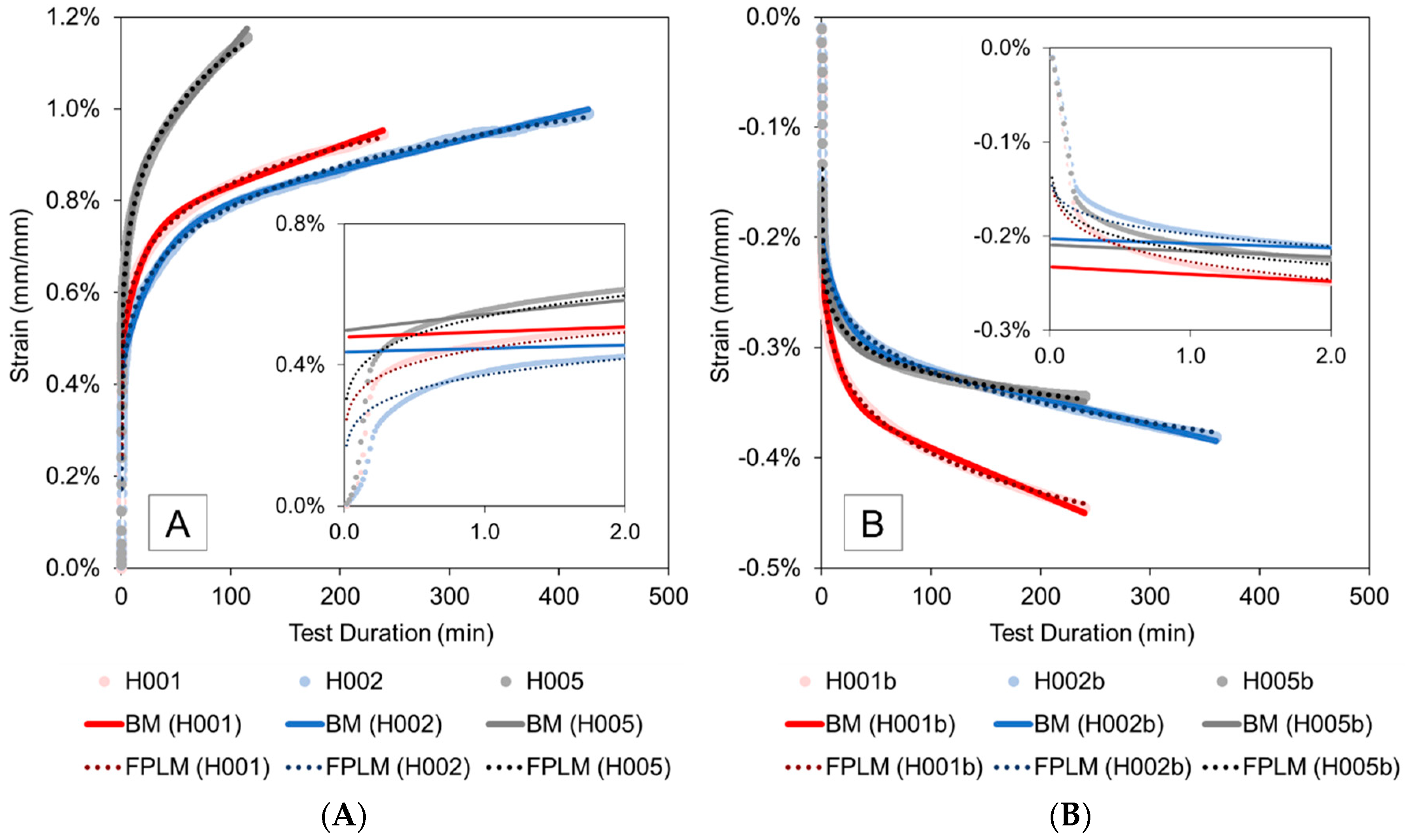
3.1. Creep Strain Results
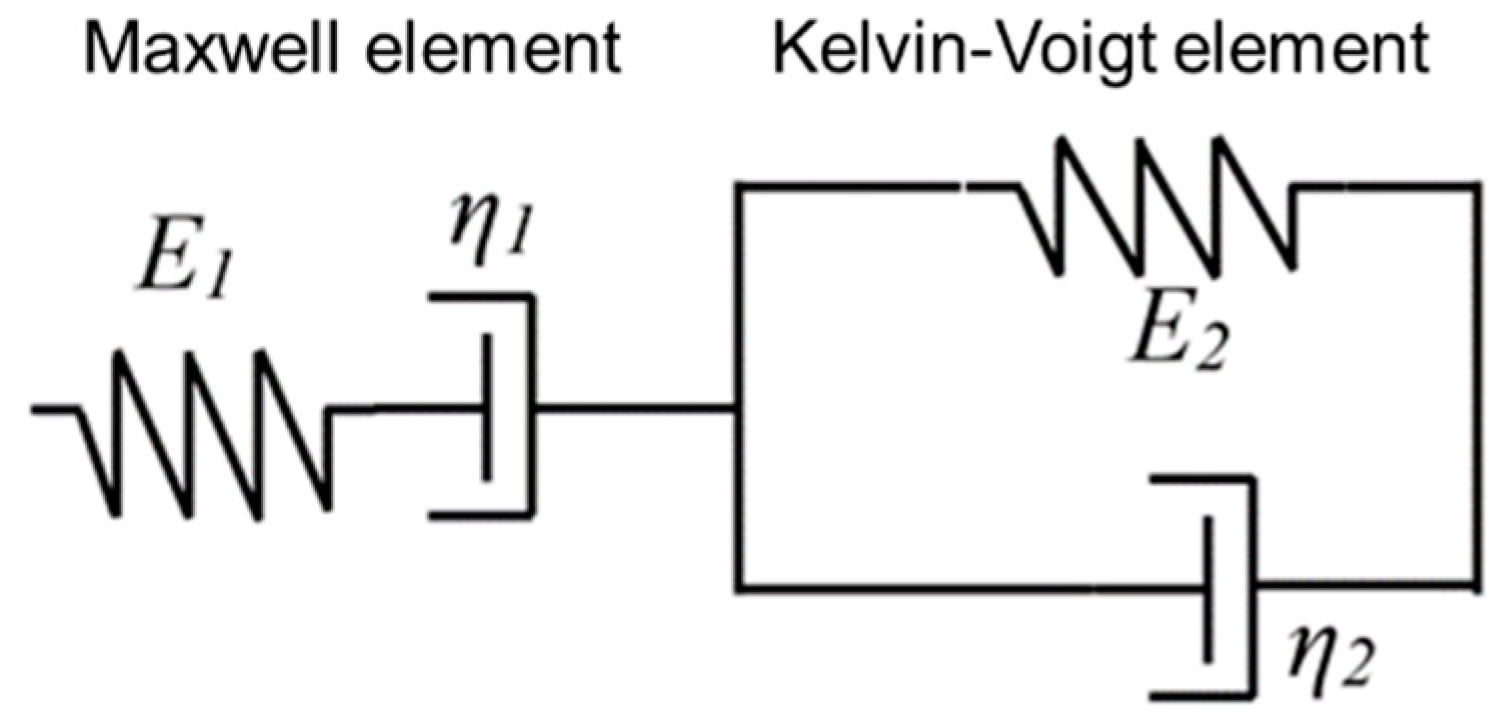
3.2. Creep Strain Modelling
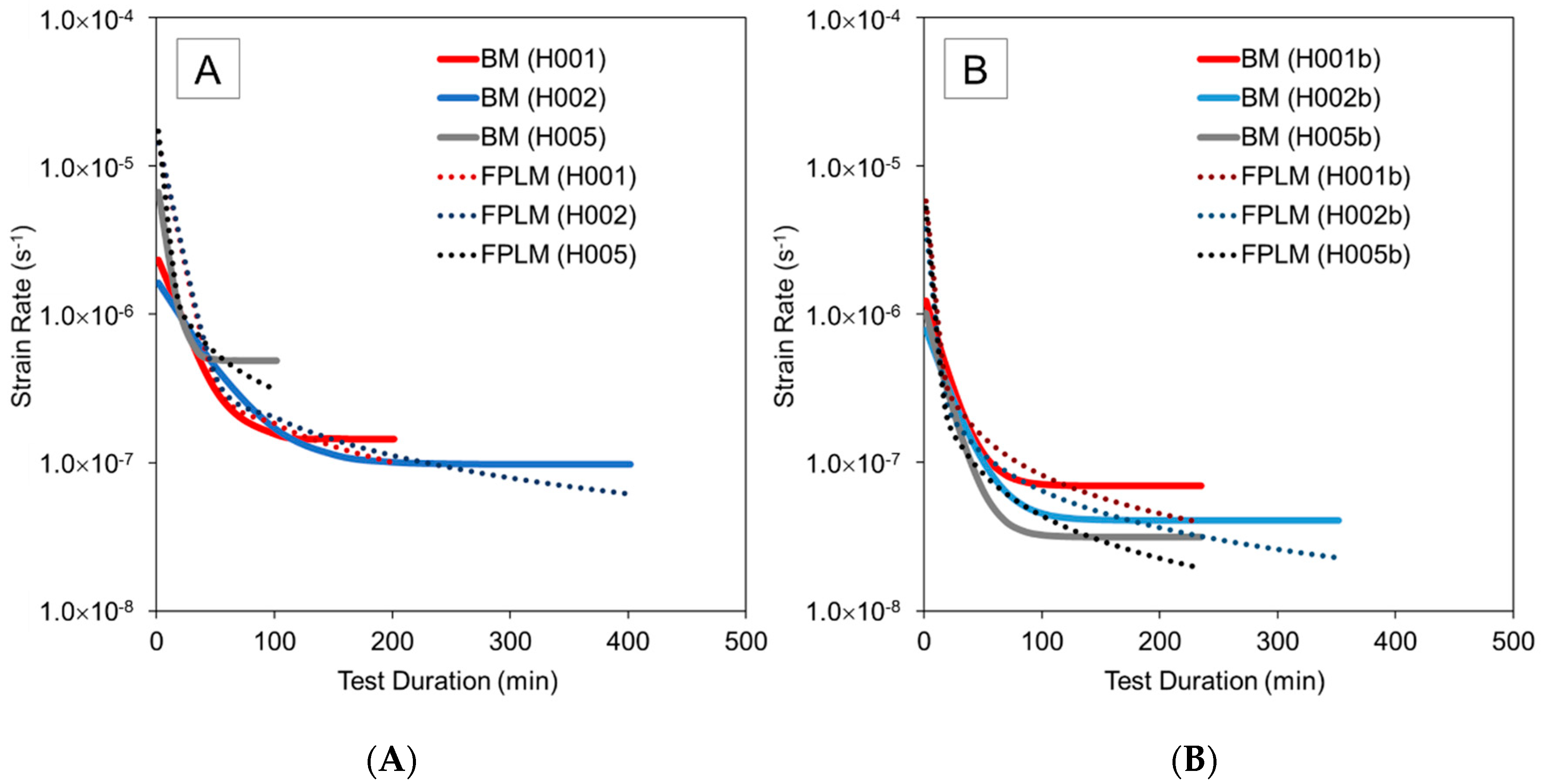
3.3. Strain Rates
3.4. Poisson’s Ratio
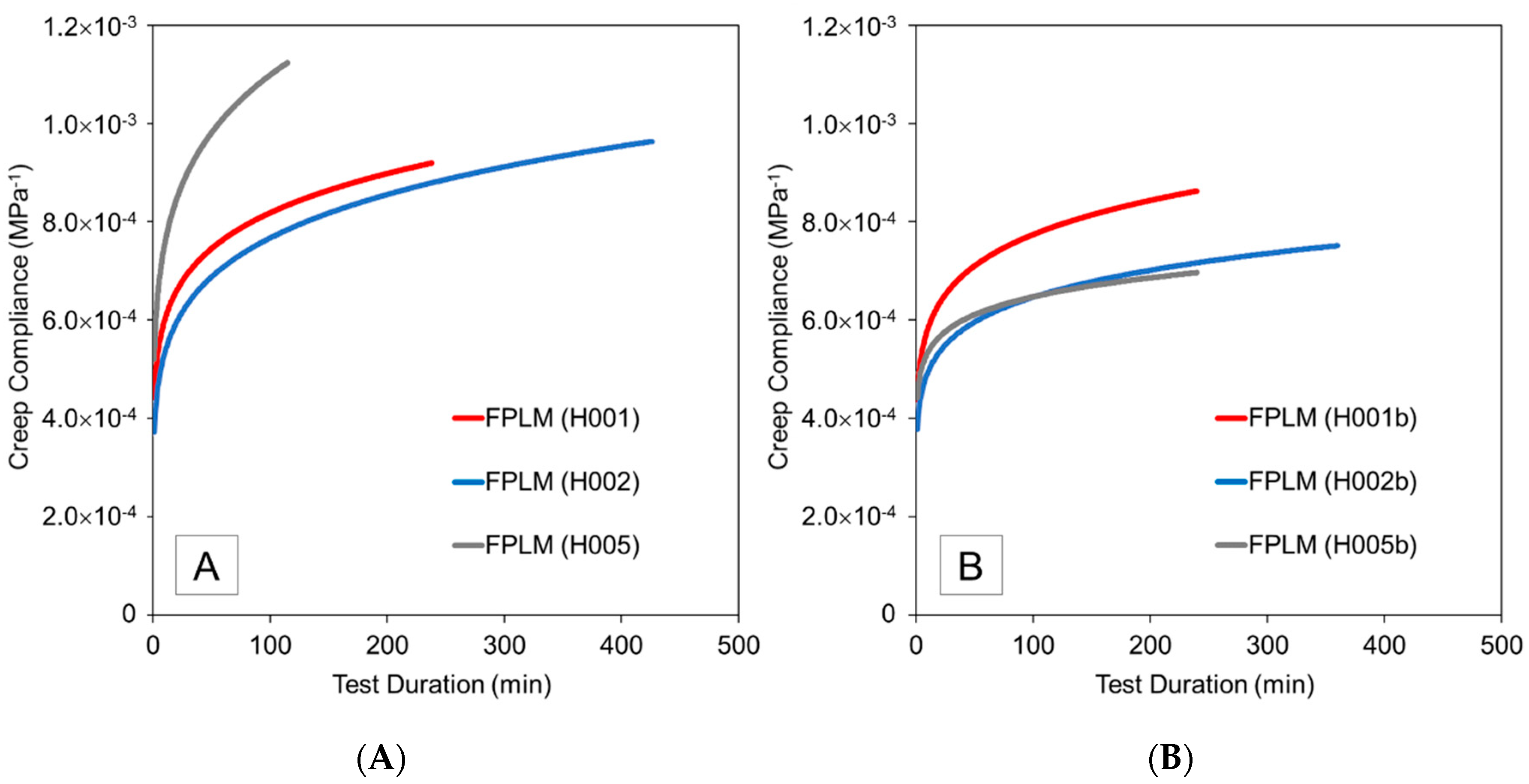
3.5. Creep Compliance
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bogner, B.E. Large diameter pipe: Lasting function in a world of growth. Reinf. Plast. 2008, 52, 28–31. [Google Scholar] [CrossRef]
- Ossai, C.I.; Boswell, B.; Davies, I.J. Pipeline failures in corrosive environments—A conceptual analysis of trends and effects. Eng. Fail. Anal. 2015, 53, 36–58. [Google Scholar] [CrossRef]
- Koch, G.H.; Brongers, M.P.; Thompson, N.G.; Virmani, Y.P.; Payer, J.H. Corrosion Cost and Preventive Strategies in the United States; NACE International: Houston, TX, USA, 2002. [Google Scholar]
- Composite Pipe Applications and Design Factors to Extend System Life. Available online: www.lbcg.com/media/downloads/events/503/12-00-otto-comin-flexpipe-systems.8597.pdf (accessed on 28 August 2019).
- The Markets: Oil and Gas 2016. Available online: www.compositesworld.com/articles/the-markets-oil-and-gas-2016 (accessed on 20 December 2017).
- Fellet, M.; Nyborg, R. Understanding corrosion of flexible pipes at subsea oil and gas wells. MRS Bull. 2018, 43, 654–655. [Google Scholar] [CrossRef]
- FlexFlow Linepipe Produced Water Transfer Line Installation. Available online: www.shawcor.com/about/success-stories/flexflow-linepipe-produced-water-transfer-line-in (accessed on 26 August 2019).
- LeBlanc, J.; Sternisha, M. Fiberglass pipe is helping solve the world’s drinking water shortage. Pipelines 2016, 2016, 1589–1599. [Google Scholar]
- Rafferty, K.D. Piping. In Geothermal Direct-Use Engineering and Design Guidebook; Lienau, P., Lunis, B., Eds.; Oregon Institute of Technology: Klamath Falls, OR, USA, 1991; pp. 242–259. [Google Scholar]
- Papanicolaou, G.C.; Zaoutsos, S.P. Viscoelastic constitutive modeling of creep and stress relaxation in polymers and polymer matrix composites. In Creep and Fatigue in Polymer Matrix Composites; Guedes, R.M., Ed.; Woodhead Publishing: Cambridge, UK, 2011; pp. 3–47. [Google Scholar]
- Kaddour, A.S.; Hinton, M.J.; Soden, P.D. Behaviour of ±45° glass/epoxy filament wound composite tubes under quasi-static equal biaxial tension-compression loading: Experimental results. Compos. Part B 2003, 34, 689–704. [Google Scholar] [CrossRef]
- Yu, K.; Morozov, E.V.; Ashraf, M.A.; Shankar, K. A review of the design and analysis of reinforced thermoplastic pipes for offshore applications. J. Reinf. Plast. Compos. 2017, 36, 1514–1530. [Google Scholar] [CrossRef]
- Brauner, C.; Herrmann, A.S.; Niemeier, P.M.; Schubert, K. Analysis of the non-linear load and temperature-dependent creep behaviour of thermoplastic composite materials. J. Thermoplast. Compos. Mater. 2017, 30, 302–317. [Google Scholar] [CrossRef]
- Ebewele, R.O. Polymer Science and Technology; CRC Press: Boca Raton, FL, USA, 2000. [Google Scholar]
- Lakes, R. Viscoelastic composite materials. In Viscoelastic Materials; Cambridge University Press: Cambridge, UK, 2009; pp. 341–376. [Google Scholar]
- Ashby, M.F.; Jones, D.R.H. Engineering Materials 1—An Introduction to Properties, Applications, and Design; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Yoon, S.H.; Oh, J.O. Prediction of long term performance for GRP pipes under sustained internal pressure. Compos. Struct. 2015, 134, 185–189. [Google Scholar] [CrossRef]
- Faria, H.; Guedes, R.M. Long-term behaviour of GFRP pipes: Reducing the prediction test duration. Polym. Test. 2010, 29, 337–345. [Google Scholar] [CrossRef]
- Tuttle, M.E.; Brinson, H.F. Prediction of the long-term creep compliance of general composite laminates. Exp. Mech. 1986, 26, 89–102. [Google Scholar] [CrossRef]
- Ghorbel, I. Durability of closed-end pressurized GRP filament wound pipes under hygrothermal aging conditions. Part II: Creep tests. J. Compos. Mater. 1996, 30, 1581–1595. [Google Scholar] [CrossRef]
- Fliegener, S.; Hohe, J.; Gumbsch, P. The creep behavior of long fiber reinforced thermoplastics examined by microstructural simulations. Compos. Sci. Technol. 2016, 131, 1–11. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, H.; Ma, X.; Shang, F.; Ma, Y.; Shao, Z.; Hou, D. Flexural creep tests and long-term mechanical behavior of fiber-reinforced polymeric composite tubes. Compos. Struct. 2018, 193, 154–164. [Google Scholar] [CrossRef]
- Findley, W.N.; Lai, J.S.; Onaran, K. Creep and Relaxation of Nonlinear Viscoelastic Materials—With an Introduction to Linear Viscoelasticity; Dover Publications: Mineola, NY, USA, 1976. [Google Scholar]
- Scott, D.W.; Lai, J.S.; Zureick, A.-H. Creep behavior of fiber-reinforced polymeric composites: A review of the technical literature. J. Reinf. Plast. Compos. 1995, 14, 588–617. [Google Scholar] [CrossRef]
- Schledjewski, R. Thermoplastic tape placement process—In situ consolidation is reachable. Plast. Rubber Compos. 2009, 38, 379–386. [Google Scholar] [CrossRef]
- Xiao, X. Studies of the viscoelastic behaviour of a thermoplastic resin composite. Compos. Sci. Technol. 1989, 34, 163–182. [Google Scholar] [CrossRef]
- Nguyen, D.H.; Ogale, A.A. Compressive and flexural creep behavior of carbon fiber/PEEK composites. J. Thermoplastc Compos. Mater. 1991, 4, 83–99. [Google Scholar] [CrossRef]
- Mittelstedt, C.; Becker, W. Free-edge effects in composite laminates. Appl. Mech. Rev. 2007, 60, 217. [Google Scholar] [CrossRef]
- International Organization for Standardization. Plastics—Determination of Creep Behaviour—Part 2: Flexural Creep by Three-Point Bending; ISO 899-2:2003; International Organization for Standardization: Geneva, Switzerland, 2003. [Google Scholar]
- International Organization for Standardization. Plastics Piping Systems—Glass-Reinforced Thermosetting Plastics (GRP) Pipes—Determination of Time to Failure under Sustained Internal Pressure; ISO 7509:2015; International Organization for Standardization: Geneva, Switzerland, 2015. [Google Scholar]
- International Organization for Standardization. Plastics Piping Systems—Glass-REINFORCED Thermosetting Plastics (GRP) Pipes—Determination of the Creep Factor under Dry Conditions; ISO 7684:1997; International Organization for Standardization: Geneva, Switzerland, 1997. [Google Scholar]
- Funck, R.; Neitzel, M. Improved thermoplastic tape winding using laser or direct-flame heating. Compos. Manuf. 1995, 6, 189–192. [Google Scholar] [CrossRef]
- Clancy, G.; Peeters, D.; Oliveri, V.; Jones, D.; O’Higgins, R.M.; Weaver, P.M. A study of the influence of processing parameters on steering of carbon fibre/PEEK tapes using laser-assisted tape placement. Composites Part B 2019, 163, 243–251. [Google Scholar] [CrossRef]
- Mazumdar, S.K.; Hoa, S.V. Determination of manufacturing conditions for hot-gas-aided thermoplastic tape winding. J. Thermoplast. Compos. Mater. 1996, 9, 35–53. [Google Scholar] [CrossRef]
- Behjat, Y.; Cheng, J.J.; Polak, M.A.; Asce, M.; Penlidis, A. Effect of molecular structure on the short-term and long-term mechanical behavior of high-density polyethylene. J. Mater. Civ. Eng. 2014, 26, 795–802. [Google Scholar] [CrossRef]
- Kaw, A. Mechanics of Composite Materials; Taylor and Francis: Milton Park, UK, 2006. [Google Scholar]
- Agarwal, V.; Mccullough, R.L.; Schultz, J.M. The thermoplastic laser-assisted consolidation process—Mechanical and microstructure characterization. J. Thermoplast. Compos. Mater. 1996, 9, 365–380. [Google Scholar] [CrossRef]
- Xia, X.C.; Zhang, Q.P.; Wang, L.; Feng, J.M.; Fu, X.R.; Yang, M.B. Role of gas cooling time on crystalline morphology and mechanical property of the HDPE parts prepared by gas-assisted injection molding. Colloid Polym. Sci. 2014, 292, 1129–1142. [Google Scholar] [CrossRef]
- Xu, Y.; Wu, Q.; Lei, Y.; Yao, F. Creep behavior of bagasse fiber reinforced polymer composites. Bioresour. Technol. 2010, 101, 3280–3286. [Google Scholar] [CrossRef] [PubMed]
- Xu, H.L.; Cao, Y.; Wang, W.H.; Wang, Q.W. Creep model of natural fiber reinforced polymer composite. Mater. Sci. Forum 2016, 850, 86–90. [Google Scholar] [CrossRef]
- Wang, W.-H.; Huang, H.-B.; Du, H.-H.; Wang, H. Effects of fiber size on short-term creep behavior of wood fiber HDPE composites. Polym. Eng. Sci. 2015, 55, 693–700. [Google Scholar] [CrossRef]
- Nomula, S.S.R.; Rathore, D.K.; Ray, B.C.; Prusty, R.K. Creep performance of CNT reinforced glass fiber/epoxy composites: Roles of temperature and stress. J. Appl. Polym. Sci. 2019, 136, 1–15. [Google Scholar] [CrossRef]
- Pereira, A.A.C.; D’Almeida, J.R.M.; Castro, T.M.L. Evaluation of short-term creep behavior of PE-HD after aging in oil derivatives. Polym. Polym. Compos. 2018, 26, 243–258. [Google Scholar] [CrossRef]
- Peel, L.D. P97 Investigation of high and negative Poisson’s ratio laminates. In Proceedings of the 50th International SAMPE Symposium and Exhibition, Long Beach, CA, USA, 1–5 May 2005; Abrams, F., Patel, J., Eds.; Destech Publications: Lancaster, PA, USA; pp. 821–834. [Google Scholar]
- Al-Salehi, F.A.R.; Al-Hassani, S.T.S.; Hinton, M.J. An experimental investigation into the strength of angle ply GRP tubes under high rate of loading. J. Compos. Mater. 1989, 23, 288–305. [Google Scholar] [CrossRef]
- Liang, Y.; Wang, H.; Gu, X. In-plane shear response of unidirectional fiber reinforced and fabric reinforced carbon/epoxy composites. Polym. Test. 2013, 32, 594–601. [Google Scholar] [CrossRef]
- Elghazouli, A.Y.; Chryssanthopoulos, M.K.; Spagnoli, A. Experimental response of glass-reinforced plastic cylinders under axial compression. Mar. Struct. 1999, 11, 347–371. [Google Scholar] [CrossRef]
- Yao, J.; Ziegmann, G. Equivalence of moisture and temperature in accelerated test method and its application in prediction of long-term properties of glass-fiber reinforced epoxy pipe specimen. Polym. Test. 2006, 25, 149–157. [Google Scholar] [CrossRef]
- Elleuch, R.; Taktak, W. Viscoelastic behavior of HDPE polymer using tensile and compressive loading. J. Mater. Eng. Perform. 2006, 15, 111–116. [Google Scholar] [CrossRef]





| Air Temperature * (Heater Setting) | Layers | |
|---|---|---|
| Batch #1 | Batch #2 | |
| 400 °C (9) | 1 | 1 |
| 400 °C (9) | 2 to 7 | 2 to 4 |
| 420 °C (9.5) | 8 to 10 | 5 to 8 |
| 440 °C (10) | - | 9 to 10 |
| Test Name | Specimen Inner Diameter (mm) | Specimen Wall Thickness (mm) | Internal Pressure (MPa) | Axial Force (N) |
|---|---|---|---|---|
| H001 | 61.92 | 3.64 | 1.176 | −3829 |
| H001b | N/A | −3829 | ||
| H002 | 69.14 | 3.65 | 1.178 | −3548 |
| H002b | N/A | −3757 | ||
| H003 | 69.14 | 3.59 | 1.168 | −3516 |
| H004 | 69.20 | 3.65 | 1.181 | −3553 |
| H005 | 69.01 | 3.60 | 1.165 | −3495 |
| H005b | N/A | −3699 |
| Property | Glass Fiber | HDPE |
|---|---|---|
| Young’s modulus range (GPa) | 68.9–85.0 | 0.7–1.34 |
| Poisson’s ratio | 0.20 | 0.46 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Doan, H.G.M.; Mertiny, P. Creep Testing of Thermoplastic Fiber-Reinforced Polymer Composite Tubular Coupons. Materials 2020, 13, 4637. https://doi.org/10.3390/ma13204637
Doan HGM, Mertiny P. Creep Testing of Thermoplastic Fiber-Reinforced Polymer Composite Tubular Coupons. Materials. 2020; 13(20):4637. https://doi.org/10.3390/ma13204637
Chicago/Turabian StyleDoan, Hai Giang Minh, and Pierre Mertiny. 2020. "Creep Testing of Thermoplastic Fiber-Reinforced Polymer Composite Tubular Coupons" Materials 13, no. 20: 4637. https://doi.org/10.3390/ma13204637
APA StyleDoan, H. G. M., & Mertiny, P. (2020). Creep Testing of Thermoplastic Fiber-Reinforced Polymer Composite Tubular Coupons. Materials, 13(20), 4637. https://doi.org/10.3390/ma13204637






