Fast Detection of Heat Accumulation in Powder Bed Fusion Using Computationally Efficient Thermal Models
Abstract
1. Introduction
2. Reference Thermal LPBF Process Model
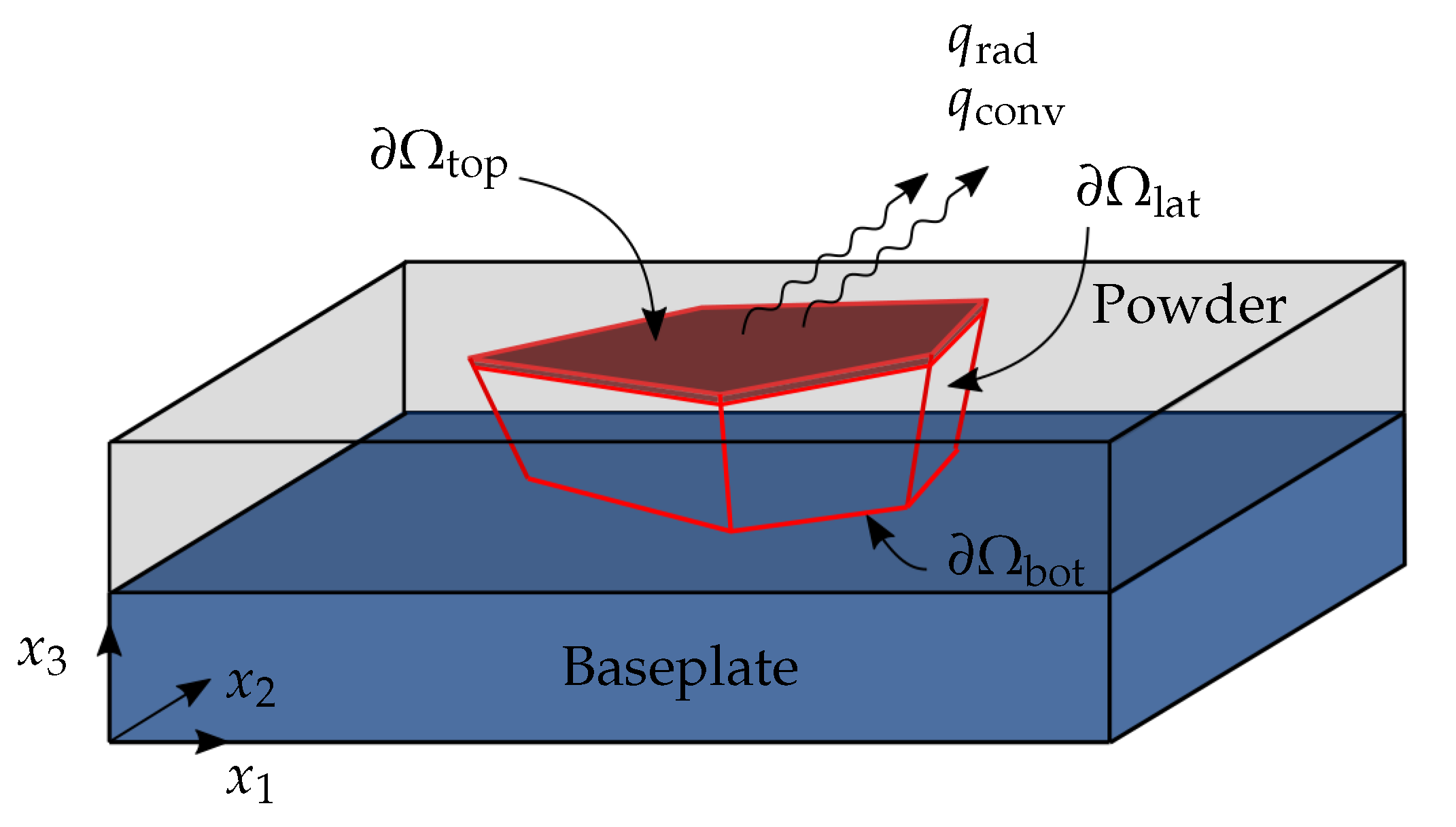
2.1. Model Description
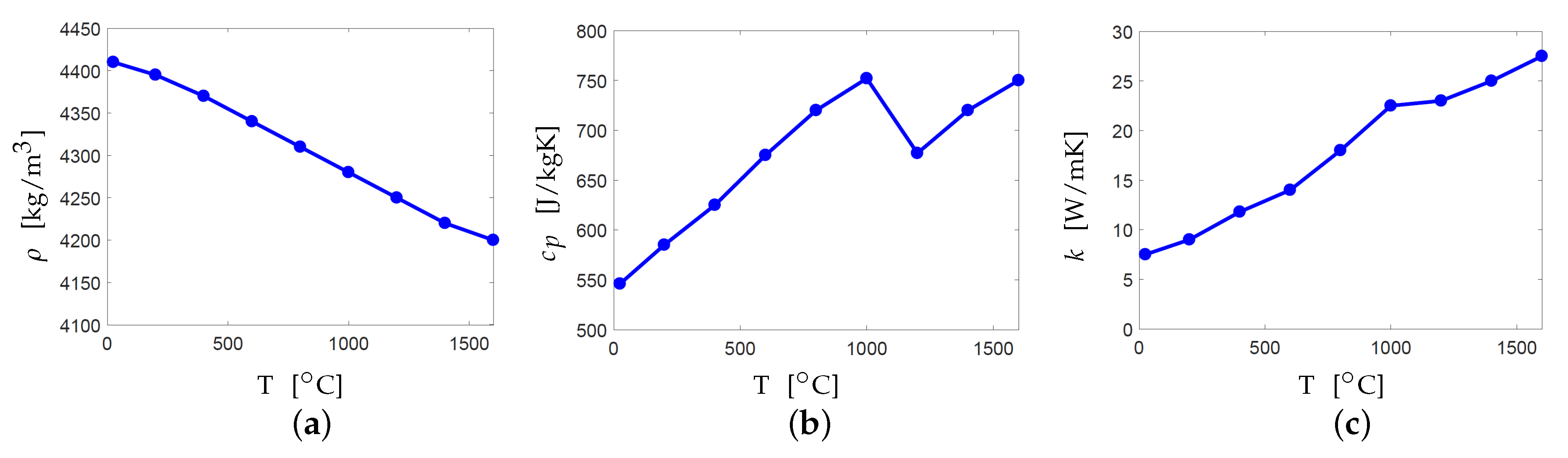
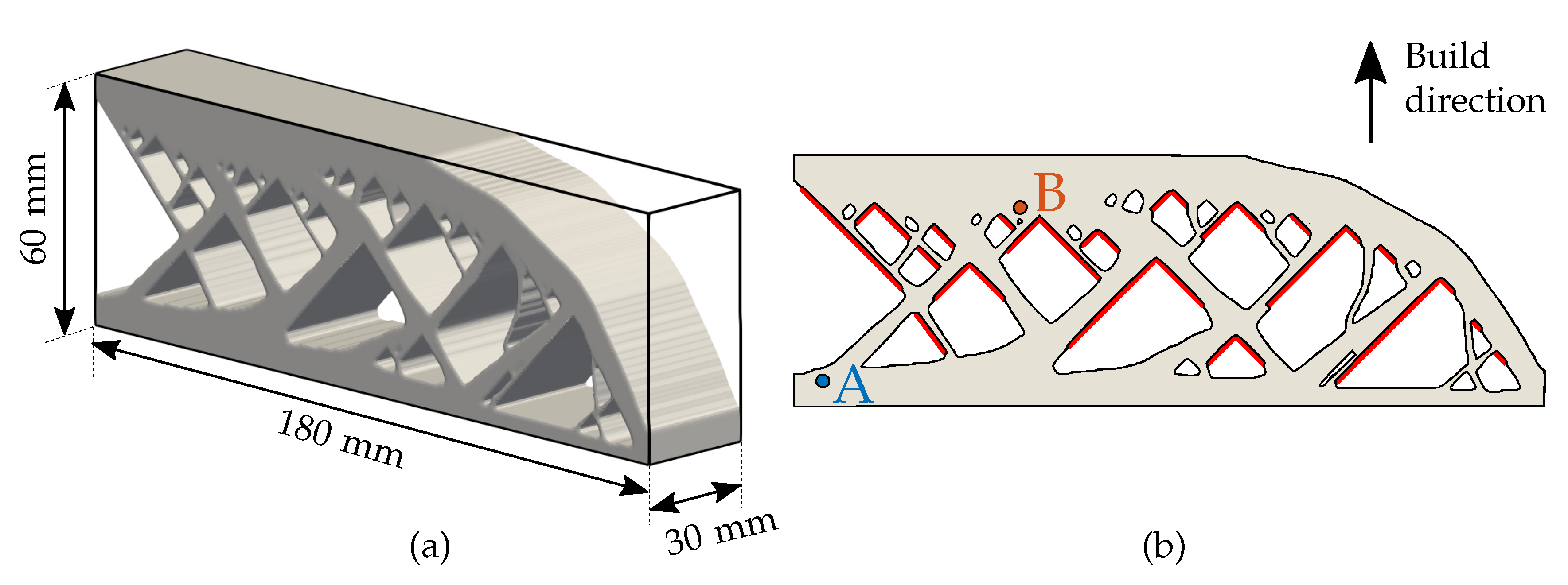
2.2. Finite Element Analysis and Simulation Parameter Setting
- Heating time for a layer with area A equals the time that the laser would take for scanning that entire layer, i.e.,where h is hatch spacing and v is laser scan velocity. Please note that by using this definition, is calculated for each super layer and it depends on the local part geometry through layer scan areas.
- It is ensured that the total deposited energy matches that of the actual process. Deposited energy per unit time is given by , where is the absorption coefficient and P is laser power. Using this principle, the volumetric heat source term can be calculated aswhere l is LPBF layer thickness.
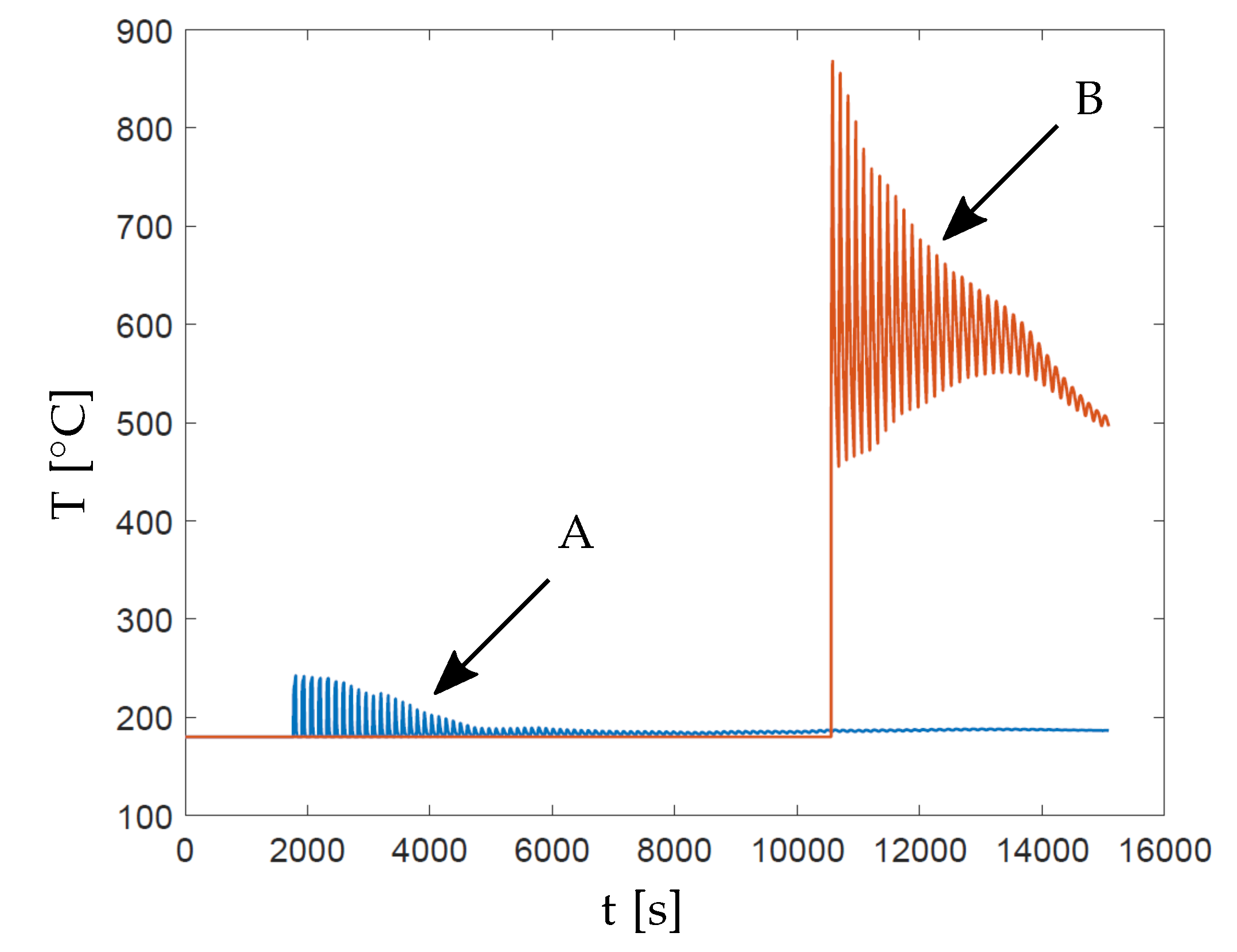
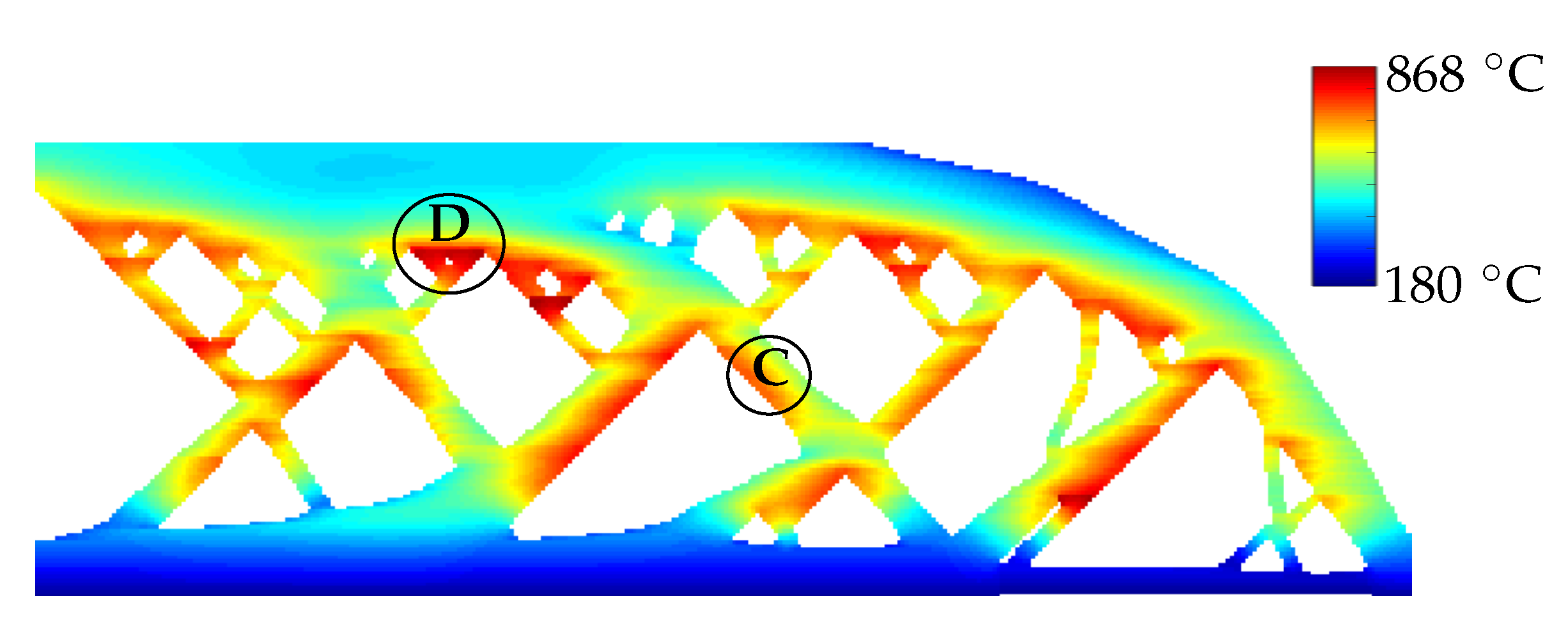
2.3. Identification of Overheating Zones
3. Thermal Modeling Simplifications and Comparison Metrics
3.1. Influence of Neglecting Convective and Radiative Heat Losses
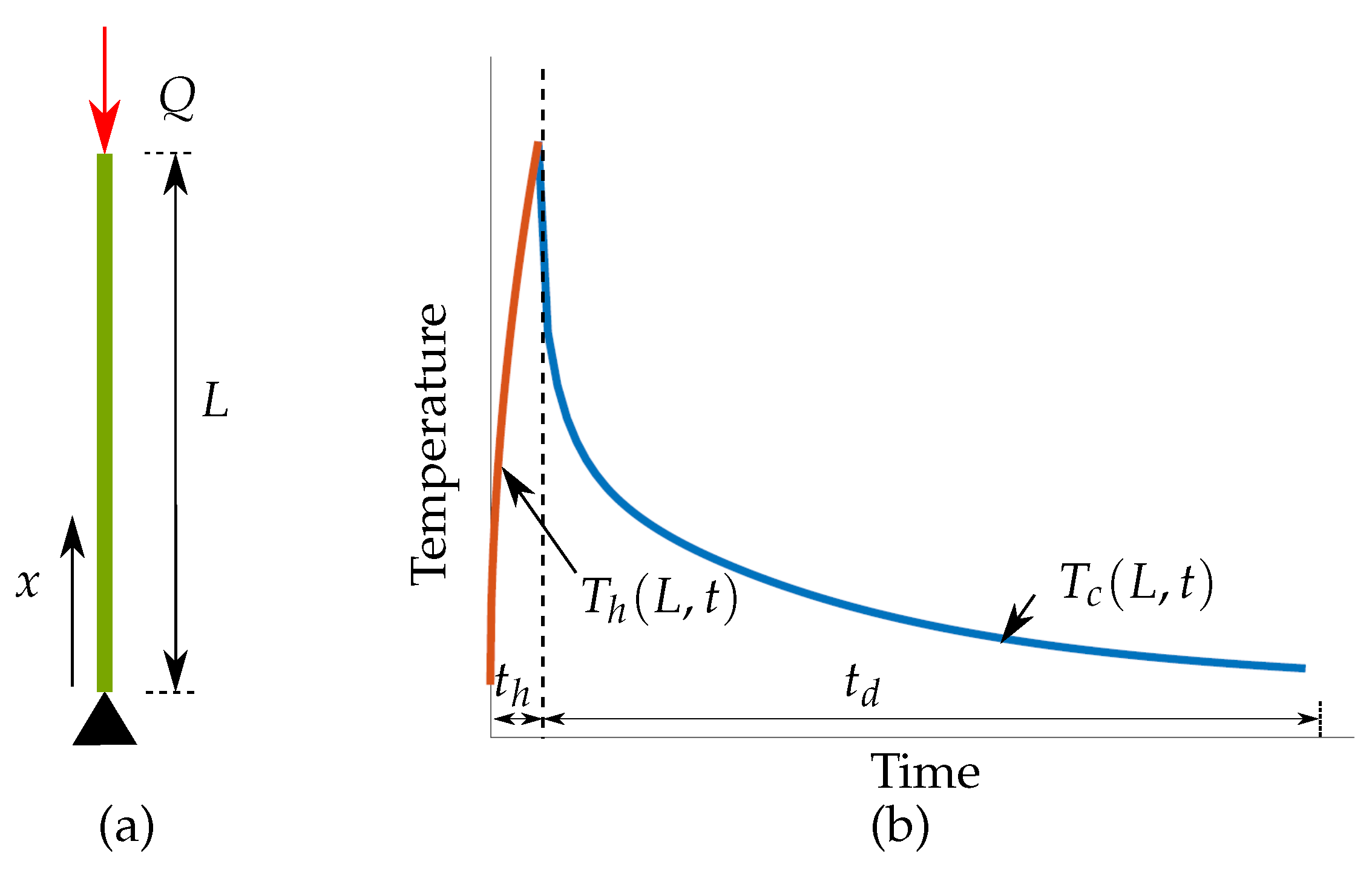
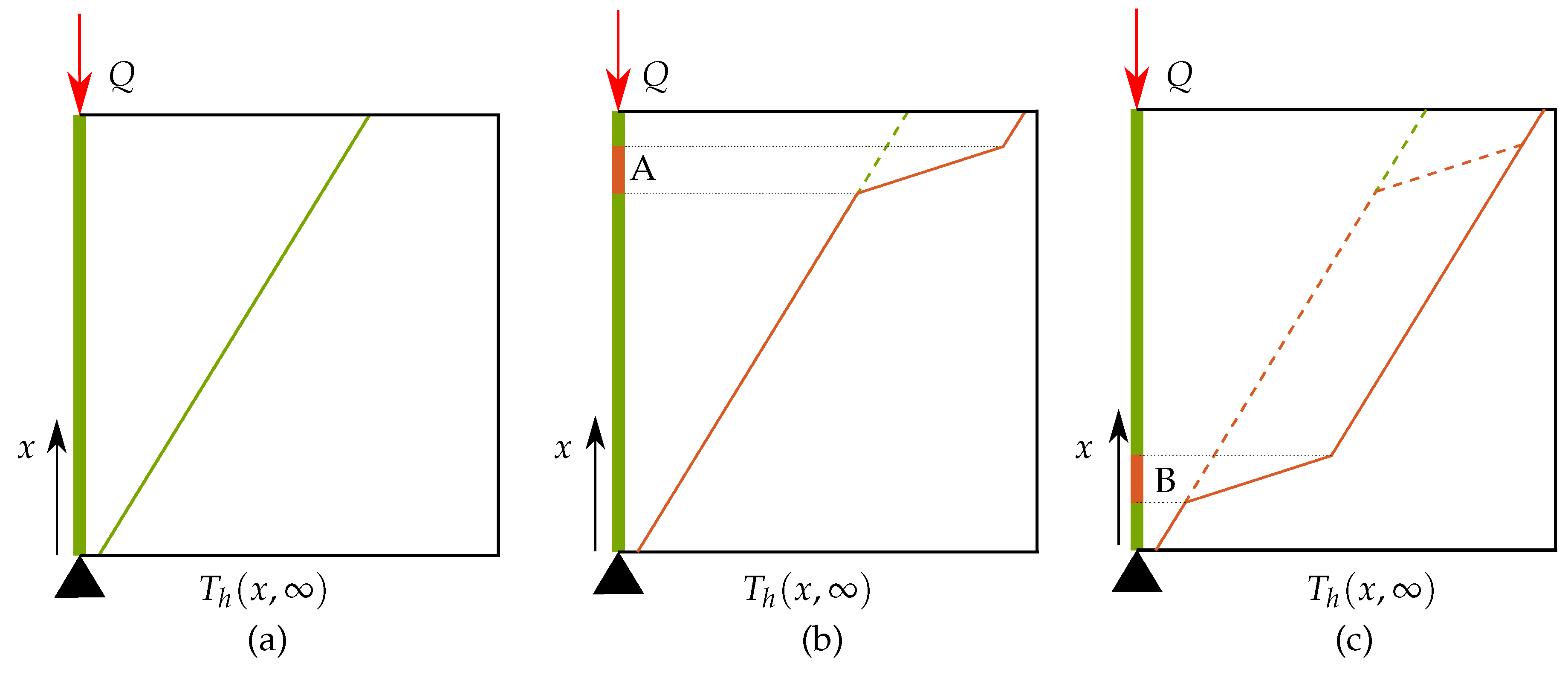
3.2. Novel Simplifications Motivated by One-Dimensional Heat Transfer Analysis
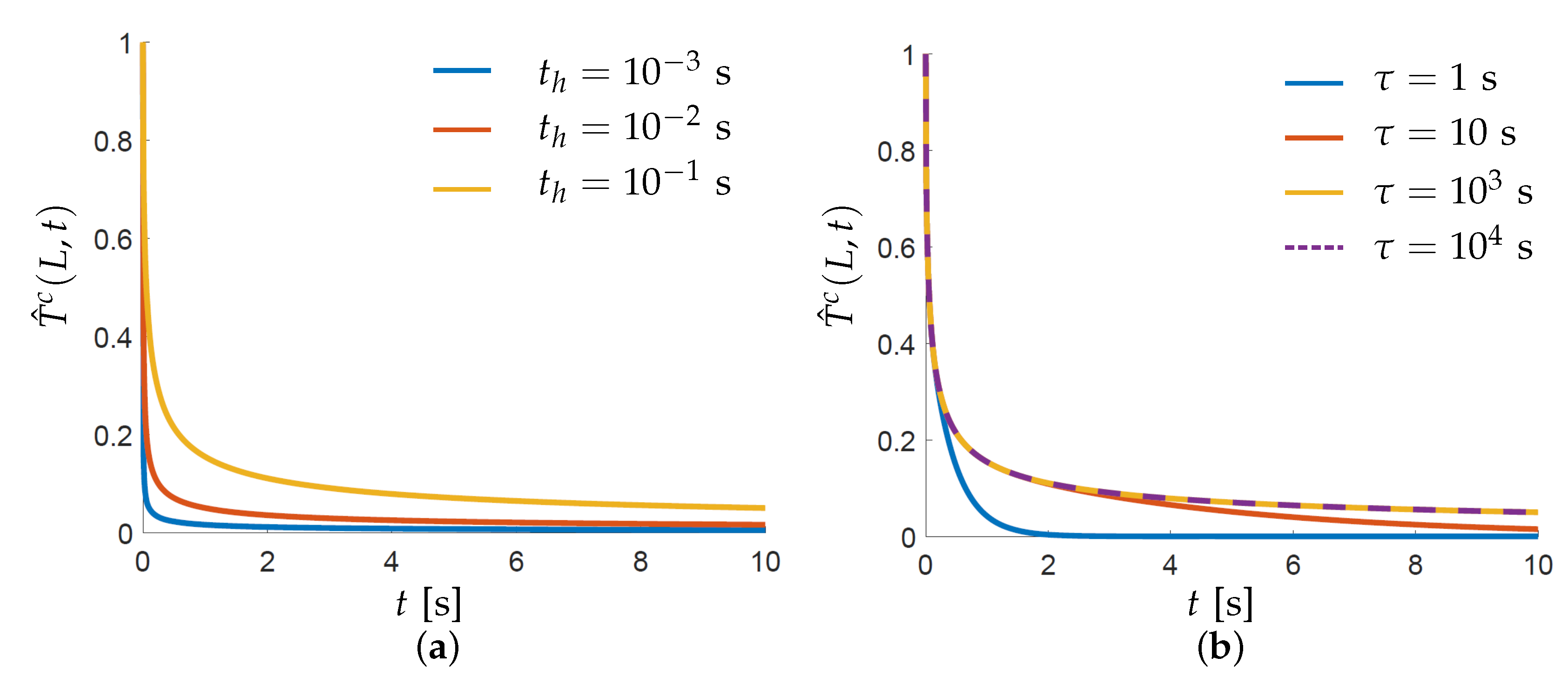
3.2.1. Observation 1: Temporal Decoupling
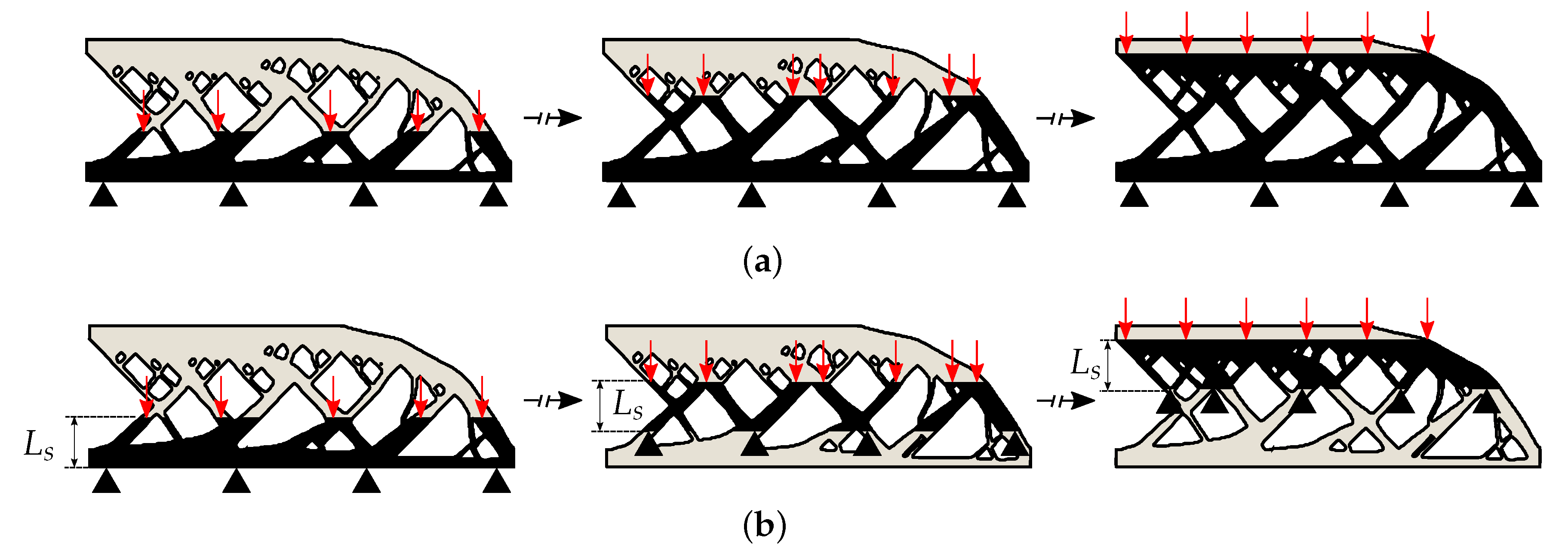
3.2.2. Observation 2: Spatial Decoupling
3.2.3. Observation 3: Steady-State Response for Detecting Overheating
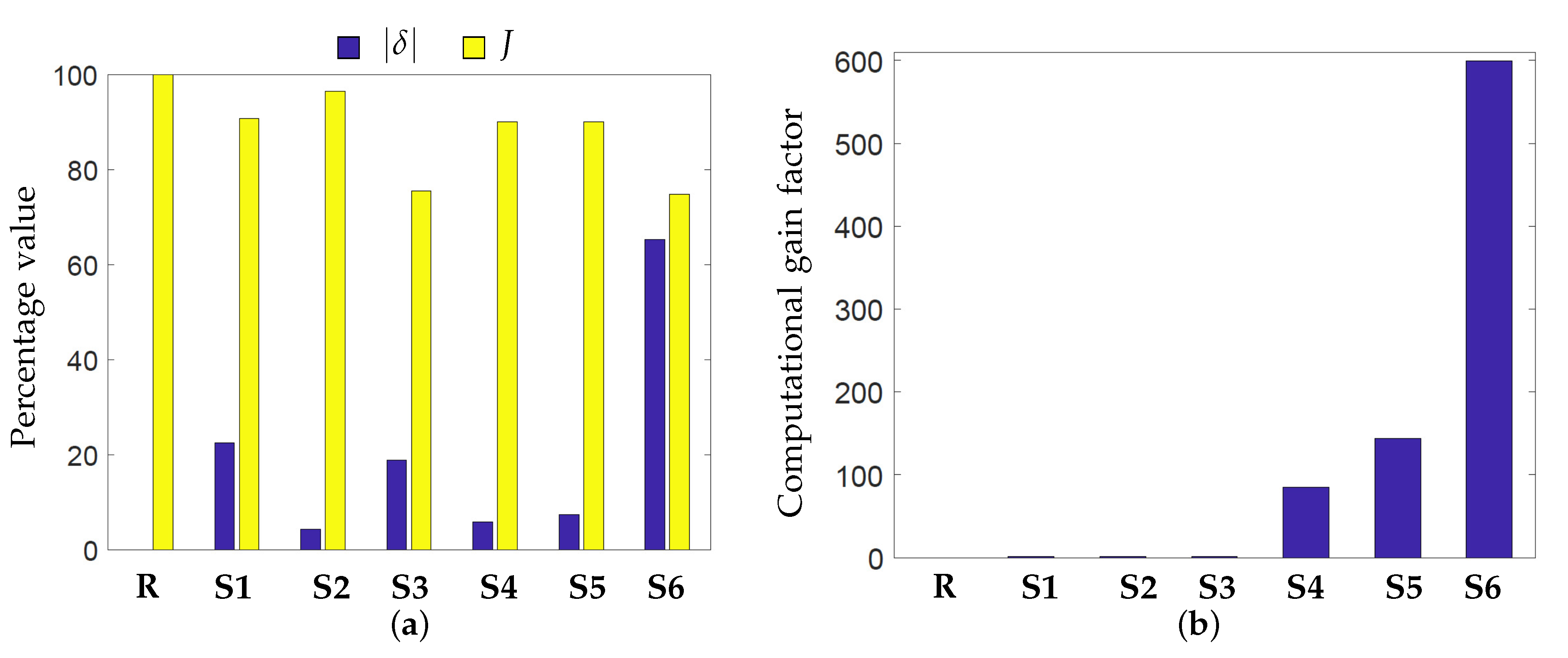
3.3. Comparison Metrics
4. Numerical Results and Discussion
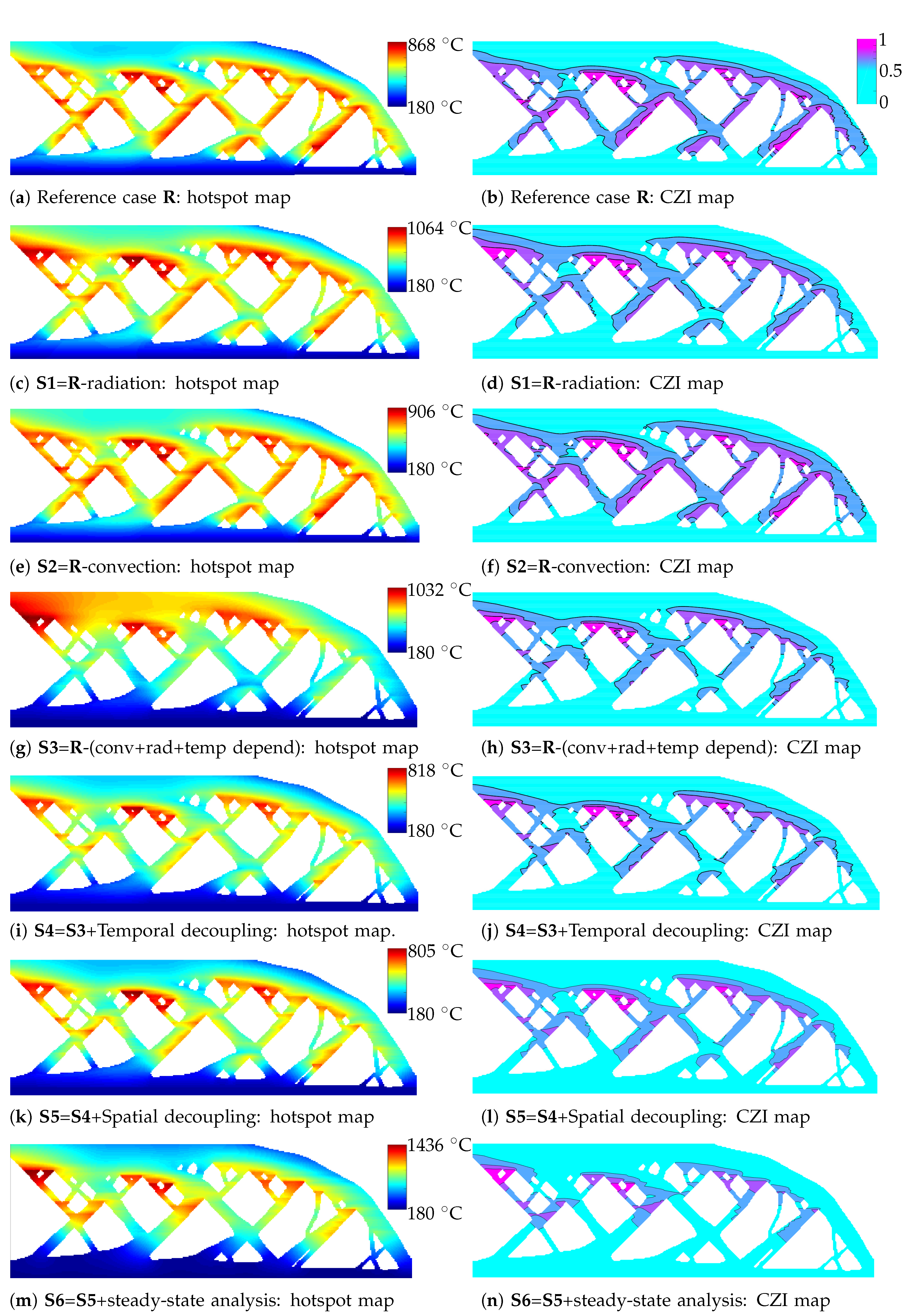
4.1. Hotspot Map without Considering Convective/Radiative Heat Losses
4.2. Hotspot Map Without Considering Temperature-Dependent Properties
4.3. Hotspot Map with Temporal Decoupling
4.4. Hotspot Map with Spatial Decoupling
4.5. Hotspot Map with Steady-State Analysis
4.6. Comparative Analysis
5. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Derivation of Analytical Solution for One-Dimensional Heat Equation
References
- Thomas-Seale, L.E.; Kirkman-Brown, J.C.; Attallah, M.M.; Espino, D.M.; Shepherd, D.E. The barriers to the progression of additive manufacture: Perspectives from UK industry. Int. J. Prod. Econ. 2018, 198, 104–118. [Google Scholar] [CrossRef]
- Leach, R.; Carmignato, S. Precision Metal Additive Manufacturing; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar] [CrossRef]
- Mertens, R.; Clijsters, S.; Kempen, K.; Kruth, J.P. Optimization of Scan Strategies in Selective Laser Melting of Aluminum Parts With Downfacing Areas. J. Manuf. Sci. Eng. 2014, 136, 061012. [Google Scholar] [CrossRef]
- Hooper, P.A. Melt pool temperature and cooling rates in laser powder bed fusion. Addit. Manuf. 2018, 22, 548–559. [Google Scholar] [CrossRef]
- Craeghs, T.; Bechmann, F.; Berumen, S.; Kruth, J.P. Feedback control of Layerwise Laser Melting using optical sensors. Phys. Procedia 2010, 5, 505–514. [Google Scholar] [CrossRef]
- Hodge, N.; Ferencz, R.; Solberg, J. Implementation of a thermomechanical model for the simulation of selective laser melting. Comput. Mech. 2014, 54, 33–51. [Google Scholar] [CrossRef]
- Charles, A.P.; Elkaseer, A.; Thijs, L.; Hagenmeyer, V.; Scholz, S. Effect of Process Parameters on the Generated Surface Roughness of Down-Facing Surfaces in Selective Laser Melting. Appl. Sci. 2019, 9, 1256. [Google Scholar] [CrossRef]
- Sames, W.J.; List, F.A.; Pannala, S.; Dehoff, R.R.; Babu, S.S. The metallurgy and processing science of metal additive manufacturing. Int. Mater. Rev. 2016, 61, 1–46. [Google Scholar] [CrossRef]
- Spranger, F.; Graf, B.; Schuch, M.; Hilgenberg, K.; Rethmeier, M. Build-up strategies for additive manufacturing of three dimensional Ti-6Al-4V-parts produced by laser metal deposition. J. Laser Appl. 2018, 30, 022001. [Google Scholar] [CrossRef]
- Yang, D.; Wang, G.; Zhang, G. Thermal analysis for single-pass multi-layer GMAW based additive manufacturing using infrared thermography. J. Mater. Process. Technol. 2017, 244, 215–224. [Google Scholar] [CrossRef]
- Mohr, G.; Altenburg, S.J.; Hilgenberg, K. Effects of inter layer time and build height on resulting properties of 316L stainless steel processed by laser powder bed fusion. Addit. Manuf. 2020, 32, 101080. [Google Scholar] [CrossRef]
- Parry, L.A.; Ashcroft, I.A.; Wildman, R.D. Geometrical effects on residual stress in selective laser melting. Addit. Manuf. 2019, 25, 166–175. [Google Scholar] [CrossRef]
- Kastsian, D.; Reznik, D. Reduction of local overheating in selective laser melting. In Proceedings of the Simulation of Additive Manufacturing (SIM-AM), Munich, Germany, 11–13 October 2017. [Google Scholar]
- Heigel, J.C.; Whitenton, E. Measurement of Thermal Processing Variability in Powder Bed Fusion. In Proceedings of the ASPE and euspen Summer Topical Meeting—Advancing Precision in Additive Manufacturing, Berkeley, CA, USA, 22–25 July 2018. [Google Scholar]
- Cloots, M.; Zumofen, L.; Spierings, A.; Kirchheim, A.; Wegener, K. Approaches to minimize overhang angles of SLM parts. Rapid Prototyp. J. 2017, 23, 362–369. [Google Scholar] [CrossRef]
- Booth, J.; Alperovich, J.; Chawla, P.; Ma, J.; Reid, T.; Ramani, K. The Design for Additive Manufacturing Worksheet. J. Mech. Des. 2017, 139. [Google Scholar] [CrossRef]
- Adam, G.A.; Zimmer, D. Design for Additive Manufacturing—Element transitions and aggregated structures. CIRP J. Manuf. Sci. Technol. 2014, 7, 20–28. [Google Scholar] [CrossRef]
- Patel, S.; Mekavibul, J.; Park, J.; Kolla, A.; French, R.; Kersey, Z.; Lewin, G. Using Machine Learning to Analyze Image Data from Advanced Manufacturing Processes. In Proceedings of the 2019 Systems and Information Engineering Design Symposium (SIEDS), Charlottesv, VA, USA, 25 April 2019; pp. 1–5. [Google Scholar]
- Paul, R.; Anand, S.; Gerner, F. Effect of Thermal Deformation on Part Errors in Metal Powder Based Additive Manufacturing Processes. J. Manuf. Sci. Eng. 2014, 136, 31009–31012. [Google Scholar] [CrossRef]
- Roberts, I.A. Investigation of residual stresses in the laser melting of metal powders in additive layer manufacturing. Ph.D. Thesis, University of Wolverhampton, Wolverhampton, UK, 2012. [Google Scholar]
- Childs, M.B.T. Further studies in selective laser melting of stainless and tool steel powders. Int. J. Mach. Tools Manuf. 2007, 47, 779–784. [Google Scholar] [CrossRef]
- King, W.E.; Barth, H.D.; Castillo, V.M.; Gallegos, G.F.; Gibbs, J.W.; Hahn, D.E.; Kamath, C.; Rubenchik, A.M. Observation of keyhole-mode laser melting in laser powder-bed fusion additive manufacturing. J. Mater. Process. Technol. 2014, 214, 2915–2925. [Google Scholar] [CrossRef]
- Peng, H.; Ghasri-Khouzani, M.; Gong, S.; Attardo, R.; Ostiguy, P.; Gatrell, B.A.; Budzinski, J.; Tomonto, C.; Neidig, J.; Shankar, M.R.; et al. Fast prediction of thermal distortion in metal powder bed fusion additive manufacturing: Part 1, a thermal circuit network model. Addit. Manuf. 2018, 22, 852–868. [Google Scholar] [CrossRef]
- Chiumenti, M.; Neiva, E.; Salsi, E.; Cervera, M.; Badia, S.; Moya, J.; Chen, Z.; Lee, C.; Davies, C. Numerical modelling and experimental validation in Selective Laser Melting. Addit. Manuf. 2017, 18, 171–185. [Google Scholar] [CrossRef]
- Malmelöv, A.; Lundbäck, A.; Lindgren, L.E. History Reduction by Lumping for Time-Efficient Simulation of Additive Manufacturing. Metals 2019, 10, 58. [Google Scholar] [CrossRef]
- Zhang, W.; Tong, M.; Harrison, N.M. Resolution, energy and time dependency on layer scaling in finite element modelling of laser beam powder bed fusion additive manufacturing. Addit. Manuf. 2019, 28, 610–620. [Google Scholar] [CrossRef]
- Chiumenti, M.; Lin, X.; Cervera, M.; Wei, L.; Zheng, Y.; Huang, W. Numerical simulation and experimental calibration of additive manufacturing by blown powder technology. Part I: Thermal analysis. Rapid Prototyp. J. 2017, 23, 448–463. [Google Scholar] [CrossRef]
- Neiva, E.; Chiumenti, M.; Cervera, M.; Salsi, E.; Piscopo, G.; Badia, S.; Martín, A.F.; Chen, Z.; Lee, C.; Davies, C. Numerical modelling of heat transfer and experimental validation in powder-bed fusion with the virtual domain approximation. Finite Elem. Anal. Des. 2020, 168, 103343. [Google Scholar] [CrossRef]
- Neiva, E.; Badia, S.; Martín, A.F.; Chiumenti, M. A scalable parallel finite element framework for growing geometries. Application to metal additive manufacturing. Int. J. Numer. Methods Eng. 2019, 119, 1098–1125. [Google Scholar] [CrossRef]
- Rombouts, M.; Froyen, L.; Gusarov, A.; Bentefour, E.H.; Glorieux, C. Photopyroelectric measurement of thermal conductivity of metallic powders. J. Appl. Phys. 2004, 97, 24905. [Google Scholar] [CrossRef]
- Romano, J.; Ladani, L.; Sadowski, M. Thermal Modeling of Laser Based Additive Manufacturing Processes within Common Materials. Procedia Manuf. 2015, 1, 238–250. [Google Scholar] [CrossRef]
- Yang, Y.; Knol, M.F.; Van Keulen, F.; Ayas, C. A semi-analytical thermal modelling approach for selective laser melting. Addit. Manuf. 2018, 21, 284–297. [Google Scholar] [CrossRef]
- Afazov, S.; Denmark, W.A.; Toralles, B.L.; Holloway, A.; Yaghi, A. Distortion prediction and compensation in selective laser melting. Addit. Manuf. 2017, 17, 15–22. [Google Scholar] [CrossRef]
- Dhondt, G. CalculiX CrunchiX User’S Manual Version 2.16. 2020. Available online: http://www.dhondt.de/ (accessed on 13 July 2020).
- Langelaar, M. An additive manufacturing filter for topology optimization of print-ready designs. Struct. Multidiscip. Optim. 2016, 55, 871–883. [Google Scholar] [CrossRef]
- Megahed, M.; Mindt, H.W.; N’Dri, N.; Duan, H.; Desmaison, O. Metal additive-manufacturing process and residual stress modeling. Integr. Mater. Manuf. Innov. 2016, 5, 61–93. [Google Scholar] [CrossRef]
- Calta, N.P.; Wang, J.; Kiss, A.M.; Martin, A.A.; Depond, P.J.; Guss, G.M.; Thampy, V.; Fong, A.Y.; Weker, J.N.; Stone, K.H.; et al. An instrument for in situ time-resolved X-ray imaging and diffraction of laser powder bed fusion additive manufacturing processes. Rev. Sci. Instrum. 2018, 89, 55101. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Van Keulen, F.; Ayas, C. A computationally efficient thermal model for selective laser melting. Addit. Manuf. 2020, 31, 100955. [Google Scholar] [CrossRef]
- Carslaw, H.S.; Jaeger, J.C. Conduction of Heat in Solids; Clarendon Press: Oxford, UK, 1959. [Google Scholar]
- Jaccard, P. The Distribution of the Flora of the Alpine Zone. New Phytol. 1912, 11, 37–50. [Google Scholar] [CrossRef]
- Jamshidinia, M.; Kovacevic, R. The influence of heat accumulation on the surface roughness in powder-bed additive manufacturing. Surf. Topogr. Metrol. Prop. 2015, 3, 14003. [Google Scholar] [CrossRef]
- Van Keulen, F.; Haftka, R.; Kim, N. Review of options for structural design sensitivity analysis. Part 1: Linear systems. Comput. Methods Appl. Mech. Eng. 2005, 194, 3213–3243. [Google Scholar] [CrossRef]


| P [W] | v [ms] | h [mm] | l [mm] | S [mm] | [C] | [C] | [WmK] | ||
|---|---|---|---|---|---|---|---|---|---|
| 200 | 0.45 | 1 | 0.14 | 0.05 | 0.5 | 180 | 25 | 10 | 0.35 |
| Model Description | Wall-Clock Time | CPU Time | J | ||
|---|---|---|---|---|---|
| R: Reference case | 21 h 28 min 32 s | 20 h 52 min 38 s | 0 | 100 | 1 |
| S1: R-radiation | 20 h 11 min 6 s | 19 h 35 min 6 s | 22.4 | 90.6 | 1.06 |
| S2:R-convection | 20 h 39 min 27 s | 20 h 3 min 30 s | 4.2 | 96.4 | 1.03 |
| S3: R-(rad, conv, temp depend) | 15 h 3 min 29 s | 14 h 48 min 16 s | 18.8 | 75.4 | 1.7 |
| S4: S3+Temporally decoupled | 15 min 7 s | 13 h 20 min 27 s | 89.9 | 85.2 | |
| S5: S4+Spatially decoupled | 8 min 6 s | 7 h 18 min 7 s | 89.9 | 144.2 | |
| S6: S5+Steady-state model | 2 min 9 s | 1 h 25 min 29 s | 65.3 | 74.8 | 599.3 |
| Model Description | Disadvantage |
|---|---|
| S1: R-radiation | Conservative prediction, risk of false positives |
| S2:R-convection | Conservative prediction, risk of false positives |
| S3: R-(radiation, convection, temp. dependent) | Conservative prediction, risk of false positives |
| S4: S3+Temporally decoupled | Thermal history lost, cannot capture gradual heat build-up |
| S5: S4+Spatially decoupled | Thermal history lost, cannot capture gradual heat build-up |
| S6: S5+Steady-state model | Qualitative indication only |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ranjan, R.; Ayas, C.; Langelaar, M.; van Keulen, F. Fast Detection of Heat Accumulation in Powder Bed Fusion Using Computationally Efficient Thermal Models. Materials 2020, 13, 4576. https://doi.org/10.3390/ma13204576
Ranjan R, Ayas C, Langelaar M, van Keulen F. Fast Detection of Heat Accumulation in Powder Bed Fusion Using Computationally Efficient Thermal Models. Materials. 2020; 13(20):4576. https://doi.org/10.3390/ma13204576
Chicago/Turabian StyleRanjan, Rajit, Can Ayas, Matthijs Langelaar, and Fred van Keulen. 2020. "Fast Detection of Heat Accumulation in Powder Bed Fusion Using Computationally Efficient Thermal Models" Materials 13, no. 20: 4576. https://doi.org/10.3390/ma13204576
APA StyleRanjan, R., Ayas, C., Langelaar, M., & van Keulen, F. (2020). Fast Detection of Heat Accumulation in Powder Bed Fusion Using Computationally Efficient Thermal Models. Materials, 13(20), 4576. https://doi.org/10.3390/ma13204576





