Printed PEDOT:PSS Trilayer: Mechanism Evaluation and Application in Energy Storage
Abstract
1. Introduction
2. Material and Methods
2.1. Formation of the IPN and Assembly of the PP–IPN
2.2. Characterization of PP–IPN
2.3. Electroactivity of the Trilayers
3. Results and Discussions
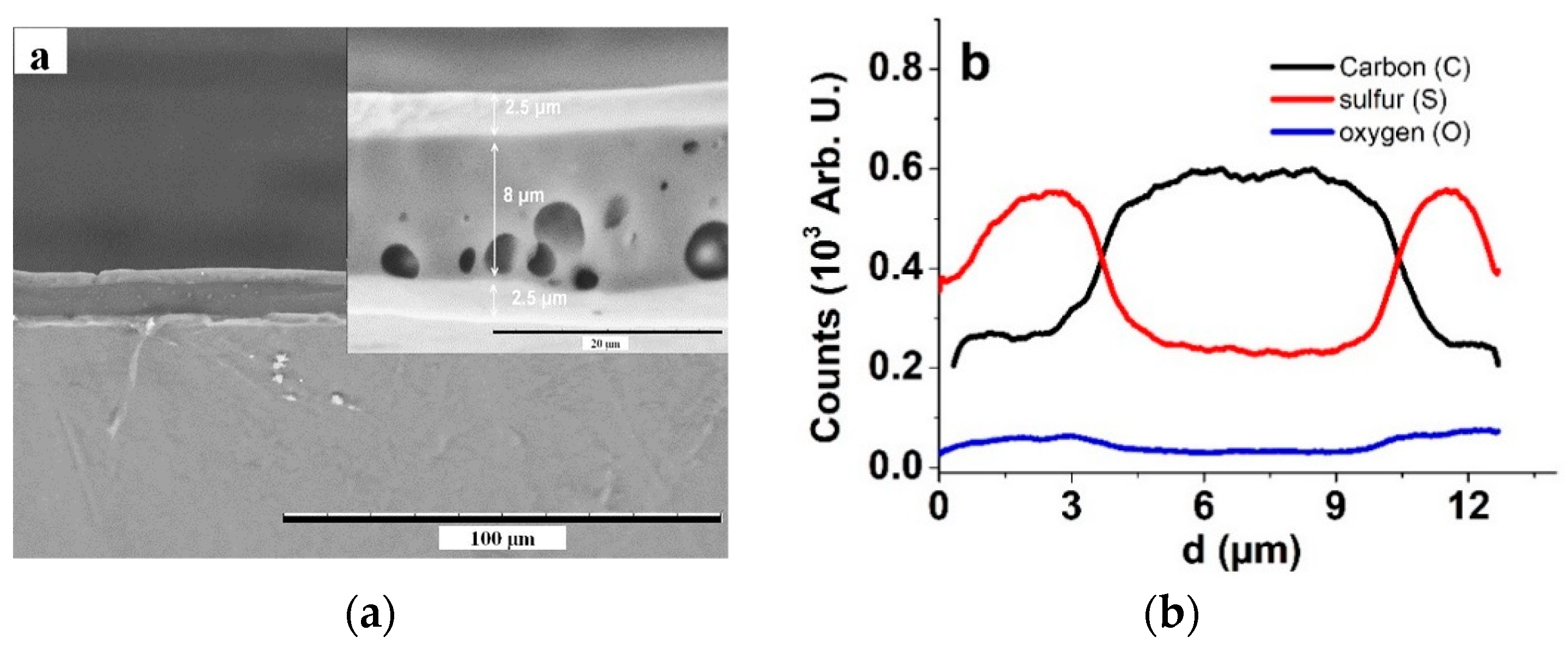
3.1. Characterization of PP–IPN Trilayers
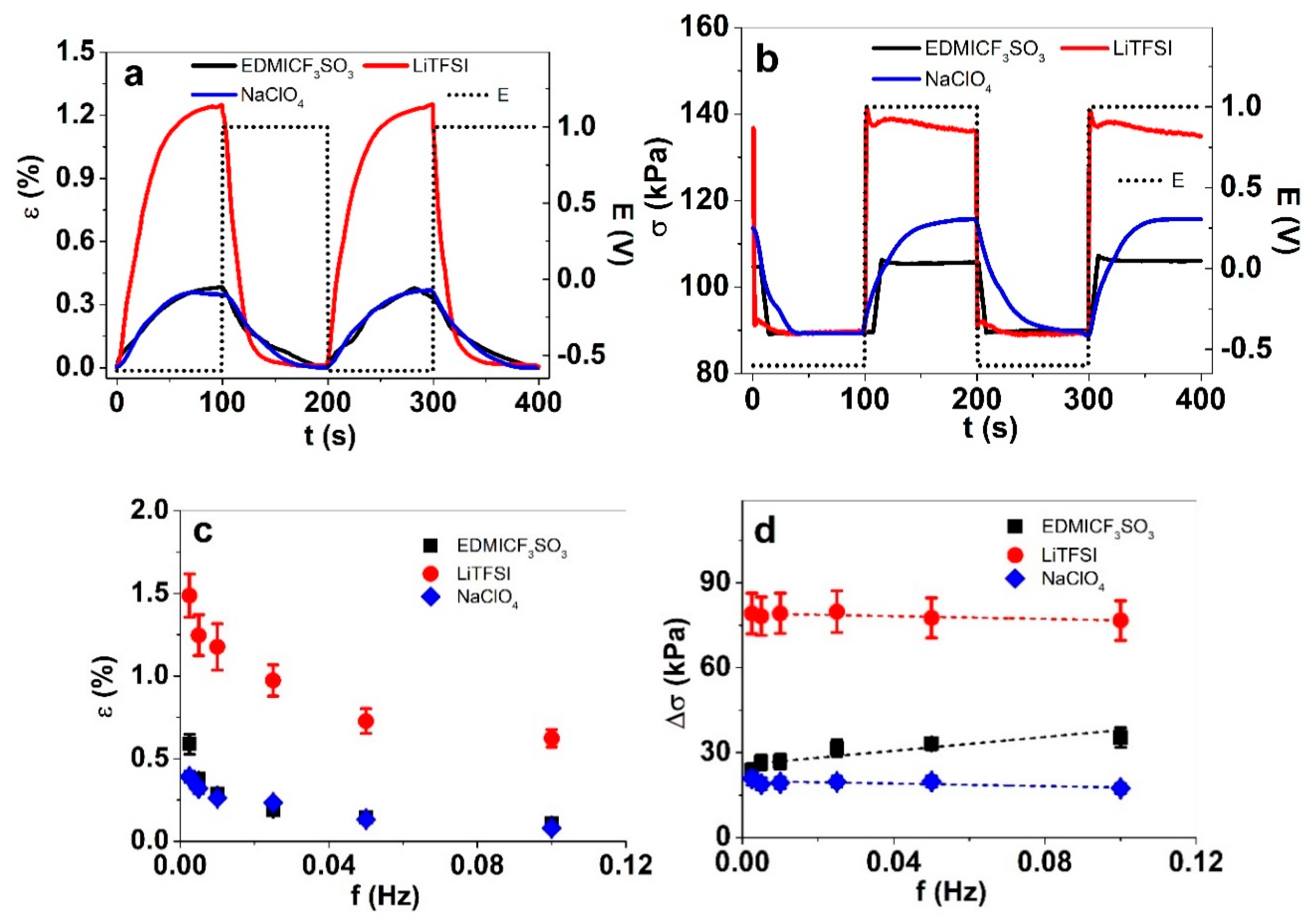
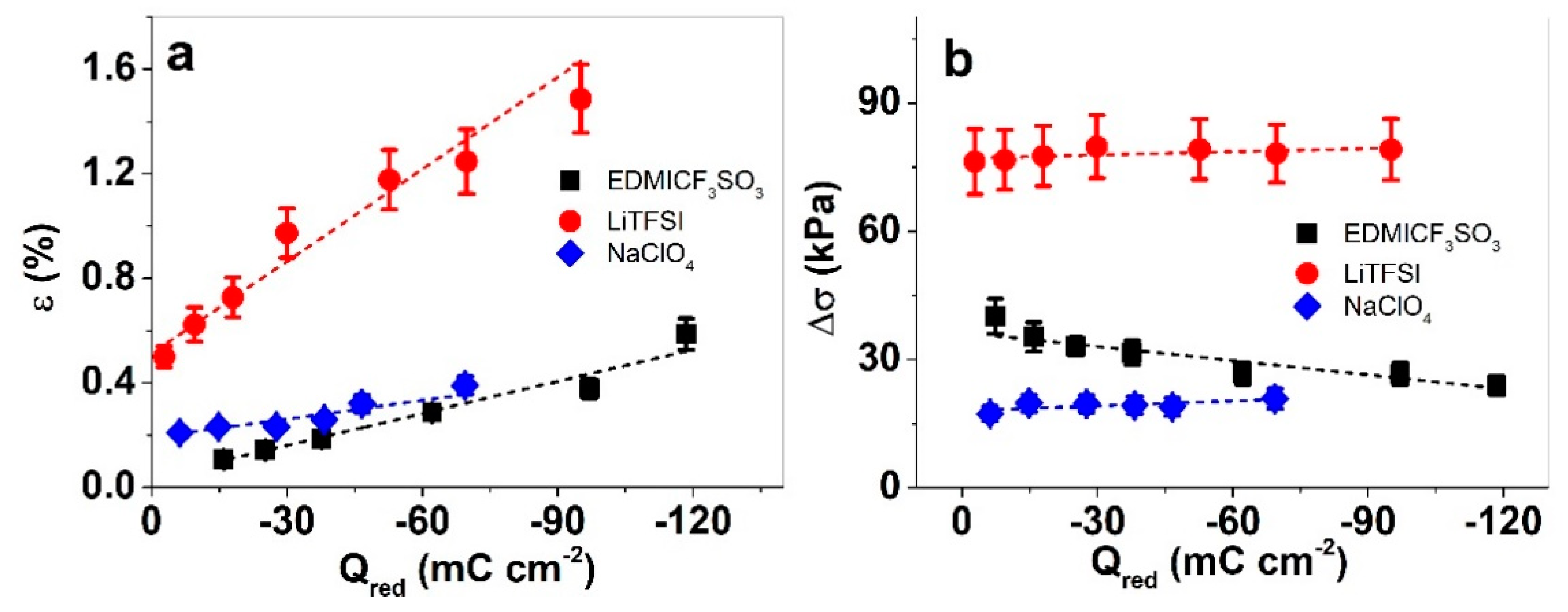
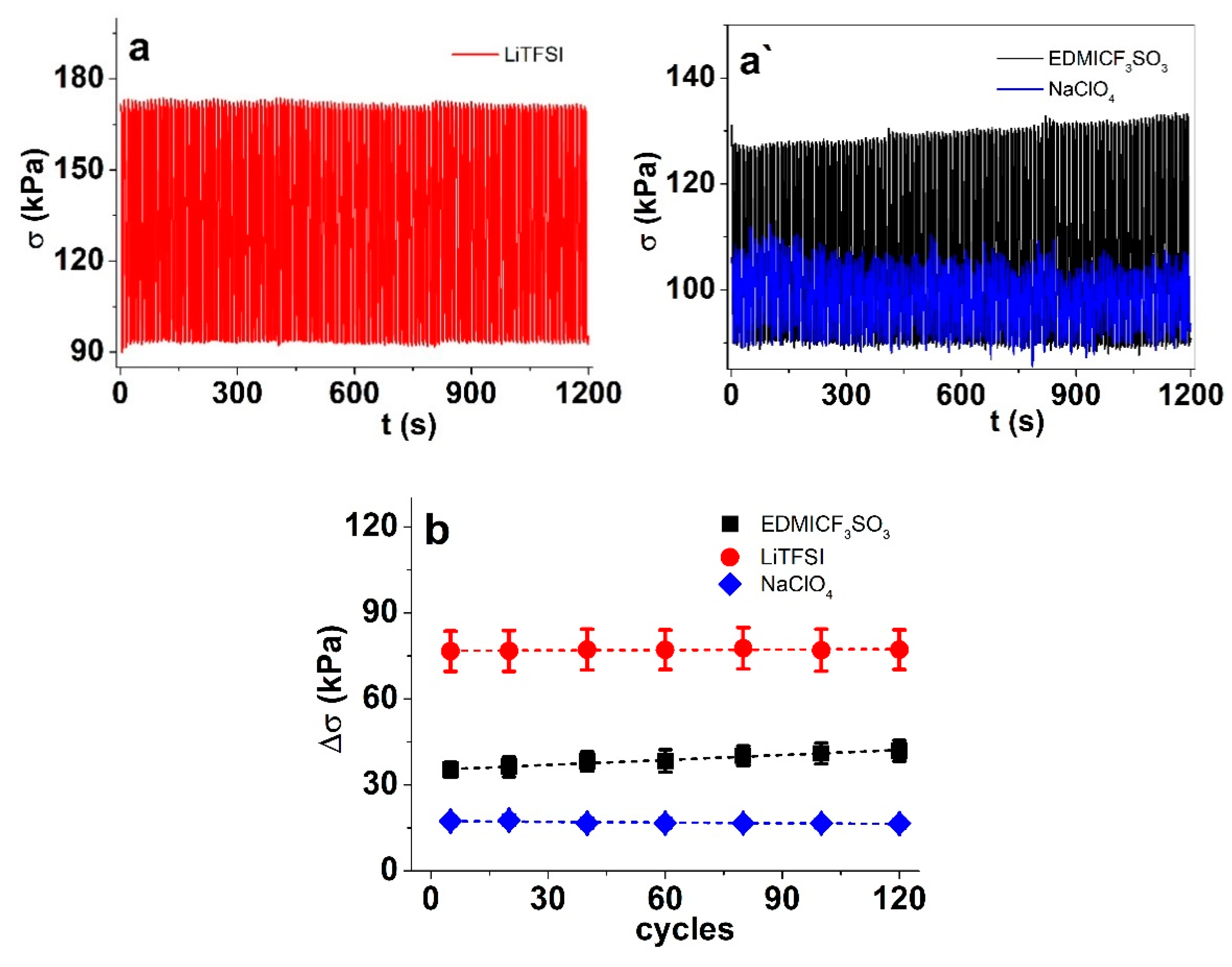
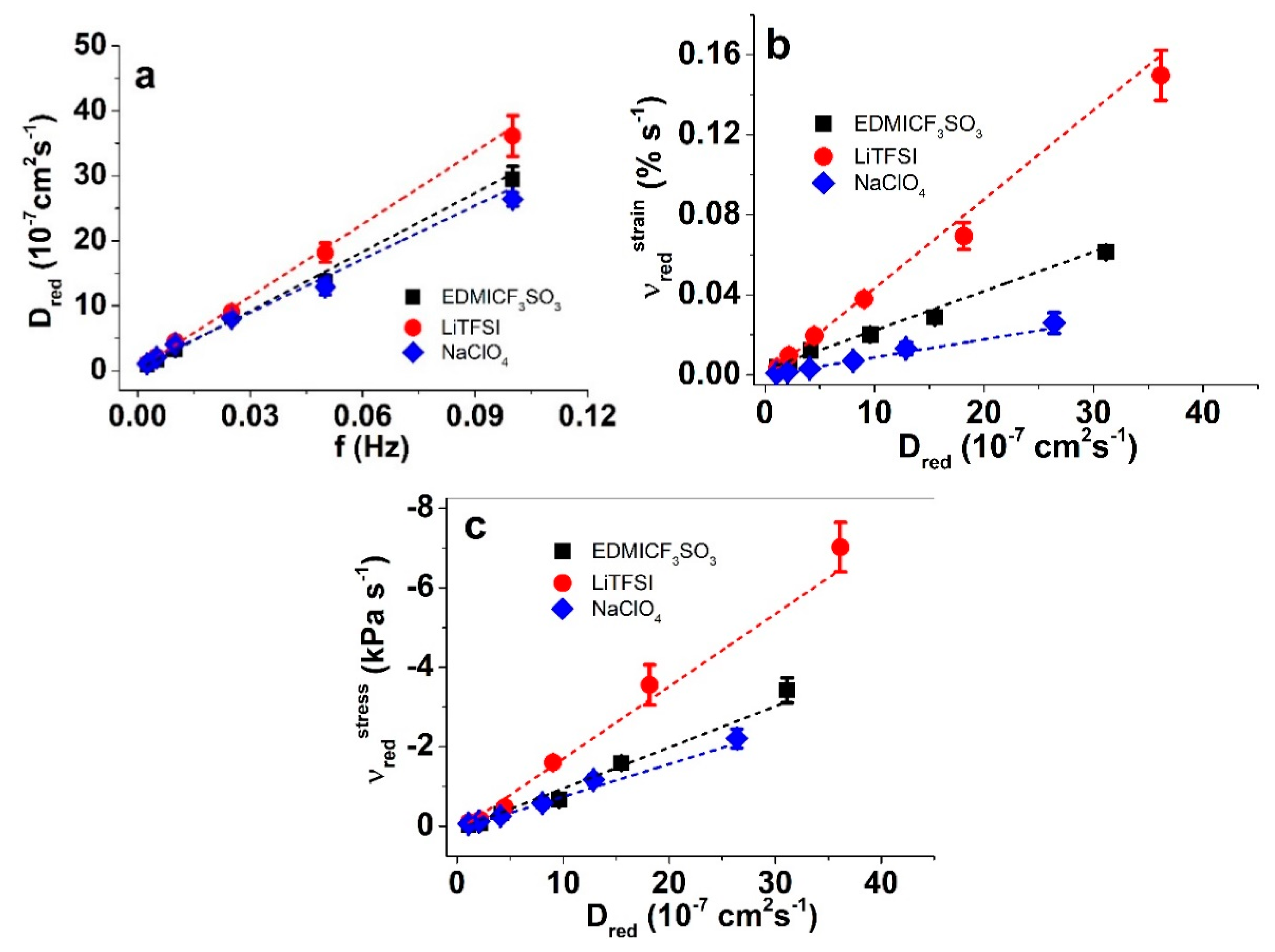
3.2. Isotonic and Isometric ECMD Measurements of PP–IPN Trilayers
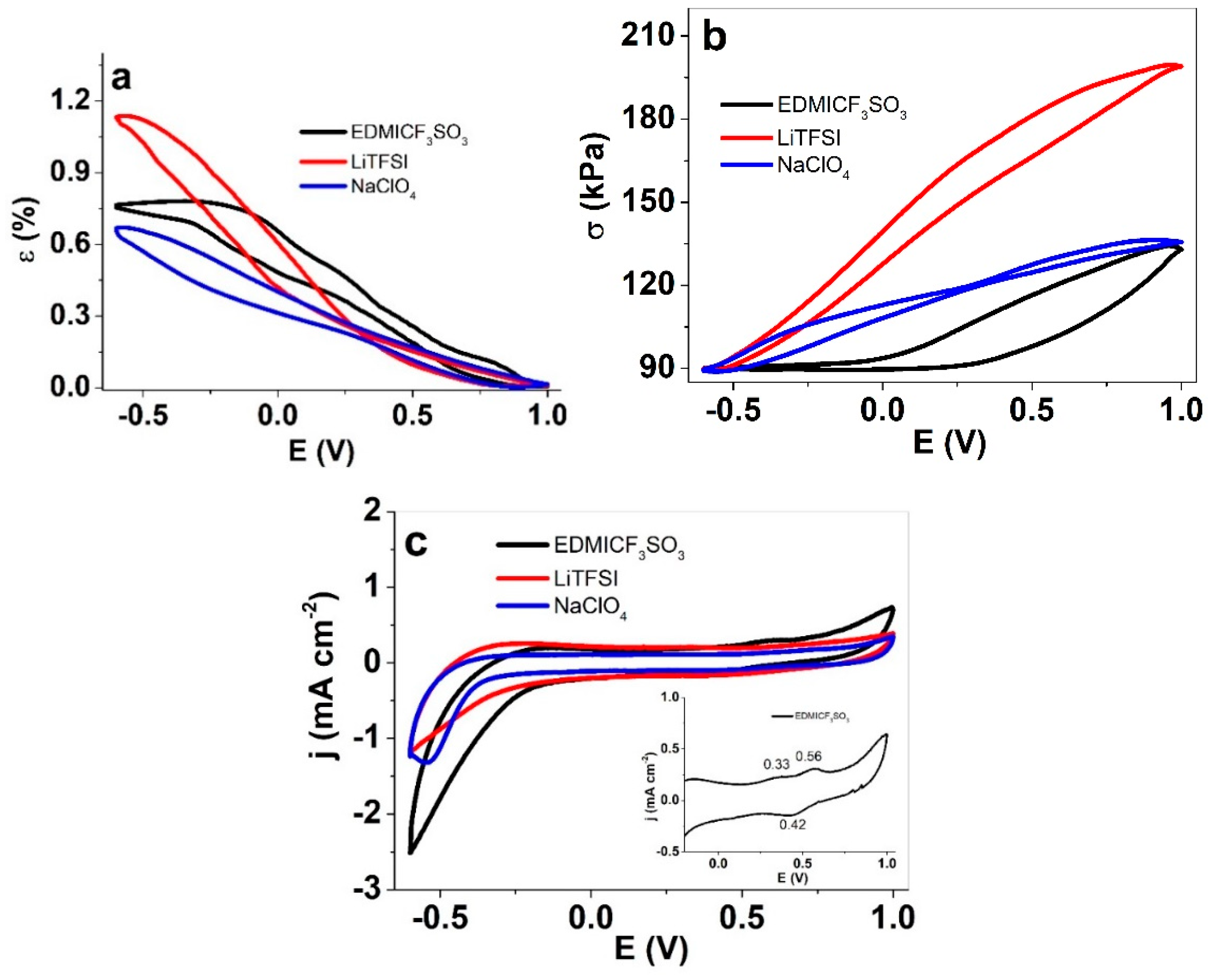
3.3. Cyclic Voltammetry Response
3.4. Square Wave Potential Step Response
3.5. Specific Capacitance
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Saetia, K.; Schnorr, J.M.; Mannarino, M.M.; Kim, S.Y.; Rutledge, G.C.; Swager, T.M.; Hammond, P.T. Spray-layer-by-layer carbon nanotube/electrospun fiber electrodes for flexible chemiresistive sensor applications. Adv. Funct. Mater. 2014, 24, 492–502. [Google Scholar] [CrossRef]
- Simon, P.; Gogotsi, Y. Materials for electrochemical capacitors. Nat. Mater. 2008, 7, 845–854. [Google Scholar] [CrossRef]
- Nuramdhani, I.; Gokceoren, A.T.; Odhiambo, S.A.; De Mey, G.D.; Hertleer, C.; Van Langenhove, L. Electrochemical impedance analysis of a PEDOT:PSS-based textile energy storage device. Materials 2018, 11, 48. [Google Scholar] [CrossRef] [PubMed]
- Afzal, A.; Abuilaiwi, F.A.; Habib, A.; Awais, M.; Waje, S.B.; Atieh, M.A. Polypyrrole/carbon nanotube supercapacitorsTechnological advances and challenges. J. Power Sources 2017, 352, 174–186. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhang, F.; Tvingstedt, K.; Barrau, S.; Li, F.; Tian, W.; Inganäs, O. Investigation on polymer anode design for flexible polymer solar cells. Appl. Phys. Lett. 2008, 92, 92–94. [Google Scholar] [CrossRef]
- Wilson, S.A.; Jourdain, R.P.J.; Zhang, Q.; Dorey, R.A.; Bowen, C.R.; Willander, M.; Wahab, Q.U.; Al-hilli, S.M.; Nur, O.; Quandt, E.; et al. New materials for micro-scale sensors and actuators: An engineering review. Mater. Sci. Eng. R Rep. 2007, 56, 1–129. [Google Scholar] [CrossRef]
- Ryu, D.; Mongare, A. Corrugated photoactive thin films for flexible strain sensor. Materials 2018, 11, 1970. [Google Scholar] [CrossRef]
- Ballarin, B.; Fraleoni-Morgera, A.; Frascaro, D.; Marazzita, S.; Piana, C.; Setti, L. Thermal inkJet microdeposition of PEDOT:PSS on ITO-coated glass and characterization of the obtained film. Synth. Met. 2004, 146, 201–205. [Google Scholar] [CrossRef]
- Sun, K.; Zhang, S.; Li, P.; Xia, Y.; Zhang, X.; Du, D.; Isikgor, F.H.; Ouyang, J. Review on application of PEDOTs and PEDOT:PSS in energy conversion and storage devices. J. Mater. Sci. Mater. Electron. 2015, 26, 4438–4462. [Google Scholar] [CrossRef]
- Eom, S.H.; Senthilarasu, S.; Uthirakumar, P.; Yoon, S.C.; Lim, J.; Lee, C.; Lim, H.S.; Lee, J.; Lee, S.H. Polymer solar cells based on inkjet-printed PEDOT: PSS layer. Org. Electron. Mater. Phys. Chem. Appl. 2009, 10, 536–542. [Google Scholar]
- Vuorinen, T.; Niittynen, J.; Kankkunen, T.; Kraft, T.M.; Mäntysalo, M. Inkjet-printed graphene/PEDOT:PSS temperature sensors on a skin-conformable polyurethane substrate. Sci. Rep. 2016, 6, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Beaujuge, P.M.; Reynolds, J.R. Color control in pi-conjugated organic polymers for use in electrochromic devices. Chem. Rev. 2010, 110, 268–320. [Google Scholar] [CrossRef] [PubMed]
- Hong, W.; Almomani, A.; Chen, Y.; Jamshidi, R.; Montazami, R. Soft ionic electroactive polymer actuators with tunable non-linear angular deformation. Materials 2017, 10, 664. [Google Scholar] [CrossRef] [PubMed]
- Taccola, S.; Greco, F.; Sinibaldi, E.; Mondini, A.; Mazzolai, B.; Mattoli, V. Soft actuators: Toward a new generation of electrically controllable hygromorphic soft actuators. Adv. Mater. 2015, 27, 1637. [Google Scholar] [CrossRef]
- Põldsalu, I.; Rohtlaid, K.; Nguyen, T.M.G.; Plesse, C.; Vidal, F.; Khorram, M.S.; Peikolainen, A.L.; Tamm, T.; Kiefer, R. Thin ink-jet printed trilayer actuators composed of PEDOT: PSS on interpenetrating polymer networks. Sens. Actuators B Chem. 2018, 258, 1072–1079. [Google Scholar] [CrossRef]
- Baughman, R.H. Conducting polymer artificial muscles. Synth. Met. 1996, 78, 339–353. [Google Scholar] [CrossRef]
- Aphale, A.; Maisuria, K.; Mahapatra, M.K.; Santiago, A.; Singh, P.; Patra, P. Hybrid electrodes by in-situ integration of graphene and carbon-nanotubes in polypyrrole for supercapacitors. Sci. Rep. 2015, 5, 1–8. [Google Scholar] [CrossRef]
- Li, Y.; Tanigawa, R.; Okuzaki, H. Soft and flexible PEDOT/PSS films for applications to soft actuators. Smart Mater. Struct. 2014, 23, 074010–074018. [Google Scholar] [CrossRef]
- Harjo, M.; Kesküla, A.; Leemets, K.; Khorram, M.S.; Saar, R.; Järvekülg, M.; Tamm, T.; Kiefer, R. Polypyrrole coatings on gelatin fiber scaffolds: Material and electrochemical characterizations in organic and aqueous electrolyte. Synth. Met. 2017, 232, 25–30. [Google Scholar] [CrossRef]
- Plaado, M.; Kaasik, F.; Valner, R.; Lust, E.; Saar, R.; Saal, K.; Peikolainen, A.; Aabloo, A.; Kiefer, R. Electrochemical actuation of multiwall carbon nanotube fiber with embedded carbide-derived carbon particles. Carbon 2015, 94, 911–918. [Google Scholar] [CrossRef]
- Presser, V.; Heon, M.; Gogotsi, Y. Carbide-derived carbons—From porous networks to nanotubes and graphene. Adv. Funct. Mater. 2011, 21, 810–833. [Google Scholar] [CrossRef]
- Maziz, A.; Plesse, C.; Soyer, C.; Chevrot, C.; Teyssie, D.; Cattan, E.; Vidal, F. Demonstrating kHz frequency actuation for conducting polymer microactuators. Adv. Funct. Mater. 2014, 24, 4851–4859. [Google Scholar] [CrossRef]
- Harjo, M.; Tamm, T.; Anbarjafari, G.; Kiefer, R. Hardware and software development for isotonic strain and isometric stress measurements of linear ionic actuators. Polymers 2019, 11, 1054. [Google Scholar] [CrossRef] [PubMed]
- Otero, T.F.; Martinez, J.G. Activation energy for polypyrrole oxidation: Film thickness influence. J. Solid State Electrochem. 2011, 15, 1169–1178. [Google Scholar] [CrossRef]
- Põldsalu, I.; Harjo, M.; Tamm, T.; Uibu, M.; Peikolainen, A.L.; Kiefer, R. Inkjet-printed hybrid conducting polymer-activated carbon aerogel linear actuators driven in an organic electrolyte. Sens. Actuators B Chem. 2017, 250, 44–51. [Google Scholar] [CrossRef]
- Martinez, J.G.; Otero, T.F.; Jager, E.W.H. Effect of the electrolyte concentration and substrate on conducting polymer actuators. Langmuir 2014, 30, 3894–3904. [Google Scholar] [CrossRef] [PubMed]
- Tahhan, M.; Truong, V.T.; Spinks, G.M.; Wallace, G.G. Carbon nanotube and polyaniline composite actuators. Smart Mater. Struct. 2003, 12, 626–632. [Google Scholar] [CrossRef]
- Khadka, R.; Zondaka, Z.; Kesküla, A.; Safaei Khorram, M.; Thien Khanh, T.; Tamm, T.; Travas-Sejdic, J.; Kiefer, R.; Minh City, C. Influence of solvent on linear polypyrrole-polyethylene oxide actuators. J. Appl. Polym. Sci. 2018, 46831, 1–7. [Google Scholar] [CrossRef]
- Khuyen, N.Q.; Zondaka, Z.; Harjo, M.; Torop, J.; Tamm, T.; Kiefer, R. Comparative analysis of fluorinated anions for polypyrrole linear actuator electrolytes. Polymers 2019, 11, 849. [Google Scholar] [CrossRef]
- Zondaka, Z.; Harjo, M.; Khan, A.; Khanh, T.T.; Tamm, T.; Kiefer, R. Optimal phosphotungstinate concentration for polypyrrole linear actuation and energy storage. Multifunct. Mater. 2018, 1, 14003. [Google Scholar] [CrossRef]
- Tamm, J.; Raudsepp, T.; Marandi, M.; Tamm, T. Electrochemical properties of the polypyrrole films doped with benzenesulfonate. Synth. Met. 2007, 157, 66–73. [Google Scholar] [CrossRef]
- Kondo, K.; Sano, M.; Hiwara, A.; Omi, T.; Fujita, M.; Kuwae, A.; Iida, M.; Mogi, K.; Yokoyama, H. Conductivity and solvation of Li + ions of LiPF6 in propylene carbonate solutions. J. Phys. Chem. B 2000, 104, 5040–5044. [Google Scholar] [CrossRef]
- Brooksby, P.A.; Fawcett, W.R. Infrared (attenuated total reflection) study of propylene carbonate solutions containing lithium and sodium perchlorate. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2006, 64, 372–382. [Google Scholar] [CrossRef] [PubMed]
- Temmer, R.; Maziz, A.; Plesse, C.; Aabloo, A.; Vidal, F.; Tamm, T. In search of better electroactive polymer actuator materials: PPy versus PEDOT versus PEDOT-PPy composites. Smart Mater. Struct. 2013, 22, 104006. [Google Scholar] [CrossRef]
- Valero, L.; Otero, T.F.; Martinez, J.G.; Martínez, J.G. Exchanged cations and water during reactions in polypyrrole macroions from artificial muscles. ChemPhysChem 2014, 15, 293–301. [Google Scholar] [CrossRef]
- Terasawa, N.; Asaka, K. High-Performance PEDOT:PSS/Single-walled carbon nanotube/ionic liquid actuators combining electrostatic double-layer and faradaic capacitors. Langmuir 2016, 32, 7210–7218. [Google Scholar] [CrossRef]

| Electrolytes in PC | Before Actuation (S cm−1) | After Actuation (S cm−1) | Swelling Rate After Actuation (%) |
|---|---|---|---|
| EDMICF3SO3 | 104 ± 8 | 114 ± 9 | 11 ± 0.8 |
| LiTFSI | 87 ± 7 | 93 ± 8 | 15 ± 1.1 |
| NaClO4 | 63 ± 4 | 54 ± 3 | 7 ± 0.6 |
| PP–IPN Trilayer Electrolytes in PC | Elastic Modulus before Actuation (kPa) | Elastic Modulus after Actuation (kPa) |
|---|---|---|
| EDMICF3SO3 | 26.7 ± 1.6 | 98.4 ± 4.8 |
| LiTFSI | 17.8 ± 1.1 | 49.0 ± 3.2 |
| NaClO4 | 22.3 ± 1.1 | 106.9 ± 5.5 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Põldsalu, I.; Rohtlaid, K.; Plesse, C.; Vidal, F.; Nguyen, N.T.; Peikolainen, A.-L.; Tamm, T.; Kiefer, R. Printed PEDOT:PSS Trilayer: Mechanism Evaluation and Application in Energy Storage. Materials 2020, 13, 491. https://doi.org/10.3390/ma13020491
Põldsalu I, Rohtlaid K, Plesse C, Vidal F, Nguyen NT, Peikolainen A-L, Tamm T, Kiefer R. Printed PEDOT:PSS Trilayer: Mechanism Evaluation and Application in Energy Storage. Materials. 2020; 13(2):491. https://doi.org/10.3390/ma13020491
Chicago/Turabian StylePõldsalu, Inga, Kätlin Rohtlaid, Cedric Plesse, Frédéric Vidal, Ngoc Tuan Nguyen, Anna-Liisa Peikolainen, Tarmo Tamm, and Rudolf Kiefer. 2020. "Printed PEDOT:PSS Trilayer: Mechanism Evaluation and Application in Energy Storage" Materials 13, no. 2: 491. https://doi.org/10.3390/ma13020491
APA StylePõldsalu, I., Rohtlaid, K., Plesse, C., Vidal, F., Nguyen, N. T., Peikolainen, A.-L., Tamm, T., & Kiefer, R. (2020). Printed PEDOT:PSS Trilayer: Mechanism Evaluation and Application in Energy Storage. Materials, 13(2), 491. https://doi.org/10.3390/ma13020491






