Universal Tool for Single-Photon Circuits: Quantum Router Design
Abstract
1. Introduction
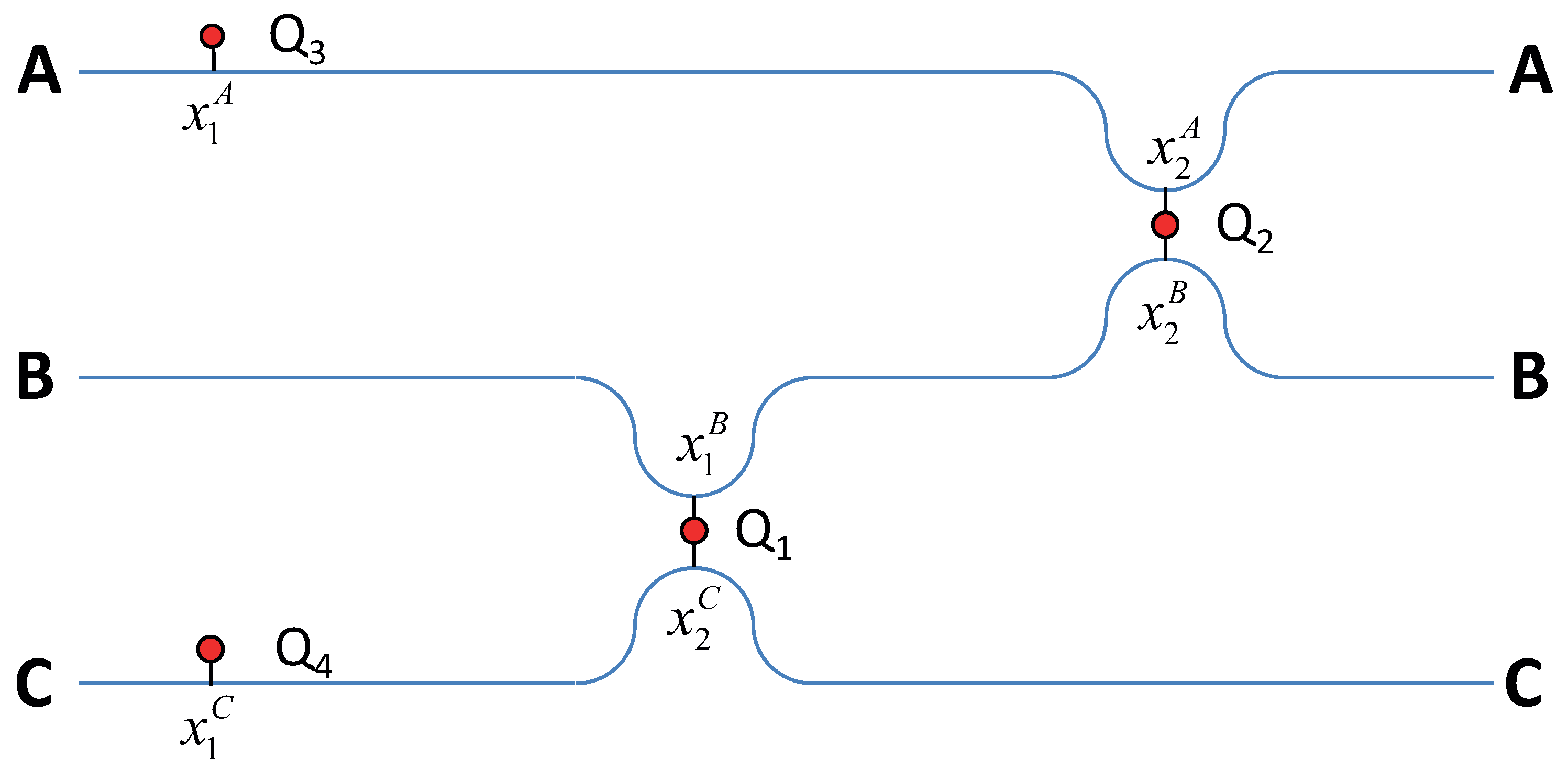
2. Quantum Router
3. Results
3.1. The System and Method Description
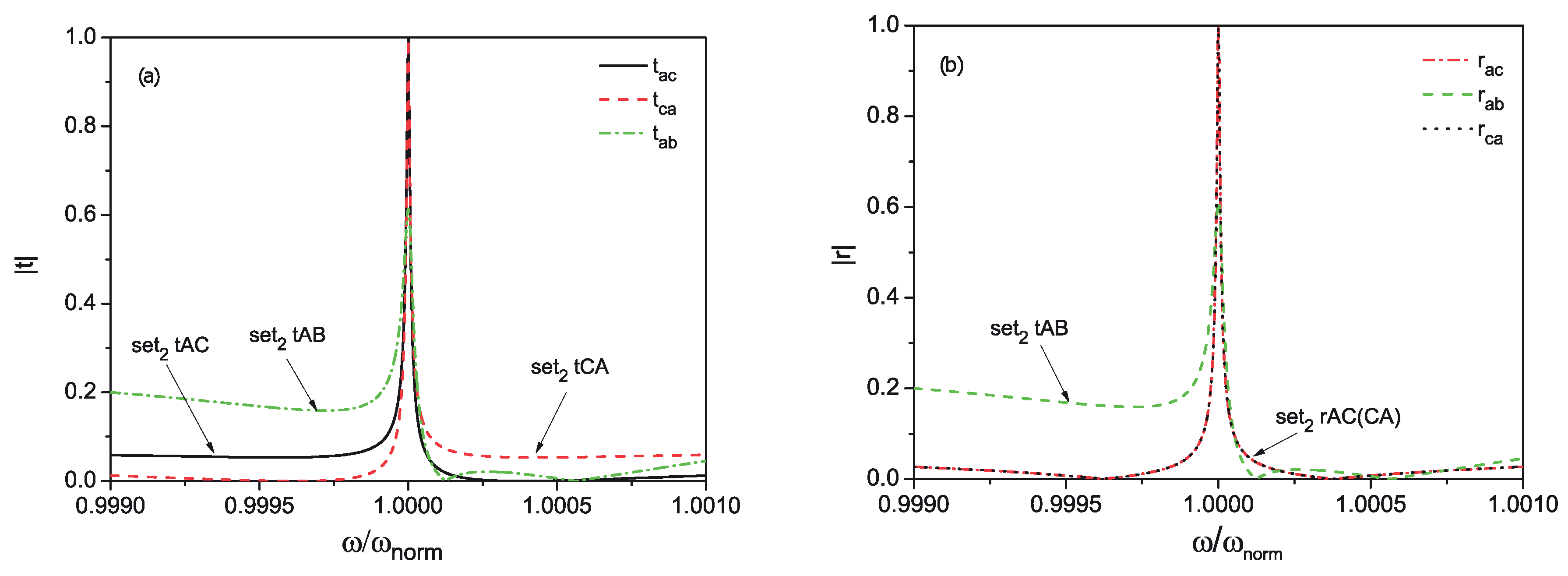
3.2. Solutions and Transmission Probabilities
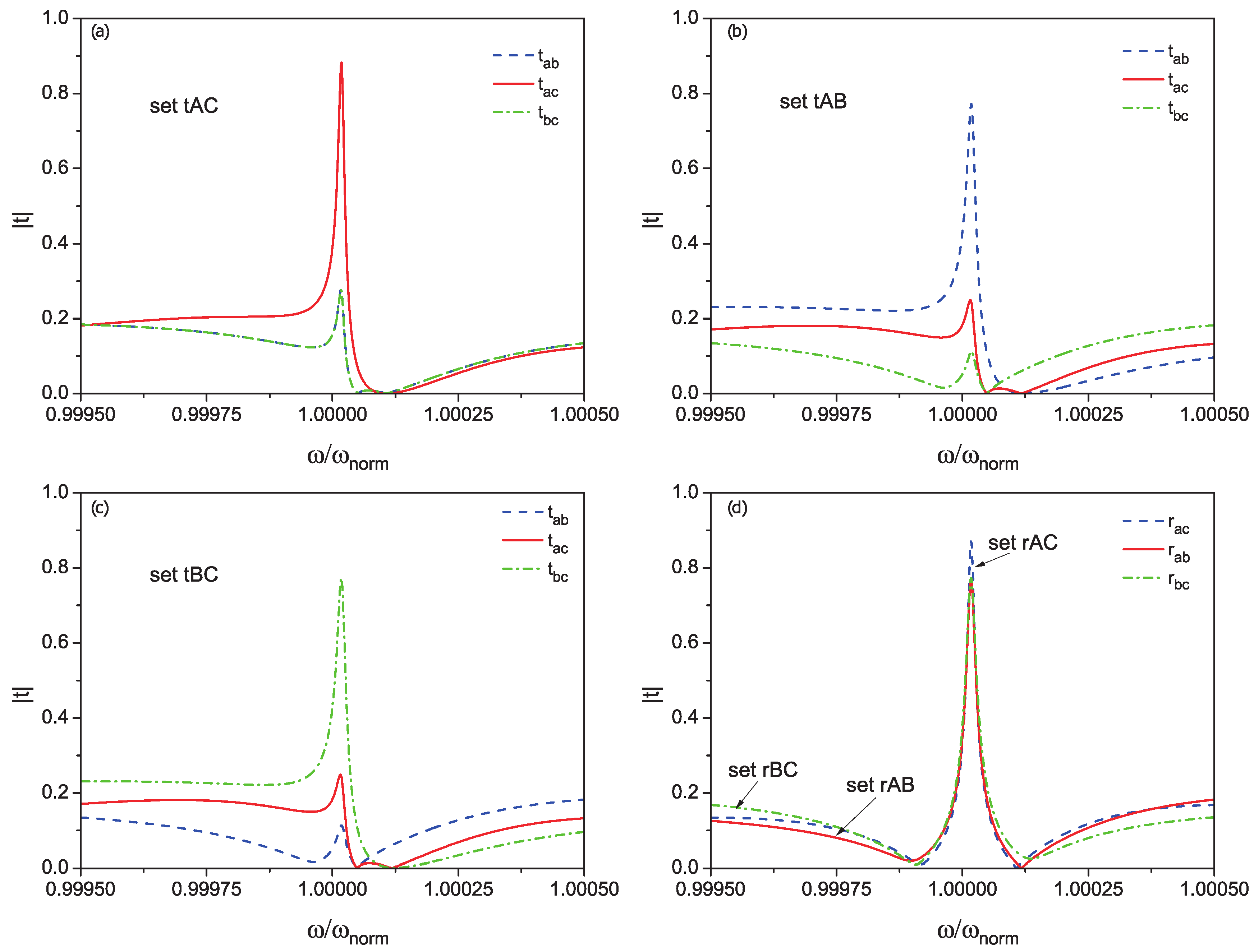
4. Simulations and Functionality of the Router
- -
- central waveguide should introduce a minimum of phase increasing because the signal between and has minimal opportunity to escape in comparison to qubits and , and we should not provide strong interference conditions in this region (for flexibility)
- -
- the couplings of qubits and to the central waveguide should be greater than other couplings because the waveguide B provides intermediate interaction between A and C waveguides.
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Conditions of One-Dimensionality

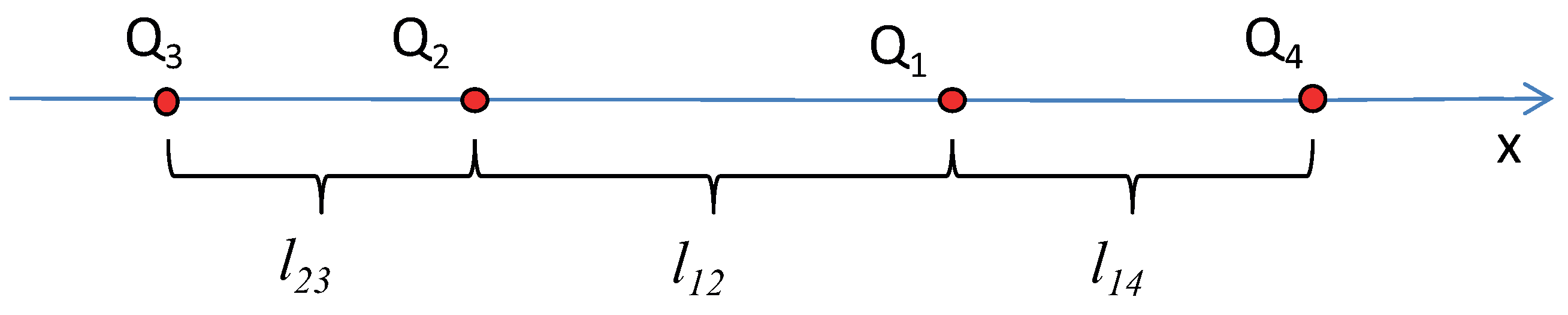
| distance between and node | |
|---|---|
| distance between and node | |
| distance between and node | |
| distance between nodes and | |
| distance between and node | |
| distance between and node | |
| distance between and node |
Appendix B. Scattering Parameters
Appendix C. Inverse Matrix R
References
- Kimble, H.J. The Quantum Internet. Nature 2008, 10, 1023. [Google Scholar] [CrossRef] [PubMed]
- Baust, A.; Hoffmann, E.; Haeberlein, M.; Schwarz, M.J.; Eder, P.; Goetz, J.; Wulschner, F.; Xie, E.; Zhong, L.; Quijandría, F.; et al. Ultrastrong coupling in two-resonator circuit QED. Phys. Rev. B 2016, 104, 214501. [Google Scholar] [CrossRef]
- Nataf, P.; Ciuti, C. Vacuum Degeneracy of a Circuit QED System in the Ultrastrong Coupling Regime. Phys. Rev. Lett. 2010, 104, 023601. [Google Scholar] [CrossRef] [PubMed]
- Ashhab, S.; Nori, F. Qubit-oscillator systems in the ultrastrong-coupling regime and their potential for preparing nonclassical states. Phys. Rev. A 2010, 81, 042311. [Google Scholar] [CrossRef]
- Beaudoin, F.; Gambetta, J.M.; Blais, A. Dissipation and ultrastrong coupling in circuit QED. Phys. Rev. A 2011, 84, 043832. [Google Scholar] [CrossRef]
- Yan, W.; Fan, H. Single-photon quantum router with multiple output ports. Sci. Rep. 2014, 4, 4820. [Google Scholar] [CrossRef]
- Xia, K.; Twamley, J. All-Optical Switching and Router via the Direct Quantum Control of Coupling between Cavity Modes. Phys. Rev. X 2013, 3, 031013. [Google Scholar] [CrossRef]
- Shomroni, I.; Rosenblum, S.; Lovsky, Y.; Bechler, O.; Guendelman, G.; Dayan, B. All-Optical Routing of Single Photons by a One-Atom Switch Controlled by a Single Photon. Science 2014, 345, 903–906. [Google Scholar] [CrossRef]
- Dayan, B.; Parkins, A.S.; Aoki, T.; Ostby, E.P.; Vahala, K.J.; Kimble, H.J. A Photon Turnstile Dynamically Regulated by One Atom. Science 2008, 319, 1062–1065. [Google Scholar] [CrossRef]
- Aoki, T.; Parkins, A.S.; Alton, D.J.; Regal, C.A.; Dayan, B.; Ostby, E.; Vahala, K.J.; Kimble, H.J. Efficient Routing of Single Photons by One Atom and a Microtoroidal Cavity. Phys. Rev. Lett. 2009, 102, 083601. [Google Scholar] [CrossRef]
- Cook, R.; Schuster, D.I.; Cleland, A.N.; Jacobs, K. Input output theory for superconducting and photonic circuits that contain weak retroreflections and other weak pseudocavities. Phys. Rev. A 2018, 98, 013801. [Google Scholar] [CrossRef]
- Feshbach, H. A unified theory of nuclear reactions. II. Ann. Phys. 1962, 19, 287. [Google Scholar] [CrossRef]
- Auerbach, N.; Zelevinsky, V. Super-Radiant Dynamics, Doorways, and Resonances in Nuclei and Other Open Mesoscopic Systems. Rep. Prog. Phys. 2011, 74, 10. [Google Scholar] [CrossRef]
- Greenberg, Y.S.; Shtygashev, A.A. Non-Hermitian Hamiltonian approach to the microwave transmission through a one-dimensional qubit chain. Phys. Rev. A 2015, 92, 063835. [Google Scholar] [CrossRef]
- Greenberg, Y.S.; Sultanov, A.N. Mollow triplet through pump-probe single-photon spectroscopy of artificial atoms. Phys. Rev. A 2017, 95, 053840. [Google Scholar] [CrossRef]
- Sultanov, A.N.; Greenberg, Y.S. Transfer of excited state between two qubits in an open waveguide. Low Temp. Phys. 2018, 44, 203. [Google Scholar] [CrossRef]
- Sultanov, A.N.; Karpov, D.S.; Greenberg, Y.S.; Shevchenko, S.N.; Shtygashev, A.A. Scattering of a single photon on a two-qubit structure with resonators. Low Temp. Phys. 2017, 43, 799. [Google Scholar] [CrossRef]
- Sultanov, A.N.; Greenberg, Y.S. Effect of the qubit relaxation on transport properties of microwave photons. Phys. Solid State 2017, 59, 2103–2109. [Google Scholar] [CrossRef]
- Greenberg, Y.S.; Sultanov, A.N. Influence of the nonradiative decay of qubits into a common channel on the transport properties of microwave photons. JETP Lett. 2017, 106, 406–410. [Google Scholar] [CrossRef][Green Version]
- Lemr, K.; Bartkiewicz, K.; Cernoch, A.; Soubusta, J. Resource-efficient linear-optical quantum router. Phys. Rev. A 2013, 87, 062333. [Google Scholar] [CrossRef]
- Agarwal, G.S.; Huang, S. Optomechanical systems as single-photon routers. Phys. Rev. A 2012, 85, 021801. [Google Scholar] [CrossRef]
- Lu, J.; Zhou, L.; Kuang, L.; Nori, F. Single-photon router Coherent control of multichannel scattering for single photons with quantum interferences. Phys. Rev. A 2014, 89, 013805. [Google Scholar] [CrossRef]
- Cirac, J.I.; Zoller, P.; Kimble, H.J.; Mabuchi, H. Quantum State Transfer and Entanglement Distribution among Distant Nodesin a Quantum Network. Phys. Rev. Lett. 1997, 78, 16. [Google Scholar] [CrossRef]
- Bermel, P.; Rodriguez, A.; Johnson, S.G.; Joannopoulos, J.D.D.; Soljačić, M. Single-photon all-optical switching using waveguide-cavity quantum electrodynamics. Phys. Rev. A 2006, 74, 043818. [Google Scholar] [CrossRef]
- Chen, X.-Y.; Zhang, F.-Y.; Li, C. Single-photon quantum router by two distant artificial atoms. J. Opt. Soc. Am. B 2016, 33, 4. [Google Scholar] [CrossRef]
- Zhou, L.; Yang, L.; Li, Y.; Sun, C.P. Quantum Routing of Single Photons with a Cyclic Three-Level System. Phys. Rev. Lett. 2013, 111, 103604. [Google Scholar] [CrossRef]
- Shapiro, J.H.; Wong, F.N. On-demand single-photon generation using a modular array of parametric downconverters with electro-optic polarization controls. Opt. Lett. 2007, 32, 2698. [Google Scholar] [CrossRef] [PubMed]
- Chang, D.E.; Sorensen, A.S.; Demler, E.A.; Lukin, M.D. A single-photon transistor using nano-scale surface plasmons. Nat. Phys. 2007, 3, 807–812. [Google Scholar] [CrossRef]
- Keil, R.; Heinrich, M.; Dreisow, F.; Pertsch, T.; Tunnermann, A.; Nolte, S.; Christidoulides, D.N.; Szameit, A. All-optical routing and switching for three-dimensional photonic circuitry. Sci. Rep. 2011, 1, 94. [Google Scholar] [CrossRef] [PubMed]
- Hoi, I.; Wilson, C.M.; Johansson, G.; Palomaki, T.; Peropadre, B.; Delsing, P. Demonstration of a Single-Photon Router in the Microwave Regime. Phys. Rev. Lett. 2011, 107, 073601. [Google Scholar] [CrossRef]
- Zhou, L.; Gong, Z.R.; Liu, Y.; Sun, C.P.; Nori, F. Controllable Scattering of a single photon inside a one-dimensional resonator waveguide. Phys. Rev. Lett. 2008, 101, 100501. [Google Scholar] [CrossRef] [PubMed]
- Longo, P.; Schmitteckert, P.; Busch, K. Few-Photon Transport in Low-Dimensional Systems: Interaction- Induced Radiation Trapping. Phys. Rev. Lett. 2010, 104, 023602. [Google Scholar] [CrossRef] [PubMed]
- Gonsalez-Ballestero, C.; Moreno, E.; Garcia-Vidal, F.J.; Gonsalez-Tudela, A. Nonreciprocal few-photon routing schemes based on chiral waveguide-emitter couplings. Phys. Rev. A 2016, 94, 063817. [Google Scholar] [CrossRef]
- Gu, X.; Kockum, A.F.; Miranowicz, A.; Liu, Y.X.; Nori, F. Microwave photonics with superconducting quantum circuits. Phys. Rep. 2017, 718–719, 1–102. [Google Scholar] [CrossRef]
- Astafiev, O.; Zagoskin, A.M.; Abdumalikov, A.A., Jr.; Pashkin, Y.A.; Yamamoto, T.; Inomata, K.; Nakamura, Y.; Tsai, J.S. Resonance Fluorescence of a Single Artificial Atom. Science 2010, 327, 840–843. [Google Scholar] [CrossRef] [PubMed]
- Konyk, W.; Gea-Banacloche, J. One- and two-photon scattering by two atoms in a waveguide. Phys. Rev. A 2017, 96, 063826. [Google Scholar] [CrossRef]
- Zheng, H.; Baranger, H.U. Persistent Quantum Beats and Long-Distance Entanglement from Waveguide-Mediated Interactions. Phys. Rev. Lett. 2013, 110, 113601. [Google Scholar] [CrossRef]
- Simons, R.N. Coplanar Waveguide Circuits, Components, and Systems; John Wiley & Sons: New York, NY, USA, 2001. [Google Scholar]
- Paauw, F.G.; Fedorov, A.; Harmans, C.J.P.M.; Mooij, J.E. Tuning the Gap of a Superconducting Flux Qubit. Phys. Rev. Lett. 2009, 102, 090501. [Google Scholar] [CrossRef]
- Castellano, M.G.; Chiarello, F.; Torrioli, G.; Carelli, P. Static flux bias of a flux qubit using persistent current trapping. Supercond. Sci. Technol. 2006, 19, 11. [Google Scholar] [CrossRef][Green Version]
- Robertson, T.L.; Plourde, B.L.T.; Reichardt, P.A.; Hime, T.; Wu, C.-E.; Clarke, J. Quantum theory of three-junction flux qubit with non-negligible loop inductance: Towards scalability. Phys. Rev. B 2006, 73, 1745256. [Google Scholar] [CrossRef]
- Casparis, L.; Connolly, M.R.; Kjaergaard, M.; Pearson, N.J.; Kringhoj, A.; Larsen, T.W.; Kuemmeth, F.; Wang, T.; Thomas, C.; Gronin, S.; et al. Superconducting gatemon qubit based on a proximitized two-dimensional electron gas. Nat. Nanotechnol. 2018, 13, 915. [Google Scholar] [CrossRef] [PubMed]

| , MHz | , MHz | , MHz | , MHz | |
|---|---|---|---|---|
| , MHz | , MHz | , MHz | , MHz | |
|---|---|---|---|---|
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sultanov, A.; Greenberg, Y.; Mutsenik, E.; Pitsun, D.; Il’ichev, E. Universal Tool for Single-Photon Circuits: Quantum Router Design. Materials 2020, 13, 319. https://doi.org/10.3390/ma13020319
Sultanov A, Greenberg Y, Mutsenik E, Pitsun D, Il’ichev E. Universal Tool for Single-Photon Circuits: Quantum Router Design. Materials. 2020; 13(2):319. https://doi.org/10.3390/ma13020319
Chicago/Turabian StyleSultanov, Aydar, Yakov Greenberg, Evgeniya Mutsenik, Dmitry Pitsun, and Evgeni Il’ichev. 2020. "Universal Tool for Single-Photon Circuits: Quantum Router Design" Materials 13, no. 2: 319. https://doi.org/10.3390/ma13020319
APA StyleSultanov, A., Greenberg, Y., Mutsenik, E., Pitsun, D., & Il’ichev, E. (2020). Universal Tool for Single-Photon Circuits: Quantum Router Design. Materials, 13(2), 319. https://doi.org/10.3390/ma13020319




