Heat Transfer Through Insulating Glass Units Subjected to Climatic Loads
Abstract
1. Introduction
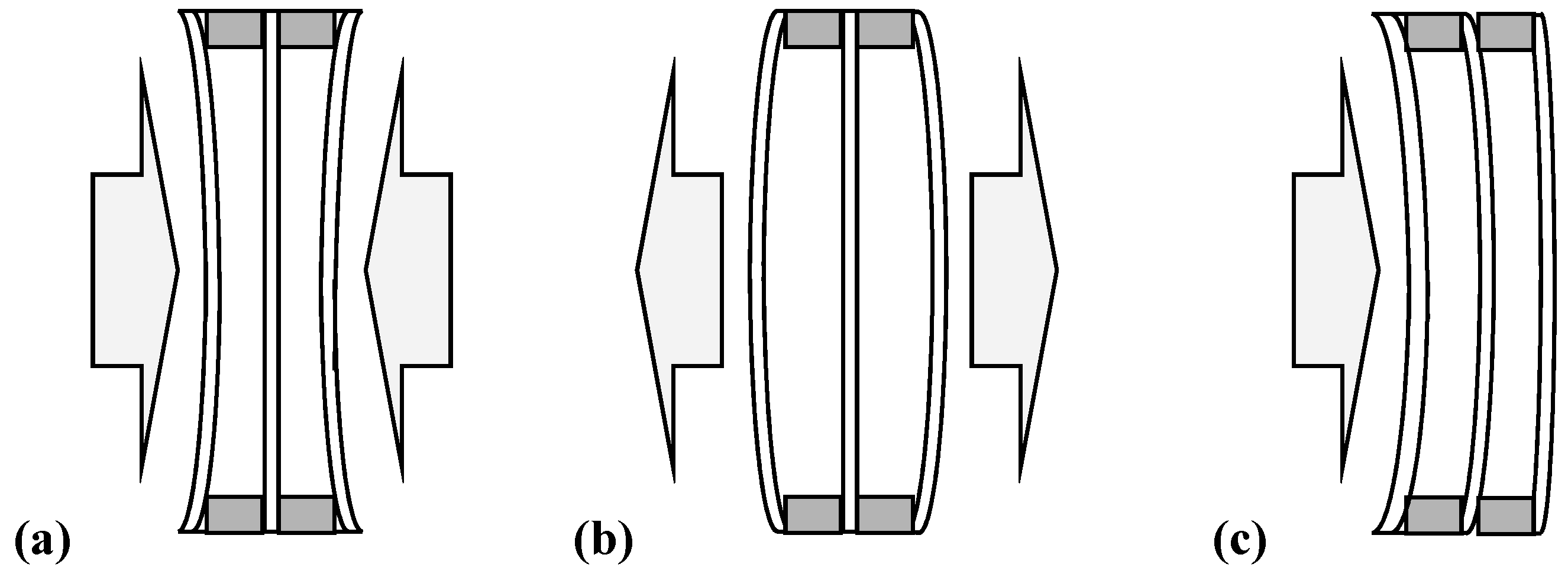
2. Methodology for the Calculation of Static Quantities in IGUs
- p0, T0, v0—initial gap gas parameters: pressure [kPa], temperature [K], volume [m3], obtained in the production process,
- pop, Top, vop—operating parameters—analogously.
- d—is the glass pane thickness [m],
- E—is the Young’s modulus of glass [kPa],
- μ—is the Poisson’s ratio [-].
- αv—is the proportionality factor, [m5/kN].
- pa—current atmospheric pressure [kPa],
- qz,ex, qz,in—load per area from outer factors, primarily wind [kN/m2], almost always qz,in = 0.
- for a double-glazed IGU
- for a triple-glazed IGU
3. Materials and Methods
- hr—is the thermal conductance by radiation [W/(m2·K)],
- hg—is the thermal conductance of gas (by conduction and convection) [W/(m2·K)].
- λg—is the thermal conductivity of gas [W/(m·K)],
- s—is the gas gap thickness [m],
- Nu—is the Nusselt number [-],
- σ—is the Boltzmann constant 5.6693 × 10−8 W/(m2·K4)
- Tm—is the average temperature of both surfaces delimiting the gap [K],
- εsur1, εsur2—are the emissivity of surfaces delimiting the gap [-].
- the type of gas; the calculation was based on the use of argon,
- location in the structure; the calculations assume a horizontal position, in units situated horizontally or diagonally convection increases.
- increasing the temperature difference on the surfaces of the glass panes limiting the gap affects the increase in convection,
- convection also increases when the average gas temperature in the gap increases.
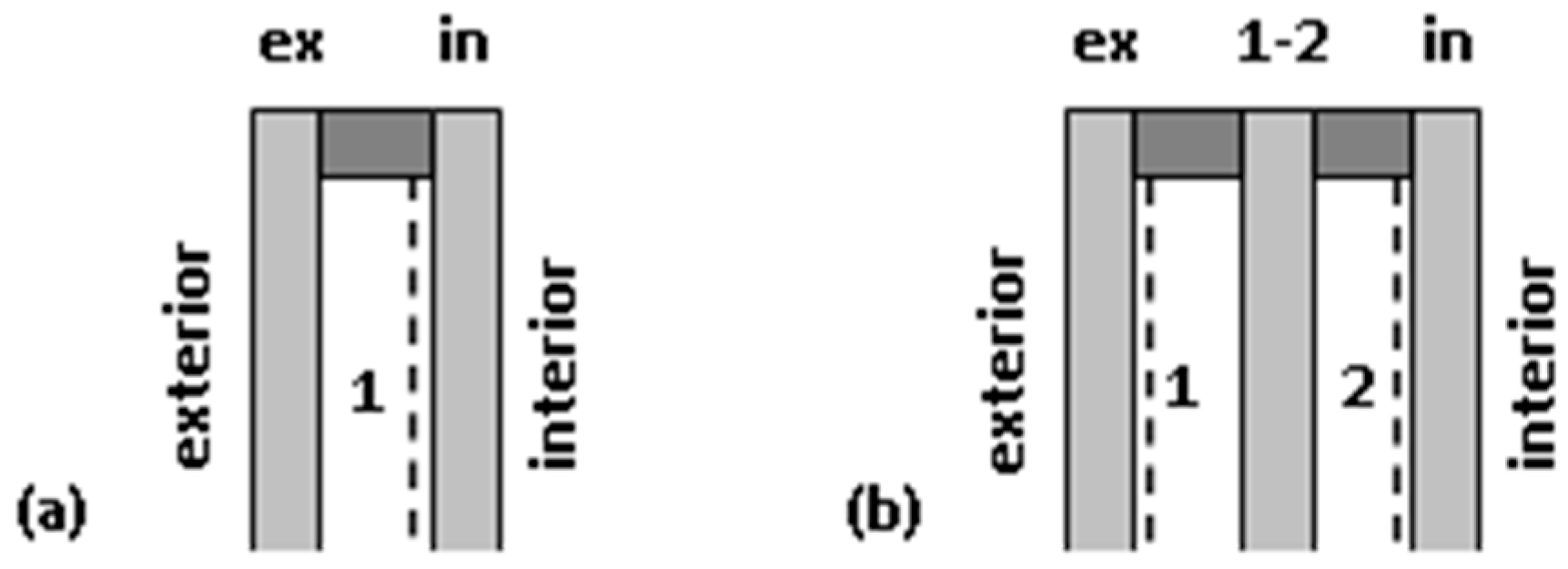
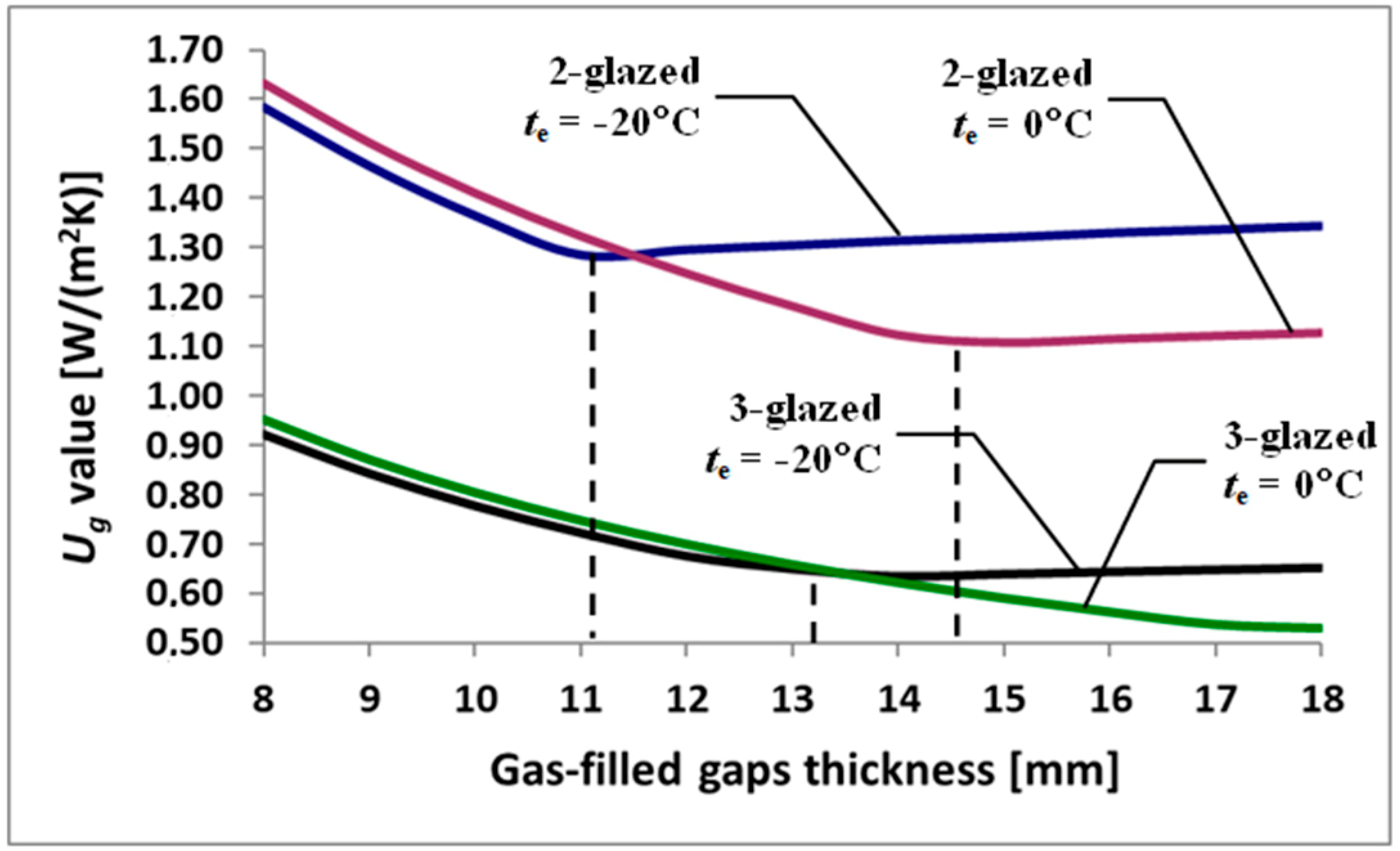
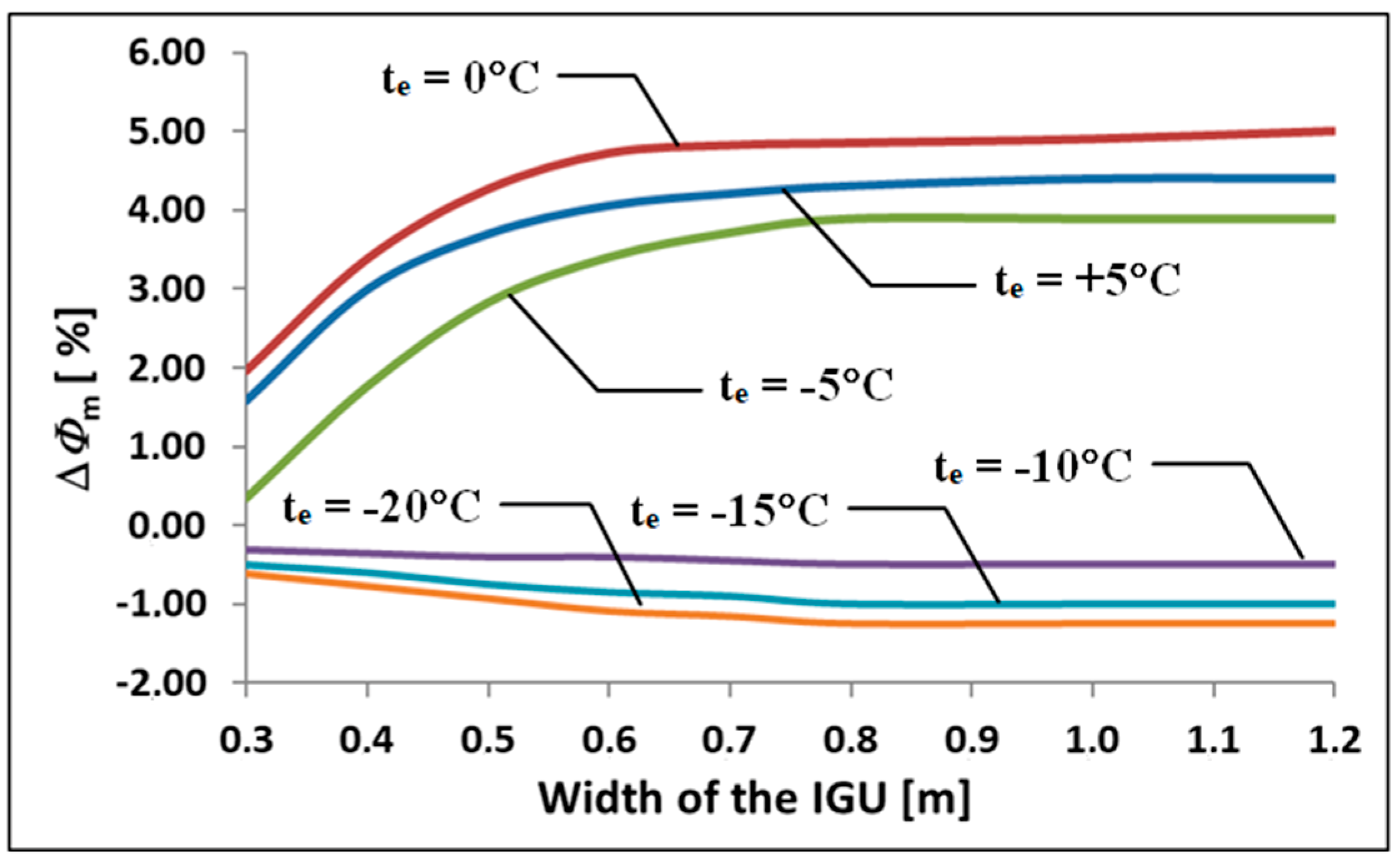
4. IGUs Under Pressure and Temperature Changes—Presentation and Discussion of Test Results
- Ug, Φg—describe heat loss without taking into account the curvature of the panes, calculated for the nominal thickness of the gaps,
- Uc, Φc—describe possible local heat loss near the IGU center, i.e., where the distance between the panes is the smallest, calculated for the thickness of the gaps sc,
- Um, Φm—describe the average heat loss through the IGU, calculated for the thickness of the gaps sm.
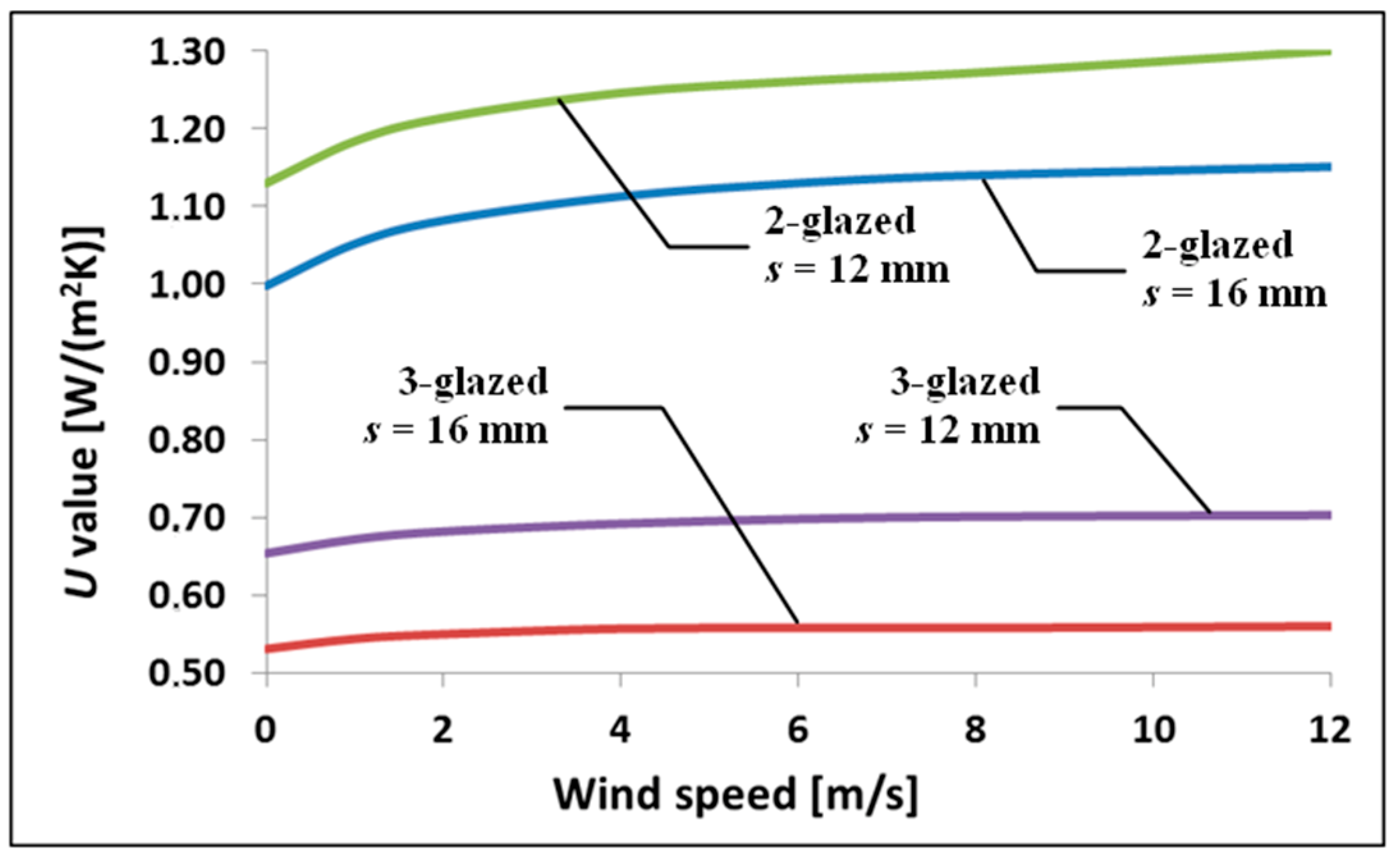
5. Notes on IGUs Wind Load
6. Conclusions
Funding
Conflicts of Interest
Nomenclature
| A | auxiliary parameter [m3] |
| a | width (of glass pane) [m] |
| B | auxiliary parameter [m5/kN] |
| b | length (of glass pane) [m] |
| c | auxiliary parameter [kPa] |
| D | flexural rigidity (of glass pane) [kNm] |
| d | thickness (of glass pane) [m] or [mm] |
| E | Young’s modulus [kPa] or [GPa] |
| h | thermal conductance [W/(m2·K)] |
| i | consecutive natural number |
| Nu | Nusselt number |
| p | pressure [kPa] |
| q | load per area, [kN/m2] |
| R | thermal resistance [(m2·K)/W] |
| s | thickness (of gas gap) [mm] |
| T | temperature (of gas in the gap) [K] |
| t | temperature (of air) [K] or [°C] |
| U | thermal transmittance [W/(m2·K)] |
| V | wind velocity [km/h] |
| v | volume (of the gap) [m3] |
| w | deflection [mm] |
| w(x,y) | function of deflection, [m] |
| x-y | coordinate system |
| Greek letters | |
| α | proportionality factor, [m5/kN] |
| α’ | dimensionless coefficient [-] |
| βi | auxiliary parameter [-] |
| ∆p | pressure change [kPa] |
| ∆T | temperature difference [K] |
| ∆v | volume change [m3] |
| ∆Φ | percentage increase in density of heat-flow rate [%] |
| ε | surface emissivity [-] |
| λ | thermal conductivity [W/(m·K)] |
| μ | Poisson’s ratio [-] |
| π | number “pi” |
| σ | Boltzmann constant [W/(m2·K4)] |
| Φ | density of heat-flow rate [W/m2] |
| Subscripts and markings | |
| 0 | initial gas parameters |
| 1, 2 | specific gas-filled gap |
| 1-2 | glass pane (between gaps) |
| c | center (of glass pane) |
| a | atmospheric |
| e | external |
| ex | exterior glass pane |
| g | regarding gas or regarding IGU (at Ug, Φg and ∆Φg) |
| i | internal |
| in | interior glass pane |
| m | mean, average |
| op | operating gas parameters |
| r | radiative |
| s | regarding gas gap |
| sur1, sur2 | regarding surfaces |
| v | regarding volume |
| w | regarding deflection |
| z | outside |
References
- Huang, S.; Wang, Z.; Xu, J.; Lu, D.; Yuan, T. Determination of optical constants of functional layer of online Low-E glass based on the Drude theory. Thin Solid Films 2008, 516, 3179–3183. [Google Scholar] [CrossRef]
- Solovyev, A.A.; Rabotkin, S.V.; Kovsharov, N.F. Polymer films with multilayer low-E coatings. Mater. Sci. Semicond. Process. 2015, 38, 373–380. [Google Scholar] [CrossRef]
- Bernier, M.; Bourret, B. Effects of Glass Plate Curvature on the U-Factor of Sealed Insulated Glazing Units. ASHRAE Trans. 1997, 103, 4038. [Google Scholar]
- Hart, R.; Goudey, H.; Arasteh, D.; Curcija, D.C. Thermal performance impacts of center-of-glass deflections in installed insulating glazing units. Energy Build. 2012, 54, 453–460. [Google Scholar] [CrossRef][Green Version]
- Penkova, N.; Krumov, K.; Zashkova, L.; Kassabov, I. Heat transfer and climatic loads at insulating glass units in window systems. Int. J. Adv. Sci. Eng. Technol. 2017, 5, 22–28. [Google Scholar]
- Derwiński, W. Okna w kamerze termowizyjnej. Świat Szkła 2014, 12, 24–26. [Google Scholar]
- Solvason, K.R. Pressures and Stresses in Sealed Double Glazing Units; Technical Paper No. 423; Division of Building Research, National Research Council Canada: Ottawa, ON, Canada, 1974.
- Feldmeier, F. Klimabelastung und Lastverteilung bei Mehrscheiben-Isolierglas. Stahlbau 2006, 75, 467–478. [Google Scholar] [CrossRef]
- Curcija, C.; Vidanovic, S. Predicting Thermal Transmittance of IGU Subject to Deflection; Lawrence Berkeley National Laboratory, Environmental Energy Technologies Division: Berkeley, CA, USA, 2012.
- Feldman, M.; Kaspar, R.; Abeln, B.; Gessler, A.; Langosch, K.; Beyer, J.; Schneider, J.; Schula, S.; Siebert, G.; Haese, A.; et al. Guidance for European Structural Design of Glass Components; Support to the Implementation, Harmonization and Further Development of the Eurocodes; Luxembourg Publications Office of the European Union: Luxembourg, 2014.
- Stratiy, P. Numerical-and-Analytical Method of Estimation Insulated Glass Unit Deformations Caused by Climate Loads. In International Scientific Conference Energy Management of Municipal Transportation Facilities and Transport EMMFT 2017; Murgul, V., Popovic, Z., Eds.; Advances in Intelligent Systems and Computing 2017; Springer International Publishing: New York, NY, USA, 2017; Volume 692, pp. 970–979. [Google Scholar]
- Velchev, D.; Ivanov, I.V. A finite element for insulating glass units. In Challenging Glass 4 & COST Action TU0905 Final Conference 2014; Louter, C., Bos, F., Belis, J., Lebet, J.P., Eds.; Taylor & Francis Group: London, UK, 2014; pp. 311–318. [Google Scholar]
- Respondek, Z. Rozkład obciążeń środowiskowych w wielokomorowej szybie zespolonej. Constr. Optim. Energy Potential 2017, 1, 105–110. [Google Scholar] [CrossRef]
- Klindt, L.B.; Klein, W. Glas als Baustoff: Eigenschaften, Anwendung, Bemessung; Verlagsgesellschaft R. Müller: Köln-Braunsfeld, Germany, 1997. [Google Scholar]
- Timishenko, S.; Woinowsky-Krieger, S. Theory of Plates and Shells; McGraw-Hill Book Company: New York, NY, USA; Toronto, ON, Canada; London, UK, 1959. [Google Scholar]
- EN 673:2011. Glass in Building—Determination of Thermal Transmittance (U Value)—Calculation Method; European Committee for Standardization (CEN): Brussels, Belgium, 2011. [Google Scholar]
- Aydın, O. Conjugate heat transfer analysis of double pane windows. Build. Environ. 2006, 41, 109–116. [Google Scholar] [CrossRef]
- Arıcı, M.; Kan, M. An investigation of flow and conjugate heat transfer in multiple pane windows with respect to gap width, emissivity and gas filling. Renew. Energy 2015, 75, 249–256. [Google Scholar] [CrossRef]
- EN 572-1:2004. Glass in Building—Basic Soda Lime Silicate Glass Products—Part 1: Definitions and General Physical and Mechanical Properties; British Standards Institution: London, UK, 2004. [Google Scholar]
- Dynamic Pressure. Available online: https://en.wikipedia.org/wiki/Dynamic_pressure (accessed on 7 September 2019).

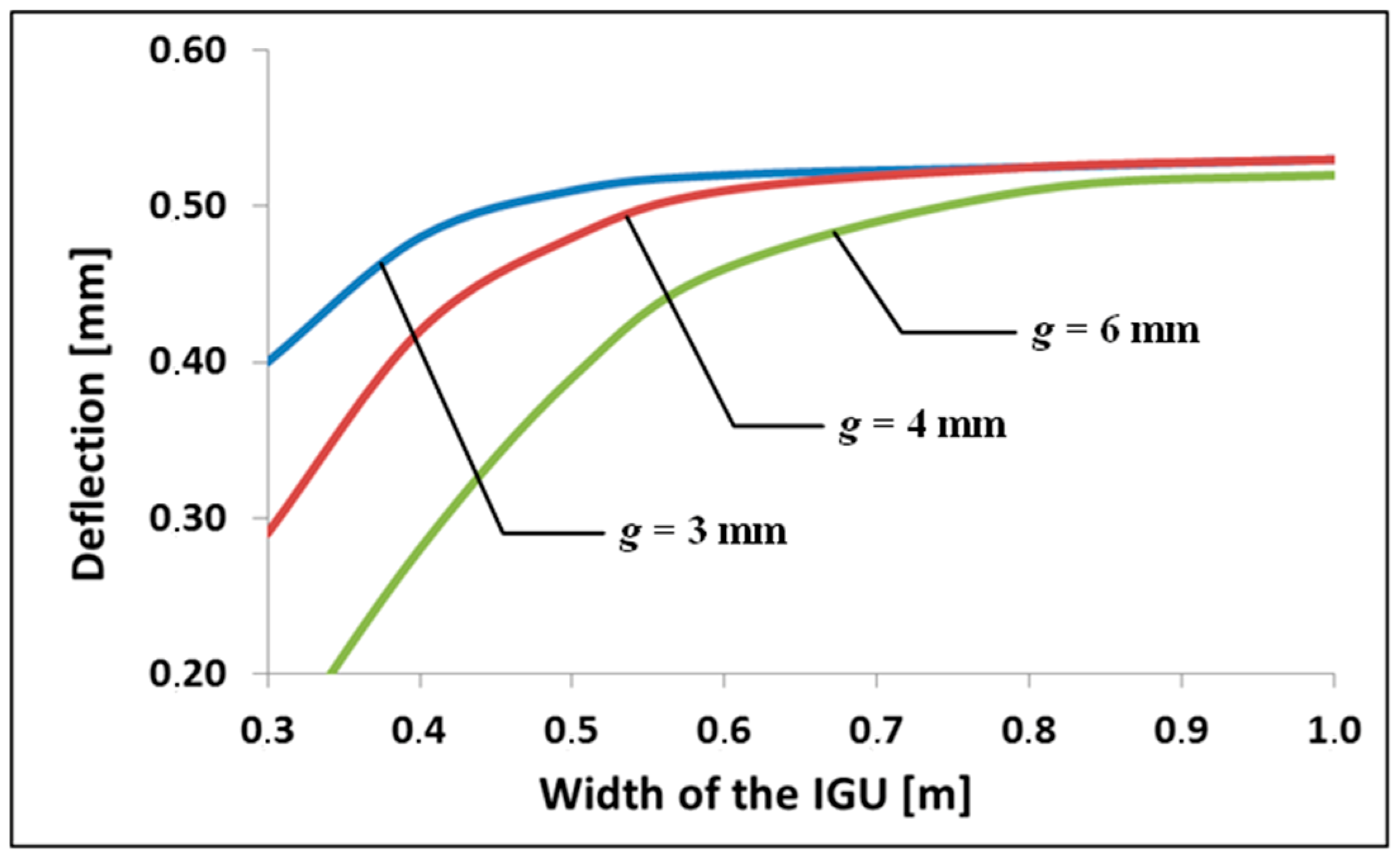
| b/a | 1.0 | 1.1 | 1.2 | 1.3 | 1.4 | 1.5 |
| α′v | 0.001703 | 0.002246 | 0.002848 | 0.003499 | 0.004189 | 0.004912 |
| α′w | 0.004062 | 0.004869 | 0.005651 | 0.006392 | 0.007085 | 0.007724 |
| b/a | 1.6 | 1.7 | 1.8 | 1.9 | 2.0 | 3.0 |
| α′v | 0.005659 | 0.006427 | 0.00721 | 0.008004 | 0.008808 | 0.017055 |
| α′w | 0.008308 | 0.008838 | 0.009316 | 0.009745 | 0.010129 | 0.012233 |
| Structure of IGU [mm] | Resultant Loading q [kN/m2] | Deflection wc (wm) [mm] | Resultant Thickness of Gap s [mm] | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ex | 1-2 | in | ex | 1-2 | in | gap 1 | gap 2 | |||
| sc1 | sm1 | sc2 | sm2 | |||||||
| dex-s1-din | Double-glazed units | |||||||||
| 4-16-4 | 0.218 | - | −0.218 | 1.36 (0.59) | - | −1.36 (−0.59) | 13.28 | 14.82 | - | - |
| 6-16-4 | 0.330 | - | −0.330 | 0.61 (0.27) | - | −2.08 (−0.90) | 13.31 | 14.83 | - | - |
| 4-12-4 | 0.164 | - | −0.164 | 1.03 (0.45) | - | −1.03 (−0.45) | 9.94 | 11.10 | - | - |
| 6-12-4 | 0.251 | - | −0.251 | 0.47 (0.20) | - | −1.57 (−0.68) | 9.96 | 11.12 | - | - |
| 3-12-3 | 0.070 | - | −0.070 | 1.04 (0.45) | - | −1.04 (−0.45) | 9.92 | 11.10 | - | - |
| dex-s1-d1-2-s2-din | Triple-glazed units | |||||||||
| 4-16-4-16-4 | 0.463 | −0.117 | −0.346 | 2.90 (1.26) | −0.73 (−0.32) | −2.16 (−0.94) | 12.37 | 14.42 | 14.57 | 15.38 |
| 6-16-4-16-4 | 0.840 | −0.311 | −0.529 | 1.56 (0.68) | −1.94 (−0.85) | −3.34 (−1.44) | 12.50 | 14.47 | 14.63 | 15.41 |
| 4-12-4-12-4 | 0.345 | −0.087 | −0.258 | 2.16 (0.99) | −0.54 (−0.24) | −1.61 (−0.70) | 9.30 | 10.77 | 10.93 | 11.54 |
| 6-12-4-12-4 | 0.631 | −0.233 | −0.398 | 1.17 (0.51) | −1.46 (−0.63) | −2.49 (−1.08) | 9.37 | 10.86 | 10.97 | 11.55 |
| 6-12-3-12-4 | 0.540 | −0.112 | −0.429 | 1.00 (0.43) | −1.66 (−0.72) | −2.68 (−1.17) | 9.34 | 10.85 | 10.98 | 11.55 |
| 3-12-3-12-3 | 0.149 | −0.037 | −0.112 | 2.21 (0.96) | −0.55 (−0.24) | −1.66 (−0.72) | 9.24 | 10.80 | 10.89 | 11.52 |
| Structure of IGU [mm] | Resultant Loading q [kN/m2] | Deflection wc (wm) [mm] | Resultant Thickness of Gap s [mm] | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ex | 1-2 | in | ex | 1-2 | in | gap 1 | gap 2 | |||
| sc1 | sm1 | sc2 | sm2 | |||||||
| dex-s1-din | Double-glazed units | |||||||||
| 4-16-4 | 0.295 | - | −0.295 | 1.84 (0.81) | - | −1.84 (−0.81) | 12.32 | 14.38 | - | - |
| 4-14-4 | 0.259 | - | −0.259 | 1.62 (0.70) | - | −1.62 (−0.70) | 10.76 | 12.60 | - | - |
| 4-12-4 | 0.233 | - | −0.233 | 1.39 (0.61) | - | −1.39 (−0.61) | 9.22 | 10.78 | - | - |
| 4-10-4 | 0.187 | - | −0.187 | 1.17 (0.51) | - | −1.17 (−0.51) | 7.66 | 8.98 | - | - |
| dex-s1-d1-2-s2-din | Triple-glazed units | |||||||||
| 4-16-4-16-4 | 0.613 | −0.114 | −0.500 | 3.83 (1.67) | −0.71 (−0.31) | −3.13 (−1.36) | 11.46 | 14.02 | 13.58 | 14.95 |
| 4-14-4-14-4 | 0.540 | −0.100 | −0.440 | 3.38 (1.47) | −0.63 (−0.27) | −2.75 (−1.20) | 9.99 | 12.26 | 11.88 | 13.07 |
| 4-12-4-12-4 | 0.460 | −0.085 | −0.375 | 2.87 (1.25) | −0.53 (−0.23) | −2.35 (−1.02) | 8.60 | 10.52 | 10.18 | 11.21 |
| 4-10-4-10-4 | 0.387 | −0.070 | −0.317 | 2.42 (1.05) | −0.44 (−0.19) | −1.98 (−0.86) | 7.14 | 8.76 | 8.46 | 9.33 |
| Structure of IGU [mm] | Resultant Loading q [kN/m2] | Deflection wc (wm) [mm] | Resultant Thickness of Gap s [mm] | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ex | 1-2 | in | ex | 1-2 | in | gap 1 | gap 2 | |||
| sc1 | sm1 | sc2 | sm2 | |||||||
| dex-s1-din | Double-glazed units | |||||||||
| 4-16-4 | 0.188 | - | −0.188 | 1.18 (0.51) | - | −1.18 (−0.51) | 13.64 | 14.98 | - | - |
| 4-14-4 | 0.165 | - | −0.165 | 1.03 (0.45) | - | −1.03 (−0.45) | 11.94 | 13.10 | - | - |
| 4-12-4 | 0.143 | - | −0.143 | 0.89 (0.40) | - | −0.89 (−0.40) | 10.22 | 11.20 | - | - |
| 4-10-4 | 0.120 | - | −0.120 | 0.75 (0.33) | - | −0.75 (−0.33) | 8.50 | 9.34 | - | - |
| dex-s1-d1-2-s2-din | Triple-glazed units | |||||||||
| 4-16-4-16-4 | 0.384 | −0.058 | −0.326 | 2.41 (1.04) | −0.36 (−0.16) | −2.04 (−0.89) | 13.23 | 14.80 | 14.32 | 15.27 |
| 4-14-4-14-4 | 0.339 | −0.050 | −0.289 | 2.12 (0.92) | −0.31 (−0.14) | −1.81 (−0.79) | 11.57 | 12.94 | 12.50 | 13.35 |
| 4-12-4-12-4 | 0.293 | −0.042 | −0.251 | 1.83 (0.80) | −0.26 (−0.11) | −1.56 (−0.68) | 9.91 | 11.09 | 10.70 | 11.43 |
| 4-10-4-10-4 | 0.246 | −0.035 | −0.212 | 1.54 (0.67) | −0.22 (−0.09) | −1.32 (−0.57) | 8.24 | 9.24 | 8.90 | 9.52 |
| Gas Gap Thickness [mm] | Thermal Transmittance [W/(m2·K)] | Density of Heat-Flow Rate Φ [W/m2] | ∆Φc [%] | ∆Φm [%] | ||||
|---|---|---|---|---|---|---|---|---|
| U | Uc | Um | Φ | Φc | Φm | |||
| Double-glazed units | ||||||||
| 16 | 1.330 | 1.299 | 1.317 | 53.20 | 51.96 | 52.68 | −2.3 | −1.0 |
| 14 | 1.314 | 1.298 | 1.302 | 52.56 | 51.92 | 52.08 | −1.2 | −0.9 |
| 12 | 1.296 | 1.441 | 1.297 | 51.84 | 57.64 | 51.88 | 11.2 | −0.1 |
| 10 | 1.364 | 1.630 | 1.467 | 54.56 | 65.20 | 58.68 | 19.5 | 7.6 |
| Triple-glazed units | ||||||||
| 16 | 0.643 | 0.653 | 0.636 | 25.72 | 26.12 | 25.44 | 1.6 | −1.1 |
| 14 | 0.634 | 0.727 | 0.648 | 25.36 | 29.08 | 25.92 | 14.7 | 2.2 |
| 12 | 0.675 | 0.817 | 0.730 | 27.00 | 32.68 | 29.20 | 21.0 | 8.1 |
| 10 | 0.776 | 0.941 | 0.839 | 31.04 | 37.64 | 33.56 | 21.3 | 8.1 |
| Gas Gap Thickness [mm] | Thermal Transmittance [W/(m2·K)] | Density of Heat-Flow Rate Φ [W/m2] | ∆Φc [%] | ∆Φm [%] | ||||
|---|---|---|---|---|---|---|---|---|
| U | Uc | Um | Φ | Φc | Φm | |||
| Double-glazed units | ||||||||
| 16 | 1.113 | 1.142 | 1.107 | 22.26 | 22.84 | 22.14 | 2.6 | −0.5 |
| 14 | 1.122 | 1.250 | 1.174 | 22.44 | 25.00 | 23.48 | 11.4 | 4.6 |
| 12 | 1.246 | 1.388 | 1.305 | 24.92 | 27.76 | 26.10 | 11.4 | 4.7 |
| 10 | 1.408 | 1.567 | 1.473 | 28.16 | 31.34 | 29.46 | 11.3 | 4.6 |
| Triple-glazed units | ||||||||
| 16 | 0.563 | 0.631 | 0.590 | 11.26 | 12.62 | 11.80 | 12.1 | 4.8 |
| 14 | 0.623 | 0.699 | 0.653 | 12.46 | 13.98 | 13.06 | 12.2 | 4.8 |
| 12 | 0.700 | 0.786 | 0.735 | 14.00 | 15.72 | 14.70 | 12.3 | 5.0 |
| 10 | 0.804 | 0.903 | 0.844 | 16.08 | 18.06 | 16.88 | 12.3 | 5.0 |
| Structure of IGU [mm] | Resultant Loading q [kN/m2] | Deflection wc [mm] | ||||
|---|---|---|---|---|---|---|
| ex | 1–2 | in | ex | 1–2 | in | |
| dex-s1-din | Double-glazed units | |||||
| 4-16-4 | 0.154 | - | 0.146 | 0.96 | - | 0.91 |
| 8-16-4 | 0.268 | - | 0.032 | 0.21 | - | 0.20 |
| 4-16-8 | 0.047 | - | 0.253 | 0.29 | - | 0.20 |
| dex-s1-d1-2-s2-din | Triple-glazed units | |||||
| 4-16-4-16-4 | 0.109 | 0.098 | 0.092 | 0.68 | 0.61 | 0.58 |
| 8-14-4-14-4 | 0.247 | 0.028 | 0.026 | 0.19 | 0.17 | 0.16 |
| 4-12-4-12-8 | 0.053 | 0.039 | 0.208 | 0.33 | 0.24 | 0.16 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Respondek, Z. Heat Transfer Through Insulating Glass Units Subjected to Climatic Loads. Materials 2020, 13, 286. https://doi.org/10.3390/ma13020286
Respondek Z. Heat Transfer Through Insulating Glass Units Subjected to Climatic Loads. Materials. 2020; 13(2):286. https://doi.org/10.3390/ma13020286
Chicago/Turabian StyleRespondek, Zbigniew. 2020. "Heat Transfer Through Insulating Glass Units Subjected to Climatic Loads" Materials 13, no. 2: 286. https://doi.org/10.3390/ma13020286
APA StyleRespondek, Z. (2020). Heat Transfer Through Insulating Glass Units Subjected to Climatic Loads. Materials, 13(2), 286. https://doi.org/10.3390/ma13020286





