Combined Fuzzy and Genetic Algorithm for the Optimisation of Hybrid Composite-Polymer Joints Obtained by Two-Step Laser Joining Process
Abstract
1. Introduction
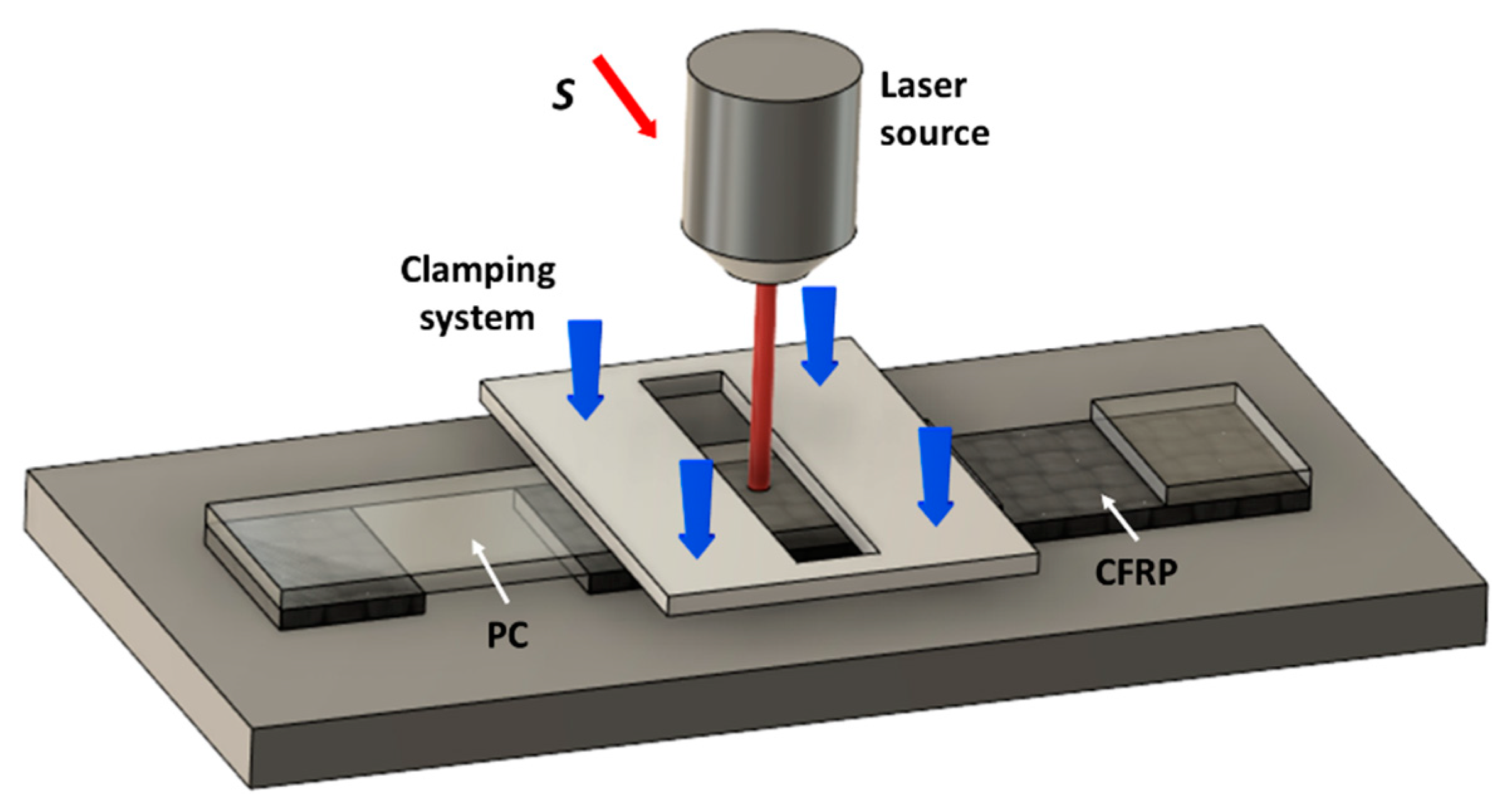
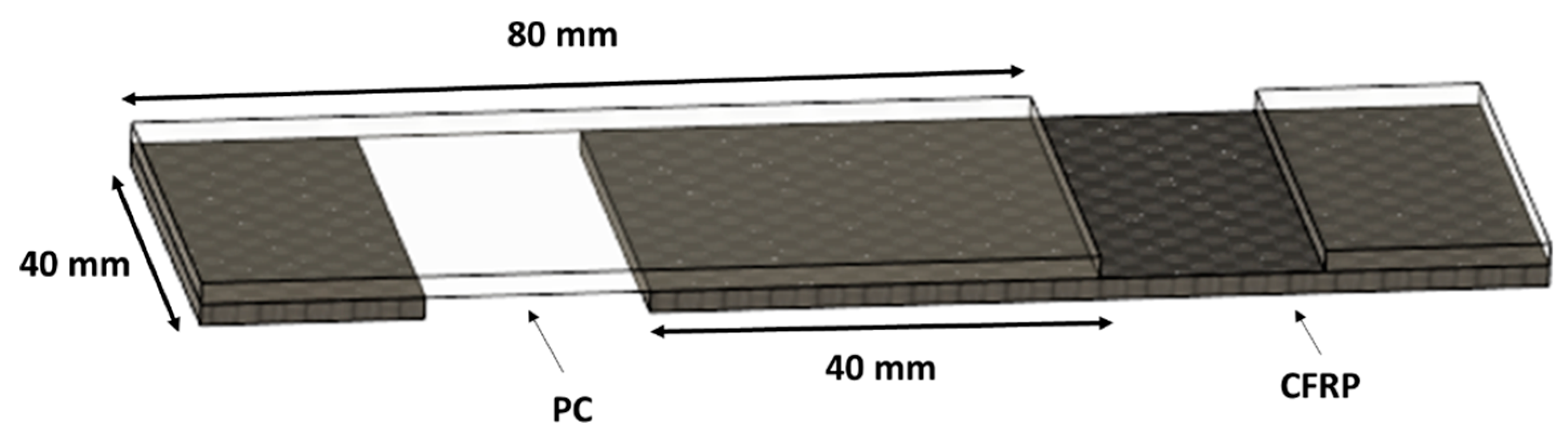
2. Materials and Methods
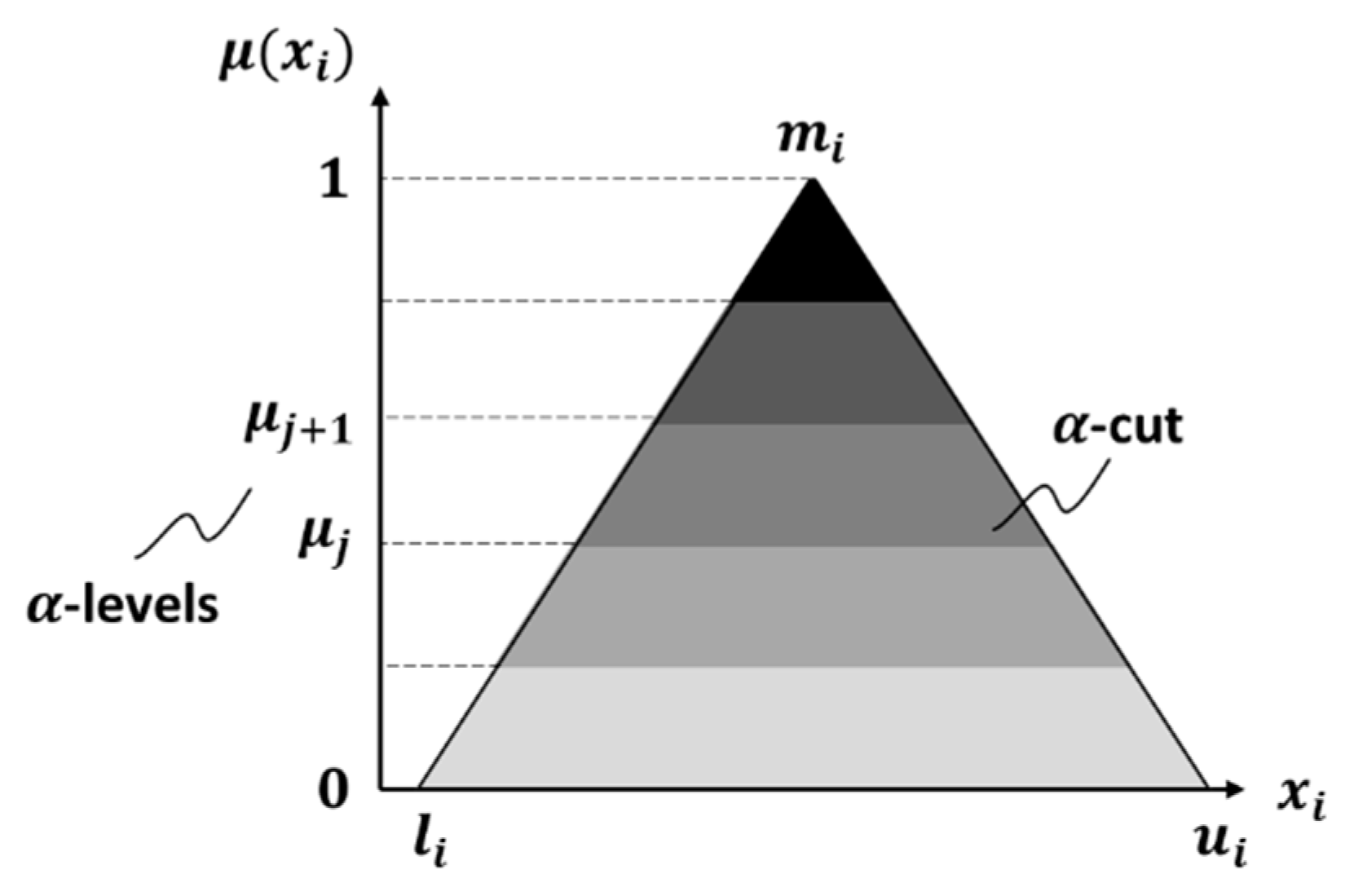
Computational
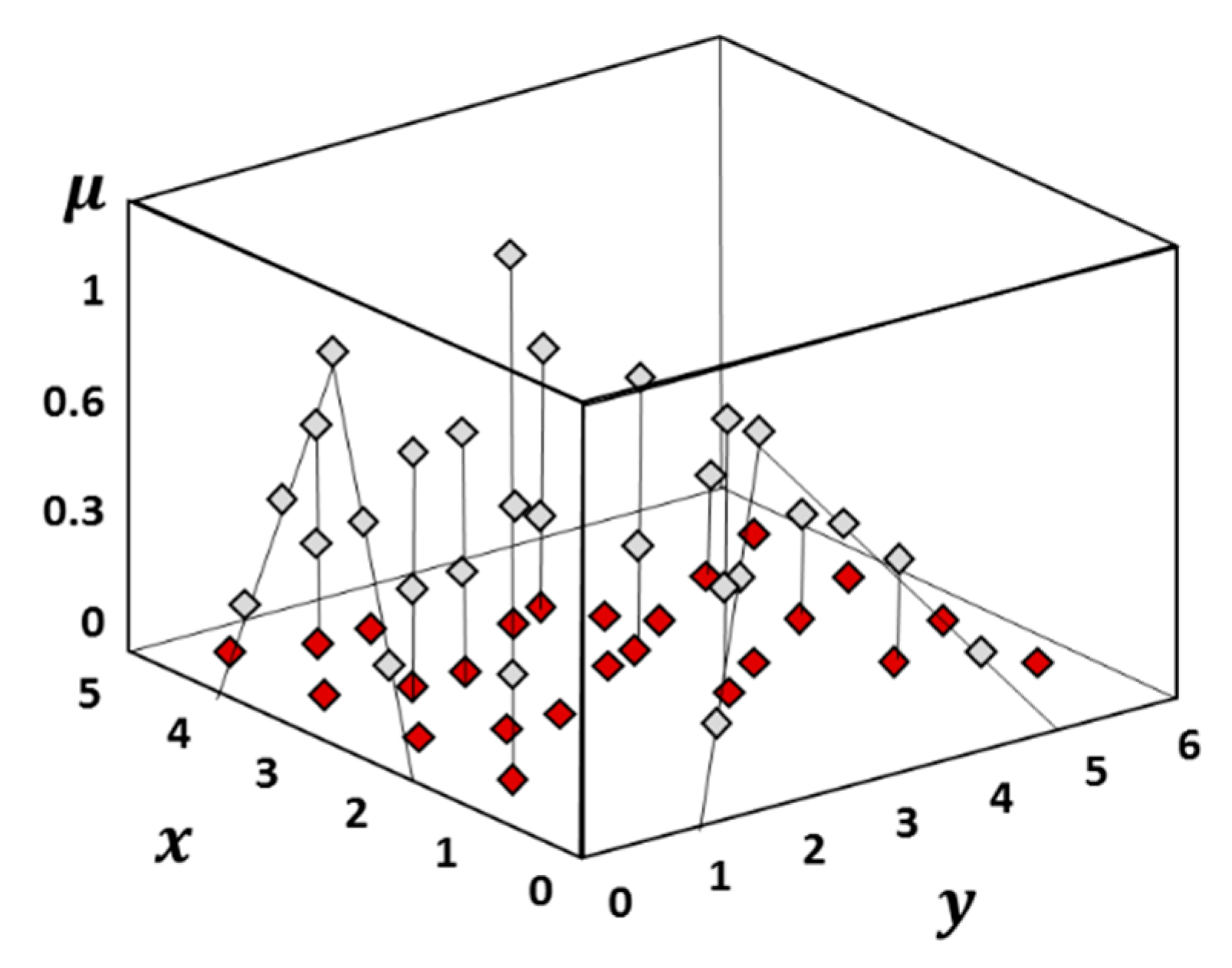
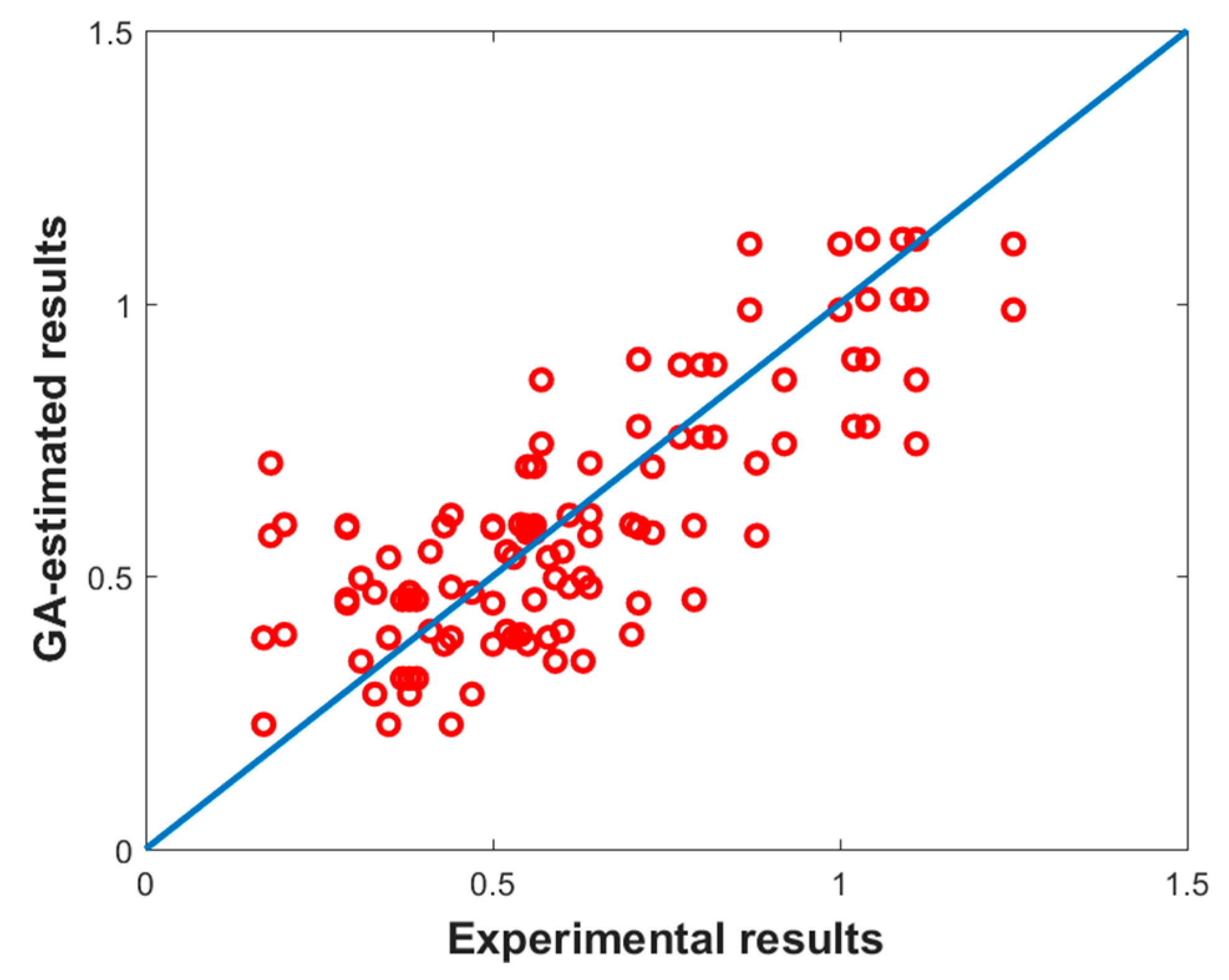
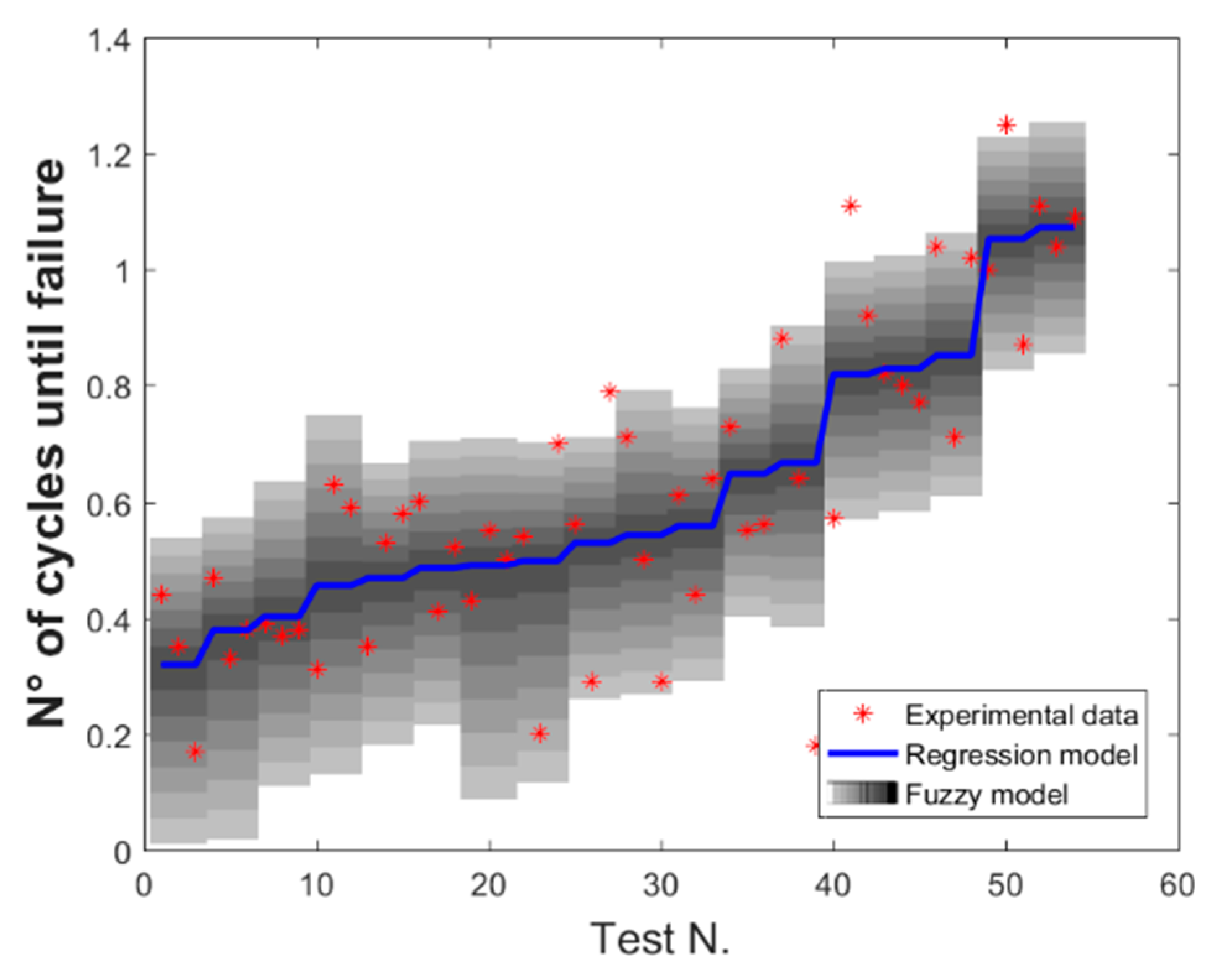
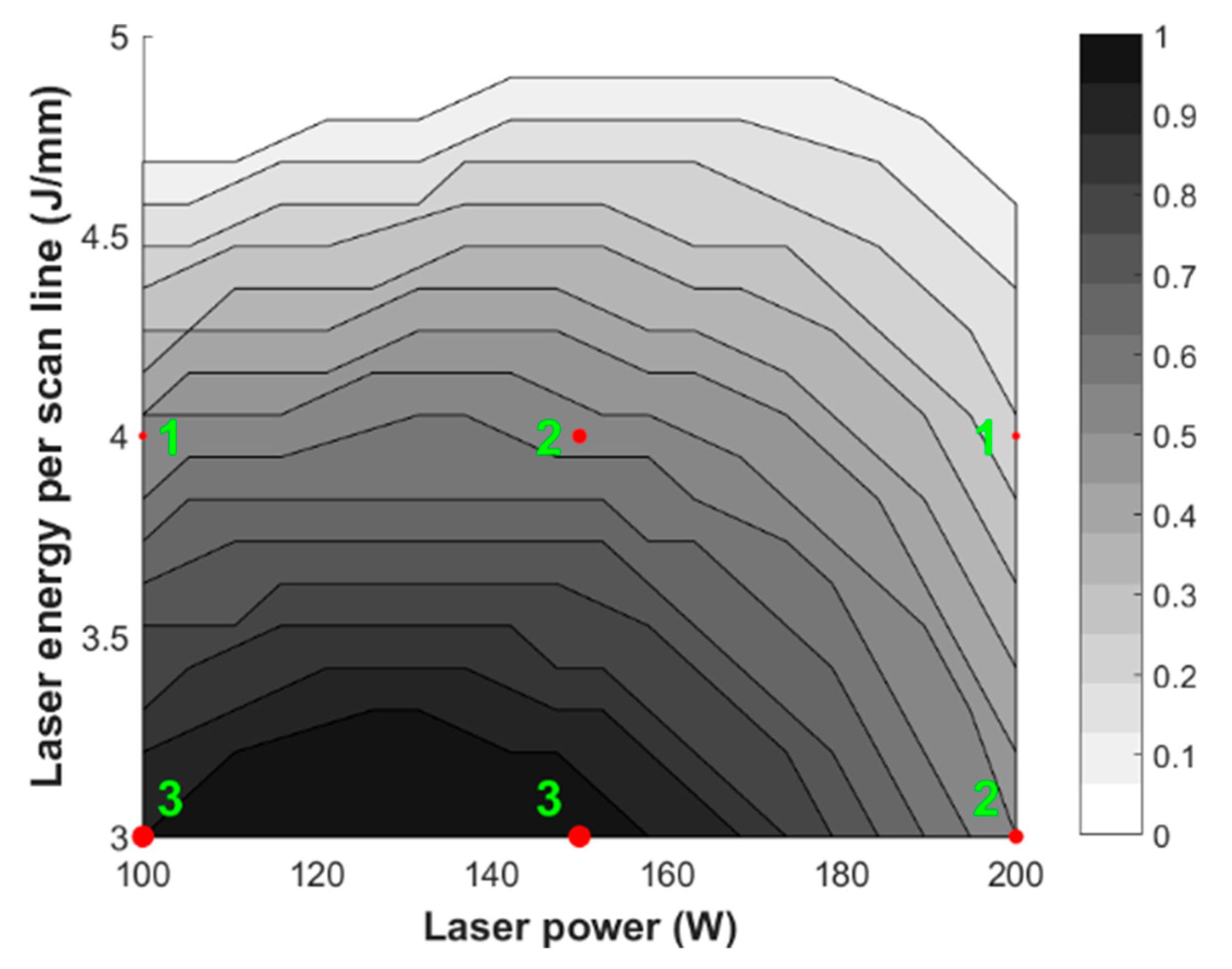
3. Results and Discussion
Optimal Fuzzy Regression Model
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ferreira, A.D.B.L.; Nóvoa, P.R.O.; Marques, A.T. Multifunctional Material Systems: A state-of-the-art review. Compos. Struct. 2016, 151, 3–35. [Google Scholar] [CrossRef]
- Pinto, S.C.; Marques, P.A.; Vesenjak, M.; Vicente, R.; Godinho, L.; Krstulović-Opara, L.; Duarte, I. Characterization and physical properties of aluminium foam–polydimethylsiloxane nanocomposite hybrid structures. Compos. Struct. 2019, 230, 111521. [Google Scholar] [CrossRef]
- Genna, S.; Lambiase, F.; Leone, C. Effect of laser cleaning in Laser Assisted Joining of CFRP and PC sheets. Compos. Part B Eng. 2018, 145, 206–214. [Google Scholar] [CrossRef]
- Lambiase, F.; Genna, S. Laser assisted joining of AA5053 aluminum alloy with polyvinyl chloride (PVC). Opt. Laser Technol. 2018, 107, 80–88. [Google Scholar] [CrossRef]
- Wang, H.; Xiao, X.; Xiao, G.; Fan, H.-T.; Arinez, J. Laser Joining of Carbon-Fiber-Reinforced Polymer and Metal with High-Strength and Corrosion-Resistant Bonds. Procedia Manuf. 2019, 34, 42–48. [Google Scholar] [CrossRef]
- Troughton, M.J. Mechanical Fastening. In Handbook of Plastics Joining; Elsevier: Amsterdam, The Netherlands, 2009; pp. 175–201. ISBN 9780815515814. [Google Scholar]
- Oplinger, D.W. Mechanical Fastening and Adhesive Bonding. In Handbook of Composites; Springer US: Boston, MA, USA, 1998; pp. 610–666. [Google Scholar]
- Kweon, J.-H.; Jung, J.-W.; Kim, T.-H.; Choi, J.-H.; Kim, D.-H. Failure of carbon composite-to-aluminum joints with combined mechanical fastening and adhesive bonding. Compos. Struct. 2006, 75, 192–198. [Google Scholar] [CrossRef]
- Gao, L.; Zhang, F.; Liu, J.; Lu, X.; Gao, H. Experimental and numerical study on the interfacial bonding characteristics of FRP-to-concrete joints with mechanical fastening. Constr. Build. Mater. 2019, 199, 456–470. [Google Scholar] [CrossRef]
- Lambiase, F.; Paoletti, A.; Grossi, V.; Ilio, A. Di Friction assisted joining of aluminum and PVC sheets. J. Manuf. Process. 2017, 29, 221–231. [Google Scholar] [CrossRef]
- Lambiase, F.; Paoletti, A.; Grossi, V.; Genna, S. Improving energy efficiency in friction assisted joining of metals and polymers. J. Mater. Process. Technol. 2017, 250, 379–389. [Google Scholar] [CrossRef]
- Huang, Y.; Meng, X.; Wang, Y.; Xie, Y.; Zhou, L. Joining of aluminum alloy and polymer via friction stir lap welding. J. Mater. Process. Technol. 2018, 257, 148–154. [Google Scholar] [CrossRef]
- Lambiase, F.; Paoletti, A. Friction-assisted clinching of Aluminum and CFRP sheets. J. Manuf. Process. 2018, 31, 812–822. [Google Scholar] [CrossRef]
- Pramanik, A.; Basak, A.K.; Dong, Y.; Sarker, P.K.; Uddin, M.S.; Littlefair, G.; Dixit, A.R.; Chattopadhyaya, S. Joining of carbon fibre reinforced polymer (CFRP) composites and aluminium alloys—A review. Compos. Part A Appl. Sci. Manuf. 2017, 101, 1–29. [Google Scholar] [CrossRef]
- Sharma, V.; Prakash, U.; Kumar, B.V.M. Surface composites by friction stir processing: A review. J. Mater. Process. Technol. 2015, 224, 117–134. [Google Scholar] [CrossRef]
- Huang, Y.; Meng, X.; Xie, Y.; Wan, L.; Lv, Z.; Cao, J.; Feng, J. Friction stir welding/processing of polymers and polymer matrix composites. Compos. Part A Appl. Sci. Manuf. 2018, 105, 235–257. [Google Scholar] [CrossRef]
- Xie, Y.; Yang, B.; Lu, L.; Wan, Z.; Liu, X. Shear strength of bonded joints of carbon fiber reinforced plastic (CFRP) laminates enhanced by a two-step laser surface treatment. Compos. Struct. 2020, 232, 111559. [Google Scholar] [CrossRef]
- Frick, T.; Schkutow, A. Laser transmission welding of polymers—Irradiation strategies for strongly scattering materials. Procedia CIRP 2018, 74, 538–543. [Google Scholar] [CrossRef]
- Engelmann, C.; Eckstaedt, J.; Olowinsky, A.; Aden, M.; Mamuschkin, V. Experimental and Simulative Investigations of Laser Assisted Plastic-metal-joints Considering Different Load Directions. Phys. Procedia 2016, 83, 1118–1129. [Google Scholar] [CrossRef]
- Lambiase, F.; Genna, S.; Leone, C.; Paoletti, A. Laser-assisted direct-joining of carbon fibre reinforced plastic with thermosetting matrix to polycarbonate sheets. Opt. Laser Technol. 2017, 94, 45–58. [Google Scholar] [CrossRef]
- Lambiase, F.; Genna, S. Laser-assisted direct joining of AISI304 stainless steel with polycarbonate sheets: Thermal analysis, mechanical characterization, and bonds morphology. Opt. Laser Technol. 2017, 88, 205–214. [Google Scholar] [CrossRef]
- Jiao, J.; Jia, S.; Xu, Z.; Ye, Y.; Sheng, L.; Zhang, W. Laser direct joining of CFRTP and aluminium alloy with a hybrid surface pre-treating method. Compos. Part B Eng. 2019, 173, 106911. [Google Scholar] [CrossRef]
- Rao, R.V. Decision Making in the Manufacturing Environment: Using Graph Theory and Fuzzy Multiple Attribute Decision Making Methods; Springer: Berlin/Heidelberg, Germany, 2007; ISBN 9781849966535. [Google Scholar]
- Lambiase, F.; Genna, S. Experimental analysis of laser assisted joining of Al-Mg aluminium alloy with Polyetheretherketone (PEEK). Int. J. Adhes. Adhes. 2018, 84, 265–274. [Google Scholar] [CrossRef]
- Lambiase, F.; Genna, S.; Kant, R. Optimization of laser-assisted joining through an integrated experimental-simulation approach. Int. J. Adv. Manuf. Technol. 2018, 97, 2655–2666. [Google Scholar] [CrossRef]
- Lambiase, F.; Genna, S.; Kant, R. A procedure for calibration and validation of FE modelling of laser-assisted metal to polymer direct joining. Opt. Laser Technol. 2018, 98, 363–372. [Google Scholar] [CrossRef]
- Verotti, M.; Di Giamberardino, P.; Belfiore, N.P.; Giannini, O. A genetic algorithm-based method for the mechanical characterization of biosamples using a MEMS microgripper: Numerical simulations. J. Mech. Behav. Biomed. Mater. 2019, 96, 88–95. [Google Scholar] [CrossRef] [PubMed]
- Ponticelli, G.S.; Guarino, S.; Giannini, O. A fuzzy logic-based model in laser-assisted bending springback control. Int. J. Adv. Manuf. Technol. 2018, 95, 3887–3898. [Google Scholar] [CrossRef]
- Ponticelli, G.S.; Guarino, S.; Tagliaferri, V.; Giannini, O. An optimized fuzzy-genetic algorithm for metal foam manufacturing process control. Int. J. Adv. Manuf. Technol. 2019, 101, 603–614. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy Sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Rodger, J.A. Application of a Fuzzy Feasibility Bayesian Probabilistic Estimation of supply chain backorder aging, unfilled backorders, and customer wait time using stochastic simulation with Markov blankets. Expert Syst. Appl. 2014, 41, 7005–7022. [Google Scholar] [CrossRef]
- Salicone, S. Measurement Uncertainty; Springer Series in Reliability Engineering; Springer US: Boston, MA, USA, 2007; ISBN 978-0-387-30655-1. [Google Scholar]
- Lambiase, F.; Ko, D.C. Feasibility of mechanical clinching for joining aluminum AA6082-T6 and Carbon Fiber Reinforced Polymer sheets. Mater. Des. 2016, 107, 341–352. [Google Scholar] [CrossRef]
- Ahamad, T.; Alshehri, S.M. Thermal degradation and evolved gas analysis of epoxy (DGEBA)/novolac resin blends (ENB) during pyrolysis and combustion. J. Therm. Anal. Calorim. 2013, 111, 445–451. [Google Scholar] [CrossRef]
- Leone, C.; Papa, I.; Tagliaferri, F.; Lopresto, V. Investigation of CFRP laser milling using a 30W Q-switched Yb:YAG fiber laser: Effect of process parameters on removal mechanisms and HAZ formation. Compos. Part A Appl. Sci. Manuf. 2013, 55, 129–142. [Google Scholar] [CrossRef]
- Genna, S.; Leone, C.; Ucciardello, N.; Giuliani, M. Increasing adhesive bonding of carbon fiber reinforced thermoplastic matrix by laser surface treatment. Polym. Eng. Sci. 2017, 57, 685–692. [Google Scholar] [CrossRef]
- Montgomery, D.C. Design and Analysis of Experiments; John Wiley: Chichester, UK, 1991. [Google Scholar]
- Dao, S.D.; Abhary, K.; Marian, R. A bibliometric analysis of Genetic Algorithms throughout the history. Comput. Ind. Eng. 2017, 110, 395–403. [Google Scholar] [CrossRef]
- Alimardani, M.; Toyserkani, E. Prediction of laser solid freeform fabrication using neuro-fuzzy method. Appl. Soft Comput. 2008, 8, 316–323. [Google Scholar] [CrossRef]
- Hanss, M. The transformation method for the simulation and analysis of systems with uncertain parameters. Fuzzy Sets Syst. 2002, 130, 277–289. [Google Scholar] [CrossRef]
- Hanss, M. Applied Fuzzy Arithmetic: An Introduction with Engineering Applications; Springer: Berlin/Heidelberg, Germany, 2005; ISBN 9783540273172. [Google Scholar]
- Reitz, V.; Meinhard, D.; Ruck, S.; Riegel, H.; Knoblauch, V. A comparison of IR- and UV-laser pretreatment to increase the bonding strength of adhesively joined aluminum/CFRP components. Compos. Part A Appl. Sci. Manuf. 2017, 96, 18–27. [Google Scholar] [CrossRef]


| Properties | Units | Material | |
|---|---|---|---|
| CFRP | PC | ||
| Young’s Modulus | GPa | 175.3 | 2.4 |
| Ultimate Tensile Strength | MPa | 962.7 | 65 |
| Melting Temperature | °C | – | 230 |
| Glass Transition Temperature | °C | 165 | 154 |
| Degradation Temperature | °C | 450 | 540 |
| Laser Parameters | Units | Values |
|---|---|---|
| Wavelength | nm | 1064 |
| Average Power | W | 30 |
| Pulse Frequency | kHz | 30 |
| Pulse Duration | ns | 50 |
| Laser Scan Speed | mm/s | 2000 |
| Hatch Distance | µm | 40 |
| Strategy | – | Line |
| Laser Parameters | Units | Values |
|---|---|---|
| Wavelength | nm | 975 |
| Peak Power | W | 200 |
| Beam Profile | – | Circular |
| Beam Diameter | mm | 6 |
| Beam Quality | mm·mrad | 22 |
| Control Factors | Symbol | Units | Levels | ||
|---|---|---|---|---|---|
| Laser Power | P | W | 100 | 150 | 200 |
| Laser Energy per scan line | E | J/mm | 3 | 4 | 5 |
| Laser Cleaning | C | – | Yes | No | |
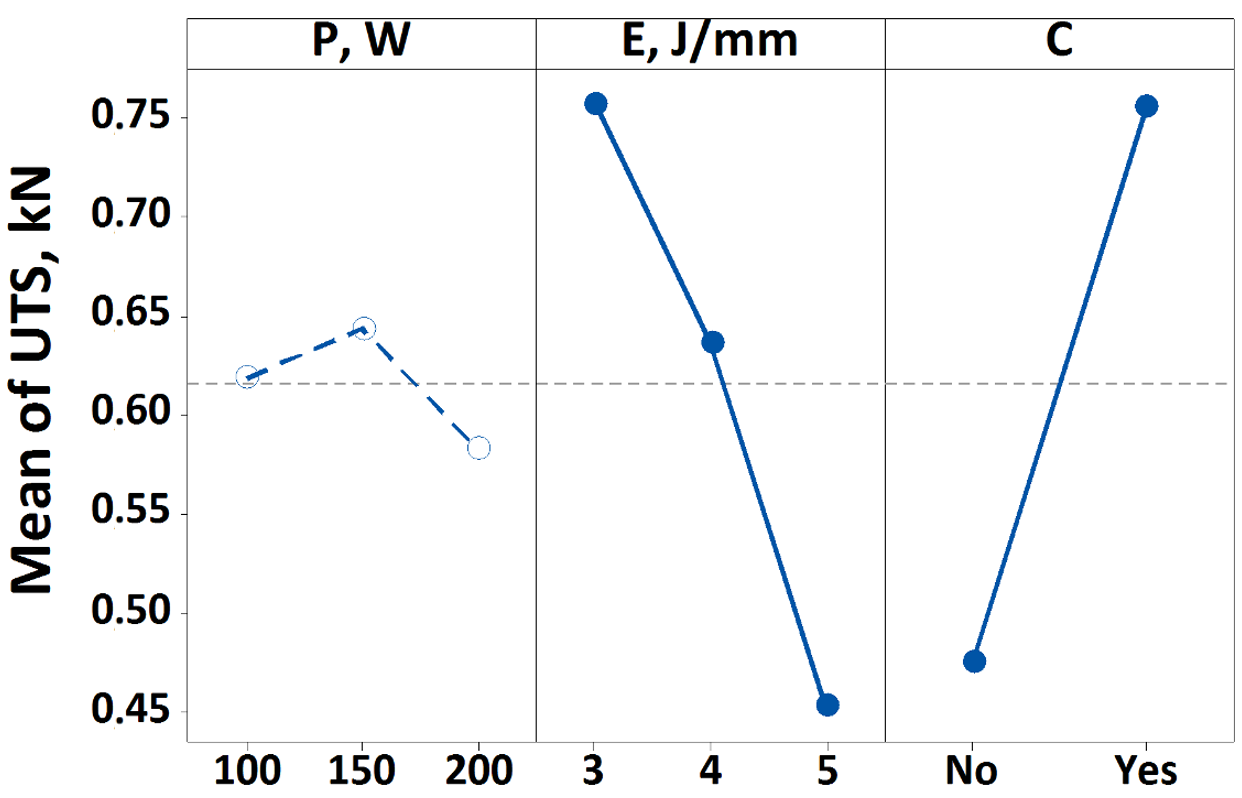
| Source | DoF | Seq.SS | Π% | Adj.SS | Adj.MS | F-Value | p-Value |
|---|---|---|---|---|---|---|---|
| P, W | 2 | 0.04032 | 1.09% | 0.03240 | 0.01620 | 0.51 | 0.603 |
| E, J/mm | 2 | 0.82507 | 22.24% | 0.80534 | 0.40267 | 12.72 | 0.000 |
| C | 1 | 1.07131 | 28.88% | 1.03587 | 1.03587 | 32.73 | 0.000 |
| P × E, | 4 | 0.06974 | 1.88% | 0.07406 | 0.01852 | 0.58 | 0.675 |
| P × C | 2 | 0.17085 | 4.60% | 0.15934 | 0.07967 | 2.52 | 0.094 |
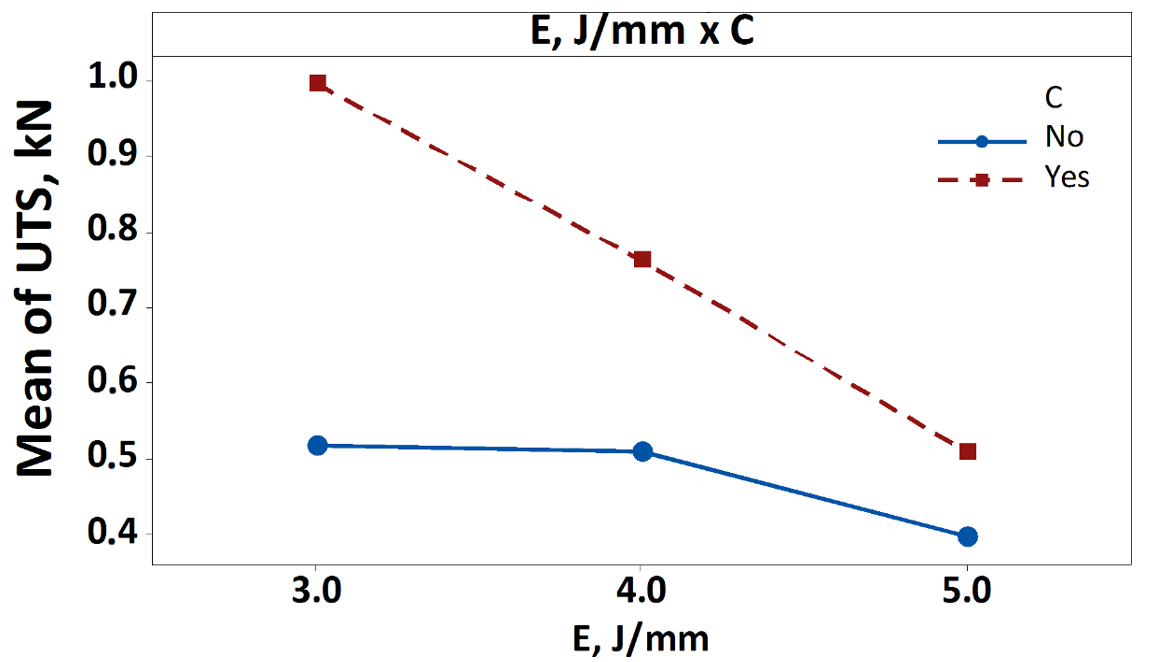
| E × C | 2 | 0.29832 | 8.04% | 0.29832 | 0.14916 | 4.71 | 0.015 |
| Error | 39 | 1.23447 | 33.27% | 1.23447 | 0.03165 | ||
| Lack-of-Fit | 4 | 0.13320 | 3.59% | 0.13320 | 0.03330 | 1.06 | 0.392 |
| Pure Error | 35 | 1.10127 | 29.68% | 1.10127 | 0.03146 | ||
| Total | 52 | 3.71008 | 100.00% |
| Term (i) | Power of P | Power of E | Power of C | |
|---|---|---|---|---|
| 1 | 2.88 | 0 | 0 | 0 |
| 2 | 5.47 × 10−6 | 1.5 | 2 | 1 |
| 3 | −1.45 × 10−5 | 2 | 0 | 1 |
| 4 | 1.18 × 10−4 | −2 | 0.5 | −1.5 |
| 5 | −419.56 | −1 | 0 | −1 |
| 6 | −0.04 | 0 | 2 | 0.5 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ponticelli, G.S.; Lambiase, F.; Leone, C.; Genna, S. Combined Fuzzy and Genetic Algorithm for the Optimisation of Hybrid Composite-Polymer Joints Obtained by Two-Step Laser Joining Process. Materials 2020, 13, 283. https://doi.org/10.3390/ma13020283
Ponticelli GS, Lambiase F, Leone C, Genna S. Combined Fuzzy and Genetic Algorithm for the Optimisation of Hybrid Composite-Polymer Joints Obtained by Two-Step Laser Joining Process. Materials. 2020; 13(2):283. https://doi.org/10.3390/ma13020283
Chicago/Turabian StylePonticelli, Gennaro Salvatore, Francesco Lambiase, Claudio Leone, and Silvio Genna. 2020. "Combined Fuzzy and Genetic Algorithm for the Optimisation of Hybrid Composite-Polymer Joints Obtained by Two-Step Laser Joining Process" Materials 13, no. 2: 283. https://doi.org/10.3390/ma13020283
APA StylePonticelli, G. S., Lambiase, F., Leone, C., & Genna, S. (2020). Combined Fuzzy and Genetic Algorithm for the Optimisation of Hybrid Composite-Polymer Joints Obtained by Two-Step Laser Joining Process. Materials, 13(2), 283. https://doi.org/10.3390/ma13020283








