Author Contributions
“Conceptualization, H.-b.N. and S.-c.G.; methodology, H.-b.N.; software, H.-b.N.; validation, H.-b.N., S.-c.G.; formal analysis, H.-b.N.; investigation, H.-b.N.; resources, H.-b.N.; data curation, H.-b.N.; writing—original draft preparation, H.-b.N.; writing—review and editing, H.-b.N.; visualization, H.-b.N.; supervision, H.-b.N.; project administration, H.-b.N.; funding acquisition, N.H. All authors have read and agreed to the published version of the manuscript.”
Figure 1.
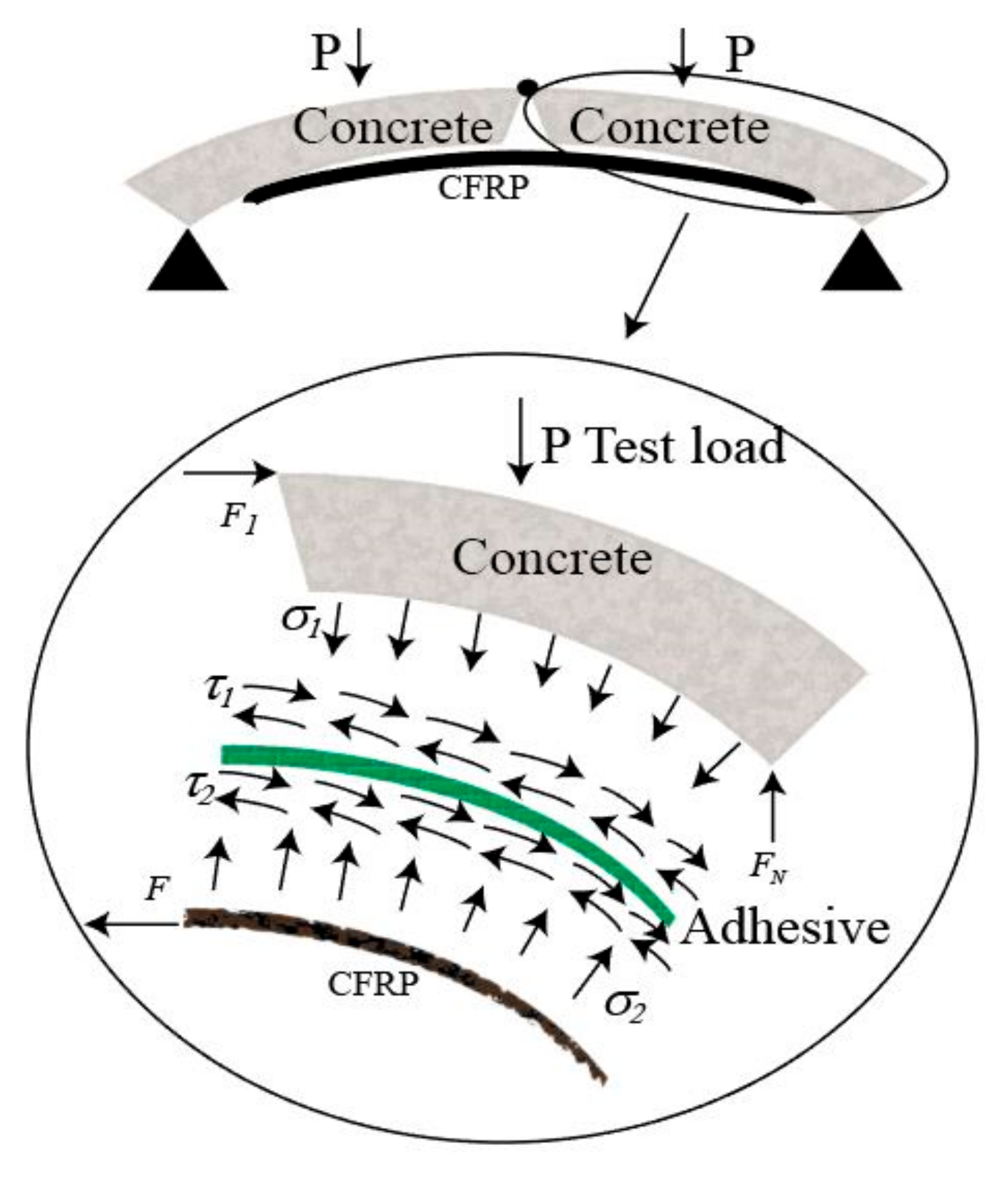
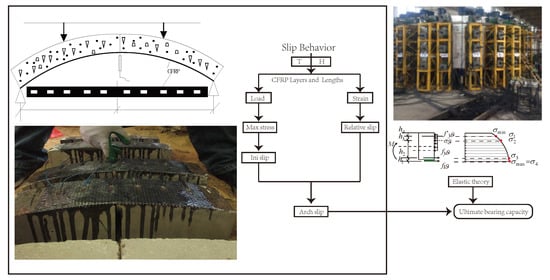
Design of problem statement. (a) Embedded methods, (b) single-shear method, (c) double-shear method, (d) reinforced notched beam, (e) bending and shear test, (f) stress model of this study.
Figure 1.
Design of problem statement. (a) Embedded methods, (b) single-shear method, (c) double-shear method, (d) reinforced notched beam, (e) bending and shear test, (f) stress model of this study.
Figure 2.
Location of strain gauge paste and rectangular CFRP. (a) Resistance strain gauge, (b) circular concrete pipe, (c) sticking CFRP.
Figure 2.
Location of strain gauge paste and rectangular CFRP. (a) Resistance strain gauge, (b) circular concrete pipe, (c) sticking CFRP.
Figure 3.
Accelerated loading of CFRP-strengthened tunnel segmental lining. (a) Test loading diagram, (b) schematic diagram.
Figure 3.
Accelerated loading of CFRP-strengthened tunnel segmental lining. (a) Test loading diagram, (b) schematic diagram.
Figure 4.
Typical failure mode of CFRP arch concrete. (a) The loading process, (b) the loading failure.
Figure 4.
Typical failure mode of CFRP arch concrete. (a) The loading process, (b) the loading failure.
Figure 5.
Typical failure mode of a tunnel segmental lining. (a) The failure of outer arch, (b) the failure of inner arch.
Figure 5.
Typical failure mode of a tunnel segmental lining. (a) The failure of outer arch, (b) the failure of inner arch.
Figure 6.
Loading of the CFRP parameters.
Figure 6.
Loading of the CFRP parameters.
Figure 7.
Deflection of the CFRP parameters.
Figure 7.
Deflection of the CFRP parameters.
Figure 8.
Limit load of CFRP parameters. (a) Temperature–load relationship under different humidity, (b) humidity–load relationship under different temperature.
Figure 8.
Limit load of CFRP parameters. (a) Temperature–load relationship under different humidity, (b) humidity–load relationship under different temperature.
Figure 9.
Limit loads under hygrothermal coupling.
Figure 9.
Limit loads under hygrothermal coupling.
Figure 10.
Relationship of shear stress and slope under different values of T and humidity. (a) Relationship between T and θ, (b) relationship between humidity and θ.
Figure 10.
Relationship of shear stress and slope under different values of T and humidity. (a) Relationship between T and θ, (b) relationship between humidity and θ.
Figure 11.
Ultimate strain of different lengths of CFRP bonding.
Figure 11.
Ultimate strain of different lengths of CFRP bonding.
Figure 12.
Ultimate strain of different CFRP layers of bonding length 350 mm.
Figure 12.
Ultimate strain of different CFRP layers of bonding length 350 mm.
Figure 13.
Ultimate strain of CFRP length 350 mm under different temperature.
Figure 13.
Ultimate strain of CFRP length 350 mm under different temperature.
Figure 14.
Ultimate strain of CFRP length 350 mm under different humidity.
Figure 14.
Ultimate strain of CFRP length 350 mm under different humidity.
Figure 15.
Interfacial shear stress and slip of CFRP bonding concrete arch. (a) Shear stress and slip curves for different CFRP lengths, (b) shear stress and slip curves for different, T.; (c) shear stress and slip curves for different CFRP layers, (d) shear stress and slip curves for different H, (e) maximum interfacial shear stress and slip curves for hygrothermal coupling.
Figure 15.
Interfacial shear stress and slip of CFRP bonding concrete arch. (a) Shear stress and slip curves for different CFRP lengths, (b) shear stress and slip curves for different, T.; (c) shear stress and slip curves for different CFRP layers, (d) shear stress and slip curves for different H, (e) maximum interfacial shear stress and slip curves for hygrothermal coupling.
Figure 16.
Tangential stress analysis.
Figure 16.
Tangential stress analysis.
Figure 17.
Ultimate load enhancement ratio of the CFRP bonding segment structure and joint.
Figure 17.
Ultimate load enhancement ratio of the CFRP bonding segment structure and joint.
Figure 18.
Comparison of the analytical and tested results. (a) Prestrengthening CFRP, (b) poststrengthening reinforced concrete.
Figure 18.
Comparison of the analytical and tested results. (a) Prestrengthening CFRP, (b) poststrengthening reinforced concrete.
Table 1.
Mechanical parameters of the CFRP and adhesive.
Table 1.
Mechanical parameters of the CFRP and adhesive.
| CFRP | Elastic Modulus
Ef(N/mm2) | | Ultimate Strength
|
|---|
| JGN | 2.5 × 105 | 1.5% | 3700 |
| Adhesive | | Ultimate Strength
| Elongation % | Bending Strength
|
| JGN-C | 26700 | 52 | 1.7 | 76 |
Table 2.
Slip testing parameters of CFRP-reinforced arch concrete sections.
Table 2.
Slip testing parameters of CFRP-reinforced arch concrete sections.
| Model Number | CFRP | Environmental Parameter | Model Number | CFRP | Environmental Parameter |
|---|
| Length | Layers | T/°C | H/% | Length | Layers | T/°C | H/% |
|---|
| 1-1 | 150 | 1 | 20 | 0% | 2-1 | 350 | 1 | 20 | 5% |
| 1-2 | 250 | 1 | 20 | 0% | 2-2 | 350 | 1 | 25 | 5% |
| 1-3 | 350 | 1 | 20 | 0% | 2-3 | 350 | 1 | 35 | 5% |
| 1-3-2 | 350 | 2 | 20 | 0% | 2-4 | 350 | 1 | 40 | 5% |
| 1-3-3 | 350 | 3 | 20 | 0% | 3-1 | 350 | 1 | 20 | 10% |
| 1-4-2 | 350 | 1 | 25 | 0% | 3-2 | 350 | 1 | 25 | 10% |
| 1-4-3 | 350 | 1 | 35 | 0% | 3-3 | 350 | 1 | 35 | 10% |
| 1-4-4 | 350 | 1 | 40 | 0% | 3-4 | 350 | 1 | 40 | 10% |
Table 3.
Limit load of damaged specimens.
Table 3.
Limit load of damaged specimens.
| Model Number | CFRP | Environmental Parameter | Loading/kN | Model Number | CFRP | Environmental Parameter | Loading/kN |
|---|
| Length | Layers | T/°C | H/% | Length | Layers | T/°C | H/% |
|---|
| 1-1 | 150 | 1 | 20 | 0% | 15.0 | 2-1 | 350 | 1 | 20 | 5% | 26.2 |
| 1-2 | 250 | 1 | 20 | 0% | 17.1 | 2-2 | 350 | 1 | 25 | 5% | 25.7 |
| 1-3 | 350 | 1 | 20 | 0% | 30.1 | 2-3 | 350 | 1 | 35 | 5% | 20.6 |
| 1-3-2 | 350 | 2 | 20 | 0% | 34.2 | 2-4 | 350 | 1 | 40 | 5% | 20.0 |
| 1-3-3 | 350 | 3 | 20 | 0% | 40.2 | 3-1 | 350 | 1 | 20 | 10% | 19.2 |
| 1-4-2 | 350 | 1 | 25 | 0% | 28.7 | 3-2 | 350 | 1 | 20 | 10% | 17.3 |
| 1-4-3 | 350 | 1 | 35 | 0% | 20.9 | 3-3 | 350 | 1 | 35 | 10% | 12.1 |
| 1-4-4 | 350 | 1 | 40 | 0% | 19.9 | 3-4 | 350 | 1 | 40 | 10% | 11.6 |
Table 4.
Related coefficients for limit load and temperature.
Table 4.
Related coefficients for limit load and temperature.
| Humidity/% | T0 | A1 | A2 | R2/% |
|---|
| 0 | 27.4 | 30.0 | 19.9 | 98.6 |
| 5 | 27.7 | 26.2 | 20.1 | 97.8 |
| 10 | 27.2 | 19.2 | 11.6 | 93.5 |
Table 5.
Related coefficients for limit load and humidity.
Table 5.
Related coefficients for limit load and humidity.
| Temperature/T °C | L0 | i | Ai | ti | R2/% |
|---|
| 20 | 30.0 | 2 | 2.03 | −8.29 | 99.7 |
| 25 | 28.7 | 2 | 0.56 | −4.19 | 96.7 |
| 30 | 20.9 | 2 | 0.01 | −1.49 | 97.8 |
| 40 | 19.9 | 2 | 1.16 × 10−6 | −0.78 | 92.8 |
Table 6.
Parameters for the relationship between the maximum shear stress and temperature.
Table 6.
Parameters for the relationship between the maximum shear stress and temperature.
| T °C | A3 | A4 | p | l0 | R2/% | leT/mm |
|---|
| 20 | 8431 | 0 | 3 | 41.8 | 99.8 | 110 |
| 25 | 7542 | 12 | 3 | 42.5 | 96.2 | 363 |
| 30 | 6024 | 10 | 3 | 40.2 | 97.5 | 409 |
| 40 | 3421 | 5 | 3 | 50.2 | 98.5 | 563 |
Table 7.
Parameters for the relationship between the maximum shear stress and humidity.
Table 7.
Parameters for the relationship between the maximum shear stress and humidity.
| Humidity | a | b | R2/% | leH/mm |
|---|
| 0% | 7169 | −58.1 | 87.7 | 110 |
| 5% | 4245 | −23.9 | 99.5 | 177 |
| 10% | 3972 | −17.6 | 98.1 | 226 |
Table 8.
Maximum interfacial shear stress and slip.
Table 8.
Maximum interfacial shear stress and slip.
| Model Number | CFRP | T/°C | H/% | d/mm | | S0 10−1 mm | | | S 10−1 mm |
|---|
| Length/mm | Layers |
|---|
| 1-1 | 150 | 1 | 20 | 0 | 12.0 | 0.94 | 0.34 | 50 | 2.16 | 1.05 |
| 1-2 | 250 | 1 | 20 | 0 | 20.0 | 1.33 | 0.96 | 75 | 6.13 | 3.03 |
| 1-3 | 350 | 1 | 20 | 0 | 30.8 | 1.50 | 1.36 | 110 | 8.73 | 5.07 |
| 1-3-2 | 350 | 2 | 20 | 0 | 25.1 | 1.37 | 1.49 | 126 | 9.61 | 5.22 |
| 1-3-3 | 350 | 3 | 20 | 0 | 14.9 | 1.01 | 1.52 | 148 | 9.76 | 5.23 |
| 1-4-2 | 350 | 1 | 25 | 0 | 31.2 | 1.54 | 1.15 | 150 | 7.36 | 4.97 |
| 1-4-3 | 350 | 1 | 30 | 0 | 35.6 | 1.59 | 0.76 | 150 | 4.88 | 3.46 |
| 1-4-4 | 350 | 1 | 40 | 0 | 40.3 | 1.67 | 0.68 | 150 | 4.36 | 2.42 |
| 2-1 | 350 | 1 | 20 | 5 | 33.2 | 1.57 | 1.01 | 150 | 6.46 | 3.97 |
| 2-2 | 350 | 1 | 25 | 5 | 34.2 | 1.58 | 0.96 | 150 | 6.19 | 3.59 |
| 2-3 | 350 | 1 | 30 | 5 | 37.9 | 1.64 | 0.73 | 150 | 4.68 | 3.11 |
| 2-4 | 350 | 1 | 40 | 5 | 42.6 | 1.69 | 0.65 | 150 | 4.18 | 2.81 |
| 3-1 | 350 | 1 | 20 | 10 | 35.3 | 1.58 | 0.70 | 150 | 4.50 | 4.53 |
| 3-2 | 350 | 1 | 25 | 10 | 36.0 | 1.63 | 0.64 | 150 | 4.09 | 3.89 |
| 3-3 | 350 | 1 | 30 | 10 | 39.2 | 1.66 | 0.42 | 150 | 2.68 | 3.29 |
| 3-4 | 350 | 1 | 40 | 10 | 45.3 | 1.81 | 0.38 | 150 | 2.45 | 2.69 |
Table 9.
Analytical and experimental results of the segment structure and joint under different humidity values.
Table 9.
Analytical and experimental results of the segment structure and joint under different humidity values.
| Spe. | Pre-Load | Ultimate Load | Ratio | Analytical Results on Slope of CFRP/MPa | Test Results of Segment Strengthened by CFRP/MPa |
|---|
| P1 | P2 | P2/P1 | | | | | | | | |
|---|
| A | 301 | 340 | 1.13 | 12.4 | 8.24 | 10.2 | 7.6 | 11.8 | 8.9 | 10.4 | 7.9 |
| B | 301 | 327 | 1.09 | 8.7 | 6.24 | 6.6 | 5.2 | 8.2 | 5.9 | 6.7 | 5.3 |
| C | 289 | 318 | 1.10 | 10.2 | 5.98 | 8.3 | 5.1 | 9.9 | 5.8 | 8.3 | 5.3 |
| D | 289 | 309 | 1.07 | 7.2 | 4.89 | 5.3 | 2.3 | 6.9 | 4.8 | 5.4 | 2.9 |
| E | 273 | 290 | 1.06 | 8.0 | 2.86 | 3.2 | 1.1 | 8.2 | 3.5 | 3.8 | 1.5 |
| F | 273 | 283 | 1.04 | 5.2 | 2.01 | 1.9 | 0.9 | 5.5 | 2.6 | 1.8 | 0.6 |
Table 10.
Comparison between the analytical and experimental results.
Table 10.
Comparison between the analytical and experimental results.
| Spe. | | | | |
|---|
| A | 1.05 | 0.92 | 0.99 | 0.96 |
| B | 1.06 | 1.06 | 0.98 | 0.98 |
| C | 1.04 | 1.03 | 1.00 | 0.97 |
| D | 1.04 | 1.02 | 0.99 | 0.82 |
| E | 0.97 | 0.81 | 0.83 | 0.70 |
| F | 0.95 | 0.78 | 1.03 | 1.39 |