Effect of Grain Refinement and Dispersion of Particles and Reinforcements on Mechanical Properties of Metals and Metal Matrix Composites through High-Ratio Differential Speed Rolling
Abstract
1. Introduction
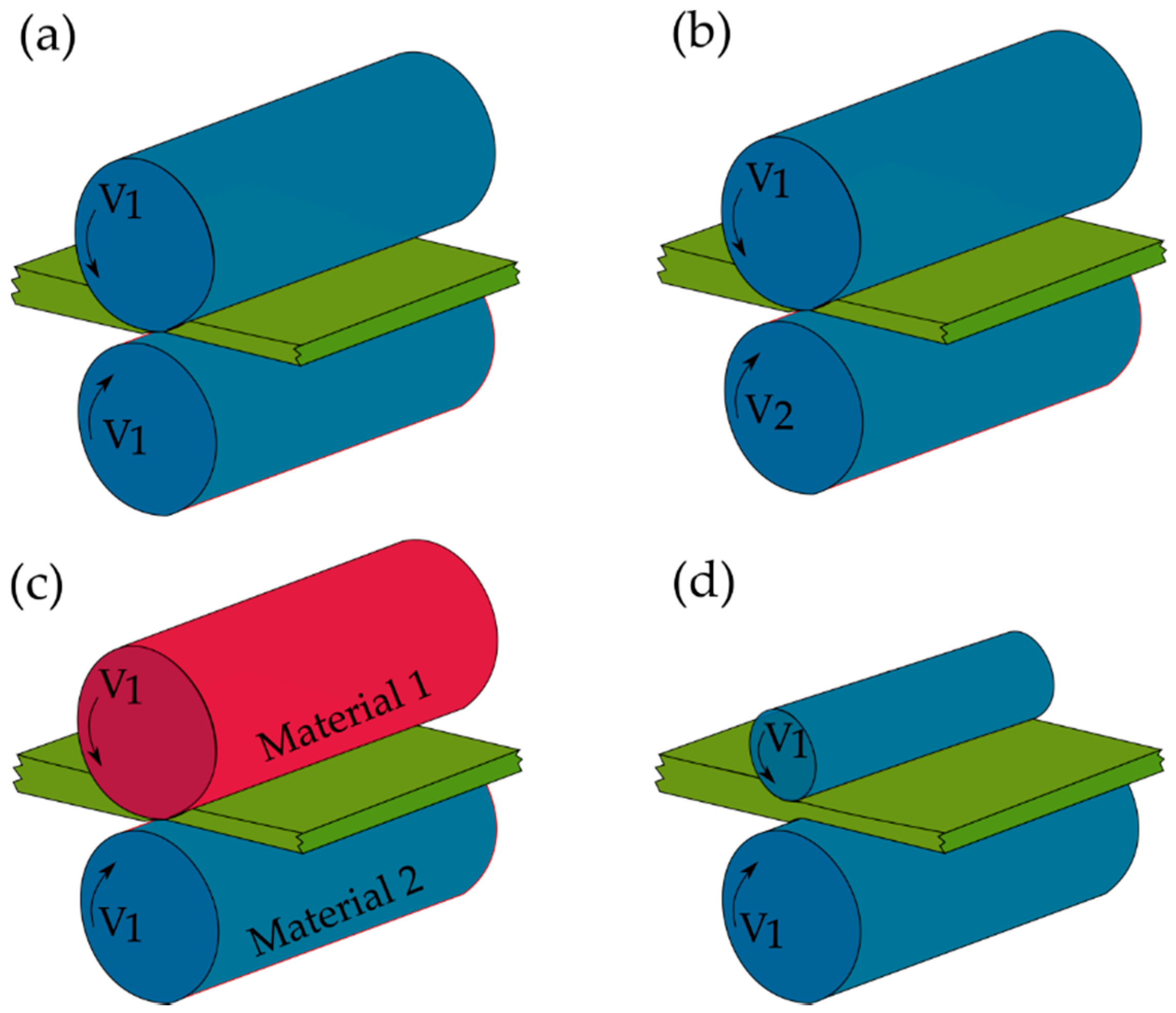
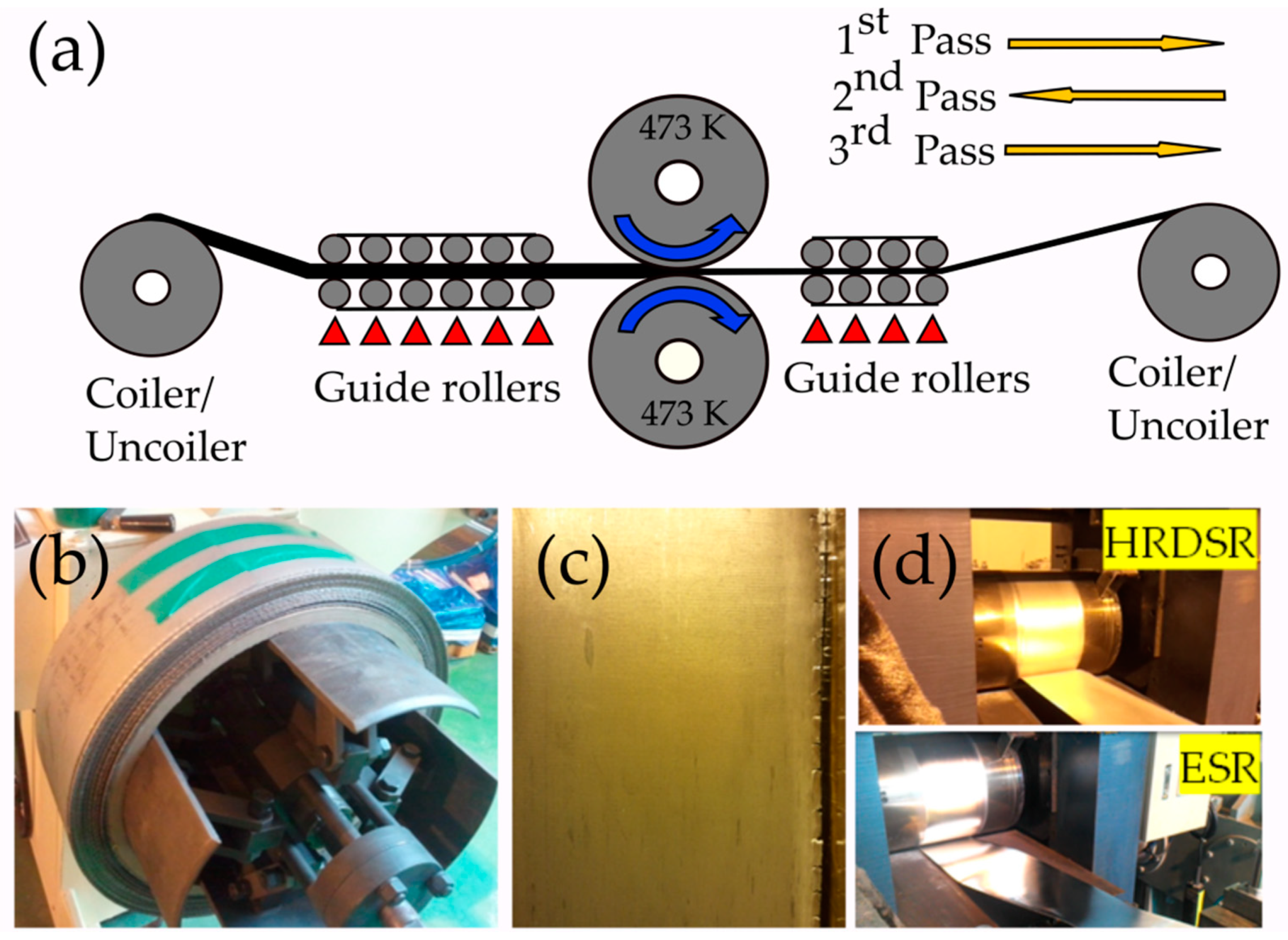
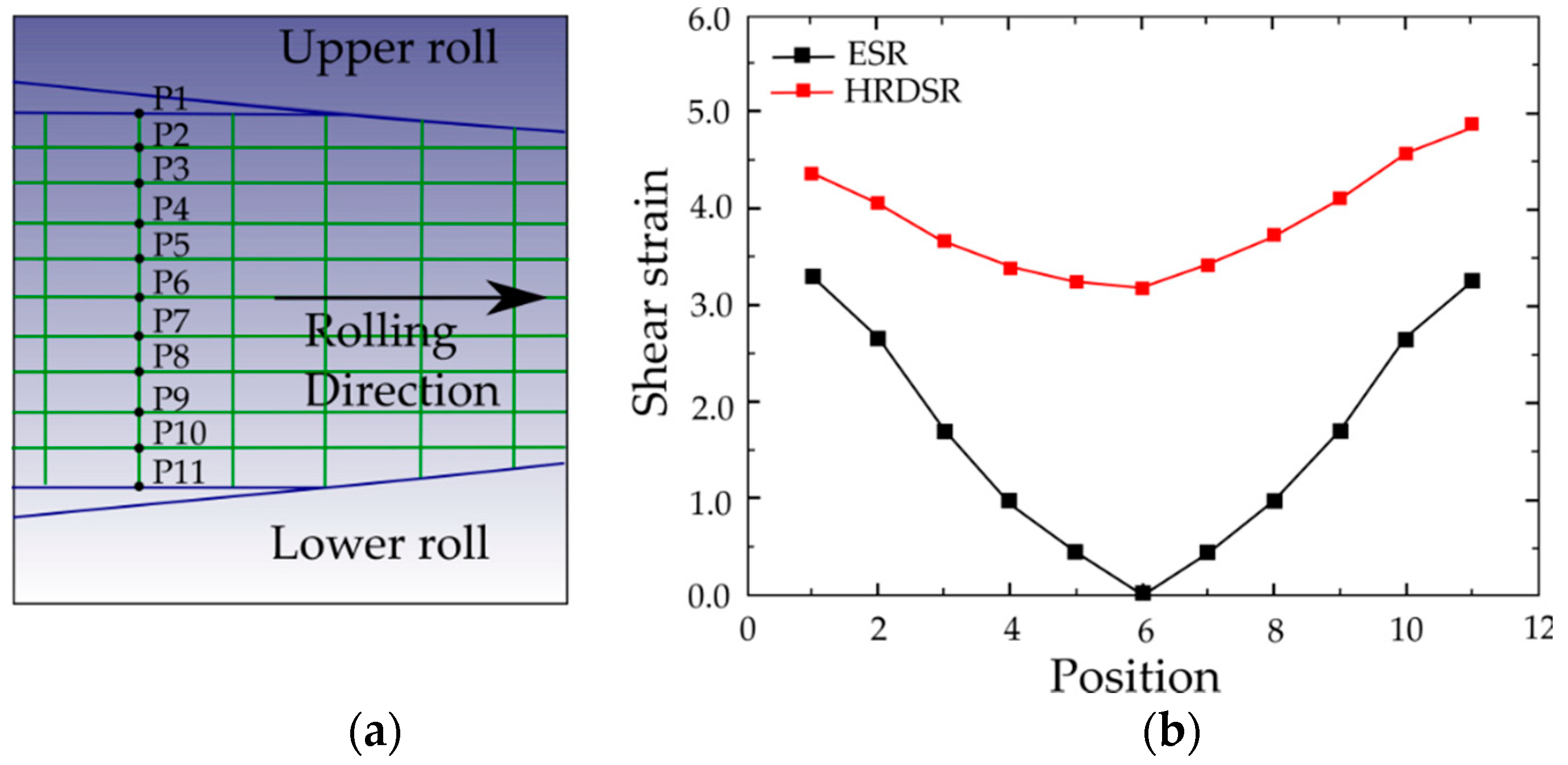
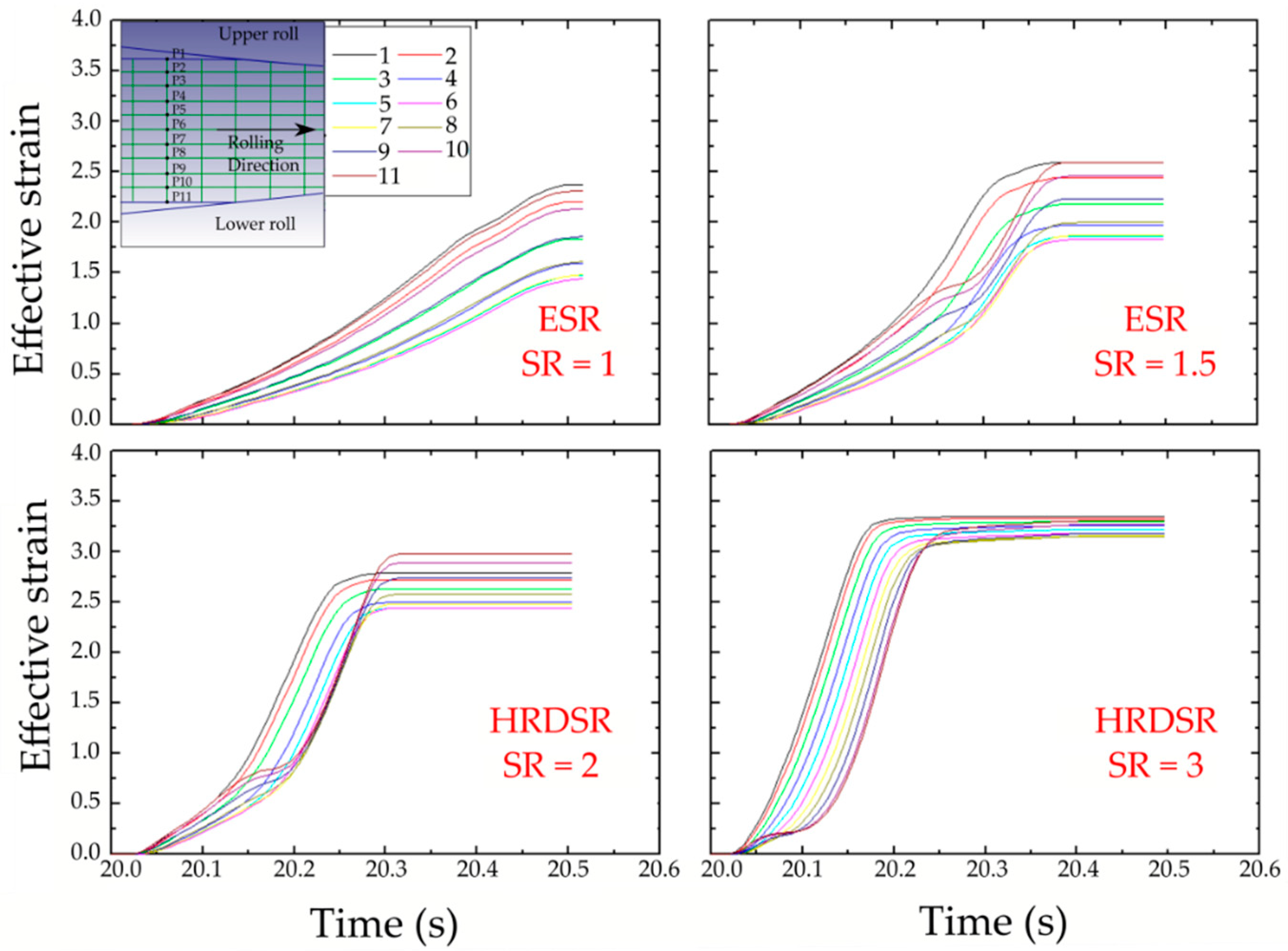
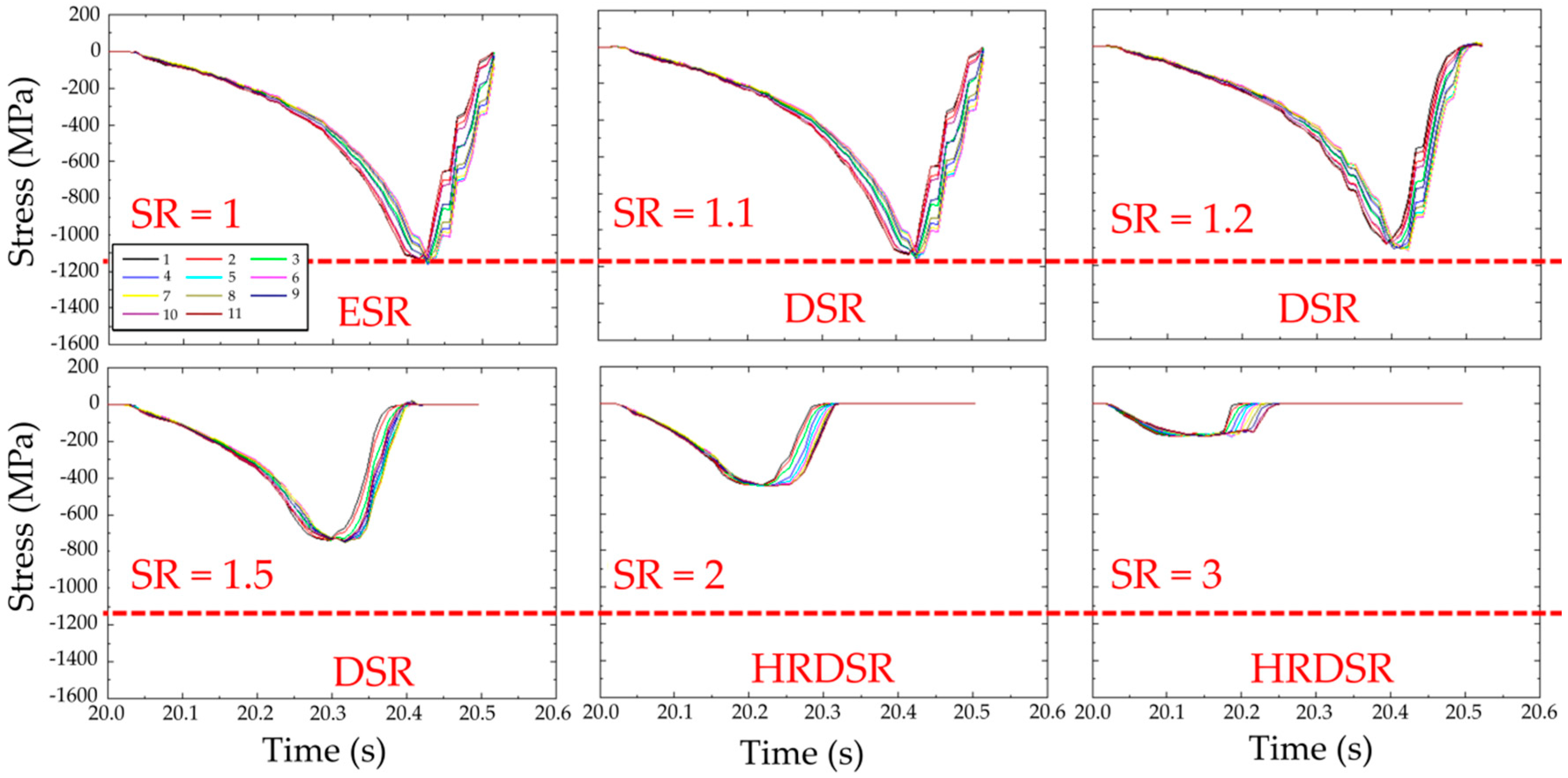
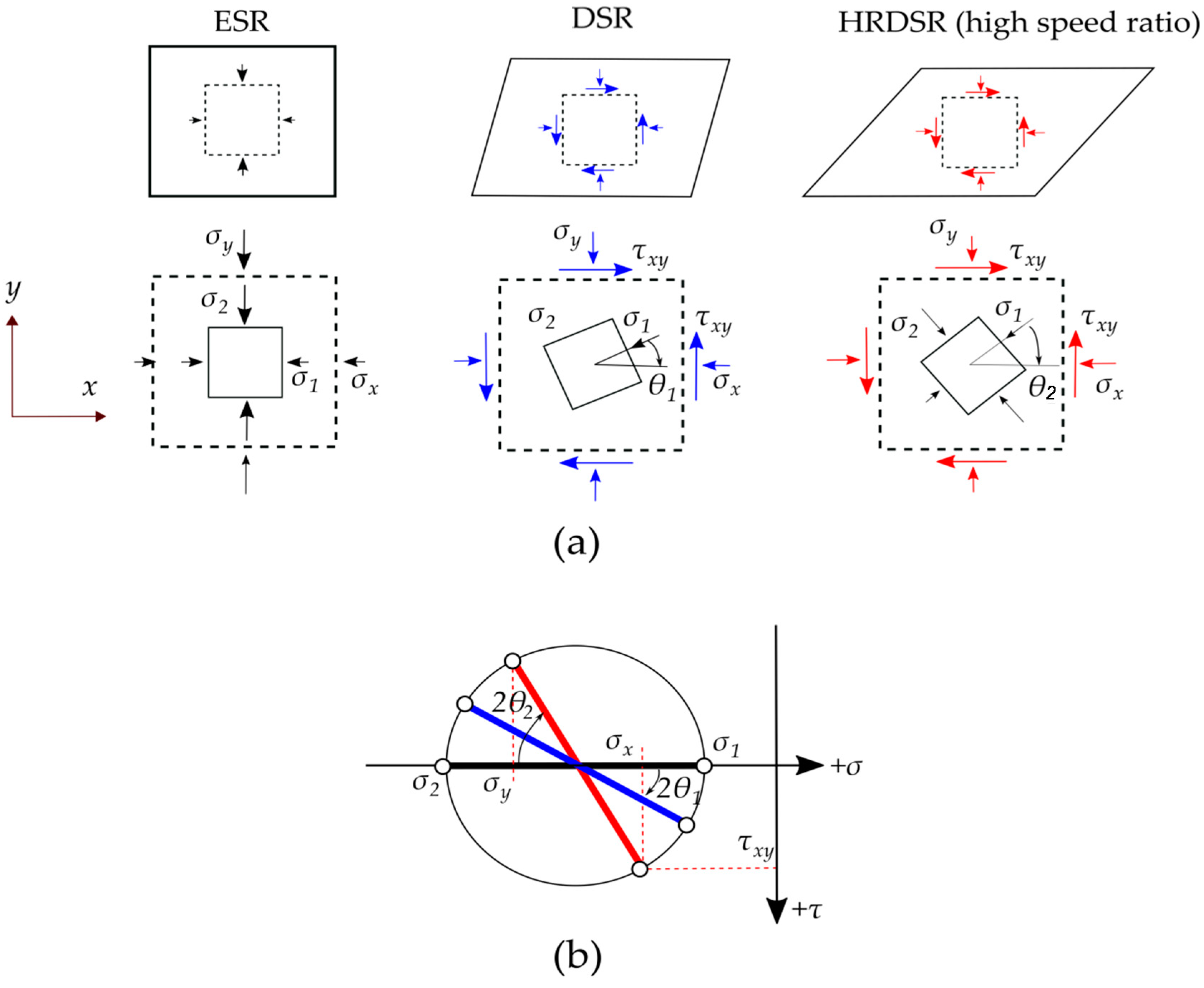
2. Method of Imposing a Large Plastic Deformation in HRDSR
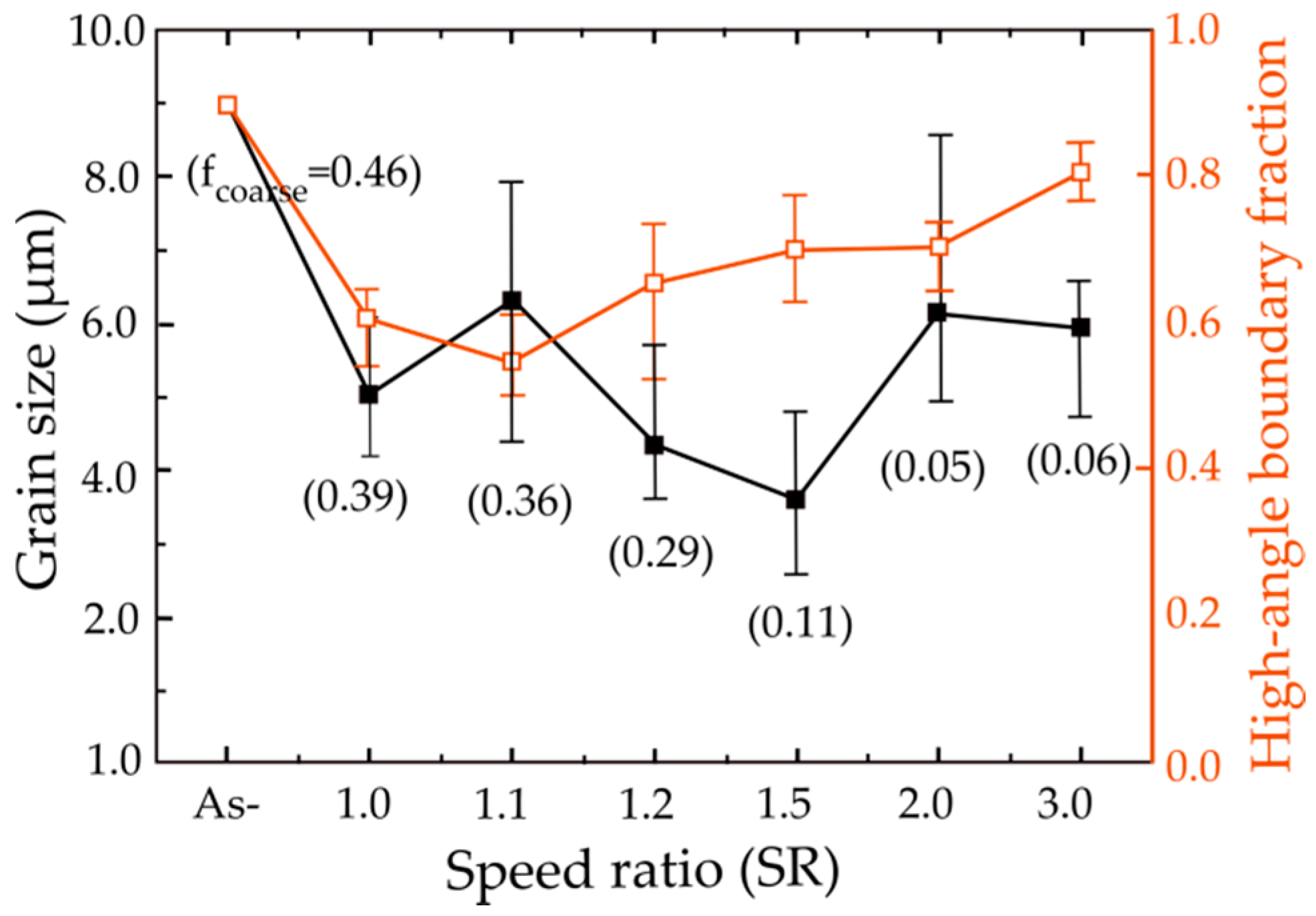
2.1. Effect of Roll-Speed Ratio on Microstructure
2.2. Principle of HRDSR
3. Enhancement of Mechanical Properties and Microstructures by HRDSR
3.1. High Strength and High Ductility
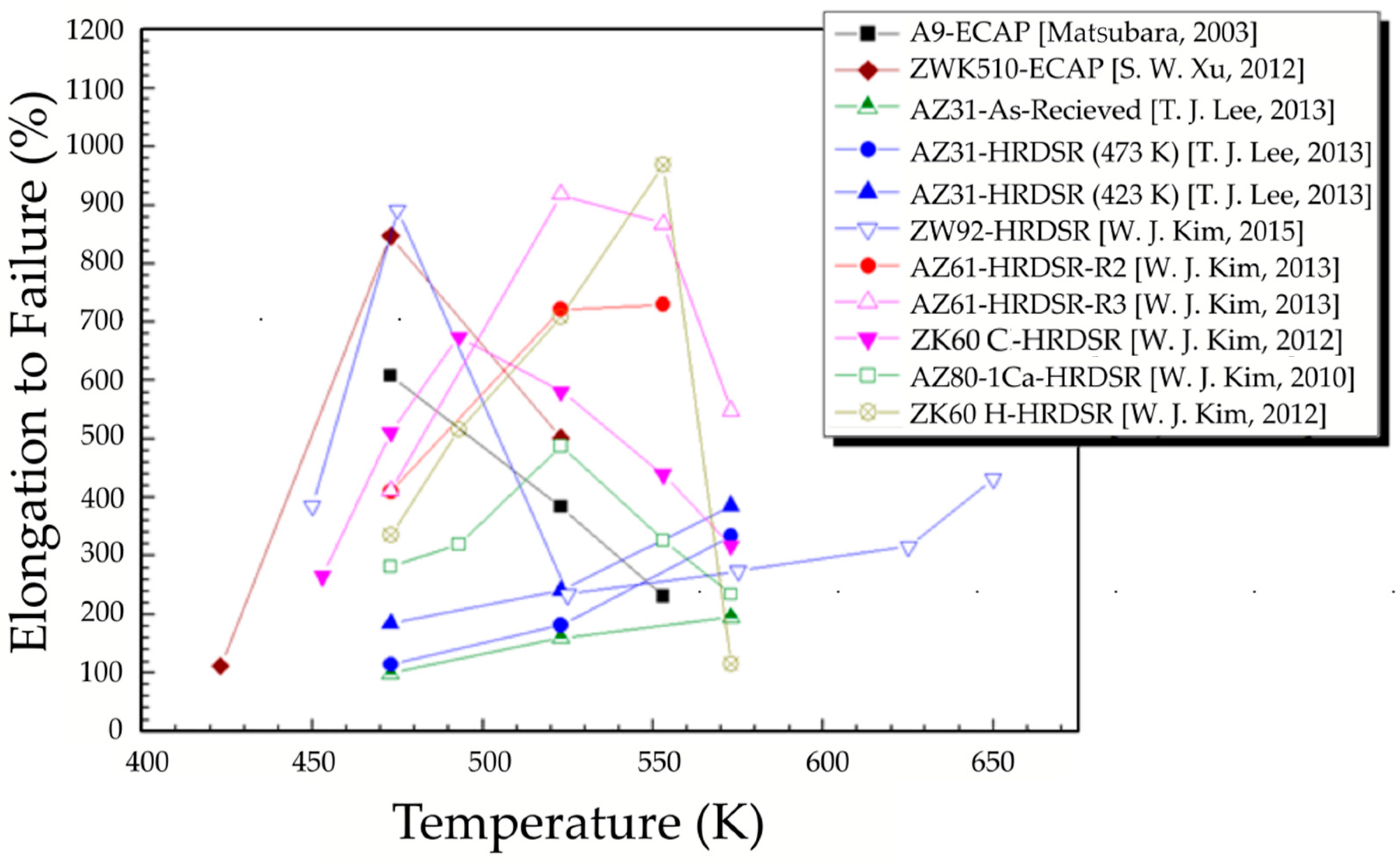
3.2. Enhanced Superplasticity
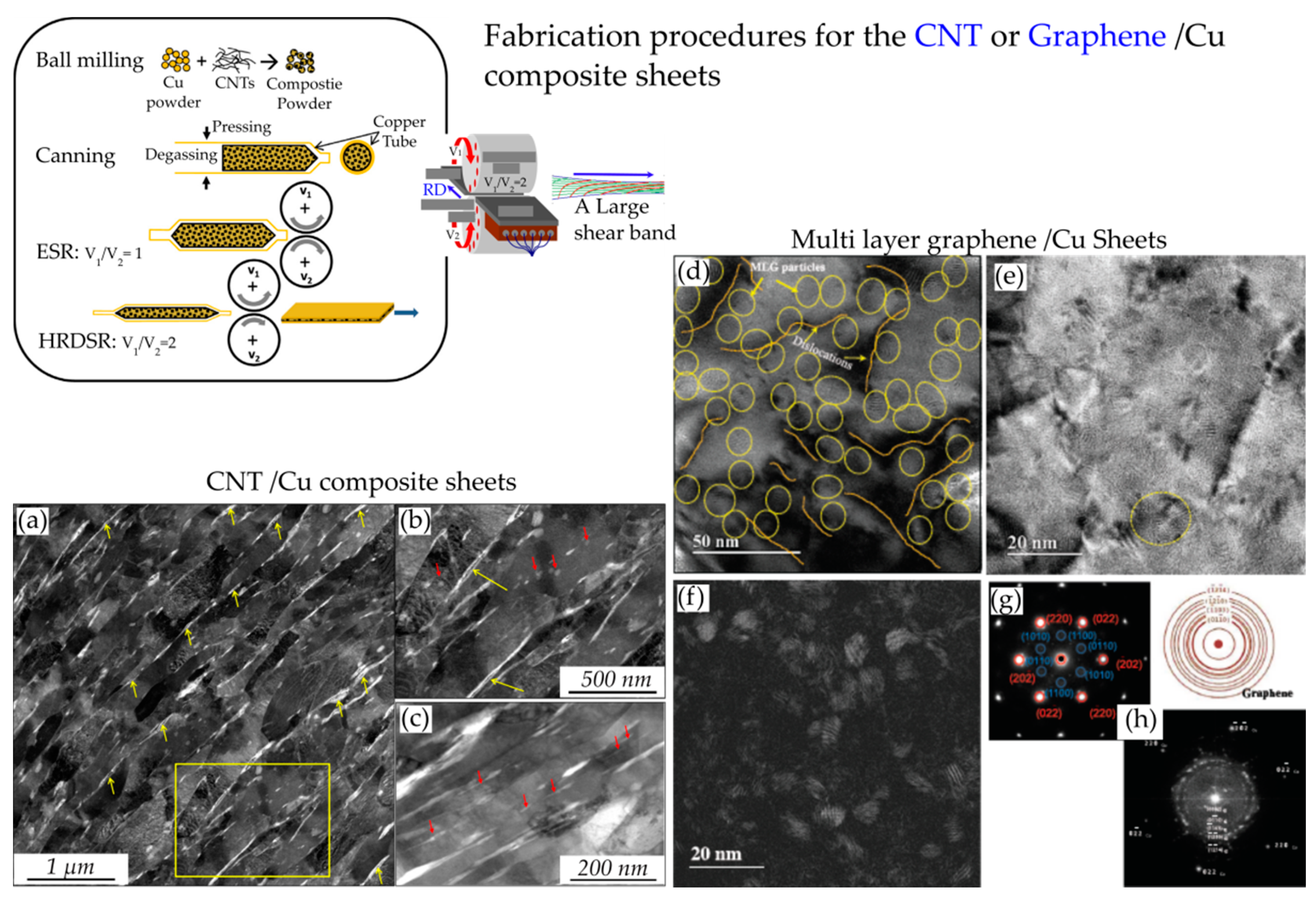
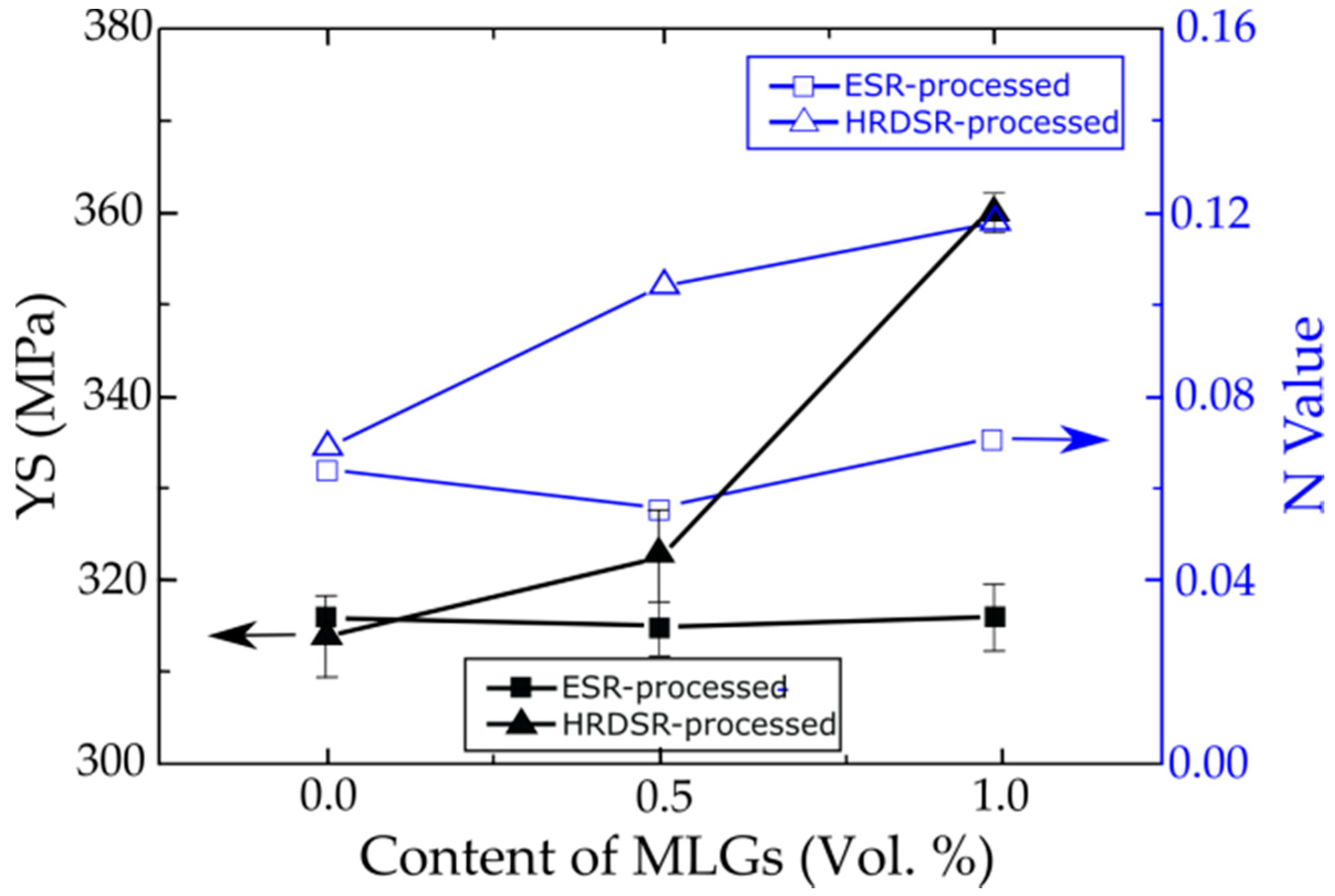
3.3. Metal Matrix Composites with Ultrafine Grains and Uniformly Dispersed Reinforcements
4. Summary and Conclusions
- HRDSR is a SPD rolling process that induces a large shear strain during thickness reduction. The key control parameter in HRDSR is the roll-speed ratio between the upper and lower rolls (≥2). Depending on the roll-speed ratio, friction condition, processing temperature and thickness reduction per pass, the texture and microstructure of materials can be controlled.
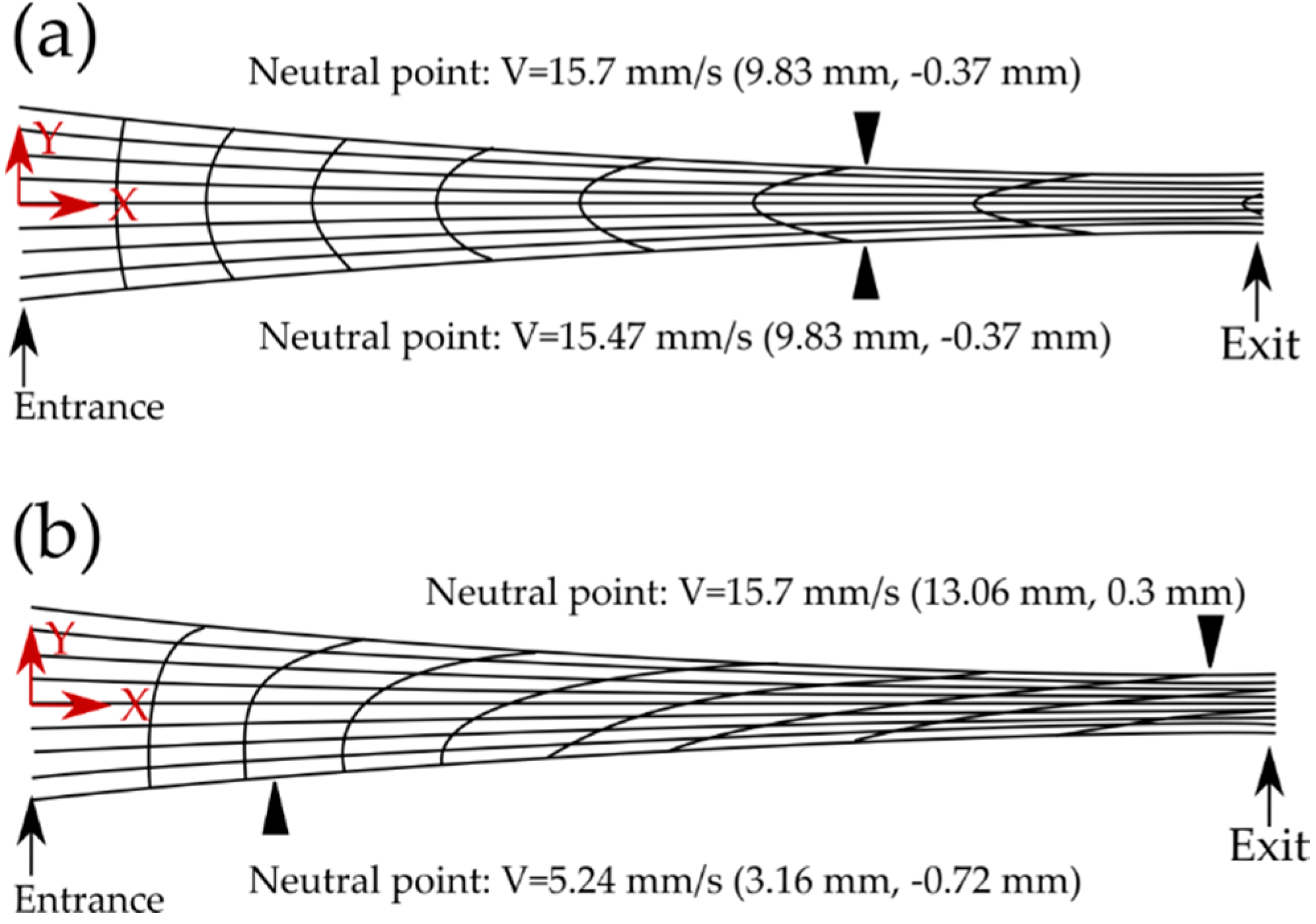
- As the accumulated effective strain in HRDSR is significantly larger than that in ESR and a much smaller lower roll force is imposed on the material in HRDSR than in ESR, ultrafine grained microstructure can be obtained in HRDSR with less effort. More homogeneously refined microstructures are also obtained in HRDSR compared to ESR, due to a more uniformly distributed strain along the thickness direction during rolling.
- Experimental results show that HRDSR is effective in improvement of strength/ductility and superplasticity through grain refinement, texture control and fragmentation and dispersion of secondary phase. HRDSR is also effective in fabricating metal matrix composites with high performance because the dispersion of reinforcement and grain refinement can be simultaneously and greatly enhanced by high shear flow induced during HRDSR.
- HRDSR has a high commercial application potential due to the possibility of scaling the product up to commercial dimensions and continuous production of the product, but there are many parameters (such as contact friction, thickness reduction per pass, the roll-speed ratio, the roll-speed and temperature, and the sheet temperature) that need to be optimized to achieve the texture controlled ultrafine-grained sheets with small surface roughness and uniform thickness distribution.
Author Contributions
Funding
Conflicts of Interest
References
- DeHoff, R.T. Engineering of microstructures. Mater. Res. 1999, 2, 111–126. [Google Scholar] [CrossRef][Green Version]
- Bahmani, A.; Arthanari, S.; Shin, K.S. Formulation of Corrosion Rate of Magnesium Alloys Using Microstructural Parameters. J. Magn. Alloys 2020, 8, 134–149. [Google Scholar] [CrossRef]
- Meyers, M.A.; Chawla, K.K. Mechanical Behavior of Materials, 2nd ed.; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Wei, Q.; Cheng, S.; Ramesh, K.T.; Ma, E. Effect of nanocrystalline and ultrafine grain sizes on the strain rate sensitivity and activation volume: Fcc versus bcc metals. Mater. Sci. Eng. A 2004, 381, 71–79. [Google Scholar] [CrossRef]
- Birbilis, N.; Ralston, K.D.; Virtanen, S.; Fraser, H.L.; Davies, C.H.J. Grain character influences on corrosion of ECAPed pure magnesium. Corr. Eng. Sci. Technol. 2010, 45, 224–230. [Google Scholar] [CrossRef]
- Chung, M.K.; Choi, Y.S.; Kim, J.G.; Kim, Y.M.; Lee, J.C. Effect of the number of ECAP pass time on the electrochemical properties of 1050 Al alloys. Mater. Sci. Eng. A 2004, 366, 282–291. [Google Scholar] [CrossRef]
- Yuan, Y.; Ma, A.; Gou, X.; Jiang, J.; Arhin, G.; Song, D.; Liu, H. Effect of heat treatment and deformation temperature on the mechanical properties of ECAP processed ZK60 magnesium alloy. Mater. Sci. Eng. A 2016, 677, 125–132. [Google Scholar] [CrossRef]
- Kim, W.J.; Hong, S.I.; Kim, Y.S.; Min, S.H.; Jeong, H.T.; Lee, J.D. Texture development and its effect on mechanical properties of an AZ61 Mg alloy fabricated by equal channel angular pressing. Acta Mater. 2003, 51, 3293–3307. [Google Scholar] [CrossRef]
- Gao, J.H.; Guan, S.K.; Ren, Z.W.; Sun, Y.F.; Zhu, S.J.; Wang, B. Homogeneous corrosion of high pressure torsion treated Mg–Zn–Ca alloy in simulated body fluid. Mater. Lett. 2011, 65, 691–693. [Google Scholar] [CrossRef]
- Ivanisenko, Y.; Kulagin, R.; Fedorov, V.; Mazilkin, A.; Scherer, T.; Baretzky, B.; Hahn, H. High pressure torsion extrusion as a new severe plastic deformation process. Mater. Sci. Eng. A 2016, 664, 247–256. [Google Scholar] [CrossRef]
- Hohenwarter, A. Incremental high pressure torsion as a novel severe plastic deformation process: Processing features and application to copper. Mater. Sci. Eng. A 2015, 626, 80–85. [Google Scholar] [CrossRef]
- Diez, M.; Kim, H.E.; Serebryany, V.; Dobatkin, S.; Estrin, Y. Improving the mechanical properties of pure magnesium by three-roll planetary milling. Mater. Sci. Eng. A 2014, 612, 287–292. [Google Scholar] [CrossRef]
- Wang, Y.L.; Molotnikov, A.; Diez, M.; Lapovok, R.; Kim, H.E.; Wang, J.T.; Estrin, Y. Gradient structure produced by three roll planetary milling: Numerical simulation and microstructural observations. Mater. Sci. Eng. A 2015, 639, 165–172. [Google Scholar] [CrossRef]
- Bahmani, A.; Shin, K.S. Effects of Severe Plastic Deformation on Mechanical Properties and Corrosion Behavior of Magnesium Alloys; Springer International Publishing: Cham, Switzerland, 2018; pp. 369–371. [Google Scholar] [CrossRef]
- Bahmani, A.; Arthanari, S.; Shin, K.S. Improvement of corrosion resistance and mechanical properties of a magnesium alloy using screw rolling. J. Alloys Compd. 2020, 813, 152155. [Google Scholar] [CrossRef]
- Morovvati, M.R.; Dariani, B.M. The effect of annealing on the formability of aluminum 1200 after accumulative roll bonding. J. Manuf. Proc. 2017, 30, 241–254. [Google Scholar] [CrossRef]
- Mashhadi, A.; Atrian, A.; Ghalandari, L. Mechanical and microstructural investigation of Zn/Sn multilayered composites fabricated by accumulative roll bonding (ARB) process. J. Alloys Compd. 2017, 727, 1314–1323. [Google Scholar] [CrossRef]
- Miura, H.; Nakamura, W.; Kobayashi, M. Room-temperature multi-directional forging of AZ80 Mg Alloy to induce ultrafine grained structure and specific mechanical properties. Procedia Eng. 2014, 81, 534–539. [Google Scholar] [CrossRef]
- Zhang, R.; Wang, D.; Yuan, S. Effect of multi-directional forging on the microstructure and mechanical properties of TiBw/TA15 composite with network architecture. Mater. Des. 2017, 134, 250–258. [Google Scholar] [CrossRef]
- Bahmani, A.; Arthanari, S.; Shin, K.S. Improved corrosion resistant and strength of a magnesium alloy using multi-directional forging (MDF). Int. J. Adv. Manuf. Technol. 2019, 105, 785–797. [Google Scholar] [CrossRef]
- Bahmani, A.; Shin, K.S. Controlling the microstructure and texture using multi-directional forging to develop a low corrosion rate Mg alloy. CORROSION 2020, 76, 750–765. [Google Scholar] [CrossRef]
- Wauthier, A.; Regle, H.; Formigoni, J.; Herman, G. The effects of asymmetrical cold rolling on kinetics, grain size and texture in IF steels. Mater. Charact. 2009, 60, 90–95. [Google Scholar] [CrossRef]
- Kim, Y.S.; Choi, E.; Kim, W.J. Characterization of the microstructures and the shape memory properties of the Fe-Mn-Si-Cr-Ni-C shape memory alloy after severe plastic deformation by differential speed rolling and subsequent annealing. Mater. Charact. 2018, 136, 12–19. [Google Scholar] [CrossRef]
- Polkowski, W. Differential speed rolling: A new method for a fabrication of metallic sheets with enhanced mechanical properties. In Progress in Metallic Alloys; InTechOpen: London, UK, 2016; pp. 111–126. [Google Scholar] [CrossRef]
- Lee, S.H.; Lee, D.N. Analysis of deformation textures of asymmetrically rolled steel sheets. Int. J. Mech. Sci. 2001, 43, 1997–2015. [Google Scholar] [CrossRef]
- Jin, H.; Lloyd, D.J. Evolution of texture in AA6111 aluminum alloy after asymmetric rolling with various velocity ratios between top and bottom rolls. Mater. Sci. Eng. A 2007, 465, 267–273. [Google Scholar] [CrossRef]
- Kim, M.G.; Kim, W.J.; Kim, G.H.; Cho, K.-K.; Han, J.H.; Kim, H.S. Microstructural evolution and electrochemical properties of HRDSR AZ61-X (X = Ca, Ti) alloys. J. Nanosci. Nanotechnol. 2018, 18, 6081–6089. [Google Scholar] [CrossRef] [PubMed]
- Loorent, Z.; Ko, Y.G. Effect of differential speed rolling strain on microstructure and mechanical properties of nanostructured 5052 Al alloy. J. Alloys Compd. 2014, 586, 205–209. [Google Scholar] [CrossRef]
- Loorent, Z.; Ko, Y.G. Microstructure evolution and mechanical properties of severely deformed Al alloy processed by differential speed rolling. J. Alloys Compd. 2012, 536, 122–125. [Google Scholar] [CrossRef]
- Ko, Y.G.; Lee, J.S.; Loorent, Z. Microstructure evolution and mechanical properties of ultrafine grained IF steel via multipass differential speed rolling. Mater. Sci. Technol. 2013, 29, 553–558. [Google Scholar] [CrossRef]
- Kim, H.S.; Kim, W.J. Enhanced corrosion resistance of ultrafine-grained AZ61 alloy containing very fine particles of Mg17Al12 phase. Corros. Sci. 2013, 75, 228–238. [Google Scholar] [CrossRef]
- Siebel, E. The theory of rolling process with separately driven rolls. Arch. Iron Steel Ind. 1941, 15, 125–128. [Google Scholar]
- Kim, W.J.; Lee, Y.G.; Lee, M.J.; Wang, J.Y.; Park, Y.B. Exceptionally high strength in Mg–3Al–1Zn alloy processed by high-ratio differential speed rolling. Scr. Mater. 2011, 65, 1105–1108. [Google Scholar] [CrossRef]
- Kim, W.J.; Lee, M.J.; Lee, B.H.; Park, Y.B. A strategy for creating ultrafine-grained microstructure in magnesium alloy sheets. Mater. Lett. 2010, 64, 647–649. [Google Scholar] [CrossRef]
- Kim, W.J.; Lee, J.B.; Kim, W.Y.; Jeong, H.T.; Jeong, H.G. Microstructure and mechanical properties of Mg–Al–Zn alloy sheets severely deformed by asymmetrical rolling. Scr. Mater. 2007, 56, 309–312. [Google Scholar] [CrossRef]
- Seong, J.W.; Kim, W.J. Development of biodegradable Mg-Ca alloy sheets with enhanced strength and corrosion properties through the refinement and uniform dispersion of the Mg2Ca phase by high-ratio differential speed rolling. Acta Biomater. 2015, 11, 531–542. [Google Scholar] [CrossRef]
- Kim, W.Y.; Kim, W.J. Fabrication of ultrafine-grained Mg–3Al–1Zn magnesium alloy sheets using a continuous high-ratio differential speed rolling technique. Mater. Sci. Eng. A 2014, 594, 189–192. [Google Scholar] [CrossRef]
- Pesin, A.; Pustovoytov, D.; Lokotunina, N. Modeling of the roll wear and material damage during high-ratio differential speed rolling of aluminium alloy 7075. In MATEC Web of Conferences; EDP Sciences: Les Ulis, France, 2016; Volume 80, p. 04006. [Google Scholar] [CrossRef]
- Pesin, A.; Korchunov, A.; Pustovoytov, D. Numerical study of grain evolution and dislocation density during asymmetric rolling of aluminum alloy 7075. Key Eng. Mater. 2016, 85, 162–166. [Google Scholar] [CrossRef]
- Kim, W.J.; Hwang, B.G.; Lee, M.J.; Park, Y.B. Effect of speed-ratio on microstructure, and mechanical properties of Mg–3Al–1Zn alloy, in differential speed rolling. J. Alloys Compd. 2011, 509, 8510–8517. [Google Scholar] [CrossRef]
- Kim, W.J.; Yoo, S.J.; Jeong, H.T.; Kim, D.M.; Choe, B.H.; Lee, J.B. Effect of the speed ratio on grain refinement and texture development in pure Ti during differential speed rolling. Scr. Mater. 2011, 64, 49–52. [Google Scholar] [CrossRef]
- Polkowski, W.; Jóźwik, P.; Polański, M.; Bojar, Z. Microstructure and texture evolution of copper processed by differential speed rolling with various speed asymmetry coefficient. Mater. Sci. Eng. A 2013, 564, 289–297. [Google Scholar] [CrossRef]
- Yu, H.; Lu, C.; Tieu, K.; Liu, X.; Sun, Y.; Yu, Q.; Kong, C. Asymmetric cryorolling for fabrication of nanostructural aluminum sheets. Sci. Rep. 2012, 2, 772. [Google Scholar] [CrossRef]
- Han, S.H.; Kim, W.J. Achievement of nearly fully amorphous structure from NiTi alloys via differential speed rolling 268 K and effect of annealing on superelasticity. Mater. Charact. 2020, 169, 110584. [Google Scholar] [CrossRef]
- Ji, Y.H.; Park, J.J.; Kim, W.J. Finite element analysis of severe deformation in Mg–3Al–1Zn sheets through differential-speed rolling with a high speed ratio. Mater. Sci. Eng. A 2007, 454–455, 570–574. [Google Scholar] [CrossRef]
- Kim, W.J.; Hong, S.I.; Lee, J.M.; Kim, S.H. Dispersion of TiC particles in an in situ aluminum matrix composite by shear plastic flow during high-ratio differential speed rolling. Mater. Sci. Eng. A 2013, 559, 325–332. [Google Scholar] [CrossRef]
- Kim, W.J. The effect of roll speed ratio on magnitude and distribution of effective strain and roll pressure in differential speed rolling. Unpublished, manuscript in preparation.
- Ji, Y.H.; Park, J.J. Analysis of thermo-mechanical process occurred in magnesium alloy AZ31 sheet during differential speed rolling. Mater. Sci. Eng. A 2008, 485, 299–304. [Google Scholar] [CrossRef]
- Jeong, H.T.; Kim, H.K.; Utsunomiya, H.; Choi, E.; Kim, W.J. Fabrication of a thin open-cell Ni foam sheet with a high specific strength and moderate porosity using severe plastic deformation via differential speed rolling. Mater. Sci. Eng. A 2019, 750, 7–13. [Google Scholar] [CrossRef]
- Yu, H.; Xin, Y.; Wang, M.; Liu, Q. Hall-Petch relationship in Mg alloys: A review. J. Mater. Sci. Technol. 2018, 34, 248–256. [Google Scholar] [CrossRef]
- Armstrong, R.; Codd, I.; Douthwaite, R.M.; Petch, N.J. The plastic deformation of polycrystalline aggregates. Philos. Mag. J. Theor. Exper. Appl. Phys. 1962, 7, 45–58. [Google Scholar] [CrossRef]
- Wang, Y.; Choo, H. Influence of texture on Hall–Petch relationships in an Mg alloy. Acta Mater. 2014, 81, 83–97. [Google Scholar] [CrossRef]
- Yuan, W.; Panigrahi, S.K.; Su, J.Q.; Mishra, R.S. Influence of grain size and texture on Hall–Petch relationship for a magnesium alloy. Scr. Mater. 2011, 65, 994–997. [Google Scholar] [CrossRef]
- Kwak, T.Y.; Kim, W.J. Mechanical properties and Hall-Petch relationship of the extruded Mg-Zn-Y alloys with different volume fractions of icosahedral phase. J. Alloys Compd. 2019, 770, 589–599. [Google Scholar] [CrossRef]
- Tong, L.B.; Zheng, M.Y.; Hu, X.S.; Wu, K.; Xu, S.W.; Kamado, S.; Kojima, Y. Influence of ECAP routes on microstructure and mechanical properties of Mg–Zn–Ca alloy. Mater. Sci. Eng. A 2010, 527, 4250–4256. [Google Scholar] [CrossRef]
- Singh, A.; Osawa, Y.; Somekawa, H.; Mukai, T. Effect of microstructure on strength and ductility of high strength quasicrystal phase dispersed Mg–Zn–Y alloys. Mater. Sci. Eng. A 2014, 611, 242–251. [Google Scholar] [CrossRef]
- Zhang, H.; Huang, G.; Roven, H.J.; Wang, L.; Pan, F. Influence of different rolling routes on the microstructure evolution and properties of AZ31 magnesium alloy sheets. Mater. Des. 2013, 50, 667–673. [Google Scholar] [CrossRef]
- Zhang, H.; Huang, G.; Wang, L.; Roven, H.J.; Pan, F. Enhanced mechanical properties of AZ31 magnesium alloy sheets processed by three-directional rolling. J. Alloys Compd. 2013, 575, 408–413. [Google Scholar] [CrossRef]
- Huang, X.; Suzuki, K.; Saito, N. Enhancement of stretch formability of Mg–3Al–1Zn alloy sheet using hot rolling at high temperatures up to 823 K and subsequent warm rolling. Scr. Mater. 2009, 61, 445–448. [Google Scholar] [CrossRef]
- Huang, X.; Suzuki, K.; Saito, N. Textures and stretch formability of Mg–6Al–1Zn magnesium alloy sheets rolled at high temperatures up to 793 K. Scr. Mater. 2009, 60, 651–654. [Google Scholar] [CrossRef]
- Kim, Y.H.; Sohn, H.T.; Kim, W.J. Ductility enhancement through texture control and strength restoration through subsequent age-hardening in Mg–Zn–Zr alloys. Mater. Sci. Eng. A 2014, 597, 157–163. [Google Scholar] [CrossRef]
- Huang, X.; Suzuki, K.; Watazu, A.; Shigematsu, I.; Saito, N. Improvement of formability of Mg–Al–Zn alloy sheet at low temperatures using differential speed rolling. J. Alloys Compd. 2009, 470, 263–268. [Google Scholar] [CrossRef]
- Yang, Q.; Ghosh, A.K. Production of ultrafine-grain microstructure in Mg alloy by alternate biaxial reverse corrugation. Acta Mater. 2006, 54, 5147–5158. [Google Scholar] [CrossRef]
- Ding, S.X.; Lee, W.T.; Chang, C.P.; Chang, L.W.; Kao, P.W. Improvement of strength of magnesium alloy processed by equal channel angular extrusion. Scr. Mater. 2008, 59, 1006–1009. [Google Scholar] [CrossRef]
- Kim, W.J.; Jeong, H.T. Grain size strengthening in equal-channel-angular-pressing processed az31 mg alloys with a constant texture. Mater. Trans. 2005, 46, 251–258. [Google Scholar] [CrossRef]
- Liao, J.; Hotta, M.; Kaneko, K.; Kondoh, K. Enhanced impact toughness of magnesium alloy by grain refinement. Scr. Mater. 2009, 61, 208–211. [Google Scholar] [CrossRef]
- Wang, Y.N.; Huang, J.C. Grain size dependence of yield strength in randomly textured Mg-Al-Zn alloy. Mater. Trans. 2007, 48, 184–188. [Google Scholar] [CrossRef]
- Kim, M.G.; Kim, J.K.; Kim, H.S.; Kim, W.J.; Han, J.H. Effect of post-annealing and strong deformation process on the mechanical and corrosion properties of a Mg-Mn alloy for biomedical application. J. Korean Phys. Soc. 2018, 72, 692–698. [Google Scholar] [CrossRef]
- Polkowski, W.A.; Polkowska, A.; Zasada, D. Characterization of high strength nickel thin sheets fabricated by differential speed rolling method. Mater. Charact. 2017, 130, 173–180. [Google Scholar] [CrossRef]
- Kim, W.J.; Park, J.D.; Kim, W.Y. Effect of differential speed rolling on microstructure and mechanical properties of an AZ91 magnesium alloy. J. Alloys Compd. 2008, 460, 289–293. [Google Scholar] [CrossRef]
- Kim, W.J.; Lee, K.E.; Choi, S.H. Mechanical properties and microstructure of ultra fine-grained copper prepared by a high-speed-ratio differential speed rolling. Mater. Sci. Eng. A 2009, 506, 71–79. [Google Scholar] [CrossRef]
- Kim, W.J.; Wang, J.Y.; Choi, S.O.; Choi, H.J.; Sohn, H.T. Synthesis of ultra high strength Al–Mg–Si alloy sheets by differential speed rolling. Mater. Sci. Eng. A 2009, 520, 23–28. [Google Scholar] [CrossRef]
- Jiang, J.; Ding, Y.; Zuo, F.; Shan, A. Mechanical properties and microstructures of ultrafine-grained pure aluminum by asymmetric rolling. Scr. Mater. 2009, 60, 905–908. [Google Scholar] [CrossRef]
- Yoo, S.J.; Han, S.H.; Kim, W.J. A combination of ball milling and high-ratio differential speed rolling for synthesizing carbon nanotube/copper composites. Carbon 2013, 61, 487–500. [Google Scholar] [CrossRef]
- Stolyarov, V.V.; Zeipper, L.; Mingler, B.; Zehetbauer, M. Influence of post-deformation on CP-Ti processed by equal channel angular pressing. Mater. Sci. Eng. A 2008, 476, 98–105. [Google Scholar] [CrossRef]
- Kim, W.J.; Yoo, S.J.; Lee, J.B. Microstructure and mechanical properties of pure Ti processed by high-ratio differential speed rolling at room temperature. Scr. Mater. 2010, 62, 451–454. [Google Scholar] [CrossRef]
- Stolyarov, V.V.; Zhu, Y.T.; Lowe, T.C.; Islamgaliev, R.K.; Valiev, R.Z. A two step SPD processing of ultrafine-grained titanium. Nanostruct. Mater. 1999, 11, 947–954. [Google Scholar] [CrossRef]
- Stolyarov, V.V.; Zhu, Y.T.; Alexandrov, I.V.; Lowe, T.C.; Valiev, R.Z. Grain refinement and properties of pure Ti processed by warm ECAP and cold rolling. Mater. Sci. Eng. A 2003, 343, 43–50. [Google Scholar] [CrossRef]
- Terada, D.; Inoue, M.; Kitahara, H.; Tsuji, N. Change in mechanical properties and microstructure of ARB processed Ti during annealing. Mater. Trans. 2008, 49, 41–46. [Google Scholar] [CrossRef]
- Kawasaki, M.; Langdon, T.G. Principles of superplasticity in ultrafine-grained materials. J. Mater. Sci. 2007, 42, 1782–1796. [Google Scholar] [CrossRef]
- Figueiredo, R.B.; Langdon, T.G. Developing superplasticity in a magnesium AZ31 alloy by ECAP. J. Mater. Sci. 2008, 43, 7366–7371. [Google Scholar] [CrossRef]
- Kim, W.J.; Chung, S.W.; Chung, C.S.; Kum, D. Superplaticity in thin Magnesium alloy sheet and deformation mechanism maps for magnesium at elevated temperatures. Acta Mater. 2001, 49, 3337–3345. [Google Scholar] [CrossRef]
- Kim, W.J.; Lee, B.H.; Lee, J.B.; Lee, M.J.; Park, Y.B. Synthesis of high-strain-rate superplastic magnesium alloy sheets using a high-ratio differential speed rolling technique. Scr. Mater. 2010, 63, 772–775. [Google Scholar] [CrossRef]
- Kwak, T.Y.; Lim, H.K.; Han, S.H.; Kim, W.J. Refinement of the icosahedral quasicrystalline phase and the grain size of Mg–9.25Zn–1.66Y alloy by high-ratio differential speed rolling. Scr. Mater. 2015, 103, 49–52. [Google Scholar] [CrossRef]
- Kim, W.J.; Lee, Y.G. Enhanced superplasticity of 1wt.%Ca-AZ80 Mg alloy with ultrafine grains. Mater. Lett. 2010, 64, 1759–1762. [Google Scholar] [CrossRef]
- Lee, T.J.; Park, Y.B.; Kim, W.J. Importance of diffusional creep in fine grained Mg–3Al–1Zn alloys. Mater. Sci. Eng. A 2013, 580, 133–141. [Google Scholar] [CrossRef]
- Kim, W.J.; Yoo, Y.J. Low temperature superplasticity of ultrafine grained Mg–9.25Zn–1.66Y alloy with an icosahedral quasicrystalline phase. Mater. Sci. Eng. A 2015, 643, 47–50. [Google Scholar] [CrossRef]
- Kim, W.J.; Park, I.B. Enhanced superplasticity and diffusional creep in ultrafine-grained Mg–6Al–1Zn alloy with high thermal stability. Scr. Mater. 2013, 68, 179–182. [Google Scholar] [CrossRef]
- Kim, W.J.; Moon, I.K.; Han, S.H. Ultrafine-grained Mg–Zn–Zr alloy with high strength and high-strain-rate superplasticity. Mater. Sci. Eng. A 2012, 538, 374–385. [Google Scholar] [CrossRef]
- Matsubara, K.; Miyahara, Y.; Horita, Z.; Langdon, T.G. Developing superplasticity in a magnesium alloy through a combination of extrusion and ECAP. Acta Mater. 2003, 51, 3073–3084. [Google Scholar] [CrossRef]
- Xu, S.W.; Zheng, M.Y.; Kamado, S.; Wu, K. The microstructural evolution and superplastic behavior at low temperatures of Mg–5.00Zn–0.92Y–0.16Zr (wt.%) alloys after hot extrusion and ECAP process. Mater. Sci. Eng. A 2012, 549, 60–68. [Google Scholar] [CrossRef]
- Lee, T.J.; Kim, W.J. Successful transition from low-temperature superplasticity to high-strain-rate superplasticity with increasing temperature in an ultrafine-grained Mg–Y–Zn–Zr alloy. J. Alloys Compd. 2020, 817, 153298. [Google Scholar] [CrossRef]
- Kim, W.J.; Lee, T.J.; Han, S.H. Multi-layer graphene/copper composites: Preparation using high-ratio differential speed rolling, microstructure and mechanical properties. Carbon 2014, 69, 55–65. [Google Scholar] [CrossRef]
- Kim, W.J.; Yu, Y.J. The effect of the addition of multiwalled carbon nanotubes on the uniform distribution of TiC nanoparticles in aluminum nanocomposites. Scr. Mater. 2014, 72–73, 25–28. [Google Scholar] [CrossRef]
- Lee, T.J.; Kim, W.J. Microstructure and tensile properties of magnesium nanocomposites fabricated using magnesium chips and carbon black. J. Magn. Alloys 2020, 8, 860–872. [Google Scholar] [CrossRef]




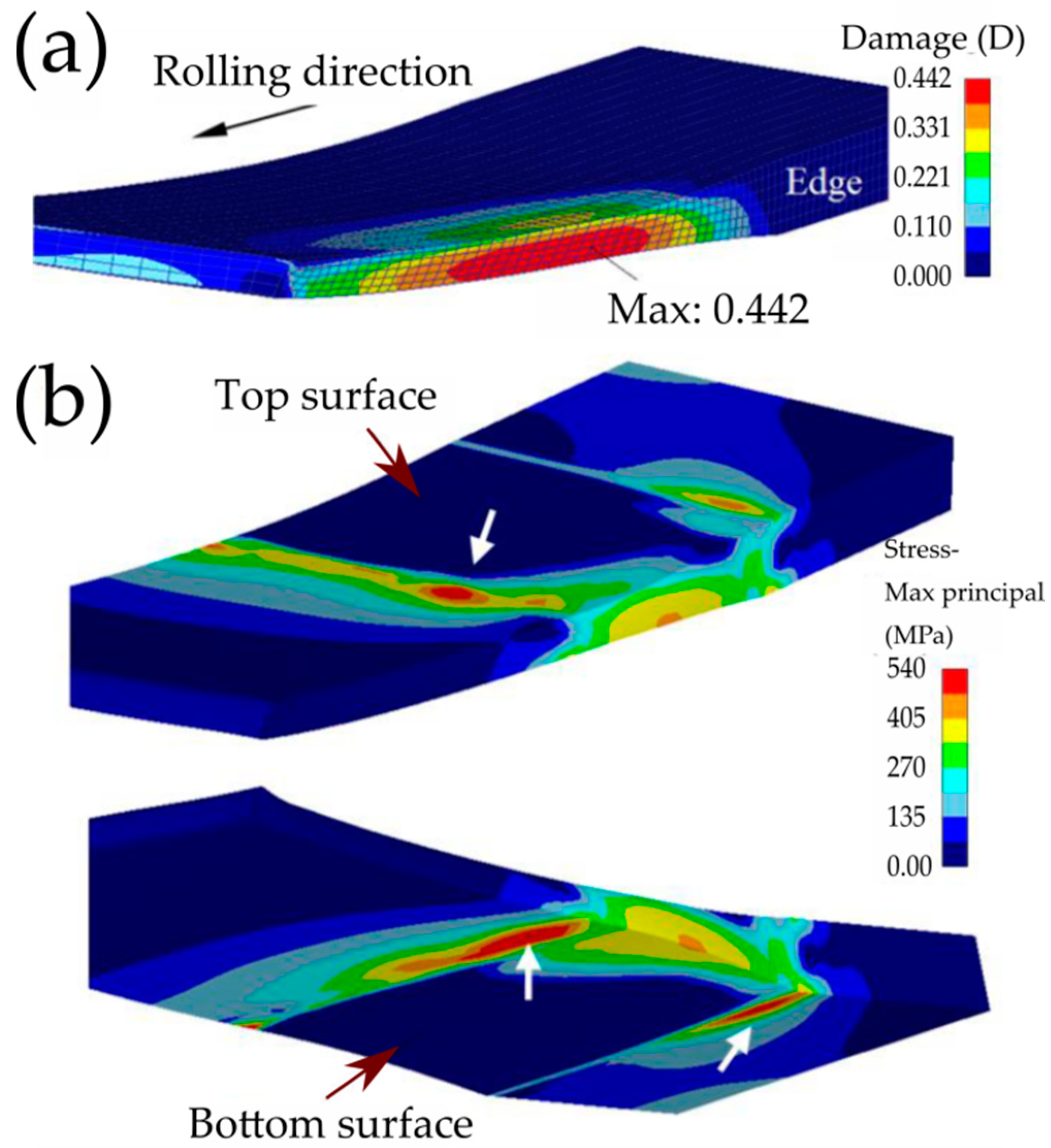
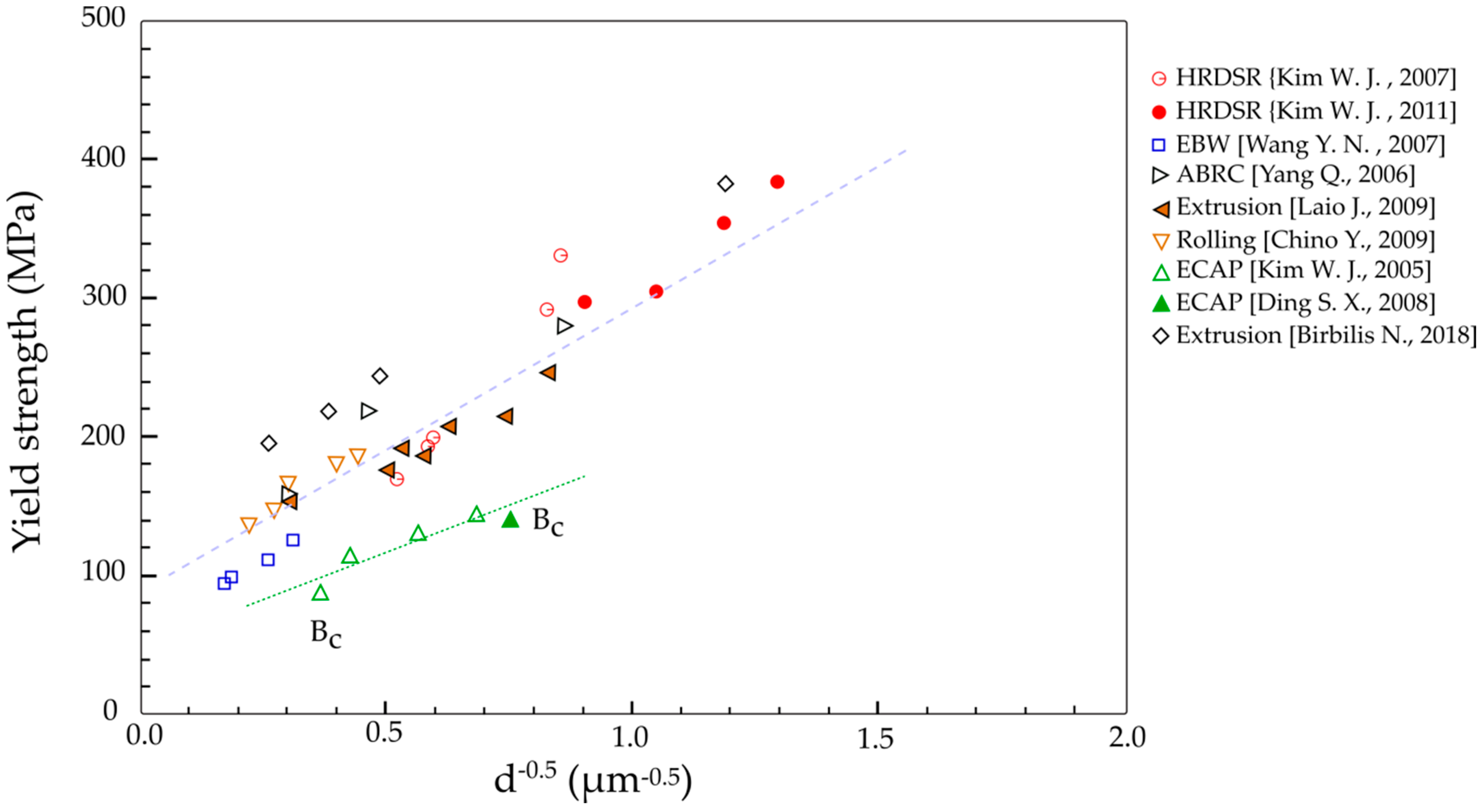
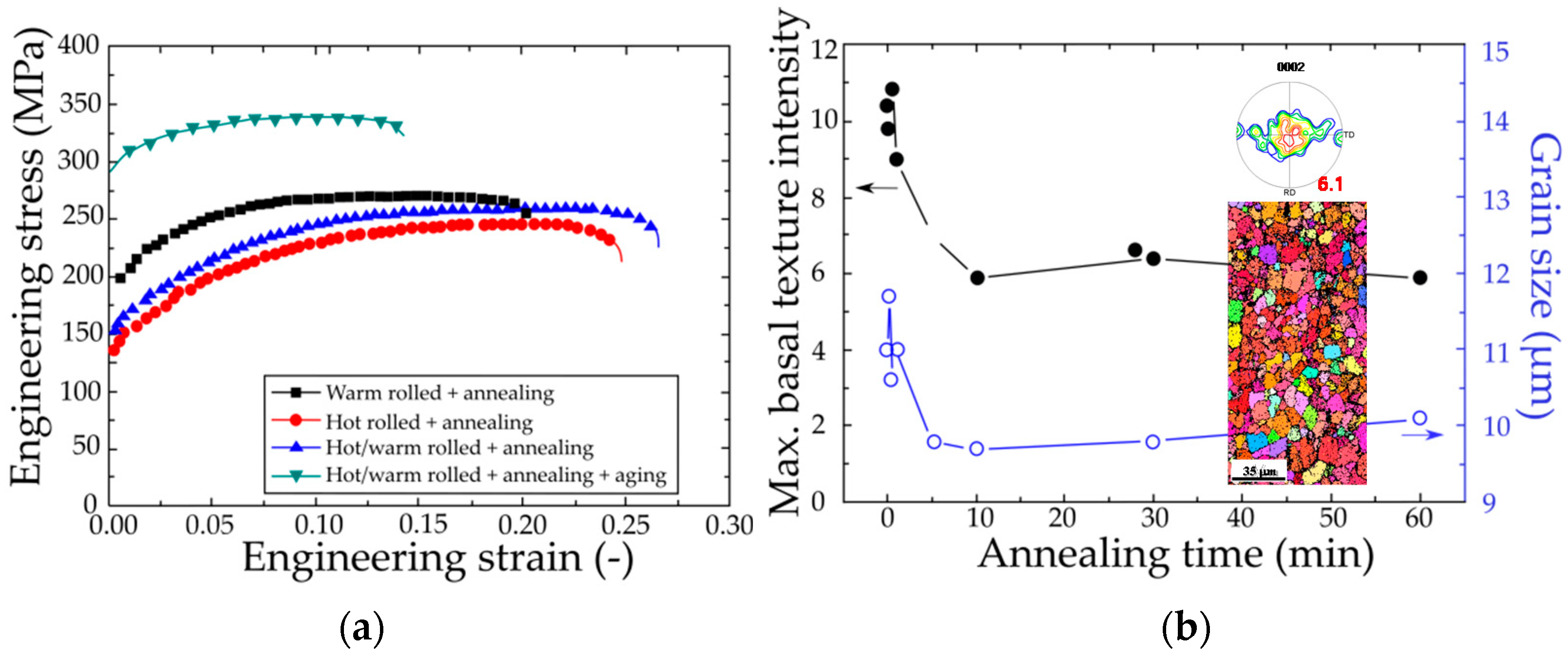
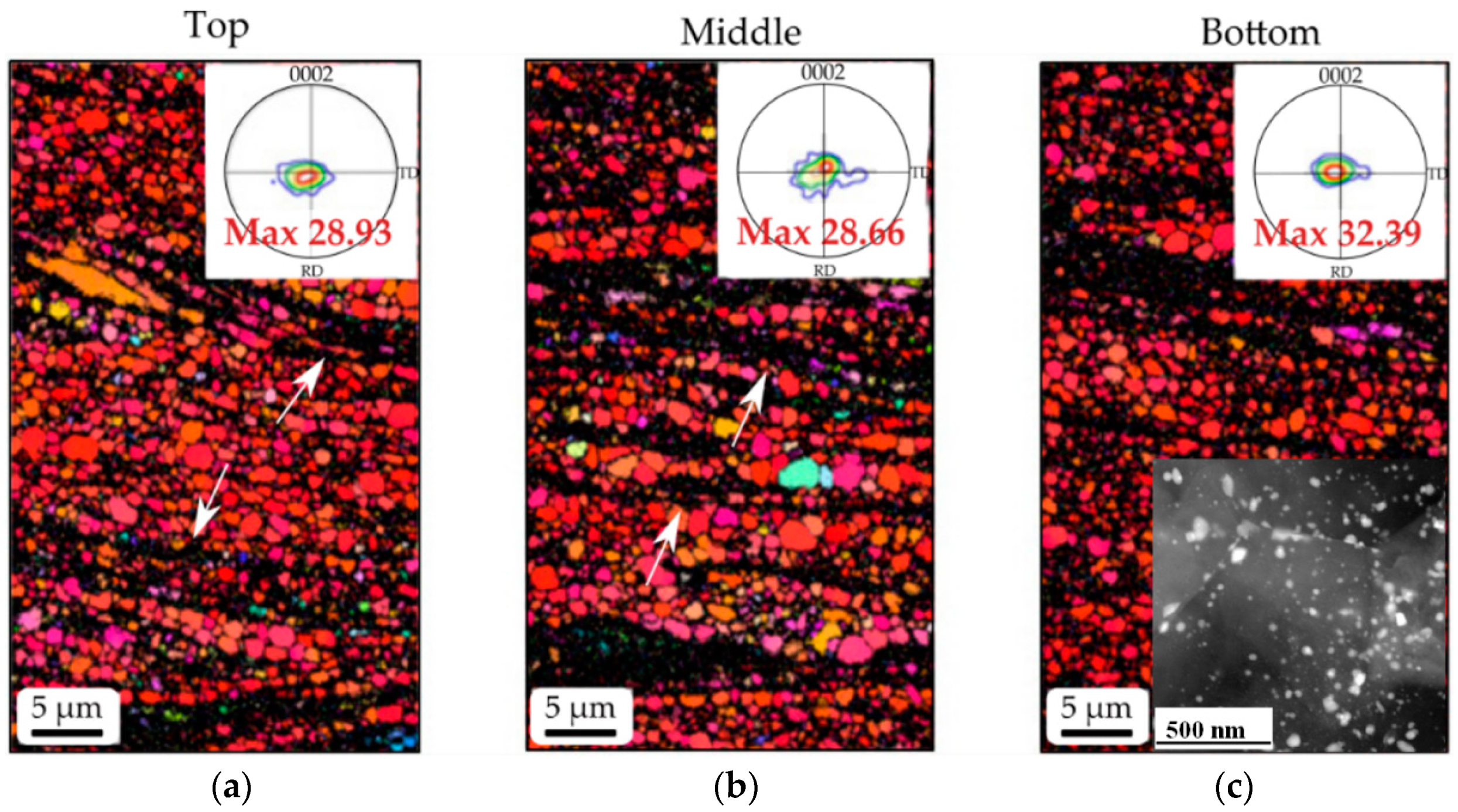



| As-Received | After HRDSR | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Alloy | Process | GS (µm) | El.% | YS (MPa) | UTS (MPa) | Hv | Processing Conditions | GS (µm) | El.% | YS (MPa) | UTS (MPa) | Hv | Ref. |
| AZ31 | Extruded | 30–60 | - | 164 | - | - | T: 433 K Thick. red.: 70% | 1.5 | 22 | 317 | 325 | - | [35] |
| AZ31 | Extruded | 20 | 16 | 225 | 270 | - | SR: 2 T: 423 K Water Quenched | 0.6 | 7 | 382 | 405 | - | [33] |
| Mg-Mn | Cast | 95 | - | - | - | 53 | SR: 3 T: 423 K | 4 | - | - | - | 80 | [68] |
| Pure nickel | 35 | 35 | ~210 | 305 | 108 | SR: 4 | 4 | 2 | 630 | 630 | 279 | [69] | |
| AZ91 | Extruded | 30–40 | - | - | - | ~80 | SR: 3 T: 473 K | 0.3–0.5 | 9 | 327 | 394 | ~95 | [70] |
| Pure Cu | 13.7 | - | 220 | 225 | ~122 | Thick. red.: 65% T: Room | 0.82 | ~40 | ~422 | 464 | ~153 | [71] | |
| 6061 Al | Plate–Slow cooled in furnace to anneal | - | 41 | 90 | 110 | 41 | SR: 3 T: 413 K Thick. red.: 70% (Aged) | 0.37 | ~6 | 455 | 485 | 145 | [72] |
| Pure Al | 35 | ~17 | ~110 | 100 | - | DSR (90%) | 0.5 | ~4 | 250 | 250 | [73] | ||
| ESR (90%) | ~6 | 155 | 155 | - | |||||||||
| 5052 Al | 50 Sheets | ~95 | 65 | 137 | 32 | - | 4 Pass; SR: 4 | 0.7 | 4.2 | 380 | 390 | - | [28] |
| Composites Cu + 3%CNT | - | - | - | - | - | - | HRDSR: SR: 2; T: 473 K | 0.6 | 417 | 500 | 12.2 | 135 | [74] |
| ESR | 1.5 | 363 | 413 | 17.8 | 115 | ||||||||
| Processing Conditions | GS (µm) | El. % | YS (MPa) | UTS (MPa) | Hv | Ref. |
|---|---|---|---|---|---|---|
| As-received | 10 | ~35 | 403 | 532 | [76] | |
| HRDSR- Thick. red.: 63%.-1P | 0.3 | 780 | 895 | |||
| HRDSR-Thick. red.: 63%.-1P-Anneal(1h) | 19% | 804 | 915 | |||
| Hot Roll (Rod) | 10 | 24 | 440 | 480 | 183.5 | [77] |
| ECAP (773–723 K) 7P | 0.3 | 16 | 520 | 540 | 239.6 | |
| ECAP (773–723 K) 7P/HPT (723 K) | 30 | 530 | 640 | 275.3 | ||
| ECAP (773–723 K) 7P/HPT (293 K) | 25 | 625 | 730 | 318.1 | ||
| As-received (Hot rolled) (Ti-grade 2) | 30–60 | 30 | 354 | 487 | [75,78] | |
| ECAP-8P | 27 | 549 | 633 | |||
| ECAP-10P | 0.45 | 20.6 | 582 | 645 | ||
| ECAP-8P+Cold roll (77%) (grade 2) | 17.6 | 665 | 938 | |||
| ECAP-10P+Cold roll (77%) (grade 2) | 0.19 | 14.5 | 736 | 945 | ||
| ECAP-10P + Hot roll (81%) (grade 2) | 18 | 736 | 928 | |||
| Cold roll (77%) (Ti-grade 4) | 15.2 | 650 | 791 | |||
| As-received | 25 | 630 | 740 | |||
| ECAP-8P | 19 | 750 | 815 | |||
| ECAP (8) + Cold roll (83%) | 10.7 | 1006 | 1135 | |||
| CR (80%) | 10 | 1130 | ||||
| As-received (Ti-VT1-0) | 10 | 27 | 380 | 460 | ||
| ECAP (8) | 0.28 | 14 | 640 | 710 | ||
| ECAP (8) + Cold roll (73%) | 12.5 | 940 | 1037 | |||
| ARB | 0.09 | 37 | 720 | 900 | [79] | |
| ARB-Ann. 373 K | 0.1 | 22 | 710 | 880 | ||
| ARB-Ann. 473 K | 0.12 | 17 | 702 | 870 | ||
| ARB-Ann. 573 K | 0.14 | 12 | 700 | 840 | ||
| ARB-Ann. 673 K | 0.27& 0.50 | 11 | 580 | 780 | ||
| ARB-Ann. 723 K | 0.33& 0.70 | 13 | 550 | 680 | ||
| ARB-Ann. 773 K | 2.3 | 8 | 500 | 520 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bahmani, A.; Kim, W.-J. Effect of Grain Refinement and Dispersion of Particles and Reinforcements on Mechanical Properties of Metals and Metal Matrix Composites through High-Ratio Differential Speed Rolling. Materials 2020, 13, 4159. https://doi.org/10.3390/ma13184159
Bahmani A, Kim W-J. Effect of Grain Refinement and Dispersion of Particles and Reinforcements on Mechanical Properties of Metals and Metal Matrix Composites through High-Ratio Differential Speed Rolling. Materials. 2020; 13(18):4159. https://doi.org/10.3390/ma13184159
Chicago/Turabian StyleBahmani, Ahmad, and Woo-Jin Kim. 2020. "Effect of Grain Refinement and Dispersion of Particles and Reinforcements on Mechanical Properties of Metals and Metal Matrix Composites through High-Ratio Differential Speed Rolling" Materials 13, no. 18: 4159. https://doi.org/10.3390/ma13184159
APA StyleBahmani, A., & Kim, W.-J. (2020). Effect of Grain Refinement and Dispersion of Particles and Reinforcements on Mechanical Properties of Metals and Metal Matrix Composites through High-Ratio Differential Speed Rolling. Materials, 13(18), 4159. https://doi.org/10.3390/ma13184159




