Thermomechanical Response of Fullerene-Reinforced Polymers by Coupling MD and FEM
Abstract
1. Introduction
2. Multiscale Analysis
3. First Simulation Scale: MD-Only Formulation
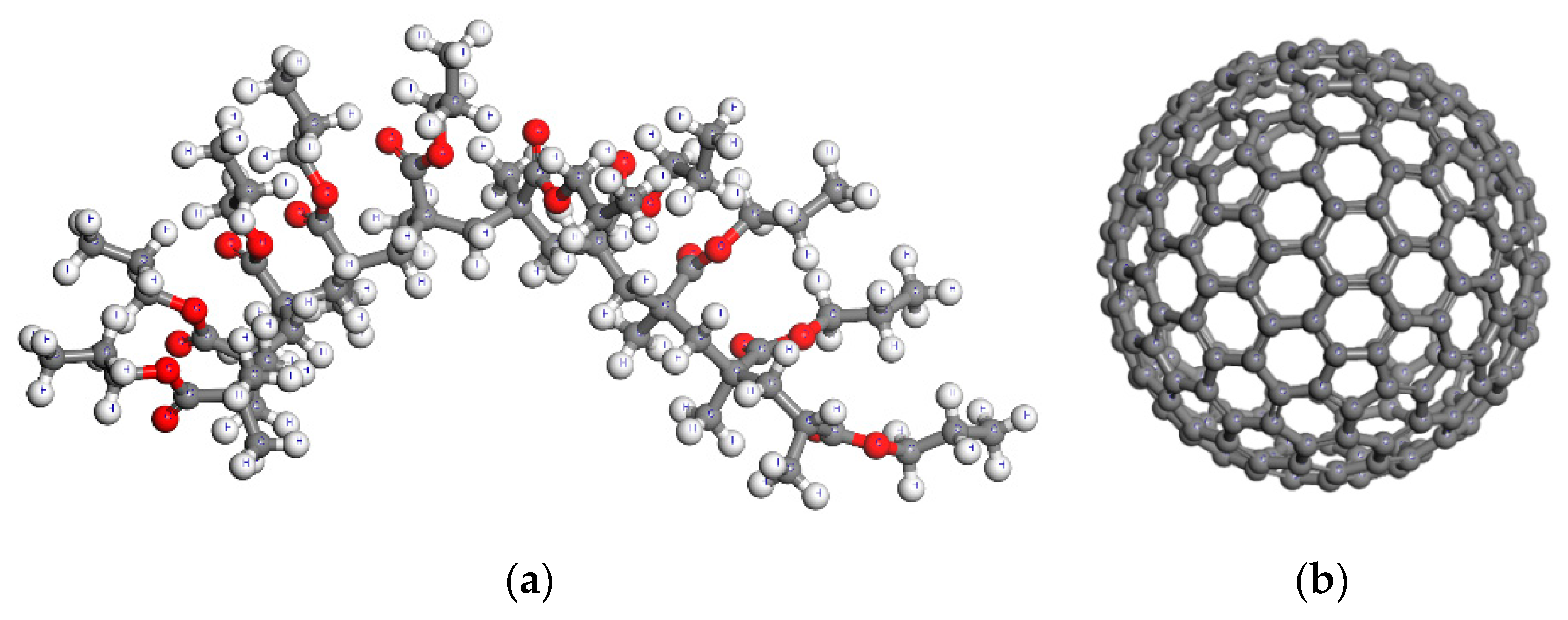
3.1. Unit Cells Construction
3.2. Geometry Optimization of Molecular Structures and Potential Model
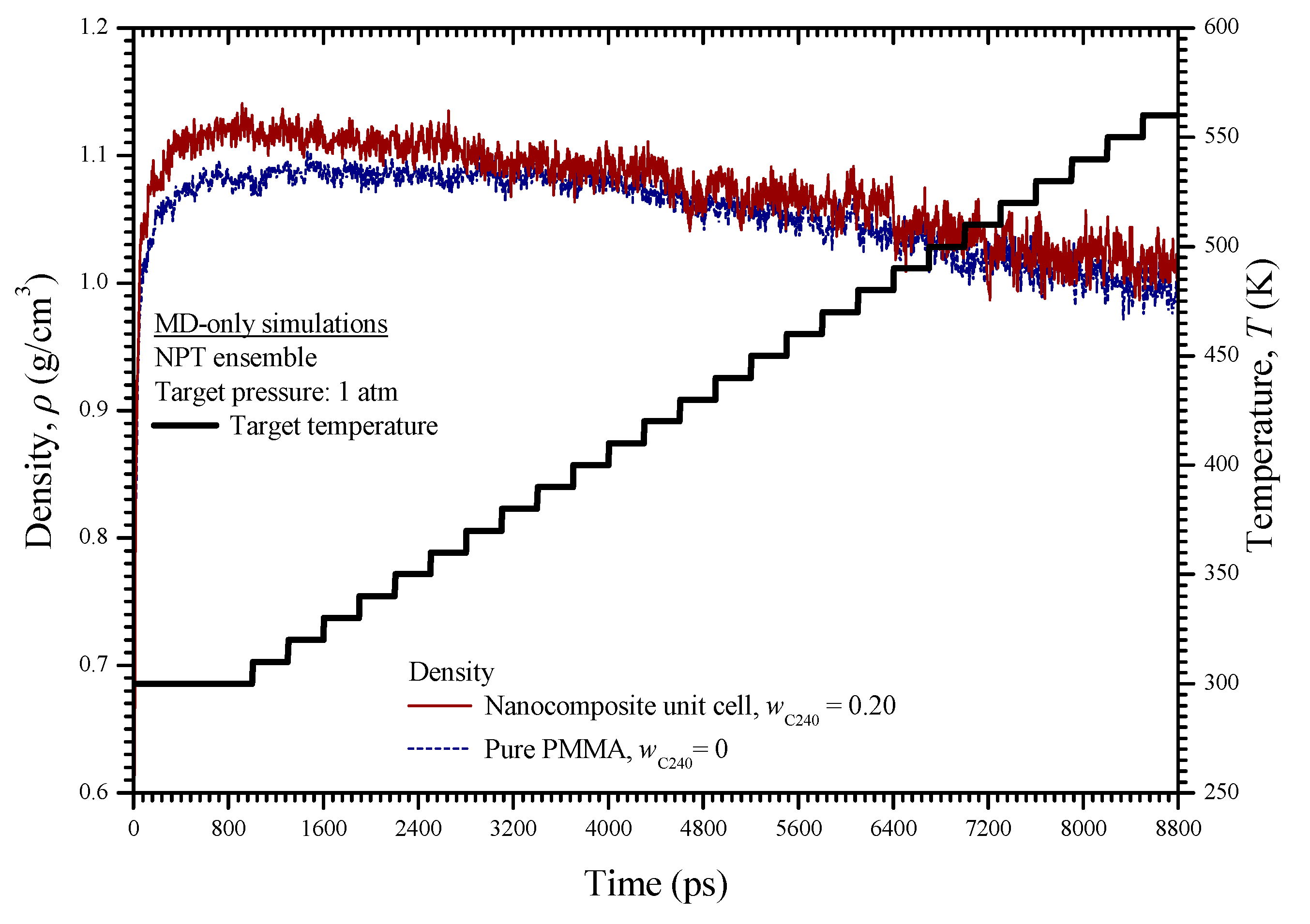
3.3. NPT Dynamic Analysis of the Unit Cells
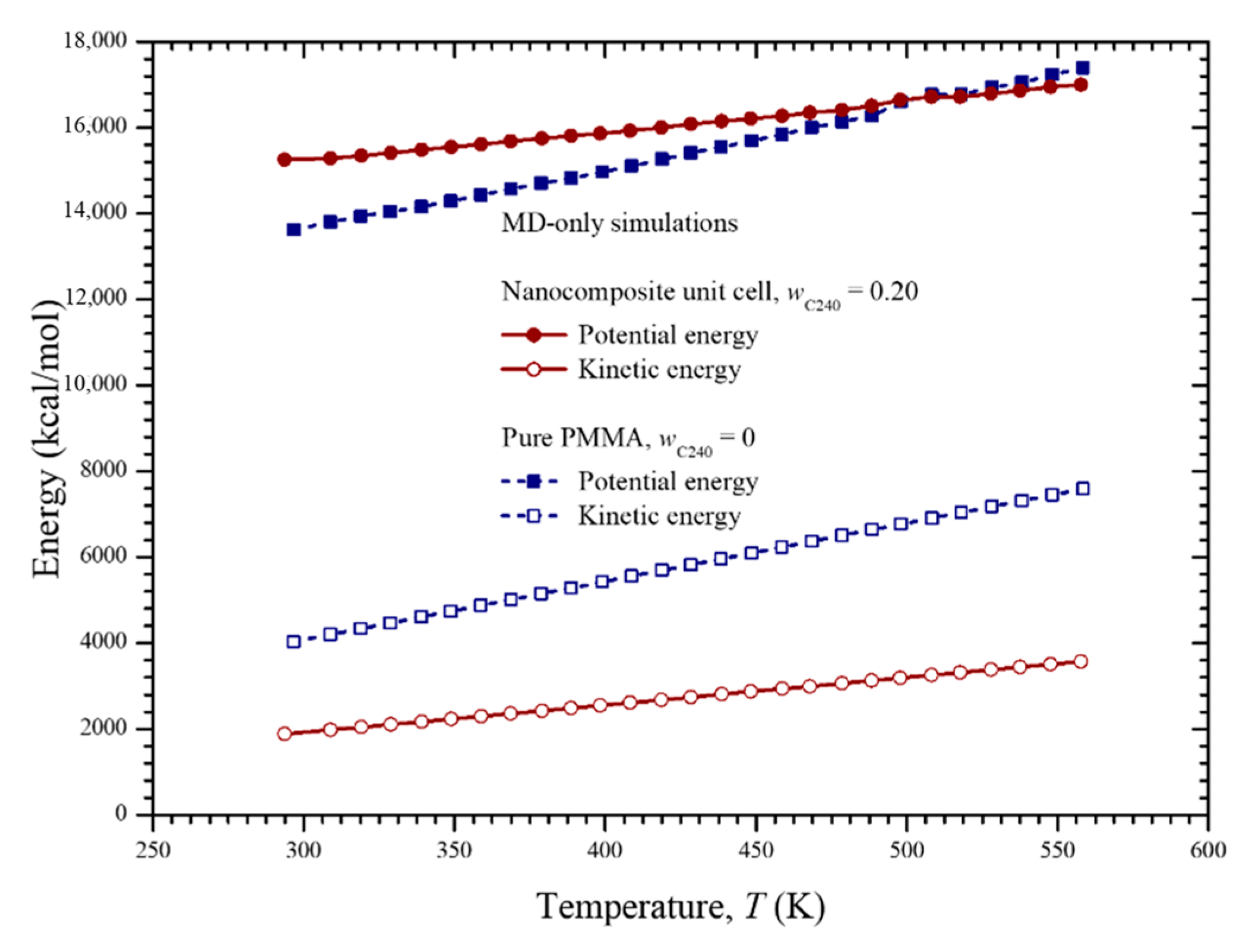
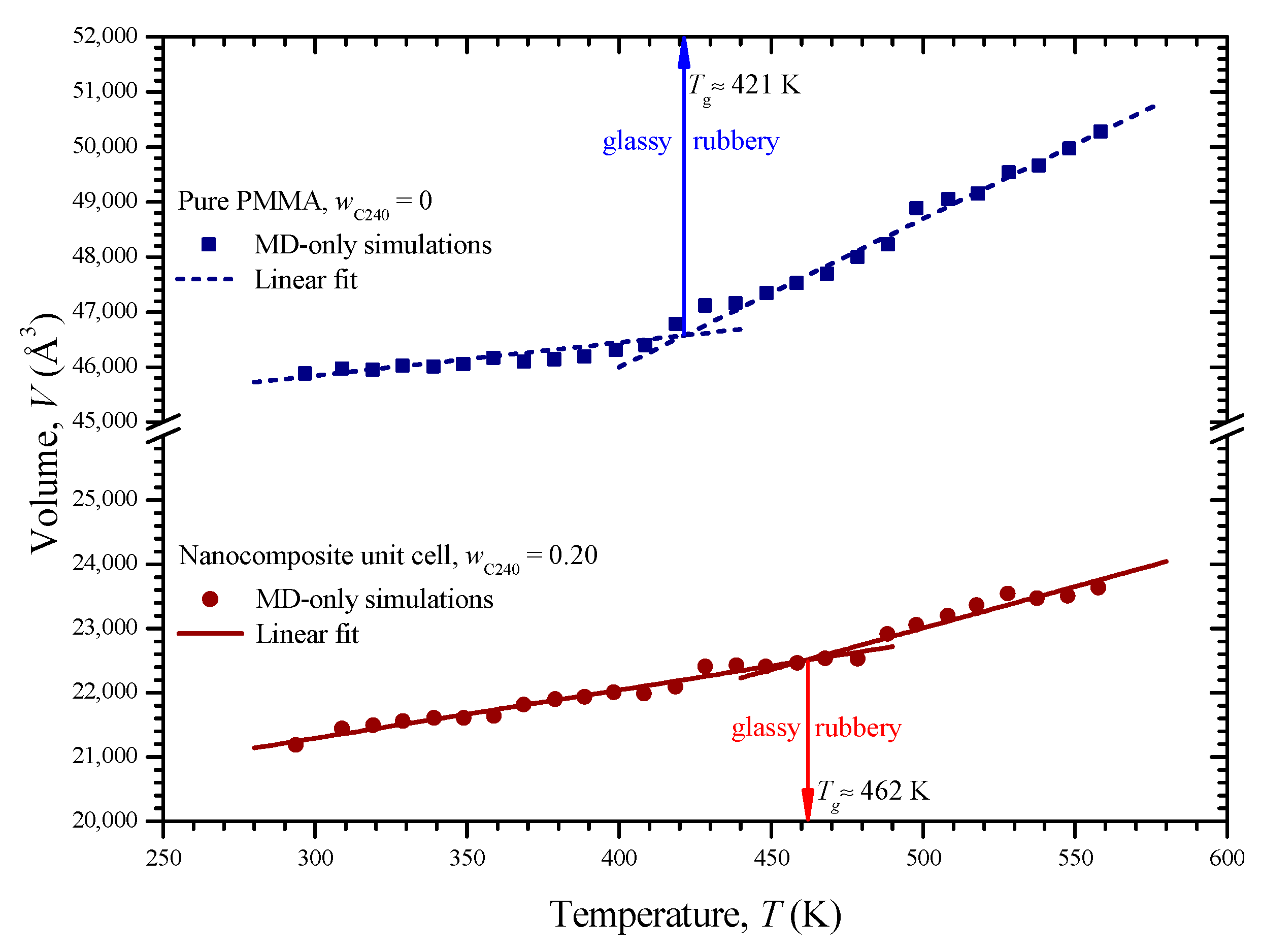
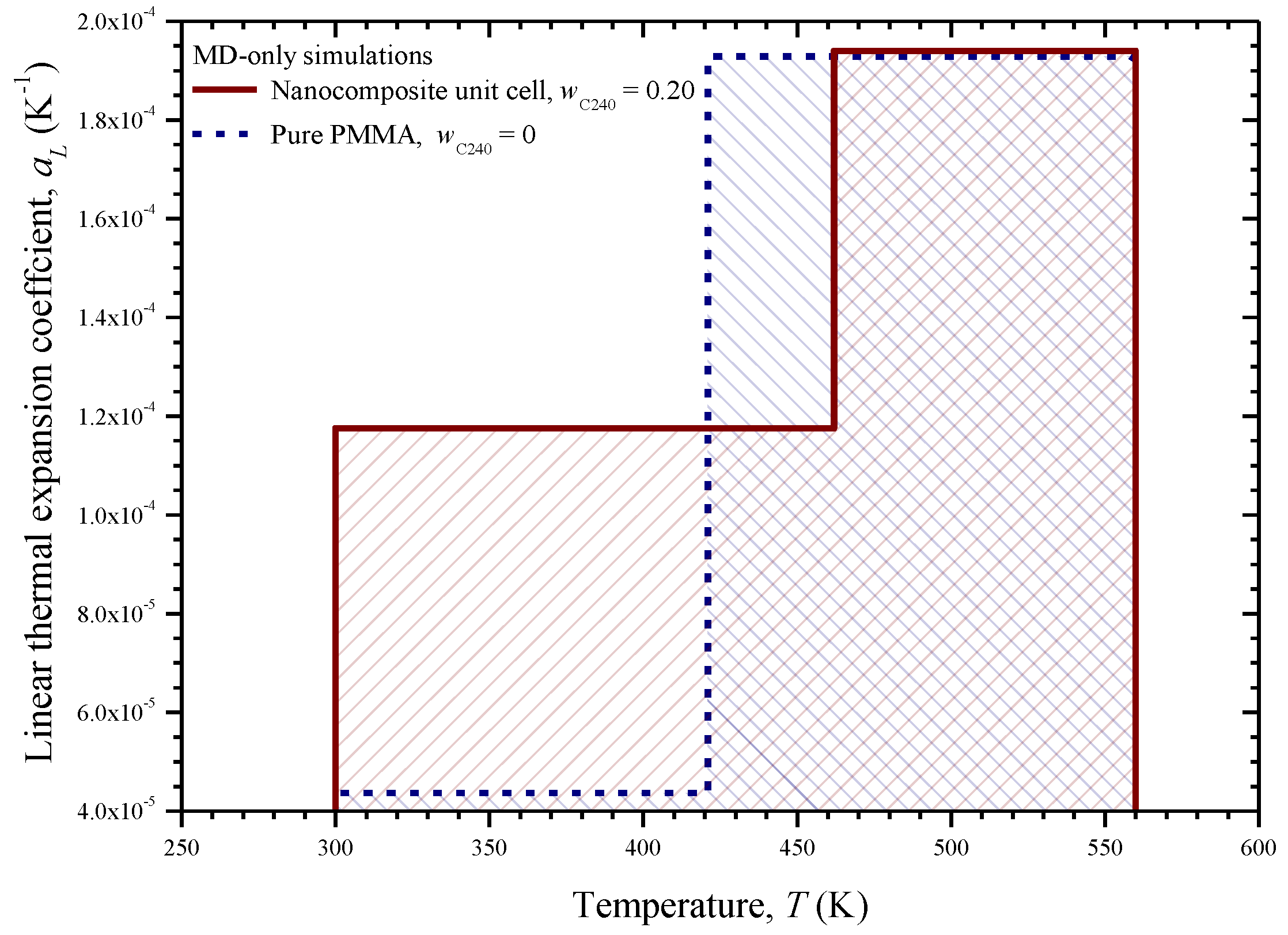
3.4. Thermomechanical Properties Calculation
4. Second Simulation Scale: FEM Formulation
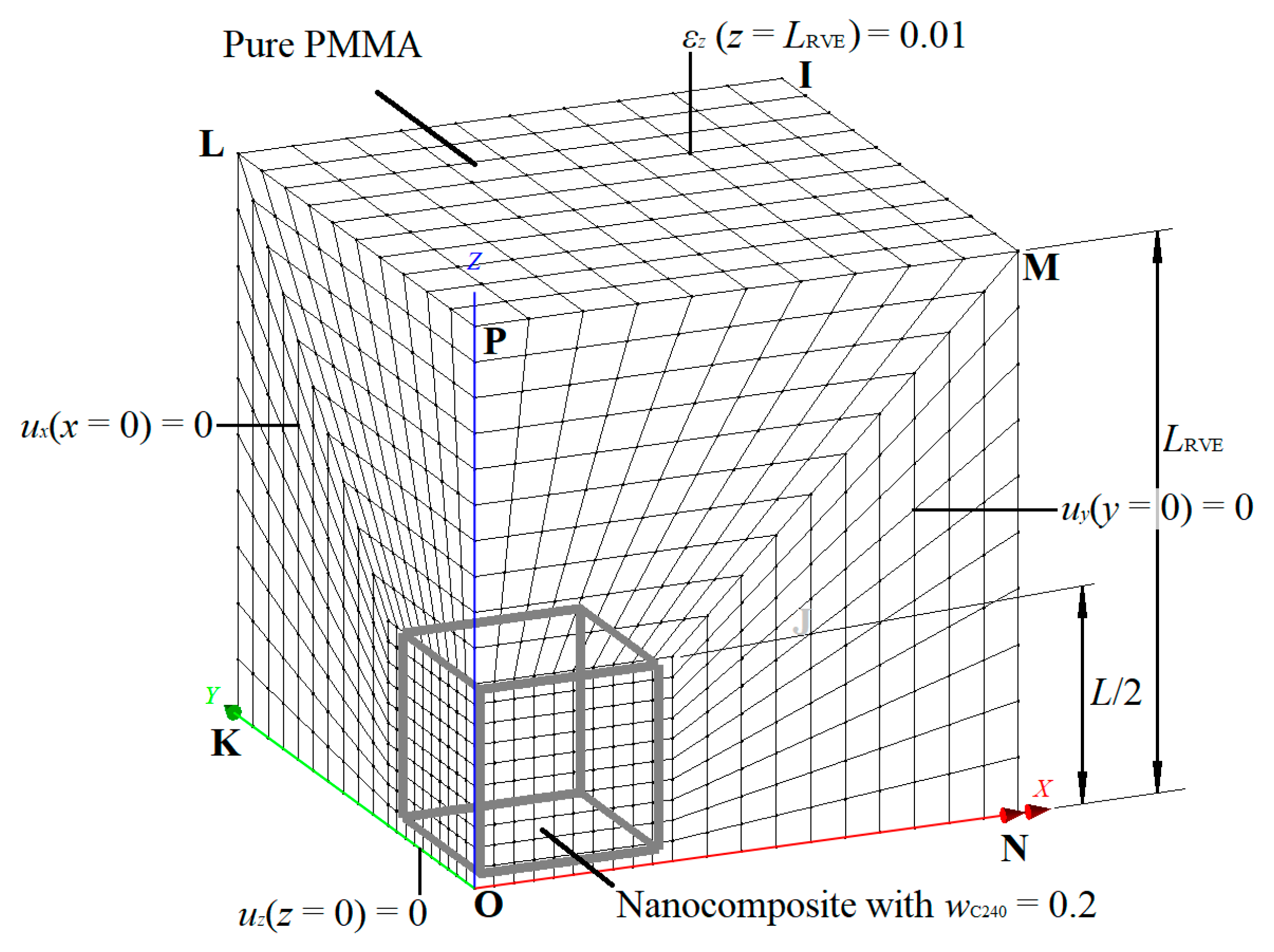
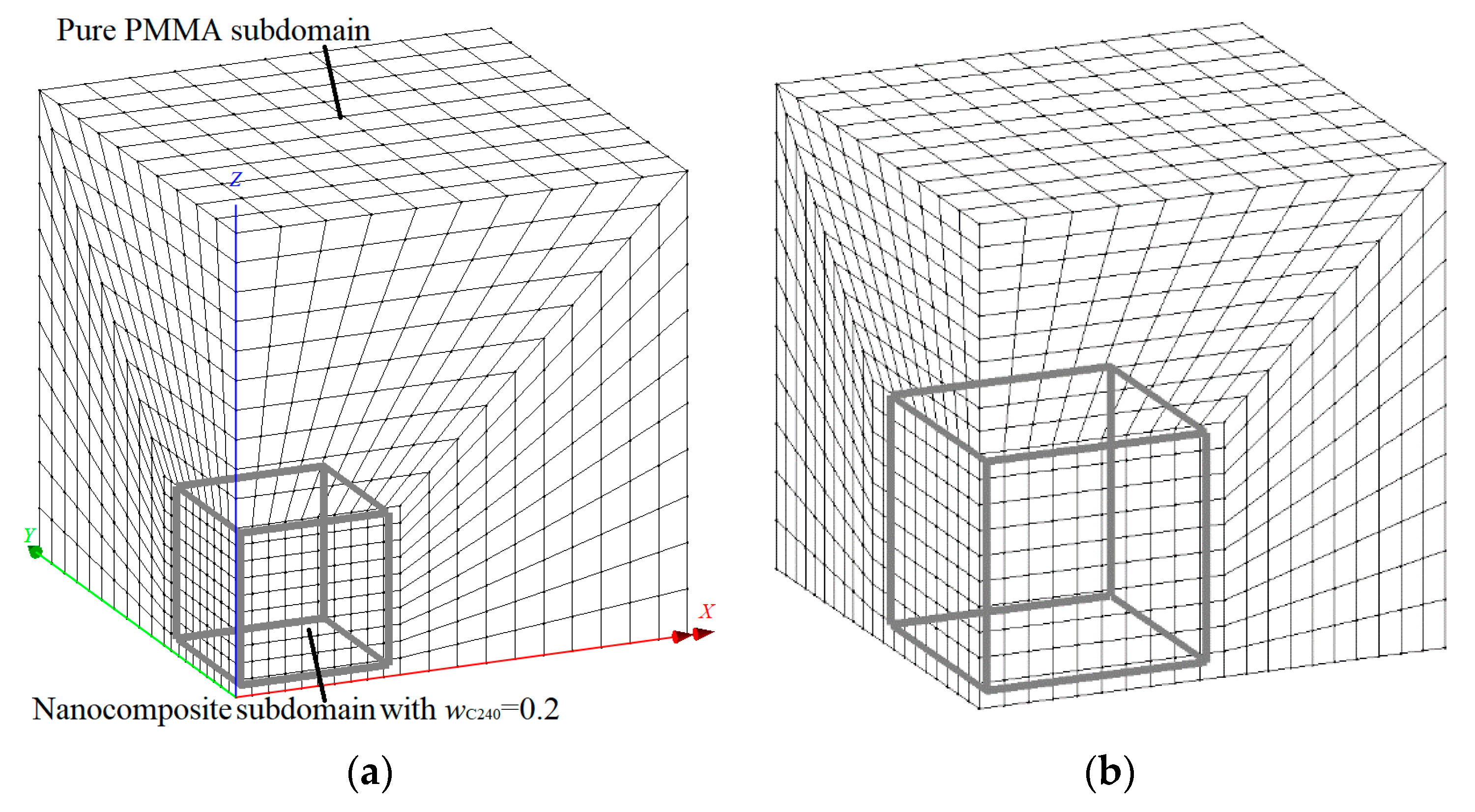
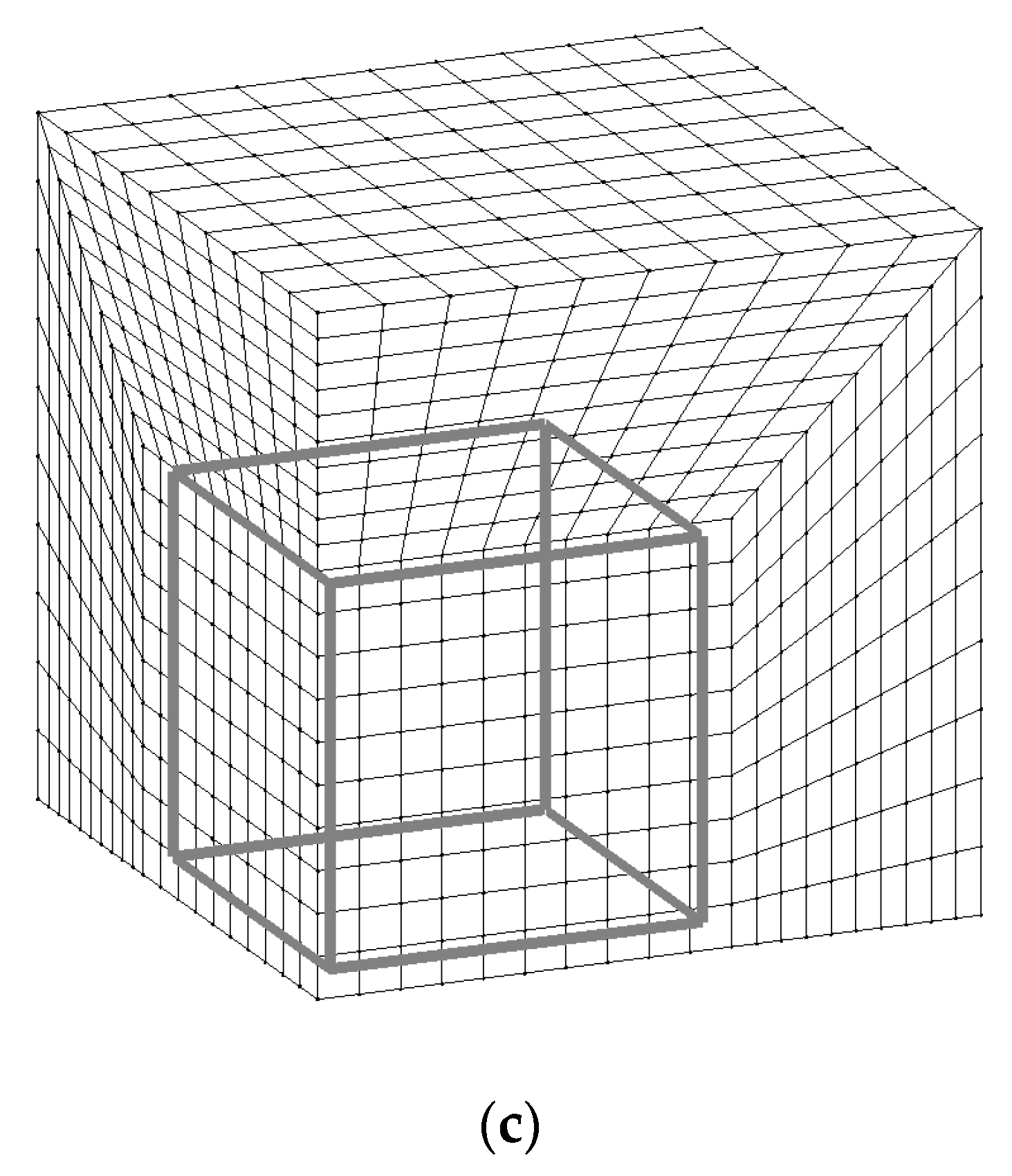
4.1. Geometry Definition and Finite Element Discretization
4.2. Material Properties Input and Output
5. Results and Discussion
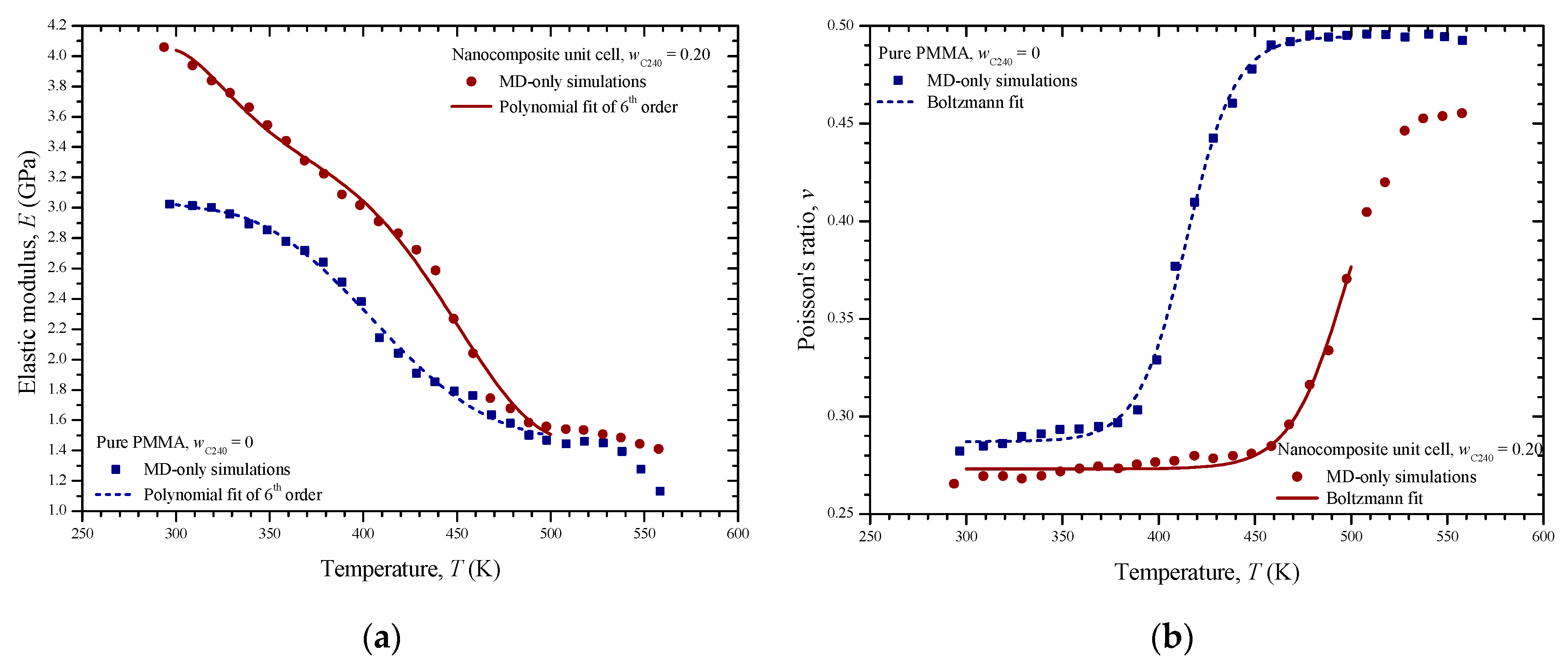
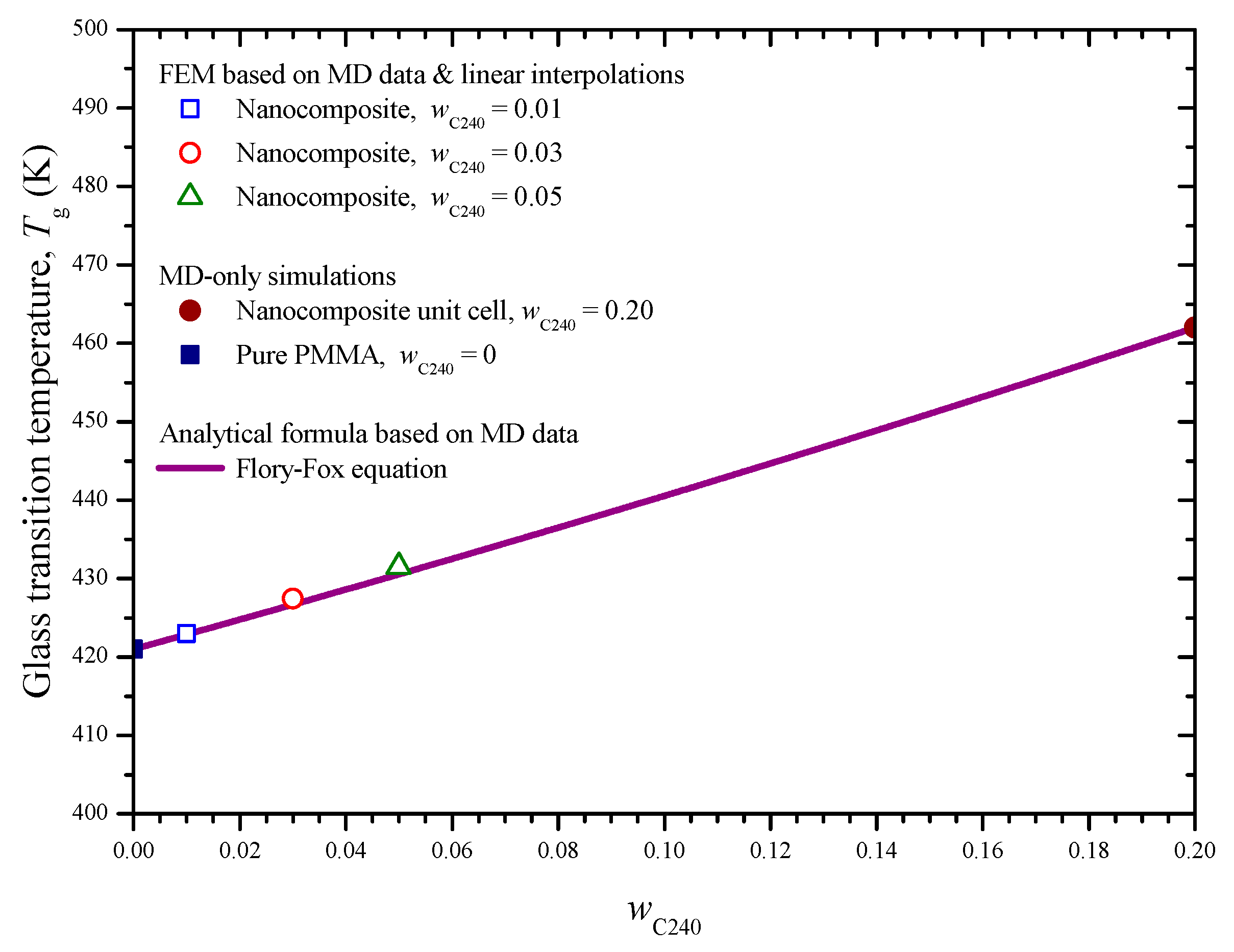
5.1. First Simulation Scale
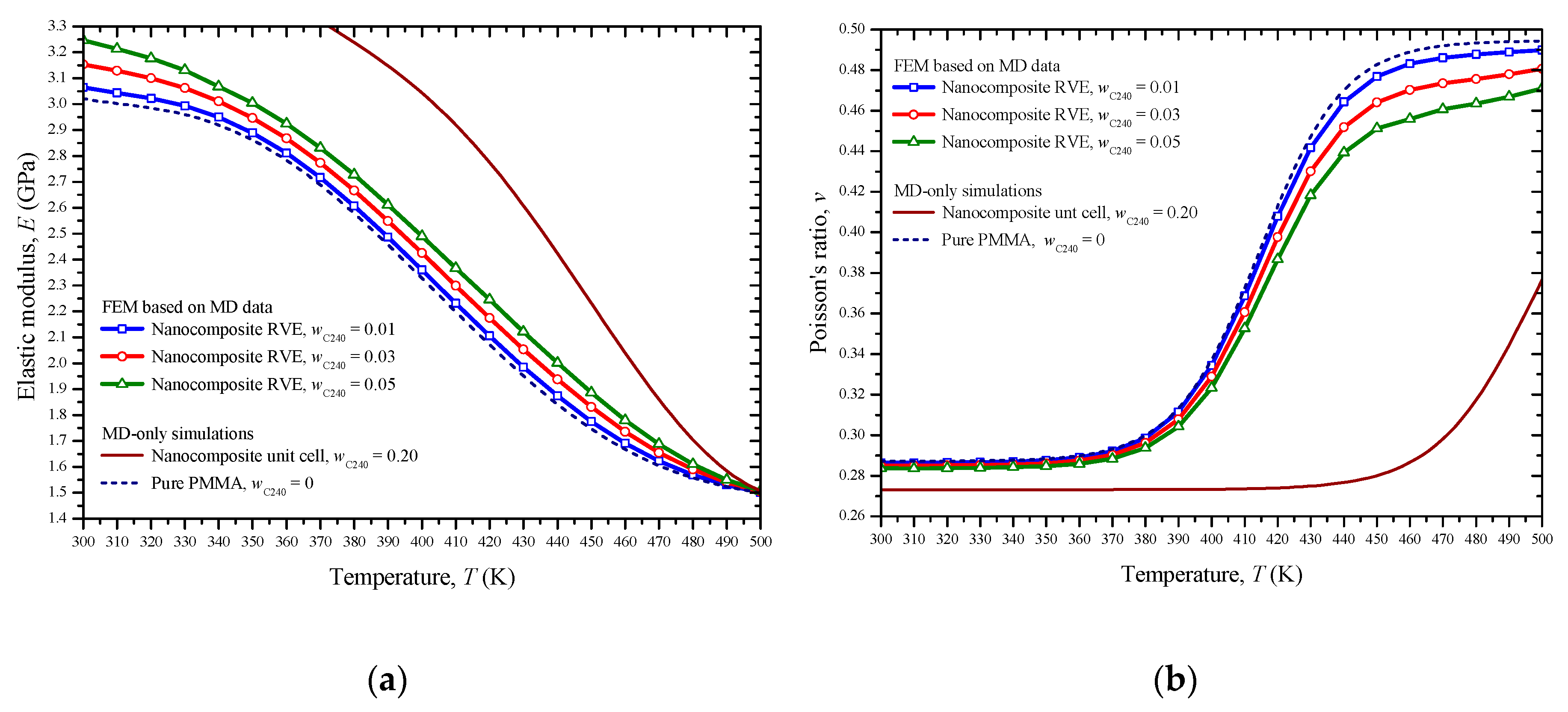
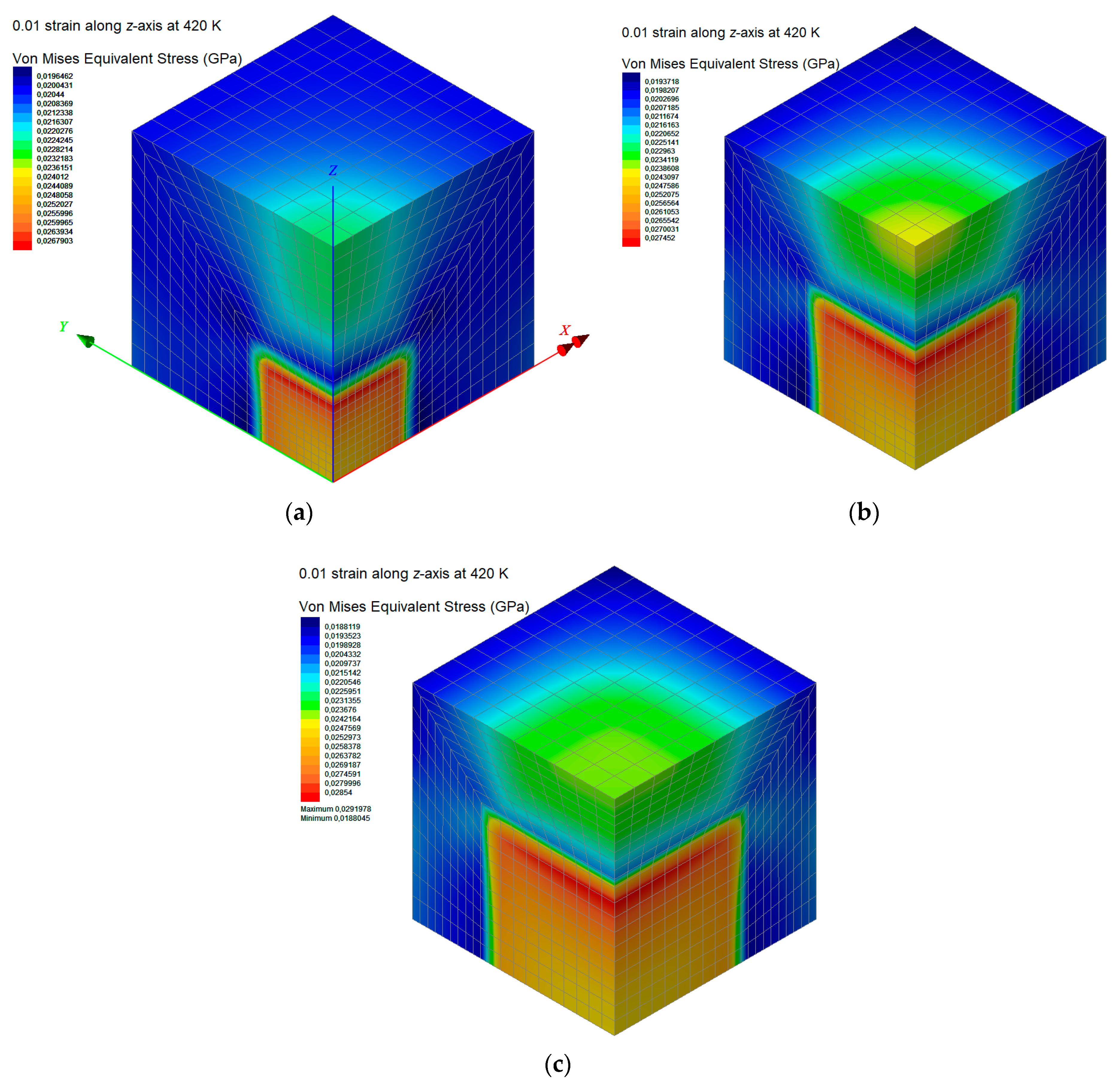
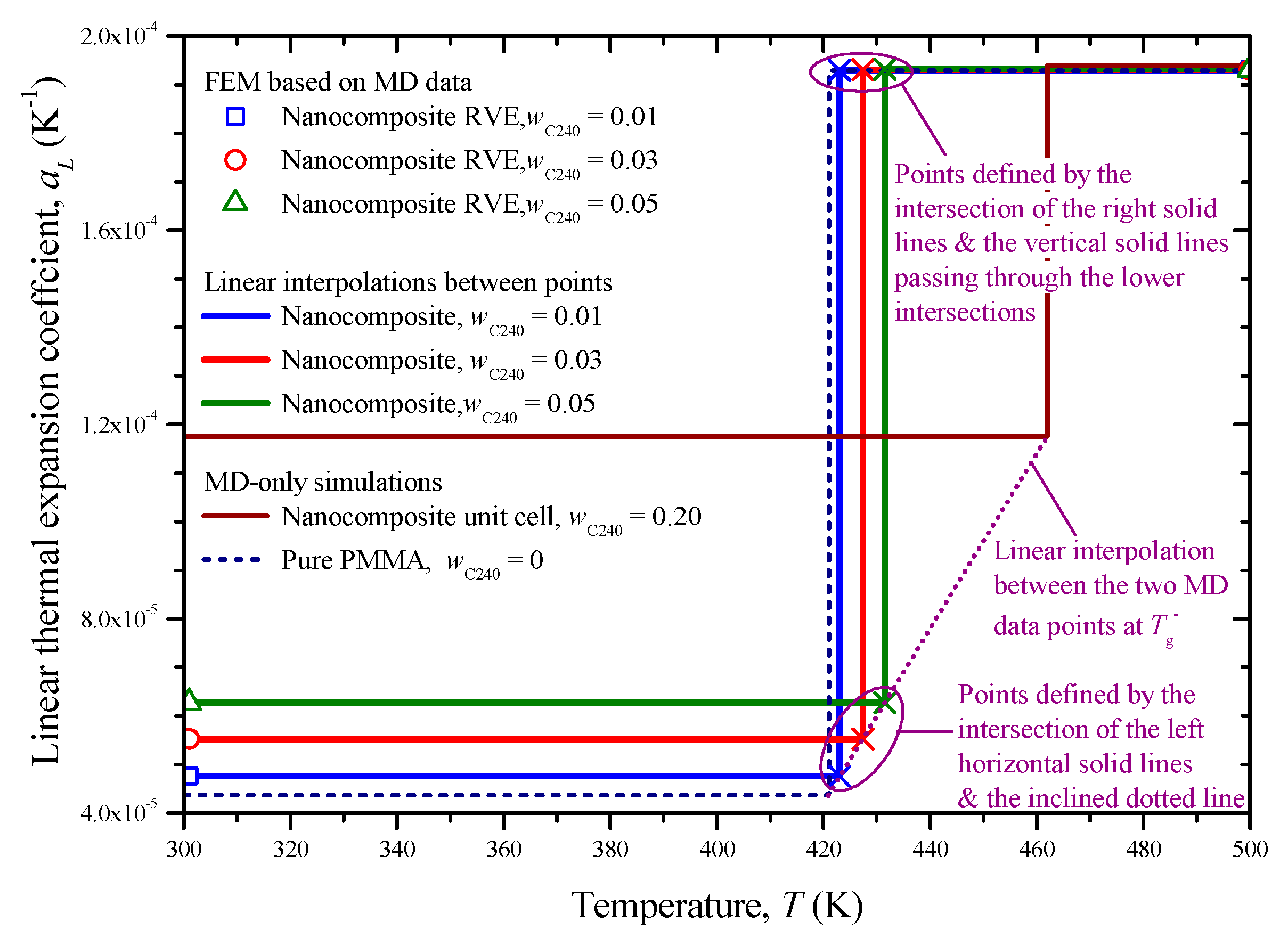
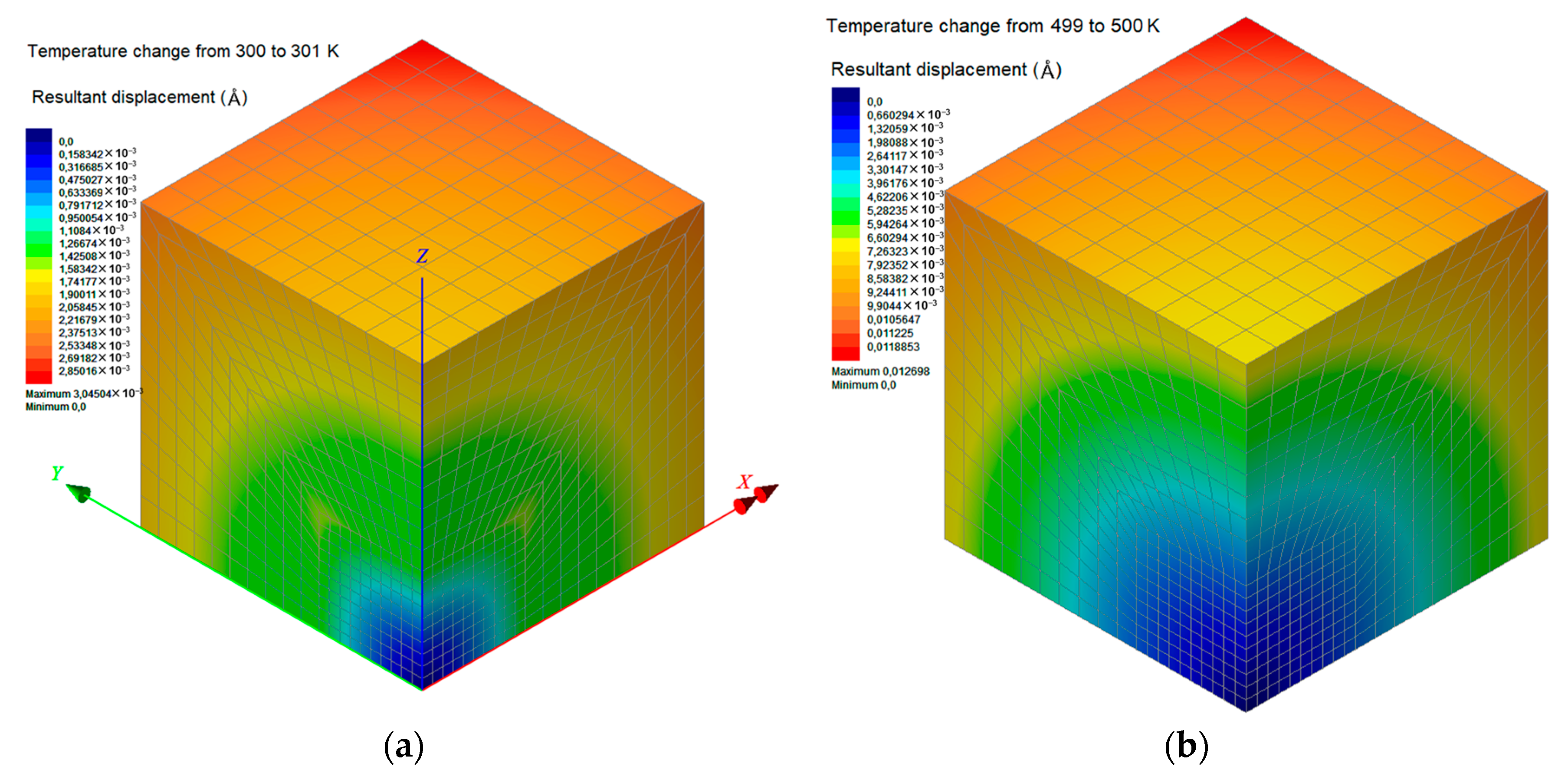
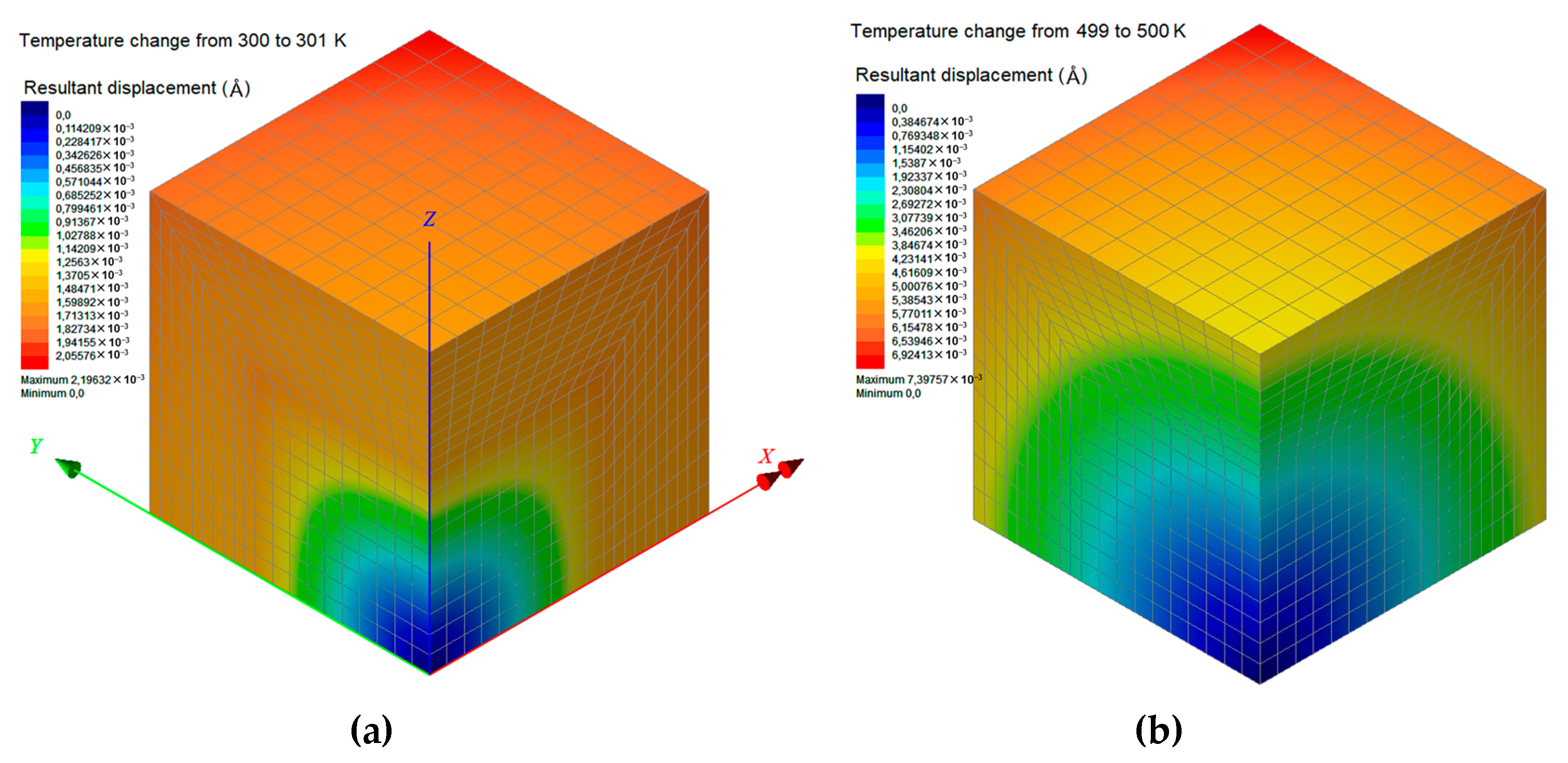
5.2. Second Simulation Scale
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Burgaz, E. Thermomechanical analysis of polymer nanocomposites. Polym. Nanocompos. Electr. Therm. Prop. 2016, 191–242. [Google Scholar]
- Cho, M.; Yang, S. Atomistic simulations for the thermal and mechanical properties of CNT-polymer nanocomposites. In Proceedings of the 48th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Honolulu, HI, USA, 23–26 April 2007; Volume 5, pp. 4718–4726. [Google Scholar]
- Allaoui, A.; El Bounia, N. How carbon nanotubes affect the cure kinetics and glass transition temperature of their epoxy composites?—A review. Express Polym. Lett. 2009, 3, 588–594. [Google Scholar] [CrossRef]
- Herasati, S.; Ruan, H.H.; Zhang, L.C. Effect of chain morphology and carbon-nanotube additives on the glass transition temperature of polyethylene. J. Nano Res. 2013, 23, 16–23. [Google Scholar] [CrossRef]
- Mohammadi, M.; Davoodi, J.; Javanbakht, M.; Rezaei, H. Glass transition temperature of PMMA/modified alumina nanocomposite: Molecular dynamic study. Mater. Res. Express 2019, 6, 035309. [Google Scholar] [CrossRef]
- Zhang, X.; Wen, H.; Wu, Y. Computational thermomechanical properties of silica-epoxy nanocomposites by molecular dynamic simulation. Polymers 2017, 9, 430. [Google Scholar] [CrossRef] [PubMed]
- Pandey, A.K.; Singh, K.; Kar, K.K. Thermo-mechanical properties of graphite-reinforced high-density polyethylene composites and its structure–property corelationship. J. Compos. Mater. 2017, 51, 1769–1782. [Google Scholar] [CrossRef]
- Dikshit, M.K.; Engle, P.E. Investigation of mechanical properties of CNT reinforced epoxy nanocomposite: A molecular dynamic simulations. Mater. Phys. Mech. 2018, 37, 7–15. [Google Scholar]
- Dikshit, M.K.; Nair, G.S.; Pathak, V.K.; Srivastava, A.K. Investigation of mechanical properties of graphene reinforced epoxy nanocomposite using molecular dynamics. Mater. Phys. Mech. 2019, 42, 224–233. [Google Scholar]
- Xue, Q.; Lv, C.; Shan, M.; Zhang, H.; Ling, C.; Zhou, X.; Jiao, Z. Glass transition temperature of functionalized graphene-polymer composites. Comput. Mater. Sci. 2013, 71, 66–71. [Google Scholar] [CrossRef]
- Park, C.; Jung, J.; Yun, G.J. Thermomechanical properties of mineralized nitrogen-doped carbon nanotube/polymer nanocomposites by molecular dynamics simulations. Compos. Part B Eng. 2019, 161, 639–650. [Google Scholar] [CrossRef]
- Singh, A.; Kumar, D. Temperature effects on the interfacial behavior of functionalized carbon nanotube–polyethylene nanocomposite using molecular dynamics simulation. Proc. Inst. Mech. Eng. Part N J. Nanomater. Nanoeng. Nanosyst. 2019, 233, 3–15. [Google Scholar] [CrossRef]
- Zhang, B.; Li, J.; Gao, S.; Liu, W.; Liu, Z. Comparison of Thermomechanical Properties for Weaved Polyethylene and Its Nanocomposite Based on the CNT Junction by Molecular Dynamics Simulation. J. Phys. Chem. C 2019, 123, 19412–19420. [Google Scholar] [CrossRef]
- Jeyranpour, F.; Alahyarizadeh, G.H.; Minuchehr, A. The thermo-mechanical properties estimation of fullerene-reinforced resin epoxy composites by molecular dynamics simulation-A comparative study. Polymer 2016, 88, 9–18. [Google Scholar] [CrossRef]
- Izadi, R.; Ghavanloo, E.; Nayebi, A. Elastic properties of polymer composites reinforced with C60 fullerene and carbon onion: Molecular dynamics simulation. Phys. B Condens. Matter 2019, 574, 311636. [Google Scholar] [CrossRef]
- Montazeri, A.; Rafii-Tabar, H. Multiscale modeling of graphene- and nanotube-based reinforced polymer nanocomposites. Phys. Lett. Sect. A Gen. At. Solid State Phys. 2011, 375, 4034–4040. [Google Scholar] [CrossRef]
- Tsiamaki, A.; Anifantis, N. Simulation of the thermomechanical behavior of graphene/PMMA nanocomposites via continuum mechanics. Int. J. Struct. Integr. 2019, 11, 655–669. [Google Scholar] [CrossRef]
- Giannopoulos, G.I. Linking MD and FEM to predict the mechanical behaviour of fullerene reinforced nylon-12. Compos. Part B Eng. 2019, 161, 455–463. [Google Scholar] [CrossRef]
- Reddy, J.N.; Unnikrishnan, V.U.; Unnikrishnan, G.U. Recent developments in multiscale thermomechanical analysis of nanocomposites. In Advances in Nanocomposites; Springer: Cham, Switzerland, 2016; pp. 177–188. [Google Scholar]
- Ruoff, R.S.; Thornton, T.; Smith, D. Density of fullerene containing soot as determined by helium pycnometry. Chem. Phys. Lett. 1991, 186, 456–458. [Google Scholar] [CrossRef]
- Shinohara, H.; Sato, H.; Saito, Y.; Izuoka, A.; Sugawara, T.; Ito, H.; Sakurai, T.; Matsuo, T. Extraction and mass spectroscopic characterization of giant fullerences up to C500. Rapid Commun. Mass Spectrom. 1992, 6, 413–416. [Google Scholar] [CrossRef]
- Wang, B.-C.; Chiu, Y.-N. Geometry and orbital symmetry relationships of giant and hyperfullerenes: C240, C540, C960 and C1500. Synth. Met. 1993, 56, 2949–2954. [Google Scholar] [CrossRef]
- Schwerdtfeger, P.; Wirz, L.N.; Avery, J. The topology of fullerenes. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2015, 5, 96–145. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.G.; Tomnek, D. Melting the fullerenes: A molecular dynamics study. Phys. Rev. Lett. 1994, 72, 2418–2421. [Google Scholar] [CrossRef] [PubMed]
- Cabrera-Trujillo, J.; Alonso, J.; Iñiguez, M.; López, M.; Rubio, A. Theoretical study of the binding of Na clusters encapsulated in the fullerene. Phys. Rev. B-Condens. Matter Mater. Phys. 1996, 53, 16059–16066. [Google Scholar] [CrossRef]
- Li, Z.; Lambros, J. Strain rate effects on the thermomechanical behavior of polymers. Int. J. Solids Struct. 2001, 38, 3549–3562. [Google Scholar]
- Van Loock, F.; Fleck, N.A. Deformation and failure maps for PMMA in uniaxial tension. Polymer 2018, 148, 259–268. [Google Scholar] [CrossRef]
- Swallowe, G.M.; Lee, S.F. Quasi-static and dynamic compressive behaviour of poly(methyl methacrylate) and polystyrene at temperatures from 293 K to 363 K. J. Mater. Sci. 2006, 41, 6280–6289. [Google Scholar] [CrossRef]
- Mohammadi, M.; fazli, H.; karevan, M.; Davoodi, J. The glass transition temperature of PMMA: A molecular dynamics study and comparison of various determination methods. Eur. Polym. J. 2017, 91, 121–133. [Google Scholar] [CrossRef]
- Accelrys, I. Materials Studio; Accelrys Software Inc.: San Diego, CA, USA, 2010. [Google Scholar]
- Sun, H. Compass: An ab initio force-field optimized for condensed-phase applications-Overview with details on alkane and benzene compounds. J. Phys. Chem. B 1998, 102, 7338–7364. [Google Scholar]
- Chen, X.P.; Yuan, C.A.; Wong, C.K.Y.; Koh, S.W.; Zhang, G.Q. Validation of forcefields in predicting the physical and thermophysical properties of emeraldine base polyaniline. Mol. Simul. 2011, 37, 990–996. [Google Scholar]
- Horrigan, D.P.W.; Williams, J.F. LUSAS Finite Element System User Examples Manual; Department of Mechanical and Manufacturing Engineering, University of Melbourne: Melbourne, Australian, 1997. [Google Scholar]
- Marx, D.; Hutter, J. Ab Initio Molecular Dynamics: Basic Theory and Advanced Methods; Cambridge University Press: New York, NY, USA, 2009. [Google Scholar]
- Murakoshi, Y.; Shan, X.C.; Shimizu, T.; Maeda, R. Hot embossing characteristics of PEEK compared to PC and PMMA. In Proceedings of the Design, Test, Integration and Packaging of MEMS/MOEMS, Cannes, France, 7 May 2003; pp. 304–311. [Google Scholar]
- Flory, P.J. Principles of Polymer Chemistry; Cornell University Press: New York, NY, USA, 1953. [Google Scholar]




| Fitting of MD Data with Functions of Temperature | ||||||
|---|---|---|---|---|---|---|
| Property | Fitting Equation (T→K) | Nanocomposite with wC240 = 0.02 | Pure PMMA | |||
| Volume, V (Å3) | Linear V = f + gT | T range | 300 ≤ T ≤ 462 | 462 < T ≤ 560 | 300 ≤ T ≤ 421 | 421 ≤ T ≤ 560 |
| f | 19,038.73973 | 16,537.08047 | 44,046.02025 | 35,216.40195 | ||
| g | 7.50775 | 13.10966 | 6.0055 | 26.96125 | ||
| Adjusted R2 | 0.96339 | 0.89922 | 0.83912 | 0.98609 | ||
| Density, ρ (g/cm3) | Linear ρ = h + lT | T range | 300 ≤ T ≤ 462 | 462 < T ≤ 560 | 300 ≤ T ≤ 421 | 421 < T ≤ 560 |
| h | 1.2401 | 1.33445 | 1.13239 | 1.3125 | ||
| l | −3.81086 × 10−4 | −5.84103 × 10−4 | −1.40928 × 10−4 | −5.71409 × 10−4 | ||
| Adjusted R2 | 0.96111 | 0.91912 | 0.85399 | 0.98549 | ||
| Elastic modulus, E (GPa) | 6th order polynomial E = A + B1T + B2T2 + B3T3 + B4T4 + B5T5 + B6T6 | T range | 300 ≤ T ≤ 500 | 300 ≤ T ≤ 500 | ||
| A | −2209.3885 | 409.32795 | ||||
| B1 | 33.54518 | −5.76718 | ||||
| B2 | −0.20948 | 0.0332 | ||||
| B3 | 6.90037 × 10−4 | −9.88824 × 10−5 | ||||
| B4 | −1.26453 × 10−6 | 1.60037 × 10−7 | ||||
| B5 | 1.22205 × 10−9 | −1.33008 × 10−10 | ||||
| B6 | −4.86522 × 10−13 | 4.40984 × 10−14 | ||||
| Adjusted R2 | 0.99509 | 0.99509 | ||||
| Poisson’ s ratio, ν | Boltzmann ν = (D1 − D2)/{1 + exp[(T − τ0)/τ]} + D2 | T range | 300 ≤ T ≤ 500 | 300 ≤ T ≤ 500 | ||
| D1 | 0.2731 | 0.28715 | ||||
| D2 | 0.46094 | 0.49459 | ||||
| τ0 | 497.04191 | 414.53197 | ||||
| τ | 14.45546 | 12.68674 | ||||
| Adjusted R2 | 0.9982 | 0.99698 | ||||
| Study | Materials Properties of Pure PMMA at T = 300 K | |
|---|---|---|
| Elastic Modulus, E (GPa) | Poisson’s Ratio, ν | |
| Present MD-only formulation | 3.065 | 0.286 |
| Different MD formulation [15] | 3.052 | 0.257 |
| Experimental [26] | 3.400 | - |
| Theoretical Study | Material Properties at T = 300 K | |
|---|---|---|
| Elastic Modulus, E (GPa) | Poisson’s Ratio, ν | |
| Present FEM combined with MD of PMMA reinforced with C240 at 5.00 wt % | 3.247 | 0.284 |
| Different MD simulation [15] of PMMA reinforced with onion C60@C240 at 5.01 wt % | 3.590 | 0.271 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giannopoulos, G.I.; Georgantzinos, S.K.; Anifantis, N.K. Thermomechanical Response of Fullerene-Reinforced Polymers by Coupling MD and FEM. Materials 2020, 13, 4132. https://doi.org/10.3390/ma13184132
Giannopoulos GI, Georgantzinos SK, Anifantis NK. Thermomechanical Response of Fullerene-Reinforced Polymers by Coupling MD and FEM. Materials. 2020; 13(18):4132. https://doi.org/10.3390/ma13184132
Chicago/Turabian StyleGiannopoulos, Georgios I., Stelios K. Georgantzinos, and Nick K. Anifantis. 2020. "Thermomechanical Response of Fullerene-Reinforced Polymers by Coupling MD and FEM" Materials 13, no. 18: 4132. https://doi.org/10.3390/ma13184132
APA StyleGiannopoulos, G. I., Georgantzinos, S. K., & Anifantis, N. K. (2020). Thermomechanical Response of Fullerene-Reinforced Polymers by Coupling MD and FEM. Materials, 13(18), 4132. https://doi.org/10.3390/ma13184132







