High-Temperature Structural and Electrical Properties of BaLnCo2O6 Positrodes
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix A.1. Chemical Expansion of Cobalt Ions upon Reduction
| Ion | Notation |
|---|---|
Appendix A.2. Reduction from Co4+ to Co3+
Appendix A.3. Reduction of Co3+ to Co2+
Appendix A.4. Chemical Expansion of Oxygen Vacancies Formation
References
- Kim, J.-H.; Manthiram, A. LnBaCo2O5+δ Oxides as cathodes for intermediate-temperature solid oxide fuel cells. J. Electrochem. Soc. 2008, 155, B385. [Google Scholar] [CrossRef]
- Tarancón, A.; Marrero-López, D.; Peña-Martínez, J.; Ruiz-Morales, J.C.; Núñez, P. Effect of phase transition on high-temperature electrical properties of GdBaCo2O5+x layered perovskite. Solid State Ion. 2008, 179, 611–618. [Google Scholar] [CrossRef]
- Kim, G.; Wang, S.; Jacobson, A.J.; Reimus, L.; Brodersen, P.; Mims, C.A. Rapid oxygen ion diffusion and surface exchange kinetics in PrBaCo2O5+x with a perovskite related structure and ordered a cations. J. Mater. Chem. 2007, 17, 2500–2505. [Google Scholar] [CrossRef]
- Szpunar, I.; Wachowski, S.; Miruszewski, T.; Dzierzgowski, K.; Górnicka, K.; Klimczuk, T.; Sørby, M.H.; Balaguer, M.; Serra, J.M.; Strandbakke, R.; et al. Electric and magnetic properties of lanthanum barium cobaltite. J. Am. Ceram. Soc. 2020, 103, 1809–1818. [Google Scholar] [CrossRef]
- Larson, A.C.; Von, R.B.; Lansce, D. General Structure Analysis System; Los Alamos National Laboratory: Los Alamos, NM, USA, 2000. [Google Scholar]
- Toby, B.H. EXPGUI, a graphical user interface for GSAS. J. Appl. Crystallogr. 2001, 34, 210–213. [Google Scholar] [CrossRef]
- Conder, K.; Podlesnyak, A.; Pomjakushina, E.; Stingaciu, M. Layered cobaltites: Synthesis, oxygen nonstoichiometry, transport and magnetic properties. Acta Phys. Pol. A 2007, 111, 7–14. [Google Scholar] [CrossRef]
- Fauth, F.; Suard, E.; Caignaert, V.; Domengès, B.; Mirebeau, I.; Keller, L. Interplay of structural, magnetic and transport properties in thelayered Co-based perovskite LnBaCo2O5 (Ln = Tb, Dy, Ho). Eur. Phys. J. B 2001, 21, 163–174. [Google Scholar] [CrossRef]
- Streule, S.; Podlesnyak, A.; Mesot, J.; Medarde, M.; Conder, K.; Pomjakushina, E.; Mitberg, E.; Kozhevnikov, V. Effect of oxygen ordering on the structural and magnetic properties of the layered perovskites PrBaCo2O5+δ. J. Phys. Condens. Matter 2005, 17, 3317–3324. [Google Scholar] [CrossRef]
- Bernuy-Lopez, C.; Høydalsvik, K.; Einarsrud, M.-A.; Grande, T. Effect of A-Site Cation Ordering on Chemical Stability, Oxygen Stoichiometry and Electrical Conductivity in Layered LaBaCo2O5+δ Double Perovskite. Materials 2016, 9, 154. [Google Scholar] [CrossRef]
- Garcés, D.; Setevich, C.F.; Caneiro, A.; Cuello, G.J.; Mogni, L. Effect of cationic order-disorder on the transport properties of LaBaCo2O6-δ and La0.5Ba0.5CoO3-δ perovskites. J. Appl. Crystallogr. 2014, 17, 325–334. [Google Scholar] [CrossRef]
- Wachowski, S.L.; Szpunar, I.; Sørby, M.H.; Mielewczyk–Gryń, A.; Balaguer, M.; Ghica, C.; Istrate, M.C.; Gazda, M.; Gunnæs, A.E.; Serra, J.M.; et al. Structure and water uptake in BaLnCo2O6-δ (Ln = La, Pr, Nd, Sm, Gd, Tb and Dy). Acta Mater. 2020. [Google Scholar] [CrossRef]
- Pralong, V.; Caignaert, V.; Hebert, S.; Maignan, A.; Raveau, B. Soft chemistry synthesis and characterizations of fully oxidized and reduced NdBaCo2O5+δ phases δ = 0, 1. Solid State Ion. 2006, 177, 1879–1881. [Google Scholar] [CrossRef]
- Frontera, C.; Caneiro, A.; Carrillo, A.E.; Oró-Solé, J.; García-Muñoz, J.L. Tailoring oxygen content on PrBaCo2O5+δ layered cobaltites. Chem. Mater. 2005, 17, 5439–5445. [Google Scholar] [CrossRef]
- Burley, J.C.; Mitchell, J.F.; Short, S.; Miller, D.; Tang, Y. Structural and Magnetic Chemistry of NdBaCo2O5+δ. J. Solid State Chem. 2003, 170, 339–350. [Google Scholar] [CrossRef]
- Aksenova, T.V.; Gavrilova, L.Y.; TsvetkoV, D.S.; Voronin, V.I.; CherepanoV, V.A. Crystal structure and physicochemical properties of layered perovskite-like phases LnBaCo2O5+δ. Russ. J. Phys. Chem. A 2011, 85, 427–432. [Google Scholar] [CrossRef]
- García-Muñoz, J.L.; Frontera, C.; Llobet, A.; Carrillo, A.E.; Caneiro, A.; Aranda, M.A.G.; Ritter, C.; Dooryee, E. Study of the oxygen-deficient double perovskite PrBaCo2O5.75. Phys. B Condens. Matter 2004, 350, E277–E279. [Google Scholar] [CrossRef]
- Mitchell, J.F.; Burley, J.; Short, S. Crystal and magnetic structure of NdBaCo2O5+δ: Spin states in a perovskite-derived, mixed-valent cobaltite. J. Appl. Phys. 2003, 93, 7364–7366. [Google Scholar] [CrossRef]
- McIntosh, S.; Vente, J.F.; Haije, W.G.; Blank, D.H.A.; Bouwmeester, H.J.M. Oxygen stoichiometry and chemical expansion of Ba0.5Sr0.5Co0.8Fe4O3-δ-measured by in situ neutron diffraction. Chem. Mater. 2006, 18, 2187–2193. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, X.-M.; Wei, H.-W.; Lin, X.-H.; Wang, C.-H.; Zhang, Y.; Chen, C.; Jing, X.-P. Effect of oxygen content on transport and magnetic properties of PrBaCo2O5.50+δ. Mater. Res. Bull. 2015, 65, 80–88. [Google Scholar] [CrossRef]
- Conder, K.; Pomjakushina, E.; Soldatov, A.; Mitberg, E. Oxygen content determination in perovskite-type cobaltates. Mater. Res. Bull. 2005, 40, 257–263. [Google Scholar] [CrossRef]
- Choi, S.; Kucharczyk, C.J.; Liang, Y.; Zhang, X.; Takeuchi, I.; Ji, H., II; Haile, S.M. Exceptional power density and stability at intermediate temperatures in protonic ceramic fuel cells. Nat. Energy 2018, 3, 202–210. [Google Scholar] [CrossRef]
- Politov, B.V.; Suntsov, A.Y.; Kellerman, D.G.; Leonidov, I.A.; Kozhevnikov, V.L. High temperature magnetic and transport properties of PrBaCo2O6–δ cobaltite: Spin blockade evidence. J. Magn. Magn. Mater. 2019, 469, 259–263. [Google Scholar] [CrossRef]
- Løken, A.; Ricote, S.; Wachowski, S. Thermal and Chemical Expansion in Proton Ceramic Electrolytes and Compatible Electrodes. Crystals 2018, 8, 365. [Google Scholar] [CrossRef]
- Korotin, M.A.; Ezhov, S.Y.; Solovyev, I.V.; Anisimov, V.I.; Khomskii, D.I.; Sawatzky, G.A. Intermediate-spin state and properties of LaCoO3. Phys. Rev. B 1996, 54, 5309–5316. [Google Scholar] [CrossRef] [PubMed]
- Shannon, R.D.; Prewitt, C.T. Effective ionic radii in oxides and fluorides. Acta Crystallogr. Sect. B Struct. Crystallogr. Cryst. Chem. 1969, 25, 925–946. [Google Scholar] [CrossRef]
- Shannon, R.D. Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Crystallogr. Sect. A 1976, 32, 751–767. [Google Scholar] [CrossRef]
- Kriegel, R.; Kircheisen, R.; Töpfer, J. Oxygen stoichiometry and expansion behavior of Ba0.5Sr0.5Co0.8Fe0.2O3-δ. Solid State Ion. 2010, 181, 64–70. [Google Scholar] [CrossRef]
- Grande, T.; Tolchard, J.R.; Selbach, S.M. Anisotropic thermal and chemical expansion in Sr-substituted LaMnO3+δ: Implications for chemical strain relaxation. Chem. Mater. 2012, 24, 338–345. [Google Scholar] [CrossRef]
- Kharton, V.V.; Yaremchenko, A.A.; Patrakeev, M.V.; Naumovich, E.N.; Marques, F.M.B. Thermal and chemical induced expansion of La0.3Sr0.7(Fe,Ga)O3-δ ceramics. J. Eur. Ceram. Soc. 2003, 23, 1417–1426. [Google Scholar] [CrossRef]
- Padilla-Pantoja, J. Spin-Lattice Coupling in Strongly Correlated Cobalt Oxides Investigated by Sychrotron and Neutron Techniques. Ph.D. Thesis, Universitat Autonoma de Barcelona, Barcelona, Spain, 2016. [Google Scholar]
- Toulemonde, O.; N’Guyen, N.; Studer, F.; Traverse, A. Spin state transition in LaCoO3 with temperature or strontium doping as seen by XAS. J. Solid State Chem. 2001, 158, 208–217. [Google Scholar] [CrossRef]
- Herrero-Martín, J.; García-Muñoz, J.L.; Valencia, S.; Frontera, C.; Blasco, J.; Barón-González, A.J.; Subías, G.; Abrudan, R.; Radu, F.; Dudzik, E.; et al. Valence change of praseodymium in Pr0.5Ca0.5CoO3 investigated by x-ray absorption spectroscopy. Phys. Rev. B Condens. Matter Mater. Phys. 2011, 84, 1–6. [Google Scholar] [CrossRef]
- Kubelka, P. New contributions to the optics of intensely light-scattering materials part I. J. Opt. Soc. Am. 1948, 38, 448. [Google Scholar] [CrossRef] [PubMed]
- Vøllestad, E.; Schrade, M.; Segalini, J.; Strandbakke, R.; Norby, T. Relating defect chemistry and electronic transport in the double perovskite Ba1-xGd0.8La0.2+xCo2O6-δ (BGLC). J. Mater. Chem. A 2017, 5, 15743–15751. [Google Scholar] [CrossRef]
- Taskin, A.A.; Ando, Y. Electron-hole asymmetry in GdBaCo2O5+x: Evidence for spin blockade of electron transport in a correlated electron system. Phys. Rev. Lett. 2005, 95, 176603. [Google Scholar] [CrossRef] [PubMed]
- Vøllestad, E.; Strandbakke, R.; Tarach, M.; Catalán-Martínez, D.; Fontaine, M.L.; Beeaff, D.; Clark, D.R.; Serra, J.M.; Norby, T. Mixed proton and electron conducting double perovskite anodes for stable and efficient tubular proton ceramic electrolysers. Nat. Mater. 2019, 18, 752–759. [Google Scholar] [CrossRef] [PubMed]
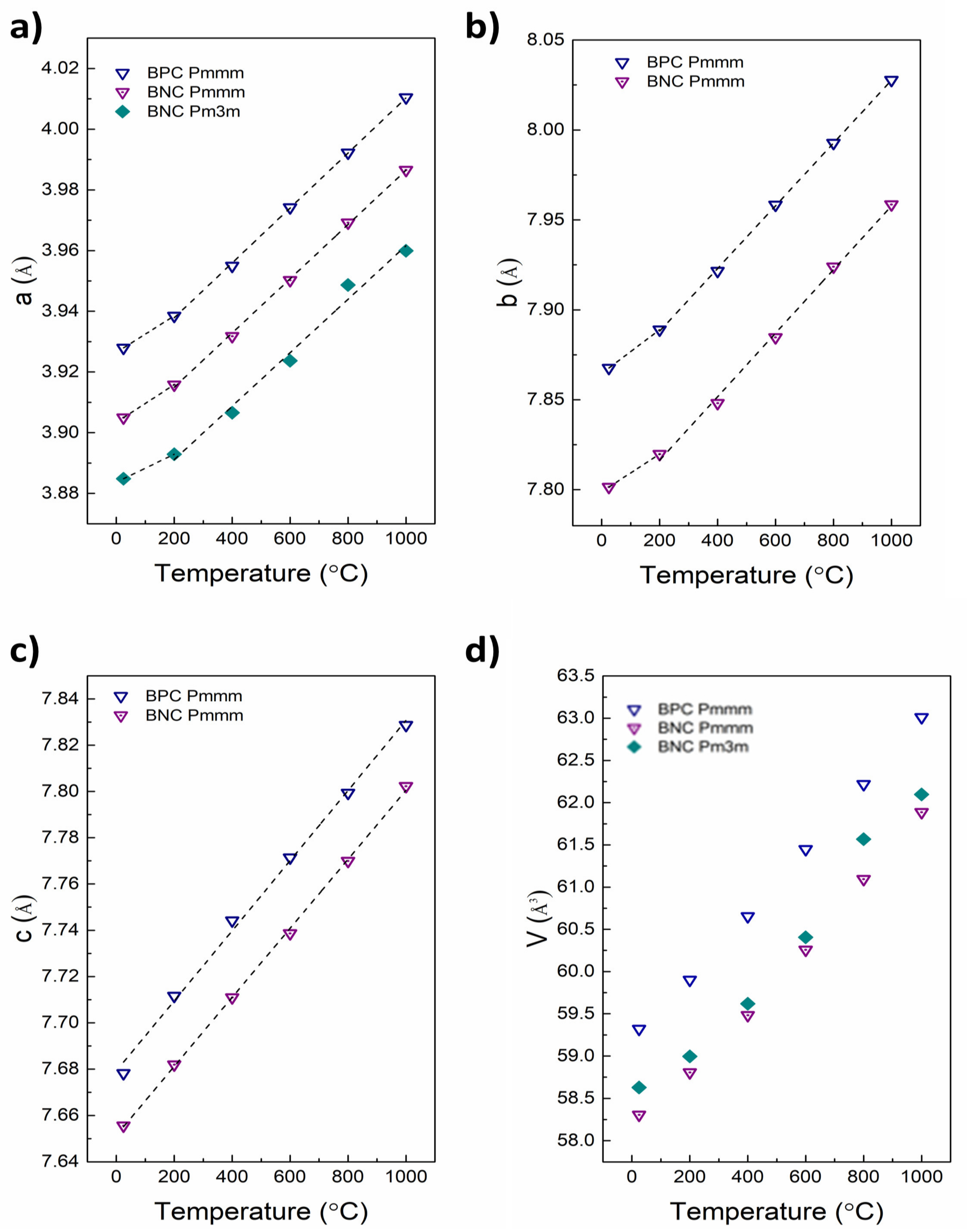
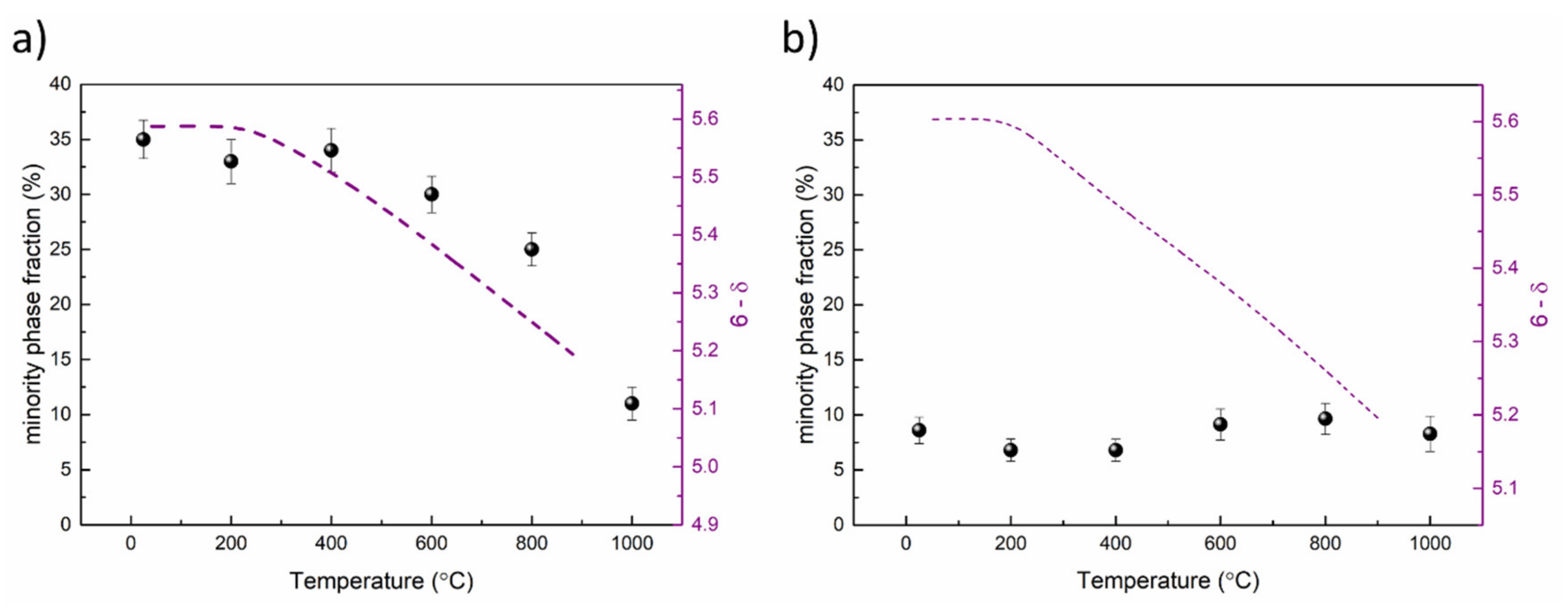
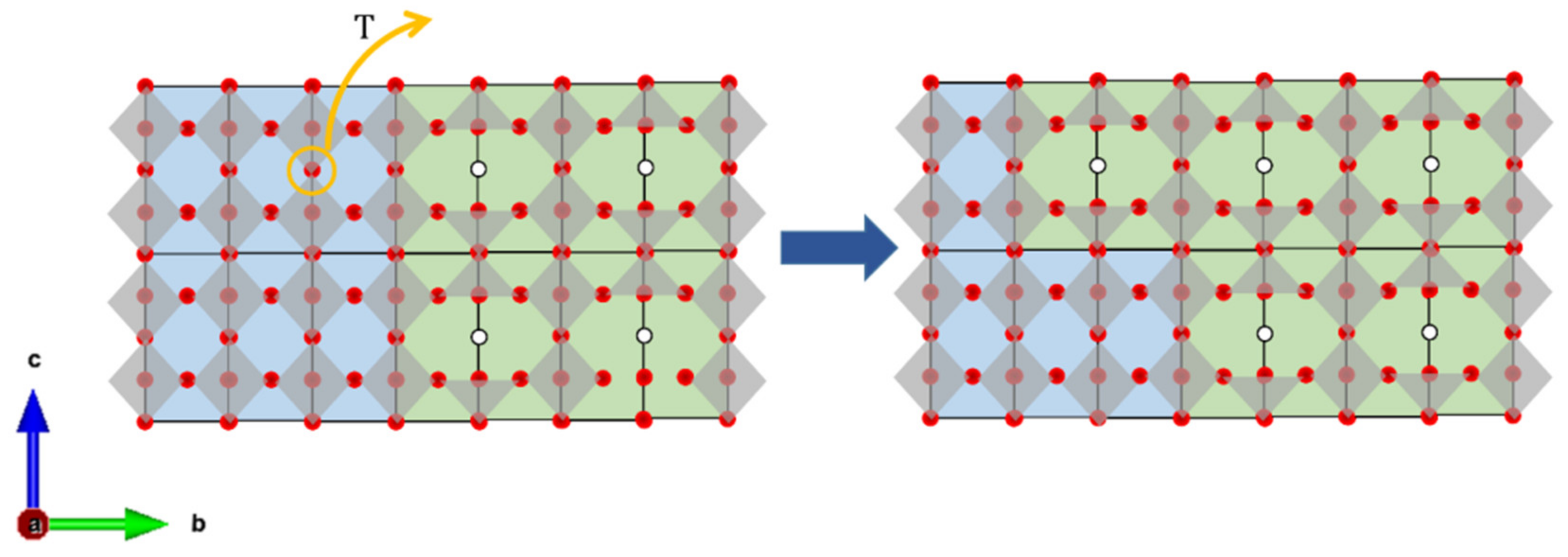
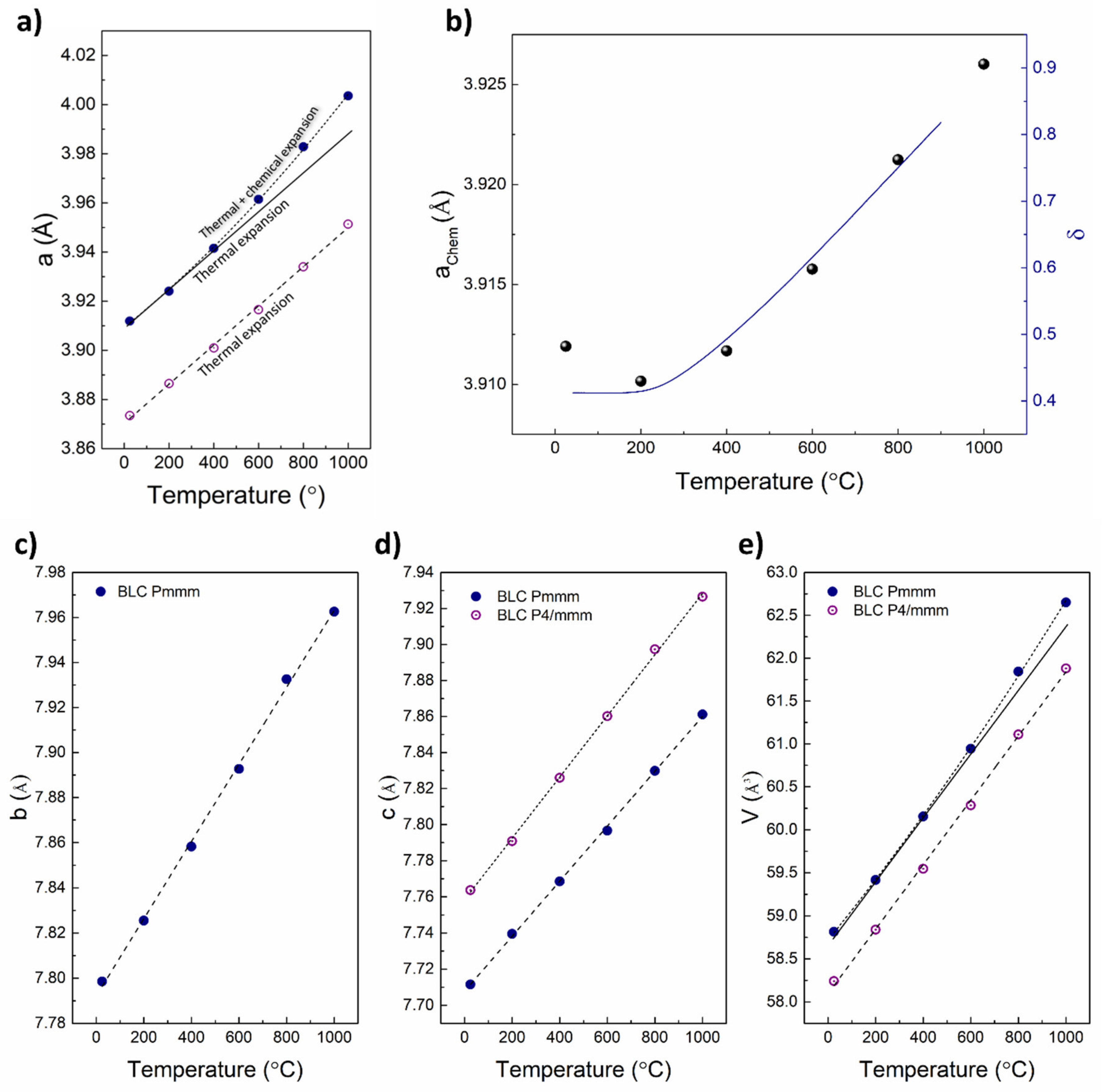
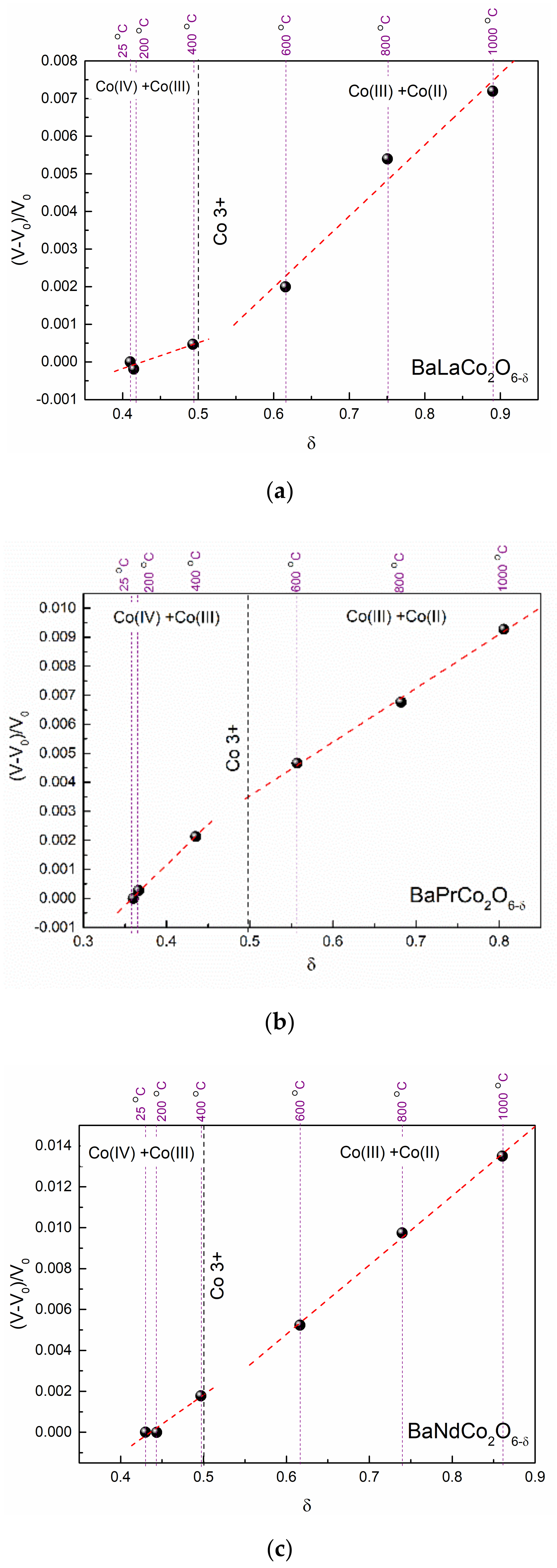
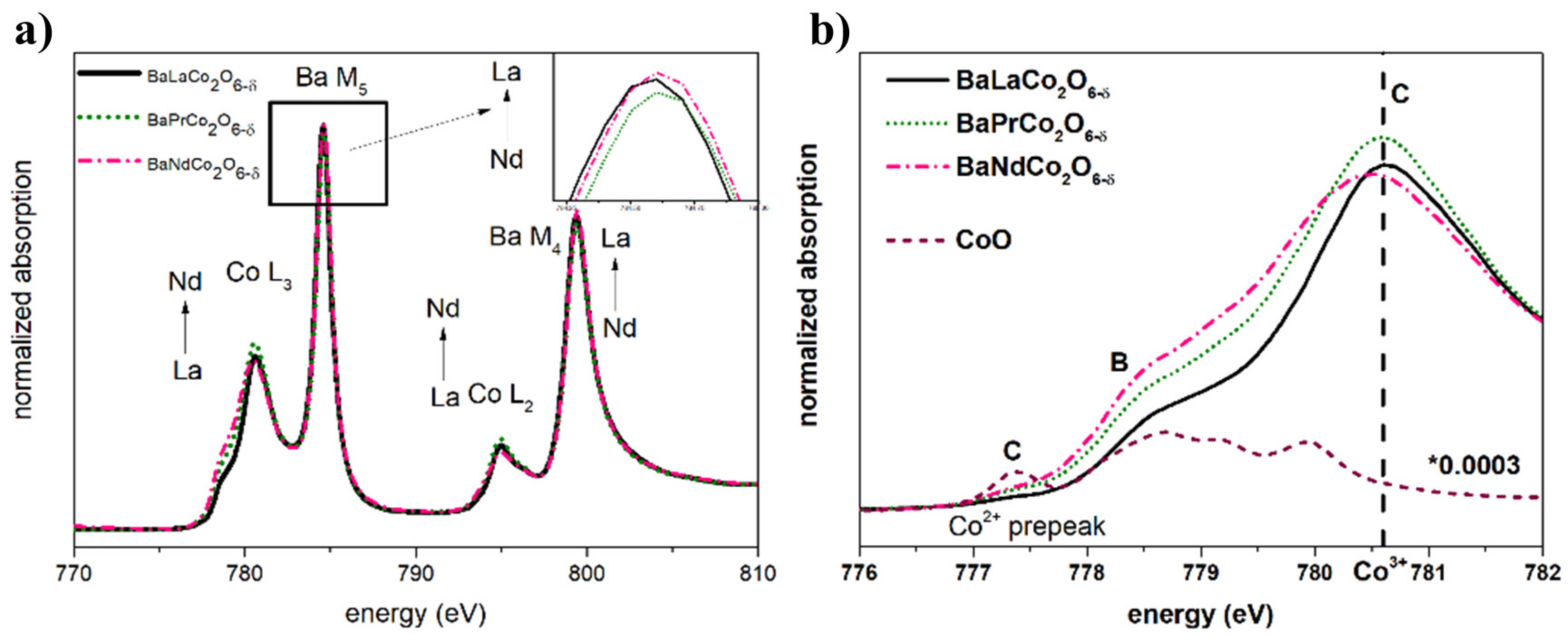
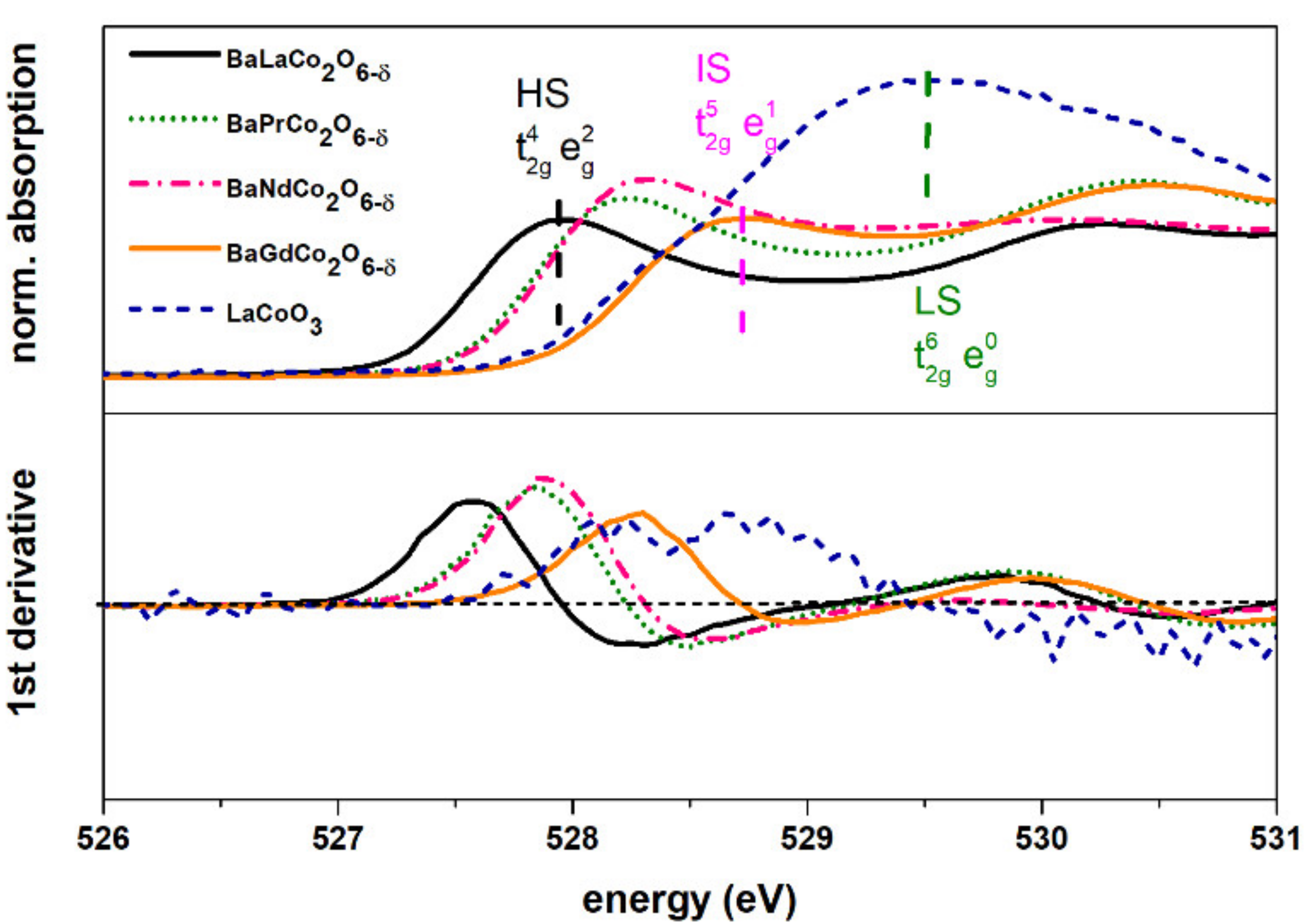
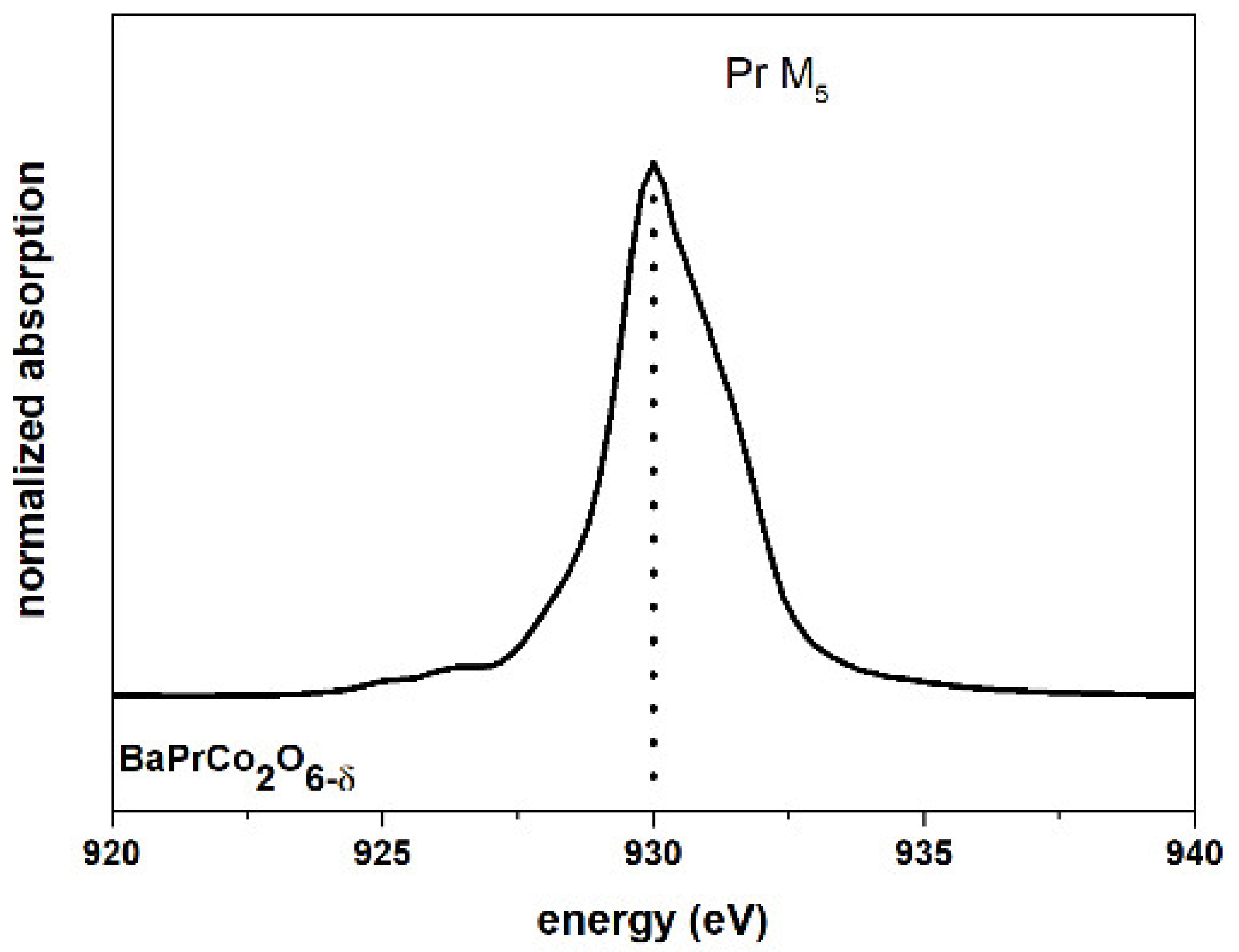
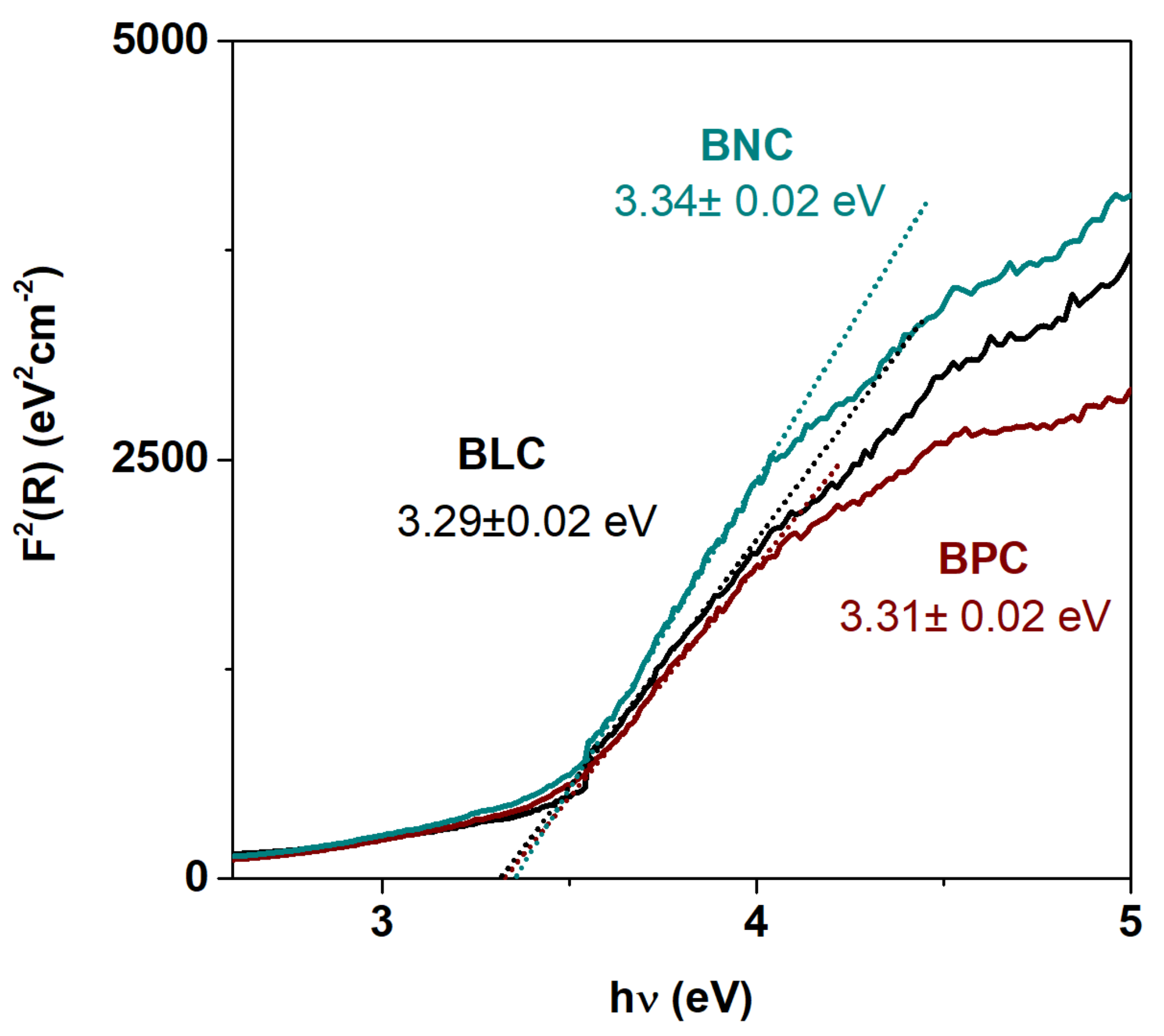
| Material (Direction) | Expansion Coefficient (below 200 °C) (×10−6) | Expansion Coefficient (above 200 °C) (×10−6) |
|---|---|---|
| BPC (a) | 15.3 | 23.0 |
| BPC (b) | 15.5 | 22.1 |
| BPC (c) | 19.7 | |
| BNC Pmmm (a) | 15.9 | 22.8 |
| BNC Pmmm (b) | 13.4 | 22.6 |
| BNC Pmmm (c) | 19.5 | |
| BNC Pm3m (a) | 11.9 | 22.6 |
| Material | Oxidation Range | |||
|---|---|---|---|---|
| BLC | δ < 0.5 | |||
| δ > 0.5 | ||||
| BNC | δ < 0.5 | |||
| δ > 0.5 | ||||
| BPC | δ < 0.5 | |||
| δ > 0.5 |
| Nominal Composition | Co Average Oxidation State | Oxygen Non-Stoichiometry |
|---|---|---|
| BaLaCo2O6 | 3.2880 | 0.2100 |
| BaPrCo2O6 | 3.2540 | 0.2460 |
| BaNdCo2O6 | 3.2332 | 0.2668 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szpunar, I.; Strandbakke, R.; Sørby, M.H.; Wachowski, S.L.; Balaguer, M.; Tarach, M.; Serra, J.M.; Witkowska, A.; Dzik, E.; Norby, T.; et al. High-Temperature Structural and Electrical Properties of BaLnCo2O6 Positrodes. Materials 2020, 13, 4044. https://doi.org/10.3390/ma13184044
Szpunar I, Strandbakke R, Sørby MH, Wachowski SL, Balaguer M, Tarach M, Serra JM, Witkowska A, Dzik E, Norby T, et al. High-Temperature Structural and Electrical Properties of BaLnCo2O6 Positrodes. Materials. 2020; 13(18):4044. https://doi.org/10.3390/ma13184044
Chicago/Turabian StyleSzpunar, Iga, Ragnar Strandbakke, Magnus Helgerud Sørby, Sebastian Lech Wachowski, Maria Balaguer, Mateusz Tarach, José M. Serra, Agnieszka Witkowska, Ewa Dzik, Truls Norby, and et al. 2020. "High-Temperature Structural and Electrical Properties of BaLnCo2O6 Positrodes" Materials 13, no. 18: 4044. https://doi.org/10.3390/ma13184044
APA StyleSzpunar, I., Strandbakke, R., Sørby, M. H., Wachowski, S. L., Balaguer, M., Tarach, M., Serra, J. M., Witkowska, A., Dzik, E., Norby, T., Gazda, M., & Mielewczyk-Gryń, A. (2020). High-Temperature Structural and Electrical Properties of BaLnCo2O6 Positrodes. Materials, 13(18), 4044. https://doi.org/10.3390/ma13184044








